北京科技大学计算的方法共70页
计算方法概论与理论基础(1,2)

如把方程组的系数舍入 成两位有效数字
x 1 0 . 50 x 2 0 . 33 x 3 1 . 8 0 . 50 x 1 0 . 33 x 2 0 . 25 x 3 1 . 1 0 . 33 x 0 . 25 x 0 . 20 x 0 . 78 1 2 3
,=2,8,10,16,
阶码
ai{0,1,2,…, -1}, Lc U F(,t.L,U)表示以上数集全体加数0,
它是计算机中使用有限离散集。
计算机中数的计算特点
1. 加法先对阶,后运算,再舍入。 2. 乘法先运算,再舍入。 3. 不在计算机数系中的数做四舍五入处理。 例如:在四位浮点十进制数的计算机上计算1+ 104
两者结果不同,因为计算机计算时做加减法要 “对 阶”,“对阶”的结果使大数吃掉了小数.产生了误差.为 了避免由于上述原因引起的计算结果严重失真,可以根 据一些具体情况,存在需要把某些算式改写成另一种等 . 价的形式.
三、防止接近零的数做除数
分母接近零的数会产生溢出错误, 因而产生大的误差,此时可以用数 学公式化简后再做.
算法的计算量 3、机器数系 4、误差的基本概念 误差的来源 模型误差;观测误差;截断误差; 舍入误差。 误差与有效数字 误差(绝对误差);误差限;相 对误差;相对误差限;有效数字。
和、差、积、商的误差; 数据的机器浮点数 浮点数的算术运算 5、问题的性态与算法的数值稳定性 良态与病态问题 算法的数值稳定性 数值计算中值得注意的事项 6、应用实例与Matlab
极限
微积分中的极限描述的是一组变元的变化趋势,其 本质是通过“充分靠近”某个固定量引入的,而体现 “靠近”的描述正是距离的意思。因此,可以在距离空 间中引入极限概念。
北科大研究生计算方法作业

计算方法姓名:学号:班级:指导教师:目录作业1 (1)作业2 (5)作业3 (8)作业4 (10)作业5 (14)作业6 (16)作业7 (17)作业11、分别用不动点迭代与Newton 法求解方程 -+=x 2x e 30的正根与负根。
解:(1)不动点迭代a.原理:将 230x x e -+=变型为1()k k x g x +=进行迭代,直到 为止变型后为有两种形式: 和 b.程序:初值为1形式: x=zeros(100,1); tol=1; i=1; x(1)=1;while tol>=10e-6; disp(x(i))x(i+1)=log(2*x(i)+3); tol=abs(x(i+1)-x(i)); i=i+1; enddisp(i-1); 形式:x=zeros(100,1); tol=1; i=1; x(1)=1;while tol>=10e-6; disp(x(i))x(i+1)=(exp(x(i))-3)/2; tol=abs(x(i+1)-x(i)); i=i+1; end disp(i-1);c.运行结果:初值为1(23)1lnk x k x ++=6110k k x x -+-<132k x k e x +-=(23)1ln k x k x ++=132k xk e x +-=迭代次数:11迭代次数:9(2)Nexton法a.原理:令()()1'kk kkf xx xf x+=-得到迭代公式为:()1232kkxkk k xx ex xe+-+=--b.程序:初值为0x=zeros(100,1);tol=1;i=1;x(1)=0;while tol>=10e-6;disp(x(i))x(i+1)=x(i)-((2*x(i)-exp(x(i))+3)/(2-exp(x(i))));tol=abs(x(i+1)-x(i));i=i+1;enddisp(i-1);初值为1x=zeros(100,1);tol=1;i=1;x(1)=1;while tol>=10e-6;disp(x(i))x(i+1)=x(i)-((2*x(i)-exp(x(i))+3)/(2-exp(x(i))));tol=abs(x(i+1)-x(i));i=i+1;enddisp(i-1)a=x(i-1);b=2*a-exp(a)+3;disp(b);c.运行结果:初值为0迭代次数:5初值为1迭代次数:8 -1.6171e -006结果分析:不动点迭代会因为迭代公式选取的不同得出不同的迭代结果,而牛顿法迭代会因为初值选取的不同而得到不同的结果。
北科大丁军计算方法作业

《计算方法》作业姓名:学号:班级:学院:2018年11月25日3-1试验目的:考察不动点迭代法的局部收敛性试验内容:分别构造方程230xx e -+=和523x 5100+-=x ,至少采用3种迭代法,迭代100次,考察收敛性,改变初值符号,再做迭代。
分析收敛与发散的原因。
(1)迭代原理:若实数p 满足()p g p =,p 称为函数()g x 的一个不动点,迭代()1,0,1,...n n p g p n +==称为不动点迭代,()g x 称为迭代函数。
由不动点方程建立迭代法()1,0,1,...n n p g p n +==,其中0p 称为初值,需要预先给定。
(2)方程230xx e -+=分别对应下列不同形式的不动点方程: 1.1()33==-+x x g x x e 2.2()(3)/2==-x x g x e 3.3()ln(23)==+x g x x取401,10,100-===p Tol N ,按()1,1,2,3n i n p g p i +==迭代,并分析收敛性。
不动点迭代法代码 1.1()33==-+x x g x x efunction [p,k] = fone( p0,max,tol ) k=1; while k<=max p=3*p0+3-exp(p0); if abs(p-p0)<tol break; end k=k+1; p0=p; enddisp(p);disp(k)运行结果:2.2()(3)/2==-x x g x efunction [p,k] = ftwo( p0,max,tol ) k=1; while k<=max p=(exp(p0)-3)/2; if abs(p-p0)<tol break; end k=k+1; p0=p; enddisp(p);disp(k) 运行结果:3.3()ln(23)==+x g x xfunction [p,k] = fthree( p0,max,tol ) k=1;while k<=maxp=log(2*p0+3);if abs(p-p0)<tolbreak;endk=k+1;p0=p;enddisp(p);disp(k)运行结果:(3)方程523x 5100+-=x 分别对应下列不同形式的不动点方程: 1.521()3x 510==++-x g x x x2.2()==x g x 3.52343x 510()1510+-==-+x x g x x x x取401,10,100-===p Tol N ,按()1,1,2,3n i n p g p i +==迭代,并分析收敛性。
北科大微机原理

CPU 结构 示意图
寄存器组
R1 R2 R3 R4
运 算 器
IP
地
指令
址
指针 寄存器
寄 存
器
数据寄存器
地址总线 AB 数据总线 DB
指令寄存器
06:34:23
标志 寄存器
指令译码器 控制电路
控制总线 CB
21
7.译码器 译码器是将输入代码转换成相应输出信号的逻辑电路。
地址总线 AB
CPU
存 I/O 输 储 接入 器 口设
备
输
I/O 接 口
出 设 备
数据总线 DB 控制总线 CB
34 06:34:23
数据总线的条数决定一次可最多传送数据的宽度。 8 根 → 一次传送 8位
16 根 → 一次传送 16位 32 根 → 一次传送 32位 64 根 → 一次传送 64位
1) 按构成分类 2) 按CPU的字长分类 3)按主机装置分类 5. IBM PC机的发展简史
9 06:34:23
一、计算机的基本组成和工作原理 ENIAC (1946)
掌上电脑(2000)
按性能可分为:巨型机,大型机, 中型机,小型机,微机 ▲ 现代计算机的结构基础:存储程序控制结构
1945年,美籍匈牙利数学家Von Neumann提出, 冯诺依曼计算机
主 要
集成电路计算机
采用微程序、流水线等技术, 提高运行速度
特
(1965—1970) 出现操作系统、诊断程序等软件 点
超大规模集成 采用半导体存储器 电路计算机 采用图形界面操作系统 (1971—至今) 器件速度更快, 软件、外设更加丰富
24 06:34:23
计算方法大作业作业((北京科技大学研究生结课考试)

《计算方法》平时作业(2010-2011学年第一学期)学 院:_________________________ 专 业:_________________________ 姓 名:_________________________ 学 号:_________________________ 联 系 方 式:_________________________机研111班机械工程学院作业(考试前交, 给出证明或计算过程、计算程序及计算结果) 1. 对向量()12Tn x x x x = 定义1211,max ,nk k k nk x x xx x ∞≤≤====∑设A 是n n ⨯矩阵,规定1111max x A Ax ==,1max x A Ax ∞∞∞==,2221max x A Ax ==证明111112max (),max (),.n nkj jk j nj nk k T A a A a A A A λ∞≤≤≤≤=====∑∑列范数行范数是最大特征值证明:1) 证明111||||max||nijj n i A a≤≤==∑1111111111||||max ||max ||||max ||||||max ||nnn nij iiji ij ij j nj nj nj ni i i i AX a x ax a x a ≤≤≤≤≤≤≤≤=====≤≤=∑∑∑∑所以 111||||111||||max ||||max||nijx j ni A Ax a=≤≤==≤∑设 1111max||||,1,0,1,0,||||1,nnijip i ip i ip j ni i aa x a x a x ≤≤====≥=-<=∑∑取若取若则11||n nip i ip i i a x a ===∑∑且。
因此,1111111||||max ||||||max ||n nn nij i ip iip ij j nj ni i i i Ax a x ax a a ≤≤≤≤=====≥==∑∑∑∑即 111||||111||||max ||||max||nijx j ni A Ax a=≤≤==≥∑ 则 111||||m a x ||nij j ni A a ≤≤==∑2)证明11||||max||niji n j A a∞≤≤==∑11111111||||m a x ||m a x ||||m a x ||||||m a x||nnnni j j i j j i j i j i ni ni ni nj j j j A X a x a x a x a ∞∞≤≤≤≤≤≤≤≤=====≤≤=∑∑∑∑ 所以 ||||111||||m a x ||||m a x ||nij x i n j A Ax a ∞∞∞=≤≤==≤∑设 111max||||,1,0,1,0,||||1,nnijpj j pj j pj i nj j aa x a x a x ∞≤≤====≥=-<=∑∑取若取若则11||nn pj j pj j j a a ===∑∑且。
北京科技大学线性代数课件ch31.ppt

am1x1 am2 x2
a1n xn b1 a2n xn b2
amn xn bm
(2) x, y V , 即Ax 0, Ay 0,
A(x y) Ax Ay 0 x y V.
(3) R, A( x) Ax 0 x V , 故V是向量空间,
构成的有序数组,现将它推广到 n 维情况:
定义3.1 n个数组成的有序数组 (a1,a2 , ,an ) 称为n维向量. 这n个数称为该向量的n个分量,
ai称为第i个分量. 分量全为实数的向量称为实向量,
至少有一个分量为复数的向量称为复向量.
例如: (1,2,3,,n)
n维实向量
(1 2i,2 3i,,n (n 1)i) n维复向量
第三章 向量空间
线性代数3-1 1
第三章 向量空间
3.1 向量空间的概念 3.2 向量的线性关系 3.3 向量组的秩 3.5 矩阵的秩 3.4 线性空间的基 维数 坐标
线性代数3-1 2
第三章 向量空间
3.1 向量空间的概念
几何空间
n 维向量
向量的运算 向量组与矩阵 向量空间
k2 k3
.
1 2 ,
2
1
在 , 所在的平面上, 故 , , 共面.
线性代数3-1 6
第三章 向量空间
3.1向量空间的概念
几何空间
n 维向量
向量的运算 向量组与矩阵 向量空间
线性代数3-1 7
2.n维向量
几何空间中的三维向量 (a1,a2 ,a3 )是由三个实数
注意: 向量的加法与数乘运算称为向量的线性运算.
北京科技大学应用计算方法作业与答案

北京科技⼤学应⽤计算⽅法作业与答案⼀、第⼀次作业(⼀)2-6计算下列向量的1-范数、∞-范数、2-范数。
(1)x=(12,-4,-6,2)T >> A=[12,-4,-6,2] A =12 -4 -6 2 >> norm(A,1) ans = 24>> norm(A,inf) ans = 12>> norm(A,2) ans =14.1421 (2) x=(1,3,-4)T >> A=[1,3,-4] A =1 3 -4 >> norm(A,1) ans = 8>> norm(A,inf) ans = 4>> norm(A,2) ans =5.0990(⼆)2-9 计算下列矩阵的⾏范数、列范数、谱范数、F 范数。
(1)--=112111113A >> A=[3,-1,1;1,1,1;2,1,-1]A =3 -1 1 1 1 1 2 1 -1 >> norm(A,1) ans = 6>> norm(A,inf)ans = 5>> norm(A,2) ans =3.7888 >> norm(A,'fro') ans =4.4721 (2)R a a a A ∈?-=,00 >> A=[0,1;-1,0] A =0 1 -1 0 >> norm(A,1) ans = 1>> norm(A,inf) ans = 1>> norm(A,2) ans = 1>> norm(A,'fro') ans =1.4142⼆、第⼆次作业⽤⽜顿迭代法求⽅程0133=--x x 在20=x 附近的根。
要求:给成程序和运⾏结果.1、⽜顿法的基本原理在求解⾮线性⽅程0)(=x f 时,它的困难在于)(x f 是⾮线性函数,为克服这⼀困难,考虑它的线性展开。
北京科技大学2012-2013计算方法考场安排
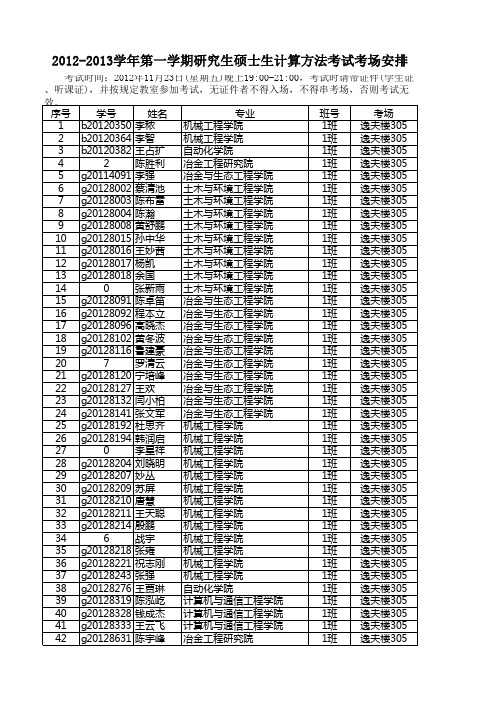
考试时间:2012年11月23日(星期五)晚上19:00-21:00,考试时请带证件(学生证 、听课证),并按规定教室参加考试,无证件者不得入场,不得串考场,否则考试无 效。 序号 学号 姓名 专业 班号 考场 1 b20120350 李秾 机械工程学院 1班 逸夫楼305 2 b20120364 李智 机械工程学院 1班 逸夫楼305 3 b20120382 王占扩 自动化学院 1班 逸夫楼305 4 B2012052 陈胜利 冶金工程研究院 1班 逸夫楼305 5 g20114091 李强 冶金与生态工程学院 1班 逸夫楼305 6 g20128002 蔡清池 土木与环境工程学院 1班 逸夫楼305 7 g20128003 陈布雷 土木与环境工程学院 1班 逸夫楼305 8 g20128004 陈瀚 土木与环境工程学院 1班 逸夫楼305 9 g20128008 黄舒鹏 土木与环境工程学院 1班 逸夫楼305 10 g20128015 孙中华 土木与环境工程学院 1班 逸夫楼305 11 g20128016 王妙茜 土木与环境工程学院 1班 逸夫楼305 12 g20128017 杨凯 土木与环境工程学院 1班 逸夫楼305 13 g20128018 余国 土木与环境工程学院 1班 逸夫楼305 14 G2012802 张新雨 土木与环境工程学院 1班 逸夫楼305 15 g20128091 陈卓笛 冶金与生态工程学院 1班 逸夫楼305 16 g20128092 程本立 冶金与生态工程学院 1班 逸夫楼305 17 g20128096 高晓杰 冶金与生态工程学院 1班 逸夫楼305 18 g20128102 黄冬波 冶金与生态工程学院 1班 逸夫楼305 19 g20128116 鲁建豪 冶金与生态工程学院 1班 逸夫楼305 20 G2012811 罗清云 冶金与生态工程学院 1班 逸夫楼305 21 g20128120 宁培峰 冶金与生态工程学院 1班 逸夫楼305 22 g20128127 王欢 冶金与生态工程学院 1班 逸夫楼305 23 g20128132 闫小柏 冶金与生态工程学院 1班 逸夫楼305 24 g20128141 张文军 冶金与生态工程学院 1班 逸夫楼305 25 g20128192 杜思齐 机械工程学院 1班 逸夫楼305 26 g20128194 韩润启 机械工程学院 1班 逸夫楼305 27 G2012820 李星祥 机械工程学院 1班 逸夫楼305 28 g20128204 刘晓明 机械工程学院 1班 逸夫楼305 29 g20128207 妙丛 机械工程学院 1班 逸夫楼305 30 g20128209 苏屏 机械工程学院 1班 逸夫楼305 31 g20128210 唐慧 机械工程学院 1班 逸夫楼305 32 g20128211 王天聪 机械工程学院 1班 逸夫楼305 33 g20128214 殷鹏 机械工程学院 1班 逸夫楼305 34 G2012821 战宇 机械工程学院 1班 逸夫楼305 35 g20128218 张雍 机械工程学院 1班 逸夫楼305 36 g20128221 祝志刚 机械工程学院 1班 逸夫楼305 37 g20128243 张强 机械工程学院 1班 逸夫楼305 38 g20128276 王贾琳 自动化学院 1班 逸夫楼305 39 g20128319 陈泓屹 计算机与通信工程学院 1班 逸夫楼305 40 g20128328 钱成杰 计算机与通信工程学院 1班 逸夫楼305 41 g20128333 王云飞 计算机与通信工程学院 1班 逸夫楼305 42 g20128631 陈宇峰 冶金工程研究院 1班 逸夫楼305 43 g20128632 刘权锐 冶金工程研究院 1班 逸夫楼305
