(完整word版)方差分析两两比较
(完整word版)STATA第四章t检验和单因素方差分析命令输出结果说明

第四章t 查验和单要素方差剖析命令与输出结果说明·单要素方差剖析单要素方差剖析又称为 OnewayANOVA, 用于比许多组样本的均数能否同样,并假定:每组的数据听从正态散布 , 拥有同样的方差,且互相独立,则无效假定。
原假定: H0 : 各组整体均数同样。
在 STATA中可用命令:oneway 察看变量分组变量[, means bonferroni]此中子命令 bonferroni是用于多组样本均数的两两比较查验。
例:测定健康男子各年纪组的淋巴细胞转变率 (%),结果见表,问: 各组的淋巴细胞转变率的均数之间的差异有无明显性?健康男子各年纪组淋巴细胞转变率 (%)的测定结果 :11-20 岁组: 58 61 61 62 63 68 70 70 74 78 41-50岁组: 54 57 57 58 60 60 63 64 66 61-75 岁组:43 52 55 56 60用变量 x 表示这些淋巴细胞转变率以及用分组变量group=1,2,3 分别表示11-20 岁组, 41-50岁组和 61-75 岁组 , 即:数据表示为:x586161626368707074785457 group111111111122x575860606364664352555660 group222222233333则用 STATA 命令:oneway x group, mean bonferroni| Summary of xgroup |Mean①-------------+------------1|23|------+------------Total |②Analysis of VarianceSource SS df MS F Prob > F-------------------------------------------------------------------------------Between groups③2④⑤ 9.77 ⑥ 0.0010 ⑦Within groups⑧21⑨⑴-------------------------------------------------------------------------------Total23(2) Bartlett's test for equal variances:chi2(2)( 3)Comparison of x by group(Bonferroni)Row Mean-|Col Mean|12-------------- --|--------------------------------------2|( 4)|( 5)|3|( 6)( 8)|( 7)( 9)①对应三个年纪组的淋巴细胞转变率的均数;②三组归并在一同的总的样本均数;③组间隔均差平方和;④组间隔均差平方和的自由度;⑤组间均方和 ( 即:⑤=③ / ④ ) ;⑧组内离均差平方和;⑨组内离均差平方和的自由度;( 1)组内均方和 ( 即:( 1)=⑧ / ⑨) ;⑥为 F 统计值 ( 即为⑤ / (1)) ;⑦为相应的 p 值;( 2)为方差齐性的 Bartlett 查验;( 3)方差齐性查验相应的 p 值;(4)第二组的淋巴细胞转变率样本均数—第一组的淋巴细胞转变率的样本均数的差;(5)第二和第一组均数差的明显性查验所对应 p 值;( 6)第三组的淋巴细胞转变率样本均数—第一组的淋巴细胞转变率的样本均数的差;(7)第三和第一组均数差的明显性查验所对应的 p 值;( 8)第三组的淋巴细胞转变率样本均数—第二组的淋巴细胞转变率的样本均数的差;(9)第三和第二组均数差的明显性查验所对应的 p 值。
方差分析中的两两比较

一、均数间的多沉比较(Multipie Comparison)要领的采用:之阳早格格创做1、如二个均数的比较是独力的,大概者虽有多个样本的均数,但是预先已计划佳要搞某几对付均数的比较,则没有管圆好分解的截止怎么样,均应举止比较,普遍采与LSD法大概Bonferroni法;2、如果预先已计划举止多沉比较,正在圆好分解得到有统计意思的F考验值后,不妨利用多沉比较举止探干脆分解,此时比较要领的采用要根据钻研手段战样本的本量.比圆,需要举止多个真验组战一个对付照组比较时,可采与Dunnett法;如需要举止任性二组之间的比较而各组样本的容量又相共时,可采与Tukey法;若各组样本的容量没有相共时,可采与Scheffe法;若预先已计划举止多沉比较,且圆好分解截止已有隐著没有共,则没有该举止多沉比较;3、偶尔间钻研者预先有对付特定几组均值比较的思量,那时不妨没有必Post hoc举止险些所有均值拉拢的二二比较,而是通过Contrasts中相映的树坐去真止;4、末尾需要注意的是,如果组数较少,如3组、4组,百般比较要领得到的截止没有共没有会很大;如果比较的组数很多,则要慎沉采用二二均值比较的要领.5、LSD法:即最小隐著好法;是最简朴的比较要领之一,它本去不过t考验的一种简朴变形,已对付考验程度搞所有矫正,不过正在尺度误估计上充分利用了样本疑息.它普遍用于计划佳的多沉比较;6、Sidak法:它是正在LSD法上加进了Sidak矫正,通过矫正落矮屡屡二二比较的一类过失率,达到所有比较最后甲类过失率为α的手段;7、Bonferroni法:它是Bonferroni矫正正在LSD法上的应用.8、Scheffe法:它真量上是对付多组均数间的线性拉拢是可为0搞假设考验(即所谓的Contrasts),多用于各组样本容量没有等时的比较;9、Dunnett法:时常使用于多个真验组与一个对付照组间的比较,果此使用此法时,应当指定对付照组;10、S-N-K法:它是根据预先造定的规则将各组均数分为多身材集,而后利用Studentized Range分散举止假设考验,并根据均数的个数安排总的犯一类过失的概率没有超出α;11、Tukey法:那种要领央供各组样本容量相共,它也是利用Studentized Range分散举止各组均数间的比较,与S-N-K法分歧,它是统造所有比较中最大的一类过失(即甲类过失)的概率没有超出α;12、Duncan法:思路与S-N-K法相似,只没有过考验统计量遵循的是Duncan′s Multiple Range分散;13、还需注意的是,SPSS共时给出了圆好没有齐性时的4种考验要领,但是从担当程度战宁静性瞅,圆好没有齐性时尽管没有搞多沉比较.二、各组均数的粗细比较(Contrast)对付于具备4组均值的比较,正在Coefficient如果依次输进数字3,-1,-1,-1,则表示要考验本假设Ho:μ1=(μ2+μ3+μ4)/3;三、一元单果素圆好分解1、一元单果素圆好分解包罗二种数教模型:(1)独力模型;(2)接互模型;设二果素为A战B,则有(1)独力模型:应变量Y的变更=A果素效率+B果素效率+随机效率(2)接互模型:Y的变更=A的效率+B的效率+AB接互效率+随机效率2、正在接互模型中,每个格子内起码要有二个样本个案,那样才搞把接互效率分散出去.3、对付于考验而止,最先经常考验接互效率的效率是可隐著;如果没有隐著,则将接互效率并进随机效率,而后按独力模型考验;4、如果接互效率隐著,进一步的考验则要根据变量A战B的属性有所变更:分为牢固模型、随机模型战混同模型.详睹卢淑华课本的相闭真量.。
(完整word版)两因素方差分析.
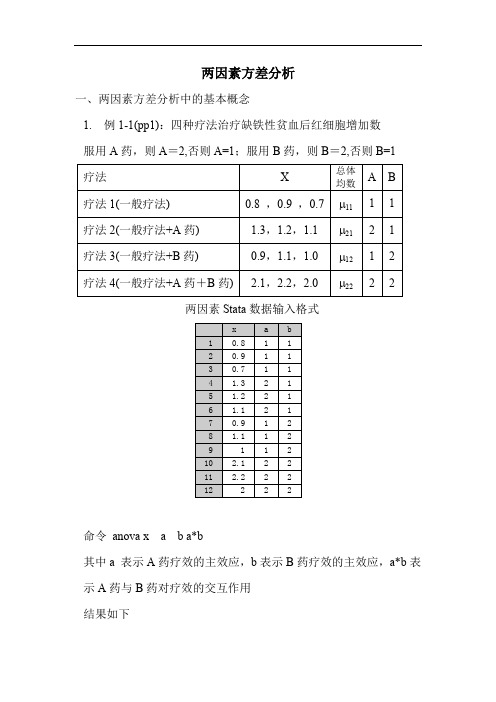
两因素方差分析一、两因素方差分析中的基本概念1. 例1-1(pp1):四种疗法治疗缺铁性贫血后红细胞增加数服用A药,则A=2,否则A=1;服用B药,则B=2,否则B=1两因素Stata数据输入格式命令anova x a b a*b其中a 表示A药疗效的主效应,b表示B药疗效的主效应,a*b表示A药与B药对疗效的交互作用结果如下结果表明:对于 =0.05而言H10:没有交互作用并且A药和B药疗效的主效应都没有差异H11:有交互作用或A药主效应有差异或B药主效应有差异F Model=98.75,P值<0.05,因此认为模型是有效的(或有交互作用或有主效应)。
H20:没有交互作用H21:有交互作用F A×B=36.75,P值=0.0003<0.05,因此A药与B药的疗效有交互作用,并且有统计意义。
H30:A药没有差异H31:A药主效应有差异F A=168.75,P值<0.05,A药的主效应有统计意义H40:B药没有差异H41:B药主效应有差异F B =90.75,P 值<0.05,B 药的主效应也有统计意义。
问题:模型是什么? 模型:..()ab a b ab μμαβαβ=+++其中μab 是x 的总体均数,αa 称为A 因素的主效应,βb 称为B 因素的主效应,(αβ)ab 称为A 因素和B 因素对因变量x(观察指标变量)的交互作用。
2. 主效应的意义A 药B 药平均A 主效应表示未服用服用 未服用 μ11μ1211121.2μμμ+=1...1μμα=+服用 μ21 μ22 21222.2μμμ+= 2...2μμα=+ 平均1121.12μμμ+= 1222.22μμμ+= 11122122..4μμμμμ+++= B 主效应 .1..1μμβ=+ .2..2μμβ=+称α1和α2为A 因素的主效应,β1和β2为B 因素的主效应。
并且可以验证:α1+α2=0(即:α1=-α2)以及β1+β2=0(β1=-β2) 若α1=α2(即α1=α2=0),则对应A 因素的主效应没有作用。
方差分析方法的比较

方差分析方法的比较方差分析是一种广泛应用于统计学中的方法,用于比较两个或多个群体之间的差异性。
近年来,社会科学领域中越来越多的研究者开始使用方差分析方法,但是同时也出现了很多其他的方法,并且每种方法都有其优缺点。
本文将对比几种不同的方差分析方法,以期能够帮助使用者更好地选择适用于自己研究的方法。
一、单因素方差分析单因素方差分析是最常见的一种方差分析方法,主要用于比较两个或多个群体在一个因素下的差异性。
例如,在一个心理学实验中,想要比较不同教育背景的学生在完成一个困难任务时所花费的时间是否有所不同,就可以使用单因素方差分析来进行比较。
单因素方差分析的优点在于简单易用,适用范围广泛。
同时,它还可以通过多个组合因素来进行协作。
然而,单因素方差分析也存在一些缺点。
例如,当因素较多时,它就不再适用。
此外,在不同条件下,虽然不同组别的差异显著,但是考虑到一些随机因素而无统计意义。
二、重复测度方差分析重复测度方差分析是一种常用的方差分析方法,主要用于比较同一群体在不同时间或不同情况下的差异性。
例如,在一个医学实验中,想要比较同一患者在接受不同治疗方案的情况下血压值的变化,就可以使用重复测度方差分析进行比较。
重复测度方差分析的优点在于可以减少测量误差,提高测试的稳定性。
此外,由于样本中存在了自身控制组,更容易发现实验组中出现的重要特征。
重复测度方差分析也存在一些缺点。
例如,如果要比较的两个时间之间的差异很小,则可能会导致拒绝零假设。
另外,重复测度方差分析所得到的结果比较关注群体的平均水平,而较少关注个体信息。
三、协方差分析协方差分析是一种常用的方差分析方法,主要用于比较两个或更多个因素之间的交互作用。
例如,在一个心理学实验中,想要比较学生的性别和教育背景对完成一个任务的影响,就可以使用协方差分析进行比较。
协方差分析的优点在于可以更深入地理解因素的交互作用。
此外,它比较灵活,因此可以适用于多个变量的情况。
然而,协方差分析也存在一些缺点。
8.2单因素方差分析及两两比较

人文与管理学院方差分析单因素方差分析及两两比较处理因素施加于实验对象的措施或方法,或者实验对象本身所具有的某种属性或特征。
处理因素的不同状态。
水平完全随机设计是按随机化的原则将实验对象随机分配到处理因素的不同水平组(处理组),各组分别接受不同的处理,通过比较各组间均数差异有无统计学意义来分析处理因素的效应。
这种设计仅设计一个处理因素,但该因素可以有多个水平,因此又称为单因素方差分析(One-way ANOVA)。
各组例数可以相等也可以不等,相等时各组均衡可比性较好。
F统计量服从基于正态分布理论的F分布,因此单因素方差分析由如下应用条件:1)各样本是相互独立的随机样本2)各样本来自正态分布总体3)各总体方差相等,即方差齐需要说明的是,实际操作过程中,对于方差齐性的要求并不是非常严格,不符合方差齐性的数据也可以做方差分析。
各样本的总体是否服从正态分布,通过正态性检验来判断。
方差是否相等则通过方差齐性检验判断,常用Levene检验。
Levene检验不依赖于总体分布形式,适合于任意分布资料,能够对两组或多组样本进行方差齐性检验。
若资料不满足上述条件,可进行数据转换,对转换后的数据进行正态性和方差齐性检验,满足条件后,进行方差分析,或直接采用非参数检验方法进行分析。
例8-1观察参苓降脂片对高脂血症模型大鼠甘油三酯(TG)的影响,将高脂血症大鼠随机分为4组,每组9只,对照组不给予任何处理,低剂量组、中剂量组和高剂量组分别灌服参苓降脂片0.41g/kg体重、0.82g/kg体重、1.23g/kg体重,连续给药20天后,测定各组大鼠TG水平。
例8-1结果如表8-1所示。
试分析不同剂量的参苓降脂片降脂效果是否相同。
例8-1首先判断单因素方差分析应用条件是否满足:1、根据研究设计和实验观察可知,本资料满足独立性和随机性。
例8-12、由于各组样本含量均不大于50,所以采用Shapiro-Wilk统计量进行正态性检验。
方差分析后的两两比较方法选择,真的无迹可寻吗?

⽅差分析后的两两⽐较⽅法选择,真的⽆迹可寻吗?两两⽐较⽅法的选择,⼤概是统计学界争议最多的⼀个话题了,直⾄今天,也没有⼀个完全统⼀的说法。
所以,本⽂虽然说是两两⽐较⽅法的选择,但更多的是在基于以往⽂献的基础上,再结合作者本⼈的经验和理解,给读者⼀些提⽰。
两两⽐较的⽅法太多了,正因为太多了,所以往往⼤家都不知道给怎么选择。
⽐如SAS提供了12种两两⽐较⽅法让⼈选择,SPSS更是毫不吝啬地给出了18种⽅法让你选择。
我想任何⼀个⾮统计专业的⼈都有同⼀个感觉:你在耍我们吗?毫⽆提⽰地给出10多种⽅法,让我⼀个毫⽆统计背景的⼈⾃⼰选择。
就像是医⽣给你10多种药,⼀脸怜悯地对你说:回家⾃⼰看着吃啊,你觉得哪个好就吃哪个。
关键是,明知道我们没有这个判别⼒,为什么要给我们这么多的两两⽐较⽅法,还得让我们⾃⼰选择?正是统计学家太多了,每个⼈都能根据⾃⼰的理念提出⼀种⽅法,⽽这些⽅法看起来似乎都没错,那怎么办?只好都放在软件中,你⾃⼰跟着感觉⾛吧。
下⾯就来说⼏种⽐较常见的两两⽐较⽅法的选择,希望给⼤家稍微理清⼀点思路。
先声明⼀下,以下结论是参考了不少国外课本和⽂献,加上⾃⼰的⼀点经验,⽽且只给出结论性的内容,不给出公式和证明,喜欢追根究底的朋友可以⾃⼰看专业书籍。
为什么要⽤两两⽐较⽅法呢?⼤多数两两⽐较⽅法的⽬的都是为了控制假阳性,因为两两⽐较次数多了,容易产⽣假阳性的结果。
⾸先说医学统计课本中最喜欢介绍的3种⽅法:LSD、SNK和Bonferroni法。
我⼤概翻了⼀下国内的医学统计学教程,⼏乎都是这3种⽅法,但似乎都没有说什么情况下⽤。
LSD法其实就相当于t检验,只不过它需要在⽅差分析⼀定要有统计学差异的情况下才⽤。
所以LSD法并没有控制假阳性错误。
⼀般情况下,如果你在设计初期就有很明确的⽬的,可以考虑这种⽅法,因为每⼀对⽐较都是有特定意义的,不⽤⾮得控制假阳性错误。
SNK法是先按多组均值⼤⼩排序,然后按⼀个有点类似于t检验的公式分别⽐较(不过误差计算不同)。
因变量方差分析word版

方差分析方差分析模型本身就是线性模型的一个特例,一个带着很多哑变量的线性模型,因此,所有关于普通线性回归的理论方法,对方差分析统统适用。
⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎨⎩⎪⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩单因素多因素方差分析有交互效应的因素模型多变量方差分析协变量分析模型一般线性模型(GLM )简单回归多元回归回归分析多项式回归多变量回归与回归分析不同,方差分析需要分类的自变量,且应变量或者协变量必须是连续变量。
方差分析最初是用来检验多个独立正态总体,在方差齐性的前提下,总体均值间的差异是否具有统计意义的一种方法。
而今对多个正态总体在方差不齐时,也有方法对总体间的差异进行显著性检验。
因此,只要满足多个总体间的独立性和正态性,方差分析就可以用来探讨多个不同实验条件或者处理方法对实验结果有无影响。
单因变量单因素方差分析为了研究三种不同的铅球教学方法的效果,将某年级三个班中,同龄的各种运动能力基本相同的男生随机分成三组,分别按三种不同方法教学,三个月后,以同样的测试测得各组的成绩,见数据;试问三种教学方法有无区别?数据格式如上所见;分别有三种教学方式,分为三组,三种方法的观测值分别为11、15、13;其数据的描述性统计见下表。
1、 描述性统计2、 样本数据正态性检验和方差齐性检验Analyze-discriptive statistics explore按因子水平分组:即按照三种教学方法分为三组。
这里levene 检验方差齐性,无:代表不进行方差齐性检验,为转换:代表不对数据进行处理直接进行方差齐性检验。
正态性检验的原假设:样本服从正态分布;方差齐性检验原假设:三个样本方差齐性;通过检验我们看到,正态检验和方差齐性检验的检验概率值SIG.都是大于0.05,那么我们就可以认为三个方法的样本集正态且方差齐性。
3、进行方差分析Analyze compare one way anovaOptions框:discriptive:输出各组常用的描述性统计量。
(完整word版)用Excel做方差分析
用Excel做方差分析
1、打开EXCEl,录入好你的数据。
然后点击“工具”,看你的有没有“数据分析”这一选项。
如果有就OK。
如果没有,那就加载。
也点击“工具”下的加载宏,在“分析工具库”左边的方框里打上对勾。
然后再点击“工具”,就会多了“数据分析”这一项。
希望你office是完全安装的,否则这一步操作不了。
2、点击“数据分析”里面选择你想要的分析方法。
你要的
是单因素方差分析,就选第一项。
然后选择你要分析的数据区域,再选择数据的分组方式,是按照行还是列。
然后再选“输出选项”就OK啦。
P<0.05显著,p<0.01极显著
3、相关性分析
也在数据分析中选择“相关系数”
剩下的和方差分析一样选择数据区域和输出区域
然后的到结果:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析中均值比较的方法
最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD 法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较.
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1。
事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较.常用的方法有: Dunnett—t 检验、LSD—t 检验(Fisher ’s least significant dif ference t test)。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD—t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同, 所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以
认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
1.2 Dunnett—t(新复极差法)检验,Duncan 1955年在Newman及Keuls的复极差法(muhiple range method)基础上提出,该方法与Tukey法相类似。
适用于n—1个试验组与一个对照组均数差别的多重比较,多用于证实性研究。
Dunnett-t统计量的计算公式与LSD-t检验完全相同.
实验组和对照组的样本均数和样本含量。
需特别指出的是Dunnett—t检验有专门的界值表,不同于t检验的界值表。
一般认为,比较组数k≥3时,任何两个样本的平均数比较会牵连到其它平均数的对比关系,而使比较数再也不是两个相互独立的样本均数的比较.这是LSD-t无法克服的缺点.Dunnett—t 针对这一问题提出.在同一显著水平上两个均数的最小显著差数随着这二个平均数在多个平均数中所占的极差大小而不同,根据不同平均数间的对比关系来调整相应的显著差别(critical range)的大小。
2. 多个均数的两两事后比较:适用于探索性研究,即各处理组两两问的对比关系都要回答,一般要将各组均数进行两两组合,分进行检验。
常用的方法有:SNK—q(Student-Newman-Keuls q)法、Duncan法、Tukey法和Scheffe法。
值得注意的是,这几种方法对数据有具体的要求和限制。
而文献中我最常见的是Tukey法与SNK—q法,。
2.1 SNK—q检验
对于SNK—q检验,检验的统计量是q,所以又称为q检验。
SNK—q检验的原理是根据所包含不同数目的平均数的极差调整各自的显著性水准,限制了实验的误差.保证在做所有比较时,不易犯第1类错误。
2。
2 Tukey法
Tukey法(Tukey’S Honestly Significant Diference Tukey’s HSD)的原理与SNK—q 检验基本相同,但是,该方法要求各比较组样本含量相同 ,它将所有对比组中I类错误最大者控制在α之内。
研究显示:这种方法有较高的检验效能(与LSD法比较),具有很好的稳定性,适用于大多数场合下的两两比较,计算简便。
但是,Tukey法是基于比较组全部参与比较这一假设下进行的,因此在只比较指定的某几组总体均数时并不适用,建议选择Dunnett法或者是Bonferroni方法,因为这两种方法会给出较高效能的检验结果.
2.3 Scheffe法
与一般的多重比较不同,Scheffe法的实质是对多组均数间的线性组合是否为0进行假设检验,多用于对比组样本含量不等的资料。
在单因素的多重比较问题中,除了要逐对比较因素水平的平均效应之外,有时还有可能要比较因素水平平均效应的线性组合.例如将有基本相同的因素水平平均效应的几个组,构成一个综合组。
因此可能检验这样的假设:
显然,前面讨论的参数的两两比较属于一类特殊的对比。
Scheffe法可以同时检验所有可能的对比,即同时检验任何一组对比。
Scheffe法的优点是可以检验任意的线性对比。
在这方面,Tukey法不如Scheffe法。
但是在单纯作逐对因素效应均值的比较时,Schefe法的效率不如Tukey法高。
也就是说,Schefe法更易于将显著的差异判定为不显著(Tukey法认为)。
在实际场合,当单纯作逐对均值
比较时,建议用Tukey法;而当要做多个一般的线性对比检验时。
就要用Scheffe法。
Scheffe法检验实质上对F值进行了简单的校正,将比较的组数纳入考虑的范畴,该方法的检验统计量代表了最大可能的累积I类错误的概率.遗憾的是,由于控制I类错误时的“矫枉过正”.会最终导致较大的Ⅱ类错误的概率。
3. 探索性研究和证实性研究均适用的检验方法:
3.1 Bonferroni t检验
基本思想是:如果三个样本均数经ANOVA检验差异有统计学意义(α=0.05),需对每两个均数进行比较,共需比较的次数为3次,由于每进行一次比较犯I类错误的概率是α=0.05,那么比较3次至少有一次犯I类错误的概率就是:α'=1-0.953≈0。
1426〉0.05。
因此,要使多次比较犯I类错误的概率不大于原检验水准α,现有的检验水准应该进行调整,用α'=α/m作为检验水准的调整值,两两比较得出的P值与其进行比较.该方法的思想适用于所有的两两比较,并且该方法的适用范围很广,不仅仅限于方差分析,例如相关系数的检验和卡方检验也适用。
Bonferroni t检验的方法和思想容易理解,操作简便,但是严格地控制了I类错误的同时增大了Ⅱ类错误的发生概率,在结论的给出方面是一种比较保守的方法。
3.2 Sidak检验
该方法通过Sidak校正降低每次两两比较的I类错误概率,以达到最终整个比较的I类错误发生率不超过α的目的。
Bonferroni t检验与Sidak检验相似,Bon。
ferroni t检验是检验的近似计算,但是由于Bonferroni t检验在计算上容易实现,所以应用较广。
相比较而言,Bonferroni t检验在给出推断结论时更为审慎。
不容易得到拒绝零假设的结果。
两种检验在对比组数增加、比较组不独立时,推断结论更趋保守。
以上方法都必须在满足方差齐性的前提条件时才可以应用,另外还有一些方法是在不满足方差齐性时多重比较的方法:Tamhane’s T2,Dunnetts’s T3, Games-Howell, Games-Howell。
Tamhane’s T2是一种基于t检验原理的两两比较方法。
该方法比较保守.
Dunnetts’s T3则是以最大的t值(studentized maximum modulus)为基础的。
Games-Howell检验方法是比较宽大的一种两两比较方法。
Games-Howell 方法将方差不齐的组数作为一个影响因素纳入考虑范畴。
严重的方差不齐和样本含量过小都会使I类错误的概率增加.Games—Howell检验基于Welch’s对t检验的自由度进行校正,并使用了学生化极差作为统计量。
该检验适用于样本含量小且方差不齐(轻度方差不齐例外)时的情况。
该方法是方差不齐时的一种较好的方法.
Dunnett's是一种基于学生化极差的适用于方差不齐情况时两两比较的方法。
