10梁模型法
迈达斯Midas_civil_梁格法建模实例

混凝土收缩变形率: 程序计算
荷载
静力荷载
>自重
由程序内部自动计算
>二期恒载
桥面铺装、护墙荷载、栏杆荷载、灯杆荷载等
具体考虑:
桥面铺装层:厚度80mm的钢筋混凝土和60mm的沥青混凝土,钢筋混凝土的重力密度为25kN/m3, 沥青混凝土的重力密度为23kN/m3。每片T梁宽2.5m,所以铺装层的单位长度质量为:
> 混凝土
采用JTG04(RC)规范的C50混凝土
>普通钢筋
普通钢筋采用HRB335(预应力混凝土结构用普通钢筋中箍筋、主筋和辅筋均采用带肋钢筋既HRB系列)
>预应力钢束
采用JTG04(S)规范,在数据库中选Strand1860
钢束(φ15.2 mm)(规格分别有6束、8束、9束和10束四类)
钢束类型为:后张拉
图7. 跨中等截面
模型/材料和截面特性/ 截面
数据库/用户> 截面号(3); 名称(端部变截面右)
截面类型>变截面>PSC-工形
尺寸
对称:(开)
拐点: JL1(开)
尺寸I
S1-自动(开),S2-自动(开),S3-自动(开),T-自动(开)
HL1:0.20;HL2:0.06 ;HL2-1: 0;HL3:1.28;HL4:0.17;HL5:0.29
(0.08×25+0.06×23)×2.5=8.45kN/m2.
护墙、栏杆和灯杆荷载:以3.55kN/m2计。
二期恒载=桥面铺装+护墙、栏杆和灯杆荷载=8.45+3.55=12kN/m2。
>预应力荷载
分成正弯矩钢束和负弯矩钢束
典型几束钢束的具体数据:
Timoshenko梁的第二频谱分析

Timoshenko梁的第二频谱分析作者:***来源:《湖南大学学报·自然科学版》2021年第11期摘要:推导Timoshenko梁振动微分方程的初参数解,结合边界条件,建立简支梁的频率方程. 当固有频率小于临界频率时,频率方程有双曲正弦函数与三角正弦函数之积的因式,当固有频率大于临界频率时,此因式变成为双三角正弦函数之积,此即Timoshenko梁产生第二频谱的理论原因. 推导出等截面等跨径的2~3跨连续Timoshenko梁的频率方程,并从理论上预测存在第二频谱现象的其他结构. 建立了简支Timoshenko梁第一、二频谱的频率计算公式. 通过实例验证第二频谱的存在. 通过微分方程求解,论证了临界频率是结构固有频率的有效组成部分,其对应的竖向位移模态无振幅、转角位移模态的振幅为常数;指出数值分析时,由于计算机截断误差的影响,所预测的临界频率有误差、所对应的竖向位移模态为不规则模态等特点.关键词:频率分析;临界频率;第二频谱;Timoshenko梁中图分类号:TU375 文献标志码:AAnalysis on the Second Frequency Spectrum of Timoshenko BeamXIA Guiyun(School of Civil Engineering,Changsha University of Science and Technology,Changsha 410114,China)Abstract:Incorporating the boundary conditions, initial parameter solutions of vibration differential equations for Timoshenko beam are used to derive the frequency equation of a simply-supported beam. When the natural frequency is less than the critical frequency, the frequency equation can be factorized into the hyperbolic sine function and the trigonometric sine function,while, when the natural frequency is greater than the critical frequency, the frequency equation can be factorized into double trigonometric sine functions, which is the crucial reason for the existence of the second frequency spectrum. Frequency equations for two-span and three-span continuous Timoshenko beams with uniform cross sections and equal spans are derived. Other structures with the second frequency spectrum are forecasted theoretically. The formulas for the first and second frequencies are deduced for simply-supported Timoshenko beam. The existence of the second frequency spectrum is confirmed through the examples. Through solving the differential equation of motion, the critical frequency is proven to be an efficient part of the natural frequencies for the framed structures. The corresponding mode shape of the critical frequency contributes to the displacement mode shape with zero amplitude and rotation mode shape with constant amplitude. Due to the truncation error of the computer, the critical frequency predicted by the finite element method shows error, and the mode shape of the displacement is very irregular.Key words:frequency analysis;cutoff frequency;second frequency spectrum;Timoshenko beam梁的彎曲振动是土木[1]、机械、石油、化工、航空航天等领域的重要问题,已有多种理论. 最早、最经典的理论是Euler梁模型,该模型考虑了梁的弯曲和截面惯性力,适应于细长杆系结构的分析计算,但对高跨比较大的深梁结构,存在静力问题计算挠度偏小[2]、动力问题高估振动频率和有无限阶次频率[3]等不足. Elishakoff等[4]评述Rayleigh梁考虑了截面转动惯量的影响,对Euler梁进行改进. Shear梁模型考虑结构弯曲、剪切变形的影响和截面惯性力,但没有考虑截面转动惯量影响(此模型不同于一般的不考虑结构弯曲的简单剪切梁模型和纯剪切梁模型[5]). 1921年Timoshenko[6-7]综合考虑截面弯曲和剪切变形、惯性力和转动惯量的影响,提出经典的Timoshenko梁模型,该模型保留梁的平截面假定,放弃直法线假定,通过引入截面剪切修正系数来弥补剪切本构关系方面的不足(假定截面剪应力不均匀、剪应变均匀)[8-9]. 相比于Euler梁、Rayleigh梁和Shear梁,Timoshenko梁有显著进步,提高了计算精度,扩大了应用范围,杆系结构的静力、动力和稳定问题都可基于Timoshenko梁理论进行分析[1]. 但该理论颇具争议,至今仍众说纷纭的第二频谱问题[10-12]和截面剪切修正系数定义问题[8,13-15],还有振动微分方程解耦后存在挠度关于时间四阶导数项,其物理意义不明确的问题,因此其后出现众多的修正理论. 1927年Love[16]根据梁段微元体平衡,提出Timoshenko梁的修正模型,即忽略挠度关于时间四阶导数项,可称为Love梁. 陈镕等[17]采用双挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能认为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)則解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分别为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振动存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:α′=■■β=■■(5)相关系数定义为:γ′ = α1 - ■,φ = β1 - ■ (6)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4的具体表达式与文献[20]一致.3)固有频率等于临界频率时(ω = ωC)微分方程退化为:■ + β2■ = 0 (7)式中:波数退化为α=0,β=■.对于常规杆系结构,如果采用Timoshenko梁单元进行结构的自由振动分析,可得到一固有频率与临界频率非常接近,位移振型较特别的模态,此模态说明临界频率是结构频谱的有效组成部分,其详细讨论在本文第5节进行.2 简支梁的第二频谱现象对于两端简支的Timoshenko梁,当ω < ωC时,由边界条件知:当x = 0时,W0 = M0 = 0;当x = L时,WL = ML = 0,得到频率方程为sinh(αL)sin(βL) = 0 (8)结构固有频率解为sin(βL) = 0,即β = ki π/L,k = 1,2,3,…,kC . 此时结构仅有一支固有频率. 此支频率的最大个数为:为Love梁. 陈镕等[17]采用双挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能认为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)则解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分別为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振动存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:α′=■■β=■■(5)相关系数定义为:γ′ = α1 - ■,φ = β1 - ■ (6)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4的具体表达式与文献[20]一致.3)固有频率等于临界频率时(ω = ωC)微分方程退化为:■ + β2■ = 0 (7)式中:波数退化为α=0,β=■.对于常规杆系结构,如果采用Timoshenko梁单元进行结构的自由振动分析,可得到一固有频率与临界频率非常接近,位移振型较特别的模态,此模态说明临界频率是结构频谱的有效组成部分,其详细讨论在本文第5节进行.2 简支梁的第二频谱现象对于两端简支的Timoshenko梁,当ω < ωC时,由边界条件知:当x = 0时,W0 = M0 = 0;当x = L时,WL = ML = 0,得到频率方程为sinh(αL)sin(βL) = 0 (8)结构固有频率解为sin(βL) = 0,即β = ki π/L,k = 1,2,3,…,kC . 此时结构仅有一支固有频率. 此支频率的最大个数为:为Love梁. 陈镕等[17]采用双挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能認为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)则解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分别为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振动存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:α′=■■β=■■(5)相关系数定义为:γ′ = α1 - ■,φ = β1 - ■ (6)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4的具体表达式与文献[20]一致.3)固有频率等于临界频率时(ω = ωC)微分方程退化为:■ + β2■ = 0 (7)式中:波数退化为α=0,β=■.对于常规杆系结构,如果采用Timoshenko梁单元进行结构的自由振动分析,可得到一固有频率与临界频率非常接近,位移振型较特别的模态,此模态说明临界频率是结构频谱的有效组成部分,其详细讨论在本文第5节进行.2 简支梁的第二频谱现象对于两端简支的Timoshenko梁,当ω < ωC时,由边界条件知:当x = 0时,W0 = M0 = 0;当x = L时,WL = ML = 0,得到频率方程为sinh(αL)sin(βL) = 0 (8)结构固有频率解为sin(βL) = 0,即β = ki π/L,k = 1,2,3,…,kC . 此时结构仅有一支固有频率. 此支频率的最大个数为:为Love梁. 陈镕等[17]采用双挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能认为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)则解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分别为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振動存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:α′=■■β=■■(5)相关系数定义为:γ′ = α1 - ■,φ = β1 - ■ (6)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4的具体表达式与文献[20]一致.3)固有频率等于临界频率时(ω = ωC)微分方程退化为:■ + β2■ = 0 (7)式中:波数退化为α=0,β=■.对于常规杆系结构,如果采用Timoshenko梁单元进行结构的自由振动分析,可得到一固有频率与临界频率非常接近,位移振型较特别的模态,此模态说明临界频率是结构频谱的有效组成部分,其详细讨论在本文第5节进行.2 简支梁的第二频谱现象对于两端简支的Timoshenko梁,当ω < ωC时,由边界条件知:当x = 0时,W0 = M0 = 0;当x = L时,WL = ML = 0,得到频率方程为sinh(αL)sin(βL) = 0 (8)结构固有频率解为sin(βL) = 0,即β = ki π/L,k = 1,2,3,…,kC . 此时结构仅有一支固有频率. 此支频率的最大个数为:为Love梁. 陈镕等[17]采用双挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能认为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)则解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分别为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振动存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:α′=■■β=■■(5)相关系数定义为:γ′ = α1 - ■,φ = β1 - ■ (6)振型函數ai(x),bi(x),ci(x),di(x),i=1,2,3,4的具体表达式与文献[20]一致.3)固有频率等于临界频率时(ω = ωC)微分方程退化为:■ + β2■ = 0 (7)式中:波数退化为α=0,β=■.对于常规杆系结构,如果采用Timoshenko梁单元进行结构的自由振动分析,可得到一固有频率与临界频率非常接近,位移振型较特别的模态,此模态说明临界频率是结构频谱的有效组成部分,其详细讨论在本文第5节进行.2 简支梁的第二频谱现象对于两端简支的Timoshenko梁,当ω < ωC时,由边界条件知:当x = 0时,W0 = M0 = 0;当x = L时,WL = ML = 0,得到频率方程为sinh(αL)sin(βL) = 0 (8)结构固有频率解为sin(βL) = 0,即β = ki π/L,k = 1,2,3,…,kC . 此时结构仅有一支固有频率. 此支频率的最大个数为:为Love梁. 陈镕等[17]采用雙挠度理论也推导出了与Love梁相同的微分方程,并认为导致Timoshenko梁模型中出现挠度关于时间四阶导数项的原因是,没有考虑剪切转角的转动惯量,如果舍弃挠度关于时间四阶导数项,则可考虑截面剪切转角的转动惯量影响. Elishakoff等[18-19]同样导出了与Love梁相同的微分方程,并认为此理论比Timoshenko梁理论更一致、更简单,其命名为截断Timoshenko梁. Love梁虽然形式比Timoshenko梁简化,微分方程求解方便,但是其没有对应的能量泛函,不能通过变分原理导出,也没有对应的有限元列式. Xia等[20]研究了考虑截面剪切变形和全转动惯量影响的Timoshenko梁振动特性,证明此种Timoshenko梁修正理论无第二频谱问题和结构固有频率有界特性.Timoshenko梁的第二频谱现象是指一种振型对应两个固有频率. 两端简支、两端导向和简支-导向的单跨Timoshenko梁,多跨连续的等截面等跨径Timoshenko梁都存在第二频谱现象. Traill-Nash[21]于1953年最先发现和报道简支Timoshenko梁存在第二频谱现象,相继得到Anderson[22]、Dolph[23]等学者的确认,但也有学者[24-27]认为第二频谱没有物理意义而应舍弃. 有些学者[4,28]则认为结构的振型包括了竖向变形和转角,如果将变形和转角同等看待,则振幅不一致的振型不能认为是同一振型,因此也就不存在第二频谱问题. 现在越来越多的实验测试结果[29-32]证实了第二频谱现象不仅存在,而且实验测试的结构固有频率与Timoshenko梁理论预测结果符合较好,因此没有理由草率地去否定、甚至舍弃第二频谱. 本文试图对Timoshenko梁第二频谱产生的原因进行理论解释,以期提高结构模态识别精度,促进以模态叠加法等为基础的动力分析方法的发展,谋求在Timoshenko梁第二频谱问题上取得共识.1 Timoshenko梁振动的理论解析Timoshenko梁振动的微分方程[1,2,20]求解采用分离变量法,设竖向位移w(x)分解为竖向位移函数W(x)和时间函数T(t),如下:w(x,t) = W(x)·T(t)(1)式中:T(t) = a1 sin(ωt) + a2 cos(ωt)则解耦后的振动微分方程为:■ + ω2■ + ■■ +■ - ■W = 0 (2)式中:D = EI、C = μGA,A、I和μ分别为截面的面积、抗弯惯性矩和剪切修正系数;E、G和ρ分别为材料的弹性模量、剪切模量和密度;ω为结构的圆频率.Timoshenko梁振动存在临界频谱(或称为移频频率,其定义为ωC = ■),式(2)可根据结构固有频率ω与临界频率ωC的大小关系有3种解.1)固有频率小于临界频率时(ω < ωC)此时结构的竖向变形、转角、剪力和弯矩用初参数(即x = 0时的W0、ψ0、Q0、M0)表示为:W(x)=a1(x)W0+b1(x)ψ0+c1(x)Q0+d1(x)M0ψ(x)=a2(x)W0+b2(x)ψ0+c2(x)Q0+d2(x)M0Q(x)=a3(x)W0+b3(x)ψ0+c3(x)Q0+d3(x)M0M(x)=a4(x)W0+b4(x)ψ0+c4(x)Q0+d4(x)M0(3)其中,波数定义为:α=■■β=■■相关系数定义为:γ = α1 + ■,φ = β1 - ■ (4)式(3)振型函数ai(x),bi(x),ci(x),di(x),i=1,2,3,4,详见文献[2,20],为节约篇幅不再列出.2)固有频率大于临界频率时(ω > ωC)此时结构的竖向变形、转角、剪力和弯矩仍可用式(3)表示,但波数、相关系数和振型函数需另行定义. 波数定义为:。
变截面梁钢筋计算方法(一)

变截面梁钢筋计算方法(一)变截面梁钢筋计算简介变截面梁是一种截面尺寸在横向或纵向上发生变化的梁,常用于大跨度的建筑结构。
为确保梁的承载能力,需要进行合理的钢筋计算。
本文将介绍几种常用的计算方法。
方法一:扭矩平衡法1.计算梁在各个截面处的弯矩分布;2.假设钢筋布置的初始尺寸和末尾尺寸,计算这两个尺寸下的截面危险截面点的弯矩;3.对比两个不同尺寸下的截面危险截面点的弯矩大小,选择出较大的一个;4.根据选择出的弯矩大小,计算在这个截面点处所需的钢筋面积;5.重复步骤3和4,直到整个变截面梁的钢筋面积满足要求。
方法二:材料力学性能计算法1.根据变截面梁的构造和受力情况,计算截面的抗弯能力;2.确定所需的截面尺寸和形状,计算整个变截面梁的抗弯能力;3.根据所需的钢筋面积,推算出所需的钢筋直径和数量。
方法三:试错法1.假设变截面梁的截面尺寸和形状;2.根据假设的尺寸和形状,计算整个梁的抗弯能力,并判断是否满足要求;3.如果不满足要求,则调整尺寸和形状,重新计算;4.重复步骤2和3,直到满足要求。
方法四:模型分析法1.建立变截面梁的有限元模型,并进行特征值分析;2.根据分析的结果,确定各个截面点的位移和应力分布;3.假设钢筋布置的初始尺寸和末尾尺寸,计算这两个尺寸下的截面危险截面点的应力;4.对比两个不同尺寸下的截面危险截面点的应力大小,选择出较大的一个;5.根据选择出的应力大小,计算在这个截面点处所需的钢筋面积;6.重复步骤4和5,直到整个变截面梁的钢筋面积满足要求。
结论根据变截面梁的特点和需要,可以选择适合的计算方法进行钢筋计算。
不同的方法有不同的优点和适用场景,需要根据具体情况选择合适的方法。
通过合理的钢筋计算,可以确保变截面梁的安全可靠性。
方法一:扭矩平衡法1.计算梁在各个截面处的弯矩分布;2.假设钢筋布置的初始尺寸和末尾尺寸,计算这两个尺寸下的截面危险截面点的弯矩;3.对比两个不同尺寸下的截面危险截面点的弯矩大小,选择出较大的一个;4.根据选择出的弯矩大小,计算在这个截面点处所需的钢筋面积;5.重复步骤3和4,直到整个变截面梁的钢筋面积满足要求。
浅谈修正Timoshenko梁的发展和应用

浅谈修正Timoshenko梁的发展和应用Timoshenko梁模型是一种广为使用的理论模型,在许多结构分析领域被广泛应用。
但是在实际应用中,Timoshenko梁模型通常需要进行修正,以更好地预测实际工程中的复杂结构行为。
本文将探讨Timoshenko梁模型的发展和修正方法,并介绍修正后模型的应用。
Timoshenko梁模型最初是由Timoshenko在20世纪初提出的,用于描述横向剪切变形对梁挠曲刚度的影响。
该模型假设梁的变形由弯曲和剪切两部分组成,其中弯曲部分由Euler-Bernoulli梁理论描述,而剪切部分则由横向剪切变形产生。
该模型在许多工程领域有着广泛的应用,例如建筑、桥梁、飞机和船舶等。
然而,在实际工程中,Timoshenko梁模型存在着一些局限性。
例如,该模型假设梁为无限刚性,而实际中很少有完全刚性的结构体系。
此外,该模型也无法考虑到梁材料的非线性特性和梁截面形状的复杂变化等因素。
这些局限性导致Timoshenko梁模型在一些实际工程问题上表现不佳,需要进行修正。
为了修正Timoshenko梁模型的局限性,一些研究学者提出了各种修正方法。
其中比较常用的方法包括扭转刚度修正、截面修正和屈曲修正等。
这些修正方法能够更好地预测梁在实际工程中的行为,从而提高分析的精度和可靠性。
在扭转刚度修正中,将梁转角的变化和横向剪切变形联系起来,从而修正了Timoshenko梁模型中忽略的扭转刚度影响。
该修正方法需要根据梁截面形态和材料性质等因素进行具体计算。
例如,在圆形截面梁中,通过计算极性惯性矩和截面面积,可以得到扭转刚度修正系数。
在截面修正中,将梁截面形状的变化与其弯曲刚度和剪切刚度联系起来,并对其进行修正。
例如,在具有不同几何形状的梁中,截面修正可以通过计算梁的剩余刚度、惯性矩和重心位置等因素进行修正。
这些修正能够更好的反映实际工程中梁的变形和应力分布情况。
在屈曲修正中,考虑到实际梁在失稳时的扭转和弯曲行为,引入屈曲修正系数对梁的挠曲刚度进行修正。
迈达斯midas梁桥专题—梁格.pdf

Integrated Solution System for Bridge and Civil Strucutres目录一、剪力-柔性梁格理论1. 纵梁抗弯刚度.......................................................................32.横梁抗弯刚度....................................................................... 43.纵梁、横梁抗弯刚度........................................................... 44.虚拟边构件及横向构件刚度.. (5)三、采用梁格建模助手生成梁格模型二、单梁、梁格模型多支座反力与实体模型结果比较1. 前言.......................................................................................72. 结构概况...............................................................................73. 梁格法建模助手建模过程及功能亮点...............................114. 修改梁格..............................................................................225. 在自重、偏载作用下与FEA 实体模型结果比较. (24)四、结合规范进行PSC 设计1.纵梁抗弯刚度【强制移轴(上部结构中性轴)法】一、剪力-柔性梁格理论a.各纵梁中性轴与上部结构中性轴基本重合b.强制移轴,使各纵梁中性轴与上部结构中性轴基本重合,等效纵梁抗弯刚度2.横向梁格抗弯刚度3.纵梁、横梁抗扭刚度4.虚拟边构件及横向构件刚度此处d’为顶板厚度。
梁类型 模型

梁类型模型
梁的类型和模型是结构工程中的重要概念。
梁是建筑物中用于支撑和传递载荷的主要结构元素之一。
根据不同的分类方式,梁有不同的类型和模型。
以下是一些常见的梁类型和模型:
1. 简支梁:简支梁是一种最简单的梁类型,它的一端固定在墙上或柱子上,另一端自由支撑。
这种梁主要用于承受垂直载荷,如楼板、屋顶等。
2. 连续梁:连续梁是一种更复杂的梁类型,它在两个或多个支点之间连续延伸。
这种梁主要用于承受更大的载荷,如大跨度桥梁、大型工业设备等。
3. 预应力梁:预应力梁是在制造过程中施加预应力的梁,以提高其承载能力和延展性。
这种梁广泛应用于大跨度桥梁和高层建筑等领域。
4. 模型梁:模型梁是指用于模拟真实世界中梁的行为的模型。
模型梁可以是简单的物理模型、数学模型或计算机模型等。
它们可以用于预测和分析梁在不同条件下的行为,如弯曲、振动、稳定性等。
总之,不同类型的梁具有不同的特性和应用场景。
在结构工程中,选择合适的梁类型和模型对于确保建筑物的安全性和稳定性至关重要。
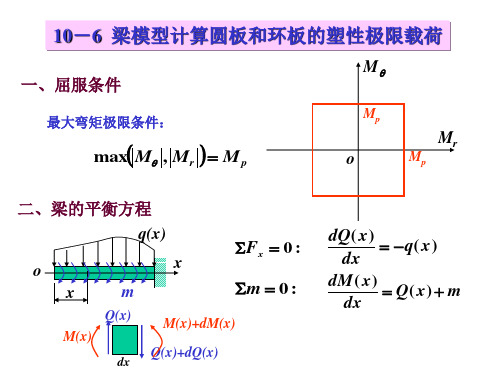
弹塑性力学10-6梁模型计算圆板和环板的塑形极限载荷(精)
r
o b
解:
o
z
r
b r a
z
a
m= 2Mp
2rM r 2 r b M p
2 r b r b 2rrq 2bq r b 2bq
b r b r 2b Mr 1 M p q r 6r
2
2
2
3
r
o
解:
o
z
r
r a
a
z
2rM r 2rM p r r 2rq 2 3
m= 2Mp
qr 2 Mr M p 6
Mr
r a
qa2 M p M p M 支圆板:
Mr
r a
0
ql 6
Mp a2
例题2:半径为 a 的简支环板,内半径为 b ,受均布载荷 q 作用,圆板单 位塑性极限弯矩为: Mp ,求塑性极限载荷。 2rq q
i 1
ai bi
( n 2) 2n 2 n
Pl M P cota i cot b i
i 1
n
正多边形(集中力作用在板中心): a i b i
( n 2) 2n 2 n
Pl M P 2 tan
i 1
n
n
Pl 2nM P tan
r
o b
解:
o
b c a
z
a
m= 2Mp
z
2 r b M p brc 2rM r 2 r b M p P r c c r a
Mr
r a
0
Pl
2 a b M p ac
力学基础-(八) 梁的弯曲

ql FQ (l ) 2
用两点式画出剪力图的斜直线。
x
4. 画弯矩图
M(0) 0
ql 2 M(l / 2)
8
M(l) 0
用三点坐标描出弯矩图的二次曲线。
13
任务八 梁的弯曲
弯曲剪力图和弯矩图
2.画剪力图和弯矩图的简便方法
(1)集中力作用处
剪力图有突变,突变幅值等于力 的大小,方向与力同向。
x
(4)集中力偶作用处 剪力图不变化。
弯矩图有突变,突变幅值等于力偶矩的大小,方向顺时针向上突变,反之 向下。
14
任务八 梁的弯曲
弯曲剪力图和弯矩图
应用举例
例 图示跨长为l的简支梁AB,中点C 作用集中力F,试用简便画法画
梁剪力图和弯矩图。
F
A
l/2 FA=F/ FQ 2 F/
C l/2
B FB=F/
MA
A FA
x
l
FQ
F
F B
x
M
Fl
x
从上例可以得出
结论1:无荷载作用的梁段上 剪力图为常量; 弯矩图为斜直线。
确定直线两点的坐标,A点的临近截 面A+的弯矩值
MA+=-Fl
B点的临近截面B -的弯矩值 MB-=-F·=0
12
任务八 梁的弯曲
弯曲剪力图和弯矩图
应用举例
例 图示的简支梁AB,作用均布荷载q,建立剪力、弯矩方程,画梁的
MA
A FA
x
l
FQ
F
M
-Fl
F
B
xC
FA
x
FQ
ql/
2
xM
l/2
ql/
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a2
4x2 ax
M pd
4b 4x a Wi
M Pd
a2
4bx ax
外力功We :
We
x 0
q
z adz x
x x
z
d
a
2
2
q b
x
2 xy
dy
a 2
y
d
0
a
a 2
D
z adz
xB
F yA
C
z (b x 2x y)dy E
x
a
b
We
qad
6
x 2 qad
12
3b 2x
a/2
a/2
和剪力的作用。 3) 不计弹性变形。
2. 破坏机构的确定规则: (1)薄板的破坏机构由若干板块组成,板内塑性铰线是相邻两板 块的转动轴。 ➢ 有塑性铰线的固支边、简支边、过支承板中心的线都是板块的 转动轴。 ➢ 板块数目等于支承边界的数目。
(2)塑性铰线在板内相交。
(3)终止在自由边界上的塑性铰线,其延长线交于相邻两板块转 动轴的交点上。该交点可能位于无穷远处。
MP
2 tan
i 1
n
Pl 2nMP tan n
n 3 : Pl 10.39M P n 4 : Pl 8M P n 5 : Pl 7.27M P n 6 : Pl 6.93M P
三、周边固支的多边形板 在O 处受集中力P 作用
C
AC=ai OD=hi
A
D
bi-1
ai
bi
O
DO
d
ji :板块AOC相对AC的转角
梁计算模型上的坐标原点
距圆板的对称轴为 r 处的圆截面
坐标为 r 的梁截面
2. 载荷与内力转换
圆板单位面积上的载荷q(r)
梁计算模型上的分布载荷 2rq(r)
圆板某一半径上的载荷P
梁计算模型相应位置处的集中力 P
圆板中的环向弯矩: Mq = Mp (极限条件)
梁计算模型上的附加均布弯矩 2 Mp
方向与外载荷在梁中产生的弯矩方向相反
n
Pl 2M P cot a i cot b i i 1
正多边形(集中力作用在板中心):
ai
bi
(n 2)
2n
2n
Pl 4nMP tan n
例题1:边长为 a 的正方形薄板,一边固支、两边简支,自由边中点A受集 中载荷 P 作用,板的塑性极限弯矩为: Mp ,求塑性极限载荷。
Da
E
b
h
A
ba
C
B
解:设A点的挠度为d
ABC与ACD的相对转角为q :
q d cot a cot b 5 d
AC
2 AC
jd
ACD与CD的相对转角为j: j d
a
内力功Wi : 外力功We : Wi We
Wi 2MPq AC M pja 6M Pd We Pd
Pl 6M P
例题2:边长为 a,b 的矩形薄板,一边自由、三边简支,板上受均布载荷 q 作用,塑性铰线如图,板的塑性极限弯矩为: Mp ,求:x=? 破坏 载荷取最小值,此最小值为多少?
q
2rq
r
o
r
ob
a
解:
z
b
r a
z
m= 2Mp
2rM r
2 r
bM p
2bq
r
b2
2
r
b 2
2rq
2bq
r
b 3
Mr
1
b r
M
p
r
b2 r
6r
2b q
Mr ra 0
ql
a
6M p
ba
2b
固支环板:Mr
r a
Mp
ql
6M p 2a b a b2 a 2b
例题3:半径为 a 的简支环板,内半径为 b ,在半径为 c 的圆周上作用线 分布载荷 p,总值为 P ,单位塑性极限弯矩为: Mp ,求塑性极 限载荷。
p
p c
r
ob
a
解:
z
o
b
c a
z
P
r
m= 2Mp
2rM r
2
2 r bM p r bM p Pr
c
b r c cra
Mr ra 0
Pl
2 a bM p
ac
10-7 多边形板的塑性极限载荷(机动法)
一、薄板的破坏机构
1. 基本假设:
1) 在薄板最大弯矩处形成塑性铰线(直线段)。 2) 沿塑性铰线的单位长度上作用着塑性极限弯矩Mp ,不计扭矩
三、板的平衡方程 dQ( x) q( x) dx
d rQr qr
dr
d (rM r dr
)
rQr
Mq
d 2rQr 2qr
dr
d(2rM r
dr
)
2rQr
2Mq
dM( x) Q( x) m dx
梁
q(x) 板
梁计算模型
q(r)
o
xo
r
x
m
r
Mx
Qx
m
q(x)
极限条件:
Mmax Mp
2rMr 2rQr 2Mq
We
qad
6
3b
x
Wi
M Pd
a2
4bx ax
6(a 2 4bx) Wi We ql M P a 2 x(3b x)
dql dx
a2 0 x
4b
b2
1 12 a2
1
ql
min
48b2 M P a2 (6b2 a2 a a2 12b2 )
2rq(r)
❖ 若梁和圆板的边界条 件在形式上相同,可 通过求解变量转换后 梁的问题得到圆板的 解答。
四、 梁模型计算圆板和环板的塑性极限载荷的步骤
1. 结构转换
o
r
o
r
r
r
z
z
圆板的半径 外边界支承圆板
梁计算模型的跨度 (只研究右半部)
梁计算模型的左端为自由端 右端与板的支承形式相同。
圆板的对称轴
ji
d
hi
固支边上形成塑性铰线
内力功Wi :
n
Wi M Pd cot a i cot b i
i 1
nd
M P i1 ai hi
ai hi
cot a i
cot b i1
n
Wi 2M Pd cot a i cot b i
i 1
外力功We : We Pd
n
Pl 2M P cot a i cot b i i 1
10-6 梁模型计算圆板和环板的塑性极限载荷
一、屈服条件
Mq
最大弯矩极限条件:
max Mq , Mr M p
Mp
o
Mr
Mp
二、梁的平衡方程
o x
q(x) x
m
Fy 0 : m 0 :
Q(x) M(x)
dx
M(x)+dM(x) Q(x)+dQ(x)
dQ( x) q( x) dx
dM( x) Q( x) m dx
li
cot a i
cot
bi
塑性极限弯矩:MP
在塑性铰线 li 上做的内力功:
qi
d
li
cot a i
cot
bi
M pliq i M Pd cot a i cot b i
M pliq i
n 多边形,总的内力功Wi :
n
n
Wi M pliq i M Pd cot a i cot b i
i 1
i 1
外力P 做的外力功We : We Pd
We Wi
n
Pl M P cot a i cot b i i 1
正多边形:a i
bi
(n 2)
2n
2
n
n
Pl M P cot a i cot b i i 1
正多边形(集中力作用在板中心):
ai
bi
(n 2)
2n
2n
n
Pl
圆板中 r 处的弯矩Mr
梁计算模型上: 2r Mr
3. 求塑性极限载荷 (梁右端边界条件)
r=a 处简支:M=0
r=a 处固支:M=-
Mp
2a Mr =0 2a Mr = - 2a Mp
例题1:半径为 a 的固支圆板,受均布载荷 q 作用,圆板单位塑性极限弯
矩为: Mp ,求塑性极限载荷。
2rq
q
r
o
r
oa
解:
z
raz源自m= 2Mp2rM r2rM p
r 2rq
2
r 3
qr 2 Mr M p 6
Mr
r a
Mp
Mp
Mp
qa2 6
简支圆板:
Mr ra 0
ql
6
Mp a2
ql
12
Mp a2
例题2:半径为 a 的简支环板,内半径为 b ,受均布载荷 q 作用,圆板单
位塑性极限弯矩为: Mp ,求塑性极限载荷。
(4)集中力作用下,塑性铰线交于载荷作用点。
二、周边简支的多边形板 在O 处受集中力P 作用
A
O
ai bi
C O
a
OA=li B
b
P
d
破坏机构:角锥体
a li tan a i b li tan b i
d
q1
q2
qi :相对转角
qi q1 q2
