sas 时间序列课后作业 相关系数
时间序列相关系数

时间序列相关系数时间序列相关系数是指在一段时间内,两个变量之间的关系的度量。
反映着一个变量的变化对另一个变量的变化程度的影响。
时间序列相关系数可以通过Pearson相关系数、Spearman等级相关系数等来计算。
Pearson相关系数基于假设研究变量是连续变量,且满足正态性假设。
在计算过程中需要依赖数据的协方差、标准差来计算。
Pearson相关系数可根据其值的正负性及非常量性分类,取值范围为[-1,1],值越大则变量之间的关系越密切。
Spearman等级相关系数则是用于序数变量之间相关性的度量,基于等级,不受数据分布的限制。
它将原始数据转换为等级,然后通过等级之间的差异来度量两个变量之间的关系。
Spearman等级相关系数的取值范围也为[-1, 1],其值的解释与Pearson相关系数类似。
时间序列相关系数的应用广泛,可以用于统计学分析、金融领域、天气预报等方面。
在金融领域,时间序列相关系数可以用于分析股票的波动性、市场行情的变化等。
在气象科学中,相关系数可以用于研究气象要素之间的关系。
需要注意的是,在计算时间序列相关系数时,需要注意样本数量是否足够,样本是否具有代表性等问题,避免在样本数量较少或不具代表性的情况下得出错误的结论。
在计算相关系数时还需要注意变量之间的因果关系。
相关系数仅能表明变量之间存在相关性,而不能证明这种相关性是因果关系。
因此在解释相关系数时需要谨慎,避免因出现错解而造成偏差。
在时间序列分析中,相关系数是一种重要的分析方法,能够帮助我们更好地理解变量之间的关系。
通过分析时间序列相关系数,我们可以更好地预测未来趋势,做出更科学的决策。
时间序列分析(SAS)第3章

结果分析:上图是数据对应的时序图,从图上曲线分析来看,数据并没有周期性或者趋向性规律,因而可以初步判断这是平稳数列。
proc arima data=ex3_1;结果分析:本过程中,我们建立了8阶自回归分析模型,图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。
由于本次实验探究的是平稳序列,因而样本逆相关图先不作分析。
结果分析:从上图可以看出,在众多模型中,MA(4)模型的BIC信息量是最小的,因而我们接下来会采用结果分析:结果分析: 结果分析:结果分析:该图为预测的图像,其中,红色线段表示预测出来的数列,绿色的两条线段分别表示95%的置信下限和95%的置信上限,而黑色的星号标识则是对应的样本数据值。
从图来分析,我们可以看出,黑色的样本数据值跟我们预测出来的线段非常的吻合,因而模型建立得很不错。
再结合上一步骤的参数结果,二、课后习题(老师布置的习题部分)17.data lianxi3_17;input x@@;time=_n_;cards;126.4 82.4 78.1 51.1 90.9 76.2 104.5 87.4110.5 25 69.3 53.5 39.8 63.6 46.7 72.979.6 83.6 80.7 60.3 79 74.4 49.6 54.771.8 49.1 103.9 51.6 82.4 83.6 77.8 79.389.6 85.5 58 120.7 110.5 65.4 39.9 40.188.7 71.4 83 55.9 89.9 84.8 105.2 113.7124.7 114.5 115.6 102.4 101.4 89.8 71.5 70.998.3 55.5 66.1 78.4 120.5 97 110;proc gplot data=lianxi3_17;plot x*time=1;symbol1c=red I=join v=star;run;结果分析:上图是数据对应的时序图,从图上曲线分析来看,数据并没有周期性或者趋向性规律,因而可以初结果分析:本过程中,我们建立了8阶自回归分析模型,图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。
时间序列相关系数

时间序列相关系数时间序列相关系数是一种用于衡量两个时间序列之间相关性的统计量。
它可以帮助我们了解两个时间序列之间的关系,以及它们之间的相互作用。
在本文中,我们将探讨时间序列相关系数的概念、计算方法以及其在实际应用中的意义。
时间序列相关系数是指两个时间序列之间的相关性程度。
它可以用来衡量两个时间序列之间的相似性或差异性。
时间序列相关系数的取值范围在-1到1之间,其中-1表示完全负相关,0表示无相关性,1表示完全正相关。
相关系数越接近1或-1,说明两个时间序列之间的相关性越强,而越接近0则说明两个时间序列之间的相关性越弱。
计算时间序列相关系数的方法有很多种,其中最常用的是皮尔逊相关系数。
皮尔逊相关系数是一种线性相关系数,它可以用来衡量两个时间序列之间的线性关系。
计算皮尔逊相关系数的公式如下:r = cov(X,Y) / (std(X) * std(Y))其中,r表示皮尔逊相关系数,cov(X,Y)表示X和Y的协方差,std(X)和std(Y)分别表示X和Y的标准差。
除了皮尔逊相关系数外,还有一些其他的相关系数,如斯皮尔曼相关系数和肯德尔相关系数等。
这些相关系数适用于不同类型的数据,可以根据实际情况选择合适的相关系数进行计算。
时间序列相关系数在实际应用中有着广泛的应用。
例如,在金融领域中,时间序列相关系数可以用来衡量不同股票之间的相关性,以及股票与市场之间的相关性。
在气象领域中,时间序列相关系数可以用来研究不同气象变量之间的相关性,以及气象变量与自然灾害之间的关系。
在医学领域中,时间序列相关系数可以用来研究不同疾病之间的相关性,以及疾病与环境因素之间的关系。
时间序列相关系数是一种重要的统计量,它可以帮助我们了解不同时间序列之间的相关性,以及它们之间的相互作用。
在实际应用中,我们可以根据具体情况选择合适的相关系数进行计算,以便更好地理解数据之间的关系。
SAS相关性分析

SAS相关性分析相关性分析处理变量之间的关系。
相关系数是两个变量之间的线性关联的度量。
相关系数的值总是在-1和+1之间。
SAS提供过程PROC CORR以找到数据集中的⼀对变量之间的相关系数。
语法在SAS中应⽤PROC CORR的基本语法是:PROC CORR DATA = dataset options;VAR variable;以下是使⽤的参数的描述:Dataset是数据集的名称。
选项是附加选项,其中包括绘制矩阵等过程。
变量是⽤于查找相关性的数据集的变量名称。
例数据集中可⽤的⼀对变量之间的相关系数可以通过在VAR语句中使⽤它们的名称来获得。
在下⾯的例⼦中,我们使⽤数据集CARS1并得到显⽰马⼒和重量之间的相关系数的结果。
PROC SQL;create table CARS1 asSELECT invoice,horsepower,length,weightFROMSASHELP.CARSWHERE make in ('Audi','BMW');RUN;proc corr data=cars1 ;VAR horsepower weight ;BY make;run;当执⾏上⾯的代码中,我们得到以下结果:所有变量之间的相关性通过简单地应⽤具有数据集名称的过程,可以获得数据集中可⽤的所有变量之间的相关系数。
例在下⾯的例⼦中,我们使⽤数据集CARS1并获得显⽰每对变量之间的相关系数的结果。
proc corr data=cars1 ;run;当执⾏上⾯的代码中,我们得到以下结果:相关矩阵我们可以通过在PROC语句中选择绘制矩阵的选项来获得变量之间的散点图矩阵。
例在下⾯的例⼦中,我们得到马⼒和重量之间的矩阵。
proc corr data=cars1 plots=matrix ;VAR horsepower weight ;run;当执⾏上⾯的代码中,我们得到以下结果:W3Cschool()最⼤的技术知识分享与学习平台此篇内容来⾃于⽹站⽤户上传并发布。
sas时间序列课后作业相关系数
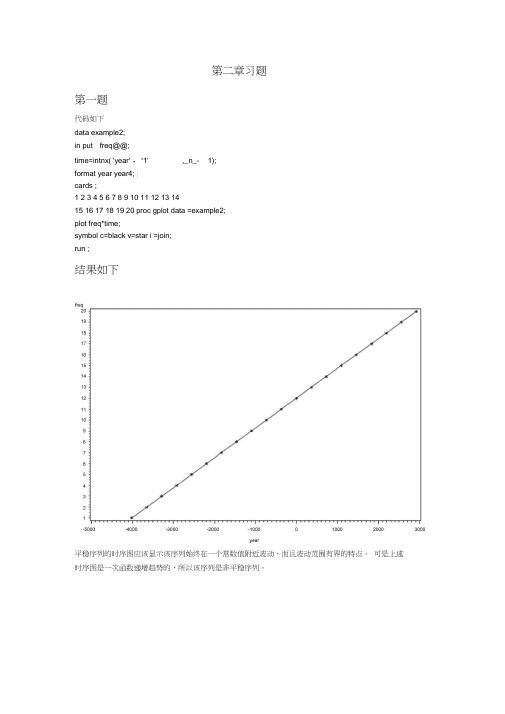
第二章习题第一题代码如下data example2;in put freq@@;time=intnx( 'year' ,‘1' ,_n_- 1);format year year4; |cards ;1 2 3 4 5 6 7 8 9 10 11 12 13 1415 16 17 18 19 20 proc gplot data =example2;plot freq*time;symbol c=black v=star i =join;run ;结果如下平稳序列的时序图应该显示该序列始终在一个常数值附近波动,而且波动范围有界的特点。
可是上述时序图是一次函数递增趋势的,所以该序列是非平稳序列。
u U LI 丘・i I 导g 朮耳m p 「; 卯皆出胃中矽gAS 累统ThursdayThe ARILiA Procedurelie of NLAC is lar&er than 25X of the 淀i i es ler^th. The ics anti conf Iderwe interveils miy bt poor.Naims of Variable = f req Me^n of fforkinr Series 10*5 Standard Deviation5.766261Number of Obscrvat ions20从图中我们发现序列的自相关系数递减到零的速度相当缓慢,在很长的时间延迟时期里, 自相关系数一直为正,而后又一直为负,在子相关图上显示出明显的三角对称性,这是具 有单调趋势的非平稳序列的一种典型自相关图形式,这和该序列时序图的单调递增是一致 的。
各个延迟阶数下的自相关系数如下K=1 ' =0.85 K=2=0.7015 K=3 ' =0.55602K=4=0.41504 K=5 =0.28008 K=6=0.152635SPSSasyuptotI c approx Inal Io used for correStd Error0 33.2500001.00000diiU-diiU-diiL JiiL H ill -iJi HiqfjHi dj di Ja di斤"「|1"心|1""1"八1""1"2TuT 1"MT 'TMT Ti T ■nT*1 28.262500 0.85000■山Ur 山山*山边山*山l| 111 ■ l| 11 p !| 1 If"■Tll|l"Tll|l"Tll|l!Tll|ll ;■2 23.325000 0.70150 ■JI I ^Lr ill L1I nj J |_L ■ J a tfj rpr|B "" 'll if ■ 'll i'p ■ T 'T'■ "lip3 18.487500 0*55602 ■桝册附榊柑{榊.4 18.800000 0.41504 附常附瀬出榊Ht0 9.312G00 0.28008附岸出壯弗常.65.075000 0.16268 11.137500 0.084218 -2.460000 -.07386 Hi9 -5.637500 -.16956 10-8.876000 -,2518811-10.61250C -,31917聃串當串}|E»:12 -12.300000 -,36992 -H {家串當串}|E 串13 -13.367500 -,40263 14 -13.825000 -.4157915 -13.56250C -.40708**»:*#*#*0.223607 0,349649 0.414070 0.449862 0.468617 0.476913 0.479349 0.479471 0.4800370,483022 0.4895450,499342 0.513343 0.52630? 0.545000Antocar re I at i on?La^ Covari anceCorral at i on"/ fiirks two standftrd errorsSeries:freAutocorrelationsLag AutocorrelationStd. Error aBox-Ljung StatisticValue dfo . bSig. 1 .850 .208 16.732 1 .000 2 .702 .202 28.761 2 .000 3 .556 .197 36.762 3 .000 4 .415 .191 41.500 4 .000 5 .280 .185 43.800 5 .000 6 .153 .178 44.533 6 .000 7 .034 .172 44.572 7 .000 8 -.074 .165 44.771 8 .000 9 -.170 .158 45.921 9 .000 10 -.252 .151 48.713 10 .000 11 -.319 .143 53.693 11 .000 12 -.370 .135 61.220 12 .000 13 -.403 .126 71.409 13 .000 14-.416.11784.08714.000File Edit 也 ew Qata Iransform B LI 旦1: fre 1 (re var 11.0022.00 33.00A 4,0055.00 6 S.OO7 7.00 a 3.009 9.001010.00 1111.0012 12.0013 13.0014H.OO15 1500161S.OO17 170018 190019 19.002020. DOReports [>BSGrp1j¥B 宝血iiw TablesCornparB Means fijerieral Lin 刚 Modeii£orrelalfi Regression LoglinsarNeural Networksdassiiy却牟 Reduction Scale ypnparameiric Tesls Tpw SeriesIMutiple RespcriEa ComplBX Semples ±S aUntitl.Al [D«t>S B iD] - £P££OueHy Control [0 RCCC^..SurviveValue Ara^sis...L t DI"Help Models 辰r 1 £resie Mocf^s.. 芮1Affily Models...Generahzed Linear iMjoctefcSeasorialDewnnposition... Spectral Anialysis...15 | -.408 | .107 | 98.729 [ 15 ] .000a. The underlying process assumed is independence (white noise).b. Based on the asymptotic chi-square approximation.fre05-y ooa-0 5--10-T i i i iTr ii i i ([ i r1 2 34 567 e9 10 1112 13 14 15L^g Number第二题代码如下 data example2; in put ppm@@; time=intnx( 'month', '01jan1975'd,_n_- 1);format time monyy.;cards ;330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.6310-□ Caefficierrt ------ U pper tonfklgnue Limit ------ L ower Confidence Limit331.63 332.46 333.36 334.45 334.82 334.32333.05 330.87 329.24 328.87 330.18 331.50332.81 333.23 334.55 335.82 336.44 335.99334.65 332.41 331.32 330.73 332.05 333.53334.66 335.07 336.33 337.39 337.65 337.57336.25 334.39 332.44 332.25 333.59 334.76335.89 336.44 337.63 338.54 339.06 338.95337.41 335.71 333.68 333.69 335.05 336.53337.81 338.16 339.88 340.57 341.19 340.87339.25 337.19 335.49 336.63 337.74 338.36 proc gplot data =example2;plot ppm*time;symbol c=black v=star i =join;run结果如下平稳序列的时序图应该显示该序列始终在一个常数值附近波动,而且波动范围有界的特点。
sas相关系数

sas相关系数
SAS相关系数是指用SAS软件计算得出的两个变量之间的相关程度。
相关系数用来衡量变量之间的线性相关程度,取值范围在-1到1之间。
当相关系数为1时,表示两个变量完全正相关;当相关系数为-1时,表示两个变量完全负相关;当相关系数为0时,表示两个变量完全不相关。
SAS中可以使用PROC CORR来计算相关系数。
该过程可以计算两个以上的变量之间的相关系数,并且还可以控制输出结果的格式和内容。
在进行相关系数计算时需要注意,数据应该是连续型的,并且需要对缺失值进行处理。
SAS还提供了其他的方法来进行相关性分析,比如使用PROC REG 来进行线性回归分析,通过分析残差来发现相关性。
此外,还可以使用PROC VARMAX来进行多元时间序列分析,其中相关系数也是一个重要的分析指标。
总之,SAS相关系数是数据分析中非常重要的一部分,它可以帮助我们理解变量之间的相互关系,从而更好地进行数据处理和预测分析。
- 1 -。
时间序列分析-sas各种模型-作业神器Word版

实验一分析太阳黑子数序列一、实验目的:了解时间序列分析的基本步骤,熟悉SAS/ETS软件使用方法。
二、实验内容:分析太阳黑子数序列。
三、实验要求:了解时间序列分析的基本步骤,注意各种语句的输出结果。
四、实验时间:2小时。
五、实验软件:SAS系统。
六、实验步骤1、开机进入SAS系统。
2、创建名为exp1的SAS数据集,即在窗中输入下列语句:3、保存此步骤中的程序,供以后分析使用(只需按工具条上的保存按钮然后填写完提问后就可以把这段程序保存下来即可)。
4、绘数据与时间的关系图,初步识别序列,输入下列程序:ods html;ods listing close;5、run;提交程序,在graph窗口中观察序列,可以看出此序列是均值平稳序列。
6、识别模型,输入如下程序。
7、提交程序,观察输出结果。
初步识别序列为AR(2)模型。
8、估计和诊断。
输入如下程序:9、提交程序,观察输出结果。
假设通过了白噪声检验,且模型合理,则进行预测。
10、进行预测,输入如下程序:11、提交程序,观察输出结果。
12、退出SAS系统,关闭计算机。
总程序:data exp1;infile "D:\exp1.txt";input a1 @@;year=intnx('year','1jan1742'd,_n_-1);format year year4.;;proc print;run;ods html;ods listing close;proc gplot data=exp1 ;symbol i=spline v=dot h=1 cv=red ci=green w=1;plot a1*year/autovref lvref=2 cframe=yellow cvref=black ;title "太阳黑子数序列";run;proc arima data=exp1;identify var=a1 nlag=24 minic p=(0:5) q=(0:5);estimate p=3;forecast lead=6 interval=year id=year out=out;run;proc print data=out;run;选取拟合模型的规则:1.模型显著有效(残差检验为白噪声)2.模型参数尽可能少3.结合自相关图和偏自相关图以及minic条件(BIC信息量最小原则),选取显著有效的参数实验二 模拟AR 模型一、 实验目的:熟悉各种AR 模型的样本自相关系数和偏相关系数的特点,为理 论学习提供直观的印象。
SAS相关分析-简单相关、偏相关讲义

350
8
10
第一组数据 a
第二组数据 b 图5.1 三组假设数据的散点图
第三组数据 c
第一节 两随机变量之间的线性关系
10 10
10 8 6 4 2 0 0 2 4 6 8 10
8 6 4 2 0 0 2 4 6 8 10
8 6 4 2 0
0
2
4
6
8
10
第一组数据 a
第二组数据 b 图5.1 三组假设数据的散点图
df = n-m
相关矩阵
c1m c2m c mm
r11 r R 21 rm1 r12 r22 rm 2 r1m r2 m rmm
CR
1
第二节 偏(净)相关分析
第一步:统计假设 H0:ij.=0,HA:ij.≠0 第二步:计算统计量
第三组
x y1 5.2 y x2 5.0 x y2 5.2 y x3 5.0 x y3 5.2 y
x1 5.0
324
2 1 2 2 2 2 2 3 2 3
350 324 350
324
350
表5.1 为说明两变量之间的线性关系而假设的三组(x,y)观察值 第一节 两随机变量之间的线性关系 组别 第一组 第二组 第三组
第一节 简单相关分析
2、统计量r显著性检验
第一步:作统计假设 H 0 : 0
HA : 0
第二步:计算统计量r,根据df =n-2,查相关 系数显著性检验表,从而获得r0.05和r0.01 。 第三步:作统计推断 1、|r|<r0.05 推断相关不显著; 2、r0.05<=|r|<r0.01 推断相关达显著; 3、|r| >= r0.01 推断相关达极显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题第一题代码如下data example2;input freq@@;time=intnx('year','1',_n_-1);format year year4;cards;1 2 3 4 5 6 7 8 9 10 11 12 13 1415 16 17 18 19 20;proc gplot data =example2;plot freq*time;symbol c=black v=star i=join;run;结果如下平稳序列的时序图应该显示该序列始终在一个常数值附近波动,而且波动范围有界的特点。
可是上述时序图是一次函数递增趋势的,所以该序列是非平稳序列。
从图中我们发现序列的自相关系数递减到零的速度相当缓慢,在很长的时间延迟时期里,自相关系数一直为正,而后又一直为负,在子相关图上显示出明显的三角对称性,这是具有单调趋势的非平稳序列的一种典型自相关图形式,这和该序列时序图的单调递增是一致的。
各个延迟阶数下的自相关系数如下K=1 ρ=0.85K=2 ρ=0.7015K=3 ρ=0.55602K=4 ρ=0.41504K=5 ρ=0.28008K=6 ρ=0.152635SPSSAutocorrelations Series:freLag Autocorrelation Std. Error aBox-Ljung Statistic Value df Sig.b1 .850 .208 16.732 1 .0002 .702 .202 28.761 2 .0003 .556 .197 36.762 3 .0004 .415 .191 41.500 4 .0005 .280 .185 43.800 5 .0006 .153 .178 44.533 6 .0007 .034 .172 44.572 7 .0008 -.074 .165 44.771 8 .0009 -.170 .158 45.921 9 .00010 -.252 .151 48.713 10 .00011 -.319 .143 53.693 11 .00012 -.370 .135 61.220 12 .00013 -.403 .126 71.409 13 .00014 -.416 .117 84.087 14 .00015 -.408 .107 98.729 15 .000a. The underlying process assumed is independence (white noise).b. Based on the asymptotic chi-square approximation.第二题代码如下data example2;input ppm@@;time=intnx('month','01jan1975'd,_n_-1);format time monyy.;cards;330.45 330.97 331.64 332.87 333.61 333.55331.90 330.05 328.58 328.31 329.41 330.63331.63 332.46 333.36 334.45 334.82 334.32333.05 330.87 329.24 328.87 330.18 331.50332.81 333.23 334.55 335.82 336.44 335.99334.65 332.41 331.32 330.73 332.05 333.53334.66 335.07 336.33 337.39 337.65 337.57336.25 334.39 332.44 332.25 333.59 334.76335.89 336.44 337.63 338.54 339.06 338.95337.41 335.71 333.68 333.69 335.05 336.53337.81 338.16 339.88 340.57 341.19 340.87339.25 337.19 335.49 336.63 337.74 338.36;proc gplot data =example2;plot ppm*time;symbol c=black v=star i=join;run;结果如下平稳序列的时序图应该显示该序列始终在一个常数值附近波动,而且波动范围有界的特点。
可是上述时序图显示每月释放的co2数据以年为周期呈现出规则的周期性,除此之外还有明显的逐年递增的趋势。
显然该序列也一定不是平稳序列。
绘制样本自相关图代码如下data example2_2;input ppm@@;time=intnx('month','1jan1975'd,_n_-1); format time monyy.;cards;330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.63 331.63 332.46 333.36 334.45 334.82 334.32 333.05 330.87 329.24 328.87 330.18 331.50 332.81 333.23 334.55 335.82 336.44 335.99 334.65 332.41 331.32 330.73 332.05 333.53 334.66 335.07 336.33 337.39 337.65 337.57 336.25 334.39 332.44 332.25 333.59 334.76 335.89 336.44 337.63 338.54 339.06 338.95 337.41 335.71 333.68 333.69 335.05 336.53 337.81 338.16 339.88 340.57 341.19 340.87 339.25 337.19 335.49 336.63 337.74 338.36 ;proc arima data=example2_2;identify var=ppm nlag=24;run;从图中我们发现自相关系数长期位于零轴一边,这是具有单调趋势序列的典型特征,同时自相关图呈现出明显的正弦波动规律,这是具有周期变化规律的非平稳序列的典型特征,这和该序列时序图的带长期递增趋势的周期性质非常吻合。
各个延迟阶数下的自相关系数如下:就是上图中第三列correlation的值K=1 ρ=0.90751K=2 ρ=0.72171K=3 ρ=0.51252K=4 ρ=0.34982K=5 ρ=0.24690K=6 ρ=0.20309后面的图中有显示所以省略。
SPSS第三题代码如下data example2;input mm@@;time=intnx('month','01jan1945'd,_n_-1);format time monyy7.;cards;69.3 80.0 40.9 74.9 84.6 101.1 225.0 95.3 100.6 48.3144.5 28.338.4 52.3 68.6 37.1 148.6 218.7 131.6 112.8 81.8 31.047.5 70.196.8 61.5 55.6 171.7 220.5 119.4 63.2 181.6 73.9 64.8166.9 48.0137.7 80.5 105.2 89.9 174.8 124.0 86.4 136.9 31.5 35.3 112.3 43.0160.8 97.0 80.5 62.5 158.2 7.6 165.9 106.7 92.2 63.226.2 77.052.3 105.4 144.3 49.5 116.1 54.1 148.6 159.3 85.3 67.3112.8 59.4;proc gplot data =example2;plot mm*time;symbol c=black v=star i=join;run;结果如下平稳序列的时序图应该显示该序列始终在一个常数值附近波动,而且波动范围有界的特点。
可是上述时序图显示每月的降雨量数据大致在一个常数波动,可以主观的认为大致趋于平稳。
绘制样本自相关图代码如下data example2_2;input mm@@;time=intnx('month','1jan1945'd,_n_-1);format time monyy7.;cards;69.3 80.0 40.9 74.9 84.6 101.1 225.0 95.3 100.6 48.3144.5 28.338.4 52.3 68.6 37.1 148.6 218.7 131.6 112.8 81.8 31.047.5 70.196.8 61.5 55.6 171.7 220.5 119.4 63.2 181.6 73.9 64.8166.9 48.0137.7 80.5 105.2 89.9 174.8 124.0 86.4 136.9 31.5 35.3 112.3 43.0160.8 97.0 80.5 62.5 158.2 7.6 165.9 106.7 92.2 63.226.2 77.052.3 105.4 144.3 49.5 116.1 54.1 148.6 159.3 85.3 67.3112.8 59.4;proc arima data=example2_2;identify var=mm nlag=24;run;从图中我们发现自相关系数大致在0轴附近波动,所以可以主观的认为它是平稳的,各个延迟阶数下的自相关系数如下:就是上图中第三列correlation的值K=1 ρ=0. 01277K=2 ρ=0.04160K=3 ρ=-0.04323K=4 ρ=-0.17869后面的图中有显示所以省略。
数据个数是72,他的四分之一是18,所以观察前三行的p值,由纯随机检验图可以看出,在延迟阶数为6时,p值大于0.05,是纯随机的,则该规律的波动没有任何统计规律可行。
而12、18阶的p值则小于0.05,拒绝原假设,所以认为月度降雨量不属于纯随机波动,说明该序列不仅可以认为是平稳的,而且还蕴含着值得提取的信息。
第四题用excel计算LB统计量2 0.95(6) 1.635χ=20.95(12) 5.226χ=所以根据自己的计算结果:当延迟阶数为6阶时,大于1.635,所以拒绝原假设,认为是非纯随机的,所以该序列是有价值的。
