磁场强度毕奥萨伐尔定律及运动电荷产生磁场大学物理
《大学物理》第八章 毕萨定律S

”
. 例Id载ly任流意2长一r直解点导:P根线的取据,磁任毕其其感意—电在应电萨流P强流点定强度元产理度BI生d为l的I?,磁试场d计为B 算方:导向线为旁Idl r
ol
ro
P
dB
各电流元产生的
o Idlsin 4dB 方r向2 垂直纸面向里。
I
1
B dB
B
ab
dr
其中B adbr、0cd与B板 d面r 等 距B离 d。0r
bc
cd
da
B
c
Bab Bcd 2Bab
而 o Ii o j ab
B
1 2
o
j
. . . . 与P点到平板的距离无关。
dl
dl
aB
b
B
1 2
o
j
与P点到平板的距离无关。
)
0m 2x3
r
B
xP
2)
在圆心处(x=0):
B
0 I
2R
(磁偶极子的场)
如考虑一段“圆弧形”载流线在圆心的磁场贡
献:
B 0I 2R 2
圆弧对圆心 所张的角
例 一直螺线管轴线上的磁场 B ?
已知:导线通有电流I,单位长度
B
2
oI R2
(
x2
R2
)
3 2
I
若令L 积分B回 d路r LL的L 绕B向dl 相反:0 若积分回L 路不包围电流I : B
I
dr
0
L
B
r
I
L
L
几点注意事项:
大学物理课件-2毕奥-萨伐尔定律

1 2
0I
2R1
(每202长1/3/1度8 相等的圆弧在O处产生的磁场大小相同);20
方向:垂直纸面向外。
大线圈在O处产生的磁场大小为: B0大
方向:垂直纸面向里。
1 2
0 I
2R2
、
B0 B0小 B0大
方向:垂直纸面向外。
0I
4
1 [ R1
1 ]
R2
(2) B0
BB00'' 大 小
B0小 B0大
以电荷为q速度为的正电荷作研究对象在电流元中其电流为i102021318lqns单个载流子产生的磁场112021318一个以速度v作匀速直线运动的电荷q与电流元是相当的在dt时间内粒子位移为dlvdt等效电流元为idlidtvqv根据毕奥萨伐尔定律在距它r处点p所激励的磁感应强度为
20XX年复习资料
它们的方向均垂直纸面向里。
B B '
‘
02021/3/108小
B0’大
ቤተ መጻሕፍቲ ባይዱ
0 I
4
1 [ R1
1 ]
R2
方向均垂直纸面向里21。
相信梦想是价值的源泉,相信眼光决定未来的一 切,相信成功的信念比成功本身更重要,相信人 生有挫折没有失败,相信生命的质量来自决不妥
协的信念。
谢谢观看
2021/3/18
22
电流元在空间某点产生的磁感应强度大小与电流
元大小成正比,与电流元和由电流元到点P的矢
量平方间成夹反角比正;弦d成B垂正直比于,I与dl电和流r元 所到组点成P的的距平离面,的
指向满足右手定则。
Idl r
dB k
2021/3/18
r3
其中: k = 0 /4 真空磁导率 : 0=410-7TmA-31
第二节毕萨定律
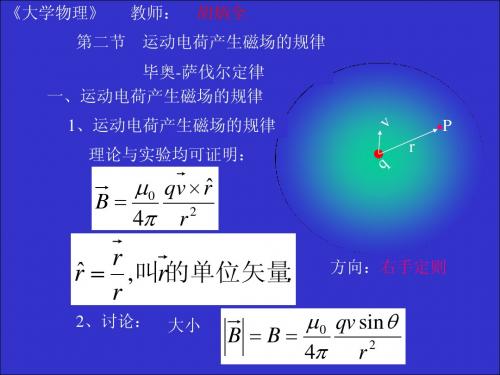
µ 0 dI dB = 2πx
I dI = dx L
R+ L
dx L
x
P
dB的方向垂直于平面向里。总磁场为:
B = ∫ dB = ∫
R
µ0 I dx 2πLx
µ0 I R + L ln B= 2πL R
《大学物理》 教师: 胡炳全 例题5、设半径为R的带电薄圆盘的电荷面密度为σ,并以 角速度ω绕通过圆盘圆心的垂直于盘面的轴转动。试求圆 盘中心处的磁感应强度。 ω 解:圆盘转动时带动电荷运动形成 + + R ++ 很多的圆电流。圆心处的磁感应强 + + 度可以看成是各个圆电流产生的磁 + O + + + r + 场的和。 + dr + + 如图取一个半径为r,宽度为dr的圆环, + 其电量为: dq = σ 2πrdr 当它以角速度ω转动时对应的电流为:
B = ∫ dBx = ∫ d B sin α =∫
l
µ 0 Idl sin α 2 4π r
《大学物理》
教师:
胡炳全 讨论: 1、圆心处的磁场
µ 0 I 2πR sin α B= 4π r2
整理可得:
B=
µ 0 IR
2
2 2 3/ 2
x = 0, B =µ0 I2R源自2( R + x )
2、磁场的方向分析
r0 = 0, B = 0
µ0 I B= 2πr0
方向讨论与磁 场分布图:
θ1 = 0,θ 2 = π
《大学物理》
教师:
胡炳全
例题2、试求一载流圆线圈在其轴线上任意一点处的磁场。 解:如图取电流元
大学物理11.2 毕萨定理
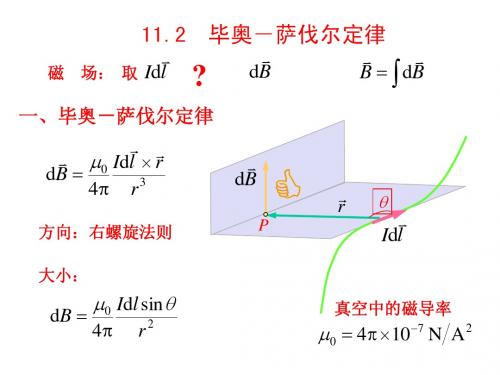
推 广
(2) o (3)
I R
×
B0
0I
4R
I R
× o
B0
0I
8R
(4)
BA
0I
4πd
d
*A
B0
(5)
I
0I
4 R2
0I
4 R1
R1
R2
* o
0I
4 π R1
例 如图,求O 点的磁感应强度。 解
B1 0
2
3 2 3 0I 8R
B2
0I
4R
0I
2πa
I
B
I
X
B
B
电流与磁感强度成右手螺旋关系
2 圆形载流导线轴线上的磁场. 解 由对称性知 B dB 0
B Bx
d B s in
r
2
Id l
R
s in R
dB
r
2
R x
2
r
o
x
*p
dB
0 Id l
4π r
2
x
dBx
dB
ndl 匝
2
d I In d l
R
P
l
圆电流在
B
P
点的磁场
2
dB
3
0 R dI
2
dB
2
0 R In d l
r R csc
2r
3
0 R In d l
2
2r
B
3
2r
0
nI
l R cot
11.3 毕奥-萨伐尔定律
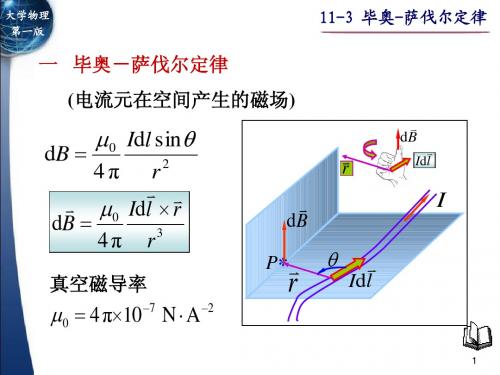
0 I (cos1 cos 2 ) 4 π r0
5
大学物理 第一版
11-3 毕奥-萨伐尔定律
B
0 I
4 π r0
(cos 1 cos 2 )
无限长载流长直导线
z
D
2
1 0பைடு நூலகம்2 π
× P
B
0 I
2 π r0
I
B
y
半无限长载流长直导线
x
C
o
1
π 1 2 2 π
二 毕奥-萨伐尔定律应用举例 例1 载流长直导线的磁场.
z
D
2
解 dB
0 Idz sin
4π r
2
dz
I
r
* P
z
1
dB
y
dB 方向均沿
x 轴的负方向
x
C
o r0
0 Idz sin B dB 4 π CD r 2
4
大学物理 第一版
11-3 毕奥-萨伐尔定律
2
cos 2 cos 1
1 π, 2 0
(1)对于无限长的螺线管
故
B 0 nI
1 * P
R
2
x
×× × ×× × ×× × ×× ×× ×
18
大学物理 第一版
11-3 毕奥-萨伐尔定律
(2)半无限长螺线管的一端
1 0.5π, 2 0
B 0 nI / 2
2
2
1
R 3csc2 d R 3 csc3 d
1 2 0 nI cos 2 cos 1 B 2
0 nI
大学物理——11-2毕奥-萨伐尔定律

1
2
μ0 I B (cos θ1 cos θ2 ) 4π a
2
μ0 I BP 4πa
I
o
a
* P
◆(3)载流直导线延长线上任一点的磁感强度
分析:根据载流直导线的磁感强度公式
μ0 I B (cos θ1 cos θ2 ) 4πa
在沿电流方向的延长线上任一点处,
P
2
2
1、5 点 : dB 0
0 Idl 3、7点 :dB 4R 2
3
7
Id l
6
2、4、6、8 点 :
R
5
4
0 Idl dB sin 45 0 4R 2
0 μ0 Idl r B dB L L 4π r2
任意形状恒定电流的磁场:
利用毕-萨定律计算磁感应强度的基本方法: (1) 将电流分解为无数个电流元 ,任取一 Idl ; (2) 写出dB 大小,图示dB方向; (3) 分析各个dB方向;将 dB 在坐标系中分解;
z
方向:电流与磁感强度 成右手螺旋定则。 A1
2
B
讨论
◆(1) 无限长载流直导 线的磁场
I
o
x
A2
r
1
P y
1 0 2
μ0 I B 2π a
无限长载流直导线的磁场方向:
μ0 I B 2π a
B I B I
X
I
B
磁感应线的绕向与电流满足右手螺旋定则。
◆(2) 半无限长载流直导线的磁场
◆ 在载流圆线圈轴线以外的空间,其磁感强度的分 布大致如下图所示: I
思考:
R B x 0 0 I o B0
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场大学物理电子教案

磁场强度毕奥萨伐尔定律及运动电荷产生的磁场一、教学目标1. 理解磁场强度的概念,掌握毕奥萨伐尔定律及其应用。
2. 了解运动电荷产生磁场的原理,能运用相关知识分析实际问题。
3. 培养学生的实验操作能力,提高其科学思维和问题解决能力。
二、教学内容1. 磁场强度的定义及其表示方法。
2. 毕奥萨伐尔定律的表述及其数学形式。
3. 毕奥萨伐尔定律在直导线、圆形电流和均匀电流环中的应用。
4. 运动电荷产生磁场的原理。
5. 运动电荷产生的磁场与电流磁场的区别与联系。
三、教学方法1. 采用讲授法,讲解磁场强度、毕奥萨伐尔定律及运动电荷产生磁场的相关概念和理论。
2. 利用示例和图示,直观展示毕奥萨伐尔定律的应用。
3. 开展讨论法,引导学生分析运动电荷产生磁场的原理及其在实际应用中的重要性。
4. 布置实验,让学生动手操作,验证毕奥萨伐尔定律及运动电荷产生磁场的理论。
四、教学准备1. 教案、教材、课件等教学资源。
2. 实验室设备:电流表、电压表、导线、磁针等。
3. 投影仪、计算机等多媒体设备。
五、教学过程1. 引入:通过简单的磁现象,引导学生思考磁场强度的概念。
2. 讲解:讲解磁场强度的定义及其表示方法,阐述毕奥萨伐尔定律的表述和数学形式。
3. 示例:分析毕奥萨伐尔定律在直导线、圆形电流和均匀电流环中的应用,演示相关计算过程。
4. 讨论:引导学生分析运动电荷产生磁场的原理,与电流磁场的区别和联系。
5. 实验:安排学生进行实验操作,验证毕奥萨伐尔定律及运动电荷产生磁场的理论。
6. 总结:对本节课的主要内容进行归纳总结,强调重点和难点。
7. 作业:布置相关练习题,巩固所学知识。
六、教学评估1. 课堂提问:通过提问了解学生对磁场强度、毕奥萨伐尔定律及运动电荷产生磁场的理解和掌握情况。
2. 实验报告:评估学生在实验过程中的操作技能、数据处理和分析问题的能力。
3. 作业完成情况:检查学生对课堂所学知识的巩固程度。
七、教学拓展1. 介绍其他磁场强度计算方法,如安培环路定律。
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场大学物理电子教案

磁场强度毕奥萨伐尔定律及运动电荷产生的磁场一、教学目标1. 让学生理解磁场强度的概念及其物理意义。
2. 掌握毕奥萨伐尔定律,并能运用其计算电流元产生的磁场。
3. 了解运动电荷产生磁场的原理。
二、教学内容1. 磁场强度的定义及物理意义。
2. 毕奥萨伐尔定律的内容及其数学表达式。
3. 运动电荷产生磁场的计算方法。
三、教学重点与难点1. 磁场强度的概念及其计算。
2. 毕奥萨伐尔定律的应用。
3. 运动电荷产生磁场的计算方法。
四、教学方法1. 采用讲授法,讲解磁场强度的定义、物理意义及计算方法。
2. 运用案例分析法,讲解毕奥萨伐尔定律的应用。
3. 利用实验法,让学生观察运动电荷产生的磁场。
五、教学过程1. 引入磁场强度的概念,讲解其物理意义。
2. 讲解电流元产生的磁场,引入毕奥萨伐尔定律。
3. 运用毕奥萨伐尔定律计算电流元产生的磁场。
4. 讲解运动电荷产生磁场的原理。
5. 运用实例分析,让学生了解毕奥萨伐尔定律在实际应用中的重要性。
6. 进行实验,让学生观察运动电荷产生的磁场。
六、教学评估1. 课堂问答:通过提问方式检查学生对磁场强度、毕奥萨伐尔定律和运动电荷产生磁场的基本理解。
2. 练习题:布置相关的计算题和应用题,评估学生运用毕奥萨伐尔定律解决问题的能力。
3. 实验报告:评估学生在实验中观察、分析和解释运动电荷产生磁场的能力。
七、课后作业1. 复习磁场强度的定义和计算方法。
2. 练习使用毕奥萨伐尔定律计算不同电流元产生的磁场。
八、课程拓展1. 介绍其他磁场计算方法,如安培环路定律。
2. 探讨磁场在现代科技中的应用,如磁悬浮列车、电机等。
3. 讨论相对论对磁场计算的影响,引入狭义相对论中的磁场计算。
九、教学反思1. 反思教学方法的有效性,如是否清晰地解释了磁场强度和毕奥萨伐尔定律的概念。
2. 考虑学生的反馈,调整教学节奏和难度,确保学生能够跟上课程进度。
3. 评估实验设计是否有助于学生理解运动电荷产生磁场的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 I 4 a
cos 1
cos 2
10
B
0 I 4a
cos 1
cos2
讨论:
1.无限长载流直导线的磁场:
10,2; NhomakorabeaB
0I 2a
l 2
Idl
lr
o
1 a
2.半无限长载流直导线的磁场:
1
,2
;
B
0I 4R sin
(cos
1)
3.载流导线延长线上任一点的磁场
Idl //
r,
Idl
r
dx x
dB
0dI 2x
0 Idx 2ax
ba
B dB ab 0Idx 0 I ln a b
b 2ax 2a b
12
例3:一载流圆环半径为R Idl
通有电流为 I,求圆环轴线
上一点的磁感应强度 B。 R
解:将圆环分割为无限 多个电流元;
I
o
电流元在轴线上产生的
r
dB
dB
dB x
x P dBx ' x
2.应用毕萨定律解题的方法 计算一段载流导体的磁场 1.建立坐标系;
B
dB
L
o
Idl
er
L 4r 2
2.分割电流元; 3. 确定电流元的磁场
dB
0 4
Id
l
r
r3
4.求 B 的分量 Bx 、By 、Bz ;
5.由 B Bx2 By2 Bz2 求总场。
9
例1:一段有限长载流直导线,通有电流为 I ,求距 a 处
的 P 点磁感应强度。 解: 分割电流元
l 2
dB
0 4
Idl sin
r2
l actg( ) actg
dl a csc2 d
r a csc
Idl
lr
o
I
1
a
dB
Px
dB
0 4
Ia
csc 2 sin d a 2 csc 2
0 I sin d 4 a
B
dB
2
1
0 I sin d 4a
f L
q B
v
当运动电荷速度与磁场方向垂直时受到洛伦兹力 fL 最大。
定义:磁感应强度
大小:B
运动电荷受到的最大洛仑兹力 电荷电量 电荷运动速度
6
B fL max qv
方向:小磁针在该点平衡时N 单位:特斯拉(T)。
极的指注向意。:B的大小和方
向是分别定义的;
四、毕奥—萨伐尔定律
研究一段电流元产生磁感应强度的规律。
N
/
A2
)
真空中的磁导率
dB
Idl
•方 为向I:dlI与dlr之r间的的方夹向角。。
r
dB 的方向垂直于Idl和r 所形
成的平面。
一段载流导线产生的磁场:B
dB
L
o
Idl
er
L 4r 2
8
直角坐标系:
Bx
dBx ,
By
dBy , Bz
dBz
B Bxi By j Bzk , B Bx2 By2 Bz2
恒定磁场—在空间的分布不随时间变化的磁场。 注意:无论电荷是运动还是静止,它们之间都存在库仑 相互作用,但只有运动着的电荷才存在着磁相互作用。
5
三、磁感应强度
描述磁场性质的基本物理量。
q
v
B
1.磁感应强度的定义
当把运动电荷放在磁场中后,
它会受到一种与其速度有关的力,
这个力称为洛仑兹力。
当电荷运动速度与磁场方向一 致时电荷受力为零。
B
B 1
B 2
B 3
I 0
R
(1
3 I
) 0 2 6R
15
例5:计算组合载流导体在 o 点的磁感应强度。
解:o 点 B 由三段载流导体产生。 a
Bo Bab Bbc Bcd
规定垂直纸面向里为正向,
b
R cd
Bo
B ab
Bbc
0I 4R
0 I
4R
0 I
4R
1
1
例6:一正方形载流线圈边长为 b,通有电流为 I,求正
磁感应强度 dB 为:
dB
0Idl 4r 2
,
dB ' dB'
Idl
由对称性可知,B 0, B Bx2 B2 B x
B dB x dB sin
sin R
B
dB sin
2R 0
0I 4r 2
Rdl r
0IR 4r 3
2R dl
0
2
r 0 IR 2
x2 R2
3/2
Ib
cI d
的磁场:
I
B
0
(cos 00 cos 300 )
1200
300
R
o
1 4 R sin 300
0
I
(1
3)
垂直纸面向里
2 R 2
cd段:B3
4
I 0
R sin
300
(cos 150 0
cos1800 )
I
0 (1
2 R
3) 2
圆弧bc 产生的磁场
B2
0I
2R
1 3
0I
6R
垂直纸面向里
13
B
2
0IR2
x2 R2
3/ 2
讨论:
R
Io
B
xP
x
1.载流圆环环心处 x = 0;
有:B o
0 I
2R
2.圆弧电流中心处
B
R
I
o
有: Bo
0I
2R
2
0I 4R
R O B
14
例4:一根无限长导线通有电流I,中部弯成圆弧形, 如图所示。求圆心o点的磁感应强度B。
解:直线段ab在o点产生 a
电流元 Idl :
•大小:Idl
Idl P
•方向:线元上通过的电流的方向。
r
表述:电流元
dB
4Id0 lI在dlr空3间rP点4产0生Id的lr磁2 e场r
dB为:
7
dBr的4方0向Id:lr从3 r电流4元0所Id在lr位2 e置r 指向场点IdPl。
P
r
dB
•大小o:dBo1c2440Id1l 0rs2i7n(
2
磁场 磁感应强度 毕奥—萨伐尔定律
3
一、磁的基本现象
I
S
N
NS
S
N
电与磁之间存在着内在的联系。
安培“分子环流假说”: 一切磁现象都起源于电流。
NI F
S
总结:一切磁现象都可以归结为运动电荷(即电流) 之间的相互作用。磁力是电荷之间的另一种力。
4
二、磁场
磁铁和运动电荷(电流)会在周围空间激发场---磁场。 磁场的基本性质:对运动电荷(电流)有力的作用。 磁场是一种物质, 其物质性体现在: 1)磁场对磁铁、对电流、对运动电荷均有作用力; 2)载流导体在磁场中移动时,磁场的作用力对它作功。 3)变化的磁场在空间传播,表明磁场具有动量。
稳恒磁场
1
前言 静止的电荷周围—电场。 运动的电荷周围—电场和磁场。 主要内容: 1.描述磁场的基本物理量——磁感应强度。
2.反映磁场性质的两条定理——磁场的高斯定理和安 培环路定理。
3.磁场对运动电荷、载流导线的作用——洛仑兹力, 安培力和磁力矩。 4.磁介质的性质。 磁现象与电现象有很多相似之处,但要注意不同之处。
0
B 0
a
P
dB
Px
I
RP
I 11
例2:一宽为 a 无限长载流平面,通有
电流 I , 求距平面左侧为 b 与电流共
面的 P 点磁感应强度 B 的大小。
解:以 P 点为坐标原点,向右为坐 标正向;
dI
I
分割电流元为无限多宽为 dx
的无限长载流直导线;
电流元电流 dI I dx a
o P B x
