初中数学常见模型之蚂蚁行程
蚂蚁行程模型

蚂蚁行程模型模型 立体图形展开的最短路径模型分析上图为无底的圆柱体侧面展开图,如果蚂蚁从点A 沿圆柱体表面爬行一周,到点B 的最短路径就是展开图中AB '的长,22AB AA A B ''''=+,做此类题目的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
模型实例例1有一圆柱形油罐,如图所示,要以A 点环绕油罐建梯子,正好到A 点的正上方B 点,已知油罐的底面周长为12m ,高AB 为5m ,问所建梯子最短需要多少米?解答:假设将圆柱体的侧面沿AB 剪开,铺平得到如图所示的长方形ABDC , 则AB=DC=5m ,AC=BD=12m ,∠BAC=∠C=∠CDB=∠B= 90° 因此沿AD 建梯子,梯子最短在△ACD 中,由勾股定理得AD 2=AC 2+CD 2=122+52=132, 解得AD=13m答:建梯子最短需要13米。
例2:如图,已知圆锥的母线长OA=8,底面圆的半径r=2.若一只蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到了A点,求蚂蚁爬行的最短路线的长.(结果保留根式)解答:小虫爬行的最短路线的长是圆锥的展开图的扇形的弧所对的弦长,例3:已知长方体的长、宽、高分别为:30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)解答:(1)展开前面右面由勾股定理得;(2)展开前面上面由勾股定理得;(3)展开左面上面由勾股定理得.,最短路程长为.1、有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离。
解答:AC的长就是蚂蚁爬行的最短距离.C,D分别是BE,AF的中点...因此,本题正确答案是:16cm.2、如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B解答:沿过A点和过B点的母线剪开,展成平面,连接AB则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程,,,,由勾股定理得:,因此,本题正确答案是:10.3、如图,桌上有个圆柱形玻璃杯,高为12 cm ,底面周长18 cm ,在杯内壁离杯口 3 cm 的 A 处有一滴蜂蜜,一只小虫从桌上爬至杯子外壁,当它正好爬至蜂蜜相对方向离桌面 3 cm 的 B 处时,突然发现了蜂蜜.问小虫怎样爬去吃蜂蜜最近? 它至少爬多少路才能到达蜂蜜所在的位置?解答:按如图所示的方向 B → C →A( 其中MNPQ 为圆柱的侧面展开图, A 与 A ′关于MQ 对称) ,小虫爬的路程为BC + CA =BA ′= 15cm .4、已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A,另一个小蚂蚁也从C点出发,绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如图所示.若沿OA剪开,则得到圆锥侧面展开图为()答案此题答案为:C.解:根据题意可知,两只蚂蚁一只从C到A,一只从C到B,选项B中第二只蚂蚁的终点不是点B,故排除B选项;第一只蚂蚁沿圆锥的前面从C到A,故路线AC是在展开图的左侧的线段,排除D 选项;第二只蚂蚁经过OA从C到B,所以展开图对称轴OB的两面都有路线,故排除A 选项.故选C.5、如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,解答:将正方体展开,右边与后面的正方形与前面正方形放在一个面上,展开图如图所示,此时AB最短,,因此,本题正确答案是:.6、如图是一个边长为6的正方体木箱,点Q在上底面的棱上,,一只蚂蚁从P点出发沿木箱表面爬行到点Q,求蚂蚁爬行的最短路程.解答:如图所示,,,,.答:蚂蚁爬行的最短路程是10.7、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?解答:将台阶展开,如下图,因为,,所以,所以,所以蚂蚁爬行的最短线路为13cm.答:蚂蚁爬行的最短线路为13cm.。
模型46 勾股定理之蚂蚁行程、弦图模型(解析版)

1.平面展开-最短路径问题(1)平面展开﹣最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.(2)关于数形结合的思想,勾股定理及其逆定理它们本身就是数和形的结合,所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型.例.如图所示,有一正方体纸盒,在点C1处有一只小虫,它要爬到点A吃食物.应该沿着怎样的路线才能使行程最短?解:如图,把侧面或上面展开与正面组成一矩形,连接AC1,则AC1就是行程最短的路线.2.赵爽弦图模型我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图1),这个正方形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2.称为勾股定理.把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论证明:由图2得,大正方形面积=4×=(a+b)2,整理得b2+c2+2ab=2ab+c2,∴c2=a2+b2,即直角三角形两直角边的平方和等于斜边的平方.例题精讲考点一:行程最短问题【例1】.如图,有一个圆柱,它的高等于16cm,底面半径等于4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是20 cm.(π取3)解:将圆柱体展开,连接A、B,根据两点之间线段最短,根据题意可得:AC是圆周的一半,∴AC=×2×4π=12,∴AB==20cm.变式训练【变式1-1】.如图,圆锥的底面圆的半径为10cm,母线长为40cm,C为母线PA的中点,一只蚂蚁欲从点B处沿圆锥的侧面爬到点C处,则它爬行的最短距离是20cm.解:由题意知,底面圆的直径AB=20,故底面周长等于20π设圆锥的侧面展开后的扇形圆心角为n°∵根据底面周长等于展开后扇形的弧长得,20π=,解得n=90°∴展开图中扇形圆心角=90°,作CE⊥PB于E,则CE=PE=10,BE=40﹣10,∵根据勾股定理求得它爬行的最短距离是=20cm∴蚂蚁爬行的最短距离为20cm【变式1-2】.如图,一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是15cm.解:由题意可得,当展开前面和右面时,最短路线长是:==15(cm);当展开前面和上面时,最短路线长是:==7(cm);当展开左面和上面时,最短路线长是:=(cm);∵15<7<,∴一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是15cm,故答案为:15.【变式1-3】.如图是一个三级台阶,它的每一级长、宽、高分别是2米、0.3米、0.2米,A,B是这个台阶上两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是 2.5米.解:三级台阶平面展开图为长方形,长为2,宽为(0.2+0.3)×3,则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B点最短路程为x,由勾股定理得:x2=22+[(0.2+0.3)×3]2=2.52,解得x=2.5.考点二:弦图模型的应用【例2】.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形EFGH拼成的大正方形ABCD.若AE=5,AB=13,则中间小正方形EFGH的面积是49.解:∵AE=5,AB=13,∴BF=AE=5,在Rt△ABF中,AF==12,∴小正方形的边长EF=12﹣5=7,∴小正方形EFGH的面积为7×7=49.故答案为:49.变式训练【变式2-1】.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=2.5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是15,则这个风车的外围周长是38.解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,AC=y,则x2=4y2+2.52,∵△BCD的周长是15,∴x+2y+2.5=15则x=6.5,y=3.∴这个风车的外围周长是:4(x+y)=4×9.5=38.故答案是:38.【变式2-2】.如图,在弦图中,正方形ABCD的对角线AC与正方形EFHI的对角线EH交于点K,对角线AC交正方形EFHI于G,J两点,记△GKH面积为S1,△JIC面积为S2,若AE=12,CD=4,则S1+S2的值为16.解:由题意可得,AF=CI,∠AFG=∠CIJ=90°,FH∥EI,∵∠AGF=∠HGK,∠IJC=∠KJE,∵FH∥EI,∴∠HGK=∠KJE,∴∠AGF=∠IJC,在△AFG和△CIJ中,,∴△AFG≌△CIJ(AAS),∴FG=IJ,∵四边形EFHI为正方形,∴EI﹣IJ=FH﹣FG,即HG=EJ,在△GHK和△JEK中,,∴△GHK≌△JEK(AAS),∴HK=EK,即点K为正方形EFHI的中心,如图,过点K作KM⊥FH于点M,∵AE=12,CD=4,∴BF=12,AD=,在Rt△ADE中,由勾股定理得DE==4,∴AF=DE=4,EF=AE﹣AF=12﹣4=8,则FH=8,KM=4,设GH=a,FG=b,则a+b=FH=8,∴=,==2b,∴S1+S2=2a+2b=2(a+b)=16.故答案为:16.1.如图所示,一只小蚂蚁从棱长为1的正方体的顶点A出发,经过每个面的中心点后,又回到A点,蚂蚁爬行最短程S满足()A.5<S≤6B.6<S≤7C.7<S≤8D.8<S≤9解:正方体展开图形为:则蚂蚁爬行最短程S=5+=5+.即6<S≤7.故选:B.2.如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan ∠ADE的值为()A.B.C.D.解:设小正方形EFGH面积是a2,则大正方形ABCD的面积是13a2,∴小正方形EFGH边长是a,则大正方形ABCD的边长是a,∵图中的四个直角三角形是全等的,∴AE=DH,设AE=DH=x,在Rt△AED中,AD2=AE2+DE2,即13a2=x2+(x+a)2解得:x1=2a,x2=﹣3a(舍去),∴AE=2a,DE=3a,∴tan∠ADE==,故选:C.3.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是()A.12B.15C.20D.30解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,因为S1+S2+S3=60,所以4m+S2+S2+S2﹣4m=60,即3S2=60,解得S2=20.故选:C.4.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么tanθ的值是()A.B.C.D.解:由已知条件可知,小正方形的边长为2,大正方形的边长为.设直角三角形中较小边长为x,则有(x+2)2+x2=()2,解得x=5.则较长边的边长为x+2=5+2=7.故tanθ==.故选:B.5.赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示).某次课后服务拓展学习上,小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1,大正方形ABCD的面积为S2,若DI=2,CI=1,S2=5S1,则GI的值是()A.B.C.D.解:如图,连接DG,∵赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形,∴AE=BF=CG=DH,AF=BG=CH=DE,CH⊥DE,∵DI=2,CI=1,∴CD=DI+CI=2+1=3,∵大正方形ABCD的面积为S2,∴S2=CD2=32=9,又∵小正方形EFGH的面积为S1,S2=5S1,∴S1=,∴EF=FG=GH=HE=,∵将EG延长交CD于点I,∴∠HGE=45°,在Rt△EHG中,由勾股定理得:EG==,设AE=BF=CG=DH=x,则AF=BG=CH=DE=x+,在Rt△CDH中,由勾股定理得:CD2=DH2+CH2,即9=x2+(x+)2,解得:x1=,x2=﹣(不合题意,舍去),即AE=BF=CG=DH=x=,∴DH=EH=,∴CH垂直平分ED,∴DG=EG=,∴∠DGH=∠HGE=45°,∴∠DGE=45°+45°=90°,∴∠DGI=90°,在Rt△DGI中,由勾股定理得:GI===,故选:A.6.如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为,高为5,则蚂蚁爬行的最短距离为13.解:因为圆柱底面圆的周长为2π×=12,高为5,所以将侧面展开为一长为12,宽为5的矩形,根据勾股定理,对角线长为=13.故蚂蚁爬行的最短距离为13.7.如图,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A点出发,绕侧面一周又回到A点,它爬行的最短路线长是.解:由题意知,底面圆的直径为2,故底面周长等于2π.设圆锥的侧面展开后的扇形圆心角为n°,根据底面周长等于展开后扇形的弧长得,2π=,解得n=90°,所以展开图中圆心角为90°,根据勾股定理求得到点A的最短的路线长是:==4.8.将四个全等的直角三角形分别拼成正方形(如图1,2),边长分别为6和2.若以一个直角三角形的两条直角边为边向外作正方形(如图3),其面积分别为S1,S2.则S1﹣S2=12.解:设四个全等的直角三角形的两条直角边分别为a,b(a>b),根据图1得:a+b=6,根据图2得:a﹣b=2,联立解得:,∴S1=16,S2=4,则S1﹣S2=12.故答案为:12.9.如图1,四个全等的直角三角形围成一个大正方形,中间是一个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.连接四条线段得到如图2的新的图案,如果图1中的直角三角形的长直角边为5,短直角边为3,图2中阴影部分的面积为S,那么S的值为16.解:由题意作出如下图,得AC=,BD=2,AB=CD,△ABD是直角三角形,则大正方形面积=AC2=34,△ADC面积=(5×3﹣2×3)=4.5,阴影部分的面积S=34﹣4×4.5=16,故答案为:16.10.如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB==cm;(2)展开底面右面由勾股定理得AB==5cm;所以最短路径长为5cm,用时最少:5÷2=2.5秒.11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E 的边长为7cm,则图中五个正方形A、B、C、D、E的面积和为98cm2.解:设正方形A、B、C、D的边长分别是a、b、c、d,则正方形A的面积=a2,正方形B的面积=b2,正方形C的面积=c2,正方形D的面积=d2,又∵a2+b2=x2,c2+d2=y2,∴正方形A、B、C、D、E的面积和=(a2+b2)+(c2+d2)+72=x2+y2+72=72+72=98(cm2).即正方形A,B,C,D、E的面积的和为98cm2.故答案为:98.12.我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).图2为小明同学根据弦图思路设计的,在正方形ABCD中,以点B为圆心,AB为半径作,再以CD为直径作半圆交于点E,若边长AB=10,则△CDE的面积为20.解:如图,取CD的中点F,连接BF、BE、DE、EF,由题意可得,FE=FC,BE=BC,∴BF是EC的垂直平分线,∴∠FBC+∠BCE=90°,∵∠BCD=90°,∴∠DCE+∠BCE=90°,∴∠FBC=∠DCE,又∵∠BCF=∠CED=90°,∴△BCF∽△CED,∴==,∵BC=CD=AB=10,CF=5,∠BCF=90°,∴BF===5,∴==,解得:CE=4,ED=2,=×CE×DE=×4×2=20,∴S△CDE故答案为:20.13.图1是一个勾股定理演示教具的正面示意图,当它倒过来时,大正方形中的全部墨水恰能注满两个小正方形.王老师有一个内长为11寸,内宽为9寸的木质盒子(如图2).现要自制一个这样的教具(由三个正方形和一个直角三角形组成),使得教具恰好摆入这个盒子中,以便保护和携带(如图3所示,A,B,C,D,E五点均紧贴盒子边缘,教具的厚度等于木盒的内高).此时盒子的空间利用率为.解:如图,过点A作AM⊥EG的延长线于点M,过点F作FR⊥GH于点R,过点B作BN⊥GH,过点F作FN∥GH,延长GH交CK于K,∵四边形AGFL、DEGH、BCHF均为正方形,∴AG=FG,BF=FH=CH,EG=GH,∠AGF=∠BFH=90°=∠AMG=∠FRG=∠BNF =∠CKH,∴∠AGM+∠FGM=∠FGR+∠FGM,∴∠AGM=∠FGR,∴△AGM≌△FGR(AAS),∴AM=FR,GM=GR,同理,△BFN≌△HFR≌△CHK(AAS),∴FR=FN=HK=AM,BN=HR,设AM=x,BN=y,AM=FR=z,则FR=FN=HK=AM=x,BN=HR=y,由勾股定理得:FH2=x2+y2,FG2=x2+z2,GH=y+z,根据题意,得:FH2+FG2=GH2,∴x2+z2+x2+y2=(y+z)2,∴x2=yz①,∵AM+GR+RH+HK=9,BN+FR+EG=11,∴2x+y+z=9②,x+2y+z=11③,②﹣③,得:x﹣y=﹣2,即y=x+2④,②×2﹣③,得:3x+z=7,即z=7﹣3x⑤,将④⑤代入①,得:x2=(x+2)(7﹣3x),解得:x1=2,x2=﹣(舍去),∴y=4,z=1,∴GH=5,FG2=5,FH2=20,∴勾股定理演示教具的正面面积为:S=25+5+20+××2=55,∵教具的厚度等于木盒的内高,∴盒子的空间利用率为:=,故答案为:.14.我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形,如图,若拼成的大正方形为正方形ABCD,面积为9,中间的小正方形为正方形EFGH,面积为2,连接AC,交BG于点P,交DE﹣S△CGP=,③DH+HC=4,④HC=2+,于点M,①△CGP≌△AEM,②S△AFP以上说法正确的是①③④.(填写序号)解:∵Rt△BCG≌Rt△DAE,∴CG=AE,∠CGP=∠AEM,∵CH∥AF.∴∠GCP=∠MAE,∴△CGP≌△AEM(ASA),=S△AEM,CP=ME,∴S△CGP﹣S△CGP=S四边形MEFP∴S△AFP∵HE=GF,∴HM=PF,=S四边形MHGP=S正方形EFGH=1,∴S四边形MEFP﹣S△CGP=1,∴S△AFP∵DH2+CH2=DC2=9,∴(DH+CH)2=DH2+CH2+2DH•CH=9+2DH•CH,∵CH﹣DH=HG,∴(CH﹣DH)2=HG2=2,∴CH2+DH2﹣2DH•CH=2,∴2DH•CH=7,∴(DH+CH)2=9+7=16,∴DH+CH=4,∵CH﹣DH=,∴HC==2+,故答案为:①③④.15.一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,(1)请问:长为12.5dm的铁棒能放进去吗?(1)如果有﹣只蚂蚁要想从D处爬到C处,求爬行的最短路程.解:(1)如图1,连接BD,∵AD=12,AB=4,∴BD2=AD2+AB2=122+42=160,∴CD===13(dm).∵13dm>12.5dm,∴长为12.5dm的铁棒能放进去;(2)如图2所示,CD==dm.如图3所示,CD==dm,如图4所示,CD==dm,∵>>,∴爬行的最短路程是dm.16.如图①,美丽的弦图,蕴含着四个全等的直角三角形.(1)如图①弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a.较短的直角边为b,斜边长为c,可以验证勾股定理;(2)如图②,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、2、S3,若S1+S2+S3=16,则S2=.(1)证明:,另一方面,即a2﹣2ab+b2=c2﹣2ab,则a2+b2=c2;(2)解:设正方形MNKT的面积为x,八个全等的直角三角形的面积均为y,∵S1+S2+S3=16,∴S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=12y+3x=16,∴4y+x=,∴S2=4y+x=.故答案为:.17.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是:大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式c2=,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.解:(1)在Rt△ABC中,由面积的两种算法可得:,解得:CD=.(2)在Rt△ABD中AD2=42﹣x2=16﹣x2,在Rt△ADC中AD2=52﹣(6﹣x)2=﹣11+12x﹣x2,所以16﹣x2=﹣11+12x﹣x2,解得=.。
初二数学蚂蚁绕圆柱问题

初二数学蚂蚁绕圆柱问题蚂蚁绕圆柱问题是初中数学中一个经典的几何问题。
它考察了学生对立体几何、视角和空间方向的理解与运用能力。
这个问题可以通过应用几何思维和空间想象力来解决,让我们一起来进行探讨。
问题描述:假设有一个半径为r的圆柱体,高度为h。
在圆柱体的最上方,有一只蚂蚁。
蚂蚁以固定速度匀速沿着圆柱体的表面爬行,它同时在水平方向和垂直方向都保持匀速运动。
当蚂蚁从最上面开始运动时,求它在整个圆柱体表面上总共走过的路程。
解题思路:要解决这个问题,我们需要先了解蚂蚁爬行的路径形式。
由于蚂蚁同时以匀速在水平和垂直方向移动,所以我们可以将问题简化为一个二维平面上的运动问题。
首先考虑在水平方向上的运动。
当蚂蚁从最上面开始向下移动时,它会遍历整个圆柱底部边缘的距离为2πr。
而当它再次回到圆柱顶部时,它在水平方向上又遍历了一次2πr的距离。
所以蚂蚁在水平方向上走过的总路程为4πr。
接下来考虑在垂直方向上的运动。
蚂蚁从最上面开始向下移动,经过了整个圆柱体的高度h。
当它再次回到最顶端时,它在垂直方向上又走过了一段等于h的距离。
所以蚂蚁在垂直方向上走过的总路程为2h。
综合考虑水平和垂直两个方向,我们可以得出结论:蚂蚁在整个圆柱体表面上总共走过的路程为4πr+2h.实际应用:这个问题看似简单,但涉及到几何思维和空间想象力。
学生通过解决这个问题能够锻炼自己对立体几何概念的理解和运用能力。
此外,这个问题也有一定的实际应用价值。
例如,在建筑设计中,我们需要计算建筑物外墙表面材料或者油漆需要多少来做预算,并且还需要考虑施工队伍和材料供应商的配合等实际因素。
通过解决这个问题,学生可以培养几何思维、空间想象力和创新能力。
同时,因为它涉及到多个数学概念的综合应用,也有助于学生全面理解和掌握这些数学概念。
拓展思考:除了蚂蚁绕圆柱体问题,我们还可以进一步讨论其他几何问题。
例如,在三维空间中如何计算球体、锥体或者棱柱的表面积和体积等等。
总结回顾:在初二数学中,蚂蚁绕圆柱问题是一个经典而有趣的几何问题。
专题24 勾股定理中的蚂蚁爬行模型--2024年中考数学核心几何模型重点突破(学生版)
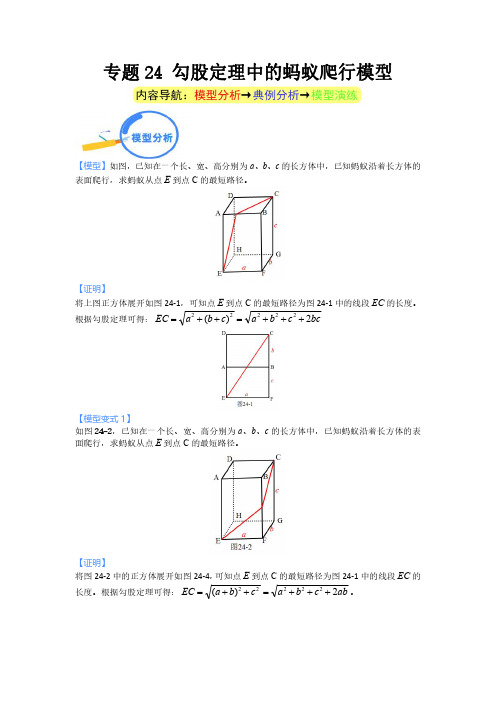
专题24勾股定理中的蚂蚁爬行模型【模型】如图,已知在一个长、宽、高分别为a 、b 、c 的长方体中,已知蚂蚁沿着长方体的表面爬行,求蚂蚁从点E 到点C 的最短路径。
【证明】将上图正方体展开如图24-1,可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。
根据勾股定理可得:bcc b a c b a EC 2)(22222+++=++=【模型变式1】如图24-2,已知在一个长、宽、高分别为a 、b 、c 的长方体中,已知蚂蚁沿着长方体的表面爬行,求蚂蚁从点E 到点C 的最短路径。
【证明】将图24-2中的正方体展开如图24-4,可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。
根据勾股定理可得:ab c b a c b a EC 2)(22222+++=++=。
【模型变式2】如图24-3,已知在一个长、宽、高分别为a 、b 、c 的长方体中,已知蚂蚁沿着长方体的表面爬行,求蚂蚁从点E 到点C 的最短路径。
【证明】将图24-3中的正方体展开如图24-5,可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。
根据勾股定理可得:ac c b a b c a EC 2)(22222+++=++=。
【例1】如图,长方形的长为15,宽为10,高为20,点B 离点C 的距离为5,蚂蚁如果要沿着长方形的表面从点A 爬到点B ,需要爬行的最短距离是()A .35B .1055C .25D .21【例2】如图,在圆柱的截面ABCD中,AB=16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为_____.【例3】如图,一个长方体形盒子的长、宽、高分别为4cm,4cm,6cm(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?(2)若将一根木棒放进盒子里并能盖上盖子,则能放入该盒子里的木棒的最大长度是多少cm?(结果可保留根号)一、单选题1.如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体的对角顶点G处,若AB=3cm,BC=5cm,BF=6cm,则最短的爬行距离是()A.10B.14C D2.如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的A 处,则蚂蚁到达蜂蜜的最短距离是()A .15cmB .16cmC .17cmD .18cm3.如图所示,圆柱的高AB =3,底面直径BC =6,现在有一只蚂蚁想要从A 处沿圆柱侧面爬到对角C 处捕食,则它爬行的最短距离是()A .B .C .9D .4.如图是一个三级台阶,它的每一级的长,宽,高分别是20dm,3dm,2dm ,A 和B 是这个台阶相对的端点,点A 处有一只蚂蚁,想到B 处去吃食物,则这只蚂蚁爬行的最短距离为()A .25dmB .26dmC .24dmD .27dm5.图,长方体的长为8,宽为10,高为6,点B 离点C 的距离为2,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是()A .B .C .D .6.如图,在长方体透明容器(无盖)内的点B 处有一滴糖浆,容器外A 点处的蚂蚁想沿容器壁爬到容器内吃糖浆,已知容器长为6cm ,宽为4cm ,高为3cm ,点A 距底部2cm ,请问蚂蚁需爬行的最短距离是(容器壁厚度不计)A .B .10cmC .D .二、填空题7.如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是_____.8.如图,一只蚂蚁沿长方体的表面从顶点A 爬到另一顶点M ,已知AB =AD =2,BF =3.这只蚂蚁爬行的最短距离_____.9.如图,圆柱形容器外壁距离下底面3cm 的A 处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm 的B 处的米粒,若圆柱的高为12cm ,底面周长为24cm .则蚂蚁爬行的最短距离为_______.10.如图,圆柱形玻璃杯高为12cm 、底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为_______cm .11.如图一只蚂蚁从长为4cm ,宽为3cm ,高为2cm 的长方体纸箱A 点沿纸箱爬到B 点,那么它爬行的最短路线的长是_________cm12.在底面周长为6cm ,高为3cm 的圆柱体侧面上,用一条无弹性的丝带从A 至C 按如图所示的圈数缠绕,则丝带的最短长度为_________.三、解答题13.如图,长方体的透明玻璃鱼缸,假设其长80cm AD =,高60cm AB =,水深为40cm AE =,在水面上紧贴内壁G 处有一鱼饵,G 在水面线EF 上,且60cm EG =;一小虫想从鱼缸外的A 点沿壁爬进鱼缸内G 处吃鱼饵,求小动物爬行的最短距离.(鱼缸厚度忽略不计)14.(1)如图1,长方体的长、宽、高分别为3m ,2m ,1m ,如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点C ,那么所用细线最短需要______m ;(2)如图2,长方体的棱长分别为6cm AB BC ==,114cm AA =,假设昆虫甲从盒内顶点1C 开始以1cm/s 的速度在盒子的内部沿棱1C C 向下爬行,同时昆虫乙从盒内顶点A 以相同的速度在盒内壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?15.如图,长方体盒子(无盖)的长、宽、高分别是12cm ,8cm ,30cm .(1)在AB 的中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)若此长方体盒子有盖,则能放入木棒的最大长度是多少?16.如图①,长方体长AB 为8cm ,宽BC 为6cm ,高BF 为4cm .在该长体的表面上,蚂蚁怎样爬行路径最短?(1)蚂蚁从点A 爬行到点G ,且经过棱EF 上一点,画出其最短路径的平面图,并标出它的长.(2)设该长方体上底面对角线EG 、FH 相交于点O (如图②),则OE =OF =OG =OH =5cm .①蚂蚁从点B 爬行到点O 的最短路径的长为cm ;②当点P 在BC 边上,设BP 长为a cm ,求蚂蚁从点P 爬行到点O 的最短路的长(用含a 的代数式表示).17.如图,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A ,C 嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是______.(2)如图①,求该长度最短的金属丝的长.(3)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝最短长度是多少?18.在每个小正方形的边长为1的网格中,每个小正方形的顶点称为格点.我们将从一个格5.....(1)在图15(2)在图2中有一只电子小马从格点M出发,经过跳马变换到达与其相对的格点N,则最少需要跳马变换的次数是次.的正方形网格中,一只电子小马从格点S经过若干次跳马变换到达(3)如图3,在2020与其相对的格点T,则它跳过的最短路程为.19.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,为了吃到蜂蜜,蚂蚁从外壁A处沿着最短路径到达内壁B处.(1)右图是杯子的侧面展开图,请在杯沿CD上确定一点P,使蚂蚁沿A-P-B路线爬行,距离最短.(2)结合右图,求出蚂蚁爬行的最短路径长.20.现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).(1)求线段BG的长;(2)现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)。
勾股定理的应用蚂蚁路径最短问题

勾股定理的应用蚂蚁路径最短问题一、勾股定理的应用蚂蚁路径最短问题蚂蚁是一种非常有趣的昆虫,它们在寻找食物的过程中,会形成一条长长的队伍,这条队伍就像一条直线一样,非常整齐。
那么,为什么蚂蚁会形成这样的队伍呢?这与勾股定理有着密切的关系。
勾股定理是古希腊数学家毕达哥拉斯发现的一个定理,它告诉我们:直角三角形的斜边的平方等于两直角边的平方和。
这个定理在很多领域都有着广泛的应用,比如建筑、地理、物理等。
而在蚂蚁寻找食物的过程中,勾股定理也起到了关键的作用。
二、勾股定理在蚂蚁寻找食物中的应用1.1 蚂蚁的行进路线规划蚂蚁在寻找食物的过程中,会先释放一种叫做信息素的物质,这种物质可以帮助它们找到食物的方向。
当一只蚂蚁找到了食物后,它会回到巢穴,并释放更多的信息素。
其他蚂蚁在接收到这些信息素后,就会沿着这条路线前进,最终找到食物。
在这个过程中,蚂蚁需要选择一条最优的行进路线。
而这条路线就是由勾股定理来决定的。
具体来说,假设有一只蚂蚁A从巢穴出发,它需要走一段距离才能释放信息素。
这段距离可以看作是一个直角三角形的斜边。
那么,根据勾股定理,这段距离的平方等于A到巢穴的距离和A到食物的距离的平方和。
因此,A会选择一条使得这个等式成立的路线,这样才能使得整个队伍的行进速度最快。
1.2 蚂蚁之间的协作在蚂蚁寻找食物的过程中,并不是每只蚂蚁都能独立地找到食物。
有时候,它们需要和其他蚂蚁一起合作才能找到食物。
这时候,勾股定理同样发挥了重要的作用。
假设有一只蚂蚁B和一只蚂蚁C同时找到了食物。
那么,它们需要将食物带回巢穴。
在这个过程中,B和C之间需要保持一定的距离,以免发生碰撞。
这个距离也可以看作是一个直角三角形的斜边。
根据勾股定理,这个距离的平方等于B到食物的距离和C到食物的距离的平方和减去(B到C的距离)^2。
因此,B和C需要选择一条使得这个等式成立的路线,这样才能保证它们能够安全地将食物带回巢穴。
三、结论通过以上分析,我们可以看出,勾股定理在蚂蚁寻找食物的过程中发挥了非常重要的作用。
初中数学解题模型专题讲解12---蚂蚁行程

初中数学解题模型专题讲解初中数学解题模型专题讲解专题12 12 蚂蚁行程蚂蚁行程蚂蚁行程模型模型 1 1 立体图形展开的最短路径立体图形展开的最短路径模型分析上图为无底的圆柱体侧面展开图,如图蚂蚁从点 A 沿圆柱表面爬行一周,到点 B 的最短路径就是展开图中 AB′的长。
做此类题目的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之 和大于第三边”准确找出最短路径。
模型实例模型实例例 1.有一圆柱体油罐,已知油罐底面周长是 12m,高 AB 是 5m,要从点 A 处 开始绕油罐一周建造房子,正好到达 A 点的正上方 B 处,问梯子最短有多长?例 2.如图,一直圆锥的母线长为 QA=8,底面圆的半径r =2,若一只小蚂蚁从 A 点出发,绕圆锥的侧面爬行一周后又回到 A 点,则蚂蚁爬行的最短路线长是多少?例3.已知长方体的长、宽、高分别为 30cm、20cm、10cm,一只蚂蚁从 A处出发到 B 处觅食,求它所走的最短路径。
(结果保留根号)模型练习模型练习1.有一个圆锥体如图,高 4cm,底面半径 5cm,A 处有一蚂蚁,若蚂蚁欲沿侧 面爬行到 C 处,求蚂蚁爬行的最短距离。
2.如图,圆锥体的高为 8cm,底面周长为 4cm,小蚂蚁在圆柱表面爬行,从 A 点到 B 点,路线如图,则最短路程是多少?3.桌上有一个圆柱形无盖玻璃杯,高为 12 厘米,底面周长 18 厘米,在杯口 内壁离杯口距离 3 厘米的 A 处有一滴蜜糖,一只小虫 22 杯子外壁,当它正好在蜜糖相对方向离桌面 3 厘米的 B 处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在的位置。
4.已知 O 为圆锥顶点,OA、OB 为圆锥的母线,C 为 OB 的中点,一只小蚂蚁 从点 C 开始沿圆锥侧面爬行到点 A,另一只小蚂蚁也从 C 点出发绕着圆锥侧面爬行到点 B,它们所爬行的最短路线的痕迹如图所示,若沿 OA 剪开,则得到的圆锥侧面展开图为 ( )5.如图,一只蚂蚁沿着边长为到点 B,如果它运动的路径是6.如图是一个边长为 6 的正蚂蚁从 P 点出发沿木箱表面爬7.如图,是一个三级台阶,边长为 2 的正方体表面从点 A 出发,经过 路径是最短的,则最短距离为多少?的正方体木箱,点 Q 在上底面的棱上,AQ=2表面爬行到点 Q,求蚂蚁爬行的最短路线。
蚂蚁怎样走最近 (题型全面)

B
A
◆在长30cm、宽50 cm、高40 cm的木箱中,如果在箱 内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要 爬多远?
.B
C
40
.A
50 30
D
.B
40
.A
C
30 50
B
40
A C
D
30
D
50
80 40 8000 图①
2 2
C
40
50
.B
B
50
. A
C
30
D
2
C
40
30 90 9000 A 30
B
A
以小组为单位, 研究蚂蚁爬行的最 短路线
A
B
A’
d
B
A’
B
A
A
蚂蚁A→B的路线
O
B B
A
A
怎样计算AB?
A’ r O B A’ B
h
侧面展开图
A
A
在Rt△AA’B中,利用勾股定理可得,
AB 2 AA2 A' B 2
其中AA’是圆柱体的高,A’B是底面圆周长的一半(π r)
若已知圆柱体高为12cm,底面半径 为3cm,π取3,则:
2
D
图②
C
40
30
.B
B
30
.A
D
C 50
C
40
D 50 70 7400
2 2
50
A
图③
小 结:
把几何体适当展开成平面图形,再利 用“两点之间线段最短”,或点到直线“垂 线段最短”等性质来解决问题。
解:AC = 6 – 1 = 5 , BC = 24 × 1 = 12, 2
北师大版八年级数学上册《蚂蚁怎样走最近》课件

A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
利用勾股定理解答最短路径问题
想一想 蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
若已知圆柱体高为12 cm,底面周长为18 cm,则:
侧面展开图
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为 x米,即AB=x米,而AC=2米,BC=1.5米, 有x2=1.52+22 ,x =2.5
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km), B组行了9×2=18(km), 又因为A,B两组相距30km, 且有242+182=302, 所以A,B两组行进的方向成直角.
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9, 在AB上取点N使AN=12, 测量MN是否是15,是,就是垂直; 不是,就是不垂直.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蚂蚁行程
模型1 立体图形展开的最短路径
模型分析
上图为无底的圆柱体侧面展开图,如图蚂蚁从点A 沿圆柱表面爬行一周。
到点B 的最短路径就是展开图中AB ′的长,22''''AB AA A B =+。
做此类题日的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
模型实例
例1.有一圆柱体油罐,已知油罐底面周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周建造房子,正好到达A 点的正上方B 处,问梯子
最短有 多长?
例2.如图,一直圆锥的母线长为QA=8,底面圆的半径2r =, 若一只小蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到A 点,则蚂蚁爬行的最短
路线长是 。
例3.已知长方体的长、宽、高分别为30cm 、20cm 、10cm ,一只蚂蚁从A 处出发到B 处觅食,求它所走的最短路径。
(结果保留根号)
热搜精练
1.有一个圆锥体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲沿侧面爬行到C处,求蚂蚁爬行的最短距离。
2.如图,圆锥体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为。
3.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长18厘米,在杯口内壁离杯口距离3厘米的A处有一滴蜜糖,一只小虫22 杯子外壁,当它正好在蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在的位置。
4.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬行到点B,如果它运动的路径是最短的,则最短距离为。
5.如图是一个边长为6的正方体木箱,点Q 在上底面的棱上,AQ=2,一只蚂蚁从P点出发沿木箱表面爬行到点Q,求蚂蚁爬行的最短路线。
6.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。
请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是多少?。
