相对论的速度变换公式
4-2 相对论速度变换公式 modified

2 ′ 1 v u / c − ⋅ dt x , = dt 1 − v2 / c2
1− β 2 . u’ 和u 之间的变换关系 y y v 1 − 2 ux c
1− β 2 同 理 , u ′z = . u’z和uz之间的变换关系 v 1 − 2 ux c uz
5/16
洛仑兹速度变换式
u = (ux , u y , uz )
x
u = u '+ v
x′
在 K′系来看,P的速度为: u ' = ( u ' x , u ' y , u ' z ) 在经典伽利略变换下,速度满足:
速度分量满足:?….
问题: 在洛仑兹坐标变换下, u 和 u’ 之间满 足什么关系?
2/16
洛仑兹速度变换
从最根本的定义出发,进行推导。
洛仑兹速度变换式讨论
d . 在洛仑兹速度变换下,光速不变。 K’系相对K系沿X轴 正向以v运动, 设在K系中, 光沿x轴传播, 即光速ux=c, uy=0, uz=0, 根据洛仑兹速度变换,
O
y K
y′
K'
v
c
O′
x′ x
ux − v c−v u′x = = 2 2 1 − v ⋅ ux / c 1 − v ⋅ c / c
例题:设想一飞船以0.80c 的速度在地球上空飞行(沿x 轴),如果在飞船上沿y方向发射一光子, 问:从地面上看,光子速度如何?
K'
解: 选择地面参考系为K系, 飞船参考系为K’系
K
v
c
∴ v = 0 .8 0 c
在飞船(K’系)中,光子速度:
v
uz ' = 0.
16-2狭义相对论时空观16-3速度变换公式解析

由洛仑兹变换:如果在S 系中物体的横向速 度为零,沿 x轴方向的速度为u,则在S′系中 观测,物体的横向速度也为零,而沿x′ 轴方 ux v 向的速度: u
x
v 1 2 ux c
第十六章 狭义相对论基础 狭义相对论基础 狭义相对论基础
由洛仑兹变换得:洛伦兹速度变换式
正变换
ux v u x v 1 2 ux c uy u y v 1 2 u x c uz u z v 1 2 u x c
考察 s' 系观测两事件: y y ' v s' s' 系同一地点B 发 s d 生两事件 发射光信号 ( x ' , t '1 ) o 接受光信号 ( x ' , t '2 )
o'
12
9 6
3
B
x' x
t1 2d c Δt t2 时间间隔 原时(固有时间):在一参考系中,同一 地点发生的两事件的时间间隔 t '。
第十六章 狭义相对论基础 狭义相对论基础 狭义相对论基础
洛伦兹首先导出洛伦兹变换,相对性 原理也是由庞加莱首先提出的,但是他们 都没有抓住同时性的相对性这一关键性、 革命性的思想。
洛伦兹和庞加莱都走近了相对论,却 没能创立相对论。只有26岁的爱因斯坦敢 于质疑人们关于时间的原始观念,坚持同 时性是相对的,才完成了这一历史的重任。
第十六章 狭义相对论基础 狭义相对论基础 狭义相对论基础
讨论
t
3
v c 时,Δt Δt 过度为牛顿力学。
4 由于同时性具有相对性,所以对不同参 考系而言,沿相对速度方向发生的同样的 两个事件之间的时间间隔是不同的,即时 间的量度是相对的。
洛伦兹速度变换

其逆变换式为:
uz
'
uz 1
1
v ux c2
2
u x
ux 'v
1
v ux c2
'
u
y
uy 1
1
v ux c2
'
2
u
z
uz ' 1 2
1
v ux c2
'
5
从相对论速度变换公式,可以得出下列结论:
⑴当速度u,v远小于光速c时,相对论速度变换公式就转化为伽利略 速度变换公式u'=u-v。说明在一般低速情况下,伽利略速度变换是 适用的,只有当u,v接近光速时,才需要相对论速度变换。
⑵相对论速度变换遵循光速不变原理。
令u' c, 解得u
u'v 1 u'v / c
cv 1 cv / c2
c
可见,对K,K'坐标系而言,光速都是c。
6
• 例:
在地面上测得两个飞船A,B分别以+0.9c和-0.9c的速度沿相 反方向飞行,如图所示,求A相对于B的速度大小。
设K系在B上,则B相对于K静止,而地面对K的速度是v=0.9c,以地面为K',则A 相对于K的速度为u'=0.9c,带入速度变换公式:
x' x vt y' y z' z t' t
推倒得速度变换公式 vpk vpk' vkk'
3
二、相对论速度变换
• 类似于伽利略变换导出速度变换公式,洛伦兹变换也可导出相对论速度变换
公式: 在K坐标系中速度表达式:
ux
dx dt ,uy
dy dt ,uz
教科版选修3-4 第6章 第4节 相对论的速度变换公式 质能关系
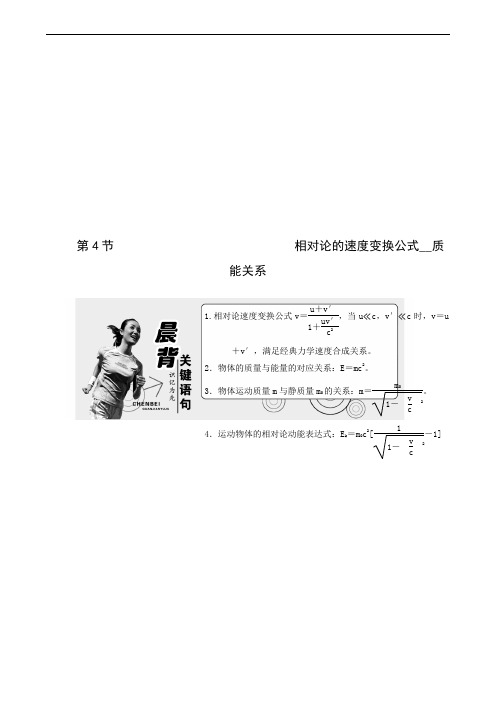
第4节相对论的速度变换公式__质能关系1.相对论速度变换公式v =u +v′1+uv′c2,当u ≪c ,v′≪c 时,v =u+v′,满足经典力学速度合成关系。
2.物体的质量与能量的对应关系:E =mc 2。
3.物体运动质量m 与静质量m 0的关系:m =m 01-v c 2。
4.运动物体的相对论动能表达式:E k =m 0c 2[11-v c2-1]v′沿着火车前进的方向相对火车运动,那么这个人相对地面的速度v 为v =u +v′1+uv′c2。
理解这个公式时请注意:(1)如果车上的人的运动方向与火车的运动方向相反,则v′取负值。
(2)如果u ≪c ,v′≪c ,这时v′uc 2可忽略不计,这时相对论的速度合成公式可近似变为v =v′+u 。
(3)如果v′与u 的方向垂直或成其他角度时,情况比较复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u′+v 的关系是( )A .u =u′+vB .u <u′+vC .u >u′+vD .以上均不正确解析:选B 按照经典的时空观,u =u′+v ,而实际上人对地面的速度按照相对论速度公式计算,u =u′+v1+u′v c2,因此u 比u′与v 之和要小,但只有在u′和v 的大小接近光速时才能观察此差别。
相对论质量和能量[自读教材·抓基础]1.质能关系式E =mc 2。
式中m 是物体的质量,E 是它具有的能量。
由此可见,物体质量越大,其蕴含的能量越大。
能量与质量成正比。
2.相对论质量 m =m 01-v 2c2(m 0指静质量); 与静质量对应的静能量为E 0=m 0c 2。
[跟随名师·解疑难]1.对质速关系m =m 01-v c2的理解(1)式中m 0是物体静止时的质量(也称为静质量),m 是物体以速度v 运动时的质量。
6.5 速度变换定理和多普勒效应

u
S''
v
O''
O
O'
x
l0
l 1 v 2 / c 2
1 v 2 / c 2 l l0 1 v 2 / c 2 l' 1 v 2 / c 2
l 1 u 2 / c 2 l 1 v u/c 2
v v u 2 由速度逆变换式有 1 v u/c
vx u u 1 2 v x c
2
v y 1 β v y u 1 2 vx c
v z
第6章相对论
dz 1 2 dz z u dt dt 2 dx c
2
v z 1 β u 1 2 vx c
2
例1 一宇宙飞船以速度 u 远离地球沿 x 轴方向飞行,发现 飞船前方有一棒形不明飞行物,平行于 x 轴。飞船上测得 此物长为l ' ,速度大小为 v ' ,方向沿 x 轴正向。 求 地面上的观测者测得此物长度。 S 解 令地球参照系为 S 系,飞船为 S' 系,不明飞行物为S'' 系,则在S'' 系中测得不明飞行物的长度为原 长 l 0 ,由长度收缩公式有
θ 0 ν l ν 0
1 β 1β
(1) 若光源离开观察者,上式中 取正号,这时l <0 ,实测频 率 l 小于光源固有频率0 (2) 若光源趋近观察者,上式中 取负号,这时l >0 ,实测频 率 l 大于光源固有频率0 2. 光的横向多普勒效应
“红移 ” “蓝移 ”
红移
9
第6章相对论
例1 一遥远的河外星系以很高的速率离开地球退行而去, 其谱线发生红移。与固有频率 0 相对应的波长为 0 = 434 nm 的谱线,地面上观测记录的该谱线的波长 = 600 nm. 求 此河外星系的退行速率。
高中物理教科版高二选修3-4课件:第6章_4_相对论的速度变换公式_质能关系、5_广义相对论点滴(选学)

应用广义相对论的原理解决时空变化问题的方法 1.应该首先分析研究的问题或物体做怎样的运动,是处于怎样的参考系 中.无论是匀加速运动的参考系,还是均匀的引力场中,其规律是相同的. 2.然后根据“引力使时间变慢,空间变短”的理论分析其所在位置或运动 情况会产生怎样的变化.
学业分层测评(二十二) 点击图标进入…
量的粒子(如光子),它却可以有动质量 m.
(2)质能方程 ①爱因斯坦质能关系式 E=mc2. ②理解这个公式请注意 a.质能方程表达了物体的质量和它所包含的能量的关系;一定的质量总是 和一定的能量相对应. b.静止物体的能量为 E0=m0c2,这种能量叫做物体的静能量.每个有静质 量的物体都具有静能量.
【答案】 ACE
4.在适当的时候,通过仪器可以观察到太阳后面的恒星,这说明星体发出 的光在________引力场作用下发生了________.
【解析】 根据爱因斯坦的广义相对论可知,光线在太阳引力场作用下发 生了弯曲,所以可以在适当的时候(如日全食时)通过仪器观察到太阳后面的恒 星.
【答案】 太阳 弯曲
2.电子的静止质量 m0=9.11×10-31kg. (1)试用焦和电子伏为单位来表示电子的静质能; (2)静止电子经过 106 V 电压加速后,其质量和速率各是多少?
【解析】 (1)由质能方程得:
E = m0c2 = 9.11×10 - 31×(3×108)2
J = 8.2×10 - 14
J
=
【提示】 一定变化.由质能方程 ΔE=Δmc2 可知,质量变化时,一定对应 能量的变化.
1.相对论速度变换公式的理解 假设高速火车对地面的速度为 v,车上的一高速粒子以速度 u′沿火车前进 的方向相对火车运动,那么此粒子相对于地面的速度为 u=1u+′u+′c2vv. (1)若粒子运动方向与火车运动方向相反,则 u′取负值.
狭义相对论的其他结论、广义相对论简介 课件

一、对质速关系式 m=
m0 的理解 1-vc 2
1.式中 m0 是物体静止时的质量(也称为静质量),m 是 物体以速度 v 运动时的质量.这个关系式表明:物体的 质量会随物体速度的增大而增大.
2.v≪c 时,vc2=0,此时有 m=m0,也就是说:低速运动 的物体,可认为其质量与物体运动状态无关. 3.微观粒子的速度很高,因此粒子运动的质量明显大 于静质量.
(_2)_结__论_:_光_速__c_是_宇. 宙速度的_极__限__,且相对任何参考 系,光速都是__不__变__的.
●2.相对论质量 ●(1)经典力学:物体的质量是__不__变__的,一定的 力作用在物体上产生的加速度_一__定__,足够长时 间后物体可以达到_任__意___的速度.
●(2)相对论:物体的质量随物体速度增大而 _增__大___.
长度的相对性.线密度 ρ=ml ,当棒沿棒长方向运动 时,m、l 都发生变化,这时要通过推算来解决,考虑 问题时不能漏了 m 或 l 的变化.当棒沿垂直长度方 向运动时,只有 m 发生变化.
质能方程的应用
例2 电子静止时质量为9.1×10-31 kg,被加速器 加速后,其能量为1.28×109 eV,问加速后电子的质 量是多少?是静止质量的多少倍? 【思路点拨】 电子被加速后的能量是电子的总 能量,而不只是电子具有动能,满足公式E=mc2.
三、广义相对论的几个结论 1.光线在引力场中偏转:根据广义相对论,物质的引 力会使光线弯曲,引力场越强,弯曲越厉害.通常物 体的引力场都太弱,但太阳引力场却能引起光线比 较明显的弯曲. 2.引力红移:按照广义相对论,引力场的存在使得空 间不同位置的时间进程出现差别.例如,在强引力的 星球附近,时间进程会变慢,因此光振动会变慢,相 应的光的波长变长、频率变小,光谱线会发生向红 光一端移动的现象.光谱线的这种移动是在引力作 用下发生的,所以叫“引力红移”.
爱因斯坦相对论公式简介与说明

爱因斯坦相对论公式简介与说明爱因斯坦相对论公式简介与说明[日期: 2007-12-14 ] 阅读:33029 次爱因斯坦(1879-1955)是20世纪最伟大的自然科学家,物理学革命的旗手。
1879年3月14日生于德国乌耳姆一个经营电器作坊的小业主家庭。
一年后,随全家迁居慕尼黑。
父亲和叔父在那里合办一个为电站和照明系统生产电机、弧光灯和电工仪表的电器工。
在任工程师的叔父等人的影响下,爱因斯坦较早地受到科学和哲学的启蒙。
1894年,他的家迁到意大利米兰,继续在慕尼黑上中学的爱因斯坦因厌恶德国学校窒息自由思想的军国主义教育,自动放弃学籍和德国国籍,只身去米兰。
1895年他转学到瑞士阿劳市的州立中学;1896年进苏黎世联邦工业大学师范系学习物理学,1900年毕业。
由于他的落拓不羁的性格和独立思考的习惯,为教授们所不满,大学一毕业就失业,两年后才找到固定职业。
1901年取得瑞士国籍。
1902年被伯尔尼瑞士专利局录用为技术员,从事发明专利申请的技术鉴定工作。
他利用业余时间开展科学研究,于1905年在物理学三个不同领域中取得了历史性成就,特别是狭义相对论的建立和光量子论的提出,推动了物理学理论的革命。
同年,以论文《分子大小的新测定法》,取得苏黎世大学的博士学位。
1908年兼任伯尔尼大学编外讲师,从此他才有缘进入学术机构工作。
1909年离开专利局任苏黎世大学理论物理学副教授。
191 1年任布拉格德语大学理论物理学教授,1912年任母校苏黎世联邦工业大学教授。
1914年,应M.普朗克和W.能斯脱的邀请,回德国任威廉皇帝物理研究所所长兼柏林大学教授,直到1933年。
1920年应H.A.洛伦兹和P.埃伦菲斯特(即P.厄任费斯脱)的邀请,兼任荷兰莱顿大学特邀教授。
回德国不到四个月,第一次世界大战爆发,他投入公开的和地下的反战活动。
他经过8年艰苦的探索,于1915年最后建成了广义相对论。
他所作的光线经过太阳引力场要弯曲的预言,于1919年由英国天文学家A.S.爱丁顿等人的日全食观测结果所证实,全世界为之轰动,爱因斯坦和相对论在西方成了家喻户晓的名词,同时也招来了德国和其他国家的沙文主义者、军国主义者和排犹主义者的恶毒攻击。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意
长度收缩是一种1相对效应, 此结果反之亦然 .
当 u c 时 l l .
洛伦兹收缩: 运动物体在运动方向上长度收缩 .
时空相对性的实验验证
1966年用μ子作了一个类似于双生子旅游的实验, 让μ子沿一直径为14米的圆环运动再回到出发点,实 验结果表明运动的μ子的确比静止的μ子寿命更长。
ABC
m m0
1
v2 c2
《物理世界奇遇记》 ----城市速度极限
1
汤普金斯先生
自行车和车 上的年轻人在运动方 向上都难以置信地缩
1
扁了.
-----运动物体的收缩
1
1
——同时的相对性
二、运动时钟的变慢
二、运动时钟的变慢
v
M
h
v
v
v
M
M
M
cΔt 2h
A
A vΔt
B
2
对于车厢内的人:t
2h c
对于车厢外的人:t 4h2 c2 v2
t t 1 v 2 c
时间延缓效应并
不是说由于相对运动 而使钟发生了结构性 变化,是由于不同观 测者进行量度时引起 的一种观测效应。这 种效应是相对的。对
按伽利略速率变换公式:
v u v 1.4c
V大于光速可能吗?
P105页
一、相对论的速度变换
根据时空相对性,狭义相对论给出:在
以速率u相对于参考系S运动的参考系S'中,
一物体沿与u相同的方向以速率v' 运动时,
在参考系S中,它的速率为:
u v
v
1
uv c2
s y s' y'
u
二、相对论的质量和能量
E mc2
二、相对论的质量和能量
m m0
1
v2 c2
E0 m0c 2
二、相对论的质量和能量
E0 m0c 2
二、相对论的质量和能量
E0 m0c 2
二、相对论的质量和能量
根据狭义相对论可得出:
E mc2
m m0
1
v2 c2
E0 m0c 2
o o'
x'
x
z
z'
在地面上空以u=0.9c飞行的飞船, 向前发射一导弹,导弹对飞船的速率为
v 0.5c
按伽利略速率变换公式:
v u v 1.4c
按相对论时空观:
u v 0.9c 0.5c
v
1
uv c2
1
0.9c 0.5c c2
0.966c c
注意:速度要接近光速时,相对论效应才会明显。
一、“同时”的相对性
在一个参考系中是同时发生的两件事,在 相对于此参考系运动的另一个参考系中观测不 是同时发生,这就是“同时”的相对性。
说明同时具有相对性,时间的量度是相对的 .
结论 :
沿两个惯性系相对运动方向发生的两个事 件,在其中一个惯性系中表现为同时的, 在 另一惯性系中观察则不同时。
1971年,科学家将铯原子钟放在喷气式飞机中作 环球飞行,然后与地面的基准钟对照.实验结果与理 论预言符合的很好.这是相对论的第一次宏观验证。
第六章 相对论
4、相对论的速度变换公式 质能关 系
高二物理备课组
在地面上空以u=0.9c飞行的飞船, 向前发射一导弹,导弹对飞船的速率为
v 0.5c
个事件之间的时间间隔 叫固有时。
固有时最短
93 6
93 6
时间延缓 :运动的钟走得慢 .
三、长度的相对性
一个物体相对于观察者静止时,它的长 度测量值最大。相对于观察者运动时,观察 者在运动方向上观测,它的长度缩短,速度 越快,缩得越短。即运动的尺子要缩短。
v0
v
三、长度的相对性
固有长度:棒静止时测得的它的长度叫棒的静长或固 有长度 .(最长)
第六章 相对论
4、相对论的速度变换公式 质能关 系
高二物理备课组
复习:1.惯性参考系:
凡是牛顿定律成立的参考系,称为惯性参 考系,简称惯性系。
2.伽利略相对性原理 对于所有的惯性系,力学规律都是相同的。
3.经典时空观(绝对时空观) 时间均匀向前,空间静止不动。 时间和空间彼此独立、互不关联,且不
受物质或运动的影响。
t t
1
v
2
c
于同一参考系,v=0,
就不存在这种效应了。
当v接近光速时,
这种偏差是非常大的。
时间延缓 :
y'
s'
t= t 1u2 c2
d
12
9 6 3 x'
t t' t0
o'
A
y
s
u
x1
o 12
1
12
93
6
x2
x
12
固有时:在某一参考系中
同一地点先后发生的两
①相对性原理: 对于不同的惯性系,物理规律
(包括力学和电磁学)都是一样的。
②光速不变原理: 光速与惯性系的选择无关。
经典时空观
相对论时空观
同时的绝对性
主 要
时间间隔的绝对性
结 论
空间距离的绝对性
质量不变
同时的相对性 运动的时钟变慢 运动的尺子变短 质量随速度的增大而增大
主 要 内 容
时间和空间彼此独立, 时间和空间相互关联,质 互不关联,且不受物 量随物体的运动状态的改 质或运动的影响。 变而改变。
