高中电路化简(1).doc
电路化简

请画出其等效电路图
A
a
R1
c b
R2 R3
b
R4
c
等电势点法
1、将各结点用字母标上 2、判定各结点电势的高低 将各结点按电势高低自左向右依次排列, 3、将各结点按电势高低自左向右依次排列,再将各结 点之间的支路画出 4、将画出的等效图加工整理
请画出其等效电路图 尖子生102-9 尖子生102 102-
复杂混联电路的等效化简
一、电路化简的原则 无电流(电势差) 无电流(电势差)的支路可去除 等电势的各点化简时可合并 理想导线无电阻, 理想导线无电阻,可任意长短 理想电流表可认为短路,理想电压表 理想电流表可认为短路, 可认为断路 电路稳定时, 电路稳定时,电容 断直流,通交流” 器“断直流,通交流”
c
R2
b
A
R1
R3
R4
d
L1
c
c
L
a
E
S
请画出其等效电路图
R2
R1 R4 R6
R3 R5
请画出其等效电路图
L2 R L1
S E L3
二、常用的等效化简
顺电流法
1、将各元件的连结点用字母标上 让电流从外电路上高电势点流出, 2、让电流从外电路上高电势点流出,在不重复经过同 一元件原则下流向低电势点, 一元件原则下流向低电势点,有几条路就有几条独立支 路 3、未包含在独立之路内的剩余元件按照它在电路中的位 、 置来确定该元件的解法
高中电路化简(1)

电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源网络可等效于一个电压源,其电动势等于网络的开路电压,内阻等于从网络两端看除电源以外网络的电阻。
如图2-4-3所示为两端有源网络A 与电阻R 的串联,网络A可视为一电压源,图2-4-1图2-4-2图2-4-3图2-4-4等效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于网络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理 又叫诺尔顿定理,内容是:两端有源网络可等效于一个电流源,电流源的0I 等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除电源外网络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2图2-4-5图2-4-62I <0,表明电流从2ε负极流出。
(完整版)高中物理电路简化

(完整版)高中物理电路简化(3)将各个电路元件对号入座,画出规范的等效电路图,如图3所示。
例谈综合法简化电路一、简化电路的具体方法1支路电流法:电流是分析电路的核心。
从电源正极出发顺着电流的走向,经各电阻外电路巡行一周至电源的负极,凡是电流无分叉地依次流过的电阻均为串联,凡是电流有分叉地依次流过的电阻均为并联。
例1:试判断图1中三灯的连接方式。
图1【解析】由图1可以看出,从电源正极流出的电流在A 点分成三部分。
一部分流过灯部分流过灯L3,然后在B 点汇合流入电源的负极,从并联电路的特点可知此三灯并联。
【题后小结】支路电流法,关键是看电路中哪些点有电流分叉。
此法在解决复杂电路时显得有些力不从心。
2 .等电势法:将已知电路中各节点(电路中三条或三条以上支路的交叉点,称为节点)编号,按电势由高到低的顺序依次用1、2、3 数码标出来(接于电源正极的节点电势最高,接于电源负极的节点电势最低,等电势的节点用同一数码)。
然后按电势的高低将各节点重新排布,再将各元件跨接到相对应的两节点之间,即可画出等效电路。
例2:判断图2各电阻的连接方式。
【解析】(1)将节点标号,四个节点分另怖上 1、2。
(2)将各个节点沿电流的流向依次排在一条直线上。
L1, 一部分流过灯 L2,图3(4)从等效电路图可判断,四个电阻是并联关系。
【题后小结】等电势法,关键是找各等势点。
在解复杂电路问题时,需综合以上两法的优点。
二、综合法:支路电流法与等电势法的综合。
注意点:(1)给相同的节点编号。
(2)电流的流向:由高电势点流向低电势点(等势点间无电流),每个节点流入电流之和等于流出电流之和。
例3:由5个1Q电阻连成的如图4所示的电路,导线的电阻不计,贝U A、B间的等效电阻为__________ Q o【策略】采用综合法,设A点接电源正极,B点接电源负极,将图示电路中的节点找出,凡是用导线相连的节点可认为是同一节点,然后按电流从A端流入,从B端流出的原则来分析电流经过电路时的各电阻连接形式就表现出来了。
(word完整版)电路化简
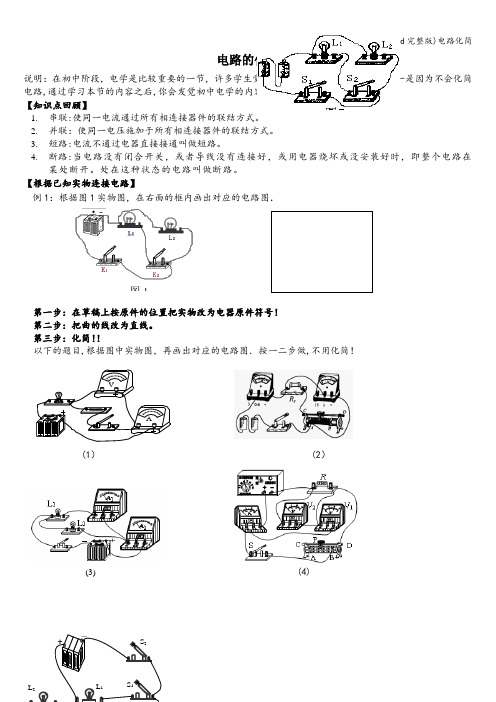
电路的化简说明:在初中阶段,电学是比较重要的一节,许多学生觉得电学内容比较难懂,其原因之一是因为不会化简电路,通过学习本节的内容之后,你会发觉初中电学的内容其实是非常简单的! 【知识点回顾】1. 串联:使同一电流通过所有相连接器件的联结方式。
2. 并联:使同一电压施加于所有相连接器件的联结方式。
3. 短路:电流不通过电器直接接通叫做短路。
4. 断路:当电路没有闭合开关,或者导线没有连接好,或用电器烧坏或没安装好时,即整个电路在某处断开。
处在这种状态的电路叫做断路。
【根据已知实物连接电路】例1:根据图1实物图,在右面的框内画出对应的电路图.第一步:在草稿上按原件的位置把实物改为电器原件符号! 第二步:把曲的线改为直线。
第三步:化简!!以下的题目,根据图中实物图,再画出对应的电路图.按一二步做,不用化简!(1) (2)(3)(4)图1V__ _A(5)(6)(7)(8)(9)(10)【化简电路】从上述化简的结果可以得知,某些复杂的电路图是由于实物连接所得,通过化简将有利于我们计算.例2:化简以下电路图:通过化简。
.。
.。
例3:化简以下电路图:(11)通常的学生会认为上述中有其中一个灯泡被短路了,事实上三者都是并联的!!电路化简的方法:一,电路化简的原则:1)电流表在电路中相当于短路,电压表相当于断路!!2)电流优先流过没有电阻的地方!3) 只要有电流流经用电器就不是短路,哪怕两者的电阻相距很大! 二,电路化简的步骤: 以下图为例:(12) 第一步:去电表!第二步:先别着急判断短路,从电源正极出发,经R1为一回路,再从电源正极出发经R2为一回路,再从正极出发,经R3又一回路!。
.。
第三步:判断电表测那里的电流电压! 【课堂检测】1.把前面实物连接所得的电路进行化简2.对以下的电路图进行化简并判断对应电表测哪里的电流电压!(13) (14)(15) (16)L 1L 2A 1A 2(17)(18)(20)(19)(word完整版)电路化简(21)(22)(23)(24)(26)(25)(28)(27)。
高中电路化简

电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源网络可等效于一个电压源,其电动势等于网络的开路电压,内阻等于从网络两端看除电源以外网络的电阻。
如图2-4-3所示为两端有源网络A 与电阻R 的串联,网络A可视为一电压源,图2-4-1图2-4-2图2-4-3图2-4-4等效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于网络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理 又叫诺尔顿定理,内容是:两端有源网络可等效于一个电流源,电流源的0I 等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除电源外网络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2图2-4-5图2-4-62I <0,表明电流从2ε负极流出。
物理电路化简节点法(万能法)含实物图
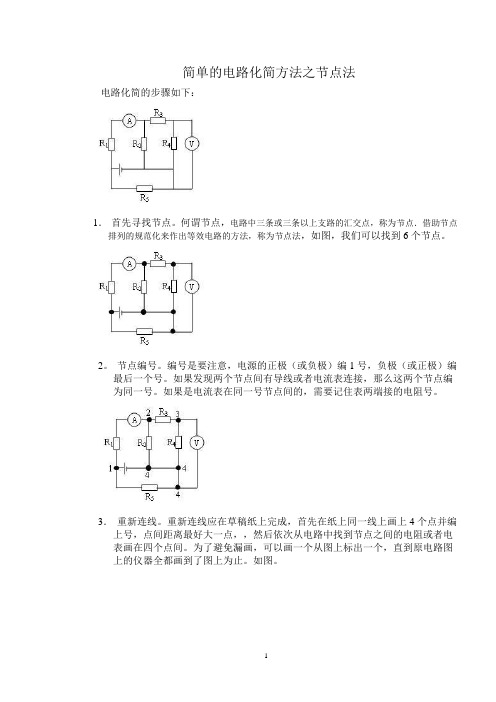
简单的电路化简方法之节点法电路化简的步骤如下:1.首先寻找节点。
何谓节点,电路中三条或三条以上支路的汇交点,称为节点.借助节点排列的规范化来作出等效电路的方法,称为节点法,如图,我们可以找到6个节点。
2。
节点编号。
编号是要注意,电源的正极(或负极)编1号,负极(或正极)编最后一个号。
如果发现两个节点间有导线或者电流表连接,那么这两个节点编为同一号。
如果是电流表在同一号节点间的,需要记住表两端接的电阻号。
3.重新连线。
重新连线应在草稿纸上完成,首先在纸上同一线上画上4个点并编上号,点间距离最好大一点,,然后依次从电路中找到节点之间的电阻或者电表画在四个点间。
为了避免漏画,可以画一个从图上标出一个,直到原电路图上的仪器全都画到了图上为止。
如图。
A 1A 3VA 2R 1R 2R 34. 转化为规范化电路图。
相信做完上一步后,您已经可以看出电路的组成了,如果发现点与点之间有断开的情况,只要将点适当的移位就可。
关于这道题的规范化电路图,在此就省略吧。
练习1.画出等效电路图2.画出等效电路图3.当闭合开关S 0、S 1,断开开关S 2时 当闭合开关S 2,断开开关S 0、S 1时V 2V 1AR 1R 2P S图12SVAL 1 L 2 S 0S 1S 2R 3R 4图394.当S 1、、S 2 均闭合且滑片P 滑到a 端时 当S 1、S 2 均断开且滑片P 在a 端时5.当闭合开关S 1,断开开关S 2和S 3, 当闭合开关S 1、S 2,断开S 3时 当闭合开关S 3,断开S 1 、S 2时6.当S 1、S 2闭合,滑动变阻器的滑片P 在a 端时 当S 1、S 2都断开,滑片P 在b 端时7.只闭合开关3S ,滑动变阻器的滑片P 在最左端时 只断开开关1S ,滑片P 移至最右端时 只闭合开关1S ,滑片P 在最右端时图23a VA 1A 2S 1S 2R 2R 1Lb1.将滑动变阻器的滑片P置于中点M,且只闭合开关S1时将滑动变阻器的滑片P置于B端,断开开关S1,闭合开关S2时将滑动变阻器的滑片P置于A端,闭合开关S1和开关S2时2.当滑动变阻器的滑片P在B端,只闭合S2时滑片P在B端,开关都断开时当滑片在A端,只闭合S1时图25。
电路化简
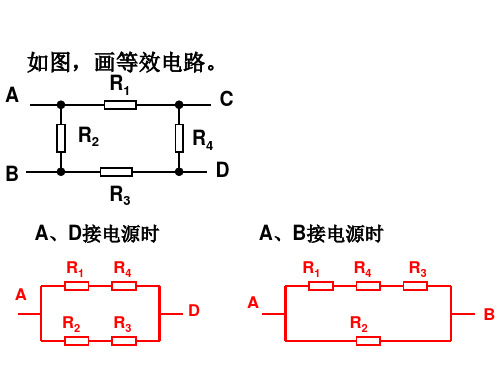
2R2 A R3 B
1、将电路中的所有理想安培表视为短路,所 有理想电压表视为开路; 2、寻找电路中的所有等势点:凡是用无阻导 线相连点,都是电势相等的点。 3、将电路中电势不等的点用不同的字母标示 出来; 4、按电流的流向将电势不同的点按电势降低 顺次序从左向右排列出来; 5、将各用电器按对号入座的原则放到相应的 等势点中去; 6、再按原电路图,将电流表和电压表放到相 应位置上去;将各用电器用导线连接起来。
4.若已知:UAB=U,R=R1=R2=R3,求 两表的读数。
A
R2 A R1
V
R3 B
电流表读数:U/I
电压表读数:U
电路如图所示,R1=R2 =R3=R4,在A B两端加电压U,安培表A1和A2的示数 都是0.6安,求安培表A3的示数多大?
0.9A
求:φ A, φ B的大小关系。
R 2R 结论:相等
电路中,R1=R2=R3=R4=3欧,则:A、 B间的总电阻多少?
A1
R2 A R1
A2
R3 B
u
5Ω 2.1A 12V
如图,R1=R2=R3=5Ω,R4=R5=10Ω, 求1、AB间的总电阻? 2、U=14v,如果在图中按入电流表,示 数为多少? 3、如果不小心装错了装成电压表, 那么示数为多少?
A B
2R 4R
若在间连一根导线呢? 或接一个电阻呢? 结论:无电流
.画下图的等效电路。
R 2R 2R 4R
无电流支路可去除
如图,画等效电路。
A R2 B R3 A、D接电源时
R1 A R2 R3 D R4 A R2
R1
R4
C
D A、B接电源时
R1 R4 R3 B
高考物理中复杂电路的简化方法——百度文库

R1 b R2
R3 d R4
R5 b R6
R7 d
第 2 步——梳理节点。将 A、a、b、c、d、B 节点依次标在一条直线上,如图所示。
A
a
b
c
d
B
第 3 步——嵌入元件。分别将 R1~R7 共 7 个元件嵌入第 1 步标示的 2 个节点之间。
A
a
R1
b
R2
c
R3
d
B
R5
R6
R7
R4
第 4 步——整理计算。把电阻和导线整理成直角拆线样式,根据串并联关系计算。
A1
R2
R3
R1 A2
S
解析:第 1 步——标节点序号。原电路中的节点如图所示,A、B 为电路中电源外电路 的两个端口。
A1
b1 R2
R3 b2
a1 R1
a2
A2
S
AB
第 2 步——梳理节点。将 A、a1、a2、b1、b2、B 节点依次标在一条直线上,如图所示。
A
a1
a2
b1 b2
B
第 3 步——嵌入元件。分别将 R1~R3、A1 表、A2 表共 5 个元件嵌入第 1 步标示的 2 个 节点之间。
并联关系,利用电阻的串并联公式计算电阻。
【实例 1】(电路简化——节点法)如图所示,电路中的各个电阻值均为 10Ω,则两个
端口 A、B 间的电阻 RAB=________。
A
B
R1
R2
R3
R4
R5
R6
R7
解析:第 1 步——标节点序号。原电路中的节点如图所示,A、B 为电路的两个端口。
Aa
c
a
c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电路化简2.4.1、等效电源定理实际的直流电源r R I0r R可以看作电动势为,阻为零的恒压源图 2-4-1 图 2-4-2与阻 r 的串联,如图2-4-1 所示,这部分电路被称为电压源。
不论外电阻 R 如何,总是提供不变电流的理想电源为恒流源。
实际电源、r 对外电阻 R 提供电流 I 为IrR r r R r其中 / r 为电源短路电流I0,因而实际电源可看作是一定的阻与恒流并联的电流源,如图 2-4-2 所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维a a有源网络bRR宁定理,容是:两端有源网络r0b可等效于一个电压源,其电动图 2-4-3图 2-4-4势等于网络的开路电压,阻等于从网络两端看除电源以外网络的电阻。
如图 2-4-3 所示为两端有源网络 A 与电阻 R 的串联,网络 A 可视为一电压源,等效电源电动势0 等于 a 、b 两点开路时端电压,等效阻r等于网络中除去电动势的阻,如图 2-4-4 所示。
等效电流源定理又叫诺尔顿定理,容是:两端有源网络可等效于一个电流源,电流源的I等于网络两端短路时流经两端点的电流,阻等于从网络两端看除电源外网络的电阻。
例 4、如图 2-4-5 所示的电路中,3.0V ,1.0V , r 0.5 , r 1.0 ,R10.0 , R5.10r 1 ,R 31 2 1 2 12 EDR4.5 , R 19.0BR234R 1( 1)试用等效电压源定理计算从电源 2、r 2AC正极R 4流出的电流I2 ;( 2)试用等效电流源定理计算从结点2r 2B 流向节点 A 的电流 I1。
图 2-4-5分析: 根据题意,在求通过 2 电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过R1 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设 ABCDE 等效电压源电动势0 ,阻 r0 ,如图 2-4-6 所示,由等效电压源定理,应有R 11.5Vr 21r 1 R 1 R 2R 3r 0R 1 r 1R 2 R 352r 2R 4r 1 R 1 R 2 R 3电源、r0 与电源2、r2 串联,故图 2-4-6I 220.02Ar 0 R 4 r 2I2 <0,表明电流从 2 负极流出。
(2)将 A 、B 两个节点短接,构成等效电流源(I 0、r0 )如图 2-4-7 所示,由等效电流源定理,I0为原电路流经A、B短接后的支路电流。
因为有1、2两电源,必须用线性叠加原理,所谓叠加原理与力学中“力的独立作用原理”极为相似,其容为:若电路中有多个电源,则通过任一支路的电流等于各个电动势单独存在时该支路产生的电流之和。
由叠加原理I 0r0I 0 1 2 0.35Ar1 R3 R2 r2 R4A R1B(r1 R3 R2 )( r2 R4I 1 )r0R3 R2 r2 R4 6.7图 2-4-7r1由r0 和R1 的分流关系I 1 r0 I 0 0.14 Ar0 R12.4.2、Y—△变换在某些复杂的电路中往往会遇到电阻的Y 型或△,如图 2-4-8 所示,有时把Y 型联接代换成等效的△型联接,或把△型联接代换成等效的Y 型联接,可使电路变为串、并联,从而简化计算,等效代换要求Y 型联接三个端纽的电压U 12、U 23、U 31及流过的电流 I 1、I 2、I 3与△型联接的三个端纽相同。
在 Y 型电路中有I1R1 I 2R2 U12I 3R3 I1R1 U 31 I 1 I2 I3 0可解得I 11 2 1 R122 R I 2I 1 I 2R1 2O R31 R23R3I 3 I 33 3图 2-4-8R3U 12 R2U 31I 1R2 R3 R3 R1 R1R2 R2 R3 R3 R1 R1 R2在△型电路中I 12 U12 R12I 31 U31 R31I 1 I12I31I 1 U12U31 R12 R31等效即满足:U 12 U 31 R3U12 R2U 31R12 R31 R1R2 R2 R3 R3R1 R2 R3 R3R1R1R2R12 R1R2 R2 R3 R3 R1R3即①R31 R1R2 R2 R3 R3 R1R2 ②R23R1 R2 R2 R3 R3 R1R1类似方法可得③①、②、③式是将Y 型网络变换到△型电路中的一组变换。
同样将△型电路变换到Y 型电路,变换式可由①、②、③式求得:④、⑤、⑥R1 R12 R31R23 R31R12 ④R2 R12 R23R23 R31R12 ⑤R3 R31 R23R23 R31R12 ⑥I11 16 64 V例 5、试求如图 2-4-9 所示电路中的电流。
2312 1 36分析: 这是包含一个 Y 型电路和一个△型图 2-4-9电路的网络,解决问题的方向可将左边 Y 型网络元变换成△型网络元,或将右侧△型网络元变换成Y 型网络元。
解:将左侧 Y 型网络换成△型,如图 2-4-1011 R 12 R316 612314 V3所示已知 RRR2R 2332 6则有R 1 R 2 R 2 R 3R 3 R 1图 2-4-103R 12R 3R 1 R 2 R 2 R 3R 3 R 13R 23R 1R 1 R 2 R 2 R 3 R 3 R 13R 31R 24V22 66由图 2-4-10,可进一步电路整理为图 2-4-11264所示。
R 总图 2-4-113R总4将右侧△型网络元换成 Y 型网络元同样可求得3,这里不再叙述。
2.4.3、 对称性原理①等势节点的断接法在一个复杂电路中, 如果能找到一些完全对称的点,(以两端连线为对称轴),那么可以将接在等电势节点间的导线或电阻或不含电源的支路断开(即去掉),也ACBD图 2-4-12可以用导线或电阻或不含电源的支路将等电势节点连接起来,且不影响电路的等效性。
例 6、用导线连接成如图 2-4-12 所示的框架, ABCD 和 ABCE 是正四面体,每段导线的电阻都是 1。
求 AB 间的总电阻。
解: 设想 A 、B 两点上存在电势差UAUB,由于电路的对称性可以知道D 、C 、两点的电势都应该介乎UA与UB的中间,即U (UAU B) / 2,所以两点应是等电势的。
这样,去掉CD 段导线,对 A 、B 间的总电阻不会有影响。
当去掉 CD 段导线后,就成为三路并联, 即 A —D —B ,A — C —B ,和 AB 。
于是:11 1 1 2R 总22R 总 0.5( )②电流分布法设有电流 I 从 A 点流入、 B 点流出,应用电流分流的思想和网络中两点间不同路径等电压的思想, (即基耳霍夫定理),建立以网络中各支路的电流为未知量的方程组,解出各支路电流与总电流 I 的关系,然后经任一路径计算 A 、B 两R AB U ABI 即可求出等效电阻。
点间的电压UAB ,再由例 7、 10 根电阻均为 r 的电阻丝接成如图 2-4-13 所示的网络,试求出 、A B 两点之间的等效电阻RAB 。
由结构对称性,要求电流 I 从A 点流入后在 A 点B的电流分布应与电流 I 从 B 点流出前的电流分布相A同,中间四方形必具有上、下电流分布对称和左、右图 2-4-13电流分布对称,因此网络电流分布应如图 2-4-14 所示。
对图中 C 点和 D 点,有电流关联I I 1 I 2 I 1 I 2 I 1I 2 I 2II 1I 1 I 21 I ①解得 2由 A 、E 两点间不同路线等电压的要求,得E I 1I2II 1BI 1 2r (I I 1 ) rI 2 rDA即 3I 2I 1I I I 1CI1I 2②图 2-4-14解①、②两式得3 1 I 1I,I 2I88选择线路 AEDB ,可得U AB I 1 2r I 1 I 2 rII 1 r15 Ir 8因此, A 、B 间等效电阻便为U AB15 R ABrI82.4.4、 无穷网络等效变换法若xa aaa ,(a >0)在求 x 值时,x 注意到是由无限多个a 组成,所以去掉左边第一个 a对x 值毫无影响,即剩余部分仍为 x ,这样,就可以将原式等效变换为 xa x ,即 x 2x a 0。
所以x 11 4a2这就是物理学中解决无限网络问题的基本思路。
例 8、如图 2-4-15 所示,框架是用同种金属丝制成的,单位长度的电阻为,一连串接等边三角形的数目可认AB为趋向无穷,取 AB 边长为 a ,以下每个三角形的边长依 图 2-4-15次减小一半,则框架上 A 、B 两点间的电阻为多大?从对称性考虑原电路可以用如图2-4-16 所示的等效电路来代替,同时我们用电阻为R AB/ 2的电阻器来代替由无数层“格子”所构成的“”三角,并且电阻是 R AB 这样的, R ABR x ,Ra 因此R / 2R / 2RR x / 2RR x / 2 R x / 2R RR / 2 R / 2R x R RR R x/ 2BR R x/ 2A R 解此方程得到R AB R x7 1 R 1 7 1 a3 3图 2-4-162.4.5、 电流叠加法解题步骤是:先考虑一支流入或流出系统的电流, 把它看作在给系统充电或放电,利用对称性求出系统中的电荷分布和电流场分布, 求出每一支电流造成的分布后进行叠加,使得电荷分布全部抵消,而电流场叠加作为所求的电流场。
例 9、有一个无限平面导体网络,它由大小相同的正六边3 214cab9g形网眼组成,如图 2-4-17 所示。
所有六边形每边的电阻为R 0,5d 6e 87求:(1)结点 a 、b 间的电阻。
图 2-4-17(2)如果有电流 I 由 a 点流入网络, 由 g 点流出网络,那么流过 de 段电阻的电流 I de 为多大。
解:(1)设有电流 I 自 a 点流入,流到四面八方无穷远处,那么必有I / 3 电流由 a 流向 c,有I / 6 电流由 c 流向 b。
再假设有电流 I 由四面八方汇集 b 点流出,那么必有 I / 6 电流由 a 流向 c,有I / 3电流由 c 流向 b。
将以上两种情况综合,即有电流 I 由 a 点流入,自 b 点流出,由电流叠加原理可知I I IIac6 2 (由a流向c)3I cbI I I3 6 2 (由c流向b)因此, a、b 两点间等效电阻U AB I ac R0 I cb R0R0R ABII(2)假如有电流 I 从 a 点流进网络,流向四面八方,根据对称性,可以设I 1 I 4 I 7 I AI 2 I3 I5 I6 I 8 I9 I B应该有3I A 6I B I、d 两点关于 a 点对称,所以因为 bI de I be 1 I A 2同理,假如有电流 I 从四面八方汇集到g 点流出,应该有I de I B最后,根据电流的叠加原理可知I de I de I de 1I A I B 1 3IA 6I B1 I2 6 6以上几种方法可实现电路的化简。
