理论力学习题集
理论力学习题册答案
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。
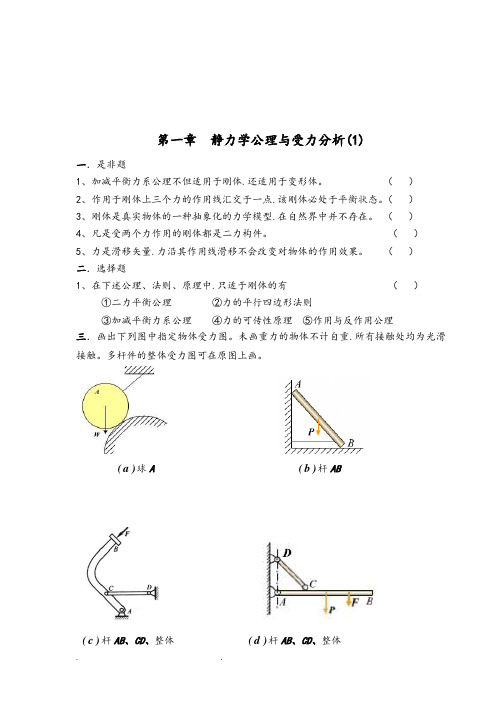
()二.选择题1、在下述公理、法则、原理中.只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N.放在水平梁AC的中央.如图所示。
(完整版)理论力学习题集册答案解析
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
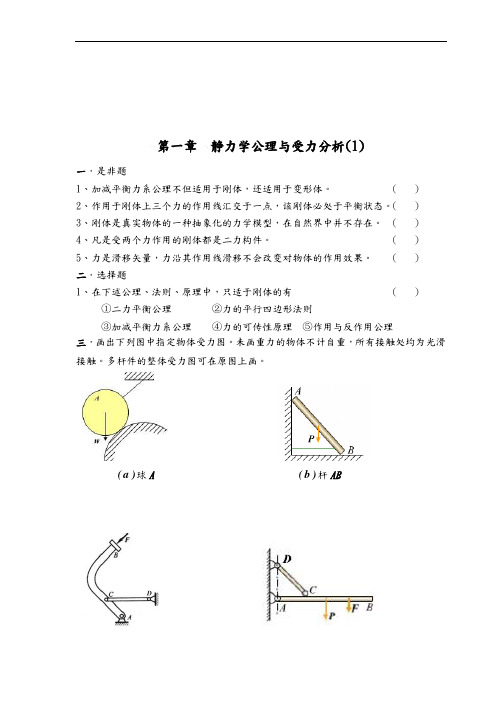
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆AB)a(球A )d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题集

理论力学习题集班级 ________________________________________ 姓名 ________________________________________ 学号 ________________________________________2009-9-7一、是非题(正确用",错误X,填入括号内。
)1、二力平衡条件中的两个力作用在同一物体上;作用力和反作用力分别作用在两个物体上。
()2、三力平衡汇交定理表明:作用在物体上汇交于一点的三个力必是平衡力系。
()3、刚体的平衡条件是变形体平衡的必要条件,而非充分条件。
()二、选择题(将答案的序号填入划线内。
)1、作用在物体A上的两个大小不等的力F 4和F 2,沿同一直线但方向相反。
则其合力可表为()① F4- F 2② F2-F4③ F4- F 2④ F2- F 1 ⑤ F1 + F22、加减平衡力系公理适用于_______________ 。
①刚体;②变形体;③刚体和变形体。
三、物体受力分析(要求解除约束、取分离体,画上所有作用力)1、画出下列各图中物体A、AB、ABC的受力图。
未画重力的物体的重量不计,所有接触处均为光滑2、画岀下列每个标注字符的物体的受力图,各题的整体受力图。
未画重力的物体的重量均不计,一、是非题(正确用",错误x,填入括号内。
)1、约束力的方向必与该约束所阻碍的物体位移方向相反。
()2、滚动支座的约束力必沿支座平面垂线方向,且指向物体内部。
()二、选择题(将答案的序号填入划线内。
)1、力的可传性只适用于________________ 。
①刚体②变形体2、考虑力对物体作用的运动效应和变形效应,力是 __________ 。
①滑动矢量②自由矢量③定位矢量三、物体受力分析•受力图(要求取分离体,画上所有的主动力和约束反力)画岀下列每个标注字符的物体的受力图,各题的整体受力图。
未画重力的物体的重量均不计,一、是非题(正确用",错误用X,填入括号内。
理论力学习题集
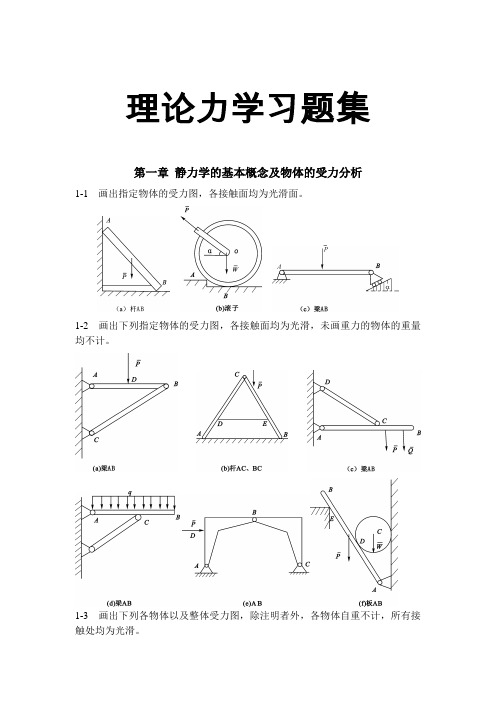
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学习题集1

第一章点的运动学1-7 如图所示。
杆AB长为l,以等角速度ω绕点B转动,其转动方程为φ=ωt。
而与杆铰接的滑块B 按规律s=a+b sinωt沿水平线作谐振动。
其中a和b均为常数。
求点A轨迹。
1-8 如图所示,曲柄OB以匀角速度ω=2rad/s绕O轴顺时针转动,并带动杆AD上点A在水平槽内运动。
已知AB=OB=BC=CD=12 cm,求点D的运动方程和轨迹,以及当φ=45o时点D的速度和加速度。
1-9 如图所示。
摇杆机构的滑杆AB以等速u向上运动,试建立摇杆OC上C点的运动方程,并求点在π4ϕ=时的速度。
假定初瞬时0ϕ=,摇杆长OC=a,距离OD=l。
1-12 如图所示,在曲柄摇杆机构中,曲柄110cmO A r==,摇杆224cmO B l==,1210cmO O=,若曲柄以π4tϕ=rad绕O1轴转动,当t=0时0ϕ=,求点B的运动方程、速度和加速度。
题1-7图题1-9图u题题1-11图题1-12图θ210(m/s)10(m/s )t v x t a v ====()()220rad s 20rad s t v R t a R ωα====2222224210(m/s )20(m/s )1014(m/s )t n t n a v a v R t a a a t =====+=+()()()()()11121221121211122222222221110rad/s 30330104rad/s 7533100.3m/s 30301640.75m/s 93100100.3m/s 93AB BC CD DA AB CD BC DA n r i r r r n v v v v r a a a r a r πωπωωωωπππωππωππωππ======⋅======⋅=⋅====⋅=⋅==⋅=⋅=第二章 刚体的简单运动 2-2 试画出图中刚体上的M 点的轨迹以及在图示位置时的速度和加速度。
2-6 升降机装置由半径为R =50cm 的鼓轮带动,如图所示。
理论力学习题集

1-1、画出下列每个标注字符的物体(不包含销钉与支座)的受力图与系统整体受力图。
题图中未画重力的各物体自重不计,所有接触处均为光滑接触。
(整体受力图在原图上画)2-1、物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起。
设滑轮的大小、AB与CB杆自重及磨擦略去不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB处受的力。
2-2、图示结构中,各构件的自重略去不计。
在构件AB上作用一力偶矩为M的力偶,求支座A和C的约束力。
2-3、直角弯杆ABCD与直杆DE及EC铰接如图,作用在杆DE上力偶的力偶矩M=,不计各杆自重,不考虑摩擦,尺寸如图,求支座A,B处的约束力及杆EC的受力。
3-1、图示平面任意力系中F1=402N,F2=80N,F3=40N, F4=110N,M=。
各力作用位置如图所示。
求:(1)力系向点O简化的结果;(2)力系的合力的大小、方向及合力作用线方程。
3-2、无重水平梁的支承和载荷如图 (b)所示。
已知力F、力偶矩为M的力偶和强度为q的均布载荷。
求支座A和B处的约束力。
3-3、图示水平梁AB由铰链A和杆BC所支持。
在梁上D处用销子安装半径为r=的滑轮。
有一跨过滑轮的绳子,其一端水平地系于墙上,另一端悬挂有重P=1800N的重物,如AD=,BD=, =45°,且不计梁、杆、滑轮和绳的重量。
求铰链A和杆BC对梁的约束力。
3-4、如图所示,组合梁由AC和DC两段铰接构成,起重机放在梁上。
已知起重机重 P1=50kN,重心在铅垂线上EC,起重载荷 P2=10kN。
如不计梁重,求支座A,B和D三处的约束力。
3-6、由AC和CD构成的组合梁通过铰链C连接。
它的支承和受力如图所示。
已知均布载荷强度q=10kN/m,力偶矩M=40 kN·m,不计梁重。
求支座A,B,D的约束力和铰链C处所受的力。
4-1、图示构架中,物体重1200N,由细绳跨过滑轮E而水平系于墙上,尺寸如图,不计杆和滑轮的重量。
《理论力学》习题集含答案

理论力学习题集答案
理论力学教研室
目录
目录 (1)
第一章:静力学的基本概念 (2)
第二章:平面基本力系 (6)
第三章:平面任意力系 (10)
第五章:空间基本力系 (24)
第六章:空间任意力系 (25)
第七章:重心 (32)
第八章:点的运动 (34)
第九章:刚体的基本运动 (36)
第十章:点的复合运动 (38)
第十一章:刚体的平面运动 (52)
第十二章:刚体的转动合成 (66)
第十四章:质点动力学基础 (70)
第十五章:质点的振动 (75)
第十七章:动能定理 (82)
第十八章:动量定理 (94)
第十九章:动量矩定理 (100)
第二十章:碰撞理论 (115)
第二十一章:达朗伯原理 (118)
第二十二章:虚位移原理 (125)
第一章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1、画出下列每个标注字符的物体(不包含销钉与支座)的受力图与系统整体受力图。
题图中未画重力的各物体自重不计,所有接触处均为光滑接触。
(整体受力图在原图上画)2-1、物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D上,如图所示。
转动铰车,物体便能升起。
设滑轮的大小、AB与CB杆自重及磨擦略去不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB处受的力。
2-2、图示结构中,各构件的自重略去不计。
在构件AB上作用一力偶矩为M的力偶,求支座A和C的约束力。
2-3、直角弯杆ABCD与直杆DE及EC铰接如图,作用在杆DE上力偶的力偶矩M=40kN.m,不计各杆自重,不考虑摩擦,尺寸如图,求支座A,B处的约束力及杆EC的受力。
3-1、图示平面任意力系中F1=402N,F2=80N,F3=40N, F4=110N,M=200N.mm。
各力作用位置如图所示。
求:(1)力系向点O简化的结果;(2)力系的合力的大小、方向及合力作用线方程。
3-2、无重水平梁的支承和载荷如图(b)所示。
已知力F、力偶矩为M的力偶和强度为q的均布载荷。
求支座A和B处的约束力。
3-3、图示水平梁AB由铰链A和杆BC所支持。
在梁上D处用销子安装半径为r=0.1m的滑轮。
有一跨过滑轮的绳子,其一端水平地系于墙上,另一端悬挂有重P=1800N的重物,如AD=0.2m,BD=0.4m, =45°,且不计梁、杆、滑轮和绳的重量。
求铰链A和杆BC对梁的约束力。
3-4、如图所示,组合梁由AC和DC两段铰接构成,起重机放在梁上。
已知起重机重P1=50kN,重心在铅垂线上EC,起重载荷P2=10kN。
如不计梁重,求支座A,B和D三处的约束力。
3-6、由AC和CD构成的组合梁通过铰链C连接。
它的支承和受力如图所示。
已知均布载荷强度q=10kN/m,力偶矩M=40 kN·m,不计梁重。
求支座A,B,D的约束力和铰链C处所受的力。
4-1、图示构架中,物体重1200N,由细绳跨过滑轮E而水平系于墙上,尺寸如图,不计杆和滑轮的重量。
求支承A和B处的约束力,以及杆BC的内力F BC。
4-2、图示结构由直角弯杆DAB与直杆BC及CD铰接而成,并在A处与B处用固定绞支座和可动绞支座固定。
杆DC受均布载荷q的作用,杆BC受矩为M=qa2的力偶作用。
不计各杆自重。
求铰链D所受的力。
4-3、构架尺寸如图所示(尺寸单位为m),不计各杆自重,载荷F=60kN。
求A,E铰链的约束力及杆BD,BC的内力。
4-4、桁架受力如图所示,已知F1=10kN,F2=F3=20kN。
试求桁架4,5,7,10各杆的内力。
5-1、水平圆盘的半径为r,外缘C处作用有已知力F。
力F位于铅垂平面内,且与C处圆盘切线夹角为60°,其他尺寸如图所示。
求力F 对x , y , z轴之矩。
5-2、使水涡轮转动的力偶矩为M z= 1200N.m。
在锥齿轮B处受到的力分解为三个分力:切向力F t,轴向力F a和径向力F r。
这些力的比例为F t:F a:F r=1:0.32:0.17。
已知水涡轮连同轴和锥齿轮的总重为P=12kN,其作用线沿轴Cz,锥齿轮的平均半径OB=0.6m,其余尺寸如图所示。
求止推轴承C和轴承A 的约束力。
5-3、图示六杆支撑一水平板,在板角处受铅直力F作用,设板和杆自重不计,求各杆的内力。
5-4、工字钢截面尺寸如图所示,求此截面的几何中心。
6-1、尖劈顶重装置如图所示。
在块B上受力P的作用。
A与B块间的摩擦因数为f s(其他有滚珠处表示光滑)。
如不计A和B块的重量,求使系统保持平衡的力F的值。
6-2、图示摇杆滑道机构中的滑块M同时在固定的圆弧槽BC和摇杆OA的滑道中滑动。
如弧BC的半径为R,摇杆OA的轴O在弧BC的圆周上,摇杆绕O轴以等角速度ω转动,当运动开始时,摇杆在水平位置,分别用直角坐标法和自然法给出点M的运动方程,并求其速度和加速度。
6-3、已知搅拌机的主动齿轮O1以n=950r/min的转速转动。
搅拌ABC用销钉A、B与齿轮O2 ,O3相连,如图所示。
且AB=O2O3,O3A=O2B=0.25m,各齿轮齿数为z1=20,z2=50,z3=50。
求搅杆端点C的速度和轨迹。
6-4、图示曲柄CB以等角速度ω0 绕C轴转动,其转动方程为ϕ=ω0 t。
滑块B带动摇杆OA绕轴O转动。
设OC=h,CB=r。
求摇杆的转动方程。
7-1、图示车床主轴的转速n=30r/min,工件的直径d=40mm。
如车刀横向走刀速度为v=10mm/s,求车刀相对工件的相对速度。
7-2、在图(a)和(b)所示的两种机构中,已知O1O2=a=200mm,ω1 = 3rad/s。
求图示位置时杆O2A的角速度。
7-3、图示平底顶杆凸轮机构,顶杆AB可沿导槽上下移动,偏心圆盘绕轴O转动,轴O位于顶杆轴线上,工作时顶杆的平底始终接触凸轮表面,该凸轮半径为R,偏心距OC=e,凸轮绕轴O转动的角速度为ω,OC与水平线成夹角ϕ。
求当ϕ =0º时,顶杆的速度。
7-4、图示铰接四边形机构中,O1A=O2B=100mm,又O1O2 =AB,杆O1A以等角速度ω=2rad/s绕轴O1转动,杆AB上有一套筒C,此套筒与CD相铰接。
机构的各部件都在同一铅直面内,求当ϕ=60º时,杆CD的速度和加速度。
8-1、如图所示,曲柄OA长0.4m,以等角速度ω=0.5rad/s绕O轴逆时针转向转动。
由于曲柄的A端推动水平板B,而使滑杆C沿铅直方向上升。
求当曲柄与水平线间的夹角θ =30o时,滑杆C的速度和加速度。
8-2、图示偏心轮摇杆机构中,摇杆O1A借助弹簧压在半径为R的偏心轮C上。
偏心轮C绕轴O往复摆动,从而带动摇杆绕轴O1摆动。
设OC⊥OO1时,轮C的角速度为ω,角加速度为零,θ=60º。
求此摇杆O1A的角速度ω1和角加速度α1。
8-3、图示直角曲杆OBC绕O轴转动,使套在其上的小环M沿固定直杆OA滑动,已知:OB=0.1m,OB 与BC垂直,曲杆的角速度ω=0.5 rad/s,角加速度为零,求当ϕ =60º时,小环M的速度和加速度。
8-4、图示椭圆规尺AB由曲柄OC带动,曲柄以角速度ω0绕O轴匀速转动。
如OC=BC=AC=r,并取C 为基点,求椭圆规尺AB的平面运动方程。
8-5、如图所示,在筛动机构中,筛子的摆动是由曲柄连杆机构所带动,已知曲柄OA的转速n OA =40r/min,OA=0.3m,当筛子BC运动到与点O在同一水平线上时,∠BAO=90°。
求此瞬时筛子BC 的速度。
9-1、图示四连杆机构中,连杆AB上固连一块三角板ABD。
机构由曲柄O1A带动。
已知:曲柄的角速度ω O1A=2rad/s; 曲柄O1A= 0.1m,水平距离O1O2=0.05m,AD=0.05m,当O1A⊥O1O2时,AB平行于O1O2,且AD与O1A在同一直线上,角ϕ =30°。
求三角板ABD的角速度和点D的速度。
9-2、图示机构中,已知:OA=BD=DE=0.1m,EF=0.13m, 曲柄OA的角速度ω=4rad/s。
在图示位置时,曲柄OA与水平线OB垂直;且B、D和F在同一铅直线上,又DE垂直于EF。
求杆EF的角速度和点F的速度。
9-3、图示机构中,曲柄OA长为r,绕O轴以等角速度ωο 转动,AB=6r,BC=3r, 求图示位置时,滑块C的速度和加速度。
9-4、图示直角刚性杆,AC=CB=0.5m。
设在图示瞬间,两端滑块沿水平与铅垂轴的加速度如图,大小分别为a A=1m/s2,a B=3m/s2, 求此时直角杆的角速度和角加速度。
10-1、曲柄OA以加速度ω =2rad/s绕O轴转动,并带动等边三角板ABC作平面运动。
板上点B与杆O1B铰接,点C与套管铰接,而套管可在绕轴O2转动的杆O2D上滑动,如图所示,已知OA=AB= O2C=1m,当OA水平、AB与O2D铅直、O1B与BC在同一直线上时,求杆O2D的角速度。
10-2、平面机构的曲柄OA长为2l ,以匀角速度ω0绕O轴转动。
在图示位置时,AB=BO,并且∠OAD=90º。
求此时套筒D相对于杆BC的速度和加速度。
10-3、在图示离心浇注装置中,电动机带动支承轮A,B作同向转动,管模放在两轮上靠摩擦传动而旋转。
使铁水浇入后均匀地紧贴管模的内壁而自动成型,从而得到质量密实的管形铸件。
如已知管模内径D=400mm,试求管模的最低转速n。
水平抛出,如图所示,空气阻力可视为与速度的一次方成正比,10-4、物体由高度h处以速度v即F=-kmv,其中m为物体的质量,v为物体的速度,k为常系数。
求物体的运动方程和轨迹。
11-1、图示水平面上放一均质三棱柱A,在其斜面上又放一块均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A的质量m A为三棱柱B质量m B的三倍,其尺寸如图所示。
设各处磨擦不计,初始时系统静止。
求当三棱柱B沿三棱柱A滑下接触到水平面时,三棱柱A移动的距离。
11-2、图示椭圆规尺AB的质量为2m1,曲柄OC的质量为m1,而滑块A和B的质量均为m2 。
已知:OC=AC=CB=l;曲柄和尺的质心分别在其中点上;曲柄绕O轴转动的角速度 为常量。
当开始时,曲柄水平向右,求此时质点系的动量。
11-3、图示曲柄滑杆机构中,曲柄以等角速度 绕O轴转动。
开始时,曲柄OA水平向右。
已知:曲柄的质量为m1,滑块A的质量为m2 ,滑杆的质量为m3 ,曲柄的质心在OA的中点,OA=l;滑杆的质心在点C。
求:(1)机构质量中心的运动方程;(2)作用在轴O的最大水平约束力。
11-4、水流以速度v0=2m/s流入固定水道,速度方向与水平面成90º角,如图所示。
水流进口截面积为0.02m2,出口速度v1=4m/s,它与水平面成30º角。
求水作用在水道壁上的水平和铅直的附加压力。
