运筹学单纯形法计算步骤
合集下载
运筹学单纯形法
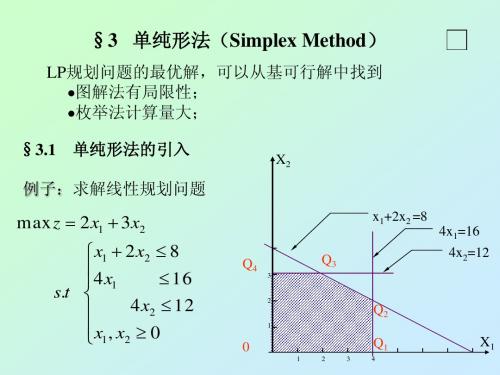
只要取 x5=min{-，8/2，12}=4 就有上式成立。 x5=4时， x4=0，故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ，令x3 ，x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解，新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能： 1、有唯一解； 2、无穷多最优解； 3、无界解； 4、无可行解。 何时达最优解, 何种最优解？
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步：将LP线性规划变标准型，确定一个初始可行解 （顶点）。 •第二步：对初始基可行解最优性判别，若最优，停止；否 则转下一步。 •第三步：从初始基可行解向相邻的基可行解（顶点）转 换，且使目标值有所改善—目标函数值增加，重复第二和 第三步直到找到最优解。
运筹学课件 单纯形法的计算步骤
第二阶段：以第一阶段的最优解(不含人工变量)为初 始解，以原目标函数为目标函数。
例8 试用两阶段法求解线性规划问题
min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4 x1 2 x1
x2
2x3 3 x3 1
x1 , x2 , x3 0
0 0 -1 0 0
x2
3 5 11/5
Z0=0
Z1=15
x1
如果将x1换入基底，得 另一解，由可行域凸性 易知，有两个最优解必 有无穷多组最优解 当非基底变量的检验数 中有取零值，或检验数 中零的个数大于基变量 个数时，有无穷多解。
四、无（有）界解
max z=x1+x2 -2x1+x2 4 x1- x2 2 -3x1+x23 x1 ,x2 0
反之，若加了人工变量的问题解后最优解中仍含人工变量为 基变量，便说明原问题无可行解。例3的单纯形表格为：
Cj
3
-1
-1
0
0
-M
CB XB b
x1
x2
x3
x4
x5
x6
0 x4 1
1
-2
1
1
0
0
-M x6 13 -4
1
2
0
-1
1
-M x7 1 -2
0
[1] 0
0
0
j
3-6M M-1 3M-1 0
-M
x1 2 x2 x3 x4
11
4 2
x1 x1
x2
2
x3 x3
例8 试用两阶段法求解线性规划问题
min z =-3x1+x2+x3
x1 2 x2 x3 11
s.t.
4 x1 2 x1
x2
2x3 3 x3 1
x1 , x2 , x3 0
0 0 -1 0 0
x2
3 5 11/5
Z0=0
Z1=15
x1
如果将x1换入基底，得 另一解，由可行域凸性 易知，有两个最优解必 有无穷多组最优解 当非基底变量的检验数 中有取零值，或检验数 中零的个数大于基变量 个数时，有无穷多解。
四、无（有）界解
max z=x1+x2 -2x1+x2 4 x1- x2 2 -3x1+x23 x1 ,x2 0
反之，若加了人工变量的问题解后最优解中仍含人工变量为 基变量，便说明原问题无可行解。例3的单纯形表格为：
Cj
3
-1
-1
0
0
-M
CB XB b
x1
x2
x3
x4
x5
x6
0 x4 1
1
-2
1
1
0
0
-M x6 13 -4
1
2
0
-1
1
-M x7 1 -2
0
[1] 0
0
0
j
3-6M M-1 3M-1 0
-M
x1 2 x2 x3 x4
11
4 2
x1 x1
x2
2
x3 x3
运筹学课件1-4单纯形法计算步骤
b 21 4
9 4
3 x1 1 -1 3 4 -1 12
9 x2 3 1 9 0 1 0
0 x3 1 0 0 1 0 0
0 x4 0 1 0 -3 1 -9
θ 7 4
9/4 -
所以把x3换出为非基变量，x1为换入变量即新的基变量。
第20页
cj
CB 0 0
0 9 3
XB x3 x4 cj-zj x3 x2 cj-zj x1
cj-zj
x3 x1 x5 cj-zj
6
0 1 0
5
5/2 1/2 1
0
1 0 0
0
-1/2 1/2 -1
0
0 0 1
75 5
0
2
0
-3
0
5
x2
5
0
1
0
-1
1
第10页
cj CB 0 0 0 0 6 0 XB x3 x4 x5 b 90 75 80 105/2 75/2 5
6 x1 1 2 2
5 x2 3 1 2
9/4
-
3 9
9/4 25/4
1 0 0
25
第24页
cj CB 0 0 XB x3 x4 cj-zj b 21 4
3 x1 1 -1 3
9 x2 3 1 9
0 x3 1 0 0
0 x4 0 1 0 θ 7 4
0
9
x3
x2 cj-zj x1 x2 cj-zj
9
4
4
-1 12
0
1 0 0 1 0
1
0 0 1/4 1/4 -3
i 1
第1页
单纯形表求解线性规划问题
第四节 单纯形法的计算步骤
上表中由于所有σ 上表中由于所有 j>0 ，表明已求得最优解 x1=4， x2=2， x3=0， x4=0， x5=0， x6=4， ， ， ， ， ， ， Z=14。 。 当确定x 为换入变量计算θ值时 值时， ◆当确定 6为换入变量计算 值时，有两个相 同的最小值： 同的最小值：2/0.5=4，8/2=4。任选其中一 ， 。 个作为换出变量时， 个作为换出变量时，则下面表中另一基变 量的值将等于0，这种现象称为退化 退化。 量的值将等于 ，这种现象称为退化。含有 一个或多个基变量为0的基可行解称为 的基可行解称为退化 一个或多个基变量为 的基可行解称为退化 的基可行解。 的基可行解。
18
迭代
xB
次数
cB
x1
x2
x3
x4
x5 bi
θi
50
x1
100
0
0
0
50 0 100
1 0 0
0
0 0 1
0
1 -2 0
- 50
0 1 0
0
-1 1 1
- 50
50 50 250 -27500
2
x4 x2
σj
2010年8月
管理工程学院
18
《运筹学》 运筹学》
19
所有的检验数 σ j ≤ 0, 此基本可行解： 此基本可行解：
2010年8月
管理工程学院
5
《运筹学》 运筹学》
6
c1 … cl b b1´
⋮
c j→ cB c1
⋮
… cm … xm …0 …⋮ 0 …1 …
⋮
…cj …xj …a1j´ …⋮ a2j´ …⋮ amj´
… ck … cn … xk …xn …0 …⋮ 1 …0
单纯形法的计算步骤
运筹学基础及应用
解：化标准型
max
z 2 x1 x2 0 x3 0 x4 0 x5 5 x2 x3 15 6 x 2 x x4 24 1 2 x5 5 x1 x2 x1 , , x5 0
运筹学基础及应用
表1：列初始单纯形表 （单位矩阵对应的变量为基变量）
运筹学基础及应用
单纯形表
- Z x1基变量 x 2 ... xm XB 0 1 1E 0 单位阵 ....... 0 1 1 c c 0... c 1 2 m xm xNn 非基变量 1 .... X a1m 1 ...a1n a 2 m 1N...a 2 n
非基阵 ......
在上一节单纯形法迭代原理中可 知，每一次迭代计算只要表示出当前的约 束方程组及目标函数即可。
a1m 1 xm 1 ..... a1n xn b1 x1 x a2 m 1 xm 1 ..... a2 n xn b2 2 .......... .......... .......... ..... xm amm 1 xm 1 ..... amn xn bm Z c1 x1 ... cm xm cm 1 xm 1 ... cn xn 0
3
0 1 5/4 -15/2 1*3/2 0 0 1/4 -1/2 +0*15/2 检验数<=0 1 0 -1/4 3/2
cj z j
8.5
0
0
-1/4
-1/2
最优解为X=(7/2,3/2,15/2,0,0) 目标函数值Z=8.5
cj
CB
0 0 0
2
1
0最小的值对应 0 0
运筹学单纯形法各个步骤详解
运筹学单纯形法各个步骤详解1. 引言大家好，今天咱们来聊聊一个听起来有点高深莫测，但其实特别有意思的东西——运筹学的单纯形法。
别看它名字复杂，其实它就是解决线性规划问题的绝招，像一把钥匙，打开了优化的宝藏。
想象一下，如果你有一大堆资源，要把它们分配到不同的地方，听起来就像玩拼图一样。
好了，废话不多说，咱们直接进入正题！2. 单纯形法的基本概念2.1 线性规划的起源首先，线性规划是啥？简单来说，它就是在一系列限制条件下，想要最大化或最小化某个目标函数。
这听起来像是在做一场抉择，你得在各种选择中找到最优解。
有点像在超市里，看到一堆零食，犹豫不决，最后只能选那包最爱吃的，既美味又划算。
2.2 单纯形法的基本思路而单纯形法就是解决这个问题的武器。
它的核心思想很简单，跟追求完美一样，咱们要一步步地朝着最优解迈进。
想象你在爬山，每一步都在找那个最容易走的路，直到你站在山顶，俯瞰整个美景，啊，真是太棒了！3. 单纯形法的步骤3.1 初始化那么，怎么开始呢？首先，咱们得把问题转化为标准形式。
这就像把一个繁杂的图案简化成几何图形，让它看起来更清晰。
要把不等式转换为等式，添加松弛变量，这样就可以把问题整理得干干净净。
3.2 构建初始单纯形表接下来，咱们构建初始单纯形表。
这个表就像一本菜单，上面列出了所有可能的选择和它们的成本。
每个变量都有自己的“价格”，而咱们的目标就是尽量少花钱，最大化收益。
想想你逛街时，总是想着要花最少的钱买到最好的东西，嘿，这就是单纯形法的精神！3.3 寻找基变量和入基变量然后，咱们得找出“基变量”和“入基变量”。
基变量就像在舞台上表演的演员，而入基变量就是准备加入的“新人”。
在这个过程中，咱们得判断哪个新人能让整个表演更精彩。
如果找对了，舞台瞬间就能变得熠熠生辉，若是找错了，哎呀，那可就尴尬了。
3.4 更新单纯形表一旦找到了合适的入基变量，咱们就得更新单纯形表。
这一步就像在调味，添加新的元素，让整体味道更加丰富。
运筹学02-单纯形法
反之，若经过迭代，不能把人工变量都变
为非基变量，则表明原LP问题无可行解。
19
第2章
单纯形法
2.3 人工变量法
2.3.1 大M法
在原问题的目标函数中添上全部人工变量，并令其系数 都为-M，
而M是一个充分大的正数。即
max z = c1x1 + c2x2 + c3x3 + … + cnxn – M( xn+1 + xn+2 +…+ xn+m )
思路：由一个基本可行解转化为另一个基本可行解。 等价改写为 目标方程 max z max z = 3x1+5x2 z -3x1 -5x2 = 0 z -3x1 -5x2 x1 +x3 x1 +x3 = 8 2x2 +x4 2x2 +x4 = 12 s.t. s.t. 3x1+4x2 +x5 3x1 + 4x2 +x5 = 36 x1 ， x2 ，x3，x4，x5 x1 ， x2 ，x3，x4，x5 ≥ 0
以主列中正值元素为分母，同行右端常数为分子，求比值；
6
第2章
单纯形法
2.1 单纯形法的基本思想
(Ⅰ)
用换基运算 将X0 转化为 另一个基本 可行解 X1。
z- 3x1 -5x2 = 0 0 换基运算—— x1 +x3 = 8 ① 方程组的初等变换 目的是把主列变为 22x2 +x4 = 12 ② 单位向量：主元变 3x1 + 4x2 +x5 = 36 ③ 为1，其余变为0。 X0 = ( 0, 0, 8, 12, 36 )T z0 = 0
⑴ 当前基：m阶排列阵
运筹学第2章单纯形法
==８ ==6
① ② ③
－２Ｘ４＋Ｘ５ ＝１２
得到新的基本可行解 X1 =(0,6,8,0,12)T
(1)、决定进基变量：1=--3, X1进基 (2)、决定离基变量：最小比值规则来确定主 元与离基变量.
则Xl为进基变量。 MIN(8/1,-,12/3)=12/3 此时可以确定X5为离基变量
Z
X(0) =(0, 0, 10, 15 )T
Z0 =0
Z-30X1-20X2 =0 选中X1从0↗，X2 =0 X3=10-(-X1 )0
X4=15-(-3X1 )0 求X1， X1→+ ,Z→+
2.2.3 单纯形法计算之例
2-3 人工变量法 (Artificial Variable)
+1/2X4
+X5 =42 =6
X3 +2/3X4 -1/3X5 =4
X2 +1/2X4
X1 -2/3X4+1/3X5=4 令X4 =X5 =0 X =(4, 6, 4, 0, 0)T Z =42
。此时4=1/2,
Z值不 再增大了,X值是最优基本解
5
=1,
* T * 即:X =(4,6) ,Z =42
检验数
当目标方程中基变量系数全为0时，非基 变量的系数可以作为检验当前的基本可 行解是否最优的标志，称之为检验数。
(2)、判定解是否最优 Z-3X1-5X2 =0 当X1从0↗或X2从0↗ Z从0↗ ∴ X0 不是最优解
(3)、由一个基可行解→另一个基可行解。 ∵ -5<-3 选X2从0↗，X1 =0 X3 =8 X4 =12-2X2 0 X2 12/2
N
沿边界找新 的基本可行解
结束
① ② ③
－２Ｘ４＋Ｘ５ ＝１２
得到新的基本可行解 X1 =(0,6,8,0,12)T
(1)、决定进基变量：1=--3, X1进基 (2)、决定离基变量：最小比值规则来确定主 元与离基变量.
则Xl为进基变量。 MIN(8/1,-,12/3)=12/3 此时可以确定X5为离基变量
Z
X(0) =(0, 0, 10, 15 )T
Z0 =0
Z-30X1-20X2 =0 选中X1从0↗，X2 =0 X3=10-(-X1 )0
X4=15-(-3X1 )0 求X1， X1→+ ,Z→+
2.2.3 单纯形法计算之例
2-3 人工变量法 (Artificial Variable)
+1/2X4
+X5 =42 =6
X3 +2/3X4 -1/3X5 =4
X2 +1/2X4
X1 -2/3X4+1/3X5=4 令X4 =X5 =0 X =(4, 6, 4, 0, 0)T Z =42
。此时4=1/2,
Z值不 再增大了,X值是最优基本解
5
=1,
* T * 即:X =(4,6) ,Z =42
检验数
当目标方程中基变量系数全为0时，非基 变量的系数可以作为检验当前的基本可 行解是否最优的标志，称之为检验数。
(2)、判定解是否最优 Z-3X1-5X2 =0 当X1从0↗或X2从0↗ Z从0↗ ∴ X0 不是最优解
(3)、由一个基可行解→另一个基可行解。 ∵ -5<-3 选X2从0↗，X1 =0 X3 =8 X4 =12-2X2 0 X2 12/2
N
沿边界找新 的基本可行解
结束
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
已知 b x1 x2
b '1
A
bm'
c0m 0cn
xm xn min
— 24/6 5/1
z0
检验数
单纯形表
单纯形表结构
c j
2
CX
B
B
b
x1
c1 x1 b '1
cm xm bm'
c j
z j
z0
基可行解：
X (b1,, bm ,0,,0)
1
0C 0 0
Z c1x1 ... cm xm cm1xm1 ... cn xn 0
单纯形表
- Z x1 基x变2量..X.B xm
0 1
0 1B
基矩....阵...
0
1
1 c1 c20... cm
xm非1基.变..量.XxN n
a1m1 ...a1n
30
xx
2
3
21
00
40
30
0
xx
4
5
0
1
0
0
X 0 (0, 0,8,16,12)T
表1：列初始单纯形表
（单位矩阵对应的变量为基变量）
c j
CX
B
B
b
x x x x x 2
0 1
3
2
00
最小的值对应的行
为主行
3
4
5 min
0
x 3
8
1 21 0
4
0
x 4
16 0 4
0
0
1
—
0
x 5
12
xn min
c1 x1 b '1 Z Z0 j x j
A jm1
cm xm bm'
— 24/6 5/1
z c z
j
求j 0
有时不写
此项
检验数
m
m
令：Z0 cibi' 单纯形表 i1
Z j ciai'j
i 1
n
Z 单Z纯0 形j表m1(结c j 构 Z j )x j
00
4
0
0
3
c z
j
j
12
3 0主元化0为1
0
主列单位向量
正检验数中最大者对应的列 为主列
x5 换出
x2 换入
表2：基变换
（初等行变换，主列化为单位向量，主元为1）
c j
CX
B
B
b
x x x x x 2
0 1
3
2
0 0 最小的值对应的行 为主行
3
45 min0 Nhomakorabeax 3
2
1 0 1 0 -2
0
x 4
16 1/24
3 x2 3 0 0
c z
j
j
1/42
z 33 9
00 1
4
1主元化0为1 0
—
主列单位向量
0 x30换出
-
0 x1 换入 3/4
正检验数中最大者对应的列
X 1 (为0,主3列, 2,16, 0)T
表3：基变换
（初等行变换，主列化为单位向量，主元为1）
c j
CX
x1
x2
a1m1xm1 ..... a1n xn b1 a2m1xm1 ..... a2n xn b2 ...................................
xm amm1xm1 ..... amn xn bm
x2 xmxn min
—
A
24/6 5/1
检验数
单纯形表令：Z0
m
cibi'
i 1
m
Z j ciai'j i 1
n
单纯形表结构Z Z0 (c j Z j )x j
c j
CX
B
B
j m1
b
2令x1：1xj 2
(c
n
j0CZ
j
)
0
xm
0 检验 数
单纯形表结构 i
a
bi'
' imk
a' imk
0
bl' a'
lmk
c j
2
CX
B
B
b
x1
c1 x1 b '1
cm xm bm'
z c z
j
j0
1 0C
x2
A
0 0
xm xn min
a1,mk 主行 —
am ,mk
25求4/1l/6
检验数 mk
B
B
230 0
b
0x x x x
1
2
3
4
x5 min
2 x1
0 3
xx 42
21 8 1/20 3 20
01 0 -4 10
0-—
1
4
0
12
c z
j
j
1/40 0 -2
0
z* 2 2 313/4 13
X 2 (2,3, 0,8, 0)T
表4：最终单纯形表
c j
2
x b C X
...
......
amm1
...
m
cm1 ciai,m1 i 1
xn
a1n a2n
amn
m
cn ciain i 1
b
b1
b2
bm
m i 1
cibi
单纯形表
单纯形表结构
c j
CX
B
B
c1 x1
cm xm
c z
j
j
C 2c1 c1 2 0
令：c j j
(c j
Z
j2)
x n
b ZCB Z0XB j x j 1
c1
x1j m
1
b
'
1
cm xm bm'
1 检验 0C数 0 c j0
x2 xmxn min
a1 j
—
A
24/6
am j
5/1
z c z
j
j0
检验数 求j
单纯形表
min
a2mN1 ...a2n ...非... 基阵
a mm 1 ...a mn cm1 N cn
b
b1
b2
bm 0
单纯形表
-Z x1 x2... xm
0
1
0 1
.......
0
1
1 0 0 ... 0
xm1
....
a1m1
...
a2m1
第四节 单纯形法的计算步骤
单纯 为书写规范和便于计算，对单纯形法的计算设计了 形表。每一次迭代对应一张单纯形表，含初始基可行解的单纯 形表称为初始单纯形表，含最优解的单纯形表称为最 终单纯形表。本节介绍用单纯形表计算线性规划问题的
步骤。
在上一单节纯单纯形形表法迭代原理中可知，每一
次迭代计算只要表示出当前的约束方程组 及目标函数即可。
B
B
x1 2x2 x3
8
s.t.
4
x1
4 x2
x4
16
x5 12
x1, x2 , x3, x4 , x5 0
表1：列初始单纯形表
（单位矩阵对应的变量为基变量）
c j
CX
B
B
b
0
x 3
8
0
x 4
16
0 x 12 5
c z
j
j
z0
2
0x 1
1 04 00 12 0
不妨设此为
主列
单纯形表
单纯形表结构
c j
2
CX
B
B
b
x1
c1 x1 b '1
cm xm bm'
z c z
j
j0
主元
1 0C
x2
A
0 0
xm xn min
a1,mk
—
a l,m k
am ,mk
254/1l/6
检验数 mk
用单纯形表求解例1
max z 2x1 3x2 0x3 0x4 0x5