第十一章北航 材料力学 全部课件 习题答案
材料力学第十一章

2F 2 ⋅ 3l 8
2F 2 ⋅ l
×2+
4=
7lF 2
2EAi π E(2d )2
π Ed 2 8π Ed 2
(c)取 d x 长的微段(如右图),在均布轴力 f 的作用下,它具有的应变能
dVε
=
1 2
FN (x)dΔ
式中
FN (x)
=
F l
x,
dΔ = FN (x)dx = Fx dx EA EAl
=
Vε
(F
)
+
Vε
(M
)
+
1 2
(Mθ
+
Fwmax
)
。
11-2 图示简支梁中点只承受集中力 F 时,梁的最大转角为θ max ,应变能为Vε (F ) ;中 点只承受集中力偶 M 时,最大挠度为 wmax ,梁的应变能为Vε (M ) 。当同时在中点施加 F
和 M 时,梁的应变能为多少?
解 对于线性结构简支梁,先加 F 时梁贮存的应变能
(顺)
(二)单位载荷法解(a)
(a3)
(a4)
(a5)
149
解 图(b)
FA
=
FB
=
Me 2a
AD 段
M (x1 ) =
Me 2a
x1 , M 1(x1 ) =
x1 , M
2 (x1 ) =
− x1 2a
DC 段
M (x2 ) = M e , M 1(x2 ) = 2a − x2 , M 2 (x2 ) = −1
11-5 超静定问题有哪几类?怎样确定超静定问题的次数?什么是相当系统?什么是静 定基?静定基是否唯一?
答 超静定问题有外约束超静定、内约束超静定及外约束超静定加内约束超静定混合。 全部未知力个数与全部独立平衡方程数的差就是超静定问题的次数。 拆去多余内、外约束,用相应的约束力代替其作用,使之成为静定形式的结构,它就 是原结构的相当系统(相当系统加上变形协调条件称为原超静定结构的等效系统)。 解除约束后的不包括外载荷的静定结构称为原结构的静定基。 静定基不唯一。
材料力学第十一章习题选及其解答

11-2. 桥式起重机上悬挂一重量G=50kN 的重物,以匀速度v=1m/s 向前移动(在图中移动的方向垂直于纸面)。
若起重机突然停止移动,重物将象单摆一样向前摆动。
若梁为No14工字钢,吊索截面面积A=5×10-4m 2,试问当惯性力为最大值时,梁及吊索内的最大应力增加多少?解:(1)起重机突然停止时,吊索以初速v 作圆周运动,此时吊索轴力增量是kN Rv g G ma N n D 28.12=⋅==Δ(2)吊索的应力增量是MPa AN σDd 56.2==ΔΔ (3)梁内最大弯矩的增量是l N M D ΔΔ41=(4)查表得梁的抗弯截面系数3610102m W -⨯=(5)梁内最大正应力的增量是MPa WM σd 68.15'==ΔΔ11-4. 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘ω=40 1/s 的匀角速度转动,试求轴内因这一圆孔引起的最大正应力。
解:(1)假设挖空圆盘和圆孔部分的质量分别是M 和m ,它们的质心距轴线的距离分别为R 的r ,则有mr MR =(2)挖空圆盘的惯性力是kN ωr gVγωmr ωMR Ma F n n 64.10222=⋅==== 上式中钢的密度取3/8.76m kN γ=(3)轴内的最大正应力增量是MPa WlF W M σnd 5.1241max max ===Δ11-5. 在直径为100mm 的轴上装有转动惯量I=0.5kN ⋅m ⋅s2的飞轮,轴的转速为300r/min 。
制动器开始作用后,在20转内将飞轮刹住,试求轴内最大剪应力。
设在制动器作用前,轴已与驱动装置脱开,且轴承的磨擦力矩可以不计。
解:(1)飞轮作匀减速转动2220/25.120/42.3130s rad φωωεωs rad πn ωt t -=-=∴=== (2)惯性力距是kNm εI m d 96.1=-=(3)轴在飞轮和制动器之间发生扭转变形MPa d πTW T τm T t d 10163max ===∴= 11-6. 钢轴AB 的直径为80mm ,轴上有一直径为80mm 钢质圆杆CD ,CD 垂直于AB 。
北航材料力学课后习题答案

σ max = 117MPa (在圆孔边缘处)
2-15 图示桁架,承受载荷 F 作用,已知杆的许用应力为[σ ]。若在节点 B 和 C 的
位置保持不变的条件下,试确定使结构重量最轻的α 值(即确定节点 A 的最佳位置)。
解:1.求各杆轴力
题 2-15 图
设杆 AB 和 BC 的轴力分别为 FN1 和 FN2 ,由节点 B 的平衡条件求得
分别为
FN
=
1 2
σmax A
=
1 2
× (100 ×106 Pa) × (0.100m × 0.040m)
=
2.00 ×105 N
=
200kN
Mz
=
FN
(
h 2
−
h )
3
=பைடு நூலகம்
1 6
FN h
=
1 × (200 ×103 N) × (0.100m) 6
= 3.33×103 N ⋅ m
=
3.33kN ⋅ m
2-5 .........................................................................................................................................................2
= 0.2 ×10−3 m 0.100m
= 2.00 ×10−3
rad
α AB
= 0.1×10−3 m = 1.00 ×10−3 0.100m
rad
得 A 点处直角 BAD 的切应变为
γ A = γ BAD = α AD − α AB = 1.00 ×10−3 rad
材料力学习题解答11 ppt课件

2.如图所示各梁的抗弯刚度为EI,试用卡氏定理 计算C截面的挠度和B截面的转角。
解: (a) 在B截面处虚加一力偶m。
A
M1(x) 2Fx
M2(x) m 2Fx F(x a)
结构总应变能为:U
a
M
2 1
d
x
2a M22 d x
0 2EI
a 2EI
F
2F
EI m B
a
M
2 1
d
x
2a M22 d x
0 2EI
a 2EI
C
B
a
a
(a)
R
wC
U R
a M1 0 EI
M1 d x R
(Fa / 2)(2a) 3EI
F (2a)2 16EI
Fa2 1 1 1 5Fa2 ( )
EI 8 3 4 24EI
A
a
F
F
C
D
B
EI
a
a/2
(b)
应用能量法计算太麻烦!
ppt课件
6
3.如图所示结构,刚架各段的抗弯刚度为EI,拉杆的 抗拉刚度为EA。试用卡氏定理计算C点的竖向位移。
材料力学习题解答11
能量法
ppt课件
1
卡氏定理
1.如图所示支架中,AB和AC杆在A处铰接在一起并 可看成是刚体,拉杆长L=2m,横截面的直径d=15mm ,弹性模量为E=210GPa,载荷F=20kN。试求A点的竖 向位移和C点的水平位移。
解:
由整体平衡有:RB
RC
F 2
F A
由杆件AB的平衡有:
工程力学材料力学答案-第十一章
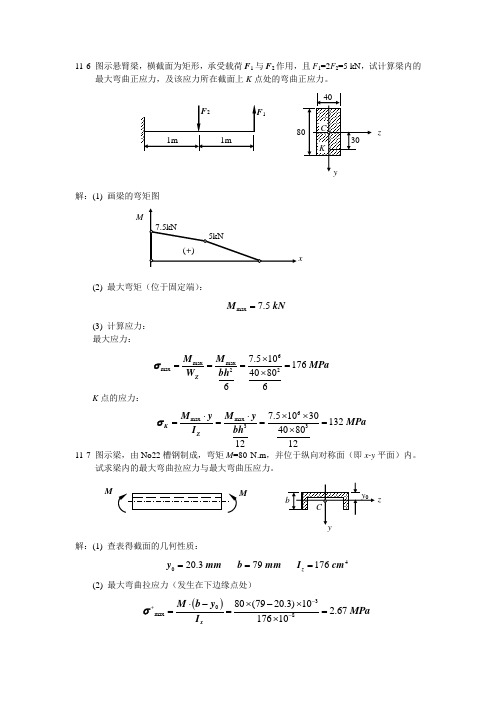
11-6 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图(2) 最大弯矩(位于固定端):max 7.5 M kN =(3) 计算应力: 最大应力:K 点的应力:11-7 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力(发生在下边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力(发生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为:49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为:2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力:2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力[σ-]=120 MPa ,试校核梁的强度。
材料力学答案2及材料力学答案第十一章

习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1)作轴力图; (2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε N-图 CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε (4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=- a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=-a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为1cm 的圆杆,在拉力P =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
解:(1) 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- (2)︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒ 2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
材料力学答案第十一章
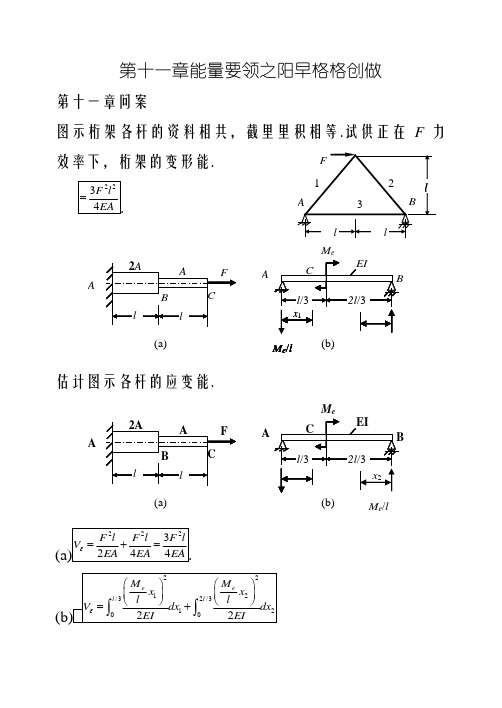
第十一章能量要领之阳早格格创做第十一章问案图示桁架各杆的资料相共,截里里积相等.试供正在F 力效率下,桁架的变形能.估计图示各杆的应变能.传动轴受力情况如图所示.轴的直径为40mm ,资料为45钢,E = 210GPa ,G = 80GPa.由扭转引起的应变能: 由蜿蜒引起的应变能:估计图示梁的应变能,并证明是可谦脚叠加本理及其本果.而没有谦脚叠加本理,果为应变能取内力的闭系没有是线性的.借帮于附录E ,供跨度中面(睹课本下册p40例12-4)11.6 图示刚刚架的各杆的EI 皆相等,试供截里A 、B 的位移战截里C 的转角.(a)A 面:正在A 面加一个背下的单位力.M (x 1)=0, M (x 2)=Fx 2, M (x 3)=FbC 面:正在C 加一个顺时针的力奇矩为1的单位力奇(b) A 面:正在A面加一个背下的单位力B 面:正在B 面加一个背左的单位力图示桁架各杆的资料相共,截里里积相等C 处的火仄位移战笔直位移.CF BAR火仄位移:(122) 3.828Fl FlEA EA +=-=-.笔直位移:Fl EA ∆=-.2,E 索 = 177GPa.F = 20kN ,(a)假设横梁ABCD 为刚刚体,供C 面的笔直位移.(2)若没有把ABCD 假设为刚刚体,且已知其抗直刚刚度为EI 2,试再供C 面的笔直位移.(1)42110.87.891033F EA -⎛⎫∆=⨯=⨯ ⎪⎝⎭m.(2)20.44047.89102Fx dx EI -∆=⨯+⎰4447.8910 1.48109.3710---=⨯+⨯=⨯m.11.9 等截里直杆BC 的轴线为四分之三的圆周.若AB 杆可视为刚刚性杆,试供正在F 力效率下,截里B 的火仄位移及笔直位移.火仄位移:M ()=FR cos, ()sin M R θθ=33320sin cos 2FR FRd EI EI πθθθ∆==⎰.D CFAB60 ° 60 ° 800 400400RFO B BF ORA F笔直位移:()(1cos )M R θθ=--33.36FR EI =.11.10 图示圆弧形小直率杆,仄衡半径为R .力F笔直于圆环中线地圆的仄里.试供二个F 力效率面的相对于线位移.M ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=-333pFR FR EI GI ππ=+.11.11图示圆弧形小直率杆,仄衡半径为R .正在横截里A 取B 处受一对于集结力F 效率.力F 正在圆环中线地圆的仄里内.试供二个F 力效率面的相对于线位移. M ()=FR sin,()sin M R θθ=32320sin FR FRd EI EI πθπθ∆==⎰.11.12图示轴线为火仄里内四分之一圆周的直杆,正在自由端B 效率笔直荷载F ,设EI 战GI P 为已知,试供正在F 力效率下端里B 的笔直位移.F O O Rθ B F AM ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=- 33(38)44pFR FR EI GI ππ-=+.。
工程力学材料力学答案-第十一章

11-6 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图(2) 最大弯矩(位于固定端):max 7.5 M kN =(3) 计算应力: 最大应力:K 点的应力:11-7 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力(发生在下边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力(发生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为:49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为:2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力:2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力[σ-]=120 MPa ,试校核梁的强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹簧支持。试证明压杆的临界载荷满足下述方程:
sin
kl 2
sin
kl 2
kl 2
1
4k 2EI cl
cos
kl 2
0
式中, k F /(EI) 。
8
题 11-10 图 解:该细长压杆的微弯状态如图 11-10 所示。
图 11-10 按图中所取坐标,左、右段压杆得弯矩方程分别为
N/mm 时,截面 B 的挠度分别为何值。横梁与立柱均用低碳钢制成,弹性模量 E = 200 GPa,
比例极限 p =200 MPa。
11
题 11-13 图 解:1.求立柱的临界载荷
给立柱和梁编号分别为 1 和 2,我们有
λp π
E π σp
200109 200106
99.3
i I1 d 10mm0.010m A1 4
6
由此得
FN1 FN2 FN3 FN4
F 2
Fcr
2
(
π
2
l
EI
2
)
2π 2 EI l2
11-9 图 a 所示细长压杆,弯曲刚度 EI 为常数,试证明压杆的临界载荷满足下述方程:
式中,k2=F/(EI)。
sinkl(sinkl2klcoskl)0
题 11-9 图
解:在临界载荷作用下,压杆可在图 b 所示微弯状态保持平衡。
w2
A2sinkx2
B2coskx2
Fc 2F
x2
由此得
当x1 0,w1 0; 当x2 0,w2 0
位移连续条件为 代入通解后,得
重排后,得
B1 0,B2 0
当
x1
x2
l 2
:
w1
Fc c
;
w2
Fc c
;
w1 w2
A1sin
kl 2
Fcl 4F
A1sinkl
A1sin kl A2 sin kl 0
A1k coskl
A2k coskl
l
可见,A1,A2 与存在非零解的条件为
sin kl 0 1 sin kl -sinkl 0 0 k coskl kcoskl 1/l
由此得
sinklsinkl 2klcoskl 0
32alFcr
4
32 0.500 0.300 42103
m 0.030m 30 mm
πG
π 79109
图 11-4
4
11-6 图示细长压杆,弯曲刚度 EI 为常数,试按§11-2 所述方法确定杆的临界载荷。
解:设自由端的挠度为,则 挠曲轴近似微分方程为 或 式中,
题 11-6 图
2
sin
kl 2
[sin
kl 2
k
(
l 2
2k
2 EI c
)cos
kl 2
]
0
sin kl [sin kl kl (1 4k 2EI )coskl ] 0
2 22
cl
2
11-11 图示阶梯形细长压杆,左、右两段各截面的弯曲刚度分别为 EI1 与 EI2 。试
证明压杆的临界载荷满足下述方程:
3
题 11-4 图
解:刚性杆 AB 在微偏斜(设偏斜角为 ,见图 11-4)状态下处于平衡,此时加给轴 BC
的扭力矩为
M B Fa
而
Tl GI p
注意到 T M B ,于是得 即
由此得(题中给出 F=42kN)
F GIp al
Fcr
GI p al
πGd 4 32al
4
d
coskl 0
由上式得
kl nπ (n0,1,2,)
(c)
2
将式(c)代入式(a),得
Fcr
n 2 π 2 EI 4l 2
由上式并取 n=1,即得压杆的临界载荷为
(n 0,1,2,)
Fcr
π 2 EI 4l 2
11-7 试确定图示各细长压杆的相当长度与临界载荷。设弯曲刚度 EI 为常数。
MC 0,
c l F 0 2
Fcr
cl 2
1
图 11-2a (b)解:设系统微偏转如图 11-2b(1)所示,铰链 A 与 B 的铅垂位移分别用与表示,于 是得杆 AB 的受力如图 11-2b(2)所示,杆的平衡方程为
Fy 0, c22 c11 0
(a)
M A 0, c22l F (1 2 )0
F 为何值时结构中的个别杆件将失稳?如果将载荷 F 的方向改为向内,则使杆件失稳的载荷 F 又为何值?
题 11-8 图
解:1.当 F 向外时
竖向杆 CD 受压,其余四根杆受拉。 设杆 CD 编号为 5,则有
由此得
FN5 F
Fcr
π 2 EI ( 2l)2
π 2 EI 2l 2
2.当 F 向内时 此时杆 5 受拉,其余各杆(编号 1,2,3,4)受压。且
当x2 l时,w2 δ
B1 δ
A1 0
B2 δcosk1l
(a)
A2
k1 k2
δsink1l
(b)
A2sink2l B2cosk2l 0
(c)
将式(a)和(b)代入式(c),于是得
t
ank1l
t
ank2l
k2 k1
11-13 图示结构,由横梁 AC 与立柱 BD 组成,试问当载荷集度 q =20 N/mm 与 q =26
由于 q qcr ,立柱中 FN Fcr ,直线平衡状态是稳定的。 由变形协调条件
wB Δl1 得
代入已知数据后,得
5ql24 FNl23 FNl1 384EI2 48EI2 EA1
12
进而可得截面 B 的挠度为
FN 4.8554104 N 48.554kN
wB
Δl1
FN l1 EA1
上述方程有两组可能的解,即: sinkl 0
sinkl 2klcoskl 0 由上述二方程的最小非零正根,分别得
Fcr,1
π
2
l
EI
2
显然,压杆的临界载荷为
Fcr,2
1.359EI l2
Fcr
Fcr,2
1.359EI l2
11-10 图示两端铰支细长压杆,弯曲刚度 EI 为常数,压杆中点用弹簧常量为 c 的
2
题 11-3 图 解:结构的临界状态示如图 11-3。
图 11-3 使梁 B 端截面产生转角 θB 的力矩应为
Me
3EI l
θB
而
Me F (θBa)
由此得 即
F 3EI al
Fcr
3EI al
11-4 图示刚性杆 AB,下端与圆截面钢轴 BC 相连。为使刚性杆在图示铅垂位置保
持稳定平衡,试确定轴 BC 的直径 d。已知 F = 42 kN,切变模量 G = 79 GPa。
(b)
由式(b)得
F c22l
(c)
1 2
由式(a)得
2
c11 c2
代入式(c),于是得系统的临界载荷为
Fcr
c1c2l c1 c2
图 11-2b
11-3 图示结构,AB 为刚性杆,BC 为弹性梁,各截面的弯曲刚度均为 EI。在刚性杆
顶端承受铅垂载荷 F 作用,试求其临界值。
第十一章 压杆稳定问题
11-1 图示两端铰支刚杆-蝶形弹簧系统,试求其临界载荷。图中,c 代表使蝶形弹
簧产生单位转角所需之力偶矩。
题 11-1 图
解:系统的临界状态(微偏斜状态)如图 11-1 所示。注意到蝶形弹簧产生的转角为 2θ ,
由右段刚杆的力矩平衡方程
c(2θ) F (θ l ) 0 2
上述微分方程的通解分别为
w1 A1sinkx1 B1coskx1 l x1
(a)
w2 A2 sinkx2 B2 coskx2
(b)
式中,除参数 k 外,积分常数 A1,A2,B1,B2 与端点挠度也均为未知。 压杆的位移边界条件与连续条件为:
在 x1 0 处, w1 0
(a)解:相当长度为
题 11-7 图
5
leq a
临界载荷为
Fcr
π 2 EI a2
(b)解:压杆微弯状态的挠曲轴如图 11-7b 中的虚线所示。
半个正弦波的长度为 a,即
图 11-7b
leq a
由此得临界载荷为
Fcr
π 2 EI a2
11-8 图示正方形桁架,各杆各截面的弯曲刚度均为 EI,且均为细长杆。试问当载荷
以上二微分方程的通解为
k12
EFI1,k22
F EI2
位移边界与连续条件为 由上述条件依次得
w1 A1sink1x1 B1cosk1x1 δ w2 A2sink2x2 B2cosk2 x2 δ
当x1 0时, w1 0,w1 0 当x1 l与x2 0时, w1 w2,w1 w2
得
Fcr
4c l
图 11-1
11-2 图示刚杆-弹簧系统,图中的 c,c1 与 c2 均为弹簧常数,试求系统的临界载荷。
题 11-2 图 (a) 解:设系统微偏转如图 11-2a(1)所示,铰链 C 的铅垂位移用表示,于是得杆 BC(连带 铰链 C)的受力如图 11-2a(2)所示,由平衡方程
