机械工程测试技术课后题答案解析[清华出版_韩建海主编]
机械工程测试技术习题课后题解答

1 求周期方波的傅立叶级数(复指数函数形式),画出|cn|-ω和ϕ-ω图。
(1)方波的时域描述为:(2) 从而:2 . 求正弦信号的绝对均值和均方根值。
(1)(2)3.求符号函数和单位阶跃函数的频谱解:(1)因为不满足绝对可积条件,因此,可以把符合函数看作为双边指数衰减函数:其傅里叶变换为:(2)阶跃函数:4. 求被截断的余弦函数的傅里叶变换。
解:(1)被截断的余弦函数可以看成为:余弦函数与矩形窗的点积,即:(2)根据卷积定理,其傅里叶变换为:5.设有一时间函数f(t)及其频谱如图所示。
现乘以余弦函数cosω0t(ω0>ωm)。
在这个关系中函数f(t)称为调制信号,余弦函数cosω0t称为载波。
试求调幅信号的f(t)cosω0t傅氏变换,并绘制其频谱示意图。
又:若ω0<ωm将会出现什么情况?解:(1)令(2) 根据傅氏变换的频移性质,有:频谱示意图如下:(3) 当ω0<ωm时,由图可见,出现混叠,不能通过滤波的方法提取出原信号f(t)的频谱。
6.求被截断的余弦函数的傅立叶变换。
解:方法一:方法二:(1)其中为矩形窗函数,其频谱为:(2)根据傅氏变换的频移性质,有:第二章4. 求指数衰减函数的频谱函数,()。
并定性画出信号及其频谱图形。
解:(1)求单边指数函数的傅里叶变换及频谱(2)求余弦振荡信号的频谱。
利用函数的卷积特性,可求出信号的频谱为其幅值频谱为a a`b b`c c`题图信号及其频谱图注:本题可以用定义求,也可以用傅立叶变换的频移特性求解。
5 一线性系统,其传递函数为,当输入信号为时,求:(1);(2);(3);(4)。
解:(1) 线性系统的输入、输出关系为:已知,则由此可得:(2) 求有两种方法。
其一是利用的傅立叶逆变换;其二是先求出,再求,其三是直接利用公式求。
下面用第一种方法。
(3)由可得:(4) 可以由的傅立叶逆变换求得,也可以直接由、积分求得:第三章1.说明线性系统的频率保持性在测量中的作用。
机械工程测试技术课后解答.doc

机械工程测试技术课后解答思考问题和练习0-1说明了什么是测试。
答:(1)测试示例:为了确定一端固定的悬臂梁的固有频率,可以用锤击法激励悬臂梁。
信号波形由压力传感器、电荷放大器和波形记录器记录,悬臂梁的固有频率可由衰减的振荡波形计算出来。
(2)结论:从这个例子可以看出,测试是指用于确定待测物体悬臂梁的固有频率的所有操作。
通过一定的技术手段——⑴测试实例: 为了确定一端固定的悬臂梁的固有频率,可以用锤击法激励悬臂梁。
信号波形由压力传感器、电荷放大器和波形记录器记录,悬臂梁的固有频率可由衰减的振荡波形计算出来。
(2)结论:从这个例子中可以看出,测试是指确定待测物体悬臂梁固有频率的所有操作。
通过一定的技术手段:(1)测试系统框图如图0所示——测试系统框图如图0所示:各部分功能如下。
传感器是将测量信息转换成特定电信号的装置;信号调理是将来自传感器的信号转换成适合传输和处理的形式。
信号处理部分可以对来自信号调节部分的信号执行各种操作。
过滤和分析;信号显示和记录链接将显示或存储来自信号处理链接的信号;模数转换和数模转换是模拟信号和数字信号的相互转换,以便于计算机处理。
0-信号调节是将来自传感器的信号转换成适合传输和处理的形式;信号处理部分可以对来自信号调节部分的信号执行各种操作。
过滤和分析;信号显示和记录链接将显示或存储来自信号处理链接的信号;模数转换和数模转换是模拟信号和数字信号的相互转换,以便于计算机处理。
0:这门课非常实用。
只有在学习过程中,紧密联系实际,加强实验,注重物理概念,才能真正掌握相关知识。
在教学过程中安排了与本课程相关的必要实验和练习。
只有学生积极参与实验并完成相应的练习,才能培养他们正确的实验能力,才能以一种微妙的方式获得一个相对完整的动态测试工作的概念。
只有通过这种方式,他们才能在一开始就有能力处理实际的测试工作。
思维问题和练习1-1的信号类型和特征是什么?(1)、根据信号随时间的变化规律分为确定性信号和确定性信号,确定性信号分为周期性信号(包括谐波信号和一般周期性信号)和非周期性信号(准周期性信号等非周期性信号);非确定性信号包括平稳随机信号(包括遍历信号和非遍历信号)和非平稳随机信号。
机械工程测试技术习题及解答答案

《机械工程测试技术》习题与题解第二章 习题解答2-1.什么是信号?信号处理的目的是什么?2-2.信号分类的方法有哪些?2-3.求正弦信号()t A t x ωsin =的均方值2x ψ。
解:()24sin 4222cos 12sin 2sin 11222022022022022A T T A T dtt A T tdt A T dtt A T dt t x T T T T T x =⎪⎭⎫ ⎝⎛-=-====⎰⎰⎰⎰ωωωωωψ 也可先求概率密度函数:221)(xA t p -=π则:⎰∞∞-==2)(222A dx x p x xψ。
2-4.求正弦信号())sin(ϕω+=t A t x 的概率密度函数p(x)。
解: 2221)(111,arcsin xA Ax A dx dt Ax t -=-=-=ωωϕω代入概率密度函数公式得:22222200122221lim 1lim)(xA x A x A T T dt dx T t x x p x x -=-=-=⋅=⎥⎥⎦⎤⎢⎢⎣⎡∆∆=∑→∆→∆πωπωω 2-5.求如下图所示周期性方波的复指数形式的幅值谱和相位谱txT 1-T 1T-T解 在x(t)的一个周期中可表示为⎩⎨⎧<<≤=21)(11T t T T t t x该信号基本周期为T ,基频ω0=2π/T ,对信号进行傅里叶复指数展开。
由于x (t )关于t =0对称,我们可以方便地选取-T /2≤t ≤T /2作为计算区间。
计算各傅里叶序列系数c n 当n =0时,常值分量c 0:T T dt T a c T T 1002111===⎰- 当n ≠0时,110110011T T t jn T T tjn n eTjn dt eTc -----==⎰ωωω最后可得⎥⎦⎤⎢⎣⎡-=-j e e T n c t jn t jn n 22000ωωω注意上式中的括号中的项即sin (n ω0 T 1)的欧拉公式展开,因此,傅里叶序列系数c n 可表示为0)(sin 2)sin(210010≠==n T n c TT n T n c n ,ωπωω其幅值谱为:)(sin 211T n c TT c o n ω=,相位谱为:ππϕ-=,,0n 。
机械工程测试技术课后答案

思考题与习题0-1 举例说明什么是测试?答:⑴测试的例子:为了确定一端固定的悬臂梁的的固有频率,可以采用锤击法对梁尽享激振,在利用压力传感器、电荷放大器、波形记录器记录信号波形,由衰减的振荡波形便可以计算出悬臂梁的固有频率。
⑵结论:由本例可知,测试是指确定被测对象悬臂梁固有频率的全部操作,是通过一定的技术手段—激振。
拾振、记录、数据处理等,获取悬臂梁固有频率的信息过程。
0-2以方框图的形式说明测试系统的组成,简述主要组成部分的作用。
答:⑴:测试系统的方框图如图0—1所示。
⑵:各部分的作用如下.传感器是将被测信息转换成某种电信号的器件;信号调理是把来自传感器的信号转换成适合传输和处理的形式;信号处理环节可对来自信号调理环节的信号,进行各种运算.滤波和分析;信号显示、记录环节将来至信号处理环节的信号显示或存储;模数转换和数模转换是进行模拟信号与数字信号的相互转换,以便于用计算机处理。
0—3 针对工程测试技术课程的特点,思考如何学习该门课程?答:本课程具有很强的实践性,只有在学习过程中密切联系实际,加强实验,注意物理概念,才能真正掌握有关知识。
在教学环节中安排与本课程相关的必要的实验及习题,学习中学生必须主动积极的参加实验及完成相应的习题才能受到应有的实验能力的训练,才能在潜移默化中获得关于动态测试工作的比较完整的概念,也只有这样,才能初步具有处理实际测试工作的能力。
思考题与习题1-1信号的分哪几类以及特点是什么?⑴、按信号随时间的变化规律分为确定性信号和分确定性信号,确定信号分为周期信号(包括谐波信号和一般周期信号)和非周期信号(准周期信号和以便非周期信号);非确定性信号包括平稳随机信号(包括各态历经信号和非各态历经信号)和非平稳随机信号.⑵、按信号幅值随时间变化的连续性分类,信号包括连续信号和离散信号,其中连续信号包括模拟信号和一般模拟信号,离散信号包括一般离散信号和数字信号.⑶、按信号的能量特征分类,信号包括能量有限信号和功率有限信号。
机械工程测试技术答案韩建海版

3.13何为滤波器的分辨力?它与哪些因素有关?
答:滤波器的分辨力是指滤波器分辨相邻频率成分的能力。
与滤波器带宽B、品质因数Q、倍频程选择性、滤波器因数等有关。
带宽越小、品质因数越大、倍频程选择性越小、滤波器因数越小,分辨力越高。
5.8测试系统实现不失真测量的条件是什么?并说明二阶系统取ﻍ=0.6~0.7的原因。
4.2某复合信号由频率分别为724HZ、600HZ、500HZ、44HZ的同相正弦波叠加而成。
若要对该复杂信号进行不失真采样,采样频率应如何选择?
4.7求余弦信号x(t)=Xcoswt的均方根值
4.8求正弦信号x(t)=Xsinwt的均值、均方值。
机械工程测试技术基础习题解答-23页文档资料
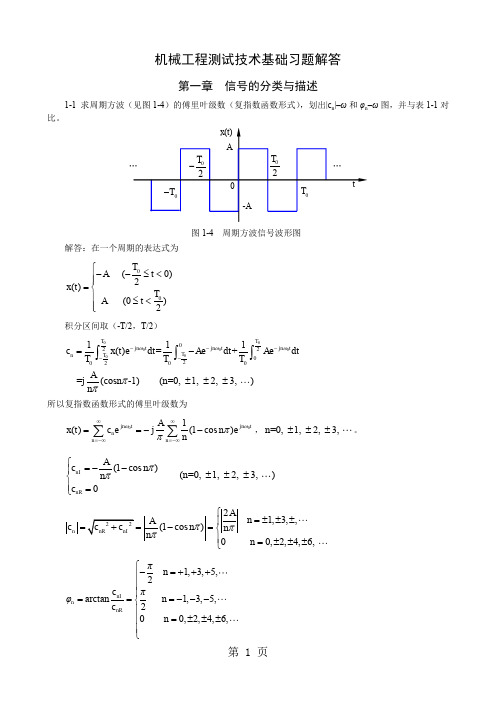
机械工程测试技术基础习题解答第一章 信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn tnn n Ax t c ejn en ∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ2221,3,,(1cos )00,2,4,6,n nR nI An A c c c n n n n ⎧=±±±⎪=+=-=⎨⎪=±±±⎩πππ1,3,5,2arctan 1,3,5,200,2,4,6,nI n nR πn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩图1-4 周期方波信号波形图0 tx (t ) T 02-T 020T -……A-AT 0没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。
解答:00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰222200rms000111cos 2()d sin d d 22T T T x x ωtx x t t x ωt t t T T T-====⎰⎰⎰1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。
机械工程测试技术_课后习题及答案
机械工程测试技术课后习题及答案第一章传感器及检测系统的基本概念1、检测系统由哪几部分组成?说明各部分的作用2、怎样选择仪表的量程大小?3、测量误差可以分为哪几类?引起各类误差的原因是什么?4、传感器按照被测物理量来分,可以分为哪几种?5、某电路中的电流为10A,用甲乙两块电流表同时测量,甲表读数为10.8A,乙表读数为9.5A,请计算两次测量的绝对误差和相对误差。
6、用1.0级量限100V的电压表甲,0.5级量限250V的电压表乙分别测量某电压,读数皆为80V,试比较两次测量结果的准确度。
7、有三台测温仪表,量程均为0~800℃,精度等级分别为2.5级、2.0级和1.5级,现要测量500℃的温度,要求相对误差不超过2.5%,选哪台仪表合理?解答:1、一个完整的工程检测系统包括:传感器、信号调理电路、信号处理电路和显示记录部分。
各部分作用:传感器——感受被测量,并将其转换为电信号;信号调理电路——将传感器输出信号进行放大和转换;信号处理电路——对电信号进行计算和分析;显示记录部分——显示记录测试结果。
2、应根据被测量的大小,兼顾仪表的准确度等级和量程,使其工作在不小于满度值2/3以上的区域。
3、测量误差可以分为:系统误差、随机误差和疏失误差三类。
引起的原因如下:系统误差——仪器误差、零位误差、理论误差、环境误差和观察者误差等随机误差——温度、磁场,零件摩擦、间隙,气压和湿度的变化,测量人员分辨本领的限制等疏失误差——操作、读数、记录和计算等方面的人为误差等4、传感器按被测物理量可以分为:位移传感器、速度传感器、加速度传感器、温度传感器、压力传感器等。
5、绝对误差:△I= I﹣I=10.8-10=+0.8A;△I= I﹣I=9.5-10=﹣0.5A相对误差:γ甲=△I甲/ I0=+0.8/10=8%;γ乙=△I乙/ I0=﹣0.5/10=﹣5%6、最大绝对误差:△V m甲=±K%·V m甲=±1.0%×100=±1.0V;△V m乙=±K%·V m乙=±0.5%×250=±1.25V最大相对误差:γm甲=△V m甲/ V=±1.0/80=±1.25%;γm乙=△V m乙/ V=±1.25/80=±1.56%故:甲表测量结果的准确度高于乙表。
《机械工程测试技术》课后习题答案机工版
2 44, 724,500, 600 2 22,362, 250,300 11,181,125,150
所以该信号的周期为 0.25s。
1-7 求正弦信号 x(t) Asin( 2 t) 的单边、双边频谱,如果该信号延时 T 后,其频谱如何变
T
4
化?
0 ea jwt dt ea jwdt
0
11 a jω a jω
2a a2 ω2
双边指数信号的傅里叶变换是一个正实数,相频谱等于零。由于双边指数信号为实偶对
称函数,因此 X ω 为 ω 的实偶对称函数。
5
1-5 设有一组合信号,有频率分别为 724Hz, 44 Hz,500 Hz,600 Hz 的同相正弦波叠加而 成,求该信号的周期。
答:在时域范围内,实现不失真的条件是:输出信号 y t 与输入信号 x t 相比,只要是幅
值上扩大 A0 ,时间上滞后 t0 ,即 y t A0x t t0 。
2-6 从频域说明测量系统不失真测量条件是什么? 答:在频域内实现不失真测试的条件即为幅频特性是一条平行于 轴的直线,相频特性
1
在教学环节中安排与本课程相关的必要的实验及习题,学习中学生必须主动积极地参加 实验及完成相应的习题才能受到应有的实验能力的训练,才能在潜移默化中获得关于动态测 试工作的比较完整的概念,也只有这样,才能初步具有处理实际测试工作的能力。
2
思考题与习题
1-1 信号的分哪几类以及特点是什么? 答:按信号随时间的变化规律分为确定性信号和分确定性信号,确定信号分为周期信号
则 有 输 出 y1 t , 且 y1 t
2
2
11
1
cos 10t
机械工程测试技术课本习题及参考答案
第二章 信号描述及其分析【2-1】 描述周期信号的频率结构可采用什么数学工具? 如何进行描述? 周期信号是否可以进行傅里叶变换? 为什么?参考答案:一般采用傅里叶级数展开式。
根据具体情况可选择采用傅里叶级数三角函数展开式和傅里叶级数复指数函数展开式两种形式。
不考虑周期信号的奇偶性,周期信号通过傅里叶级数三角函数展开可表示为:001()sin()(1,2,3,)n n n x t a A n n ωϕ∞==++=∑2021()T T a x t dt T-=⎰n A =(2022()cos T n T a x t n tdt T ω-=⎰ 202()sin T n T b x t n tdt T ω-=⎰ )tan n n n b a ϕ=式中,T 为信号周期, 0ω为信号角频率, 02T ωπ=。
n A ω-图为信号的幅频图, n ϕω-图为信号的相频图。
周期信号通过傅里叶级数复指数函数展开式可表示为:0()(0,1,2,)jn t nn x t C e n ω∞=-∞==±±∑0221()T jn t n T C x t e dt Tω--=⎰n C 是一个复数,可表示为:n j n nR nI n C C jC C e ϕ=+=n C = arctan n nI nR C ϕ=n C ω-图为信号的幅频图, n ϕω-图称为信号的相频图。
▲ 不可直接进行傅里叶变换,因为周期信号不具备绝对可积条件。
但可间接进行傅里叶变换。
参见书中第25页“正弦和余弦信号的频谱”。
【2-2】 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。
参考答案:由非周期信号的傅里叶变换,()()j t X x t e dt ωω∞--∞=⎰,得22()()j tA a j X x t edt A a j a ωωωωω∞--===++⎰由此得到,幅频谱为:()X ω=相频谱为: ()arctan()a ϕωω=-【2-3】 求周期三角波(图2-5a )的傅里叶级数(复指数函数形式)参考答案:周期三角波为: (2)20()(2)02A A tT t x t A A T tt T +-≤<⎧=⎨-≤≤⎩则0221()T jn t n T C x t e dt T ω--=⎰积分得 02222204(1cos )(1cos )2n A T AC n n n T n ωπωπ=-=- 即 22()1,3,5,00,2,4,n A n n C n π⎧=±±±=⎨=±±⎩又因为周期三角波为偶函数,则0nb =,所以arctan 0n nI nR C C ϕ==所以,周期三角波傅里叶级数复指数形式展开式为:00(21)222()(0,1,2)(21)jn t j k tn n n A x t C e e k k ωωπ∞∞+=-∞=-∞===±±+∑∑【2-4】 求图2-15所示有限长余弦信号()x t 的频谱。
机械工程测试技术课后答案第二章
2-1 一个测试系统与其输入和输出间的关系各有哪几种情形?试分别用工程实例加以说明。
答:测试系统与输入、输出的关系大致可以归纳为以下三类问题:(1)当输入和输出是可观察的或已知量时,就可以通过他们推断系统的传输特性,也就是求出系统的结构与参数、建立系统的数学模型。
此即 系统辨识 问题。
(2)当系统特性已知,输出可测时,可以通过他们推断导致该输出的输入量,此即滤波与预测问题,有时也称为载荷识别问题。
(3)当输入和系统特性已知时,则可以推断和估计系统的输出量,并通过输出来研究系统本身的有关结构参数,此即系统分析问题。
2-2什么是测试系统的静特性和动特性?两者有哪些区别?如何来描述一个系统的动特性?答:当被测量是恒定的或是缓慢变化的物理量时,便不需要对系统做动态描述,此时涉及的就是系统的静态特性。
测试系统的静态特性,就是用来描述在静态测试的情况下,实际的测试系统与理想的线性定常系统之间的接近程度。
静态特性一般包括灵敏度、线性度、回程误差等。
测试系统的动态特性是当被测量(输入量)随时间快速变化时,输入与输出(响应)之间动态关系的数学描述。
静特性与动态性都是用来反映系统特性的,是测量恒定的量和变化的量时系统所分别表现出的性质。
系统的动态特性经常使用系统的传递函数和频率响应函数来描述。
2-3传递函数和频率响应函数均可用于描述一个系统的传递特性,两者有何区别?试用工程实例加以说明。
答:传递函数是在复数域中描述系统特性的数学模型。
频率响应函数是在频域中描述系统特性的数学模型。
2-4 不失真测试的条件时什么?怎样在工程中实现不失真测试?答:理想情况下在频域描述不失真测量的输入、输出关系:输出与输入的比值为常数,即测试系统的放大倍数为常数;相位滞后为零。
在实际的测试系统中,如果一个测试系统在一定工作频带内,系统幅频特性为常数,相频特性与频率呈线性关系,就认为该测试系统实现的测试时不失真测试。
在工程中,要实现不失真测试,通常采用滤波方法对输入信号做必要的预处理,再者要根据测试任务的不同选择不同特性的测试系统,如测试时仅要求幅频或相频的一方满足线性关系,我们就没有必要同时要求系统二者都满足线性关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《机械工程测试技术》习题答案第一章:略。
第二章: 2.1略。
2.2略。
2.3 解答:因为 5310410102010510F E EA σε--====⨯⨯⨯ R S Rε∆= 所以 32101200.24R S R ε-∆==⨯⨯=Ω 2.4 解答:由于线性电位器空载时满足:CB CB AB R U x AB R U ==,即C B C B 150m m 30k 12VR U x==Ω CB O AB 2212V 8V 33150mmR x xU U U U U R AB =-=-=⨯- (1)当O 0V U =时,100mm x =(2)当10~140mm x =时,O 7.2V ~3.2V U =-2.5 解答:(1)126632608.8510 3.14410(110) 4.9410pF 0.310A C εδδ-----⨯⨯⨯⨯∆≈∆=⨯±⨯=±⨯⨯ (2)31264.94101005 2.5/m 10C S S S μδ--∆⨯==⨯⨯≈∆格 (3)312 4.94101005 2.5n S C S S δ-=⨯∆=∆⨯⨯=±⨯⨯⨯=±格 2.6 解答:因为 12Z Z Z ==,22232()40(24003010)85.32Z R L ωπ-=+=+⨯⨯⨯≈Ω所以 12o 12410()0.23V 42285.32Z Z u u Z u Z Z Z ∆∆∆=-==⨯≈ 2.7解答: q x o f f 1000.550mV 1000S a q u C C ⨯≈-=-=-= 2.8 解答:由输出波形图可知,输出信号频率15150Hz 0.1f == 旋转轴的转速为:6060150750r/min 12f n Z ⨯=== 2.10 解答:晚上无光照时,流过光敏二极管D1V 的电流很小,A 点为低电位,晶体管1V 截止、2V 导通,继电器K 线圈通电,常开触点1K 吸合,路灯点亮。
白天有光照时,流过光敏二极管D1V 的电流增大,A 点电位升高,晶体管1V 导通、2V 截止,继电器K 线圈断电,常开触点1K 断开,路灯熄灭。
D2V 为继电器K 提供放电回路,保护晶体管V 2。
第三章: 3.1略。
3.2 解答:设运放反相输入端电势为Ua ,R3左边电势为Uo ,右端电势为Ut 则有综上 由于12435R R R R R ===+,且53R R >>,则运算放大器A 输出电压为3.3 解答:设计的I/V 转换电路如下图所示(答案不是唯一的)ou 2R bU 4R 3R AΔ∞i1R i u由图可知:i 1u iR =,22o i b 33(1)R Ru u U R R =+- 取1250R =Ω,则4~20mA i =,对应i 1~5V u =,o 0~10V u =,即22b 3322b 33(1)10(1)510R R U R R R R U R R ⎧+⨯-=⎪⎪⎨⎪+⨯-=⎪⎩解得:2332R R =,b 5V 3U =,取320k R =Ω,则230k R =Ω,423//12k R R R ==Ω3.4略。
3.5解答:(1)由题3.5图可知,为了测量拉力P ,电桥应满足相加特性,接桥如下图所示UoU 1R 4R 3R 2R(2)电桥输出电压为:o 13241324()()44U UU R R R R S R εεεε=∆-∆+∆-∆=-+- 由于12500εεμε==,3410.3500150εενεμε==-=-⨯=-则6o 12(1)2(10.3)50010 1.3mV 22U U S νε-=+=⨯⨯+⨯⨯= 3.6 解答:为了实现一次性贴片,测量弯矩M 和测量轴向力P 布片相同,如下图所示PM1R 2R 3R 4R(1)欲测量弯矩M 接桥如下图所示UoU 1R 4R 3R 2R(2)欲测量轴向力P 接桥如下图所示UoU 1R 4R 3R 2R3.7 解答:由题3.7图可知,并联a R 、b R 和c R 时产生的电阻变化量分别为6a a 612010//1200.014412010R R R R ⨯∆=-=-≈+ 5b b 5120510//1200.028*******R R R R ⨯⨯∆=-=-≈+⨯5c c 512010//1200.14412010R R R R ⨯∆=-=-≈+ 因为RS Rε∆=,所以并联a R 、b R 和c R 时产生的应变分别为 a a 0.0144602120R SR εμε∆===⨯b b 0.028********R SR εμε∆===⨯c c 0.1446002120R SR εμε∆===⨯ 3.8略。
3.9解答:m c ()(10030cos 220cos 6)cos 2x t f t f t f t πππΩΩ=++c c c c c 100cos 215cos 2()15cos 2()10cos 2(3)10cos 2(3)f t f f t f f t f f t f f tπππππΩΩΩΩ=+++-+++- m ()x t 所包含的各频率分量及幅值分别为幅值 100 15 15 10 10 频率(kHz )1010.59.511.58.53.10 解答:m 11()(1cos )cos100cos100cos101cos9922x t t t t t t =+=++ 带通滤波器的幅频特性为:2211()1(2100)1(100)A f ωπω==+-+-带通滤波器的相频特性为:()arctan(2100)arctan(100)f ϕωπω=--=-- 当100ω=时,()1A ω=,()0ϕω= 当101ω=时,1()2A ω=,()4πϕω=-当99ω=时,1()2A ω=,()4πϕω=调幅波通过带通滤波器后的输出为22()cos100cos(101)cos(99)4444y t t t t ππ=+-++ 3.11 解答:由题3.11图得:i o ()()u t iR u t =+,o ()du t i Cdt=,则 o i o ()()()du t u t RCu t dt=+令RC τ=,并对上式求拉普拉斯变换得:i o ()(1)()U s s U s τ=+(1)滤波器的传递函数、频率响应函数、幅频特性和相频特性表达式分别为1()1H s s τ=+ 1()1H j j ωωτ=+21()1()A ωωτ=+()arctan()ϕωωτ=-(2)当输入信号i 10sin1000u t =时,即1000ω=,幅频特性和相频特性分别为2362111()21()1(10001010)A ωωτ-===++⨯⨯ 36()arctan()arctan(10001010)4πϕωωτ-=-=-⨯⨯=-滤波器的输出信号为()52sin(1000)4y t t π=-3.12略。
3.13略。
3.14略。
第四章:4.1 解答:()()12sin(30)2o f t t t μ=-⋅4.2解答:错误!未找到引用源。
的周期为错误!未找到引用源。
,错误!未找到引用源。
的周期为错误!未找到引用源。
,则:()()ααπ<<-=t e t x t 10cos 2的周期为1/10。
4.3 解答:已知矩形单位脉冲信号()t x 0的频谱为()⎪⎭⎫⎝⎛=2sin 0ωττωc A X ,又知错误!未找到引用源。
是()t x 0经以T 为周期的周期延拓,幅值放大A 倍,即 错误!未找到引用源。
由傅里叶变换时域卷积性质,错误!未找到引用源。
的频谱函数为:4.4 解答:已知单个矩形脉冲()⎩⎨⎧=01t ut t t t >≤的频谱函数为:()f U ()02sin ft c πτ=余弦信号的傅里叶变换为:()()[]000212cos f f f f t f -++⇔δδπ又知错误!未找到引用源。
t 错误!未找到引用源。
则:错误!未找到引用源。
的傅里叶变换为错误!未找到引用源。
其中:错误!未找到引用源。
4.5 解答:设错误!未找到引用源。
是宽度为2、幅度为1的三角波信号,由于错误!未找到引用源。
可由两个单位脉冲方波错误!未找到引用源。
的卷积求得,即错误!未找到引用源。
,错误!未找到引用源。
的傅里叶变换为:错误!未找到引用源。
,由傅里叶变换的时域卷积性得:错误!未找到引用源。
的傅里叶变换为:错误!未找到引用源。
,利用傅里叶变换的线性和展缩特性可得错误!未找到引用源。
的傅里叶变换为:错误!未找到引用源。
4.6 解答:()2201T x x t dt T ψ=⎰ ()()()t d t x t x TR Tx⎰+=01ˆττ所以有x ψ2=错误!未找到引用源。
错误!未找到引用源。
=错误!未找到引用源。
x ψ2=错误!未找到引用源。
=6400 则其均方根值为:80 4.7 解答:()2201T x x t dt Tψ=⎰错误!未找到引用源。
=错误!未找到引用源。
=X 2/2 则其均方根值为:X/错误!未找到引用源。
4.8 解答:()01Tx x t dt T μ=⎰错误!未找到引用源。
=0 ()2201T x x t dt Tψ=⎰错误!未找到引用源。
=X 2/2 4.9 略。
第五章:5.1 解答:由引用误差n n nΔ100%100%x x x x γ-≈⨯=⨯可得,两温度计的绝对误差分别为 1n1n1Δ0.5%300=1.5C x γ==⨯ 2n2n2Δ1%120=1.2C x γ==⨯两支温度计的相对误差分别为11Δ 1.5100%=100%=1.5%100γμ=⨯⨯ 22Δ 1.2100%=100%=1.2%100γμ=⨯⨯ 由于第二支温度计比第一支温度计的相对误差小,因此应选用第二支温度计。
5.2 本题解法不是唯一的,答案也有所差别。
若用平均法求拟合直线:解答:将数据整理如下拉力F/N 0 10 20 30 40 50 平均应变ε/10-61 80 160 240 320 400 理论应变ˆε/10-60.4380.33160.23240.13320.03399.93设拟合直线方程为:01ˆa a F ε=+ 由上表可得01012413309603120a a a a =+⎧⎪⎨⎪=+⎩ 求得010.437.99a a ≈⎧⎪⎨⎪≈⎩则拟合直线方程为:ˆ0.437.99F ε=+ 传感器的灵敏度为:617.9910/N S a -≈=⨯最大偏差max (0.437.9930)22812.13L ∆=+⨯-= 传感器的线性度为:L 12.13100%3%400γ=⨯≈ 传感器的滞后量为:H 252228100%6%400γ-=⨯≈5.3 解答: 由2211Δ()1121()1()A Tωπωττ=-=-++可得当5s T =时,21Δ()18.5%21(0.35)5A ωπ=-≈-+⨯当1s T =时,21Δ()158.6%1(20.35)A ωπ=-=-+⨯当2s T =时,21Δ()132.7%21(0.35)2A ωπ=-=-+⨯5.4 解答:幅值误差不大于5%,即222111()0.951()1(2)1(200)A f ωωτπτπτ===≥+++由此解得:523s τμ≤5.5 解答:(1)由/u ()1e20%t y t τ-=-=解得u 28.96s ln[1()]ln[10.2]t y t τ=-=≈--(2)由/u ()1e95%t y t τ-=-=解得u ln[1()]8.96ln[10.95]26.84s t y t τ=--=--≈5.6 解答:由题意可得,炉温的表达式为:5405002()520sin 52020sin 240x t t t T ππ-=+=+ 当40πω=时,2211()0.7871()1(10)40A ωπωτ==≈++⨯()arctan()arctan(10)0.66540πϕωωτ=-=-⨯≈-(1)()520200.787sin(0.665)52015.74sin(0.665)4040y t t t ππ=+⨯-=+-(2)()arctan()0.665rad ϕωωτ∆=-=- (3)()0.6658.47s /40t ϕωωπ==≈ 5.7 解答:由1()1H j j ωω=+可知,该一阶系统的时间常数1s τ=,幅频特性和相频特性分别为2211()1()1()A ωωτω==++()arctan()arctan()ϕωωτω=-=-(1)当1ω=时,1(1)2A =,(1)45ϕ=- 当3ω=时,1(3)10A =,(3)71.6ϕ=- 稳态输出信号为:210()cos(45)cos(3116.6)450y t t t =-+- (2)不失真条件为:()A ω=常数,()ϕωω=常数本题(1)(3)A A ≠幅值失真,(1)(3)13ϕϕ≠相位失真,即测量结果波形失真。
