山西太原市高中数学竞赛解题策略-几何分册第10章三角形的内切圆2
山西太原市高中数学竞赛解题策略-几何分册第1章直角三角形

第一编 点击基本图形 第1章 直角三角形直角三角形是含有内角为90︒的特殊三角形,它是一类基本图形. 直角三角形的有趣性质在处理平面几何问题中常发挥重要作用.性质1 一个三角形为直角三角形的充要条件是两条边长的平方和等于第三条边长的平方(勾股定理及其逆定理).性质2 一个三角形为直角三角形的充要条件是一边上的中线长等于该边长的一半. 推论1 直角三角形的外心为斜边的中点.性质3 ABC △为直角三角形,且C 为直角顶点的充要条件是当C 在边AB 上的射影为D 时,下列五个等式之一成立. (1)2AC AD AB =⋅. (2)2BC BD AB =⋅. (3)2CD AD DB =⋅.(4)22BC AB CD AD=. (5)22AC AB CD DB=. 事实上,由2AC AD AB =⋅,有AB ACAC AD=.注意到A ∠公用,知ACB △∽ADC △.而90ADC ∠=︒,故90ACB ∠=︒.即可得(1)的充分性. 我们又由22222BC AB BC CD AB ADCD AD CD AD --=⇒=22DB DBCD AD⇒=,即2CD AD DB =⋅. 即可证得(4)的充分性.其余的证明略.推论2 非等腰ABC △为直角三角形,且C 为直角顶点的充要条件是当C 在边AB 上的射影为D 时,22AC ADBC DB=. 事实上,由性质3中的(1)、(2)相除或(4)、(5)相除即证.下面,另证充分性.由222222AD AC AD CD DB BC CD DB +==+, 有 2()()0CD AD DB AD DB -⋅-=.而AD DB ≠,即有2CD AD DB =⋅.由此即可证.性质4 ABC △为直角三角形,且C 为直角顶点的充要条件是当C 在边AB 上的射影为点D ,过CD 中点P 的直线AP (或BP )交BC (或AC )于E ,E 在AB 上的射影为F 时,2EF CE EB =⋅(或2EF =CE EA ⋅). 证明 必要性.如图11-,过D 作DG AE ∥交BC 于G ,则图1-1BAFDPGECCE EG =,且AD EG DB GB =,即有AD EGAD DB EG BG=++, 即 AD CEAB EB=. ① 又EF CD ∥,有EF EBCD CB=② 在Rt ABC △中,有22,CD AD DB BC DB AB =⋅=⋅, ③将③代入②2得22EB ADEF AB⋅=④将①代入④得2EF CE EB =⋅.充分性.由2EF CE EB =⋅,注意到②2及①,有22BC ABCD AD=再注意到性质3(4)即证.对于2EF CE EA =⋅的情形也类似上述证明.性质5 ABC △为直角三角形,且C 为直角顶点的充要条件是当D 为边AB 上异于端点的任一点时,222()()()AB CD AC BD BC AD ⋅=⋅+⋅. 证明必要性.如图12-,作BK DC ∥交AC 的延长线于K ,则图1-2DBnla AbC K,AB BDBK CD CK AC AD AD=⋅=⋅. 由222BK CK BC =+.将前述式代入上式化简即可证.充分性.令,,,,,BC a AC b AB c CD l AD n DB m ======,在ABC △与ADC △中,应用余弦定理得2222222m l a n l b ml nl-+-+--=注意到m n c +=,化简得222cl cmn na mb ==+,所以22222222222()()()c l c mn na mb m n mn a b b m a n +=++=+++. 而已知有222222c l b m a n =+,从而222c a b =+即证.性质6 如图13-,在Rt ABC △中,CD 为斜边AB 上的高,1I ,2I 分别为ACD △和CDB △的内心,过1I ,2I 的直线交AC 于M ,交BC 于N ;延长1CI 交AD 于P ,延长2CI 交DB 于Q ;设I 为ABC △的内心,则图1-3I 2I 1DN BG I HPAMC(1)45PCQ ∠=︒.(2),AQ AC BP BC ==.(3)CM CD CN ==,且2221212MI I N I I +=.(4)三直线2PI ,1QI ,CD 共点. (5)12CI I I ⊥,且12CI I I =. (6)90PIQ ∠=︒. 证明(1)11145222PCQ ACD DCB ACB ∠=∠+∠=∠=︒.(2)由1122ACQ ACD DCB B DCB AQC ∠=∠+∠=∠+∠=∠,知AQ AC =. 同理BP BC =.(3)由Rt ADC △∽Rt CDB △,有12DI ACDI BC=. 又121902I DI ADB ACB ∠=∠=︒=∠,则12I DI △∽ACB △,即21I I D A ∠=∠.故M ,A ,D ,1I 共圆,则11145CMI ADI CDI ∠=∠==︒.于是 11221,,MI DI I N DI CMI ==∠≌1CDI △,即 11,CM CD MI DI ==. 同理22,CN CD I N DI ==.在12Rt I DI △中,有2221212I D I D I I +=.由此即证得2221212MI I N I I +=.(4)由AQ AC =,及1I 在A ∠的平分线上,则1I 在CQ 的中垂线上,即11CI I Q =,又45PCQ ∠=︒,则190CI Q ∠=︒.同理290CI P ∠=︒,故2PI 与1QI 相交于CPQ △的垂心,而CD PQ ⊥,故CD 过此垂心,即三直线2PI ,1QI ,CD 共点.(5)联结AI ,BI ,易知1I ,2I 分别在AI ,BI 上,且有AI CQ ⊥,BI PC ⊥,即I 为12CI I △的垂心,得12CI I I ⊥.又1245I CI ∠=︒,设1I I 交2CI 于G ,有1CG I G =,则Rt GIG △≌12Rt I I G △.故 12CI I I =.(6)延长AI 交CQ 于G ,延长BI 交CP 于H ,则1I ,2I 分别在AG ,BH 上. 由AC AQ =,BC BP =,可知AG 为QC 的中垂线,BH 为CP 的中垂线,有 ,IQ IC IP IC ==,即 IP IQ IC ==. 故I 为CPQ △的外心,于是290PIQ PCQ ACB ∠=∠=∠=︒.即 90PIQ ∠=︒.性质7 如图14-,在Rt ABC △中,C ∠为直角,CD AB ⊥于D ,ACB △,ADC △,CDB △的内心分别为I ,1I ,2I ;圆1I 与圆2I 的另一条外公切线交CD 于G ,交AC 于E ,交BC 于F ;12I I 所在直线交CD 于K ,交AC 于M ,交BC 于N ;设圆I ,圆1I ,圆2I 的半径分别为r ,1r ,2r ,则G I 2I 1O 3K JI FQ T NBHL D AM SP E C图1-4(1)12I DI △∽ACB △. (2)12I G I G =. (3)CEF △∽CBA △. (4)22212r r r +=.(5)当,,ABC ADC CDB △△△的半周长分别为p ,1p ,2p 时,2221122()()()p r p r p r ±+±=+.(6)C ,I ,1I ,2I 为一垂心组. (7)2ABC MCN S S △△≥.(8)以边AB 上的中线HC 为直径的圆必与内切圆圆I 相切. (9)CG p c r =-=,12r r r CD ++=. (10)21AI C BI C ∠=∠.(11)设12DI I △的内心为3O ,则132II O I 为平行四边形.(12)延长31O I 交AC 于S ,延长32O I 交BC 于T ,则S 、I 、T 三点共线.(13)设圆1I 切AC 于P ,圆2I 切BC 于Q ,圆1I 与圆2I 的另一条内公切线(不同于CD )交AB 于L ,则P ,1I ,L 及Q ,2I ,L 分别三点共线.(14)延长AI 交BC 于U ,延长BI 交AC 于V ,则2ABUV AIB S S =△. (15)111BC AC CK+=.证明(1)由Rt ADC △∽Rt BDC △知12I D ACI D BC=. 而1290I DI ∠=︒,故12Rt I DI △∽Rt ACB △.(2)由121290I DI I GI ∠=︒=∠,知1I ,D ,2I ,G 共圆,从而12122145I I G I DG I DG I I G ∠=∠=︒=∠=∠,故12I G I G =.(3)由12245I I G I NC ∠=︒=∠,知2I G NC ∥.故2221CFE FGI I GD I I D A ∠=∠=∠=∠=∠.同理,CEF B ∠=∠,故CEF △∽CBA △. 由上亦推之A ,B ,F ,E 四点共圆. (4),(5)由Rt ACB △∽Rt ADC △∽Rt BDC △,知221122ADC ACB S r p S r p ==△△,222222BDC ACB S r p S r p ==△△. 而ADC BDC ACB S S S +=△△△,从而有22212r r r +=,22212p p p +=,1122r p r p rp +=.前两式之和加或减第三式的2倍即证得(5).(6)设BI 的延长线交1CI 于T ,由12135I II ∠=︒,知1145I IT CI I ∠=︒=∠,从而知21I I CI ⊥.同理12I I CI ⊥,即知I 为12CI I △的垂心,故C ,I ,1I ,2I 为一垂心组. (7)设H 为AB 中点,则CD CH ≤.由(2),则212ABC S AB CD AH CD CD =⋅=⋅△≥, 21122MCN S CM CN CD =⋅=△.故2ABC MCN S S △△≥.(8)由于H 为AB 的中点,则H 为Rt ABC △的外心.设HC 的中点为J ,则圆I 与圆J 相切⇔2IJ =22()2R r JC r ⎛⎫-=- ⎪⎝⎭(其中R 为ABC △的外接圆半径),注意到IJ 为IHC △的中线,则2222222242242(2)(2)IJ CI IH CH r R Rr R R r =+-=+--=-,其中,222IH R Rr =-,即2IJ =22R r ⎛⎫- ⎪⎝⎭,由此即证. (9)利用切线长关系即可推得前式,后式由内切圆半径与边长关系即可推得. (10)由111909022AI D ACD ABC ∠=︒+∠=︒+∠,212ABI ABC ∠=∠,知1221122()AI I ABI AI D DI I ABI ∠+∠=∠+∠+∠119022ABC BAC ABC =︒+∠+∠+∠90180ABC BAC =︒+∠+∠=︒.从而知A ,B ,2I ,1I 四点共圆,则有21AI B AI B ∠=∠.又2111909022BI C BDC ADC AI C ∠=︒+∠=︒+∠=∠,故222360AI C AI B BI C ∠=︒-∠-∠ 111360AI B AI C BI C =︒-∠-∠=∠.(11)显然,3O 在CD 上.由CM CD NC ==及(6)知,1AI DN ∥(因212,DN CI I I CI ⊥⊥).又 2312221122DI O I I D B NBI NDI ∠=∠=∠=∠=∠,从而 32DN O I ∥. 即有132I I O I ∥.同理,312O I I I ∥.故132II O I 为平行四边形.(12)因132II O I 为平行四边形,可证1323,CI SO CI O T ⊥⊥,则2131II I O SI ==,1322II O I I T ==,1122SI I I II II T ∠=∠=∠,从而1SI I △≌21I II △≌2II T △,有112221,SII II I TII II I ∠=∠∠=∠,即1122180SII I II I IT ∠+∠+∠=︒.故S ,I ,T 三点共线.(13)由121180902I LI ∠=⨯︒=︒,知2I ,L ,D ,1I 四点共圆,则1I LD ∠或221I DL I I D A ∠=∠=,即2I L CA ∥.又AC BC ⊥,则2I L BC ⊥.又2I Q BC ⊥,则L ,2I ,Q 三点共线. 同理P ,1I ,L 三点共线.(14)注意到22()ab pr p p c ==-.ab CU b c =+,abCV a c=+,由 ()()ABUV ABCCUV abcpS S S cr a c b c =-==++△△,即证.(15)证法1令ACD α∠=,则90DCB α∠=︒-,由张角定理,有sin90sin(90)sin CK CM CNαα︒︒-=+. 而sin(90)sin CD CMA AC ACα︒-===, sin sin CD CNB BC BCα===. 于是111CK AC BC=+. 证法2 延长AC 至R ,使CR CB =. 由AM AN =,知BAR △∽KCN △.从而 AR CK AB CN ⋅=⋅, 即 ()AC CR CK AB CD +⋅=⋅, 亦即 ()AC CB CK AC CB +⋅=⋅.故111CK AC BC=+. 性质8 在RT ABC △中,AB 为斜边,则(1)ABC △的内切圆半径2AC BC ABr +-=.(2)当圆Γ与AB 边上的高CD 、DB 及ABC △的外接圆均相切且切BD 于点T 时,圆Γ的半径1r =AT TBAT TB⋅+,且CT 平分BCD ∠.事实上,对于(2)设O 为AB 的中点,1O 为圆Γ的圆心,令AT x =,TB y =,则1()2OA OB x y ==+,1||2OT x y =-.111()2OO x y r =+-,11O T r =.由22211OO OT O T =+,即知1xy AT TBr x y AT TB ⋅==++. 又令,AD a DB b ==,则1x a r =+,1y b r =-.由1xyr x y=+有 21120r ar ab +-=,即1r a =,从而AT AD DT =+=而AC ==AT AC =.从而119022DCT CTA CAT BCD ∠=︒-∠=∠=∠,即知CT 平分BCD ∠.例1 (2008年克罗地亚数学竞赛题)若ABC △通过同一顶点的高线、角平分线、中线将该角四等分.求ABC △的三个内角.解 如图15-,不失一般性,设AH 、AT 、AM 分别为过顶点A 的高线、角平分线、中线. 设BAH θ=△,则π2ABC θ∠=-, πππ322ACB θθθ⎛⎫∠=-4--=- ⎪⎝⎭.H θθθθ图1-5MTCBA在ABM △和AMC △中应用正弦定理,有πsin cos 2sin3sin3BM BM AM θθθθ⎛⎫⋅- ⎪⋅⎝⎭==, πsin 3cos32sin sin CM CM AM θθθθ⎛⎫⋅- ⎪⋅⎝⎭==. 从而cos cos3sin3sin θθθθ=,即sin2sin6θθ=. 而4πθ<,故π8θ=.故ππ3π,,288BAC ACB ABC ∠=∠=∠=.例2 (2008年克罗地亚数学竞赛题)已知ABC △的边BC 的中线和高恰好将BAC ∠等分.求ABC △的三个内角.解 如图16-,设AH 、AM 分别为BC 边上的高和中线.图1-6CA则,2BH HM MC BM HM ===.由角平分线性质,有12AH HM AC MC ==. 即2AC AH =,从而30C ∠=︒.于是336090,6022A HACB ∠=∠=⋅︒=︒∠=︒.例3 (2004年第12届土耳其国家数学奥林匹克题)已知ABC △满足B C ∠>∠,A ∠的平分线和过顶点的高线、中线与边BC 分别交于点L 、H 、D .证明HAL DAL ∠=∠的充分必要条件是90BAC ∠=︒.证明 充分性:若90BAC ∠=︒,因为AD 为中线,则BD AD DC ==,即DAC ACD BAH ∠=∠=∠.又BAL CAL ∠=∠,故HAL DAL ∠=∠. 必要性:如图17-,若HAL DAL ∠=∠,图1-7KLH DCBA又BAL LAC ∠=∠,则BAH CAD ∠=∠. 作CK AC ⊥交AD 的延长线于点K ,则9090AKC DAC BAH ABC ∠=︒-∠=︒-∠=∠.所以,A 、B 、K 、C 四点共圆.从而,90ABK ∠=︒.于是,AK 为四边形ABKC 的外接圆的直径.易知AD 与BC 不垂直,又AK 平分BC ,所以,BC 也为外接圆的直径.因为BD DC =,所以D 为圆心.即DA DB DC ==,故ABC △为直角三角形,90BAC ∠=︒. 例4 设x m 、x h 分别表示三角形顶点x 所对边上的中线长,高线长,ABC △为直角三角形,且C 为直角顶点的充要条件是下列两式之一成立.(1)2225A B C m m m+=.(2)A B C h h h ⋅=.证明提示 (1)注意到三角形的中线长公式(如22221(22)4A m b c a =+-)及性质1即证.(2)注意到面积关系111CA B h h h a b c==及性质1即证. 例5 ABC △为直角三角形,且C 为直角顶点的充要条件是下述条件成立.设C m ,C h ,C t 分别为C ∠所对边上的中线长,高线长及C ∠的平分线长时,22()2C C C C C m h t m h +=⋅.证明 设CD 、CH 、CL 分别是AB 边上的中线、高线、C ∠的平分线.Rt CDH △中,由角平分线的判定与性质知,CL 平分DCH ∠的充要条件是DH CHLH CD CH⋅=+.而例3 结论CC CDH h DH CH LH DC CH m h ⋅⋅⇔==++222222C C CC Cm h CL h LH m h ⋅⇔=+=+(其中222C C DH m h =-)22()2C C C C C m h t m h ⇔+⋅=⋅.例6 在Rt ABC △中,C 为直角顶点.(1)设内角,,A B C 所对的边长分别为,,a b c ,记1()2p a b c =++,则1()()()2ABC S p p c p a p b ab =-=--=△.(2)设AB 被内切圆切点D 分为两段,则ABC S AD DB =⋅△. 证明 (1)略.(2)设内切圆半径为r ,由11()()()()22AD r DB r AB BC AC r AD DB r r ++=++=++. 即()ABC AD DB AD DB r r S ⋅=++=△.例7 在ABC △中,D 在AB 上,AD AB λ=,BC a =,CA b =,CD m =,则90C ∠=︒的充要条件是22222(1)(0)m a b λλλ=+-<<1. 证明 设CA =b ,CB =a ,则AB =-a b ,AD AB λλ= =(-)a b ,(1)CD CA AD λλ=+=+-a b , 22()((1))CD λλ=+-a b .即 22222(1)2(1)m λλλλ=+-+-⋅a b a b .90C ∠=︒的充要条件为0⋅=a b ,即22222(1)m λλ=+-a b .例8 如图18-,在ABC △中,T 为AB 上异于A ,B 的点,AT d =,BT e =,CT t =,CTB α∠=,则90ACB ∠=︒的充要条件是α图1-8t BeTd AabC2()cos 0t t d e de α+--=①证明 必要性.设AC b =,BC a =,由余弦定理,得 2222cos a t e te α=+-,② 2222cos b t d td α=++.③ ②,③两式相加,由于90ACB ∠=︒,得222222()22()cos d e a b d e t t d e α+=+=+++-.整理即得①.充分性.由①出发,得2222()22()cos d e d e t t d e α+=+++-,应用余弦定理,得222()d e a b +=+.故 90ACB ∠=︒. 例9 如图19-,设Rt ABC △(A ∠为直角)的内切圆圆I 与ABC △的三边分别切于D ,E ,F ,DEF △,BDF △,CDE △的垂心分别为1H ,2H ,3H .则123H H H △是等腰直角三角形.H 3图1-9H 2H 1I DGCBE FA证明 延长AI 交BC 于G ,联结BI ,CI ,由已知得2H ,3H 分别在BI ,CI 上.其余连线如图19-所示.易知AEIF 是正方形,所以 90EIF ∠=︒, 且AI EF =.又因为1452EDF EIF ∠=∠=︒,1H 是DEF △的垂心,由含45︒角的三角形性质2,知1DH EF =,所以1AI DH =.另一方面45AGC BAG B B ∠=∠+∠=︒+∠,11(90)902C H DC H DE EDC DEF ⎛⎫∠=∠+∠=︒-∠+︒- ⎪⎝⎭190904522B DIF ∠⎛⎫⎛⎫=︒-∠+︒-︒- ⎪ ⎪⎝⎭⎝⎭190(180)4522BB ∠=︒-︒-∠+︒+45B =︒+∠.所以 1AGC H DC ∠=∠. 即得1AI DH ∥.从而1AIDH 是平行四边形,所以1AH DI ==∥. ③又因为222BIH D H DB ∠∠=+∠ 909022B BB ∠∠=+︒-∠=︒-, 902BBID ∠∠=︒-. 所以2DI DH =.且因为2H 是等腰DBF △的垂心,所以22DH FH =,所以2DI FH =. 同时因为DI ,2FH 都垂直BC ,所以2DI FH ==∥.④由③,④知12AH FH ∥,所以12AH H F 是平行四边形,所以12AF H H ==∥. 同理13AE H H ==∥.结合AEF △是等腰直角三角形.知123H H H △是等腰直角三角形.例10 设AD 是Rt ABC △斜边BC 上的高(设AB AC <),1I ,2I 分别是ABD △,ACD △的内心,12AI I △的外接圆圆O 分别交AB ,AC 于点E ,F ,直线EF 与直线BC 交于点M ,则1I ,2I 分别是ODM △的内心与旁心.证明 如图110-,因90BAC ∠=︒,则知12AI I △的外接圆圆心O 在EF 上.联结1OI ,2OI ,1I D ,2I D ,则由1I ,2I 为内心,知1245I AI ∠=︒,所以121212290I OI I AI I DI ∠=∠=︒=∠图1-10I 2I 1NMCBDO F EA于是O ,1I ,D ,2I 四点共圆,所以211245I I O I I O ∠=∠=︒.又因为221245I DO I I O I DA ∠=∠=︒=∠,则知点O 在AD 上,即O 为EF 与AD 的交点. 设AD 与圆O 的另一交点为N ,由11EAI I AN ∠=∠,22NAI FAI ∠=∠,可知1I ,2I 分别为EN ,NF 的中点,所以1122,EOI DOI DOI FOI ∠=∠∠=∠.因此,1I ,2I 分别为OMD △的内心与旁心.注 (1)由例10知EF 为圆1I 与圆2I 的公切线,且可推证N 为12DI I △的内心.(2)此例即为2008年江西省竞赛题. 练习一 1.(2003年第29届俄罗斯数学奥林匹克题)已知ABC △中,C ∠为直角,D 为边AC 上一点,K 为边BD 上一点,且ABC KAD AKD ∠=∠=∠.证明:2BK DC =. 2.(2003年第17届北欧数学竞赛题)已知正ABC △内一点D ,满足150ADC ∠=︒.证明:由线段AD 、BD 、CD 为边构成的三角形是直角三角形. 3.(2007—2008年匈牙利数学奥林匹克题)设D 是ABC △的边BC 的中点,ABD △、ADC △的外心分别为E 、F ,直线BE 、CF 交于点G .若22008BC DG ==,1255EF =.求AEF △的面积.4.(2003年泰国数学奥林匹克题)在Rt ABC △中,90B ∠=︒,P 是ABC △内A ∠的角平分线上的点,M (异于A 、B )是边AB 上的点,直线AP ,CP 、MP 分别交边BC 、AB 、AC 于点D 、E 、N .如果MPB PCN ∠=∠,NPC MBP ∠=∠.求APC ACDE SS △四边形.5.(2004年克罗地亚数学竞赛题)在ABC △中,90BCA ∠=︒,a ,b 是直角边,c 是斜边,圆k 是ABC △的外接圆.设圆1k 是与斜边c 、高CD 及圆k 的劣弧BC 相切的圆,圆2k 是与斜边c 、高CD 及圆k 的劣弧AC 相切的圆,又设1r ,2r 分别是圆1k 、圆2k 的半径,证明:12r r a b c +=+-.6.(2005年国家集训队培训题)在直角三角形ABC 中,90B ∠=︒,它的内切圆分别与边BC 、CA 、AB 相切于点D 、E 、F ,联结AD ,与内切圆相交于另一点P ,联结PC 、PE 、PF .已知PC PF ⊥,求证:PE BC ∥.7.(《数学通报》数学问题1489号)在Rt ABC △中,AD 是斜边BC 上的高,1O ,2O 分别是ABD △,ACD △的内切圆,两圆的另一条外公切线分别交直线AB ,AC ,AD 于P ,Q ,M 点,求证: (1)2AP AQ AMAB AC AD+=;(2)1290PO Q PO Q ∠=∠=︒. 8.(《中学数学》2006(7)数学奥林匹克问题179)在正方形ABCD 中,以边AB 的中点1O 为圆心,2AB长为半径画半圆1O ,半圆2O 的圆心2O 在边BC 上,并与边CD 相切,与半圆1O 外切于点P .求证:DP 是1O 和2O 的公切线.9.在Rt ABC △中,CD ⊥斜边AB 于D ,1O ,2O 分别为ACD △,CDB △的内心,过1O ,2O 的直线交AC 于E ,交CD 于K ,交CB 于F ,交直线AB 于G ,过C 作ABC △的外接圆的切线交直线BA 于T ,CTB ∠的平分线交AC 于R ,交BC 于S ,则(1)BG FBAG EA=;(2)12RS O O ∥. 10.ABC △中,CD AB ⊥于D ,ABC △的内切圆半径为r ;ABC △,ADC △,BCD △的内心分别为I ,1I ,2I ,12II I △的外接圆半径为0R ,则ABC △为直角三角形的充要条件是0R r =.11.ABC △中,CD AB ⊥于D ,ACD △,BCD △的内切圆分别切AC ,BC 于E ,F ,则ABC △为直角三角形的充要条件90EDF ∠=︒.12.ABC △为直角三角形的充分与必要条件为:ABC △可以被分成两个彼此无公共内点且都与ABC △相似的小三角形.13.在Rt ABC △中,CD 是斜边上的高,记1I ,2I ,I 分别是ADC △,BCD △,ABC △的内心,I 在AB 上的射影为1O ,CAB ∠,ABC ∠的平分线分别交BC ,AC 于P ,Q ,PQ 与CD 相交于2O .求证:四边形1122I O I O 为正方形.14.(2003年中国国家队选拔赛题)在锐角ABC △中,AD 是BAC ∠的内角平分线,点D 在边BC 上,过点D 分别作DE AC ⊥,DF AB ⊥,垂足分别为E 、F .联结BE 、CF ,它们相交于点H ,AFH △的外接圆交BE 于点G .求证:以线段BG 、GE 、BF 组成的三角形是直角三角形.。
《三角形的内切圆》 讲义

《三角形的内切圆》讲义一、引入同学们,在我们的数学世界中,三角形是一种非常基础且重要的图形。
而今天,我们要来一起探索三角形中的一个神秘而有趣的部分——三角形的内切圆。
想象一下,在一个三角形内部,有一个圆与三角形的三条边都相切,这个圆就像是被三角形紧紧地拥抱着,它有着独特的性质和规律等待我们去发现。
二、三角形内切圆的定义那什么是三角形的内切圆呢?简单来说,三角形的内切圆就是与三角形的三条边都相切的圆。
这个圆的圆心叫做三角形的内心,它是三角形三条角平分线的交点。
为了更直观地理解,我们可以画一个三角形 ABC,然后试着画出它的内切圆。
三、三角形内切圆的性质1、圆心到三角形三边的距离相等由于内切圆与三角形的三条边都相切,所以圆心到三条边的距离就是内切圆的半径,而且这个距离是相等的。
这是因为切线的性质决定了圆心到切线的距离等于圆的半径。
2、三角形的面积与内切圆半径之间的关系我们知道三角形的面积可以用底乘以高除以 2 来计算。
对于一个三角形 ABC,设其面积为 S,三边分别为 a、b、c,内切圆的半径为 r。
那么三角形的面积 S 还可以表示为:S = 1/2×(a + b + c)×r 。
这是一个非常有用的公式,通过它我们可以在已知三角形的边长和内切圆半径的情况下,轻松求出三角形的面积,或者在已知三角形的面积和边长的情况下,求出内切圆的半径。
3、内心的性质内心是三角形三条角平分线的交点,这意味着从内心到三角形三边的距离相等。
而且,内心是三角形内切圆的圆心,它决定了内切圆的位置。
四、三角形内切圆的画法那怎么画出一个三角形的内切圆呢?我们可以按照以下步骤进行:1、先作出三角形的两条角平分线,它们的交点就是内心。
2、以内心为圆心,从内心到三角形任意一边的距离为半径画圆,这个圆就是三角形的内切圆。
为了让大家更清楚,我们通过一个具体的例子来实际操作一下。
五、三角形内切圆的应用在实际生活中,三角形内切圆有很多应用。
三角形的内切圆ppt

C
第10页,本讲稿共23页
一 判断题:
1. 三角形的内心到三角形各个顶点的距离相等( )错 2. 三角形的外心到三角形各边的距离相等 ( 错) 3. 等边三角形的内心和外心重合 ( 对)
4. 三角形的内心一定在三角形的内部( )对 5. 菱形一定有内切圆( 对) 6. 矩形一定有内切圆( 错)
第11页,本讲稿共23页
第2页,本讲稿共23页
小明在一家木料厂上班,工作之余想对厂里的 三角形废料进行加工:裁下一块圆形用料,且使 圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。
A
B
C
第3页,本讲稿共23页
合
作 思考下列问题:
A
探 究
1.如图,若⊙O与∠ABC的两
边相切,那么圆心O的位置有什
: 么特点?
M
O
三 角
圆心0在∠ABC的平分线上。
B
NC
形
2.如图2,如果⊙O与
A
内 △ABC的内角∠ABC的两边相
切 圆
切,且与内角∠ACB的两边也相 切,那么此⊙O的圆心在什么 位置?
O
的 作
B
图2
C
法 圆心0在∠ABC与∠ACB的两个角的角平分线的
交点上。
第4页,本讲稿共23页
3.如何确定一个与三角形
三边都相切的圆的圆心位置
第23页,本讲稿共23页
作直线n与⊙O相切于点E,
直线m和直线n相交于点A;
B
③作直线l与圆O相切于点F, 直线l分别与直线m、直线n相交于点B、C.
nm
A
D
E
.O
C
F
l
1. 和三角形各边都相切的圆叫做三角形的内切圆,内切 圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形
山西太原市高中数学竞赛解题策略-几何分册第10章三角形的内切圆1

第10章 三角形的内切圆三角形的内切圆中,有一系列有趣的结论,它们在处理有关问题中常常发挥着重要的作用. 性质1 三角形内切圆与边的切点及这条边所在直线和另两切点所在直线的交点内分、外分该边的比相等.证明 如图101-,设D ,E ,F 分别为ABC △的内切圆与边BC ,CA ,AB 的切点,又设直线BC 与直线FE 交于点T ,则对ABC △及截线FET 应用梅涅劳斯定理,有图10-1ABCDEFT1AF BT CEFB TC EA⋅⋅=. 注意到AF AE =,BF BD =,CE CD =,即有BD BTDC TC=. 注:D ,T 内分、外分BC 所成的比相等时,亦称为D ,T 调和分割BC .若FE BC ∥时,则T 为无穷远点,此时D 为BC 的中点,也认为是内分、外分所成的比相等.性质2 三角形的顶点和对边上的内切圆切点的连线与内切圆的交点以及三个切点为顶点构成的圆内接四边形,对边的乘积相等.证明 如图102-,设D ,E ,F 分别为ABC △的内切圆与边BC ,CA ,AB 的切点,AD 交内切圆于点P ,则由AEP △∽ADE △,AFP △∽ADF △,有A E P E A D E D =,AF PFAD FD=.此两式相除,并注意到AE AF =,有PE PFED FD=,即PE FD PF ED ⋅=⋅. H GA BCE F P 图10-2注:对边乘积相等的圆内接四边形,亦称为调和四边形,图102-中,若PC ,PB 分别交内切圆于G ,H ,则四边形DGEP ,四边形PFHD 均为调和四边形.性质3 ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线AD 交内切圆于点P ,交EF 于点Q ,则A ,Q 调和分割PD .证明 如图103-,设I 为内切圆圆心,联结AI 交EF 于L ,则AL EF ⊥,有2A L A I A F A P A D ⋅==⋅,即知L ,I ,D ,P 四点共圆,从而,ALP IDP IPD ILD ∠=∠=∠=∠,即知AL 平分PLD ∠的外角.而LQ AL ⊥,即知LQ 平分PLD ∠.于是有DQ LD DAQP LP AP==,即A ,Q 调和分割PD . 图10-3A BCDE FI L P Q注:过A 作内切圆的割线交内切圆于P ,D (不一定是切点),交切点弦EF 于点Q ,同上述证法也推证得A ,Q 调和分割PD .性质4 ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线AD 交内切圆于点P ,直线PC ,PB 分别交内切圆于点G ,H ,直线AG ,AH 分别交内切圆于M ,N .则: (1)EH ,FG ,AD 三线共点; (2)四边形DGPH 为调和四边形; (3)BG ,CH ,AD 三线共点; (4)HM ,GN ,AD 三线共点.证明 如图104-,(1)注意到圆内接四边形FHDP ,DGEP 均为调和四边形,有HF HDFP DP=,PEEG PD DG =,此两式相乘,得1PE GD HFEG DH FP⋅⋅=. 图10-4A BCDE F GHMNP于是,由第一角元形式塞瓦定理的推论(参见第22章),即知EH ,FG ,AD 三线共点. (2)设EH ,FG ,AD 三线共点于K ,由PKG △∽FKD △,有PK PGFK FD=. 同理FK PF KD DG =.从而PK PG PF DK DG DF =⋅.同理PK HP PEKD DH ED=⋅. 又PF AF AE PE FD AD AD ED ===,则PG HPDG DH=.故四边形DGPH 为调和四边形. (3)由CDG △∽CPD △,有DG PD GC CD =.同理,有PD DHDB BH=.注意到有PG HP DG DH =,这三式相乘,得1PG CD BHGC DB HP⋅⋅=.于是,由塞瓦定理的逆定理,即知BG ,CH ,AD 三线共点. (4)由APM △∽AGD △,有PM APGD AG=. 同理,EG AG ME AE =,ED AD EP AE =,EP CP EG CE =,DG PD CD CP =,PD PB DH BD =,HF BFFP PB=. 上面七式相乘,并注意CE CD =,BD BF =,2AE AP AD =⋅,得1PM ED HFME DH FP⋅⋅=,由此式即知HM ,AD ,EF 三线共点.同理,GN ,AD ,EF 三线共点,故HM ,GN ,AD 三线共点.性质5 ABC △的内切圆I 分别切BC ,CA ,AB 边于点D ,E ,F ,直线AI 交内切圆于点P 、Q ,则P ,Q 分别为AEF △的内心和旁心.证明 如图105-,联结PE ,PF ,则由对称性知PE PF =,即有PEF PFE ∠=∠.又AEP PFE ∠=∠,即知EP 平分AEF ∠.于是,知点P 为AEF △的内心.联结EQ ,则知90PEQ ∠=︒,即知EQ 平分么FEC ∠.故知点Q 为AEF △的旁心.图10-5ABD性质6 三角形一内角平分线上的点为三角形一顶点的射影的充分必要条件是另一顶点关于内切圆的切点弦直线与这条内角平分线的交点. 证明 如图106-,在ABC △中,内切圆I 分别切BC ,CA ,AB 边于点D ,E ,F ,AI ,BI ,CI 分别为三条内角平分线.图10-6I NHG ABCDEFS MK L T下面先证直线CI 上的点G ,有,,CG AG D F G ⊥⇔三点共线. 充分性.由D ,F ,G 共线,联结FI ,则180AIG AIC ∠=︒-∠1180902B ⎛⎫=︒-︒+∠ ⎪⎝⎭1902B BFD AFG =︒-∠=∠=∠,于是,A ,G ,F ,I 四点共圆,即有90AGI AFI ∠=∠=︒,故CG AG ⊥.必要性.由CG AG ⊥,联结FI ,IF AB ⊥,知A ,G ,F ,I 四点共圆.又I 为内心,知1902AIC B ∠=︒+∠,则1180902AFG AIG AIC B ∠=∠=︒-∠=︒-∠.由BD BF =,知1902BFD B AFG ∠=︒-∠=∠,故D ,F ,G 三点共线.类似地,有直线CI 上的点H ,,,CH BH E H F ⊥⇔三点共线, 直线BI 上的点M ,,,BM AM D E M ⊥⇔三点共线. 直线BI 上的点N ,,,BN CN D N F ⊥⇔三点共线, 直线AI 上的点T ,,,AT BT E D T ⊥⇔三点共线. 直线AI 上的点S ,,,AS CS D S F ⊥⇔兰点共线,在图106-中,设L 为AB 的中点,联结LM 交AC 于点K ,则由AM BM ⊥知LM 为Rt AMB △斜边上的中线,由此即推知LM BC ∥,即知K 为AC 的中点.联结GK 交AB 于L ',也可证L '为AB 的中点,即L '与L 重合,由此即知G ,M 在与BC 平行的ABC △的中位线上.于是可得如下结论.推论1 三角形的一条中位线,与平行于此中位线的边的一端点处的内角平分线及另一端点关于内切圆的切点弦直线,这三条直线相交于一点,且该点为与中位线对应的顶点在这条内角平分线上的射影.性质7 ABC △的内切圆I 切BC 边于点D ,M 为BC 的中点,AH 是BC 边上的高,Q 为AH 上的一点,则AQ 等于内切圆半径r 的充分必要条件是M ,I ,Q 三点共线.证明 如图107-,充分性.当M ,I ,Q 共线时,令BC a =,CA b =,AB c =,则12M C a =,1()()2DC a b c p c =+-=-,222cos 2a b c HC AC C a +-=⋅=.联结ID ,由Rt IMD △∽Rt QMH △,有A B图10-7()22()2QH HM MC HC a HC b cID DM MC DC c b a-⋅-+====-⋅-. 又2()ABC AH a S r a b c ⋅==++△,有AH a b cr a++=.于是1AQ AH QH AH QH a b c b cr r r ID a a-+++==-=-=,故AQ r =. 必要性.当AQ r =时,则()()a b c r b c rQH AH AQ r a a++⋅+⋅=-=-=. 设直线QI 交BC 于M '(当c b >时),则由22222222a b c a b c ab ac b c DH a a+-+---+=-=.有IDQH= M DM H''.即有ID M D QH ID DH ''=-,亦即22()()2()2()2ab ac b c r ID DH b c a c b c b a M D b c r QH ID b c a ra --+⋅⋅+---'=====+⋅-+--22a abc MC DC MD +--=-=. 从而M '与M 重合,故Q ,I ,M 三点共线.性质8 设ABC △的内切圆I 切BC 边于点D ,P 为DI 延长线上一点,直线AP 交BC 于点Q ,则BQ DC =的充要条件是点P 在I 上.证明 如图108-,过P 作B C BC ''∥交AB 于点B ',交AC 于点C '.BA图10-8充分性.当P 在I 上时,则知B C ''切I 于点P .易知AB C ''△∽ABC △.由于在BAC ∠内它们的旁切圆分别为I 与A I ,则在以A 为中心的位似变换下,使I 变为A I ,此时切点P 变为切点Q ,即Q 为直线AP 与BC 的交点.于是,BQ p c DC =-=(其中BC a =,CA b =,AB c =,1()2p a b c =++).必要性.当BQ DC p c ==-时,即Q 为ABC △的BAC ∠的旁切圆的切点,由AB C ''△∽ABC △,则存在以A 为中心的位似变换,将BC 上的点Q 变为B C ''上的点P ',且P '为AB C ''△的BAC ∠的旁切圆的切点.注意到B C BC ''∥,则知P '在过D 与BC 垂直的直线上,从而P '与P 重合,故点P 在I 上.推论2 设Q 为ABC △的BC 边上一点,则Q 为BAC ∠内的旁切圆的切点的充要条件是AB BQ += AC CQ +.性质9 设ABC △的内切圆I 分别切BC ,CA ,AB 边于点D ,E ,F ,设K 是DI 延长线上一点,AK 的延长线交BC 于点M ,则M 为BC 的中点的充要条件是点K 在线段EF 上. 证明 如图109-,过点K 作ST BC ∥交AB 于点S ,交AC 于点T ,则IK ST ⊥.联结SI ,FI ,TI ,EI .ADC图10-9充分性.当点K 在EF 上时,注意到F ,S ,I ,K 及I ,E ,T ,K 分别四点共圆,有ISK IFK ∠=∠=IEK ITK ∠=∠,即知SIT △为等腰三角形. 注意到IK ST ⊥,知K 为ST 的中点. 由于ST BC ∥,则知M 为BC 的中点.必要性.当M 为BC 的中点时,则知K 为ST 的中点.由于IK ST ⊥,则知IS IT =,从而Rt ISF △≌Rt ITE △,即有SIF TIE ∠=∠.注意到F ,S ,I ,K 及I ,E ,T ,K 分别四点共圆,有SKF SIF TIE TKE ∠=∠=∠=∠.于是,E ,K ,F 三点共点,即点K 在线段EF 上.推论3 设ABC △的内切圆I 切BC 边于点D ,M 为BC 边的中点,Q 为BC 边上一点,则Q 为BAC ∠内的旁切圆的切点的充分必要条件是IM AQ ∥.事实上,参见图109-,证充分性时,过点A 作AQ IM ∥交DI 于点P ,证点P 在I 上即可.证必要性时,延长DI 交I 于点P ,作直线AP 交BC 于Q ,证明IM AQ ∥.性质10 ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,BC 边上的高AD 交EF 于点H ,则H 为ABC △的垂心的充要条件是D H EF ⊥. 证明 如图1010-,联结BH ,CH .A H FEDP CC 'BT图10-10充分性.当D H EF ⊥时,设直线FE 与直线BC 交于点T ,由性质1,知D ,T 调和分割BC ,则HB ,HC ,HD ,HT 为调和线束,由其性质知当D H H T ⊥时,DH 平分BHC ∠,于是可得FBH ECH ∠=∠.作C 点关于AP 的对称点C ',则C '在BC 上.联结AC ',HC ',则AC H ACH ECH FBH ABH '∠=∠=∠=∠=∠,从而A ,B ,C ',H 四点共圆,于是,BAH HC C HCC ''∠=∠=∠,即有90HCC CBA BAH CBA '∠+∠=∠+∠=︒,从而知CH AB ⊥.故H 为ABC △的垂心.必要性.当H 为ABC △的垂心时,由90FBH A ECH ∠=︒-∠=∠,BFH CEH ∠=∠,知BFH △∽CEH △,于是,BH BF BDCH CE CD==,从而即知DH 平分B H C ∠,即F H D F H B B H D E ∠=∠+∠=∠ CHD EHD +∠=∠,故知D H EF ⊥.(或由DH 平分BHC ∠,及D ,T 调和分割BC ,即知有D H EF ⊥见(第15章).)注:可由BFH △∽CEH △,有BH BF BDCH CE CD==,即知DH 平分BHC ∠. 性质11 设ABC △的内切圆分别切BC ,CA ,AB 三边于点D ,E ,F . 令BC a =,CA b =,AB c =,1()2p a b c =++,内切圆半径为r ,则(1)tan2r AE AF p a ==-=,tan2r BD BF p b ==-=,tan2r CD CE p c C ==-=;(2)1()2EDF B C ∠=∠+∠,1()2DEF A C ∠=∠+∠,1()2DFE A B ∠=∠+∠.(证略)性质12 设ABC △的内切圆的圆心为I ,IBC △的外接圆分别和射线AB ,AC 交于点D ,E ,则DE 与I 相切.证明 如图1011-,显然D ,B ,I ,E ,C 五点共圆.A(2)图10-11对于图1011(1)-,有IDB ICB ∠=∠,IDE ICE ∠=∠.而ICB ICE ∠=∠,从而IDB IDE ∠=∠.由于AD 与I 相切,由对称性,知DE 也与I 相切. 对于图1011-(2),注意IBC IEC ∠=∠,IBD IED ∠=∠,而I B C I B D ∠=∠,从而IEC IED ∠=∠.因EA 与I 相切,故ED 也和I 相切.性质13 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F .记以A 为圆心,AE 为半圆的圆为叫ω,直线DE 交圆ω于点G ,点H 在圆ω上,则GH 为圆ω的直径的充要条件是H ,F ,D 三点共线.证明 如图1012-,注意到AEG △、CED △均为等腰三角形,且底角相等,则知其顶角相等,即GAE ECD ∠=∠,从而AG DC ∥.于是,ωLH GF A BCE图10-12GH 为圆ω的直径HA BD HAF FBD ⇔⇔∠=∠∥,注意到A H F △、BDF △均为等腰三角形⇔其对应底角相等,即,,AFH BFD H F D ∠=∠⇔三点共线.推论4 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线DE ,DF 分别交过点A 且与BC 平行的直线于点G ,H ,直线AD 交内切圆于点L ,则AG AH =,且180GDH GLH ∠+∠=︒.事实上,由AE AF =并注意到图中的等腰三角形即得AG AH =;由G A L L D B L E D ∠=∠=∠知A ,L ,E ,G 四点共圆,有ALG CDG ∠=∠.同理ALH BDH ∠=∠.由此即可得180GDH GLH ∠+∠=︒.性质14 设ABC △的内切圆I 分别切BC ,CA ,AB 边于点D ,E ,F ,L 为劣弧EF 上一点,过点L 作内切圆的切线与BC 所在直线交于点G ,则G ,E ,F 三点共线的充要条件是A ,L ,D 三点共线.证明 充分性.当A ,L ,D 共线时,如图1013-,联结AI 交EF 于点K ,则KI EF ⊥. ①L K GFA BCDE R I图10-13联结EI ,DI ,KD ,则22ID EI IK IA ==⋅,即ID IKIA ID=. 注意到DIK ∠公用,则IDA △∽IKD △,即有IDA IKD ∠=∠. ②联结IL ,则ILD ID A IKD ∠=∠=∠,从而,知D ,L ,K ,I 四点共圆. 又I ,D ,G ,L 四点共圆,从而I ,D ,G ,L ,K 五点共圆,于是 90IKG ILG ∠=∠=︒,即KI KG ⊥. ③ 由①,③可知,G ,E ,F 三点共线.必要性.当G ,E ,F 三点共线时,如图1013-,联结GI 交DL 于点R ,则IR DL ⊥. 类似于充分性证明,由22FI ID IR IG ==⋅,可证得F ,I ,R ,E 四点共圆.又A 、F 、I 、E 四点共圆,即有90IRA IEA ∠=∠=︒,即IR AR ⊥.故A 、L 、D 三点共线.性质15 设ABC △的内切圆为I ,点D ,E ,F 依次为I 上三点(点D 在优弧EF 上,且与A ,I 不共线),EF 与AI 交于点K ,且K 为EF 的中点,则E 为AC 与I 的切点(或F 为AB 与I 的切点)的充要条件是IDK △∽IAD △. 证明 如图1014-,显然AI EF ⊥.A图10-14充分性.当IDK △∽IAD △时,有IK IDID IA=,即有22IK IA ID IE ⋅==. 于是IK IEIE IA=,注意到EIK ∠公用,则IEK △∽IAE △,即知90IEA IKE ∠=∠=︒.所以AE 与I 切于点E ,且AE 为过定点A 与I 右侧相切的直线,而这样的直线是唯一的,所以E 为AC 与I 相切的切点.同理,F 为AB 与I 的切点.必要性.当E 为AC 与I 的切点时,则由对称性(即K 为EF 中点)知F 必为AB 与I 的切点,反之亦真.此时,显然有IDA IKD ∠=∠,即有IDK △∽IAD △.性质16 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,点H 在线段EF 上,则D H EF ⊥的充要条件是FH BDHE DC=. 证明 如图1015-,联结BH ,CH . M HGF ABCDE 图10-15充分性.当FH BD HE DC =时,注意到BF BD =,EC DC =,则有FH BFHE CE=.又B F H C E H ∠=∠,从而BHF △∽CHE △.于是,BHF CHE ∠=∠,且BH BF BDCH CE DC==. 由角平分线性质定理的逆定理,知DH 平分B H C ∠.从而DHF DHB BHF DHC CHE ∠=∠+∠=∠+∠ DHE =∠,故D H EF ⊥.必要性.当D H EF ⊥时,若FE BC ∥,则ABC △为等腰三角形,结论显然成立.若\FE BC ∥,则可设直线FE 与直线交于点G ,如图1015-.1BG CE AFGC EA FB⋅⋅=. 注由性质1,有BD DCBG GC=. 过点D 作MN HG ∥交直线BH 于点M ,交直线HC 于点N ,则D H M N ⊥,且M D B D D C D NH G B G G C H G ===, 即有MD DN =.由等腰三角形性质,知DH 平分MHN ∠,即有BHF CHE ∠=∠.又BFH CEH ∠=∠,所以BHF △∽CHE △.故FH BF BDHE CE DC==. 性质17 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线AD 交EF 于点H ,若直线FE 与直线BC 交于点G ,则FH FGHE GE=. 证明 如图1016-,由性质1,有BG CGDB DC=. Y JH GFABC DE I 图10-16联结AG ,过点D 作IJ AG ∥交AB 于点I ,交直线AC 于点J ,则AG BG CG AGDI DB DC DJ===. 从而D 为IJ 的中点,过点H 作XY IJ ∥交AB 于点X ,交AC 于点Y ,则知H 为XY 的中点,即XH HY =.于是,FH XH HY HE FG AG AG EG ===,故FH FGHE GE=. 推论5 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线AD 交内切圆于点L ,过点L 作内切圆的切线分别与直线DF ,DE ,BC 交于点S ,T ,G ,则S L S GL T G T=.证明 如图1017-,由性质14,知F ,E ,G 三点共线.XZ L SHF A BC DE I JYT图10-17设直线AD 与EF 交于点H ,则由性质17,知FH HEFG GE=. 过点H 作XY BC ∥交直线DF 于点X ,交直线DF 于点Y ,则XH FH HE HYDG FG GE DG===. 由上即知H 为XY 的中点,过点L 作IJ XY ∥交直线DF 于点I ,交直线DE 于点J ,则知L 为IJ 的中点,即IL LJ =,于是SL IL LJ LT SG DG DG TG ===.故SL SGLT GT=. 注:特别地,设AF 与SL 交于点Z ,则对GZB △,应用上述性质17,亦有DH DAHL AL=.对G Z B △及截线DFS 应用梅涅劳斯定理也可推证推论5.推论6 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,联结AD 交内切圆于点L ,过L 作内切圆的切线分别与直线DF ,DE 交于点S ,T ,则直线AD ,BT ,CS 共点.证明 如图1018-,当ST BC ∥时,则推知ABC △为等腰三角形,此时结论显然成立.FABC DES L T X X'图10-18为\ST BC ∥时,可设直线ST 与直线BC 交于点G .于是,由性质14,知F ,E ,G 三点共线.由性质1,知有BG CGDB DC=. 又由推论5,知SL LTSG GT=. 设BT 交AD 于点X ,CS 交AD 于点X ',则对DGL △及截线BXT ,对DGL △及截线CX S'分别应用梅涅劳斯定理,有1DB GT LX BG TL XD ⋅⋅=,1DC GS LX CG SL X D'⋅⋅='.于是,LX BG TL CG SL LX XD DB GT DC GS X D'=⋅=⋅='. 由上式知X 与X '重合,故直线AD ,BT ,CS 共点.注:性质17及推论5中的结论,应用线段的调和分割性质证明更简捷(参见第15章). 性质18 设ABC △的内切圆I 分别切BC ,CA 边于点D ,E ,直线DI 交I 于另一点P ,直线AP 交边AB 于点Q ,点S 在边AC 上,BS 与AQ 交于点L ,则SC AE =的充要条件是AP LQ =.证明 如图1019-,由性质8,即知BQ DC =.A B图10-19兖分性.当AP LQ =时,此时PQ AL =.应用正弦定理,有sin sin sin sin AS AS BS ABS CSC BS SC A CBS ∠∠=⋅=⋅∠∠ sin sin sin sin sin sin sin sin C ABS BQA BAQ A BAQ CBS BQA ∠∠∠∠=⋅⋅⋅∠∠∠∠ c AL BL BQ p c AL a BL LQ c a LQ-=⋅⋅⋅=⋅. ①过点P 作B C BC ''∥交AB 于点B ',交AC 于点C ',则B C ''为I 的切线.设r ,A r 分别为AB C ''△、ABC △在BAC ∠内的旁切圆半径,S △为ABC △的面积,则A S AP r p a p aAQ r p S p--==⋅=△△.②于是,()LQ AP AP p a p a AL PQ AQ AP p p a a--====---.③将③代入①式得 AS p c a p cSC a p a p a --=⋅=--. 从而AC AS SC p c p a b SC SC p a p a+-+-===--. 故SC p a AE =-=.必要性.当SC AE =时,即有SA CE =.对AQC △及截线应用梅涅劳斯定理,有1AL QB CS LQ BC SA ⋅⋅=. 即有AL BC SA BC CE BC aLQ QB CS CD CS CS p a =⋅=⋅==-. 从而11AQ AL LQ AL a pLQ LQ LQ p a p A+==+=+=--. 再注意到②式,有 AQ p AQAP p a LQ==-. 故AP LQ =.性质19 设ABC △的内切圆分别切BC ,CA ,AB 边于点D ,E ,F ,直线FD ,DE ,EF 分别与直线CA ,AB ,BC 交于点U ,V ,W ,则U ,V ,W 三点共线.证明 若FE BC ∥,则视W 为无穷远点,UV BC ∥时,也视U ,V ,W 三点共线.当\FE BC ∥时,如图1020-分别对AFE △及截线WBC ,对BDF △及截线UAC ,对DCE △及截线VAB 应用梅涅劳斯定理,有WUFAB CD E LM N图10-201AB FW EC BF WE CA ⋅⋅=, 1BC DU FACD UF AB⋅⋅=, 1DB CA EVBC AE VD⋅⋅=. 注意到AF AE =,BF BD =,CD CE =,上述三式相乘,得1FW EV DUWE VD UF⋅⋅=. 对DEF △应用梅涅劳斯定理的逆定理,知U ,V ,W 三点共线. 注:U 、V 、W 三点所在的直线称为莱莫恩(Lemoine )线. 性质20 三角形外心、内心及内切圆切点三角形的重心三点共线.证明 如图1021-,设O ,I 分别为ABC △的外心和内心,I 切边BC ,CA ,AB 分别于点D ,E ,F ,点G '为DEF △的重心.图10-21联结AI 并延长交I 于点K ,AI 交EF 于点H ,则K 为劣弧BC 的中点,且在BC 的中垂线上,AH 垂直平分EF .联结OK ,KC ,ID ,IE ,则由OK BC ⊥,ID BC ⊥知ID OK ∥,且由内心性质,知IK KC =.令KAC θ∠=,则HEI θ∠=.设O 的半径为R ,直线OI 与HD 交于点G ,则sin sin DIG HIG S DG ID DIGGH S IH HIG⋅∠==⋅∠△△ sin sin ID IOK ID IKIH OIK IH OK⋅∠==⋅⋅∠ 22sin IE IK AI IK IK IK IH R IE R R KCθ=⋅=⋅===⋅. 从而知G 为DEF △的重心,即G 与G '重合.故O ,I ,G '三心共线.下面给出上述性质应用的一些例子.例1(2006年福建竞赛题)如图1022-,O为ABC△的外接圆,AM,AT分别为中线和角平分线,过点B,C的O的切线相交于点P,联结AP与BC和O分别相交于点D,E.求证:点T是AME△的内心.R图10-22证明如图,过点A的切线与PB,PC的延长线交于点R,Q,由性质2知,四边形ABEC 为调和四边形,有AB EC BE AC⋅=⋅.注意到托勒密定理,有AB EC BE AC AE BC⋅+⋅=⋅,即2AB EC AE⋅=⋅2BC BM AC=⋅,亦即AB AC BM EC=.而ABM AEC∠=∠,从而ABM△∽AEC△.即知BAM EAC∠=∠.于是,知AT平分MAE∠.又由性质3,知D,P调和分割AE,在调和线柬MA,ME,MD,MP中,由于M D M P⊥,即知MD平分AME∠.故点T是AME△的内心.例2(2007年罗马尼亚国家队选拔赛题)设E,F分别为ABC△内切圆I与边AC,AB 的切点,M为BC的中点,AM与EF交于点N,以BC为直径的圆M分别交BI、CI于点X,Y.证明:NX NYACAB=.证明如图1023-,首先证明点X,Y在直线EF上.B图10-23由题设知X,Y分别为C,B在直线BI,CI上的射影,则由性质6,知点X,Y均在内切圆的切点弦EF上.其次证N,I,D三点共线.设DI的延长线与EF交于点N',则直线AN'与BC的交点(由性质9)为BC的中点,而M为BC 中点,AM 与EF 交于N ,则N '与N 重合,从而N ,I ,D 三点共线. 延长BY ,CX 交于点S ,则I 为SBC △的垂心,从而S 在直线ND 上. 又I 为DXY △的内心(三角形垂心的垂足三角形性质),从而1122ABC DBI CYX DYX ∠=∠=∠=∠, 即知ABC DYX ∠=∠. 同理,ACB DXY ∠=∠.于是sin sin sin sin NX XD DYX ABC ACNY DY DXY ACB AB∠∠====∠∠. 例3 (2005年南昌市数学竞赛题)如图1024-,ABC △的内切圆分别切BC ,CA ,AB 三边于D ,E ,F .M 是EF 上的一点,且D M EF ⊥.求证:DM 平分BMC ∠.FABEM图10-24证明 由性质16,有FM BD BFME DC CE==. 因BFM CEM ∠=∠,则BFM △∽CEM △.即有BMF CME ∠=∠,由此即可得DM 平分BMC ∠.类似于例3,可推证《数学教学》1999年3期数学问题481:已知ABC △的内切圆在BC ,CA ,AB 上的切点分别为D ,E ,F ,且DG EF ⊥,G 为垂足,求证:GD 平分BGC ∠. 例4 (2008年第34届俄罗斯数学奥林匹克题)ABC △的内切圆圆ω分别与边BC ,CA ,AB 切于点A ',B ',C ',圆周上的点K ,L 满足180AKB BKA ALB BLA ''''∠+∠=∠+∠=︒.求证:A ',B ',C '到直线KL 的距离彼此相等. 证明 如图1025-,对于劣弧A B ''上的点P ,有180APB BPA A PB ''''∠+∠<∠<︒,知点K ,L 均在优弧B C A '''上.设圆ω的圆心为I .图10-25注意到AKBALB '''''∠=∠及题设条件,有180180AKB A KB A LB ALB ''''∠=︒-∠=︒-∠=∠,从而,有A ,B ,L ,K 四点共圆. 联结B C '',A C '',由性质11(2),有180180AKB A KB A C B '''''∠=︒-∠=︒-∠1180()2A B AIB =︒-∠+∠=∠.从而知A ,B ,L ,I ,K 五点共圆. 设AI 与B C ''交于点X ,则X 为B C ''的中点.注意到B C '',KL ,AI 分别为圆ω,AB IC '',AKILB 两两的根轴,因而它们共点于X .因此,B ',C '到KL 的距离相等. 同理,A ',C '到KL 的距离相等.例5 (2008年第10届香港地区数学奥林匹克题)设D 为ABC △边BC 上一点,且满足AB BD +=AC CD +,线段AD 与ABC △的内切圆交于点X ,Y ,且X 距点A 更近一些,ABC △的内切圆与边BC 切于点E .证明: (1)EY AD ⊥;(2)2XD IA '=,其中I 为ABC △的内心,A '为边BC 的中点. 证明 如图1026-,(1)由推论2,知点D 为BAC ∠内的旁切圆与边BC 的切点,再由性质8知XE 为I 的直径,则90XYE ∠=︒,故EY AD ⊥.图10-26(2)由推论3,知IA XD '∥,而I 为XE 的中点,故2XD IA '=.例6 (2003年CMO 题)设点I ,H 分别为锐角ABC △的内心和垂心,点1B ,1C 分别为边AC ,AB 的中点.已知射线1B I 交边AB 于点22()B B B ≠,射线1C I 交AC 的延长线于点2C ,22B C 与BC 相交于K ,1A 为BHC △的外心.试证:A ,I ,1A 三点共线的充分必要条件是2BKB △与2CKC △的面枳相等.证明 如图1027-,先证2260BKB CKC S S BAC =⇔∠=︒△△.TF 1C 1C 2E 1B 1K ABCA 1B 2LIE F H 图10-27设I 分别切AC ,AB 于点E ,F ,直线EI 交I 于点T ,直线BT 交AC 于点1E ,则由性质8,知1AE C E =,即知1E 为ABC ∠内的旁切圆与AC 的切点.又由推论3,知211BB B E ∥,亦有211AB AB AB AE =. 同理,可得点L ,1F ,亦有211AC AC AC AF =. 令BC a =,CA b =,AB c =,1()2p a b c =++,由性质,则111,,22b cAB AC AE CE p c ====-,1AF BF p b ==-. 于是,22222241()()BKB AB C CKC ABC bcS S AB AC S S AB AC p b p c ⋅====⋅--△△△△. 从而,由2224()()60p b p c bc a b c bc BAC --=⇔=+-⇔∠=︒. 其次,再证A ,I ,1A 三点共线60BAC ⇔∠=︒.设O 为ABC △的外心,则180BHC BAC ∠=︒-∠,12(180)2BAC BHC BAC ∠=︒-∠=∠.因此,BAC ∠=1160180BAC BAC A ︒⇔∠+∠=︒⇔在O 上AI ⇔与1AA 重合(1A 在BC 的中垂线上)⇔A ,I ,1A 三点共线.例7 (2004年第18届韩国数学奥林匹克题)在等腰ABC △中,AB AC =,O 是ABC△的内切圆,与三边BC ,CA ,AB 的切点依次为K ,L ,M .设N 是直线OL 与KM 的交点,Q 是直线BN 与CA 的交点,P 是点A 到直线BQ 的垂足.若2BP AP PQ =+,求ABBC的所有可能的取值.解 如图1028-,由性质9,知Q 为AC 的中点.BA(1)(2)图10-28当点P在ABC△内时,如图1028-(1),在BQ的延长线上取点R,使Q R Q P=,又取点S,使RS AP=.联结CR,AS,CS,则知CR AP=,2PS PQ AP BP=+=.从而ABS△,ACS△,RCS△均为等腰三角形,则QAP QCR RSA ABQ∠=∠=∠=∠,从而(90)90BAC ABQ QAP∠=︒-∠+∠=︒.此时ABBC==当点P在ABC△外时,如图1028-(2),作CR BP⊥于R,则由Q为AC中点知CR AP=,RQ PQ=,于是2BR BP PQ AP=-=,即知BCR△为等腰直角三角形.此时,RCQ PBA∠=∠,知Rt RCQ△∽Rt PBA△,由2AB AC QC==,知22AP QR PQ==,亦即知2RC PQ=.于是,2AB QC===,BC==.故ABBC.综上,ABBC,。
《三角形的内切圆》PPT课件

= a·r
2
+
b·r 2
+
c·r 2
B
= (a+b+c)·r
2
A
r Ir
r
a
c
C
练习:
⑴边长为3,4,5的三角形的内切圆半径是_1_
⑵边长为5,5,6的三角形的内切圆半径是_1_.5
课堂小结:
1、本节课从实际问题入手,探索得出三角形内切圆 的作法 .
2、通过类比三角形的外接圆与圆的内接三角形概念 得出三角形的内切圆、圆的外切三角形概念,并介 绍了多边形的内切圆、圆的外切多边形的概念。
范文下载: .
试卷下载: . /shiti/
教案下载: .
ppt论坛: . .cn
ppt课件: .
语文课件: . /kejian/yuwen/ 数学课件: .
英语课件: . /kejian/yingyu/ 美术课件: .
科学课件: . /kejian/kexue/ 物理课件: .
化学课件: . /kejian/huaxue/ 生物课件: .
(3)若∠BOC=100 °,则∠A=
度。
2
试探讨∠BOC与∠A之间存在怎样的数量关系?
请说明理由.
∠BOC=90ຫໍສະໝຸດ °+12
∠A
名称
确定方法
图形
性质
外心 (三角形 外接圆的 圆心)
三角形三 边中垂线 的交点
B
A
(1)OA=OB=OC
(2)外心不一定在
O
三角形的内部.
C
内心
(三角形 内切圆的 圆心)
三角形三条 角平分线的 交点
A
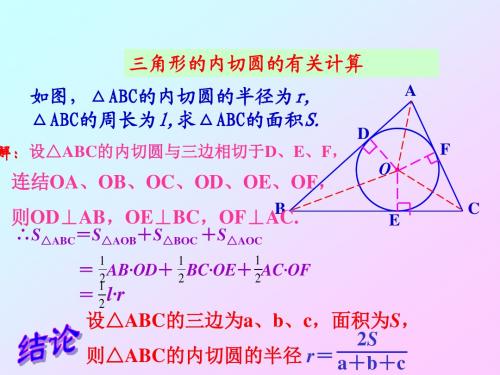
已知: △ABC(如图)
三角形内切圆 (2)
5
E
如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为 Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、 BC都相切,求⊙O的半径r的取值范围。
解:(1)设Rt△ABC的内切圆与三边相
切于D、E、F,连结OD、OE、OF则 OA⊥AC,OE⊥BC,OF⊥AB。 在Rt△ABC中,BC=3,AC=4, ∴AB=5 ∵ ⊙O与Rt△ABC的三边都相切 ∴AD=AF,BE=BF,CE=CD
A D O F
解:设△ABC的内切圆与三边相切于D、E、F,
·
C
B
E
设△ABC的三边为a、b、c,面积为S, 2S 则△ABC的内切圆的半径 r= a+b+c
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r. 解:设Rt△ABC的内切圆与三边相切于D、E、F, 连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。 A ∵ ⊙O与Rt△ABC的三边都相切 ∴AD=AF,BE=BF,CE=CD 设AD= x , BE= y ,CE= r 则有 x+r=b y+r=a x+ y= c
A
∴OB=BC=3 ∴半径r的取值范围为0<r≤3
D
O ·
几何问题代数化是 解决几何问题的一 种重要方法。
C
B
基础题:
1.既有外接圆,又内切圆的平行四边形是正方形 ______. 2.直角三角形的外接圆半径为5cm,内切圆半径为1cm, 22cm 则此三角形的周长是_______. 3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O 2cm 于P点,交AB、BC于E、F,则△BEF的周长是_____.
山西太原市高中数学竞赛解题策略-几何分册第3章含有45内角的三角形
第3章 含有45︒内角的三角形含有45︒内角的三角形也是一类特殊的基本图形,它出现在等腰直角三角形中,出现在正方形图形中,出现在直角三角形等图形中.它也有一系列有趣的性质及广泛的应用.性质1 含有45︒内角的三角形中,其外心与45︒角所对的边的两端点构成直角三角形的顶点,且外心为直角顶点.性质2 含有45︒内角的三角形中,其垂心与45︒角的顶点的距离等于45︒角所对的边长. 证明 如图31-,点H 为ABC △的垂心,45BAC ∠=︒.设AD 、BE 分别是边BC 、AC 上的高,D 、E 分别为垂足,则ABE △为等腰直角三角形,于是有AE BE =.HE DCBA图3-1HEDC BA又90AHE HAE BCE ∠=︒-∠=∠,则有Rt AHE △≌Rt BCE △.故AH BC =.性质3 在锐角AMN △中,45A ∠=︒,AH MN ⊥于H ,则A M N △可内接于一个以A 为一个顶点,边长等于AH 的正方形ABCD .证明 如图32-,分别以AM 、AN 为对称轴,作AH 的对称图形AB 、AD ,则ABM △≌AHM △,ADN △≌AHN △,此时290BAD MAN ∠=∠=︒,90ABM ADN ∠=︒=∠.延长BM 、DN 交于点C ,则A B C D 为矩形.又AB AH AD ==,故A B C D 为正方形,且AMN △内接于此正方形.图3-2HN MD CBA性质4 在锐角AMN △中,45A ∠=︒,AH MN ⊥于H ,则AMN △可内接于以A 为直角顶点,AH 为斜边上的高的直角三角形ABC .证明 如图33-,分别以AM 、AN 为角平分线作BAM M AH ∠=∠,作CAN NAH ∠=∠,与MN 两端的延长线分别交于B ,C ,则290BAC MAN ∠=∠=︒,且AH BC ⊥,故ABC △为直角三角形,且AMN △内接于此直角三角形.图3-3HN M CB A性质5 在锐角AMN △中,45A ∠=︒,AH MN ⊥于H ,则2222AH MH AH MHAH NH AH NH++=++. 证明 如图33-,设AH h =,MH m =,HN n =,MAH α∠=,则45NAH α∠=︒-,tan m h α=⋅,tan(45)n h α=⋅︒-.于是2222AH MH AH NH ++222222tan tan (45)h h h h αα+⋅=+⋅︒- 2221tan (1tan )21tan 11tan αααα++==-⎛⎫+ ⎪+⎝⎭, tan tan(45)AH MH h h AH NH h h αα++⋅=++⋅︒-21tan (1tan )211tan αααα++==++.由此即证.性质6 在锐角AMN △中,45A ∠=︒,作ME AN ⊥于E ,作NF AM ⊥于F ,则EF 平分AMN △的面积,即AEF MNEF S S =△四边形.证明 如图34-,由45MAN ∠=︒,则45AME ∠=︒,45ANF ∠=︒,从而AE EM =,AF FN =,且ME 与FN 所成的锐角为45︒.图3-4MF NEA于是11sin 45sin 4522AEF MNEF S AE AF EM FN S =⋅⋅︒=⋅⋅︒=△四边形. 即知线段EF 平分AMN △的面积.性质7 在锐角AMN △中,作ME AN ⊥于E ,作N F A M ⊥于F ,设K 为AMN △的外心,则45A ∠=︒的充要条件是K 为AEF △的垂心.证明 如图35-,设ME 与FN 交于点C ,则C 为AMN △的垂心.图3-5MCK NFE A联结AC ,AK ,MK ,NK ,FK ,则A 、F 、C 、E 四点共圆,且由三角形垂心与外心的性质,知FAK EAC ∠=∠.于是,CFE CAE FAK ∠=∠=∠,而90CFA ∠=︒,从而AFE ∠与FAK ∠互余,故AK FE ⊥. 4590A MKN MFN M ∠=︒⇔∠=︒=∠⇔、N 、K 、F 四点共圆⇔注意由MNC KNE ∠=∠有MNK FNE ∠=∠,此时有AME FNE MNK AFK ∠=∠=∠=∠ FK MN FK AE ⇔⇔⊥∥,其中注意到ME AE K ⊥⇔为AEF △的垂心. 下面,我们从四个方面介绍有关问题的求解例子,从这些例子中可看到这类问题的求解方法. 1.在等腰直角三角形中例1 设P 为等腰直角三角形ACB 斜边AB 上任一点,PE 垂直AC 于点E ,PF 垂直BC 于点F ,PG 垂直EF 于点G ,延长GP 并在其延长线上取一点D ,使得PD PC =. 试证:BC BD ⊥,且BC BD =.证明 如图36-,由题设,有EPG EFP CPF ∠=∠=∠.图3-6PE G DABFC从而4545DPB APG EPG CPF BPF CPF BPC ∠=∠=︒+∠=︒+∠=∠+∠=∠. 又PC PD =,PB 公共,则PDB △≌PCB △,有BC BD =. 注意到45PBD CBP ∠=∠=︒,则90CBD ∠=︒. 故BC BD ⊥.例2 如图37-,在等腰直角ABC △中,1AB =,90A ∠=︒,点E 为腰AC 的中点,点F 在底边BC 上,且FE BE ⊥.求CEF △的面积.图3-7DF ECBA解 过点C 作CD CE ⊥与EF 的延长线交于点D .因90ABE AEB ∠+∠=︒,90CED AEB ∠+∠=︒,则A B E C E D ∠=∠,于是Rt ABE △∽Rt CED △.从而214CDE AEB S CE S AB ⎛⎫== ⎪⎝⎭△△,且2CE ABCD AE== 又45ECF DCF ∠=∠=︒,则CF 是DCE ∠的平分线,从而点F 到CE 和CD 的距离相等.于是2CEF CDF S CES CD==△△. 故221211133434224CEF CDE AEB ABC S S S S ==⋅=⋅⋅=△△△△.此即为所求.2.在正方形中例3 如图38-,在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点,满足EF BE DF =+,AE 、AF 分别与对角线BD 交于点M ,N .图3-8E 1M1N MFED CBA求证:(1)45EAF ∠=︒;(2)222MN BM DN =+.证明 (1)延长CD 至点1E ,使1DE BE =,联结1AE ,则1ADE △≌ABE △,从而1DAE BAE ∠=∠,且1AE AE =,于是190EAE ∠=︒.在AEF △和1AE F △中,11EF BE DF E D DF E F =+=+=,则AEF △≌1AE F △,于是1EAF E AF ∠=∠11452EAE =∠=︒. (2)在1AE 上取一点1M ,使得1AM AM =,联结1M D ,1M N ,则ABM △≌1ADM △,ANM △≌1ANM △.于是有1ABM ADM ∠=∠,1BM DM =,1MN M N =,亦即有190NDM ∠=︒, 亦即有22211M N M D ND =+,故222MN BM DN =+.注:由此例,在图38-中,有45EAF EF BE DF ∠=︒⇔=+,亦有22245EAF MN BM DN ∠=︒⇔=+.例4 如图39-,正方形ABCD 的边长为1.点M 、N 分别在BC 、CD 上,使得CMN △的周长为2.图3-9LNMDCB A求:(1)MAN ∠的大小;(2)MAN △面积的最小值.解 (1)延长CB 至L ,使B L D N =,则Rt ABL △≌Rt ADN △.从而AL AN =,LAB NAD ∠=∠,90NAL DAB ∠=∠=︒.又211MN CN CM CN CM DN BM BL BM ML =--=-+-=+=+=,及AM 公用,所以AMN △≌AML △,故190452MAN MAL ∠=∠=⋅︒=︒.(2)设CM x =,CN y =,MN z =, 则2222222,2,.x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩于是222(2)y z y z --+=,即22(24)(44)0y z y z +-+-=. 因0y >,考虑其判别式24(2)32(1)0z z ∆=---≥,即(220z z +++-≥.又0z >,则2z ≥,当且仅当2x y ==时等号成立.由于11122AMN AML S S ML AB z ==⋅=△△,故AMN △1.注:由此例,在图39-中,有45MAN CMN ∠=︒⇔△的周长等于正方形ABCD 周长的一半.例5 如图310-,A 、B 、C 三个村庄在一条东西走向的公路沿线上,2km AB =,3km BC =,在B 村的正北方向有一个D 村,测得45ADC ∠=︒.今将ADC △区域规划为开发区,除其中24km 的水塘外,均作为建筑或绿化用地,试求这个开发区的建筑及绿化用地的面积是多少?图3-10E D解 问题显然就是求BD 的长.注意到ADC △是含有45︒的锐角三角形,可分别以AD 、CD 为对称轴作DB 的对称线段得正方形DEGF ,如图310-. 设DB x =,则2AG EG EA DB BA x =-=-=-, 3CG GF CF DB BC x =-=-=-. 由勾股定理,得22(2)(3)25x x -+-=. 解得6x =或1-,其中1x =-不合题意舍去. 故6x =.由此可得面积2156411(km )2⋅⋅-=.例6 如图311-,正方形ABCD 被两条与边平行的线段EF 、GH 分割成四个小矩形,P 是EF 与GH 的交点.若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定HAF ∠的大小并证明你的结论.E图3-11yx ba PG HCFBMD A解 猜测45FAH ∠=︒.证明如下:设AG a =,BG b =,AE x =,ED y =,则联立方程 ,2a b x y ax by +=+=得a x y b -=-,亦即 222222224a ax x y by b y ax b -+=-+=-+,从而222()a x b y +=+,亦即a x FH +=,于是DH BF FH +=.延长CB 至M ,使BM D H =,联结AM ,由Rt ABM △≌Rt ADH △,有AM AH =,M AB H AD ∠=∠.从而90MAH MAB BAH BAH HAD ∠=∠+∠=∠+∠=︒. 再由AMF △≌AHF △(边,边,边),知M AF H AF ∠=∠.故1452HAF MAH ∠=∠=︒.注:由此例,在图311-中,有452PFCH AGPE HAF S S ∠=︒⇔=.3.在直角三角形中例7 已知Rt ABC △中,CD 是斜边AB 上的高,O 、1O 、2O 分别是ABC △、ACD △、BCD △的角平分线的交点.求证:(1)12O O CO ⊥;(2)12OC O O =.证明 (1)如图312-,由题设1O 、O 都在A ∠的平分线上,设该平分线交2CO 于E .图3-12O 2O 1OE F DBCA由于A DCB ∠=∠,则2EAC O CB ∠=∠,从而290EAC ACE O CB ACE ∠+∠=∠+∠=︒,于是90AEC ∠=︒.故12O O CO ⊥.或者由O 、1O 都在A ∠的平分线上,设该平分线交2CO 于E ,联结1CO ,则1245O CO ∠=︒,111114522EO C O AC ACO A ACD ∠=∠+∠=∠+∠=︒,从而90AEC ∠=︒,故12O O CO ⊥.(2)由于点1O 、2O 分别在ACD ∠和DCB ∠的平分线,从而1245O CO ∠=︒. 由(1)知190O EC ∠=︒,有1CE EO =.同理,设直线2O O 交1CO 于F ,则2O F CF ⊥,245OO E ∠=︒,有2O E EO =. 又21CEO O EO ∠=∠,则CEO △≌12O EO △,从而12CO O O =. 注:由此例,在图312-中,有12CO O O ⊥,即O 为12CO O △的垂心.例8 如图313-,设P 、Q 是Rt ABC △的斜边AB 上两点,满足AQ AC =,BP BC =,在AC 、BC 上分别取点M ,N ,使CM CN =且等于AB 边上的高.又G 、H 分别是线段CP 、CQ 上的点,则CPQ △的外心O 为CGH △的垂心的充要条件是M 、G 、H 、N 四点共线.图3-13321POHD N MBAC证明 作CD AB ⊥于D ,则ACD B ∠=∠,且CD CN =.由AQ AC =,有B D C Q A C D D C Q A C Q A Q C B ∠+∠=∠+∠=∠=∠=∠+∠,从而D C Q Q C B ∠=∠,即QC 平分DCB ∠.同理,PC 平分ACD ∠.故知45PCQ ∠=︒. 此时,还有CDH △≌CNH △.充分性:当M 、G 、H 、N 四点共线时,由CM CN =,知45CNH ∠=︒. 于是,45CDH ∠=︒,即知DH 平分CDB ∠,从而H 为CDB △的内心.又O 为CPQ △的外心,即O 在PC 的中垂线上,则在等腰CBP △中,B 、H 、O 三点共线,即HO CG ⊥.同理,GO CH ⊥.故O 为CGH △的垂心.必要性:当CPQ △的外心O 为CGH △的垂心时,联结HN ,GQ ,则GO 为QC 的中垂线. 于是QG GC =.而45PCQ ∠=︒,则45GQH GQC ∠=∠=︒.联结PH .同理45H P G H P C ∠=∠=︒.于是,P 、Q 、H 、G 四点共圆,即有1CHG CPQ ∠=∠=∠.又H 在PC 的中垂线上,有HC HP =,且45HPC ∠=︒,推知PH CQ ⊥. 注意到CD PQ ⊥,从而C 、P 、D 、H 四点共圆,有2QHD CPQ ∠=∠=∠. 联结QN ,由CD CN =及QC 平分DCB ∠,知CDQ △≌CNQ △,有DQ QN =.又由C D H △≌CNH △,有D HH N =,从而DHQ △≌HNQ △,即有23DHQ QHN ∠=∠=∠=∠.于是123CHG QHN ∠=∠=∠=∠=∠,即知G 、H 、N 三点共线. 同理M 、G 、H 三点共线.故M 、G 、H 、N 四点共线. 4.在其他图形中例9 (2008年陕西省竞赛题)如图314-,AB 是半圆O 的直径,C 是AB 的中点,M 是弦AC 的中点,CH BM ⊥,垂足为H .求证:2CH AH OH =⋅.图3-14M HOBAC证明 联结OC 、BC ,则90BOC BHC ∠=∠=︒.从而O 、B 、C 、H 四点共圆. 故45OHB OCB ∠=∠=︒.又因为90BCM ∠=︒,CH BM ⊥,且M 为AC 的中点,所以22AM CM MH MB ==⋅,即HM AMAM BM=. 于是AMH △∽BMA △,即有M AH BM A ∠=∠,45AHM BAM ∠=∠=︒.从而AHM BHO ∠=∠,可知AMH △∽BOH △,即AH MHBH OH=. 亦即AH OH MH BH ⋅=⊥. 又因为2CH MH HB =⋅,故2CH AH OH =⋅.例10 (2004年第7届香港地区数学奥林匹克)在ABC △中,P 、Q 分别是边AB 、AC 上的点,且使得45APC AQB ∠=∠=︒,过点P 作边AB 的垂线与BQ 交于点S ,过点Q 作边AC 的垂线与CP 交于点R .设D 是BC 上的点,且使得AD BC ⊥.证明:PS 、AD 、QR 三线共点,且SR BC ∥.证明 如图315-,设QR 、AD 的延长线交于点E .下面证明直线PE 和PS 重合.图3-15P RQSEDCBA注意到135ABQ BAC ACP ∠=︒-∠=∠,则B 、P 、Q 、C 四点共圆. 于是APQ ACB ∠=∠.又90AEQ EAC ACB ∠=︒-∠=∠,从而A 、P 、E 、Q 四点共圆. 于是18090APE AQE ∠=︒-∠=︒,所以PE AB ⊥. 因此,PE 、PS 重合且PS 、AD 、QR 三线共点.由9045BQE CPE ∠=︒-︒=∠,即知P 、Q 、R 、S 四点共圆.从而QPR QSR ∠=∠.因为B 、P 、Q 、C 四点共圆,所以QPR QBC ∠=∠. 因此,QBC QSR ∠=∠,即SR BC ∥.例11 (《中等数学》2001(2)数学奥林匹克问题高98)如图316-,AM 和AN 是O 的切线,M 、N 是切点,L 是劣弧MN 上异于M 、N 的点,过点A 平行于MN 的直线分别交直线ML 、NL 于点P 和Q .若45POQ ∠=︒,求证:2πOOPQ SS =△.O图3-16βαL M NPAQ证明 连接OA ,OM ,设AOP α∠=,AOQ β∠=.由AM 、AN 是O 的两条切线,知AM AN =,且AO MN ⊥. 因PQ MN ∥,则AO PQ ⊥,从而cos cos()cos cos sin sin POQ αβαβαβ∠=+=⋅-⋅ 2OA OA AP AQ OA AP AQ OP OQ OP OQ OP OQ-⋅=⋅-⋅=⋅. 又AMP MNL AQN ∠=∠=∠,APM PMN ANQ ∠=∠=∠,则AMP △∽AQN △,有AM APAQ AN =,即有2AP AQ AM AN MA ⋅=⋅=, 从而222cos OA AM OM POQ OP OQ OP OQ-∠==⋅⋅.当45POQ ∠=︒时,有2OM OQ =⋅,从而2πOS OM OP OQ ==⋅.又1sin 2OPQ S POQ OP OQ OQ =∠⋅⋅=⋅△. 故2πOPOQ SS =△.练习三1.在梯形ABCD 中,AD BC ∥(BC AD >),90D ∠=︒,12BC CD ==,45ABE ∠=︒.若10AE =,则CE 的长度为___________.2.在梯形A B C D 中,A D B C ∥,AD CD ⊥,2BC CD AD ==,E 是CD 上一点,45ABE ∠=︒.则tan AEB ∠的值等于________________.3.已知ABC △中,AB c =,AC b =,BC a =.BC 边上的高为a h ,AC 边上的高为b h ,且有a a h ≤,b b h ≤.求ABC △的三个内角的度数.4.从正方形ABCD 的顶点A 引两射线,使其夹角为45︒,分别与BC 、CD 交于E 、F ,与BD 交于P ,Q .求证:2AEF APQ S S =△△.5.设ABCD 为正方形,M 在BC 上,N 在CD 上,且45MAN ∠=︒.求证:2ABCD MAN S ABS MN =△. 6.在正方形ABCD 的边BC 、CD 上各有一点M 、N ,满足45MAN ∠=︒.求证:AMAN=7.(2007年爱沙尼亚国家队选拔考试)在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点.设AE 与BD 交于点G ,FG AE ⊥,K 为FG 上一点,且满足AK EF =.求EKF ∠.8.(2007年克罗地亚国家集训考试题)已知在以AB 为直径、S 为圆心的半圆上有两点C 、D ,满足点C 在弧AD 上且90CSD ∠=︒,点E 、F 分别为直线AC 与BD 、AD 与BC 的交点.证明:EF AB =. 9.(《中学教学》2003(12)数学问题601号)Rt ABC △中,AC BC =,90ACB ∠=︒,D 、E 是AB 上的点,过C 、D 、E 的圆交AC 于P ,交BC 于Q .求证:AP BQ PQ +=成立的充要条件是45DCE ∠=︒.。
《三角形的内切圆》 讲义
《三角形的内切圆》讲义一、三角形内切圆的定义在三角形中,如果一个圆与三角形的三边都相切,那么这个圆就叫做三角形的内切圆。
内切圆的圆心是三角形三条角平分线的交点,这个交点被称为三角形的内心。
想象一下,一个三角形就像是一块被包围的土地,而内切圆就是在这块土地中间挖的一个正好与三边都接触的圆形水池。
二、三角形内切圆的性质1、内心到三角形三边的距离相等因为角平分线的性质,内心到三角形三边的距离都等于内切圆的半径。
这就好比从圆心向三条边引垂线,这些垂线的长度都是一样的。
2、三角形的面积与内切圆半径的关系三角形的面积可以用“三角形的周长乘以内切圆半径的一半”来计算。
假设三角形的三条边分别为 a、b、c,周长为 L,内切圆半径为 r,那么三角形的面积 S = 1/2 × L × r 。
我们可以这样理解,把三角形分成三个小三角形,分别以三边为底,内切圆半径为高,那么三个小三角形的面积之和就是大三角形的面积。
3、内切圆半径的计算公式对于一个已知三边长度为 a、b、c 的三角形,其内切圆半径 r 可以通过公式 r =(a + b c) / 2 计算(前提是 c 为最长边)。
例如,一个三角形的三边分别为 6、8、10,因为 10 是最长边,所以内切圆半径 r =(6 + 8 10) / 2 = 2 。
三、三角形内切圆的作图方法1、角平分线法(1)首先作出三角形的两条角平分线,它们的交点就是内心。
(2)过内心向三角形的一边作垂线,这条垂线的长度就是内切圆的半径。
(3)以内心为圆心,以内切圆半径为半径作圆,这个圆就是三角形的内切圆。
2、切线长法(1)分别测量三角形的三边长度 a、b、c 。
(2)以三角形的顶点为圆心,分别以切线长(切线长可以通过公式:切线长=(a + b c) / 2 计算)为半径作弧,三条弧的交点就是内切圆的圆心。
(3)以内切圆的圆心为圆心,以切线长为半径作圆,即为三角形的内切圆。
四、三角形内切圆的应用1、求三角形的面积当知道三角形的三边长度时,可以先求出内切圆半径,然后利用面积公式计算三角形的面积。
山西太原市高中数学竞赛解题策略-几何分册第12章圆与圆相交2
1PT EN FKTE NF KP⋅⋅=.① 上述两式相除得CK DM EN FKTD MC NF TE ⋅=⋅. ② 由题设有DM EN MC NF =,则由②式有CK FKTD TE =, 即有KC TD KF TE =,亦即KC TD CF DE=. ③ 对于③式,应用性质35,知Q ,T ,P ,K 四点共圆.即知QTPK ⊙, Q DCP ⊙,QEFP ⊙有公共弦PQ .此时,又由性质35,当QTPK ⊙,QEFP ⊙, P QAB ⊙有公共弦PQ 时,有 BF AE FK ET =, 亦即KB TK FK ET=, 从而有 KB FKTA TE=. ④ 设直线KN 交AB 于L ',对PAB △及截线KTL '应用梅涅劳斯定理,有1PT AL BKTA L B KP'⋅⋅='.由上式和①式两式相除,得BK AL EN FKTA L B NF TE'⋅=⋅' ⑤ 将④式代入⑤式,得AL EN L B NF '='.注意到已知条件EN AL NF LB =,有AL ALL B LB'='. 从而L '与L 重合,故M ,N ,L 三点共线. 由推论9,即得如下结论:推论10在凸(或折)四边形ABCD 中,E ,F 分别在线段AD ,BC 上,点M ,N ,L 分别在线段DC ,EF ,AB 或其延长线上,且满足DE CF EA FB =,DM EN ALMC NF LB==,则M ,N ,L 三点共线.推论11 三个圆两两相交(或相切)有公共弦PQ (或公切点P ),过点P 的割线段PA ,PB 依次交三个圆于D 、E 、A ,C 、F 、B ,则PDC △,PEF △,PAB △的三个重心共线,且三个垂心共线.证明仅就图12-37的情形给出证明.图12-37设,,PAB PEF PDC △△△的重心分别为1G 、2G 、3G ,又1M 、2M 、3M 分别为PB ,PF ,PC 的中点,则注意到性质35,有121223231()21()2BP FP M M M P M P BF AEM M M P M P FC ED FP CP --====--. 而123,,G G G 分别在线段123,,AM EM DM 上,且3121122332DG AG EG G M G M G M ===,则由推论10,知123,,G G G 三点共线.设123,,O O O 分别为PAB △,PEF △,PDC △的外心,则由性质34,知123,,O O O 三点共线,且由性质35必要性证法1中,知12122323O O M MO O M M =.再注意到欧拉线定理,三角形的外心,重心,垂心共线,且其间距离成比例,从而由推论10知PAB △,PEF △,PDC △的垂心1H ,2H ,3H 共线. 由性质35还可得到如下结论:推论12 两圆相交的公共弦为PQ ,过点P 的割线XY 与X Y ''分别交第一个圆于X ,X ',交第二个圆于Y ,Y '.若有一点O ,使得OXY △与OX Y '△反向相似,则OQ QP ⊥.证明 在图12-38,1O XY △与1O X Y ''△以及2O XY △与2O X Y ''△似乎顺向相似,但1O 、2O 是不存在的.反向相似存在于图12-38(2)中.设O 在直线XY ,X Y ''上的射影分别为Z 、Z ',则由反向的OXY OX Y '△∽△,知OYZ OY Z ''△∽△,即有XY X Y YZ Y Z ''=''. XZPOQYX′Z′Y′O 1Z 1OY′QYZZ′X′O 1P Z 1Z 1(1) (2)图12-38此时,P ,Z ',O ,Z 四点共圆,且PO 为其直径.注意到性质35,知P 、Q 、Z '、Z 四点共圆,即知P 、Q 、Z '、O 、Z 五点共圆. 于是90PQO ∠=︒,故OQ QP ⊥.推论13 两圆相交的公共弦为PQ ,过点P 的割线XZ 与X Z ''分别交第一个圆于X ,X ',交第二个圆于Z ,Z '.若线段XZ 的中垂线与线段X Z ''的中垂线相交于点O ,则O Q Q P ⊥. 证明 如图12-39,设Y ,Y '分别为XZ ,X Z ''的中点,则OY XZ ⊥,OY X Z '''⊥.从而,即知P 、Y 、O 、Y '四点共圆,且PO 为其直径.X PZX′Y′Z′YO QX′Y′Q XYZP OZ′PQOX YZY′X′Z′(1) (2) (3)图12-39此时,1XY X Y YZ Y Z ''=='',注意到性质35,知P ,Y ,Y ',Q 四点共圆. 于是,P 、Y 、O 、Y '、Q 五点共圆,有90PQO ∠=︒,故OQ QP ⊥. 推论14两圆相交的公共弦为PQ ,过点P 的割线XZ 与X Z ''分别交第一个圆于X 、X ',交第二个圆于Z 、Z '.若X 、Z 、Z '、X '四点共圆,圆心为O ,则OQ QP ⊥. 证明 如图12-40,设Y ,Y '分别为XZ XZ ,X Z ''的中点,则OY XZ ⊥,OY X Z '''⊥.从而即知P 、Y 、O 、Y '四点共圆,且PO 为其直径,此时1XY X Y YZ Y Z ''=='',注意到性质35,知P 、Y 、O 、Y '、Q 五点共圆,有90PQO ∠=︒,故OQ QP ⊥. PX YZZ′Y′X′QOY′XTZQO YP (1) (2)图12-40注:此推论即为前面的性质10.性质36 三个圆两两相交,一条与三圆相交(异于公共弦的端点)的直线依次与各圆交于六点,过第一、五、六点分别作该圆的直径,则这三个圆共一条公共弦,且三条直径的另一端点为顶点的三角形的垂心在公共弦所在直线上的充分必要条件是这三条直弪的端点构成完全四边形的六个顶点.证明 如图12-41,三个圆的圆心分别为M ,N ,L .点A ,B ,C 相应为直线与三个圆的交点,D ,F ,E 分别为三条直径的另一端点,EF 图12-41充分性.当A ,B ,C ,D ,E ,F 构成完全四边形的六个顶点时,则M ,N ,L 分别为完全四边形的三条对角线AD ,BF ,CE 的中点,设1H ,2H ,3H ,4H 分别为DEF △,ACF △,ABE △,BCD △的垂心.注意到三角形垂心的性质:三角形的垂心是所有过任一条高的两个端点的圆的根心,即知1H 三个圆的根心,对于DEF △,在它的边所在直线上的点C ,B ,A ,1H 关于以CE ,BF ,AD 为直径的圆的幂相等,即1H 在这三个圆两两的根轴上.同样,对ACF △.在它的边所在直线上的点B ,D ,E .其垂心2H 关于以CE ,BF ,AD 为直径的圆的幂相等,即2H 在这三个圆两两的根轴上. 同理,3H ,4H 也都在这三个圆两两的根轴上.于是,1234,,,H H H H 均在这三个圆两两的根轴上,即这三个圆两两的根轴重合,亦即共轴.三个圆两两相交时,三个圆共公共弦PQ 如图,显然DEF △的垂心1H 在直线PQ 上. 必要性 .设M ⊙,N ⊙,L ⊙共公共弦PQ ,且DEF △的垂心1H 在直线PQ 上时. 联结AF ,BD ,CD ,由于1H .在直线PQ 上,则知1H 在这三个圆两两的根轴上,即1H 关 于以CE ,BF ,AD 为直径的圆的幂相等,从而知这三个圆分别过DEF △的三条高EY ,FX ,DZ (如图)的端点,于是知C ,B ,A 分别在边FD ,ED ,EF 所在直线上.故BE 与CF 交于点,点A ,F ,E 三点共线,即A ,B ,C ,D ,E ,F 为完全四边形的六个顶点,结论证毕.(注:三圆两两不相交时,也有类似于性质36的结论.)推论15完全四边形的三条对角线的中点共线,且三中点所在直线垂直于以对角线为直径的三圆的公共根轴, 事实上,这可由性质34及性质36证明后的注即证.三条对角线的中点所在直线也常称为牛顿线或高斯线.下面给出应用上述结论处理问题的几个例子:例1(第21届俄罗斯数学奥林匹克题)试证:若五边形ABCDE 中,ABC ADE ∠=∠,AEC ADB ∠=∠,则BAC DAE ∠=∠. 证明 如图12-42,设BD 与CE 交于点F ,联结AF ,则由ADF ADB ∠=∠=AEC AEF ∠=∠,知A ,E ,D ,F 四点共圆.此时,AFE ADE ABC ∠=∠=∠,即知A ,F ,C ,B 四点共圆.CDEABF图12-42于是AFCB ⊙与AEDF ⊙相交于A ,F 两点,BD 和CE 是过点F 的两条割线段,由推论1,知AEC ADB △∽△,故BAC DAE ∠=∠.例2 (2006年全国女子数学奥林匹克题)设凸四边形ABCD 的对角线交于点O ,OAD △,OBC △的外接圆交于O ,M 两点,直线OM 分别交OAB △,OCD △的外接圆于T ,S 两点.求证:M 是线段TS 的中点.证明 如图12-43,联结DS ,DM ,由AOD ⊙与COD ⊙相交于D ,O 两点,应用推论1,有DAC DMS △∽△,亦即有DA DMAC MS=. ① S CD BMOA图12-43T联结AT ,AM ,同理,由AOB ⊙与AOD ⊙相交于A ,O 两点,有ABD ATM △∽△,亦有AD AMBD TM=. ② 联结MB ,MC ,MAC MDB △∽△,有AC BDMA MD=③ 由①÷②再代入③即得MS TM =.故M 是线段TS 的中点.例 3 (1992年冬令营试题)凸四边形ABCD 内接于圆O ,对角线AC 与BD 相交于P .ABP △,CDP △的外接圆相交于P 和另一点Q ,且O ,P ,Q 三点两两不重合.试证:90OQP ∠=︒证明 如图12-44,由于CDP ⊙与ABP ⊙相交于P ,Q ,且AC ,DB 为过点P 的两条割线段,因A ,B ,C ,D 四点共圆,则由性质10,即知OQ QP ⊥,即90OQP ∠=︒.(C 与D 重合,A 与B 重合,则变为1997年全国高中联赛题)图12-44例4 (2007年中国国家队集训第5次测试题)凸四边形ABCD 内接于O ⊙,BA ,CD 的延长线相交于点H ,对角线AC 、BD 相交于点G ,1O 、2O 分别为AGD △、BGC △的外心.设12O O 与OG 交于点N ,射线HG 分别交1O ⊙,2O ⊙于点P ,Q .设M 为PQ 的中点,求证:NO NM =.证明 如图12-45,过点G 作1GT O G ⊥,则知TG 切1O ⊙于G .图12-45于是AGT ADG ACB ∠=∠=∠,即知TG BC ∥,从而1O G BC ⊥,而2O OB C⊥,则12O G OO ∥.同理,12OO GO ∥,即知12O OO G 为平行四边形,所以N 分别为OG ,12O O 的中点. 在射线HG 上取点M ',使HG HM HA HB '⋅=⋅,则知G ,A ,B ,M '四点共圆. 而HD HC HA HB ⋅=⋅,亦知C ,D ,G ,M '四点共圆,即知ABM G '⊙与GM CD '⊙相交于G ,M ',且AC ,BD 为过点G 的两条割线段,则由性质9,即知M '为PQ 的中点,亦知M '与M 重合.又2BOC BAC BAC BDC BMQ QMC BMC ∠=∠=∠+∠=∠+∠=∠,知B ,C ,M ,O 四点共圆,则111(180)(180)(1802)222OMB OCB BOC BMC BMQ ∠=∠=︒-∠=︒-∠=︒-∠=90BMQ ︒-∠,即知OM PQ ⊥.于是,在Rt GOM △中,NM 为斜边OG 上的中线,故NO NM =.注:证得M 为PQ 的中点后,应用性质11,知NM NG =,即有NO NM =.例5(2010年中国数学奥林匹克题)两圆1Γ,2Γ过点B 的一条直线分别交圆1I ,n 于点C ,D ,过点交于点A ,B 过点B 的一条直线分别交圆1Γ,2Γ于点E ,F ,直线CF 分别交圆1Γ,2Γ于点P ,Q .设M ,N 分别是弧PB ,QB 的中点.若CD EF =,求证:C ,F ,M ,N 四点共圆.证明 如图12-46,圆1Γ与圆2Γ相交于A ,B ,而CD ,EF 为过点B 的两条割线段,则由推论3知AB 平分CBF ∠ .CBN DP AQ E MFI Г1Г2图12-46联结CM ,FN ,因M 是弧PB 的中点,则知CM 是BCF ∠的平分线. 同理,FN 是CFB ∠的平分线.在FCB 中,BA ,CM ,FN 三线共点于其内心,设内心为I .在圆1Γ,2Γ中,由圆幂定理,有CI IM AI IB ⋅=⋅,AI IB NI IF ⋅=⋅.于是,有CI IM NI IF ⋅=⋅.故由圆幂定理的逆定理知C ,F ,M ,N 四点共圆.例6 (1999年第25届全俄数学奥林匹克题)点D 是锐角ABC △的外心,过A ,B ,D 作圆分别交AC ,BC 于M ,N .证明:ABD △和MNC △的外接圆相等.证明 如图12-47,联结MB ,则ABD △与MNB △内接于同一个圆.而MNB △与MNC △有公共边,因此要证明ABD △与MNC △的外接圆相等,由性质6,知只需证明MBC △是等腰三角形,即证MBN MCN ∠=∠.ABCDN图12-47M事实上,由DB DC DA ==,有,DBN DCN MAD MCD ∠=∠∠=∠. 在ABC ⊙中,有MAD MBD ∠=∠,于是,MBN MBD DBN ∠=∠+∠MAD DCN =∠+∠MCD DCN =∠+∠MCN =∠. 故ABD △和MNC △的外接圆相等. 例7(2003年国家集训队训练题)设D 是ABC △的边BC 上一点,但不是其中点,设1O 和2O 分别是ABD △和ADC △的外心,求证:ABC △的中线AK 的垂直平分线过线段12O O 的中点.证明 如图12-48,联结AD ,12O O ,则由性质1,知12O O 是AD 的垂直平分线.图12-48设O 为12O O 的中点,则AO OD =. 联结OK ,则由性质11,知OK OD =.于是,AO OK =.这说明O 在线段AK 酌中垂线上. 故AK 的垂直平分线过线段12O O 的中点. 例8 (2007年中国国家集训队训练题)锐角ABC △的外接圆在A 和B 处的切线于点D ,M 是AB 的中点.证明:ACM BCD ∠=∠.证明 如图12-49,过点A 作与CB 切于点C 的1O ⊙,1O ⊙与CD 交于点Q ,与DA 的延长线交于点K ,联结AQ ,QB ,则AQD AKC ACB ABD ∠=∠=∠=∠,K图12-49于是,A ,D ,B ,Q 四点共圆.注意到DA DB =, 则AQD DQB ∠=∠.此时,180180AQC AQD DQB CQB ∠=︒-∠=︒-∠=∠. 又QAC QCB ∠=∠,从而AQC CQB △∽△.于是,AQC CBQ ∠=∠,此说明过B ,Q ,C 的圆即2O ⊙与AC 切于点C . 由性质14,知ACM BCD ∠=∠.例9 (2004年中国国家集训队测试题)圆心为1O 和2O ⊙的两个半径相等的圆相交于P ,Q 两点,O 是公共弦PQ 的中点,过P 任作两条割线AB 和CD (AB 、CD 均不与PQ 重合),点A ,C 在圆1O 上,点B ,D 在圆2O 上,联结AD 和BC ,点M ,N 分别是AD ,BC 的中点,已知1O 和2O 不在两圆的公共部分内,点M ,N 均不与点O 重合.求证:M ,N ,O 三点共线.证明 如图12-50,设S ,T 分别为CD ,AB 的中点,联结OS ,OT ,则由性质11,知OS OP OT ==,即知OST △为等腰三角形,亦即知点O 在ST 的中垂线上.N 图12-50O 2O 1AB CDOPS MT QO O 1O 2P N S MT ABCD联结AC ,BD ,则由性质5(2),知AC BD =.又联结MT ,MS ,NT ,NS ,则由中点性质,知12SN BD ∥,12MT BD ∥,12NT AC ∥,12MS AC ∥.从而,知MSNT 为菱形,它的对角线互相垂直平分,即M ,N 也在线段ST 的中垂线上.故M ,N ,O 三点共线, 例10 (IM049预选题)设P ,Q 是凸四边形ABCD 内的两点,且满足四边形PQDA 和四边形QPBC 均为圆内接四边形.若在线段PQ 上存在一点E ,使得PAE QDE ∠=∠,PBE QCE ∠=∠.证明:四边形ABCD 为圆内接四边形.证明 如图12-51,由性质20,知PQ 与EAD △的外接圆切于点EQ ABCDP EX图12-51假若直线AD 与PQ 交于点X ,则由切割线定理有2XE XA XD =⋅.又XA XD XP XQ ⋅=⋅,所以2XE XP XQ =⋅.若直线BC 与PQ 交于点Y ,亦有2YE YP YQ =⋅.从而X Y =,即AD ,BC ,PQ 三条直线交于一点.由此即证得ABCD 为圆内接四边形.若BC PQ ∥,则四边形QPBC 为等腰梯形,由PBE QCE ∠=∠,可得E 是PQ 的中点,这与2XE XP XQ =⋅.矛盾假若AD PQ BC ∥∥,则四边形PQDA ,QPBC 均为等腰梯形,从而四边形ABCD 为等腰梯形,因此,四边形ABCD 为圆内接四边形.例11 (2010年中国国家集训队测试题)如图12-52,在ABC △中,AD 是边BC 上的高,圆1Γ与2Γ圆相交于D ,K 两点,且圆1Γ过边AB 的中点M ,圆2Γ过边AC 的中点N ,直线MN 是圆1Γ与圆2Γ的一条公切线,过BC 边上的任一点P P 作直线AB ,AC 的平行线,分别与边AC ,AB 交于点E ,F .求证:K ,E ,A ,F 四点共圆.图12-52Γ2Γ1ABCDE FPNM L证明 注意到MN BC ∥,有A N M N C D D N M ∠=∠=∠,AMN MBD NMD ∠=∠=∠,从而有 DMN AMN △≌△,即有BM MA =,CN NA ND ==. 设L 为BC 的中点,则LN PE ∥,LM PF ∥,BL LC =,从而EN EN PL CN BL CN ND FM PL FM LC BM BM MD=⋅=⋅==. 由性质17(2),有ND KN MD KM =.因此EN KNFM KM=. 另一方面,由题设可知,MNK NDK ∠=∠,KMN KDM ∠=∠,所以由性质3(1), NDM NDK KDM MNK KMN ∠=∠+∠=∠+∠,故180NDM NKM ∠+∠=︒.但NDM MAN ∠=∠,所以180MAN NKM ∠+∠=︒,从而A ,M ,K ,N 四点共圆,于是,KNE KMF ∠=∠. 综上所述即知KNE KMF △∽△,所以KEN KFN ∠=∠. 不失一般性,设P 在B ,L 之间,则N 在C ,E 之间,F 在M ,B 之间,于是,KEN KFM ∠=∠,这表明KEC KFA ∠=∠.故K ,E ,A ,F 四点共圆.例12 两圆1O ⊙与2O ⊙相交于P ,Q 两点,过点P 的割线段AB ,CD 分别交1O ⊙于A ,C ,交2O ⊙,于B ,D 直线CA 与直线BD 交于点D .求证:QA QD QB QC QP QS ⋅=⋅=⋅.证明 如图12-53,由性质5(3)知Q A C Q B D △∽△,有Q A Q CQ B Q D=,从而QA QD QB QC ⋅=⋅. 图12-53O 2O 1QPABCDS又由性质5(2),知S ,A ,Q ,B 四点共圆,从而QBP QBA QSA QSC ∠=∠=∠=∠.注意到Q P B Q C A Q ∠=∠=∠,于是Q B P Q S △∽△,即有QB QPQS QC=,故Q B Q C Q P ⋅=⋅. 例13 两圆1O ⊙与2O ⊙相交于P ,Q 两点,过点P 的割线段AB 交1O ⊙于点A ,交2O ⊙于点B ,两圆在A ,B 处的切线交于点S ,直线SQ 交123O O O △的外接圆于另一点T .求证:ST 等于123O O O △的外接圆的直径.证明 如图12-54,设直线1AO 与直线2BO 交于点C ,则知S ,A ,C ,B 四点共圆.又由推论1知S ,A ,Q ,B 四点共圆,故知S ,A ,C ,Q ,B 五点共圆.因此,90CQS CBS ∠=∠=︒图12-54O 2O 1S 'A'B 'T Q A BCDS P分别延长1QO ,2QO 交圆于A ',B ',设两圆在A ',B '的切线交与S ',则由性质5(1)知A S B ASB '''∠=∠,注意到性质5(2)知1212O CO O QO ∠=∠,于是,知点C 在12O O Q △的外接圆上.由上即知CT 为12O O Q △的外接圆直径.于是1TO AC ⊥,即有1AS O T ∥.设直线AC 与直线SQ 交于点D ,则由1AS O T ∥及1DQO DCT △∽△,有1111AO O Q ST CTTD O D O D TD===,即知ST CT =. 即ST 等于12O O Q △的外接圆直径.例14(2009年土耳其数学奥林匹克题)已知圆Γ和直线l 不相交,P ,Q ,R ,S 为圆Γ上的点,PQ 与RS ,PS 与QR 分别交于点A ,B ,且A ,B 在直线l 上. 试确定所有以AB 为直径的圆的公共点,解 令圆Γ的圆心为O ,半径为r ,作ASP △的外接圆交AB 于点K ,联结SK ,则AKS QPS SRB ∠=∠=∠,于是,知S ,K ,B ,R 四点共圆.由性质24,知OK AB ⊥. 由圆幂定理,有222BO r BS BP BK BA BK BK KA -=⋅=⋅=+⋅,即有2AK KB BO ⋅=- 2222BK r OK r -=-.对任何一对满足条件的点{,}A B ,因为O ,K ,r 是固定的,所以,以AB 为直径的圆一定过直线OK 上的两点,其到直线l图12-55ΓABKOQPS lR例15 (2006年第35届美国数学奥林匹克题)在四边形ABCD 中,点E 和F 分别在边AD和BC 上,且AE BFED FC=.射线FE 分别交线段BA 和CD 的延长线于S 和T .求证:SAE △,SBF △,TCF △和TDE △的外接圆有一个公共点. 证明 如图12-56,延长BS 交直线TC 于点K .图12-56ABCDE FPS T对TED △及截线ASK ,对T F C △及截线BSK 分别应用梅涅劳斯定理,有1TS EA DKSE AD KT⋅⋅=,1TS FB CK SF BC KT⋅⋅=. 上述两式相除得EA DK FB CKAD SE BC SF⋅=⋅(*) 由题设AE BF ED FC =,AE FBAD BC=. 于是,由(*)式有DK CK SE SF =,即有KD SEDC EF=. (**) 设TCF △与TDE △的外接圆的另一交点为P ,对(**)式应用性质35,知SKT ⊙也公共弦PT ,即S ,K ,T ,P 四点共圆.由S ,K ,T ,P 及E ,D ,T ,P 分别四点共圆,有180PSK PEK PED ∠=︒-∠=∠,从而它们的补角相等,即ASP AEP ∠=∠.于是,知A ,E ,S ,P 四点共圆. 故SAE △,SBF △,TCF △与TDE △的外接圆有一个公共点P .例16 (2006年瑞士国家队选拔赛题)在锐角ABC △中,AB AC ≠,H 为ABC △的垂心,M 为BC 的中点,D ,E 分别为AB ,AC 的点,且AD AE =,D ,H ,E 三点共线.求证:ABC △的外接圆与ADE △的外接圆的公共弦垂直于HM .证明 如图12-57,设直线BH ,CH 分别与AC ,AB 交于点B ',C ',ABC △的外接圆与ADE △的外接圆交于A ,K 两点(因AB AC ≠).由HBD HCE ∠=∠,BDH CEH ∠=∠.则知HDB △与HEC △反向相似,于是,由推论12,知HK AK ⊥.图12-57B'C 'HABCDE K M又HC AB '⊥,HB AC '⊥,所以A ,C ',H ,B ',K 五点共圆.而B ',C '在以BC 为直径的圆上,M 为其圆心,于是,由推论14,知MK AK ⊥. 因此,,,M H K 三点共线.故AK HM ⊥.例17 (2009年西部数学奥林匹克题)设H 为锐角ABC △的垂心,D 为边BC 的中点,过点H 的直线分别交边AB ,AC 于点F ,E ,使得AE AF =,射线DH 与ABC △的外接圆交于点P .求证:P ,A ,E ,F 四点共圆.证明 如图12-58,分别延长BH ,CH 交AC 于点B ',交AB 于点C ',则知A ,C ',H ,B '四点共圆,设其圆心为O .又设O ⊙与ABC △的外接圆除交于点A 外,另一交点P '.C B 图12-58HAB CDEFOP由于AH 为O ⊙的直径,则知HP AP ''⊥.注意到B ,C ,B ',C '四点共圆,其圆心为D ,则由推论14,知DP AP ''⊥. 于是,D ,H ,P '三点共线.又P '在ABC ⊙上,即知P '与P 重合. 又由Rt Rt C FH B EH ''△∽△,FHB EHC △∽△, 有C F FH FB B E EH EC '==', 即C F B E FB EC''=. 由上式,应哟那性质35,即知AFE △的外接圆,O ⊙,ABC ⊙有公共弦AP . 故P ,A ,F ,E 四点共圆.例18 (2003年德国国家第二轮数学竞赛题)已知圆内接四边形ABCD 的两条对角线AC ,BD 的交点为S ,S 在边AB ,CD 上的射影分别为E ,F .证明:EF 的中垂线平分线段BC ,AD .证明 若AB DC ∥,则四边形ABCD 为等腰梯形,此时,E ,S ,F 三点共线,eF 的中垂线就是等腰梯形的中位线.故结论显然成立.当AD ∥DC 时,可设直线BA 与直线CD 交于点P ,如图12-59.图12-59A BCD EFOPNSM L由SE AB ⊥,SF CD ⊥,则知P ,E ,S ,F 四点共圆,且PS 为其直径.设O ,L 分别为PS ,EF 的中点,则OL 为EF 的中垂线.设M ,N 分别为AD ,BC 的中点,在完全四边形PABSCD ,应用推论15,则知O ,M ,N 三点共线,即O 在直线MN 上.由Rt Rt EBS FCS △∽△,Rt Rt AES DFS △∽△,有BE ES EA CF FS FD ==,即AE DFEB FC =. 又M ,L ,N 分别为AD ,EF ,BC 的中点,即有AM EL BNMD LF NC==. 于是,由推论10即知M ,L ,N 共线,亦即L 在直线MN 上. 故EF 的中垂线OL 过BC ,AD 的中点N ,M .结论获证. 练习十二 l .(2006年波兰数学奥林匹克题)已知C 是线段AB 的中点,过点A ,C 的圆1O ⊙.与过点B 、C 的圆2O ⊙相交于C ,D 两点,P 是O ⊙上AD (不包含点C )的中点,Q 是2O ⊙上BD (不包含点C )的中点.求证:PQ CD ⊥. 2.(2006年瑞士国家队选拔赛题)设P 是ABC △内部一点,D 是AP 上不同于P 的一点,1Γ,2Γ分别是过B ,P ,D 三点的圆和过C ,P ,D 三点的圆,圆1Γ,2Γ分别与BC 交于E ,F ,直线PF 与AB 交于X ,直线PE 与AC 交于点Y .求证:XY BC ∥. 3.(2009年巴尔干地区数学奥林匹克题)在ABC △中,点M ,N 分别在边AB ,AC 上,且MN BC ∥,BN 与CM 交于点P ,BMP △与CNP △的外接圆的另一个交点为Q .证明:BAQ CAP ∠=∠. 4.(2010年湖南省夏令营题)1O ⊙与2O ⊙相交于D ,P 两点,AB 为两圆的外公切线(离D 点较近).AD 与2O ⊙相交于点C ,线段BC 的中点为M .求证:DPM BDC ∠=∠. 5.(IM046试题)给定凸四边形ABCD ,BC AD =,且BC 不平行于AD ,设点E 和F 分别在边BC 和AD 的内部,满足BE DF =.直线AC 和BD 相交于点P ,直线EF 和BD 相交于点Q ,直线EF 和AC 相交于点R .证明:当点E 和F 变动时,PQR △的外接圆经过除点P 外的另一个定点. 6.(2006年第35届美国数学奥林匹克题)设E ,F 分别是凸四边形ABCD 的边AD 和BC 上的点,满足AE BFED FC=,射线FE 分别与射线BA 和CD 交于点S 和T .证明:SAE △、SBF △、TCF △和TDE △的外接圆有一个公共点. 7.(1995年第21届俄罗斯,1996年罗马尼亚国家队选拔,1997年伊朗数学奥林匹克题)设AB 是O ⊙的一条直径,一直线与O ⊙交于C ,D 两点,与直线AB 交于点M ,AOC △的外接圆与BOD △的外接圆交于点(0)N N ≠.证明:ON MN ⊥. 8.(2009年越南国家队选拔赛题)设以AB 为直径的圆为O ⊙,M 为O ⊙内的动点,AMB ∠的角平分线与O ⊙交于点N ,AMB ∠的外角平分线与NA 、NB 分别交于点P 、Q ,AM 、BM 分别与以NQ 、NP 为直径的圆交于R 、S .证明:NRS △中过点N 的中线过一个定点. 9.(2009年哥伦比亚数学竞赛题)在ABC △中,P 是边BC 上一点,1I ,2I 分别是APB △,APC △的内心,圆12,ΓΓ分别是以1I ,2I 为圆心且过点P 的圆.设Q 是圆1Γ,2Γ不同于点P 的交点,1X ,1Y 分别是圆2Γ.与AB ,BC 靠近点C 的交点.11X Y ,22X Y 分别是圆2Γ与AC 、BC 靠近点C 的交点,证明:11X Y ,22X Y ,PQ 三线共点. 10.(2003年第35届加拿大数学奥林匹克题)三个圆有公共弦AB ,任一条过点A 的直线l与三个圆的交点依次为X ,Y ,Z ,其中x B ≠.证明:XYYZ为定值.11.(IM026试题)已知ABC △,以O 为圆心的圆经过三角形的顶点A ,C 且与边AB ,BC 分别交于另外的点K ,N .ABC △和KBN △的外接圆交于点B ,M .试证:OMB ∠是直角. 12.(2006年国家集训队测试题)设K ,M 是ABC △的边AB 上的两点,L ,N 是边AC 上的两点.K 在M ,B 之间,L 在N ,C 之间,且BK CLKM LN=.求证:ABC △,AKL △,AMN △的垂心在一条直线上. 13.(《中等数学》2010(5)数学奥林匹克训练题)ABC △的三条高线AD ,BE ,CF 交于点H ,P 是ABC △内任意一点,求证:APD △,BPE △,CPF △的外心1O ,2O ,3O 三点共线.14.(《中等数学》2011(2)训练题)已知锐角()⊙与边AC,ABC AB AC△,过点B,C的O△外接圆的弧BAC上一点.证明:BD,CE,OP三线AB分别交于点D,E,P为ABC共点的充分必要条件是PBD△的内心重合.△的内心与PCE。
山西省太原市高中数学竞赛解题策略-几何分册第23章角元形式的梅涅劳斯定理
第23章 角元形式的梅涅劳斯定理第一角元形式的梅涅劳斯定理设A '、B '、C '分别是ABC △的三边BC 、CA 、AB 所在直线(包括三边的延长线)上的点,则A '、B '、C '共线的充要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''∠∠∠⋅⋅='''∠∠∠证明如图23-1,由sin sin ABA AA C S BA AB BAA A C S AC A AC''''⋅∠==''⋅∠△△, 图23-1B C 'CB'A及sin sin CB BC CBB B A AB B BA ''⋅∠=''⋅∠, sin sin AC AC ACC C B BC C CB''⋅∠=''⋅∠. 这三式相乘,运用梅涅劳斯定理及其逆定理,知结论成立.第二角元形式的梅涅劳斯定理设A '、B '、C '分别是ABC △的三边BC 、CA 、AB 所在直线上的点,点O 不在ABC △三边所在直线上,则A '、B '、C '三点共线的充要条件是 sin sin sin 1sin sin sin BOA COB AOC A OC B OA C OB'''∠∠∠⋅⋅='''∠∠∠.证明如图23-2.注意到sin sin BOA A OC'∠'∠C 'A'BOCBA 图23-2OC BA OB A C '=⋅'(其中BOA A OC S BA S A C '''='△△),sin sin COB B OA'∠'∠ OA CB OC B A '=⋅',sin sin AOC OB AC C OB OA CB ''∠=⋅'∠. 所以sin sin sin sin sin sin BOA COB AOC A OC B OA C OB'''∠∠∠⋅⋅'''∠∠∠ BA CB AC A C B A C B'''=⋅⋅'''.而由梅涅劳斯定理及逆定理知A '、B '、C '共线1BA CB AC A C B A C B'''⇔⋅⋅='''. 故知结论成立.注:在上述两定理中,若采用有向角(规定角的终边绕逆时针方向时角为正值,否则为负值)时,两条件式的右端均为1-,有向角记为. 下面给出运用如上定理处理问题的例子.例1如图23-3,设ABC △的三边BC 、CA 、AB 所在的直线E E'D F'FDCB A图23-3上的点D 、E 、F 共线,并且直线AD 、BE 、CF 关于A ∠、B ∠、C ∠平分线的对称直线AD '、BE '、CF '分别与BC 、CA 、AB 所在直线交于D '、E '、F ',则D '、E '、F '也共线. 证明对ABC △及截线FED 应用第一角元形式的梅涅劳斯定理,有sin sin sin 1sin sin sin BAD CBE ACFDAC EBA FCB∠∠∠⋅⋅=∠∠∠.由题设知,CAD BAD '∠=∠,D AB DAC '∠=∠,BCF ACF '∠∠=,F CA FCB '∠=∠,ABE CBE '∠=∠,E BC EBA '∠=∠.从而有sin sin sin 1sin sin sin CAD ABE BCF D AB E BC F CA '''∠∠∠⋅⋅='''∠∠∠,即sin sin sin 1sin sin sin BAD CBE ACF D AC E BA F CB'''∠∠∠⋅⋅='''∠∠∠. 由第一角元形式的梅涅劳斯定理知,D '、E '、F '三点共线.例2若三角形的三条外角平分线皆与对边所在直线相交,则三交点共线.证明如图23-4,设ABC △的三条外角平分线分别与对边所在直线相交于D 、E 、F ,则知1902BAD A =︒+∠,1902DAC A ⎛⎫=-︒-∠ ⎪⎝⎭,1902CBE B =︒+∠,1902EBA B ⎛⎫=-︒-∠ ⎪⎝⎭,1902ACF C ⎛⎫=-︒-∠ ⎪⎝⎭,1902FCB C =︒+∠.ACBFDE图23-4故有sin sin sin sin sin sin BAD CBE AZFDAC EBA FCB⋅⋅111cos cos cos 2221111cos cos cos 222A B CA B C∠∠-∠=⋅⋅=--∠-∠∠. 故D 、E 、F 三点共线.例3分别过三角形的三顶点作其外接圆的切线,证明:若三切线皆与其对边所在直线相交,则三交点共线.图23-5证明设过ABC △的三顶点A 、B 、C 的切线与对边BC 、CA 、AB 所在直线分别交于D 、E 、F .则弦切角定理BAD C =-∠,180DAC C A B =∠+∠=︒-∠,CBE A =-∠,180EBA A B C =∠+∠=︒-∠,180ACF C A B =∠+∠=︒-∠,FCB A =-∠. 故有sin sin sin sin sin sin BAD CBE ACFDAC EBA FCB⋅⋅sin sin sin 1sin sin sin C A BB C A --=⋅⋅=--. 故D 、F 、E 三点共线.例4在筝形ABCD 中,AB AD =,BC CD =,过BD 上一点P 作一条直线分别交AD 、BC 于E 、F ,再过点P 作一条直线分别交AB 、CD 于G 、H .设GF 与EH 分别交BD 于I ,J .求证:PI PJPB PD=. 证明如图23-6,过B 作AD 的平行线交直线EF 于E ',再过B 作CD 的平行线交直线GH 于H ',则E BP EDP PBG '∠=∠=∠,HBPHDP PBF '∠∠∠==, JE'H 'G HPJ FED CBA图23-6进而H BG H BP GBP ''∠∠=∠=PBF PBE E BF ''∠-∠∠==,所以 sin sin sin sin sin sin PBH GBI FBE H BG IBF E BP ''∠∠∠⋅⋅''∠∠∠ sin sin sin 1sin sin sin FBP GBP FBE E BF PBF PBG'∠∠∠=⋅⋅='∠∠∠.使H '、I 、E '分别为PGF △三边所在直线上的点,且点B 不在PGF △三边所在直线上,由第二角元形式的梅涅劳斯定理,即知H '、I 、E '三点共线.于是,由PBE PDE '△∽△,PH B PHD '△∽△,有E H EH ''∥.因此,PI PE PBPJ PE PD '==. 故PI PJPB PD=. 注:当PB PD =即P 为BD 中点时为1989年的冬令营选拔赛题.例5设ABC △为非直角三角形,AD 、BE 、CF 为三边上的高,D 、E 、F 为垂足,过ABC △的垂心H 分别作边BC ,CA ,AB 的平行线与直线EF 、FD 、DE 对应相交于P 、Q 、R .求证:P 、Q 、R 三点共线.证明如图23-7,有EHP HBC =,PHF HCB =,FHQ BCA =,QHD HAC =,DHR HAB =,RHE HBA =.从而PRHF E DCBA Q图23-7sin sin sin sin sin sin EHP FHQ DHRPHF QHD RHE ⋅⋅sin sin sin sin sin sin HBC HCA HABHCB HAC HBA =⋅⋅sin sin sin sin sin sin HBC HCA HABBCH CAH ABH=-⋅⋅1HC HA HBHB HC HA=-⋅⋅=-. 因ABC △为非直角三角形,点H 不在ABC △三边上,故由第二角元形式的梅涅劳斯定理知P 、R 、Q 三点共线.例6设E 、F 分别为四边形ABCD 的边BC 、CD 上的点,BF 与DE 交于点P .求证: BAE FAD ∠∠=,则BAP CAD ∠∠=.证明只需证明:当AF 关于BAD ∠的等角线交BE 于P 时,B 、P 、F 共线即可,如图23-8所示.PFED CBA图23-8事实上,B 、P 、F 分别为CDE △三边所在直线上的三点,A 不在其三边所在直线上,而FAD EAB =-,DAP BAC =-,PAE CAF =-.故sin sin 1sin sin sin EAB CAF DAPBAC FAD PAE⋅⋅=-.故由第二角元形式的梅涅劳斯定理,知B 、P 、F 三点共线. 注:注AC 平分BAD ∠时,即为1999年全国高中联赛题. 例7设P 为ABC △所在平面上一点,过点P 作PA 的垂线交直线BC 于D ,作PB 的垂线交直线CA 于E ,作PC 的垂线交AB 于F .求证:D 、E 、F 共线.FEDCBA 图23-9证明当点P 在ABC △的某边所在直线上时,结论显然成立.下设点P 不在ABC △的边所在直线上,则90BPD APB =︒-△,90DPC CPA =︒-,90CPE BPC =︒-,90EPA APB =︒-,90APF CPA =︒-,90FPB BPC =︒-. 于是,sin sin sin sin sin sin BPD CPE APFDPC EPA FPB⋅⋅cos cos cos 1cos cos cos APB BPC CPACPA APB BPC-=⋅⋅=---.故由第二角元形式的梅涅劳斯定理,知D 、F 、E 三点共线. 练习题二十三1.1四边形ABCD 的对角线交于O ,在直线AC 上取一点E ,设DE 交AB 于F ,FO 交CD 于G ,BG 交CO 于H ,BE 交AD 于I ,DH 交BC 于J ,证明:I 、O 、J 三点共线.JH OIFE D CBA2.设ABC △与A B C '''△的对应顶点的连线交于一点O ,D 、E 、F 分别为ABC △的三边所在直线上的点,直线OD 、OE 、OF 分别交A B C '''的三边B C '',C A '',A B ''所在直线于D '、E '、F '.求证:D 、E 、F 三点共线的充分必要条件是D '、E '、F '三点共线.1 萧振钢.再谈Menelaus 定理的第二角元形式[]J .中学数学研究,2007(9):16-18.EFF'E'O D 'B'A'C 'D CBA3.设P 为ABC △所在平面上一点,D 、E 、F 分别为ABC △的三边BC 、CA 、AB 所在直线上的三点,PD 关于BPC ∠的等角线交BC 于D ',PE 关于CPA ∠的等角线交CA 于E ',PF 关于APB ∠的等角线交AB 于F ',则D '、E '、F '三点共线的充分必要条件是D 、E 、F 三点共线.D 'PE'FDCB AE4.设ABC △的外心为O ,OAB △与OCA △的垂心分别为1H 、2H ,直线12H H 交BC 于D ,求证:AD BC ⊥.5.设P 为ABC △的顶角A 的外角平分线上一点,BAC ∠的两条等角线分别交直线PB 、PC 于E 、F ,EF 与BC 交于D ,则AD 平分BAC ∠.6.圆内三弦AD 、BE 、CF 交于一点O 、P 为圆周上一点,直线PD 、PE 、PF 分别交直线BC 、CA ,AB 于L 、M 、N ,求证:O 、L 、M 、N 四点共线.LPMF EDOBA7.(第7章推广7)在ABC △中,D 为边BC 上任意一点,从D 在形内作一条射线DP ,使BDP ADC ∠∠=.H 是DP 上任意一点,BH 与AC 交于点E ,CH 与AB 交于点F .求证:FDP EDA ∠∠=. 8.(第7章推广8)任意四边形ABCD 中,从顶点A 在形内作射线AP ,使BAP DAC ∠=∠,在CD 上取一点E ,BE 与AP 交于点F ,DF 与BC 交于点G .求证:GAP EAC ∠=∠.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例8 (2010年中国国家集训队测试题)锐角ABC △中,已知AB AC >,设ABC △的内心为I ,边AC ,AB 的中点分别为M ,N ,点D ,E 分别在线段AC ,AB 上,且满足BD IM ∥,CE IN ∥,过内心I 作DE 的平行线与直线BC 交于点P ,点P 在直线AI 上的投影为Q .证明:点Q 在ABC △的外接圆上.证明 如图1029-,由B D IM ∥,CE IN ∥,应用推论3,知D 为ABC ∠内的旁切圆与边AC 的切点,E 为ACB ∠内的旁切圆与边AB 的切点.Q (Q 1)SA BCD EM IKNTP (P 1)图10-29令BC a =,CA b =,AB c =,1()2p a b c =++,BAC α∠=,ABC β∠=,ACB γ∠=,R ,r 分别为ABC △的外接圆、内切圆半径. 由性质11(1),c o t 2A E p b r β=-=⋅,cot2AD p c r γ=-=⋅,从而cottan22cot tan 22AE AD βγγβ==. 设AI 与BC 交于点K ,与ABC △的外接圆交于点1Q ,则1Q 为弧BC 的中点,过点1Q 作1AQ 的垂线与直线BC 交于点1P .下面证明1PI DE ∥.设1P I 与AC ,AB 分别交于点S ,T ,对ABK △及截线1PTI 应用梅涅劳斯定理, 有111BP AT KITB P K IA ⋅⋅=. 因为1sin sin sin sin 22BKQ IA AC AKC KI KC γγ∠∠===,111111111sinsin sin 2sin sin(90)cos PQ PBQ CBQ BP PQ BAQ B γγ∠∠===∠︒-∠, 所以11111sin sin 2PK PKBKQ AT IA TB BP KI BP α∠=⋅=⋅1111cos sin2PQ BP αγ==⋅. 于是,有 22sin 2tan 1cos 22cos 2AB R AT R γγγγ⋅===⋅+.同理2tan2AS R β=⋅.由于tan2tan 2AT AE AS ADγβ==,所以1PI DE ∥. 注意到过点I 只能引一条平行于DE 的直线,所以1P 与P 重合,又点P 在AI 上的投影是唯一的,故1Q 与Q 重合,即点Q 在ABC △的外接圆上.例9 (2006年CMO 题)在Rt ABC △中,90ACB ∠=︒,ABC △的内切圆圆O 分别与边BC ,CA ,AB 相切于点D ,E ,F ,联结AD ,与内切圆交圆O 交于点P ,联结BP ,CP .若90BPC ∠=︒,求证:AE AP PD +=.(注:90ACB ∠=︒可去掉) 证法1 如图1030-,辅助线及各点标记如图.A C图10-30由性质4(1),可设EH ,FG ,AD 三线共点于K .由90GPH ∠=︒,知O 在GH 上,又OFG OGF HEF ∠=∠=∠,则OF 是KEF △外接圆的切线.又OF AF ⊥,知KEF 的圆心在AF 上. 同理,KEF 的圆心在AE 上.故A 即KEF 的圆心,AK AE =,从而AKE AEH EGH ∠=∠=∠,则E ,G ,S ,K 四点共圆,有90OSK GEK ∠=∠=︒,即GH PD ⊥.故知点G 为弧PED 的中点.设AE x =,AP m =,PD n =,CE CD y ==,延长AD 至T ,使D T C D y ==,作C Q A T ⊥于Q ,则12T CDP CPD ∠=∠=∠,即知Q 为PT 的中点.于是,1()2PQ n y =+,1||2DQ n y =-,且 2222AC CD AQ DQ -=-(定差幂线定理)即()()()()AC CD AC CD AQ DQ AQ DQ +-=+-,亦即(2)()()x y x m n m y +⋅=++, 亦即22()()x xy m m n y m n +=+++.由切割线定理,有2()x m m n =+.代入上式有2m n x +==求得3n m =,2x m =,即有3x m m n +==,故AE AP PD +=. 证法2 (图略).由性质4(3).可设BG ,CH ,AD 三线共点于L ,DH 与BG 交于点R ,则在完全四边形BHPLCD 中,应用对角线调和分割性质,有BR LRBG LG=. 过G 作IJ DH ∥交DC ,DP 于I ,J ,则DR BR LR DRIG BG LG JG===,即有IG JG =. 又90GDH ∠=︒,则DG IJ ⊥,即IDG JDG ∠=∠,知G 是弧PED 中点.下同证法1. 证法3 (图略).联结AG 、AH 分别交内切圆于点M 、N .由性质4(4),可设HM ,GN ,AD 三线共点于W .因90GPH ∠=︒,则H M A G ⊥,GN AH ⊥,即W 为AGH △的垂心.于是AD GH ⊥.从而,直径GH 为PD 的中垂线,即G 是弧PED 的中点.下同证法1.例10 (2001年第30届美国数学奥林匹克题)已知ABC △的内切圆ω分别切BC ,AC 边于1D ,1E ,2D ,2E 分别在BC ,AC 上,且21CD BD =,21CE AE =.记2AD 与2BE 的交点为P ,圆ω与2AD 相交两点中离A 较近的点为Q .求证:2AQ D P =.证明 如图1031-,设圆ω的圆心为I ,因21CD BD =,由性质8知1D ,I ,Q 三点共线. 再由性质18,知当21CE AE =时,有2AQ D P =.E 2D 2E 1D 1A BPQ I 图10-31例11 (2003年第20届伊朗数学奥林匹克题)设I 是ABC △的内心,且I 与AB ,BC 分别切于点X ,Y ,XI 与I 交于另一点T ,X '是AB 与CT 的交点.L 在线段X C '上,且X L CT '=.证明:当且仅当A ,L ,Y 三点共线时,AB AC =.证明 如图1032-,设直线AL 交BC 于点Y ',则由性质18,知当X L CT '=时,BY CY '=.A图10-32于是,A ,L ,Y 三点共线Y '⇔与Y 重合Y ⇔为BC 的中点AB AC ⇔=.例12 (2008年印度国家队选拔考试题)设ABC △是非等腰三角形,其内切圆为圆Γ,圆Γ与三边BC ,CA ,AB 分别切于点D ,E ,F .若FD ,DE ,EF 分别与CA ,AB ,BC 交于点U ,V ,W ,DW ,EU ,FV 的中点分别为L ,M ,N .证明:L ,M ,N 三点共线. 证明 如图1020-,由性质19知,U ,V ,W 三点共线. 在四边形VUFE 中(或完全四边形VUWFDE 中),应用牛顿线定理,即知L ,M ,N 三点共线(第14章性质1).例13 (1995年第24届美国数学奥林匹克题)设ABC △是非等腰非直角三角形,设O 是它的外接圆圆心,并且1A ,1B ,1C 分别是边BC ,CA ,AB 的中点,点2A 在射线1OA 上,使得1OAA △∽2OA A △.点2B 和2C 分别在射线1OB 和1OC 上,使得1OBB △∽2OB B △和1OCC △∽2OC C △.证明:直线2AA ,2BB ,2CC 共点.证明 如图1033-,因1OAA △∽2OA A △,1OBB △∽2OB B △,1OCC △∽2OC C △,则由性质15,知2A B 与O 相切于点B ,2A C 与O 相切于点C ,2B C ,2B A ,2C A ,2C B 分别与O 相切于点C ,A ,A ,B .于是,O 是222A B C △的内切圆,切点分别为A ,B ,C .C 2ABCA 1B 1C 1A 2B 2O图10-33由切线长定理,再应用塞瓦定理,知2AA ,2BB ,2CC 三线共点.例14 (2006年第16届韩国数学奥林匹克题)在ABC △中,B C ∠≠∠,ABC △的内切圆I 与BC ,CA ,AB 的切点分别为D ,E ,F .记AD 与I 的不同于点D 的交点为P .过点P 作AD 的垂线交EF 于点Q ,X ,Y 分别是AQ 与直线DE ,DF 的交点.求证:A 是线段XY 的中点.证明 如图1034-,记过点A 且平行于BC 的直线与过点P 且与AD 垂直的直线交于点Q ',直线DI 与AQ '交于点U ,直线PQ '与I 交于点()V V P ≠.Y Q (Q ')图10-34由90VPD ∠=︒,知D ,I ,V ,U 四点共线.由90BDI ∠=︒,知90AUI ∠=︒,又90AFI AEI ∠=︒=∠,即知A ,F ,I ,E ,U 五点共圆,记此圆为1ω.又由90APV AUV ∠=︒=∠,知A ,P ,V ,U 四点共圆,记此圆为叫2ω.注意到I ,圆1ω,圆2ω两两相交的根轴EF ,PV ,AU 相交于一点(因B C ∠≠∠知圆1ω,圆2ω,I 的圆心不共线),而EF 与PV 相交于点Q ,直线AU 与PV 交于点Q ',故Q 与Q '重合,即有QA BC ∥.于是,由推论4,知AX AY =,故知A 是线段XY 的中点. 例15 (2008年中国国家代表队选拔赛题)设I 为ABC △的内切圆,切BC 边于点D ,AB AC >,联AD 交I 于E ,在DE 上取点F ,使CF CD =,延长CF 交BE 于点G ,则FG FC =.证明 如图1035-,设I 分别切AB ,AC 于点P ,Q ,过点E 的切线与直线BC 交于点K ,则由性质14,知P ,Q ,K 三点共线.又由性质1,有BD BK DC KC =,即有1BD KCDC BK⋅=.B图10-35由CF CD =,有KED ADC DFC ∠=∠=∠,知EK GC ∥.从而GE KC EB KB=.对BCG △及截线DFE 应用梅涅劳斯定理,有1BD CF GE BD CF KC CFDC FG EB DC FG KB FG=⋅⋅=⋅⋅=, 故GF FC =. 例16 (IMO46预选题,2006年伊朗国家队选拔赛题)已知ABC △的中线AM 交其内切圆Γ于点K ,L ,分别过K ,L 且平行于BC 的直线交圆Γ于点X ,Y ,AX ,AY 分别交BC 于P ,Q .证明:BP CQ =. 证明 如图1036-,设I 为ABC △的内心,I 分别切BC ,CA ,AB 于点D ,E ,F ,直线DI 与EF 交于点T ,则由性质9知,点T 在AM 上.B图10-36设过点K ,L 的两条切线交于点S ,则由性质14,知F ,E ,S 共线.又由性质17,知KA KTAL TL=.① 没直线YL 交AP 于点Z ,由KX YL ∥,有KX AKLZ AL=. ②注意到等腰梯形YLXK 中KL 对其对角线,两底的公垂线为TI ,从而KX KTYL TL=.再注意①,②式,则KX KXLZ YL=,即知L 是YZ 的中点. 因此,M 是QP 的中点,故BP CQ =. 练习十 1.(2008年东南地区数学奥林匹克题)ABC △的内切圆I 分别切BC ,AC 于点M 、N ,E 、F 分别为边AB 、AC 的中点,D 是直线EF 与BI 的交点.证明:M 、N 、D 三点共线. 2.(2010年第六届北方数学奥林匹克邀请赛题)已知O 是ABC △的内切圆,D ,E ,N 分别为AB ,AC ,BC 上的切点.联结NO 并延长交DE 于点K ,联结AK 并延长交BC 于点M .求证:M 是BC 的中点. 3.(2008年香港数学奥林匹克题)已知ABC △(AB AC ≠)的内切圆分别切BC ,CA ,AB 于点D ,E ,F ,H 是线段EF 上的点,使得D H EF ⊥.若A H B C ⊥,证明:H 是ABC △的垂心. 4.(2009年越南数学奥林匹克题)设A ,B 是定点,C 是动点,且ACB α∠=是定角,其中0α︒<180<︒,ABC △的内切圆I 在边BC ,CA ,AB 上的切点分别为F ,E ,D ,EF 分别与AI ,BI 交于点M ,N .证明:线段MN 的长是定长,且DMN △的外接圆过一个定点. 5.(1995年伊朗数学奥林匹克、1997年匈牙利数学奥林匹克、2002年保加利亚数学奥林匹克题)设ABC △的内切圆与边BC ,CA ,AB 分别相切于点D ,E ,F .求证:ABC △的外心O ,内心I 与DEF △的垂心H '三点共线. 6.(2007年保加利亚数学奥林匹克题)已知锐角ABC △的内切圆与三边AB 、BC 、CA 分别切于点P ,Q ,R ,垂心H 在线段QR 上.证明:(1)PH QR ⊥;(2)设ABC △的外心,内心分别为O ,I ,C ∠内的旁切圆切AB 于点N ,则I ,O ,N 三点共线. 7.(2010年第六届北方数学奥林匹克邀请赛题)已知PA ,PB 是O 的切线,切点分别是A ,B ,PCD 是O 的一条割线,过点C 作PA 的平行线,分别交弦AB ,AD 于点E ,F .求证:CE EF =.8.设ABC △的内切圆切BC 边于点D ,AD 交内切圆于点L ,过点L 作内切圆的切线分别交AB ,AC 于点M ,N ,则1111AB AM AC AN+=+. 9.设ABC △的内切圆I 分别切BC ,CA ,AB 三边于点D ,E ,F ,过点I 与DEF △三边平行的直线分别交BC ,CA ,AB 于点G ,H ,M ,N ,P ,Q .则1G H M NP QB C C AA B++=.10.ABC △的一个旁切圆分别切BC 及AC ,AB 的延长线于点D ,E ,F ,点I 在线段EF上,则DI EF ⊥的充要条件是FI BDIE DC=. 11.(《中等数学》2009(12)数学奥林匹克训练题)ABC △的一个旁切圆O 分别切边BC 及AB ,AC 的延长线于点D ,E ,F ,BH OC ⊥于点H ,CG OB ⊥于点G .联结GH .过点D 作DI GH ⊥,BI ,CI 分别交AC ,AB 的延长线于点M ,N .证明:EN BDFM CD=. 12.(2008年第34届俄罗斯教学奥林匹克(第四轮))ABC △的内切圆圆ω分别与边BC ,CA ,AB 切于点A ',B ',C ',圆周上的点K ,L 满足180A K B B K A A L B B L A ''''∠+∠=∠+∠=︒.求证:点A ',B ',C '到直线KL 的距离彼此相等.13.(2005年IMO46预选题、2006年波兰数学奥林匹克题、2006年法国国家队选拔赛题)已知ABC △满足3AB BC AC +=,I 为ABC △的内心,内切圆与边AB 、BC 的切点分别为D 、E .点D 、E 关于点I 的对称点分别为K 、L .证明:A 、C 、K 、L 四点共圆. 14.(IMO45预选题)已知三角形ABC ,点X 是直线BC 上的动点,且点C 点B 、X 之间.又ABX △、ACX △的内切圆有两个不同的交点P 、Q .证明:PQ 经过一个不依赖于X 的定点. 15.(《数学教学》2006(2)数学问题664号)O 是Rt ABC △的内切圆,E 、F 分别是两条直角边AC 、BC 上的切点,射线AO 、BO 交直线EF 于N 、M .求证:1154ONM ABC S S <<△△.。
