【人教版】物理必修二:5.4《圆周运动》导学案(含答案)
2021-2022学年高一物理人教版必修2导学案:第五章 4 圆周运动

4 圆周运动[目标定位] 1.理解线速度、角速度、转速、周期等概念,会对它们进行定量计算. 2.知道线速度与角速度的关系,知道线速度与周期、角速度与周期的关系. 3.理解匀速圆周运动的概念和特点.一、线速度1.定义:物体做圆周运动通过的弧长与所用时间的比值. 2.大小:v =ΔsΔt,单位:m/s . 3.方向:质点在圆周上某点的线速度方向是沿圆周上该点的切线方向. 4.物理意义:描述质点沿圆周运动的快慢. 5.匀速圆周运动(1)定义:沿着圆周,并且线速度的大小处处相等的运动. (2)性质:线速度的方向是时刻变化的,所以是一种变速运动. 想一想 做匀速圆周运动的物体相等时间内通过的位移相同吗?答案 不愿定相同.做匀速圆周运动的物体相等时间内通过的位移大小相等,但方向可能不同. 二、角速度1.定义:连接物体与圆心的半径转过的角度与所用时间的比值. 2.大小:ω=ΔθΔt ;单位:弧度每秒,符号rad/s .3.物理意义:描述物体绕圆心转动快慢的物理量. 4.匀速圆周运动是角速度不变的圆周运动. 5.周期和转速(1)周期:做圆周运动的物体运动一周所用的时间,用符号T 表示,单位为秒(s).(2)转速:做圆周运动的物体单位时间内转过的圈数.用n 表示,单位为转每秒(r/s),或转每分(r/min). n r/s =60n r/min.想一想 周期和转速都是描述物体做圆周运动快慢的物理量,二者之间的关系如何?答案 二者关系是n =1T (n 单位为r/s). 三、线速度与角速度的关系线速度的大小等于角速度大小与半径的乘积.即v =ωr .一、对匀速圆周运动的理解【例1】 关于匀速圆周运动,下列说法正确的是( ) A .匀速圆周运动是变速运动 B .匀速圆周运动的速率不变 C .任意相等时间内通过的位移相等 D .任意相等时间内通过的路程相等 答案 ABD解析 由线速度定义知,匀速圆周运动的速度大小不变,也就是速率不变,但速度方向时刻转变,故A 、B 对;做匀速圆周运动的物体在任意相等时间内通过的弧长即路程相等,C 错,D 对.借题发挥 (1)矢量的比较,首先要想到方向问题.(2)“相等时间内…”的问题,为便于比较可以取一些特殊值,但是有时取特殊值也会犯错,如本题中若取t =T ,则相等时间内位移相等,均为0,这样看来A 选项正确,所以举例时要具有普遍性.(3)匀速圆周运动中的“匀速”,是指“匀速率”的意思,匀速圆周运动是变速运动. 二、描述圆周运动的物理量及其关系1.线速度v 、角速度ω、周期T和转速n 都是用来描述质点做圆周运动快慢的,但它们描述的角度不同.(1)线速度v通过弧长描述质点沿圆周运动的快慢.(2)角速度ω、周期T、转速n通过转过的角度描述质点绕圆心转动的快慢.2.各个物理量之间的关系(1)v、T、r的关系:物体在转动一周的过程中,转过的弧长Δs=2πr,时间为T,则v=Δs Δt=2πr T.(2)ω、T的关系:物体在转动一周的过程中,转过的角度Δθ=2π,时间为T,则ω=ΔθΔt=2πT.(3)ω与n的关系:物体在1 s内转过n转,1转转过的角度为2π,则1 s内转过的角度Δθ=2πn,即ω=2πn.特殊提示(1)线速度大的物体,其角速度不愿定大,据ω=vr知,若v大,r也很大,角速度ω可能很小.(2)v、ω、r三个量中,只有先确定其中一个量不变,才能进一步明确另外两个量是正比还是反比关系.【例2】甲、乙两物体都做匀速圆周运动,其转动半径之比为1∶2,在相等的时间里甲转过60°,乙转过45°,则它们的角速度之比为________,线速度之比为________,周期之比为________.答案4∶32∶33∶4解析由ω=ΔθΔt得:ω甲ω乙=60°45°=43,由v=ωr得:v甲v乙=ω甲ω乙·r甲r乙=43×12=23由T=2πω得:T甲T乙=ω乙ω甲=34【例3】图5-4-1如图5-4-1所示,圆环以过其直径的直线AB为轴匀速转动.已知其半径R=0.5 m,周期T=4 s,求环上P点和Q点的角速度和线速度大小.答案ωP=ωQ=1.57 rad/s v P≈0.39 m/s v Q≈0.68 m/s解析由题意知P点和Q点的角速度相同,ωP=ωQ=2πT=π2rad/s=1.57 rad/s;P点和Q点绕直径AB做匀速圆周运动,其轨迹的圆心不同,P点和Q点的轨迹半径分别为r P=R sin 30°=0.25 m,r Q=R sin 60°=34m,故二者的线速度分别为v P=ωP r P≈0.39 m/s;v Q=ωQ r Q≈0.68 m/s.借题发挥应用关系式v=ωr解题的关键是看哪个量保持不变,本题中物体在圆环上各点时的角速度ω相等,它的线速度v与做圆周运动的半径r成正比,故确定圆周运动半径又是解决本题的另一个关键.三、常见传动装置及其特点1.同轴转动图5-4-2如图5-4-2所示,A点和B点在同轴的一个圆盘上,圆盘转动时:ωA =ωB ,v A v B =rR ,并且转动方向相同.2.皮带传动如图5-4-3所示,A 点和B 点分别是两个轮子边缘上的点,两个轮子用皮带连起来,并且皮带不打滑,则当轮子转动时:v A =v B ,ωA ωB =rR,并且转动方向相同.图5-4-3 3.齿轮传动如图5-4-4所示,A 点和B 点分别是两个齿轮边缘上的点,两个齿轮啮合,则当齿轮转动时, v A =v B ,ωA ωB =r 2r 1,两点转动方向相反.图5-4-4特殊提示 在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系.【例4】 图5-4-5所示为皮带传动装置,皮带轮为O 、O ′,R B =12R A ,R C =23R A ,当皮带轮匀速转动时,皮带与皮带轮之间不打滑,求A 、B 、C 三点的角速度之比、线速度之比、周期之比.图5-4-5答案 ωA ∶ωB ∶ωC =2∶2∶3 v A ∶v B ∶v C =2∶1∶2 T A ∶T B ∶T C =3∶3∶2解析 由题意可知,A 、B 两点在同一皮带轮上,因此ωA =ωB ,又皮带不打滑,所以v A =v C ,故可得ωC =v C R C=v A 23R A=32ωA ,所以ωA ∶ωB ∶ωC =ωA ∶ωA ∶32ωA =2∶2∶3. 又v B =R B ωB =12R A ωA =v A 2,所以v A ∶v B ∶v C =v A ∶12v A ∶v A =2∶1∶2, T A ∶T B ∶T C =2πωA ∶2πωB ∶2πωC=12∶12∶13=3∶3∶2.针对训练 小明同学在学习了圆周运动的学问后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算脚踏板转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下数据:在时间t 内脚踏板转动的圈数为N ,那么脚踏板转动的角速度ω=________;要推算自行车的骑行速度,还需要测量的物理量有__________________________;自行车骑行速度的计算公式v = ________________________.图5-4-6答案 2πNt牙盘的齿轮数m 、飞轮的齿轮数n 、自行车后轮的半径R (或牙盘的半径r 1、飞轮的半径r 2、自行车后轮的半径R ) 2πmN nt R ⎝ ⎛⎭⎪⎫或2πr 1N r 2t R解析 依据角速度的定义式ω=ΔθΔt得ω=2πNt ;要求自行车的骑行速度,还要知道牙盘的齿轮数m (或半径r 1)、飞轮的齿轮数n (或半径r 2)、自行车后轮的半径R ;因v 1=ωr 1=v 2=ω2r 2,又齿轮数与轮子的半径成正比,则有ωm =ω2n ,且ω2=ω后,v=ω后R,联立以上各式得v=mn Rω=2πmNnt R或v=r1r2Rω=2πr1Nr2t R.借题发挥处理此类问题在读题、审题时要三抓:一抓有效信息,建立物理模型;二抓物理量之间的关系;三抓解题技巧.对匀速圆周运动的理解1.关于匀速圆周运动,下列说法正确的是() A.匀速圆周运动是匀速运动B.匀速圆周运动是变速运动C.匀速圆周运动是线速度不变的运动D.匀速圆周运动是线速度大小不变的运动答案BD解析这里的“匀速”,不是“匀速度”,也不是“匀变速”,而是速率不变,匀速圆周运动实际上是一种速度大小不变、方向时刻转变的变速运动.故B、D正确.圆周运动各物理量间的关系2.如图5-4-7所示,两个小球a和b用轻杆连接,并一起在水平面内做匀速圆周运动,下列说法中正确的是()图5-4-7A.a球的线速度比b球的线速度小B.a球的角速度比b球的角速度小C.a球的周期比b球的周期小D.a球的转速比b球的转速大答案A解析两个小球一起转动,周期相同,所以它们的转速、角速度都相等,B、C、D错误;而由v=ωr可知b的线速度大于a的线速度.所以A正确.3.甲、乙两物体分别做匀速圆周运动,假如它们转动的半径之比为1∶5,线速度之比为3∶2,则下列说法正确的是()A.甲、乙两物体的角速度之比是2∶15B.甲、乙两物体的角速度之比是10∶3C.甲、乙两物体的周期之比是2∶15D.甲、乙两物体的周期之比是10∶3答案C解析由v=ωr得ω1ω2=v1r1∶v2r2=v1v2·r2r1=32×51=152,A、B错误;由ω=2πT得T1T2=ω2ω1=215,C 正确、D错误.传动问题4.如图5-4-8所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是r A=r C=2r B.若皮带不打滑,求A、B、C三轮边缘上a、b、c三点的角速度之比和线速度之比.图5-4-8答案1∶2∶21∶1∶2解析a、b两点比较:v a=v b由v=ωr得:ωa∶ωb=r B∶r A=1∶2b、c两点比较ωb=ωc由v=ωr得:v b∶v c=r B∶r C=1∶2所以ωa∶ωb∶ωc=1∶2∶2v a∶v b∶v c=1∶1∶2(时间:60分钟)题组一 对匀速圆周运动的理解1.做匀速圆周运动的物体,下列不变的物理量是( )A .速度B .速率C .角速度D .周期答案 BCD解析 物体做匀速圆周运动时,速度的大小虽然不变,但它的方向在不断变化,选项B 、C 、D 正确.2.质点做匀速圆周运动,则( )A .在任何相等的时间里,质点的位移都相等B .在任何相等的时间里,质点通过的路程都相等C .在任何相等的时间里,质点运动的平均速度都相同D .在任何相等的时间里,连接质点和圆心的半径转过的角度都相等 答案 BD解析 如图所示,经T 4,质点由A 到B ,再经T4,质点由B 到C ,由于线速度大小不变,依据线速度的定义,Δs =v ·T4,所以相等时间内通过的路程相等,B 对;但位移x AB 、x BC 大小相等,方向并不相同,平均速度不同,A 、C 错;由角速度的定义ω=ΔθΔt知Δt 相同,Δθ=ωΔt 相同,D 对.题组二 圆周运动各物理量间的关系3.一般的转动机械上都标有“转速××× r/min ”,该数值是转动机械正常工作时的转速,不同的转动机械上标有的转速一般是不同的.下列有关转速的说法正确的是( )A .转速越大,说明该转动机械正常工作时转动的线速度确定越大B .转速越大,说明该转动机械正常工作时转动的角速度确定越大C .转速越大,说明该转动机械正常工作时转动的周期确定越大D .转速越大,说明该转动机械正常工作时转动的周期确定越小答案 BD解析 转速n 越大,角速度ω=2πn 确定越大,周期T =2πω=1n 确定越小,由v =ωr 知只有r确定时,ω越大,v 才越大,B 、D 对.4.假设“神舟”十号实施变轨后做匀速圆周运动,共运行了n 周,起始时刻为t 1,结束时刻为t 2,运行速率为v ,半径为r .则计算其运行周期可用 ( ) A .T =t 2-t 1nB .T =t 1-t 2nC .T =2πrvD .T =2πvr答案 AC解析 由题意可知飞船匀速圆周运动n 周所需时间Δt =t 2-t 1,故其周期T =Δt n =t 2-t 1n ,故选项A 正确;由周期公式有T =2πrv ,故选项C 正确.5.汽车在大路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长.某国产轿车的车轮半径约为30 cm ,当该型号的轿车在高速大路上行驶时,驾驶员面前速率计的指针指在“120 km/h ”上,可估算出该车轮的转速约为( )A .1 000 r/sB .1 000 r/minC .1 000 r/hD .2 000 r/s答案 B解析 由公式ω=2πn ,得v =rω=2πrn ,其中r =30 cm =0.3 m ,v =120 km/h =1003 m/s ,代入得n =1 00018πr/s ,约为1 000 r/min.6. 如图5-4-9,静止在地球上的物体都要随地球一起转动,a 是位于赤道上的一点,b 是位于北纬30°的一点,则下列说法正确的是( )A .a 、b 两点的运动周期都相同B .它们的角速度是不同的图5-4-9C.a、b两点的线速度大小相同D.a、b两点线速度大小之比为2∶3答案AD解析如题图所示,地球绕自转轴转动时,地球上各点的周期及角速度都是相同的.地球表面物体做圆周运动的平面是物体所在纬度线平面,其圆心分布在整条自转轴上,不同纬度处物体做圆周运动的半径是不同的,b点半径r b=r a32,由v=ωr,可得v a∶v b=2∶ 3. 7.甲、乙两个做匀速圆周运动的质点,它们的角速度之比为3∶1,线速度之比为2∶3,那么下列说法中正确的是()A.它们的半径之比为2∶9B.它们的半径之比为1∶2C.它们的周期之比为2∶3D.它们的周期之比为1∶3答案AD解析由v=ωr,得r=vω,r甲r乙=v甲ω乙v乙ω甲=29,A对,B错;由T=2πω,得T甲∶T乙=2πω甲∶2πω乙=13,C错,D对.题组三传动问题8. 如图5-4-10所示,一个匀速转动的半径为r的水平圆盘上放着两个木块M和N,木块M放在圆盘的边缘处,木块N放在离圆心13r的地方,它们都随圆盘一起运动.比较两木块的线速度和角速度,下列说法中正确的是()A.两木块的线速度相等B.两木块的角速度相等C.M的线速度是N的线速度的3倍D.M的角速度是N的角速度的3倍答案BC解析由传动装置特点知,M、N两木块有相同的角速度,又由v=ωr知,因r N=13r,r M=r,故木块M的线速度是木块N线速度的3倍,选项B、C正确.9. 如图5-4-11所示是一个玩具陀螺.a、b和c是陀螺上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是()A.a、b和c三点的线速度大小相等B.a、b和c三点的角速度相等C.a、b的角速度比c的大D.c的线速度比a、b的大答案B解析a、b和c均是同一陀螺上的点,它们做圆周运动的角速度都是陀螺旋转的角速度ω,B对,C错;三点的运动半径关系r a=r b>r c,据v=ωr可知,三点的线速度关系v a=v b>v c,A、D错.10. 如图5-4-12所示为常见的自行车传动示意图.A轮与脚蹬子相连,B轮与车轴相连,C为车轮.当人蹬车匀速运动时,以下说法中正确的是()A.A轮与B轮的角速度相同B.A轮边缘与B轮边缘的线速度相同C.B轮边缘与C轮边缘的线速度相同D.B轮与C轮的角速度相同答案BD解析A、B两轮以链条相连,其边缘线速度相同,B、C同轴转动,其角速度相同.11. 无级变速是指在变速范围内任意连续地变换速度,其性能优于传统的挡位变速器,很多高档汽车都应用了“无级变速”.图5-4-13所示为一种“滚轮—平盘无级变速器”的示意图,它由固定在主动轴上的平盘和可随从动轴移动的圆图5-4-10图5-4-11图5-4-12图5-4-13柱形滚轮组成.由于摩擦的作用,当平盘转动时,滚轮就会跟随转动,假如认为滚轮不会打滑,那么主动轴的转速n 1、从动轴的转速n 2、滚轮半径r 以及滚轮中心距离主动轴轴线的距离x 之间的关系是 ( ) A .n 2=n 1xrB .n 1=n 2xr C .n 2=n 1x 2r 2D .n 2=n 1x r答案 A解析 由滚轮不会打滑可知,主动轴上的平盘与可随从动轴转动的圆柱形滚轮在接触点处的线速度相同,即v 1=v 2,由此可得x ·2πn 1=r ·2πn 2,所以n 2=n 1xr ,选项A 正确. 题组四 综合应用12.某转盘每分钟转45圈,在转盘离转轴0.1 m 处有一个小螺帽,求小螺帽做匀速圆周运动的周期、角速度、线速度.答案 1.33 s 4.71 rad/s 0.471 m/s 解析 由周期和转速的关系可求周期 T =1n =6045 s ≈1.33 s角速度ω=ΔθΔt =2πT =3π2 rad/s ≈4.71 rad/s线速度v =ωr =3π2×0.1 m/s =0.471 m/s13.做匀速圆周运动的物体,10 s 内沿半径为20 m 的圆周运动100 m ,试求物体做匀速圆周运动时:(1)线速度的大小; (2)角速度的大小; (3)周期的大小.答案 (1)10 m/s (2)0.5 rad/s (3)4π s解析 本题考查了对圆周运动的各物理量的理解. (1)依据线速度的定义式v =Δs Δt 可得v =Δs Δt=10010 m/s =10 m/s.(2)依据v =ωr 可得ω=v r =1020 rad/s =0.5 rad/s. (3)T =2πω=2π0.5 s =4π s14.如图5-4-14所示,小球A 在光滑的半径为R 的圆形槽内做匀速圆周运动,当它运动到图中a 点时,在圆形槽中心O 点正上方h 处,有一小球B 沿Oa 方向以某一初速度水平抛出,结果恰好在a 点与A 球相碰,求:图5-4-14(1)B 球抛出时的水平初速度; (2)A 球运动的线速度最小值. 答案 (1)Rg2h (2)2πRg 2h解析 (1)小球B 做平抛运动,其在水平方向上做匀速直线运动,则R =v 0t ① 在竖直方向上做自由落体运动,则h =12gt 2② 由①②得v 0=Rt =Rg 2h .(2)设相碰时,A 球转了n 圈,则A 球的线速度 v A =2πR T =2πRt /n =2πRng 2h当n=1时,其线速度有最小值,即g v min=2πR2h.。
人教版高中物理必修2第五章 曲线运动4. 圆周运动 导学案(4)

圆周运动教学学案一.线速度:1.物理意义:描述质点沿圆周运动的。
2.定义:质点做圆周运动通过的和所用时间的比值叫做线速度。
3.大小:4.单位:5.方向:质点在圆周某点的线速度方向沿圆周上该点的。
二.匀速圆周运动:1.物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
2.注意:匀速圆周运动是一种运动3.注意:匀速圆周运动中的“匀速”指速度。
三.角速度:1.物理意义:描述质点转过的快慢。
2.定义:质点所在的半径转过和所用的比值叫做角速度。
3.大小:4.单位:5.说明:匀速圆周运动是不变的运动。
越高表明物体运转得越快!越大表明物体运动得越快!总结:描述匀速圆周运动快慢的物理量1、线速度:单位:m/s 线速度是矢量,它既有大小,也有方向2、角速度:单位:rad/s3、转速:n 单位:转/秒 (r/s)或转/分 (r/min)4、周期:T 单位:s5、频率:f 单位:Hz或s-1小试身手:1、做匀速圆周运动的物体,线速度不变,时刻在变,线速度是(恒量或变量),匀速圆周运动的性质是,匀速的含义是。
2.一个做半径为r的圆周运动的物体其线速度为v,请你表示出其运动周期?3.一个做半径为r的圆周运动的物体其角速度为ω,请你表示出其运动周期?4.若已知物体做半径为r匀速圆周运动的角速度为ω,求其运动的线速度?5.某钟表上秒针、分针的长度比为 d1:d2=1:2,求:A:秒针、分针转动的角速度之比是__________B:秒针、分针尖端的线速度之比是__________6.自行车车轮每分钟转120周,车轮半径为40cm,则自行车前进的速度多大?。
[精品]新人教版必修二高中物理5.4圆周运动导学案及答案
![[精品]新人教版必修二高中物理5.4圆周运动导学案及答案](https://img.taocdn.com/s3/m/28b9662116fc700abb68fca2.png)
54 《圆周运动》导案[]【习目标】1.解线速度、角速度和周期的物意义,知道它们之间的关系(高考要求Ⅰ)[*****]2.知道匀速圆周运动的特点3.应用线速度、角速度和周期公式求解匀速圆周运动的有关问题。
【重点难点】线速度、角速度和周期的物意义;应用线速度、角速度和周期公式求解匀速圆周运动的有关问题。
【法指导】仔细观察教材的图片,体会圆周运动的特点;解描述圆周运动的几个物量的意义【知识链接】1.对速度的解速度:描述物体运动_______和运动_______的物量,是______对时间的变率,是矢量。
速度是一个用比值定义的物量,定义式为__________。
平均速度:在变速直线运动中,运动物体的_______和所用时间的________,称为平均速度公式为____________,方向为_________的方向。
瞬时速度:对应于某一_______(或某一位置)的速度,方向为物体的运动方向。
速率:_______速度的大小即为速率;2.做曲线运动物体在某一点的速度方向是:_______________________________________。
【习过程】一、物体做圆周运动的实例教材P16例1:电风扇工作时______上的点、时钟的_______、通过田径场________时的运动员等,都在做________运动。
例2:以运动的自行车为例,说明做圆周运动的部件有哪些_________________________________________________________________________。
问题探究1:如何描述质点做圆周运动的快慢呢?如:比较运动员甲和乙在弯道部分做圆周运动的快慢可用什么方法?__________________________________________________________ 比较时钟的分针和时针做圆周运动的快慢可用什么方法?__________________________二、描述圆周运动快慢的物量——线速度、角速度、周期、转速1.线速度:物体做圆周运动时通过的__________和时间的_________,叫做线速度。
人教版高中必修二物理教学课件 第五章:曲线运动 5.4 圆周运动 ppt导学课件(含答案)

三种传动装置及其特点.
传动类型 同轴传动
皮带传动
齿轮传动
装置
A、B 两点在同 两个轮子用皮带 两个齿轮轮齿啮
轴的一个圆盘 连接,A、B 两点 合,A、B 两点分
上
分别是两个轮子 别是两个齿轮边
边缘的点
缘上的点
角速度、 特点
周期相同
线速度相同
线速度相同
转动方向 相同
相同
相反
规律
角速度与半径成 角速度与半径成
3.择式分析:若线速度大小相等,则根据 ω ∝1r分析; 若角速度大小相等,则根据 v ∝ r 分析.
1.如图所示的齿轮传动装置中,主动轮和从动轮的齿 大小相同,主动轮的齿数 z1=24,从动轮的齿数 z2=8, 当主动轮以角速度 ω 逆时针转动时,从动轮的转动情况 是( )
A.顺时针转动,周期为23πω B.逆时针转动,周期为23πω
A.①③⑤⑦ C.②④⑥⑦
B.②④⑥⑧ D.②④⑤⑧
解析:由题意知半径 R=0.25 m,线速度 v=Rω=2.5
v
2π
m/s,则角速度 ω=R=10 rad/s,②正确;周期 T= ω =
0.2π s=0.628 s,④正确;
频率
f=T1=1.59
Hz,⑥正确;转速
n= ω =5
2π π
r/s<
答案:ABC
解析:A、B 两轮通过皮带传动,皮带不打滑,则 A、 B 两轮边缘的线速度大小相等,
即 va=vb 或 va∶vb=1∶1.① 由 v=ωr 得 ωa∶ωb=rB∶rA=1∶2.② B、C 两轮固定在一起绕同一轴转动,则 B、C 两轮 的角速度相等,即 ωb=ωc 或 ωb∶ωc=1∶1.③ 由 v=ωr 得 vb∶vc=rB∶rC=1∶2.④
物理:5.4《圆周运动》导学案(一)(新人教版必修2)

5.4圆周运动(一)导学案制作人:王金龙审核人:日期:〖目标导学〗学习目标:知识与技能1.认识匀速圆周运动的概念,理解线速度的概念,知道它就是物体做匀速圆周运动的瞬时速度;理解角速度和周期的概念,会用它们的公式进行计算.2.理解线速度、角速度、周期之间的关系:v=rω=2πr/T3.理解匀速圆周运动是变速运动。
过程与方法1.运用极限法理解线速度的瞬时性.掌握运用圆周运动的特点如何去分析有关问题.2.体会有了线速度后.为什么还要引入角速度.运用数学知识推导角速度的单位.情感、态度与价值观1.通过极限思想和数学知识的应用,体会学科知识间的联系,建立普遍联系的观点.2.体会应用知识的乐趣.激发学习的兴趣.重点难点:线速度、角速度、周期公式以及它们之间的关系.易错问题:1.对匀速圆周运动中“匀速”的理解2.v、ω、r之间关系的应用.思维激活:电风扇工作时叶片上的点、时钟的分针和时针上的点、行驶中的自行车车轮上的点都在做什么运动?它们的运动轨迹是什么样子?你能说出哪些点运动得快,哪些点运动得慢?〖问题独学〗1、温故而知新:曲线运动有哪些特点:曲线运动的速度有什么特点?思考:(1)如果让你给圆周运动下一个定义,应该怎么描述?(2)这节课我想知道哪些知识与方法。
〖合作互学〗一、线速度与匀速圆周运动1、阅读教材及查找资料2、交流小结:线速度:(1)物理意义:描述圆周运动的物体_________的物理量.(2)定义式:注意:线速度有平均值与瞬时值之分,若Δt足够小,得到的是瞬时线速度,若Δt较大,得到的是平均线速度.(3)矢量性:线速度的方向和半径________,和圆弧________.(4)匀速圆周运动:线速度大小___________的圆周运动.注意:匀速圆周运动是一种变速运动,这里的“匀速”是指速率不变.3、典例剖析:例1、关于匀速圆周运动的说法,正确的是( )A.匀速圆周运动是匀速运动B.匀速圆周运动的速率不变C.匀速圆周运动在任何相等时间里,质点的位移都相同D.匀速圆周运动在任何相等的时间里,质点通过的路程都相等二、角速度1、阅读教材及查找资料2、交流小结:角速度:(1)角度制和弧度制角度制:将圆周等分成360等份,每一等份对应的圆心角定义为1度。
2020年新人教版物理必修二5.4圆周运动(导学提纲案2)含答案
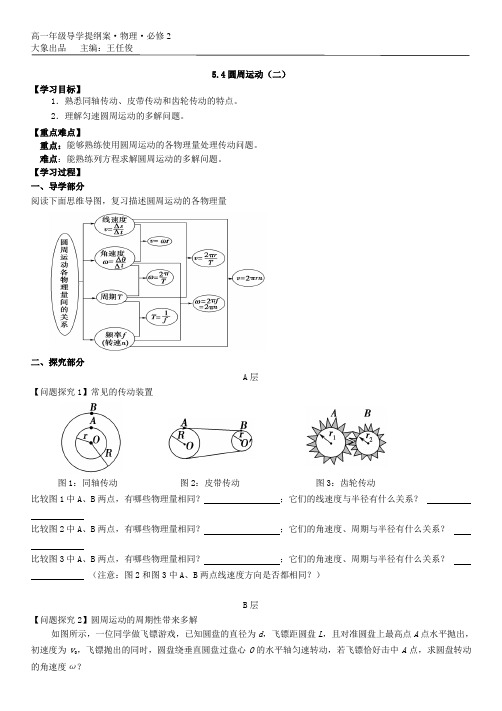
高一年级导学提纲案·物理·必修2大象出品主编:王任俊5.4圆周运动(二)【学习目标】1.熟悉同轴传动、皮带传动和齿轮传动的特点。
2.理解匀速圆周运动的多解问题。
【重点难点】重点:能够熟练使用圆周运动的各物理量处理传动问题。
难点:能熟练列方程求解圆周运动的多解问题。
【学习过程】一、导学部分阅读下面思维导图,复习描述圆周运动的各物理量二、探究部分A层【问题探究1】常见的传动装置图1:同轴传动图2:皮带传动图3:齿轮传动比较图1中A、B两点,有哪些物理量相同?;它们的线速度与半径有什么关系?比较图2中A、B两点,有哪些物理量相同?;它们的角速度、周期与半径有什么关系?比较图3中A、B两点,有哪些物理量相同?;它们的角速度、周期与半径有什么关系?(注意:图2和图3中A、B两点线速度方向是否都相同?)B层【问题探究2】圆周运动的周期性带来多解如图所示,一位同学做飞镖游戏,已知圆盘的直径为d,飞镖距圆盘L,且对准圆盘上最高点A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘绕垂直圆盘过盘心O的水平轴匀速转动,若飞镖恰好击中A点,求圆盘转动的角速度ω?讨论1:对准A就能在最高点直接射中A吗?讨论2:飞镖射中A时A转动到哪个位置?讨论3:飞镖射中A时A一定转动半圈吗?三、当堂检测A层例1 如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C 分别为轮边缘上的三点,设皮带不打滑,求:(1)A、B、C三点的线速度大小之比v A∶v B∶v C=________。
(2)A、B、C三点的角速度之比ωA∶ωB∶ωC=________。
B层例2 如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h处沿OB方向水平抛出一小球,要使球与盘只碰一次,且落点为B,求小球的初速度及圆盘转动的角速度ω的大小。
学习小结:。
2020年新人教版物理必修二5.4圆周运动(导学提纲案1)含答案

高一年级导学提纲案·物理·必修2大象出品 主编:王任俊5.4圆周运动(一)【学习目标】1.认识匀速圆周运动的概念,理解线速度的概念,知道它就是物体做匀速圆周运动的瞬时速度;理解角速度和周期的概念,会用它们的公式进行计算.2.理解线速度、角速度、周期、频率、转速之间的关系.3.理解匀速圆周运动是变速运动.【重点难点】重点:线速度、角速度、周期的概念及引入的过程,掌握他们之间的联系。
难点:理解线速度、角速度的物理意义及概念引入的必要性。
【学习过程】一、导学部分——线速度和角速度阅读课本第16页和第17页,完成下列自学任务:①线速度 v ②角速度ω1.物理意义: . 1、定义:2.定义: . 2、大小:3.大小: .4.方向: .5.单位: . B6.什么是匀速圆周运动? rθ △L △sA二、探究部分A 层【问题探究1】角速度的单位角速度的定义式为:ω=ΔθΔt根据角速度的定义式,同学们能否得出角速度的单位? (角速度是导出单位哦)S知识链接——角度的国际单位如图所示,圆心角θ越大,它所对的圆弧的弧长S 越长,二者成正比。
因此可以用弧长与半径的比值表示角的大小。
例如,弧长是0.12m ,半径是0.1m ,那么 θ=m m1.012.0=1.2。
角度θ本来没有单位,但为了表达的方便,我们“给”θ一个单位:弧度(radian ),用符号rad 表示。
这样,刚才计算得到的角θ就是1.2弧度,记为θ=1.2rad 。
【问题探究2】描述圆周运动的其他物理量及其单位周期(T ): 单位:频率(f ): 单位:转速(n ): 单位:B 层【问题探究3】描述圆周运动的各物理量关系:完成下列各物理量关系探究1、线速度v 与角速度ω的关系 △s2、线速度v 与周期T 的关系 A3、角速度ω与周期T 、频率f 、转速n 的关系三、当堂检测A 层【例1】 做匀速圆周运动的物体,10 s 内沿半径为20 m 的圆周运动100 m ,试求物体做匀速圆周运动时:(1)线速度的大小;(2)角速度的大小;(3)周期的大小.B 层【例2】高速或超速离心机是基因提取中的关键设备,当超速离心机转速达80 000 r/min 时,则关于距离超速离心机转轴12 cm 处的质点,下列说法正确的是( )A .周期为180 000s B .线速度大小为320π m/s C .角速度为160 000π rad/sD .角速度为4 0003rad/s学习小结:5.4圆周运动(导学提纲案)答案例1、[解析](1)依据线速度的定义式v=ΔsΔt可得v=ΔsΔt=10010m/s=10 m/s.(2)依据v=ωr可得,ω=vr=1020rad/s=0.5 rad/s.(3)T=2πω=2π0.5s=4π s.[答案](1)10 m/s(2)0.5 rad/s(3)4π s例2、B[离心机转速n=80 000 r/min=4 0003r/s,半径r=0.12 m.故周期T=1n=34 000s=7.5×10-4s,A错.角速度ω=2π·n=8 000π3rad/s,C、D错.线速度v=ω·r=8 000π3×0.12 m/s=320 π m/s,B对.]。
高二物理必修二第五章曲线运动导学案(含答案,精排版)5.4圆周运动

§ 5.4 圆周运动班级:_________ 组名:. 姓名:时间:_________ 年____ 月_____日【本卷要求】:1. 动脑思考2. 听懂是骗人的,看懂是骗人的,做出来才是自己的3. 该背的背,该理解的理解,该练习的练习,该总结的总结,勿懈怠!4. 多做多思,孰能生巧,熟到条件反射,这样一是能见到更多的出题方式,二是能提高做题速度5. 循环复习6. 每做完一道题都要总结该题涉及的知识点和方法7. 做完本卷,总结该章节的知识结构,以及常见题型及做法8. 独立限时满分作答9. 步骤规范,书写整洁10. 明确在学习什么东西,对其中的概念、定律等要追根溯源,弄清来龙去脉才能理解透彻、应用灵活11. 先会后熟:一种题型弄懂了,再多做几道同类型的,总结出这种题型的做法,直到条件反射【一分钟德育】如何制定目标?――跳一跳,够得着目标分为长远目标和短期目标。
长远目标就是激励我们奋斗的核动力。
它应该足够强大,足够持久。
比如“我将来要考某某大学” 要从事某某行业”。
短期目标就是常规动力,比如“某某科要考到多少分”“我今天一定要整完某某科改错”,“本周我定要做到零违纪”等等。
它们显而易见,触手可及,伴随着我们的日常生活,让我们在学校的每一天变得充实而有意义。
每次制定目标都要是能够完成的目标,这样才能产生真正的作用。
【目标及达标标准】1. 认识圆周运动2. 理解线速度、角速度和周期的概念,会用它们的公式进行计算(重点)。
3. 理解线速度、角速度、周期之间的关系4. 理解匀速圆周运动是变速运动(难点)。
【回眸一瞥】“我数学中关于弧度的定义式【导读导思】自主学习、课前诊断先通读教材,画出本节课中的基本概念及物理规律,回答导学案预习中涉及的问题,独立完成,限时25分钟。
一、请举出一些圆周运动的实力。
、图中圆盘绕0点转动,其上有两点B C,思考,怎么描述这两个点转动的快慢?1. 参看下图,一个质点绕0点转动,从A点经过时间t到达B点,AB弧长为L,思考如何描述质点运动的快吗?试得出线速度的概念,并思考其物理意义是什么?线速度的大小计算公式是什么?方向如何确定?2. 参看下图,一个质点绕0点转动,从A点经过时间t到达B点,经过的夹角为;:,思考如何从角度变化快慢的角度描述质点运动的快慢?试得出角速度的概念,并思考其物理意义是什么?角速度的大小计算公式是什么?关于角速度的方向,只需知道角速度是矢量即可,不必再深究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时5.4圆周运动1.知道什么是圆周运动,什么是匀速圆周运动。
2.知道线速度的物理意义、定义式、矢量性,知道匀速圆周运动线速度的特点。
3.知道角速度的物理意义、定义式及单位,了解转速和周期的关系。
4.掌握线速度和角速度的关系,掌握角速度与转速、周期的关系。
5.能在具体的情景中确定线速度和角速度与半径的关系。
重点难点:理解线速度和角速度的物理意义,体会用这两个物理量描述匀速圆周运动快慢的方法。
教学建议:圆周运动是一种较为复杂的曲线运动,本节学习的一些物理量较抽象,教学中应联系各种日常生活中常见的现象,想办法多做演示实验以激发学生学习积极性,把抽象的物理量具体形象化,便于学生接受。
多用一些学生熟悉的、感兴趣的例子说明一些较难说清的问题。
导入新课:当我们开启电风扇时,风扇开始转动,叶片末端做圆周运动的速度是如何变化的?(学生回答:圆周运动的速度加快)当我们观察走时准确的挂钟和手表上的秒针的运动时,秒针的末端可看作是匀速圆周运动,那么,如果把挂钟和手表作一个比较,哪个秒针的末端圆周运动得更快一些呢? (学生可能不知道如何回答)1.如果做圆周运动的物体在相等的①时间内通过的②圆弧长度相等,这种圆周运动就叫作匀速圆周运动。
2.做匀速圆周运动的物体通过的③圆弧长与所用的④时间的比值能够表示匀速圆周运动的快慢,这个比值叫作匀速圆周运动的线速度。
3.匀速圆周运动的快慢也可以用物体沿圆周转过的⑤圆心角与所用⑥时间的比值来描述,这个比值叫作匀速圆周运动的角速度,其单位是⑦弧度/秒。
4.线速度与角速度的关系:⑧v=rω。
1.质点做圆周运动的快慢实际上可以从两个方面来讲,是哪两个方面?解答:一方面是单纯从运动快慢来说,即线速度;另一方面是单纯从转动快慢来说,即角速度。
2.两个做圆周运动的质点,线速度较大的质点是不是角速度也一定较大?解答:不一定。
3.角度2π和角度360°是什么关系?解答:角度2π和角度360°是相同的角度,只是表述时的单位不同,一个是弧度,一个是度。
主题1:线速度问题:(1)图示是正在转动的钟表:钟表的分针与秒针的末端都做圆周运动,谁的线速度更大些?你判断的依据是什么?(2)根据你对线速度的认识,回答下列问题:①线速度如何描述圆周运动的快慢?描述圆周运动时,线速度是平均速度还是瞬时速度?②线速度是矢量还是标量?方向是怎么样的?③匀速圆周运动的“匀速”同“匀速直线运动”的“匀速”一样吗?解答:(1)秒针的末端运动的线速度更大。
分针与秒针的末端做圆周运动的半径基本相同,相同时间秒针的末端转过的圈数多,运动轨迹更长,根据线速度定义可知,秒针的线速度更大。
(2)①用弧长(路程)与时间的比值来描述,线速度是瞬时速度。
②线速度是矢量,方向是圆周上各点的切线方向。
③不一样。
“匀速圆周运动”的“匀速”指的是速率,“匀速直线运动”的“匀速”指的是速度。
知识链接:圆周运动是一种特殊的曲线运动,圆周运动中的线速度相当于以前直线运动中瞬时速度的概念。
主题2:角速度和周期问题:(1)如图所示,在自行车车轮上同一半径位置上标有A、B两点,两点到圆心距离不同。
车轮转动时,A、B两点做圆周运动过程中,它们的线速度大小相同吗?角速度大小相同吗?周期大小相同吗?(2)比较线速度和角速度的物理意义有什么不同?国际单位制中,角速度的单位是什么?(3)有人说匀速圆周运动是线速度不变的运动,也有人说匀速圆周运动是角速度不变的运动,这两种说法是否正确?(4)周期与角速度有没有必然的关系?解答:(1)线速度大小不同,角速度大小相同,周期大小相同。
(2)线速度是描述质点做圆周运动快慢的物理量,角速度是描述质点绕圆心转动快慢的物理量。
国际单位制中,角速度单位是弧度/秒(rad/s)。
(3)匀速圆周运动是线速度变化(方向时刻变化)的运动;匀速圆周运动是角速度不变(大小、方向均不变)的运动,通俗地描述角速度方向可用顺时针方向和逆时间方向。
(4)周期与角速度有必然的关系,即ω==,周期越大则角速度越小。
知识链接:转速也是描述圆周运动的快慢的物理量,它表示单位时间内转动的圈数,与周期有着必然的联系。
主题3:线速度与角速度的关系情景:如图所示,自行车轮胎在转动过程中,轮胎上某点转过的弧长总是与该点转过的角度对应。
从这方面来说,线速度、角速度、周期都是用来描述匀速圆周运动快慢的物理量,它们之间一定存在某种关系。
问题:阅读课本的相关内容,推导出线速度与角速度、周期、转速之间的关系式。
解答:①一物体做半径为r的匀速圆周运动,它运动一周所用的时间叫周期,用T表示。
它在周期T内转过的弧长为2πr,由此可知线速度与周期的关系为v=。
上式表明,当半径相同时,周期小的线速度大;当半径不同时,周期小的线速度不一定大。
所以周期与线速度描述的快慢是不一样的。
②一个周期T内转过的角度为2π,由ω=得物体的角速度与周期的关系为ω=。
③线速度与角速度关系为v=rω。
④考虑到转速,则有ω=2πn,v=2πnr。
知识链接:线速度、角速度、半径三者之间的关系是:半径一定时,线速度与角速度成正比;角速度一定时,线速度与半径成正比;线速度一定时,角速度与半径成反比。
主题4:闹钟与手表之争问题:闹钟的秒针比手表的秒针长很多,闹钟说它的秒针针尖线速度比手表的快,手表说它们秒针针尖转一周时间相同,所以快慢是一样的。
关于闹钟与手表的快慢之争,小组讨论一下,说说你们小组讨论后的看法。
解答:均有道理,但作为计时工具我们只关心角速度(周期)。
知识链接:钟和表都是计量和指示时间的精密仪器。
钟和表通常是以内机的大小来区别的。
1.下列物理量是矢量的有()。
A.线速度B.周期C.频率D.转速【解析】线速度是矢量,有大小也有方向;其他量只有大小,没有方向,是标量。
【答案】A【点评】周期、频率和转速是描述同一个概念的不同方式。
2.下列关于匀速圆周运动的说法中,正确的是()。
A.它是线速度不变的运动B.它是角速度不变的运动C.它是周期不变的运动D.它是转速不变的运动【解析】线速度不但有大小,还有方向,各点线速度的方向是圆周上该点的切线方向,所以方向是变化的,A错。
角速度ω=,对匀速圆周运动而言ω为定值;同理,周期、转速也为定值,所以B、C、D都是正确的。
【答案】BCD【点评】角速度与线速度一样是矢量,但它的方向是不变的。
3.做匀速圆周运动的物体,运动半径增大为原来的2倍,则()。
A.如果角速度不变,线速度变为原来的2倍B.如果线速度不变,角速度变为原来的2倍C.如果角速度不变,运动周期变为原来的2倍D.如果线速度不变,运动周期变为原来的2倍【解析】由v=rω知,ω不变,r增大为原来的2倍,v增大为原来的2倍,A正确;v不变,ω=,r 变为原来的两倍,ω变为原来的,B错; T=,ω不变,T不变,C错; T=,v不变,r变为原来的2倍,T变为原来的2倍,D正确。
【答案】AD【点评】线速度与角速度是通过圆周运动半径联系起来的。
4.图示为一个绕中心线OO'以角速度ω转动的球,下列说法正确的是()。
A.A、B两点的角速度相等B.A、B两点的线速度相等C.若θ=30°,则v A∶v B=∶2D.以上选项都不对【解析】A、B两处角速度相等,设球半径为R,若θ=30°,则A做圆周运动的半径r=R cos θ=R,B 做圆周运动的半径为R,因为v=rω,所以v A∶v B=r∶R=∶2。
【答案】AC【点评】地球自转时,同一纬度上的物体绕同一点做圆周运动,只有赤道上的物体绕地心做圆周运动。
拓展一、圆周运动中各量间的关系1.图示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点;左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上。
若在转动过程中皮带不打滑,则()。
A.a点与b点的线速度大小相等B.a点与b点的角速度大小相等C.a点与c点的线速度大小相等D.a点与d点的线速度大小相等【分析】解决此类问题,最重要的是抓住三个关键:①明确哪些物理量相等;②知道描述圆周运动各个物理量的含义;③知道相关的公式。
【解析】左右两轮通过皮带传动,在皮带不打滑的前提下,a、c两点的线速度大小相等,b、c、d三点的角速度大小相等,即v a=v c,ωb=ωc=ωd。
由v=rω可得:v b=rω,v c=2rω,v d=4rω。
显然v d>v c>v b,则v d>v a>v b。
又v a=rωa,v b=rωb,则ωa>ωb,A、B、D三项错误,C项正确。
【答案】C【点评】研究描述圆周运动的各物理量间的关系时除了要熟练掌握公式,还要建立两种模型。
①同轴共转模型:各点具有相同的角速度、转速、周期,线速度与半径成正比。
②摩擦传动(不打滑)模型(包括皮带传动、链条传动、地面传动、齿轮传动等):各轮的边缘线速度大小相等,角速度与半径成反比。
对以上两类问题,搞清哪些物理量相等、哪些物理量不相等是解题的关键。
拓展二、圆周运动与其他知识相结合2.如图所示,小球A在光滑的半径为R的圆形槽内做匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,将一小球B沿Oa方向以某一初速度水平抛出,结果恰好在a 点与A球相碰,求:(1)B球抛出时的水平速度。
(2)A球运动的线速度最小值。
【分析】由于A、B在a点相碰,且同时开始运动,则相碰前A、B运动时间相等。
其中,对A 球来说其运动具有周期性,这一点不容忽视。
【解析】(1)小球B做平抛运动,其在水平方向上做匀速直线运动,设小球B的水平速度为v0则R=v0t在竖直方向上做自由落体运动,则h=gt2解得v0==R。
(2)A球的线速度取最小值时,A球刚好转过一圈与B球在a点相碰,则A球做圆周运动的周期正好等于B球的运动时间,即T=,所以v A==2πR。
【答案】(1)R (2)2πR【点评】对于有关圆周运动和平抛运动相结合的问题,架起这两种不同运动问题的桥梁的物理量往往是时间。
因为对于匀速圆周运动而言,它具有周期性,所以该类题中也常出现多解的情况,我们应引起重视。
