一维双原子链晶格振动光学支与声学支频隙宽度
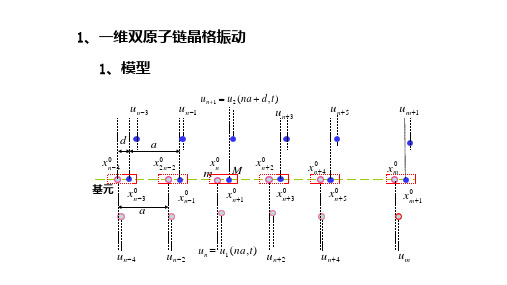
高二物理竞赛一维双原子链晶格振动课件
色散关系(频率与波矢的关系)
一维单原子链动力学方程的一般解 得到:
l 0, 1, 2,
Gl
表示同一格波,所以可以将 q e的取iN值aqq 限制1在第一N布a里q渊区:2 ,
n 1,2,3, N
l 0,1,2,
当两个原子的振动位相差为2 Aei(qx t )
的整数倍时,两个原子q的振动2位移l相,
m
d 2un dt 2
(un1
un1
2un
)
强行者有志。
胸有凌云志,无高不可攀。 贫困教会贫困者一切。 贫穷是一切艺术职业的母亲。
得到: m 2u eiaqu eiaqu 2u
n
n
n
n
学做任何事得按部就班,急不得。
壮志与毅力是事业的双翼。
立志是事业的大门,工作是登门入室的旅程。 褴褛衣内可藏志。 人若有志,万事可为。 志,气之帅也。
将动力学方程的一般解
un
u(na,t)
i( 2nat )
Ae
Aei(naqt)
人 志无之志所向 趋, ,和 无迷 远途 勿的 届盲 ,人穷一 山样 复。 海不能代限也入;志动之所力向学,无方坚程不摧,。
鸟不展翅膀难高飞。 穷人的孩子早当家。 人之所以异于禽者,唯志而已矣! 志坚者,功名之柱也。登山不以艰险而止,则必臻乎峻岭。
等,晶体原子振动以格波在晶体中传
l 0,1,2
播。
2、相邻间距为d 的两个原子的恢复力系数为
; Na
3、相邻间距为(a-d)的两个原子的恢复力系数为 2
u2 (na, t) 格波圆频率具有中心反演对称性: 若格波波长 比晶体原子间距离大得多,即
由于 q
a
a
一维双原子链

—— ω 与q之间存在着两 种不同的色散关系 —— 一维复式格子存在 两种独立的格波
2 − 2β B mω + —— 光学波 ( )+ = − A 2β cos aq
2 B mω − − 2β —— 声学波 ( )− = − A 2 β cos aq
05/ 20
q的取值 M和 m原子振动方程 相邻原胞之间位相差 波矢 q的值
2 ω− =β
(m + M ) 4mM {1 − [1 − sin 2 aq ]2 } mM ( m + M )2
1 (m + M ) 4mM {1 + [1 − sin 2 aq ] 2 } mM (m + M )2
1
2 ω+ =β
—— A、 B有非零的解,系数行列式为零
1
2 ω− =β
1 (m + M ) 4mM {1 − [1 − sin 2 aq] 2 } mM (m + M )2
33一维双原子链声学波和光学波一维复式格子的情形一维无限长链两种原子m和m构成一维复式格子m原子位于2n12n12n3同种原子间的距离2a晶格常数系统有n个0120n个原胞有2n个独立的方程两种原子振动的振幅a和b一般来说是不同的第2n1个m原子的方程第2n个m原子的方程方程解的形式iaqiaqiaqiaqab有非零的解系数行列式为零第2n1个m原子第2n个m原子方程的解aqaqmmaqmmmmaqmmmmaqmm与q之间存在着两种不同的色散关系一维复式格子存在两种独立的格波光学波声学波0520mmaqmmmmaqmm光学波声学波mmaqmm相邻原胞之间位相差aqm和m原子振动方程q的取值布里渊区大小2aq第一布里渊区允许的q值的数目晶体中的原胞数目对应一个q有两支格波
固体物理题目总汇

固体物理题目总汇填空题1、根据固体材料中原子排列的方式可以将固体材料分为晶体、非晶体和准晶体。
2、晶体结构=点阵+基元3、晶体的比热包括晶格比热和电子比热。
4、结晶学中,属于立方晶系的布拉维晶胞有简单立方、体心立方和面心立方三种。
5、密堆结构有两种:六方密堆积和立方密堆积。
6、原子电负性在一个周期内由左到右不断升高,周期表由上到下,负电性逐渐降低。
7、限定波矢q的取值范围在第一布里渊区8、金属的未满能带叫价带或导带。
1、人们利用某射线衍射测定晶体结构。
3、晶体的热学性质,如比热、热膨胀和热传导等就与晶格振动密切有关。
4、声子是一种准粒子,不具有通常意义下的动量,常把q称为声子的准动量。
5、根据晶体缺陷在空间延伸的线度晶体缺陷可分为点缺陷~线缺陷、面缺陷和体缺陷。
6、V心是F心的反型体。
1、晶体的基本结构单元称为基元2、面心立方晶胞的晶格常数为a,其倒格子原胞的体积等于323/a33、布拉维空间点阵共有14种,归为7种晶系。
5、一维双原子链的色散关系中频率较低的一支叫声学支(声频支),它很像单原子链中的声学支,;频率较高的一支则叫光学支(光频支)。
6、面缺陷有堆垛层错、小角晶界和晶粒间界三种主要形式。
8、一般情况下晶体电子的近似质量是张量,自由电子的惯性质量是标量。
9、对复式晶格,格波可分为声学波和光学波。
1、体心立方结构的第一布里渊区是菱形十二面体。
2、已知某晶体的基矢取为a1、a2、a3,某一晶面在三个基矢上的截距分别为3,2,-1,则该晶面的晶面指数为2363、倒格矢体现了晶面的面间距和法向。
8、晶体中的载流子是电子和空穴2、正格子原胞体积与倒格子原胞体积之积为233、金刚石晶体的基元含有2个原子,其晶胞含有8个碳原子。
6、准晶是介于周期性晶体和非晶玻璃之间的一种新的固体物质形态。
8、晶格振动的简化模型主要有爱因斯坦模型和德拜模型。
1、面心立方结构的第一布里渊区是十四面体。
2、代表基元中的几何点称为格点。
固体物理-一维双原子链 声学波和光学波

的声子所用的
对应电磁波的能量和波长
EO max
0.442 eV
2.8 m
E v 2 2c T
—— 要激发的声子所用的电磁波波长在近红外线波段 (Near Infrared)(NIR)
1 2
)i
本征态函数 ni (Qi )
i
exp(
2
2
)
H
ni
(
)
m d 2n
dt 2
(n1 n1 2n )
(n 1, 2, 3 , N )
得到
2 4 sin2( aq)
m
2
§3.3 一维双原子链 声学波和光学波 一维复式格子的情形 —— 一维无限长链 —— 两种原子m和M _( M > m) ____ 构成一维复式格子 —— M原子位于2n-1, 2n+1, 2n+3 …… —— m原子位于2n, 2n+2, 2n+4 …… —— 同种原子间的距离2a____晶格常数
4) 如果用电磁波激发光学波,要激发的声子所用的电磁波
波长在什么波段?
1) 声学波的最大频率
A max
3 1014
rad / s
光学波的最大频率
O max
5
2
M
6.7 1014
rad / s
光学波的最小频率
O min
2
m
6 1014 rad / s
2)相应声子的能量
EA max
0.198 eV
EO max
0.442 eV
EO min
0.396 eV
3) 某一特定谐振子具有激发能
的几率
根据归一化条件
归一化常数
高二物理竞赛课件:一维双原子链模型

4mM (m M )2
sin2
1
aq
2
独立的格波:
• 声学波(频率较低)
• 光学波(频率较高)
2 m
• 频率的禁带区
2
• 命名主要根据两种格波在长
M
波极限 ( q→0 ) 的性质
一维双原子链模型
声学波的长波极限
• 频率 q 0,
2 sin(aq) a
mM
2 q
mM
• 两种原子振幅比值
• 慢中子的能量:0.02~0.04 eV,与声子的能量同数量级; 中子的德布罗意波长:2~3×10-10 m(2~3 Å),与晶格常 数同数量级;可直接准确地给出晶格振动谱的信息
• 局限性:不适用于原子核对中子有强俘获能力的情况
典型晶格振动谱
Pb
Cu
典型晶格振动谱
Si GaAs
典型晶格振动谱
一维双原子链模型
一维双原子链模型
• 两种原子m和M (M > m) 构成一维复式格子
• M原子位于2n-1, 2n+1, 2n+3 … m原子位于2n, 2n+2, 2n+4…
• 晶格常数、同种原子间的距离:2a
• 第2n+1个M原子的方程
M
d 22n1
dt 2
(22n1 2n2
2n )
• 第2n个m原子的方程
• 离子晶体中光学波的共振能引 起对远红外光的强烈吸收,可
应用于红外光谱学
• 晶格振动谱可以利用中子、可见光光子或X光光子受晶格的 非弹性散射来测定。
• 中子(或光子)与晶格的相互作用即中子(或光子)与晶 体中声子的相互作用。中子(或光子)受声子的非弹性散 射表现为中子吸收或发射声子的过程。
固体物理:3_3 一维双原子链 声学波和光学波

m2 2 2 cos aq
在长波极限下, q 0
2 max
2
(M Mm
m)
2
B ( A)
m
2
2
2 cosqa
m M
表明:长波光学模中原胞内两原子作相对振动,而且原胞
质心保持不动。这一点很重要,例如离子晶体中,原胞内正、 负离子振动方向相反,产生迅速变化的电偶极矩,与光波耦 合必然影响其光学性质,这就是为什么称为光学模的原因。
2 min
m 2
m
2
(
B A)
m2 2 2 cos aq
B ( A)
m2 2 2 cosqa
0
表明基元中相邻原子作相对振动,这是光 学模的振动特点。
东北师范大学物理学院
3 – 3 一维双原子链
第三章 晶格振动与晶体的热学性质
相邻原子的运动情况
(声学支Acoustic branches)
24516710gmk???maxoeminoemaxaemino?15nm??maxo?4mm?maxa?41510dyncm?第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院1声学波的最大频率14max310arads???光学波的最大频率光学波的最小频率14610rads??max2am???4mm?15nm??max2o????02mmmmm????14max256710oradsm?????min2om???cmgs2m???radsgdyncm第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院max0442oeev?min0396oeev?max0198aeev?2相应声子的能量minminooe??min2om???maxmaxooe??max2o????max2am???maxmaxaae??第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院6周期性边界条件periodicboundarycondition表明
固体物理的思考题

固体物理的思考题1.解理⾯是⾯指数低的晶⾯还是⾯指数⾼的晶⾯,为什么?答:解理⾯是指⾯与⾯之间的相互作⽤⼒⽐较弱,容易解离的⾯,若⾯间距⽐较⼤,则容易形成解理,晶⾯指数越⼤,⾯间距越⼩,晶⾯指数越⼩,⾯间距越⼤,所以是⾯指数低的晶⾯容易解离。
2.⾼指数的晶⾯族与低指数的晶⾯族相⽐,对于同级衍射,那⼀晶⾯族衍射光弱?为什么?答:由布拉格衍射公式,其中θ为⼊射x射线的掠射⾓,⾼指数的晶⾯族晶⾯间距d⽐较⼩,对于同级衍射,d越⼤,则越⼩,光的透射能⼒就越弱,此时形成的衍射光就⽐较弱。
也可以从另⼀⽅⾯考虑,晶⾯指数越⼤,晶⾯间距越⼩,原⼦密度也越⼩,此时对⼊射光的反射作⽤就⽐较弱,所以⾼指数晶⾯组的衍射光弱。
3.对于x射线衍射,可否将⼊射光改为可见光?答:不可以,主要由于原⼦的间距在?的数量级,根据布拉格衍射公式,可知⼊射光波的波长也应在?的数量级,然⽽可见光的波长⼀般为⼏百nm所以不可以改为可见光⼊射,常⽤的⼊射光⼀般为Cu的线1.54?。
4.在⼀般的单式格⼦中是否存在强烈的红外吸收,为什么?答:在离⼦晶体中的长光学⽀格波有特别重要的作⽤,因为不同离⼦间的相对振动产⽣电偶极矩,从⽽可以和电磁波相互作⽤,长光学波与红外光波的共振,引起对⼊射波的强烈吸收,但是对于单式格⼦(简单晶格)⽽⾔,由于是只包含单个原⼦,并不存在光学⽀格波,所以不会引起对红外光波的强烈吸收。
5.⾊散曲线中,能否判断哪知格波的模式密度⽐较⼤,是光学⽀格波还是声学⽀格波?答:在⾊散曲线中,光学⽀格波的⾊散曲线⽐较平缓,⽽声学⽀的⾊散曲线⽐较陡峭,模式密度表⽰在频率ω附近单位频率间隔内的格波数,由于光学⽀格波⾊散曲线变化平缓,对应⼩的ω区间就具有了较⼤的波⽮q的变化,所以光学⽀格波的模式密度⽐较⼤。
6.拉曼散射中光⼦会不会产⽣倒逆散射?答:拉曼散射是长光学波声⼦与光⼦(红外光)的相互作⽤,长光学波声⼦的波⽮很⼩,响应的动量⼩,产⽣倒逆散射的条件要求波长⼩,波⽮⼤,散射⾓⼤,拉曼散射不满⾜条件所以不会产⽣倒逆散射。
固体物理(第6课)一维双原子链

v h v h2 v h3 v 1. q = 1 b + b2 + b3, h、h2、h3 ∈Z 1 1 N1 N2 N3 v q点占据的体积: 平均一个 点占据的体积:示意图 v v v 3 3 b2 b3 1 (2π ) b 1 (2π ) 1 ⋅ × = ⋅ Ω* = ⋅ = N N N N1 2 N Ω V 3 1 V v v q的分布密度(单位体积 q点的数目): 3 = 的分布密度( 中 点的数目): (2π ) (2π )3 V v q被限制在第一布里渊区
M 设 > m,则:
2β ω2min = m 2β (m+ M) ω 2m = ax mM
色散曲线
ω(q)为周期函数,周期为 ←倒易原胞长度 为周期函数,
a
π
π π + 将q限制在- , ←第一布里渊区 2a 2a
周期性边界条件
N 设晶体中有 个原胞 x1 = x2N+1 ⇒ Aei(ωt−qa) = Aei[ωt −q(2N+1)a] ⇒e−i 2qNa =1 ∴2qNa = 2π ⋅ l(l ∈Z) ⇒ q =
表示所有原子均以频 率ω振动,波矢为q。
− mω2 A = β eiqa + e−iqa B − 2βA ⇒ 2 iqa −iqa − Mω B = β e + e A− 2βB
( (
) )
2β − mω2 A−[2β cos(qa)]B = 0 −[2β cos(qa)]A+ 2β − Mω2 B = 0
一般情况下原子的振动方向既不平行也不垂直于q格波前进方向只在一些特殊方向通常是布里渊区的对称轴方向格波才可以分解成两个频率简并的横波振动方向与格波行进方向垂直和一个纵波振动方向与格波行进方向垂直支声学波而无光学波
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维双原子链晶格振动光学支与声学支频隙宽度
一维双原子链晶格是一个理想模型,用于研究晶体中原子振动的性质。
它由两种原子按特定顺序排列而成,可以看作是一条由不同类型原子组成的链。
在这个模型中,每个原子可以看作是一个质点,它们在平衡位置附近以简谐振动的方式运动。
在一维情况下,原子只能在链的方向上振动,其振动模式有两种:光学模式和声学模式。
对于一维双原子链晶格,振动可以用简谐振动的方程描述:
m₁x₁''(t) + k₁(x₁(t) - x₀(t)) + k₂(x₂(t) - x₁(t)) = 0,
m₂x₂''(t) + k₂(x₂(t) - x₁(t)) + k₃(x₃(t) - x₂(t)) = 0,
...
mₙxₙ''(t) + kₙ(xₙ(t) - xₙ₋₁(t)) + kₙ₊₁(xₙ₊₁(t) - xₙ(t)) = 0,
其中,m₁、m₂、...、mₙ分别为原子的质量,k₁、k₂、...、
kₙ分别为原子之间的弹性系数,x₁(t)、x₂(t)、...、xₙ(t)分别
为原子的位移。
这个方程组可以通过求解本征频率和模位移来描述晶格的振动性质。
根据以上方程,可以得到一维双原子链晶格的频率-波矢关系,即声学支和光学支的频率分布。
在这个关系中,频率由波矢 k 决定,光学支频率通常高于声学支频率。
对于声学支,原子振动是同相的,在低频区域可以近似看作是一组刚性振动模式。
在一维双原子链晶格中,声学支的频率在特定波矢区间内存在频隙,即不存在振动模式。
这个频隙的宽度取决于原子质量、弹性系数和晶格常数等因素。
频隙宽度越大,声学支频率范围限制的越小。
对于光学支,原子振动是异相的,在低频区域振动模式不存在。
光学支的频率范围从声学支频率频隙起始位置开始,直至无穷大。
这个频率范围内存在多个振动模式,频率越高,振动模式的数量越多。
一维双原子链晶格的声学支和光学支频隙宽度是研究材料的重要参数,能够提供有关晶体性质的信息。
频隙的宽度和位置可通过实验技术如中子散射、红外光谱和拉曼散射等手段进行测量,并与理论模型进行比较。
总之,一维双原子链晶格的声学支和光学支频隙宽度是其振动性质的重要特征,对于研究材料的声学和光学性质具有重要意义。
