双样本t检验
两独立样本t检验与两配对样本t检验的异同

• 拒绝域为
t
t0.975 6 2.4469
样本未落入拒绝域中,所以在 0.05水平上 还不能认为该道工序对提高参数值有用
三、两种t检验的对比
• 独立样本的t检验过程用于检验两个独立样本是否来自 具有相同均值的总体,相当于两个正态分布总体的均 值是否相等,即检验假设 H 0 : 1 2 是否成立,此检 验以t分布为理论基础。 • 配对样本检验用于检验两个相关的样本是否来自具有 相同均值的正态总体。即检验假设 H0 : d 0 ,实质就 是检验差值的均值和零均值之间的显著性。 ——两者的主要区别在于数据的来源和要分析的问题。
序号 加工前 加工后 1 25.6 28.7 2 20.8 30.6 3 19.4 25.5 4 26.2 24.8 5 24.7 19.5 6 18.1 25.9 7 22.9 27.8
解:数据之差为:-3.1 -9.8 -6.1 1.4 5.2 -7.8 -4.9 均值与标准差分别为 d 3.586 , sd 5.271 检验统计量
n
m
x y
2 1
n
2 2
~ N (0,1)
m
2 2 2 当 12 与 2 分别用其无偏估计 sX 代替后,记 t x y , sY 2 2 sX sY 2 2 4 4 取 s X sY 2 sX sY
l ( ) /( 2 2 ) n m n (n 1) m (m 1)
拒绝与形式为
W1 t t n m 2 1 2
b. 1 与 2 未知的一般场合
• n与m不太大 2 2 2 1 y ~ N 2, , 这是 x ~ N , ,且两者独立,从而 1
两个独立总体样本均值的t检验

1、单击Analyze Compare Means Independent-sample T Test,打开 Independent-sample T Test 主对话框如图。 2、选择要检验的变量“综合得分”进入检验框中, 选择分组变量“性别”进入分组框中 。
3、然后单击Define Group按纽,打开分组对话 框如图所示,确定分组值后返回主对话框,如果 没有分组,可以选择Cut point单选项,并在激 活的框内输入一个值作为分组界限值。
人中抽取30人,将他们培训前后的数据每加工
500个零件的不合格品数进行对比,得到数据表, 见表3。试根据表中数据检验培训前后工人的平 均操作技术水平是否有显著提高,也就是检验培 训效果是否显著。
工人培训前后不合格品数据表3
序号 培训前 培训后 序号 培训前 培训后
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Test Value = 10000 95% Confidence Interval of the Difference Mean Difference 置信区间 Lower Upper 均值差 3559.90323 1795.5916 5324.2148
t值 国有单位 4.121
Sig. df (2-tailed) 自由度 P值 30 .000
单个总体均值的 t 检验(One-Sample T Test); 两个独立总体样本均值的 t 检验 (Independent-Sample T Test);
两个有联系总体均值均值的 t 检验(PairedSample T Test);
单因素方差分析(One-Way ANOVA);
双因素方差分析(General Linear ModelUnivariate)。
实验七 两个独立样本t检验

2、确定检验统计 n1 n2
(n1 1) s1 (n2 1) s2 2 se n1 n2 2
2
2
2
两个 独立样本t 检验操作步骤: 1、选择菜单【Anaiyze】 【Independent-Samples T Test 】 弹出如下所示“Independent-Samples T Test ”对话框,将待检验 的变量送入“Test Variable(s)”框中;选择分组变量进入 “Grouping Variable”
2、在该对话框中单击“Define Groups”按纽得到下面对话框 “ Define Groups”
3
3、单击【 Continue】
4
4、单击【 Continue】
【 Ok】系统输出统计量值及p值
Group Statistics 班 级 一 班 二 班 N 20 20 Mean 26.95 31.65 Std. Deviation 8.236 6.434 Std. Error Mean 1.842 1.439
Std. Error Difference 2.337 2.337
结论:两个班成绩存在显著差异。
5
6
成 绩
Independent Samples Test Levene's Test for Equality of Variances t-test for Equality of Means 95% Confidence Interval of the Difference Lower Upper -9.431 -9.440 .031 .040
两个独立样本t检验
1
一、两个独立样本t检验的基本概念
是利用来自两个正态总体的两个独立样本的数据,来推断两个总体 的均值是否存在显著差异的一种统计推断方法。
医学统计方法课件 成组设计两样本资料的t检验

➢ 方差齐性检验统计量
F S大2 S小2
两样本进行t检验举例
➢ 可以证明:当两个总体方差齐性时,统计量F靠近 1附近,服从自由度分别为n1-1,n2-1的F分布,反 之,如果两个总体方差不等时,F值增大。故可以 上述统计量检验方差齐性的问题。
F=1.094, 查表可知:P>>0.1,故方差齐性。
成组设计续变量的两样本资料平均水平 比较
成组设计
❖成组设计:可以是实验性研究中的随机 分组,也可以是观察性研究中的不同人 群随机抽样。
在实验性研究中,将受试对象随机分成二组 或更多组,每个受试对象均有相同的机会进 入其中的任何一组。
成组设计
成组设计
(n1 1)s12 (n2 1)s22 ( 1 1 )
n1 n2 2
n1 n1
两样本进行t检验举例
❖ 两样本标准误
s X1 X2
与H0是否为真无关
❖ X1 X2 是两个总体均数之差的点估计,因此当
H0: µ1=µ2成立时,X1 X2 在大多数情况下非常小 或较小,故t检验统计量较小或比较小。
➢ 如果满足每组资料近似呈正态分布(或大样本) 并且方差齐性,则可用两样本t检验;
➢ 如果满足每组资料近似呈正态分布(或大样本) 但方差不齐,则可用两样本t’检验;
➢ 否则可以用两样本的Wilcoxon秩和检验或变量变 换
两样本进行t检验举例
例4.7 下面资料是关于18名单腿截肢者的健康足 和18名正常健康人的足部相同部位组织切片毛细 血管密度(/mm2)的测定结果,试比较健康人和截 肢者足部毛细血管密度有无差别?
成组设计
成组设计
➢ 在观察性研究中,按不同人群进行随 机抽样,得到二个或二个以上的独立 样本。
两样本t检验计算公式

两样本t检验计算公式我们来看一下两样本t检验的计算公式。
两样本t检验的计算公式如下:t = (x1 - x2) / sqrt(s1^2/n1 + s2^2/n2)其中,t为检验统计量,x1和x2分别为两个样本的均值,s1和s2为两个样本的标准差,n1和n2分别为两个样本的样本容量。
在进行两样本t检验时,我们需要先计算出两个样本的均值和标准差,然后代入上述公式进行计算。
计算得到的t值可以与t分布的临界值进行比较,从而判断两个样本的均值是否存在显著差异。
接下来,我们将通过一个实例来说明如何使用两样本t检验进行分析。
假设我们想要比较两个不同班级的学生在数学考试中的平均成绩是否有显著差异。
我们随机抽取了班级A和班级B各30名学生的成绩数据,现在我们想要利用两样本t检验来进行分析。
我们计算出班级A和班级B的平均成绩和标准差。
假设班级A的平均成绩为80,标准差为10,班级B的平均成绩为85,标准差为12。
样本容量分别为30。
将这些数据代入两样本t检验的计算公式中,我们可以得到:t = (80 - 85) / sqrt(10^2/30 + 12^2/30)计算得到的t值为-2.73。
接下来,我们需要查找t分布表,找到相应自由度下的临界值。
如果t值小于临界值,则可以认为班级A和班级B的平均成绩存在显著差异。
通过查表,我们发现当自由度为58时,t分布的临界值为-2.00。
由于计算得到的t值(-2.73)小于临界值(-2.00),因此我们可以得出结论:班级A和班级B的数学成绩存在显著差异,班级B的平均成绩高于班级A。
两样本t检验是一种常用的统计方法,可用于比较两个独立样本均值是否存在显著差异。
通过计算得到的t值与t分布的临界值进行比较,我们可以判断两个样本的均值是否存在显著差异。
在实际研究中,我们可以利用两样本t检验来进行数据分析,从而得到有关样本之间差异的结论。
需要注意的是,两样本t检验的计算公式只适用于满足一定假设条件的情况下。
sas统计分析_利用SAS解决两个独立样本的t检验

利用SAS解决两个独立样本的t检验班级:学号:指导教师:姓名:目录1. SAS简介 (2)1.1 SAS的设计思想 (2)1.2 SAS的功能 (2)1.3 SAS的特点 (3)2. 方法及原理——两个独立样本的t检验 (4)2.1假设检验的思想和步骤 (4)2.2 t检验的原理与方法 (4)2.3 检验统计量t的公式 (5)2.4两个独立样本的t检验的步骤 (5)3.SAS常用命令 (6)4.题目与解答 (6)4.1题目 (6)4.2解答与分析 (6)1. SAS简介SAS是美国使用最为广泛的三大著名统计分析软件(SAS,SPSS和SYSTAT)之一,是目前国际上最为流行的一种大型统计分析系统,被誉为统计分析的标准软件。
SAS为“Statistical Analysis System”的缩写,意为统计分析系统。
它于1966年开始研制,1976年由美国SAS软件研究所实现商品化。
1985年推出SAS PC 微机版本,1987年推出DOS下的SAS6.03版,之后又推出6.04版。
以后的版本均可在WINDOWS下运行,目前最高版本为SAS6.12版。
SAS集数据存取,管理,分析和展现于一体,为不同的应用领域提供了卓越的数据处理功能。
它独特的“多硬件厂商结构”(MV A)支持多种硬件平台,在大,中,小与微型计算机和多种操作系统(如UNIX,MVS WINDOWS 和DOS等)下皆可运行。
SAS 采用模块式设计,用户可根据需要选择不同的模块组合。
它适用于具有不同水平于经验的用户,处学者可以较快掌握其基本操作,熟练者可用于完成各种复杂的数据处理。
目前SAS已在全球100多个国家和地区拥有29000多个客户群,直接用户超过300万人。
在我国,国家信息中心,国家统计局,卫生部,中国科学院等都是SAS系统的大用户。
SAS以被广泛应用于政府行政管理,科研,教育,生产和金融等不同领域,并且发挥着愈来愈重要的作用。
SPSS生物统计分析示例2-两样本t检验
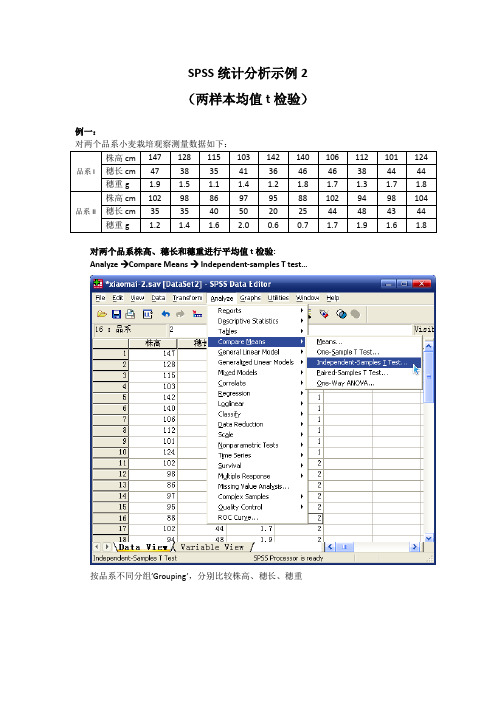
SPSS统计分析示例2(两样本均值t检验)例一:对两个品系株高、穗长和穗重进行平均值t检验:Analyze →Compare Means → Independent-samples T test…按品系不同分组’Grouping’,分别比较株高、穗长、穗重SPSS输出:汇总表:品系I 品系II t 株高cm(M±SD) 121.80±16.98 96.40±5.89 4.468**穗长cm(M±SD) 41.50±4.48 38.40±9.74 0.914穗重g (M±SD) 1.54±0.28 1.45±0.48 0.511**:P<0.01从t检验的结果看:(1)株高数据不满足方差齐性,用近似t检验,t=4.468 (df=11.136), 双侧检验P=0.001<<0.01,两品系的株高具有极显著差异,品系I株高显著大于品系II(2)穗长数据不满足方差齐性,用近似t检验,t=0.914 (df=12.640), 双侧检验P=0.378>0.05,两品系的穗长无显著差异(3)穗重数据满足方差齐性,用t检验,t=0.511 (df=18), 双侧检验P=0.615>0.05,两品系的穗重无显著差异例二:将20名某病患者随机分为两组,分别用甲乙两药治疗,测得治疗前后的血沉(mm/小时)如下表:试分甲乙两药是否有疗效?两药疗效是否有差异?并用图或表对数据和结果进行描述。
1.对两种药物治疗效果比较的统计分析(以下结果均使用SPSS统计软件获得)(1)对甲药疗效做配对t检验:治疗前后血沉值的差值的配对检验SPSS结果显示:t=5.237(df=9),单侧检验P=0.001/ 2 = 0.0005<0.01,结论甲药疗效极显著。
(2)对乙药疗效做配对t检验:治疗前后血沉值的差值的配对检验SPSS结果显示:t=5.303(df=9),单侧检验P<<0.01,结论乙药疗效极显著。
excel双样本 t检验法的计算方法

excel双样本t检验法的计算方法摘要:1.Excel双样本T检验的概念与原理2.准备工作:数据准备与输入3.执行双样本T检验:步骤与操作4.解读结果:假设检验与结论5.实际应用案例与注意事项正文:在数据分析和统计研究中,Excel双样本T检验法被广泛应用于比较两组数据的均值是否存在显著差异。
本文将详细介绍Excel双样本T检验的计算方法,包括操作步骤、结果解读以及实际应用案例。
1.Excel双样本T检验的概念与原理双样本T检验是一种统计分析方法,用于检验两个独立样本的均值是否存在显著差异。
它基于t分布理论,通过计算t统计量及其对应的p值来判断假设检验的结果。
2.准备工作:数据准备与输入在进行双样本T检验之前,需要首先准备好两组要分析的数据。
这两组数据可以来自不同来源、不同时间或不同条件下收集。
确保数据具有可比性,例如单位、尺度等要保持一致。
将数据输入Excel,建议将两组数据分别放在两个工作表中,以便于进行数据分析。
通常,第一列表示样本编号或组别,后续列表示各样本的观测值。
3.执行双样本T检验:步骤与操作在Excel中进行双样本T检验,可以遵循以下步骤:步骤1:打开Excel,点击“数据”菜单,选择“数据分析”。
步骤2:在“数据分析”对话框中,选择“t-检验:双样本假设检验”模块。
步骤3:分别选取两组数据所在的工作表和输出区域。
步骤4:点击“确定”,等待Excel计算结果。
4.解读结果:假设检验与结论Excel会输出双样本T检验的结果,包括t统计量、p值以及结论。
根据p 值与预设的显著性水平(通常为0.05)进行比较,可以得出以下结论:- 如果p值小于显著性水平,说明两组数据的均值存在显著差异;- 如果p值大于显著性水平,不能拒绝原假设,即两组数据的均值之间没有显著差异。
5.实际应用案例与注意事项实际应用中,双样本T检验可用于比较不同实验组之间的效果、评估干预措施的有效性等。
在进行双样本T检验时,请注意以下几点:- 确保数据具有可比性,如单位、尺度一致;- 检查数据是否存在异常值,如有需要,进行数据清洗;- 选择合适的显著性水平,根据实际情况调整;- 注意样本容量,确保样本足够大以获得可靠结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双样本t检验
双样本t检验是一种用于比较两个独立样本均值差异的统计方法。
它的假设是两个样本来自于正态分布总体,并且两个样本方差相等。
双样本t检验的步骤如下:
1. 建立假设:
- 零假设(H0):两个样本的均值相等。
- 备择假设(H1):两个样本的均值不相等。
2. 计算样本均值:
- 计算第一个样本的均值(X1)和标准差(s1)。
- 计算第二个样本的均值(X2)和标准差(s2)。
3. 计算t统计量:
- 计算t统计量(t)= (X1 - X2) / sqrt(sp^2/n1 + sp^2/n2),其中sp^2 = ((n1-1)s1^2 + (n2-1)s2^2) / (n1 + n2 - 2),n1和n2分别为第一个和第二个样本的样本容量。
4. 计算p值:
- 根据计算得到的t统计量和自由度(n1 + n2 - 2),查找t分布表,找到相应的临界值。
- 根据临界值和双侧检验或单侧检验的要求,计算p值。
5. 做出决策:
- 如果p值小于设定的显著性水平(通常为0.05),则拒绝零假设,认为两个样本均值存在显著差异。
- 如果p值大于设定的显著性水平,则接受零假设,认为两个样本均值无显著差异。
需要注意的是,以上步骤基于一些前提条件,如正态分布的假设和方差相等的假设。
如果数据不满足这些假设,可以考虑使用非参数方法进行比较,如Wilcoxon秩和检验或Mann-Whitney U检验。
