角平分线模型精华篇
2022年中考数学几何模型之角平分线的五种模型(讲+练)(解析版)

专题01 角平分线的五种模型模型一、角平分线垂两边例1.如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为()A.3:2B.6:4C.2:3D.不能确定【答案】A【详解】过点D作DE⊥AB于E,DF⊥AC于F.∵AD为∠BAC的平分线,∴DE=DF,又AB:AC=3:2,∴S△ABD:S△ACD=(12AB•DE):(12AC•DF)=AB:AC=3:2.故选A.例2.如图,∠AOP=∠BOP=15°,PC//OA,PD⊥OA,若PC=4,则PD的长为___.【答案】2【详解】解:过P作PE⊥OB,交OB与点E,∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,∴PD=PE,∵PC//OA,∴∠CPO=∠POD,又∠AOP=∠BOP=15°,∴∠CPO=∠BOP=15°,又∠ECP为△OCP的外角,∴∠ECP=∠COP+∠CPO =30°,在直角三角形CEP 中,∠ECP =30°,PC =4,∴PE =12PC =2,则PD =PE =2.故答案为:2. 【变式训练1】如图所示,在四边形ABCD 中,DC //AB ,∠DAB =90°,AC ⊥BC ,AC =BC ,∠ABC 的平分线交A D ,AC 于点E 、F ,则BFEF的值是___________.11221BCBC BC ==--【详解】解:如图,作FG ⊥AB 于点G ,∠DAB -90°,∴FG /AD ,∴BF EF =BGAGAC ⊥BC ,∴∠ACB =90° 又BF 平分∠ABC ,∴FG =FC 在Rt △BGF 和Rt △BCF 中BF BFCF GF=⎧⎨=⎩ ∴△BGF ≌△BCF (HL ),∴BC =BGAC =BC ,∴∠CBA =45°,∴AB =2BC1BF BG BC EF AG AB BG ∴====- 【变式训练2】如图,BD 平分ABC 的外角∠ABP ,DA =DC ,DE ⊥BP 于点E ,若AB =5,BC =3,求BE 的长.【答案】1【详解】解:过点D 作BA 的垂线交AB 于点H ,∵BD平分△ABC的外角∠ABP,DH⊥AB,∴DE=DH,在Rt△DEB和Rt△DHB中,DE DHDB DB=⎧⎨=⎩,∴Rt△DEB≌Rt△DHB(HL),∴BE=BH,在Rt△DEC和Rt△DHA中,DE DHDC DA=⎧⎨=⎩,∴Rt△DEC≌Rt△DHA(HL),∴AH=CE,由图易知:AH=AB−BH,CE=BE+BC,∴AB−BH=BE+BC,∴BE+BH=AB−BC=5−3=2,而BE=BH,∴2BE=2,故BE=1.【变式训练3,的平分线相交于点E,过点E作交AC于点F,则EF的长为.【答案】【解析】延长FE交AB于点D G H,如图所示:四边形BDEG是矩形,平分CE平分,四边形BDEG是正,,设,则,,,解得,,即,解得,.模型二、角平分线垂中间例.如图,已知,90,,BAC AB AC BD ∠=︒=是ABC ∠的平分线,且CE BD ⊥交BD 的延长线于点E .求证:2BD CE =. 【答案】见解析【详解】证明:如图,延长CE 与BA 的延长线相交于点F ,∵90,90EBF F ACF F ∠+∠=︒∠+∠=︒,∴EBF ACF ∠=∠,在ABD △和ACF 中,EBF ACF AB AC BAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABD ACF ASA △≌△,∴BD CF =,∵BD 是ABC ∠的平分线,∴EBC EBF ∠=∠.在BCE ∆和BFE ∆中,EBC EBF BE BE CEB FEB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BCE BFE ASA ≌△△, ∴CE EF =,∴2CF CE =, ∴2BD CF CE ==.【变式训练1】如图,已知△ABC ,∠BAC =45°,在△ABC 的高BD 上取点E ,使AE =BC . (1)求证:CD =DE ;(2)试判断AE 与BC 的位置关系?请说明理由;【答案】(1)见解析;(2)AE BC ⊥,理由见解析;(3)【详解】(1)证明:∵BD AC ⊥,45BAC ∠=︒,∴90,45EDA BDC ABD BAD ∠=∠=︒∠=∠=︒,∴AD BD =,在Rt ADE △和Rt BDC 中,∵AD BDAE BC =⎧⎨=⎩ ∴()Rt ADE Rt BDC HL ≅,∴CD =DE ; (2)AE BC ⊥,理由如下:如图,延长AE ,交BC 于点F , 由(1)得,90EAD EBF EAD AED ∠=∠∠+∠=︒,∵AED AEF ∠=∠,∴90BEF EBF ∠+∠=︒,∴90EFB =︒,即AE BC ⊥;【变式训练2】如图,D 是△ABC 的BC 边的中点,AE 平分∠BAC ,AE ⊥CE 于点E ,且AB =10,AC =16,则DE 的长度为________【答案】3【解答】解:如图,延长CE ,AB 交于点F .AE 平分∠BAC ,AE ⊥EC ,∴∠F AE =∠CAE ,∠AEF =∠AEC =90°在△AFE 和△ACE 中,EAF EAC AE AE AEF AEC =⎧⎪=⎨⎪=⎩∠∠∠∠,∴△AFE ≌ACE (ASA ),∴AF =AC =16,EF =EC ,∴B F =6又D 是BC 的中点,∴BD =CD ,∴DE 是△CBF 的中位线,∴DE =12BF =3,故答案为:3. 【变式训练3】如图,在ABC ∆中,CD 是ACB ∠的平分线,AD CD ⊥于点D ,DE //BC 交AB 于点E ,求证:EA EB =.【答案】见解析【解答】证明:延长AD 交BC 于点F .CD 平分ACF ∠, ACD FCD ∴∠=∠.又,,AD CD CD CD ⊥=ADC ∴∆≌FDC ∆,AD FD ∴=. 又DE ∥BC ,EA EB ∴=.模型三、角平分线+平行线构造等腰三角形例.如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于D,∠CBP 的平分线交CE 于Q ,当CQ =13CE 时,EP +BP =________.【答案】12【解答】解:如图,延长BQ 交射线EF 于点M .E 、F 分别是AB 、AC 的中点,∴EF //BC ,∴∠CBM =∠EMBBM 平分∠ABC ,∴∠ABM =∠CBM ,∴∠EMB =∠EBM ,∴EB =EM ,∴EP +BP =EP +PM =EM CQ =13CE ,∴EQ =2CQ由EF //BC 得,△EMQ ∽△CBQ∴2 212 12EM EQEM BC EP BP BC CQ==∴==∴+=【变式训练1】如图,平分于点C ,,求OC 的长?【解析】如图所示:过点D 作交OA 于点E ,则,平分,,中,,.【变式训练2C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且,则AC=.【解析】过点E于G,连接CF,如图所示:分别是,CF是的平分线,,,由勾股定理可得.模型四、利用角平分线作对称例.平分.【答案】见解析【解析】证明:在AB上截取,连接DE,如图所示:.【变式训练】AD是△ABC的角平分线,过点D作DE⊥AB于点E,且DE=3,S△ABC=20.(1)如图1,若AB=AC,求AC的长;(2)如图2,若AB=5,请直接写出AC的长.【答案】(1)203;(2)253【详解】解:(1)如图1,作DF⊥AC于F,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×AB ×3+12×AC ×3=20,解得,AC =AB =203; (2)如图2,作DF ⊥AC 于F ,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×5×3+12×AC ×3=20,解得,AC =253. 模型五、内外模型例.如图,在△ABC 中,AB=AC ,∠A=30°,E 为BC 延长线上一点,∠ABC 与∠AC E 的平分线相交于点D ,则∠D 的度数为( )A .15°B .17.5°C .20°D .22.5°【答案】A4321DA【解析】∵∠ABC与∠AC E的平分线相交于点D,∴∠DCE=∠DCA,∠CBD=∠ABD,即.的外角的平分线CP与内角BP交于点P,若,则.【解析】平分平分又,过点P的延长线,垂足分别为点E、F、G,如图所示:由角平分线的性质可得,AP是.课后训练1.如图,BD是ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE 的长为()A .2B .1.5C .1D .0【答案】C【详解】解:如图,过点D 作DF AB ⊥于F ,BD 是ABP ∠的角平分线,DF AB ⊥,DE ⊥BP ,DE DF ∴=,在Rt BDE 和Rt BDF 中,BD BDDE DF =⎧⎨=⎩,()Rt BDE Rt BDF HL ∴△≌△,BE BF ∴=,在Rt ADF 和Rt CDE △中,DA DCDE DF=⎧⎨=⎩,()Rt ADF Rt CDE HL ∴△≌△,AF CE ∴=,AF AB BF =-,CE BC BE =+,AB BF BC BE ∴-=+,2BE AB BC ∴=-,5AB =,3BC =,2532BE ∴=-=,解得:1BE =.故选:C .2.如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,32=DE ,5AB =,则AC 的长为( )A .133B .4C .5D .6【答案】A【详解】∵AD 是ABC ∆中BAC ∠的平分线,DE AB ⊥于点E ,DF AC ⊥交AC 于点F ,∴32DF DE ==. 又∵ABCABD ACDSSS=+,5AB =,∴1313752222AC =⨯⨯+⨯⨯,∴133AC =.故选:A . 3.如图,在Rt △ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,CD =2,BD =3,Q 为AB 上一动点,则DQ 的最小值为( )A.1B.2C.2.5D【答案】B【详解】解:作DH⊥AB于H,如图,∵AD平分∠BAC,DH⊥AB,DC⊥AC,∴DH=DC=2,∵Q为AB上一动点,∴DQ的最小值为DH的长,即DQ的最小值为2.故选:B.4.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是______.【答案】30【详解】过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,∵∠BCD=90°,BD平分∠ABC,∴DE=DC=4,∴四边形ABCD的面积S=S△BCD+S△BAD=12×BC×CD+12×AB×DE=12×9×4+12×6×4=30,故答案为:30.5.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为______.【答案】8【详解】解:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF=2,∴△ABC的面积=12×5×2+12×3×2=8,故答案侍:8.6.在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角∠ACD和∠ABC的平分线交于点E,则∠AEB=_____︒【答案】25【详解】解:如图示:过点E ,分别作EF BD ⊥交BD 于点E ,EG AC ⊥交AC 于点G ,EH AB ⊥,交AB 延长线于点H , ∵BE 平分ABC ∠,CE 平分ACD ∠,∴EH EF =,EG EF =,∴EH EG =,∴AE 平分HAC ∠, ∵62ABC ∠=︒,50∠=°ACB ,∴6250112HAC ABC ACB ∠=∠+∠=︒+︒=︒,∴111125622EAO HAC ∠=∠=⨯︒=︒, ∵BE 平分ABC ∠,62ABC ∠=︒∴11623122EBC ABC ∠=∠=⨯︒=︒ 在AOE △和BOC 中,OBC OCB OAE AEB ∠+∠=∠+∠∴31505625AEB OBC OCB OAE ∠=∠+∠-∠=︒+︒-︒=︒,故答案是:25. 7.如图,DE ⊥AB 于E ,DF ⊥AC 于F ,若BD =CD ,BE =CF .(1)求证:AD 平分∠BAC :(2)已知AC =18,BE =4,求AB 的长. 【答案】(1)见解析;(2)10AB =.【详解】(1)证明:DE AB ∵⊥,DF AC ⊥,90E DFC ∴∠=∠=︒,在Rt BED 和Rt CFD △中,BD CD BE CF =⎧⎨=⎩,∴Rt BED Rt CFD ≅()HL ,DE DF ∴=,DE AB ∵⊥,DF AC ⊥,AD ∴平分BAC ∠;(2)解:DE DF =,AD AD =,Rt ADE Rt ADF ∴≅()HL ,AE AF ∴=,AB AE BE AF BE AC CF BE =-=-=--,184410AB ∴=--=.8.如图1,在平面直角坐标系中,△ABC 的顶点A (-4,0),B (0,4),AD ⊥BC 交BC 于D 点,交y 轴正半轴于点E (0,t )(1)当t=1时,点C 的坐标为 ; (2)如图2,求∠ADO 的度数;(3)如图3,已知点P (0,3),若PQ ⊥PC ,PQ=PC ,求Q 的坐标(用含t 的式子表示). 【答案】(1)点C 坐标(1,0);(2)∠ADO =45°;(3)Q (-3,3-t ). 【详解】(1)如图1,当t =1时,点E (0,1), ∵AD ⊥BC , ∴∠EAO +∠BCO =90°, ∵∠CBO +∠BCO =90°,∴∠EAO =∠CBO ,在△AOE 和△BOC 中,∵90EAO CBOAO BO AOE BOC ∠=∠⎧⎪=⎨⎪∠=∠︒⎩=,∴△AOE ≌△BOC (ASA ),∴OE =OC =1,∴点C 坐标(1,0). 故答案为:(1,0);(2)如图2,过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,∵△AOE ≌△BOC ,∴S △AOE =S △BOC ,且AE =BC , ∵OM ⊥AE ,ON ⊥BC ,∴OM =ON ,∴OD 平分∠ADC ;AD ⊥BC ,90ADC ∴∠=︒∴∠ADO =1452ADC ∠=︒;(3)如图3,过P 作GH ∥x 轴,过C 作CG ⊥GH 于G ,过Q 作QH ⊥GH 于H ,交x 轴于F ,∵P (0,3),C (t ,0),∴CG =FH =3,PG =OC =t , ∵∠QPC =90°,∴∠CPG +∠QPH =90°, ∵∠QPH +∠HQP =90°,∴∠CPG =∠HQP ,∵∠QHP=∠G=90°,PQ=PC,∴△PCG≌△QPH,∴CG=PH=3,PG=QH=t,∴Q(-3,3-t).。
角平分线的几种辅助线作法与三种模型

一、角平分线的三种“模型”模型一:角平分线+平行线→等腰三角形如图1,过∠AOB 平分线OC 上的一点P ,作PE ∥OB ,交OA 于点E ,则EO=EP. AA A E P C E C D F E PO B B C O F B 图1 图2 图3例1 如图2,∠ABC ,∠ACB 的平分线相交于点F ,过F 作DE ∥BC ,交AB 于点D ,交AC 于点E.求证:BD+EC=DE. 模型二:角平分线+垂线→等腰三角形如图3,过∠AOB 平分线OC 上的一点P ,作EF ⊥OC ,交OA 于点E ,交OB 于点F ,则OE=OF ,PE=PF.例2 如图4,BD 是∠ABC 的平分线,AD ⊥BD ,垂足为D ,求证:∠BAD=∠DAC+∠C.模型三:角平分线+翻折→全等三角形 在△ABC 中,AD 是∠BAC 的平分线,沿角平分线AD 将△ABD 往右边折叠就得到如图5的图形.此时有:△ABD ≌△AB /D.此翻折相当于在三角形的一边截取线段等于另一边,或延长一边等于另一边构造出相等的线段.用此方法可解决一些不相等的线段和差类问题.D A EA P /BCD B / B C 图5 图6例3如图6,点P 是△ABC 的外角∠CAD 的平分线上的一点.求证:PB+PC>AB+AC.二、角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形1、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
求证:1()2BE AC AB =-2、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E .求证:∠ACE=∠B+∠ECD .21FEDCBAABDCE F图二、已知一个点到角的一边的距离,过这个点作另一边的垂线段1、如图所示,∠1=∠2,P 为BN 上的一点,并且PD ⊥BC于D ,AB +BC=2BD 。
求证:∠BAP +∠BCP=180°。
(完整word版)角平分线模型精华篇
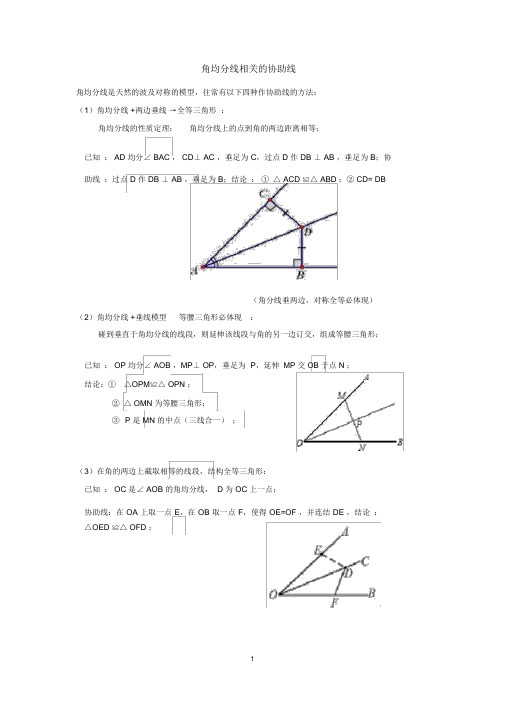
角均分线相关的协助线角均分线是天然的波及对称的模型,往常有以下四种作协助线的方法:(1)角均分线 +两边垂线→全等三角形:角均分线的性质定理:角均分线上的点到角的两边距离相等;已知: AD 均分∠ BAC , CD⊥ AC ,垂足为 C,过点 D 作 DB ⊥ AB ,垂足为 B;协助线:过点 D 作 DB ⊥ AB ,垂足为 B;结论:① △ ACD ≌△ ABD ;② CD= DB(角分线垂两边,对称全等必体现)(2)角均分线 +垂线模型等腰三角形必体现:碰到垂直于角均分线的线段,则延伸该线段与角的另一边订交,组成等腰三角形;已知: OP 均分∠ AOB ,MP⊥ OP,垂足为P,延伸 MP 交 OB 于点 N ;结论:① △OPM≌△ OPN ;② △ OMN 为等腰三角形;③P 是 MN 的中点(三线合一);(3)在角的两边上截取相等的线段,结构全等三角形:已知: OC 是∠ AOB 的角均分线, D 为 OC 上一点;协助线:在 OA 上取一点 E,在 OB 取一点 F,使得 OE=OF ,并连结 DE ,结论:△OED ≌△ OFD ;(4)作平行线①以角分线上一点作角的另一边的平行线,则△OAB等腰三角形;②过一边上的点作角均分线的平行线与另一边的反向延伸线订交,则△ODH等腰三角形;已知: OP 均分∠ MON , AB ∥ON ,已知:OC均分∠ AOD,DH∥ OC,结论:△OAB等腰三角形结论:△ODH等腰三角形一、角均分线模型应用1.角均分线 +两边垂线→全等三角形协助线:过点G作 GE射线AC已知: AD 是∠ BAC 的角均分线, CD⊥ AC ,DB ⊥ AB ,求证: CD=DB证明:∵ AD 是∠ BAC 的角均分线,∴∠ 1=∠ 2,∵CD⊥AC ,DB⊥ AB ,∴∠ ACD= ∠ABD=90 °,在△ ACD 和△ ABD 中,∠1=∠2∠ACD = ∠ABD = 90AD =AD∴△ ACD ≌△ ABD ( AAS )∴CD=BD例 1:已知:∠ 1=∠ 2,∠ 3= ∠ 4,求证: AP 均分∠ BAC .例 2:如图,AB > AC ,∠A 的均分线与BC 的垂直均分线订交于 D ,过 D 作 DE ⊥AB 、DF⊥ AC ,垂足分别为E、 F.求证: BE=CF .例 3:如图,在△ABC 中, AC >AB , M 是 BC 中点, AN 均分∠ BAC ,若 AN ⊥ BD 且交12例 4:如图,在△ABC 中,M 为 BC 的中点, DM ⊥ BC,DM 与∠ BAC 的角均分线交于点D,DE⊥ AB , DF ⊥AC ,E、 F 为垂足,求证:BE=CF .角均分线 +垂线模型等腰三角形必体现例:如图,在Rt △ABC 中, AB=AC ,∠ BAC=90°,∠ 1=∠ 2, CE⊥ BE 交 BA 的延伸于 F.求证: BD=2CE例、如图,在△ABC 中,∠ BAC 的角均分线AD 交 BC 于点 D,且 AB=AD ,作 CM ⊥ AD 交 AD 的延伸线于 M. 求证: 2AM= (AB+AC )例:如图,已知△ ABC 中, CF 均分∠ ACB ,且 AF ⊥ CF,∠ AFE+ ∠ CAF=180°,求证: EF∥ BC.截取结构全等:例. 如图, AB>AC ,∠ 1=∠ 2,求证: AB - AC>BD - CD。
角平分线四大模型总结+习题+解析(最全版)
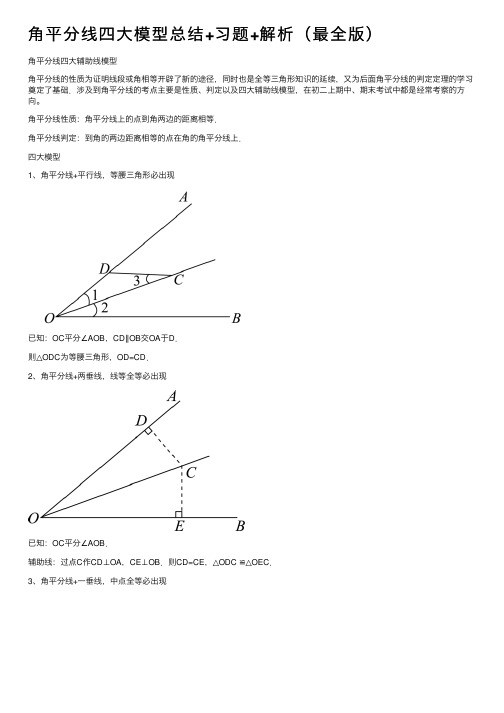
⾓平分线四⼤模型总结+习题+解析(最全版)⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径,同时也是全等三⾓形知识的延续,⼜为后⾯⾓平分线的判定定理的学习奠定了基础.涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型,在初⼆上期中、期末考试中都是经常考察的⽅向。
⾓平分线性质:⾓平分线上的点到⾓两边的距离相等.⾓平分线判定:到⾓的两边距离相等的点在⾓的⾓平分线上.四⼤模型1、⾓平分线+平⾏线,等腰三⾓形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三⾓形,OD=CD.2、⾓平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、⾓平分线+⼀垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、⾓平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核⼼考点⼀】⾓平分线的性质与判定1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:163.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB ,另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ,⼩明说:“射线OP 就是BOA ∠的⾓平分线.”他这样做的依据是( )A .⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B .⾓平分线上的点到这个⾓两边的距离相等C .三⾓形三条⾓平分线的交点到三条边的距离相等D .以上均不正确6.(2019秋?梁平区期末)如图,若BD AE ⊥于B ,DC AF ⊥于C ,且DB DC =,40BAC ∠=?,130ADG ∠=?,则DGF ∠=.7.(2018春?开江县期末)如图,在Rt ABC ?中,90C ∠=?,以顶点A 为圆⼼,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆⼼,⼤于12MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( ) A .CAD BAD ∠=∠B .若2CD =,则点D 到AB 的距离为2C .若30B ∠=?,则CDA CAB ∠=∠D .2ABD ACD S S ??=8.(2014秋?西城区校级期中)如图,点E 是AOB ∠的平分线上⼀点,EC OA ⊥,ED OB ⊥,垂⾜分别是C ,D .下列结论中正确的有( )(1)ED EC =;(2)OD OC =;(3)ECD EDC ∠=∠;(4)EO 平分DEC ∠;(5)OE CD ⊥;(6)直线OE 是线段CD 的垂直平分线.A .3个B .4个C .5个D .6个9.(2019春?杜尔伯特县期末)如图:在ABC ?中,90C ∠=?,AD 是BAC ∠的平分线,DE AB ⊥于E ,F 在AC 上,BD DF =,证明:(1)CF EB =.(2)2AB AF EB =+.10.(2019秋?垦利区期中)如图,ABC⊥⊥且平分BC,DE AB中,AD平分BAC∠,DG BC于E,DF AC⊥于F.(1)判断BE与CF的数量关系,并说明理由;(2)如果8AB=,6AC=,求AE、BE的长.11.(2017秋?遂宁期末)某地区要在区域S内(即COD∠内部)建⼀个超市M,如图所⽰,按照要求,超市M到两个新建的居民⼩区A,B的距离相等,到两条公路OC,OD的距离也相等.这个超市应该建在何处?(要求:尺规作图,不写作法,保留作图痕迹)【核⼼考点⼆】⾓平分线+⾓两边垂线12.(2019秋?肥城市期末)如图,//AB CD ,BP 和CP 分别平分ABC ∠和DCB ∠,AD 过点P ,且与AB 垂直,垂⾜为A ,交CD 于D ,若8AD =,则点P 到BC 的距离是.13.(2015?湖州)如图,已知在ABC ?中,CD 是AB 边上的⾼线,BE 平分ABC ∠,交CD 于点E ,5BC =,2DE =,则BCE ?的⾯积等于( )A .10B .7C .5D .414.(2010秋?涵江区期末)如图所⽰,在Rt ABC ?中,90C ∠=?,BC AC =,AD 平分BAC ∠交BC 于D ,求证:AB AC CD =+.15.(2012秋?蓬江区校级期末)如图,已知90∠=∠=?,M是BC的中点,DM平分B C∠.求证:ADC(1)AM平分DAB∠;(2)DM AM⊥.16.(2016秋?西城区校级期中)已知:如图,12∠=∠,P为BN上的⼀点,PF BC⊥于F,=,PA PC(1)求证:180∠+∠=?;PCB BAP(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.【核⼼考点三】⾓平分线+垂线17.(2017秋?和平区校级⽉考)如图.在ABC ?中,BE 是⾓平分线,AD BE ⊥,垂⾜为D ,求证:21C ∠=∠+∠.18.(2013秋?昌平区期末)已知:如图,在ABC ?中,AD 平分BAC ∠,CD AD ⊥于点D ,DCB B ∠=∠,若10AC =,6AD=,求AB 的长.19.如图所⽰,ABC ?中,ACB ABC ∠>∠,AE 平分BAC ∠,CD AE ⊥于D ,求证:ACD B ∠>∠.20.已知:如图,在ABC ?中,3ABC C ∠=∠,12∠=∠,BE AE ⊥.求证:2AC AB BE -=.21.(2019秋?下陆区期中)如图,BD 是ABC ∠的⾓平分线,AD BD ⊥,垂⾜为D ,20DAC ∠=?,38C ∠=?,则BAD ∠=.22.(2019秋?曲⾩市校级⽉考)如图,在ABC ?中,AB AC =,90BAC ∠=?,BD 平分ABC ∠交AC 于D ,过C 作CE BD ⊥交BD 延长线于E .求证:12CE BD =.23.(2019?沂源县⼀模)(1)如图(a)所⽰,BD、CE分别是ABC的外⾓平分线,过点A作AD BD⊥,AE CE⊥,垂⾜分别为D、E,连接DE,求证:1() 2DE AB BC AC=++;(2)如图(b)所⽰,BD、CE分别是ABC的内⾓平分线,其他条件不变,DE与ABC三边有怎样的数量关系?并证明这个数量关系;(3)如图(c)所⽰,BD为ABC的内⾓平分线,CE为ABC的外⾓平分线,其他条件不变,DE与ABC三边⼜有怎样的数量关系?并证明这个数量关系.24.(2017秋?夏⾢县期中)如图,在ABC ?中,ABC ∠、ACB ∠的平分线相交于F ,过F 作//DE BC ,交AB 于D ,交AC 于E ,那么下列结论:①BDF ?、CEF ?都是等腰三⾓形;②DE DB CE =+;③AD DE AE AB AC ++=+;④BF CF =.正确的有.25.(2019秋?垦利区期末)如图,平⾏四边形ABCD 中,3AB cm =,5BC cm =;,BE 平分ABC ∠,交AD 于点E ,交CD 延长线于点F ,则DE DF +的长度为.26.(2010秋?海淀区期末)如图,BD 是ABC ?的⾓平分线,//DE BC ,DE 交AB 于E ,若AB BC =,则下列结论中错误的是( )A .BD AC ⊥B .A EDA ∠=∠C .2AD BC =D .BE ED =27.如图,若BD 、CD 分别平分ABC ∠和ACB ∠,过D 作//DE AB 交BC 于E ,作//DF AC 交BC 于F ,求证:BC 的长等于DEF ?的周长.28.(2018秋?邳州市期中)如图,在四边形ABCD中,对⾓线AC平分BAD >,∠,AB AD 下列结论正确的是()A.AB AD CB CD->-B.AB AD CB CD-=-C.AB AD CB CD-<-D.AB AD-与CB CD-的⼤⼩关系不确定29.(2012?⿇城市校级模拟)在ABC∠的外⾓平分线,P是AD上的任意中,AD是BAC⼀点,试⽐较PB PC+与AB AC+的⼤⼩,并说明理由.30.(2018秋?万州区期中)已知:如图,在四边形ABCD中,AC平分BAD ∠,CE AB⊥于=+.E,且180B D∠+∠=?,求证:AE AD BE31.(2017秋?海淀区期中)如图,已知AD是BAC∠=?,C=+,31的⾓平分线,AC AB BD 求B∠的度数.32.(2019秋?平⼭县期中)如图,90∠=?,OM平分AOB∠,将直⾓三⾓板的顶点PAOB在射线OM上移动,两直⾓边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.33.(2016秋?丰宁县期中)如图,在ABC ?中,100A ∠=?,40ABC ∠=?,BD 是ABC ∠的平分线,延长BD ⾄E ,使DE AD =.求证:BC AB CE =+.34.(2018秋?丰城市期中)在ABC ?中,2ACB B ∠=∠,(1)如图1,当90C ∠=?,AD 为BAC ∠的⾓平分线时,在AB 上截取AE AC =,连接DE ,求证:AB AC CD =+;(2)如图2,当90C ∠≠?,AD 为BAC ∠的⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请直接写出你的结论,不需要证明;(3)如图3,当AD 为ABC ?的外⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请写出你的猜想,并说明理由.35.(2019春?利津县期末)如图,在ABC∠平分线,AD的垂直平分线分中,AD是BAC别交AB、BC延长线于F、E.求证:(1)EAD EDA∠=∠;(2)//DF AC;(3)EAC B∠=∠.36.(2014?西城区⼆模)在ABC>,AD平分BAC∠交BC于点∠为锐⾓,AB AC,BACD.(1)如图1,若ABC是等腰直⾓三⾓形,直接写出线段AC,CD,AB之间的数量关系;(2)BC的垂直平分线交AD延长线于点E,交BC于点F.①如图2,若60∠=?,判断AC,CE,AB之间有怎样的数量关系并加以证明;ABE②如图3,若AC AB+,求BAC∠的度数.⾓平分线四⼤辅助线模型--解析⼀.⾓平分线的性质与判定(共11⼩题)1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .【分析】⾸先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据⾓平分线的性质,即可求得PB 的值,⼜由垂线段最短,可求得PQ 的最⼩值.【解答】解:过点P 作PB OM ⊥于B , OP 平分MON ∠,PA ON ⊥,3PA =,3PB PA ∴==,PQ ∴的最⼩值为3.故选:C .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:16【分析】利⽤⾓平分线的性质,可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等,估计三⾓形的⾯积公式,即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐.【解答】解:AD 是ABC ?的⾓平分线,∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ,2h ,12h h ∴=,ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===,故选:B .3.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm【分析】根据⾓平分线的性质得到ED EC =,计算即可.【解答】解:BE 平分ABC ∠,DE AB ⊥,90ACB ∠=?, ED EC ∴=,3AE DE AE EC AC cm ∴+=+==,故选:B .4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn【分析】过点D 作DE AB ⊥于E ,根据⾓平分线上的点到⾓的两边距离相等可得DE CD =,然后根据三⾓形的⾯积公式即可得到结论.【解答】解:如图,过点D 作DE AB ⊥于E ,BD 是ABC ∠的平分线,90C ∠=?,DE CD m ∴==,ABD ∴?的⾯积122n m mn =??=,故选:A.5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB,另⼀把直尺压住射线OA并且与第⼀把直尺交于点P,⼩明说:“射线OP就是BOA∠的⾓平分线.”他这样做的依据是()A.⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B.⾓平分线上的点到这个⾓两边的距离相等C.三⾓形三条⾓平分线的交点到三条边的距离相等D.以上均不正确【分析】过两把直尺的交点C作CE AO=,再根据⾓⊥,CF BO⊥,根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠;【解答】解:(1)如图所⽰:过两把直尺的交点P作PE AO⊥,⊥,PF BO两把完全相同的长⽅形直尺,PE PF∴=,∠(⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上),OP∴平分AOB故选:A.。
角平分线的四大模型(Word版)

角平分线四大模型模型一:角平分线上的点向两边作垂线如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA.模型分析:利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
例1:(1)如图①,在△ABC,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到AB的距离是___cm(2)如图②,已知∠1=∠2,∠3=∠4,求证:AP平分∠BAC.练习1 如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.求证:∠BAD+∠C=180°练习2 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=()模型二:截取构造对称全等如图,P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≅△OPA.模型分析:利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等、利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。
例2:(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.(2)如图②所示.AD是△ABC的内角平分线,其他条件不变,试比较PC -PB与AC-AB的大小,并说明理由.练习 3 已知:△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,求线段BC的长。
练习4 已知,如图AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.练习5 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.模型三:角平分线+垂线构造等腰三角形如图,P是∠MON的平分线上一点,AP⊥OP于P点,延长AP交ON于点B,则△AOB是等腰三角形。
专题6 全等模型——角平分线模型

初中数学 ︵ 角平分线模型 ︶培优篇角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各类模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的几类全等模型作相应的总结,需反复掌握.【模型解读与图示】条件:如图1,OC 为AOB 的角平分线、CA OA 于点A 时,过点C 作CA OB .结论:CA CB 、OAC ≌OBC .图1常见模型1(直角三角形型)条件:如图2,在ABC 中,90C ,AD 为CAB 的角平分线,过点D 作DE AB .结论:DC DE 、DAC ≌DAE .(当ABC 是等腰直角三角形时,还有AB AC CD )图2初中数学 ︵ 角平分线模型 ︶培优篇常见模型2(邻等对补型)条件:如图3,OC 是∠COB 的角平分线,AC =BC ,过点C 作CD ⊥OA 、CE ⊥OB 。
结论:①180BOA ACB ;②AD BE ;③2OA OB AD .图3A .4 例2.如图,已知BF ,垂足分别为①CP 平分ACF ; ② APM CPN APC S S .其中结论正确的是( A .①②③B .①②③④初中数学 ︵ 角平分线模型 ︶培优篇 例3.如图所示,90BC ,E 是BC 的中点,DE 平分ADC . (1)求证:AE 是DAB 的平分线; (2)若2cm,BAD=60CD ,求AD 的长.例4.已知,OA 平分MON ,点P 在射线OA 上,点B 在射线OM 上,点C 在直线ON 上,连接PB ,PC ,且180MON BPC .(1)如图1,当90MON 时,PB 与PC 的数量关系是______.(2)如图2,当MON 是钝角时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)当120MON 时,若6OP ,2OC ,请直接写出OBP 与OCP △的面积的比值.初中数学 ︵ 角平分线模型 ︶培优篇【模型解读与图示】条件:如图1,OC 为AOB 的角平分线,AB OC .结论:△AOC ≌△BOC ,OAB 是等腰三角形、OC 是三线合一等.图1 图2 图3 条件:如图2,BE 为ABC 的角平分线,BE EC ,延长BA ,CE 交于点F . 结论:△BEC ≌△BEF ,BFC 是等腰三角形、BE 是三线合一等。
74 角平分线模型知识精讲-【初中数学】120个题型大招!冲刺满分秘籍!
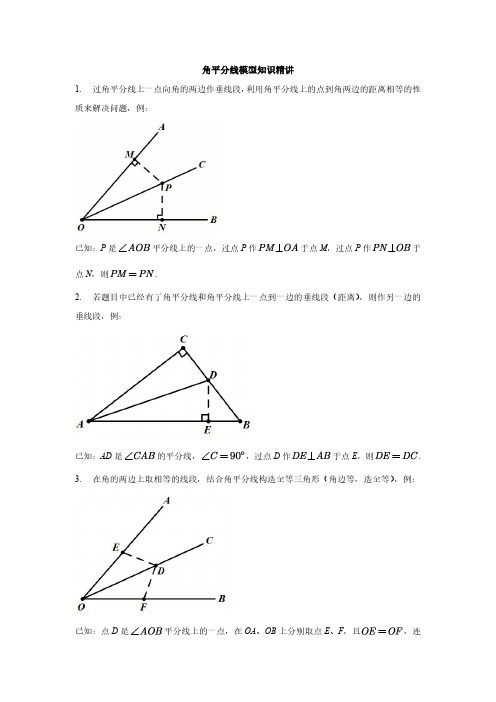
角平分线模型知识精讲1.过角平分线上一点向角的两边作垂线段,利用角平分线上的点到角两边的距离相等的性质来解决问题,例:已知:P是平分线上的一点,过点P于点M,过点P于点N.2.若题目中已经有了角平分线和角平分线上一点到一边的垂线段(距离),则作另一边的垂线段,例:已知:AD是,过点D于点E,则.3.在角的两边上取相等的线段,结合角平分线构造全等三角形(角边等,造全等),例:已知:点D是平分线上的一点,在OA、OB上分别取点E、F,且,连接DE、DF.4.过角平分线上一点作角的一边的平行线,构造等腰三角形,例:已知:点D是平分线上的一点,过点D作是等腰三角形,即.证明:是的平分线,,又,是等腰三角形.5.有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边所在直线于一点,也可构造等腰三角形,例:已知:OC平分,点D是OA上一点,过点D作交OB的反向延长线于点E,则.6.从角的一边上的一点作角平分线的垂线,使之与角的另一边相交,则可得到一个等腰三角形,例:已知:OE平分∠AOB,点D在OA上,DE⊥OE,则可延长DE交OB于点F,则DE=EF,OD=OF,∠ODF=∠OFD.7.有角平分线时,可将等角放到直角三角形中,构造相似三角形,也可以另加一对相等的角构造相似三角形,例:(1)已知:OC平分E、F分别在OA、OB上,过点E M,过点F N(2)已知:OC平分,点E、F在OC于点M于点N(3)已知:OC平分,点E、F在OC上,作,则8.利用“在同圆或等圆中,相等的圆周角(圆心角)所对的弦相等”可得相等线段,例:已知:∠BAC是圆O的圆周角,∠DOE是圆O的圆心角,AF平分∠BAC,OG平分∠DOE,连接BF、CF、DG、EG,则BF=CF,DG=EG.9.D,则.证明:平分,平分,①②,由得,即10.的一个内角平分线和一个外角平分线交于点D,则证明:平分,平分,①②由得,即.11.D,则.证明:平分平分,即①,②由①=②,得,,,即,由④可得,代入③式可得整理可得三角形几何模型-双角平分线(知识讲解)模型1:内角平分线+内角平分线模型01902BI CI ABC BIC A∠∠=+∠ 如图一、条件:、分别为ABC的内角、结论:如图一0000001902=180-+1=180-+21=180--21=902I CI ABC ACB BIC ABIC I CI ABC ACB BIC IBC ICB ABC ACB A A∠∠∠=+∠∠∠∴∠∠∠∠∠∠+∠ 已知:如图一:B 、分别为ABC的内角、的角平分线相交于点I.求证:证明:在中,B 、分别为ABC的内角、()()(180)模型2:内角平分线+外角平分线模型0190.2P ABC ACD A ∆∠∠∠+∠如图二、条件:为ABC的内角和外角的角平分线BP、CP相交于点,结论:P=如图二1211;,22=,,1()21212CP ABC ACD P AABC ACD P PBC ABC PCD ACD PCD P PBC ACD A ABC P PBC A ABC P PBC A PBCP A∠∠∠=∠∠∠∴∠=∠∠=∠∠∠+∠∠=∠+∠∴∠+∠=∠+∠∴∠+∠=∠+∠∴∠=∠ 已知:如图二:BP、分别为ABC的内角、外角的角平分线相交于点P.求证:证明:、平分线交于点,模型三:外角平分线+外角平分线模型0190.2CBE BCD A ∆∠∠∠-∠如图三、条件:ABC的外角和外角的角平分线相交于点,结论:P=如图三0000000190211;,22180()1180()21180()21180(2180)21902CP CBE BCD P AEBC DCB P PBC CBE PCB BCD P PBC PCB EBC DCB A ACB A ABC A A A∠∠∠=-∠∠∠∴∠=∠∠=∠∠=-∠+∠=-∠+∠=-∠+∠+∠+∠=-∠+-∠=-∠ 已知:如图三:BP、分别为ABC的外角、外角的角平分线相交于点P.求证:证明:、平分线交于点,模型四:飞镖+角平分线模型1、飞镖模型内角关系模型:=++.=+,=+,=++.C A BD BCD BED CDE ABE BCD CED D CED A B C A B D ∠∠∠∠∠∠∴∠∠∠∠∠∠∴∠∠∠∠ 如图四:如图,在四边形ABCD中,结论:证明:延长BC交AD于E,则、分别为、外角,图四2、飞镖模型“内角平分线+内角平分线”模型:图五+C=2ABC ADC P A P ∠∠∠∠∠如图五:条件:、平分线交于点,结论:++(1)++2,1-2-=-+=2C PBC PDC P P PBA PDA A PBC PBA PDC PDAC P P AA CP ∠=∠∠∠∠=∠∠∠∠=∠∠=∠∠∠∠∠∠∠∴∠ 略证:如图五:()()()得1.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点P .(1)若∠ABC +∠ACB =130°,求∠BPC 的度数.(2)当∠A 为多少度时,∠BPC =3∠A ?【答案】(1)115︒;(2)36A ∠=︒【分析】(1)根据角平分线的定义,求得PBC ∠,PCB ∠,再根据三角形内角和定理即可求得BPC ∠;(2)根据(1)的方法求得BPC ∠,再结合条件∠BPC =3∠A ,解方程即可求得∠A .解:(1)PB 平分ABC ∠,PC 平分ACB ∠,11,22PBC ABC PCB ACB ∴∠=∠∠=∠, ∠ABC+∠ACB =130°,1()652PBC PCB ABC ACB ∴∠+∠=∠+∠=︒,180()18065115BPC PBC PCB ∴∠=︒-∠+∠=︒-︒=︒,(2)PB 平分ABC ∠,PC 平分ACB ∠,11,22PBC ABC PCB ACB ∴∠=∠∠=∠,1()2PBC PCB ABC ACB ∴∠+∠=∠+∠,180ABC ACB A ∠+∠=︒-∠ ,1902PBC PCB A ∴∠+∠=︒-∠,180()BPC PBC PCB Ð=°-Ð+Ð1180(90)2A =︒-︒-1902A=+∠︒ ∠BPC =3∠A13902A A ∴∠=︒+∠,36A ∴∠=︒.【点拨】本题考查了与角平分线有关的角度计算,三角形内角和定理,掌握三角形内角和定理是解题的关键.类型二、内角平分线+外角平分线模型2.如图,在△ABC 中,.∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2;……;∠A 2013BC 与∠A 2013CD 的平分线相交于点A 2014,得∠A 2014.如果∠A =n 度,则∠A 2014=___________度.(直接用含n 的代数式表示)【答案】20142n解:由∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC可得∠A=∠ACD–∠ABC,∠A1=∠A1CD–∠A1BC;又因∠A1CD=12∠ACD,∠A1BC=12∠ABC,所以,∠A1=∠A1CD–∠A1BC=12∠ACD—12∠ABC=12(∠ACD—∠ABC),即可得到∠A1=12∠A.同理可得∠A2=12∠A1=12×12∠A……∠A n=1(2n∠A.所以∠A2014=20141(2∠A=20141(2n =20142n考点:三角形内角和定理;三角形外角的性质.类型三、外角平分线+外角平分线模型3.如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:(1)若∠A=60°,则∠P=°;(2)若∠A=40°,则∠P=°;(3)若∠A=100°,则∠P=°;(4)请你用数学表达式归纳∠A与∠P的关系.【答案】(1)65;(2)45;(3)40;(4)∠P=90°-12∠A,理由见解析.解:试题分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数;(2)、(3)和(1)的解题步骤类似;(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=12(∠A+∠ABC),∠CBP=12(∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.考点:三角形内角和定理;三角形的外角性质.点评:本题主要考查三角形内角和定理,三角形的外角性质.关键是熟练掌握三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义.类型四、飞镖内角平分线+内角平分线模型4.如图,BE 平分ABD ∠,CF 平分ACD ∠,BE 与CF 交于点G ,若140BDC ∠=︒,100BGC ∠=︒,则A ∠=()A .80°B .75°C .60°D .45°【答案】C【分析】连接,BC 先求解,DBC DCB ∠+∠再求解,GBC GCB ∠+∠可得,GBD GCD ∠+∠再利用角平分线的定义可得:,ABD ACD ∠+∠从而可得:,ABC ACB ∠+∠再利用三角形的内角和定理可得A ∠的大小.解:连接,BC 140,BDC ∠=︒ 18014040,DBC DCB ∴∠+∠=︒-︒=︒100,BGC ∠=︒ 18010080,GBC GCB ∴∠+∠=︒-︒=︒40,GBD GCD GBC GCB DBC DCB ∴∠+∠=∠+∠-∠-∠=︒ BE 平分ABD ∠,CF 平分ACD ∠,()280,ABD ACD GBD GCD ∴∠+∠=∠+∠=︒+8040120,ABC ACB ABD ACD DBC DCB ∴∠+∠=∠∠+∠+∠=︒+︒=︒()∴∠=︒-∠+∠=︒A ABC ACB18060.故选:.C【点拨】本题考查的是三角形的内角和定理的应用,角平分线的定义,熟练利用三角形的内角和定理求解与之相关的角的大小是解题的关键.角平分线模型巩固练习1.如图,四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=8,BD=13,BC=12,则四边形ABCD的面积为()A.50B.56C.60D.72【解答】A【解析】过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,∵∠BCD=90°,BD平分∠ABC,∴DE=DC,在Rt△BCD中,由勾股定理得:∴DE=5,在Rt△BED中,由勾股定理得:,∵AB=8,∴AE=BE﹣AB=12﹣8=4,+S△BED﹣S△AED∴四边形ABCD的面积S=S△BCD=50,故选:A.2.如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC边于点D,过点D作BC的平行线交AB于点E.已知AD=3,DE=4,则下列结论正确的是()A.AE=BE B.DE垂直平分ACC.D.【解答】D【解析】过D点作DF⊥AB于点F,∵Rt△ABC中,∠C=90°,BD平分∠ABC交AC边于点D,∴DC=DF,∵过点D作BC的平行线交AB于点E.∴DE∥BC,∴∠ADE=∠C=90°,∵AD=3,DE=4,∴,∴,∴DC=DF=≠3,故DE不能平分AC,故B说法错误;∵,∴AE≠BE,故A说法错误;∵,∴故C说法错误;∵,故D说法正确;故选:D.3.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF ⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有()A.0个B.1个C.2个D.3个【分析】C【解析】(1)证明:作PH⊥AB于H,∵AP是∠CAB的平分线,∴∠PAE=∠PAH,在△PEA和△PHA中,,∴△PEA≌△PHA(AAS),∴PE=PH,∵BP平分∠ABD,且PH⊥BA,PF⊥BD,∴PF=PH,∴PE=PF,∴(1)正确;(2)与(1)可知:PE=PF,又∵PE⊥OC于E,PF⊥OD于F,∴点P在∠COD的平分线上,∴(2)正确;(3)∵∠O+∠OEP+∠EPF+∠OFP=360°,又∵∠OEP+∠OFP=90°+90°=180°,∴∠O+∠EPF=180°,即∠O+∠EPA+∠HPA+∠HPB+∠FPB=180°,由(1)知:△PEA≌△PHA,∴∠EPA=∠HPA,同理:∠FPB=∠HPB,∴∠O+2(∠HPA+∠HPB)=180°,即∠O+2∠APB=180°,∴∠APB=90°﹣,∴(3)错误;故选:C.4.C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且,则AC=.【解析】过点E于G,连接CF,如图所示:分别是和的平分线,,CF是的平分线,,,由勾股定理可得.5.,的平分线相交于点E,过点E作交AC于点F,则EF的长为.【解答】【解析】延长FE交AB于点D G H,如图所示:四边形BDEG是矩形,平分CE平分,四边形BDEG,,设,则,,,解得,即,解得,.6.如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,CE⊥BE于点E,连接AE.若AC=BC=4,则△ABE的面积为.【解答】4【解析】作EH⊥AB于H,EK⊥BC于K.在EB上取一点J,使得EJ=EC,连接CJ.设EC=EJ=m.∵在Rt△ABC中,∠ACB=90°,AC=BC=4,∴AB=,∵BE平分∠ABC,CE⊥BE于点E,∵∠ACB=45°,BE平分∠ABC,∴∠CBE=22.5°,∵EC=EJ=m,∠CEJ=90°,∴∠EJC=45°,∵∠EJC=∠JCB+∠JBC,∴∠JCB=∠JBC=22.5°,∴JC=JB=m,∴EB=m+m,∵EC2+EB2=BC2,∴m2+(m+m)2=42,∴m2=8﹣4,=•EC•EB=•m(m+m)=•(1+)m2=2,∴S∵EB平分∠ABC,EH⊥AB,EK⊥BC,∴EH=EK,∴,∴S=2×=4.△AEB=4.解法二:延长CE交AB于点F,证明△ABE的面积等于△ABC的一半,可得S△AEB故答案为4.7.如图,,BE平分,CE平分,点E在AD上,求证:.【解答】见解析【解析】在直线BC上截取,连接EF,如图所示:在和中,,又.8.三条角平分线相交于点P,求点P到AB的距离.【解答】3【解析】过点P于点D E F,如图所示:,点P,又,即,点P到AB的距离为3.9.如图,在中,AB为直径,CD平分交于点D,求证:.【解答】见解析【解析】连接AD、BD,过点A过点B,垂足分别为点M、N,如图所示:是的直径,CD平分交于点D,,,的直径,,,又,.10.都是等腰直角三角形,的顶点A的斜边DE上,若,求两个三角形的重叠部分面积是多少?【解答】重叠部分面积为【解析】连接BD,AB与CD相交于点O,过点O M,ON⊥BD于点N,如图所示:又,,,在中,由勾股定理可得,在中,,解得,平分,又M于点N,,,,.11.已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.求证:点O到EB与ED的距离相等.【解答】见解析【解析】证明:∵AD∥BC,∴∠ADC+∠BCD=180°,∵DB平分∠ADC,CE平分∠BCD,∴∠ODC+∠OCD=90°,∴∠DOC=90°,∴∠DOC=∠BOC,又∵CO=CO,∠DCO=∠BCO,∴△DCO≌△BCO(ASA)∴CB=CD,∴OB=OD,∴CE是BD的垂直平分线,∴EB=ED,又∠DOC=90°,∴EC平分∠BED,∴点O到EB与ED的距离相等.12.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.(1)求证:AD平分∠BAC;(2)直接写出AB+AC与AE之间的等量关系.【解答】(1)见解析;(2)AB+AC=2AE.【解析】(1)证明:∵DE⊥AB于E,DF⊥AC于F,∴∠E=∠DFC=90°,∴△BDE与△CDF均为直角三角形,∵∴△BDE≌△CDF,∴DE=DF,即AD平分∠BAC;(2)AB+AC=2AE.证明:∵BE=CF,AD平分∠BAC,∴∠EAD=∠CAD,∵∠E=∠AFD=90°,∴∠ADE=∠ADF,在△AED与△AFD中,∵,∴△AED≌△AFD,∴AE=AF,∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.。
专题16 角平分线四大模型(解析版)

专题16 角平分线四大模型(解析版)角平分线是指从一个角的顶点出发,将该角分成两个相等的角的线段。
在几何学中,角平分线是一种重要且常见的构造,它具有许多有用的性质和应用。
本专题将介绍角平分线的四大模型,并对其进行解析。
1. 模型一:角内角平分线模型角内角平分线是指从一个角的内部点出发,将该角分成两个相等的内角的线段。
这种模型在解决一些与角相关的问题时非常有用。
例如,考虑一个三角形ABC,D点在角BAC的内部,且BD与CD分别是角BAC的内角平分线,我们可以推导出:∠BDC = 1/2 * ∠BAC。
这个模型在证明角内角平分线性质时发挥了关键作用。
2. 模型二:角外角平分线模型角外角平分线是指从一个角的外部点出发,将该角的外角分成两个相等的外角的线段。
这种模型在解决一些与外角相关的问题时也非常有用。
以正五边形ABCDE为例,点F在边AB延长线上,且∠BCD为角ACD的外角,则可以得出:∠BCD = 1/2 * ∠ACD。
这个模型在讨论外接角平分线性质时起到了重要作用。
3. 模型三:角平分线的垂直性模型角平分线的垂直性模型是指在一个三角形中,三条角平分线相交于一个点,且该点与三个三角形的顶点连线垂直。
以三角形ABC为例,如果AD、BE、CF为三个角平分线,且它们交于点O,则有AO ⊥BC,BO ⊥ AC,CO ⊥ AB。
这个模型在解决垂直关系问题时具有重要的应用价值。
4. 模型四:角平分线的外角关系模型角平分线的外角关系模型是指一个三角形的三个外角等于一个直角的两倍。
以三角形ABC为例,∠BAC的外角是∠ACD,∠ABC的外角是∠BCE,∠BCA的外角是∠CAD,则∠ACD + ∠BCE + ∠CAD = 2 * 90°。
这个模型在研究外角关系时起到重要的辅助作用。
综上所述,角平分线四大模型提供了解决各种与角有关问题的有力工具。
这些模型不仅在几何学中具有广泛的应用,而且在其他科学领域中也有其独特的价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角平分线有关的辅助线
角平分线是天然的涉及对称的模型,通常有下列四种作辅助线的方法:
(1)角平分线+两边垂线→全等三角形:
角平分线的性质定理:角平分线上的点到角的两边距离相等;
已知:AD平分∠BAC,CD⊥AC,垂足为C,过点D作DB⊥AB,垂足为B;辅助线:过点D作DB⊥AB,垂足为B;
结论:①△ACD≌△ABD;②CD=DB
(角分线垂两边,对称全等必呈现)(2)角平分线+垂线模型等腰三角形必呈现:
遇到垂直于角平分线的线段,则延长该线段与角的另一边相交,构成等腰三角形;
已知:OP平分∠AOB,MP⊥OP,垂足为P,延长MP交OB于点N;
结论:①△OPM≌△OPN;
②△OMN为等腰三角形;
③P是MN的中点(三线合一);
(3)在角的两边上截取相等的线段,构造全等三角形:
已知:OC是∠AOB的角平分线,D为OC上一点;
辅助线:在OA上取一点E,在OB取一点F,使得OE=OF,并连接DE,
结论:△OED≌△OFD;
(4)作平行线
①以角分线上一点作角的另一边的平行线,则△OAB等腰三角形;
②过一边上的点作角平分线的平行线与另一边的反向延长线相交,则△ODH等
腰三角形;
已知:OP平分∠MON,AB∥ON,已知:OC平分∠AOD,DH∥OC,
结论:△OAB等腰三角形结论:△ODH等腰三角形
一、角平分线模型应用
1.角平分线+两边垂线→全等三角形
辅助线:过点G作GE 射线AC
已知:AD是∠BAC的角平分线,CD⊥AC,DB⊥AB,
求证:CD=DB
证明:∵AD是∠BAC的角平分线,
∴∠1=∠2,
∵CD⊥AC,DB⊥AB,
∴∠ACD=∠ABD=90°,
在△ACD和△ABD中,
∴△ACD≌△ABD(AAS)
∴CD=BD
例1:已知:∠1=∠2,∠3=∠4,求证:AP平分∠BAC.
例2:如图,AB>AC,∠A的平分线与BC的垂直平分线相交于D,过D作DE⊥AB、DF⊥AC,
垂足分别为E、F.求证:BE=CF.
是BC中点,AN平分∠BAC,若AN
,求证:MN=1
2
(AC-AB).
例4:如图,在△ABC中,M为BC的中点,DM⊥BC,DM与∠BAC的角平分线交于点D,DE⊥AB,DF⊥AC,E、F为垂足,求证:BE=CF.
角平分线+垂线模型等腰三角形必呈现
例:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE交BA 的延长于F.
求证:BD=2CE
例、如图,在△ABC中,∠BAC的角平分线AD交BC于点D,且AB=AD,作CM⊥AD交AD的延长线于M.求证:2AM=(AB+AC)
例:如图,已知△ABC中,CF平分∠ACB,且AF⊥CF,∠AFE+∠CAF=180°,
求证:EF∥BC.
截取构造全等:
例.????如图,AB>AC,∠1=∠2,求证:AB-AC>BD-CD。
例:??如图,AB//CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD. 例:?在ABC
∆中,AB AC
>,AD是BAC
∠的平分线.P是AD上任意一点.求证:AB AC PB PC
->-.
例:?已知△ABC中,AB=AC,∠A=100°,∠B的平分线交AC于D,
O,且MN∥。
