最新船舶静力学第4章 大倾角稳性(1)
第04章 大角稳性

.05
.04 .01
.11
.07 .04
.19
.13 .06
.27
.27 .14
.42性曲线的特征
1. 静稳性曲线在原点处的斜率,等于初稳性高。 2. 稳定平衡和不稳定平衡
某一静外力矩MH与静稳性力矩曲线相交于A,C两点,在 A点处船舶有稳定平衡;在C点处于不稳定平衡。
计算步骤
4. 横倾角间隔一般取5°或10 °海船计算到70-80度,河 船算到40-60度。
5. 量取每站入水、出水点的宽度a 和b 。
2/4
计算步骤
6. 对每个吃水、横倾角用近似计算方法求倾斜水线的
v v1 v2
"
1 2 0
L/2
L / 2
(a 2 b 2 )dxd
第四章 大角稳性
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 概述 变排水量计算法 等排水量计算法 上层建筑与自由液面的影响 静稳性曲线的特征 动稳性 船舶稳性校核 临界初稳性高 船形对稳性的影响 作业
高昌古城
4.1 概述
一、大角横倾的特殊性 二、静稳性曲线 三、大角稳性讨论
.11
.11 .10
.11
.11 .11
.10
.11 .11
.09
.10 .11
.08
.09 .11
.07
.09 .10
.06
.08 .10
.04
.06 .08
1
.75 .5
.01
.01 .00
.01
.02 .01
.02
.02 .01
.03
.02 .02
.05
第四章 船舶稳性

第四章船舶稳性第一节船舶稳性的基本概念(一)船舶平衡的3种状态1、稳定平衡>0G点在M点之下,GM>0,MR2、随遇平衡G点与M点重合,GM=0,M=0R3、不稳定平衡<0G点在M点之上,GM<0,MR(二)稳性的定义船舶稳性是指船舶受给定的外力作用后发生倾侧而不致倾覆,当外力消失后仍能回复到原来的平衡位置的能力。
(三)稳性分类分类方法: 按倾斜方向、倾角大小、倾斜力矩性质、船舱是否进水┏破舱稳性稳性┫┏初稳性(小倾角稳性)┃┏横稳性┫┏静稳性┗完整稳性┫┗大倾角稳性┫┗纵稳性┗动稳性其中,倾角小于等于10-15度称为小倾角,否则称为大倾角。
倾斜力矩性质指静力或动力,或者说有无角速度、角加速度。
第二节船舶初稳性(1)(一)船舶初稳性的基本标志1.稳心M 与稳心距基线高度KM船舶小倾角横倾前、后其浮力作用线交点称为横稳心,简称稳心。
稳心M距基线的垂向坐标称为稳心距基线高度。
2.初稳性的衡准指标稳心M至重心G的垂距称为初稳性高度GM。
初稳性高度GM是衡准船舶是否具有初稳性的指标。
初稳性高度大于零,即船舶重心在稳心之下,船舶就有初稳性。
3.初稳性中的假设(对于任一给定的吃水或排水量)(1)小倾角横倾(微倾);(2)在微倾过程中稳心M和重心G的位置固定不变;(3)在微倾过程中浮心B的移动轨迹是一段以稳心为圆心的圆弧;(4)在微倾过程中倾斜轴过漂心。
(二)初稳性高度GM的表达式GM=KB+BM-KG=KM-KG第二节 船舶初稳性(2)(三) 初稳性高度的求取1、 KM 可在静水力曲线图、静水力参数表或载重表中查取。
2、 KG 的计算式中,P i —— 组成船舶总重量(含空船重量等)的第i 项载荷,tZ i —— 载荷P i 的重心距基线高度,m3、Z i 确定(1)舱容曲线图表查取法船舶资料中通常有各个货舱和液舱的舱容曲线图或数据表,利用舱容曲线图表,可方便确定舱内散货或液货的重心高度Z i ,方法如下:i )对于匀质散货或液货,已知货堆表面距基线高度,在图中左纵轴上对应点做水平线交舱容中心距基线高度曲线得B 点,过B 点做垂线交上横轴得C 点,对应值即为该舱货物重心距基线高度Z i 。
船舶静力学第四章习题答案
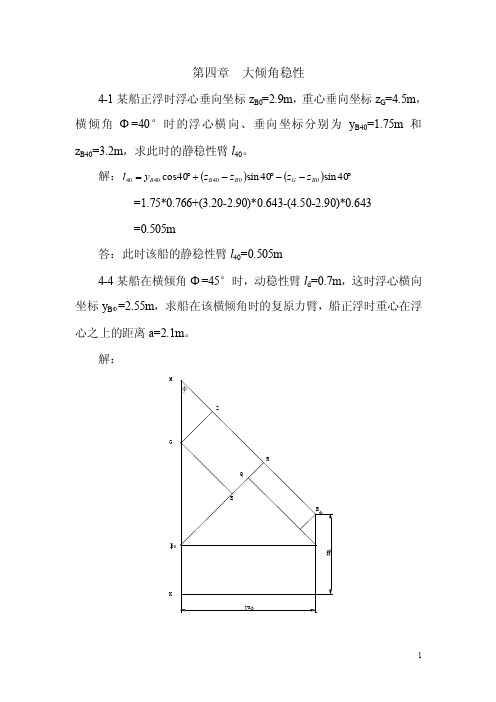
第四章 大倾角稳性4-1某船正浮时浮心垂向坐标z B0=2.9m ,重心垂向坐标z G =4.5m ,横倾角Φ=40°时的浮心横向、垂向坐标分别为y B40=1.75m 和z B40=3.2m ,求此时的静稳性臂l 40。
解:()()︒--︒-+︒=40sin 40sin 40cos 00404040B G B B B z z z z y l =1.75*0.766+(3.20-2.90)*0.643-(4.50-2.90)*0.643 =0.505m答:此时该船的静稳性臂l 40=0.505m4-4某船在横倾角Φ=45°时,动稳性臂l d =0.7m ,这时浮心横向坐标y B Φ=2.55m ,求船在该横倾角时的复原力臂,船正浮时重心在浮心之上的距离a=2.1m 。
动稳性臂的几何意义为:()G B KB z y G B G B zB l B B d 0000cos sin cos ---+=-=φφφφφφ即0.7=2.1*22+2.55*22-()0KB z B -φ*22-2.1 解得:()0KB z B -φ=0.69m()φφφφφsin sin cos 00G B KB z y l B B --+==2.55*22+0.69*22-2.1*22 =0.806m答:该船此状态的复原力臂l =0.806m 。
4-5某船在横倾角Φ=30°时的复原力臂l =2.60m ,动稳性臂l d =0.73m ,重心在龙骨以上高度z g =10.58m ,正浮时重心在浮心以上的高度a=5.99m ,求Φ=30°时浮心在龙骨以上的高度。
解:又∵()φφφφφsin sin cos 00G B KB z y l B B --+=即:()50.0*99.550.0*59.4866.0*60.2--+=φφB B z y ② 将式①②联立解得06.6=φB z ,61.5=φB y答:Φ=30°时浮心在龙骨以上的高度m z B 06.630=。
大倾角稳性介绍

船舶静稳性曲线的变排水量计算法
2 - 17
船舶静稳性曲线的变排水量计算法
有了上述稳性横截曲线图,可以根据船舶在各种装载情况 下的排水量及其重心高度,按下式(4 一12 )可很方便 地求出船舶的静稳性曲线图.
2 -4
概述
大倾角时的静稳性臂(见图4 一1 )只能用下式来表示
或写作
式中,lb——B0R为浮心沿水平横向移动的距离,其数值 完全由排水体积的形状所决定,因此称为形状稳性臂,
lb yB cos zB sin
lg=B0E-B0Gsinφ,其数值主要由重心位置所决定,因此 称为重量稳性臂。 静稳性臂l随横倾角φ的变化比较复杂,不能用简单的公 式来2表- 5示。
第4章 大倾角稳性
4 一1 概述 4 一2 船舶静稳性曲线的变排水量计算法 4 一3 船舶静稳性曲线的等排水量计算法 4 一4 上层建筑及自由液面对静稳性曲线的影响 4 一5 静稳性曲线的特征 4 一6 动稳性 4 一7 船舶在各种装载情况下的稳性校核计算 4 一8 极限(许用)重心高度曲线 4 一2 9- 1 船体几何要素等对稳性的影响
2 -7
船舶静稳性曲线的变排水量计算法
根据合力矩原理,由图4 一4 可以看出:▽φ对于NN 的 体积静矩
船舶浮于倾斜水线NN时浮力作用线至轴线的距离
令
2 -8
船舶静稳性曲线的变排水量计算法
则式(4 一4 )为
由式(4 一5)的可见,欲求得了φ的关键在于:必须先
求得人水楔形和出水楔形的体积差δ▽φ=vl 一v2,以及
2 -6
4 一2 船舶静稳性曲线的变排水 量计算法
一、基本原理 如图4 一4 所示,船舶正浮于水线WoLo,吃水为do,排水 体积为▽o,浮心在Bo处,其高度为KBo。当船舶横倾φ角 ,假定倾斜水线为WφLφ,并与 WoLo相交于O 点。V1为入水楔形 的体积,V2为出水楔形的体积, NN 为通过O 点的计算静矩的参考 轴线,c为旋转点O 至中心线的 距离(即偏离值)。水线WφLφ 下的排水体积▽φ必然是
第四节 船舶大倾角稳性

第四节船舶大倾角稳性1.液舱自由液面对静稳性力臂GZ的影响()。
A.随横倾角的增大而增大B.随横倾角的增大而减小C.不随横倾角变化D.以上均可能2.静稳性曲线的纵坐标是()。
A.复原力臂B.形状稳性力臂C.复原力矩D.A或C3.某船Δ=15000t,GM=2.3m,查得横倾角θ=20 °时的形状稳性力臂MS为0.64m,则静稳性力力矩为()t·m。
A.2250B.15000C.21450D.420004.()表示船舶重心G至浮力作用线的垂直距离。
A.GZB.GMC.KND.KH5.船舶横倾角在通常范围内增加时,其重量稳性力臂()。
A.增大B.不变C.减小D.以上均有可能6.液舱自由液面对静稳性力臂GZ的影响是()。
A.使静稳性力臂减小B.使静稳性力臂保持不变C.使静稳性力臂增大D.以上均有可能7.液舱自由液面对静稳性力矩M S的影响是()。
A.使静稳性力矩减小B.使静稳性力矩保持不变C.使静稳性力矩增大D.以上均有可能8.液舱自由液面对静稳性力矩M S的影响与()有关。
A.液面大小B.液面形状C.横倾角D.以上均是9.液舱自由液面对静稳性力臂GZ的影响与()有关。
A.液面大小B.液面形状C.横倾角D.以上均是10.通常情况下,横倾角不同时液舱自由液面对静稳性力臂GZ的影响()。
A.不同B.相同C.与横倾角无关D.以上均对11.通常情况下,横倾角不同时液舱自由液面力矩()。
A.不同B.相同C.与横倾角无关D.以上均对12.已知船舶形状稳性力臂KN|θ=30°=5.25m,船舶重心高度KG=8.20m,自由液面对初稳性的修正值为0.20m,则船舶的静稳性力臂GZ为()m。
A.0.95B.1.05C.1.15D.1.2013.某船装载后△=18000t,未经自由液面修正的KG0=7.3m,查得30°时的形状稳性力臂KN=4.5m和自由液面倾侧力矩为1080×9.81kN·m,则此时复原力臂为()m。
第一篇第4章大倾角稳性

船舶静稳性曲线的变排水量计算法
假定重心S 位置一般取在基线上 ,即KS=0。 倾角间隔一般海船取δφ=10º,算至φ=80 º;江船取 δφ=5 º,算到φ=40 º~50º,倾斜角度通常取为右倾 。
2 - 21
船舶静稳性曲线的变排水量计算法
( 3 )计算复原力臂. 分别计算各倾斜水线下的排水体积▽φ和浮心位置Bφ(yφ, zφ) ,然后按下式计算假定重心高度zs为零的复原力臂 ls;
2 - 16
船舶静稳性曲线的变排水量计算法
2 - 17
船舶静稳性曲线的变排水量计算法
有了上述稳性横截曲线图,可以根据船舶在各种装载情况 下的排水量及其重心高度,按下式(4 一12 )可很方便 地求出船舶的静稳性曲线图.
式中ls可以从稳性横截曲线图上查得。 按式(4一12 )计算不同横倾角沪时的静稳性臂ls,据此 即可绘制船舶在某一排水量时(即某一装载情况下)的静 稳性曲线。
2 -2
概述
式中l=GZ为重力作用线与浮力作用线之间的垂直距离, 称为复原力臂或静稳性臂。对于一定的船,静稳性臂l 随排水量△ 、重心高度KG及横倾角φ而变。在排水量△ 及重心高度KG一定时,GZ只随φ而变,如图4 一2 所示 。 讨论大倾角稳性的关键是确定复原力矩MR (或复原力臂 l ) ,而求复原力臂的关键是确定船舶在横倾φ后的浮 心位置Bφ( yφ,zφ)。因此计算复原力臂的途径一般是 根据水线WφLφ,计算倾斜后的浮心位置Bφ(yφ, zφ) 或利用重心移动原理计算倾斜后浮心位置的移动距离 B0Bφ。
2 -7
船舶静稳性曲线的变排水量计算法
根据合力矩原理,由图4 一4 可以看出:▽φ对于NN 的 体积静矩
船舶浮于倾斜水线NN时浮力作用线至轴线的距离
第四章 大倾角稳性

dl B M cos 2 yB sin B M sin 2 z B cos KG cos d 原点处 0, M B0 M 0,z B KB0, 0, 1, B sin cos dl | 0 B0 M 0 KB0 KG GM。 d
dM 1
按
2 l 2
l
dm dx
L
2 l 2
l
l 1 3 1 a cos ddx M 1 l2 a 3 cos ddx 0 2 3 3
1 3 0 3 b cos ddx 2 L '' 1 2 M M 1 M 2 L 0 a 3 b 3 cos ddx 2 3 按照前一章的内容:水线面对NN轴线的面积惯性矩 M2
故M ' 0 OF 0 d 0 KB0 sin C cos
三、楔形(入水、出水)计算
V1 V2
1 2
2 L
L
2
a
0
2
b 2 ddx
V2
1 2
2 l 2
l
0
b 2 ddx
1 的计算
入水楔形取一微体积元d A dV1
Ld BO G cos y B sin (Z B KBO ) cos BO G
dy B dZB dLd BOG sin cos y b cos cos ( Z B KBO ) sin d d d dZ B dy B B M sin B M cos d d
第四章 大倾角稳性

[(
)
]
三、楔形(入水、出水)计算
δφ =V1 V2 =
1 2∫
2 L
L
2
∫ (a
φ
0
2
b2 ddx
)
V2 =
1 l2 φ 2 0 b d dx l 2∫ 2∫
(1)δφ的计算
入 楔 取 微 积 dA = 水 形 一 体 元 dV1 = ∫
二、动稳性曲线与静稳性曲线的关系
1、 T = φ M dφ = φ ldφ = φ ldφ = ×l R d ∫O R ∫o ∫o 动稳性曲线是静稳性曲线的积分曲线。 动稳性曲线是静稳性曲线的积分曲线。
2、动稳性臂的物理含义
Ld物理意义是:船舶倾斜后的重心与浮心位置在垂向变化的增量。 物理意义是:船舶倾斜后的重心与浮心位置在垂向变化的增量。
结论:自由液面对静稳性曲线是不利的。 注:从0度就开始影响
φ = 300时 l300 δ φ300 δl均 δl30 取 δ 线 变 00 300的 l按 性 化
1 2 即 δl10 = δl30 ;δl20 = δl30 : 3 3
§4-5 静稳性曲线的特性
一、静稳性曲线的特征
1、曲线在原点处的曲率为初稳性高;
稳性消失角也是表示船舶稳性好坏的标志之一。 稳性消失角也是表示船舶稳性好坏的标志之一。
6、静稳性曲线下的面积
倾斜力矩所做的功 , 倾斜后船舶具有的位能等于静稳 倾斜力矩所做的功,
性曲线下的面积,面积越大,船舶稳性越好。 性曲线下的面积,面积越大,船舶稳性越好。
T = ∫ φ MH dφ = ∫ φ MRdφ 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
49
1)利用静稳性曲线确定
50
1)利用动稳性曲线确定
51
在风 浪作 用下 的稳 性曲 线
52
船舶能承受的三种最大倾斜力矩
53
4、特别说明
1)外力矩一般是随横倾角变化的,特别是风力 矩,多半随横倾角的增大而减小。前面的讨论 都是假定外力矩是不随横倾角变化的定值(中 国和日本的规范都是这样处理),且往往取可 能的最大值,这样选取在实用上偏于安全。
船舶静力学第4章 大倾角稳性 (时的静稳性臂
3
五、静稳性臂曲线图
4
§4-2 静稳性曲线的变排水量法
• 求得船舶在横 倾后浮力作用 线的位置就可 方便地进行静 稳性曲线的计 算。
5
一 基 本 原 理
6
船舶倾斜后水线下的排水体积: 根据合力矩原理,有:
外力矩主要来自风浪的作用,而风浪的大小 又与离岸距离以及水域开阔程度有关
63
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
计算时使用的稳性曲线必须经过自由液 面修正和考虑进水角影响后的曲线。
59
横摇角的计算: 根据图形查得
60
61
2、最小风倾力矩(最小风倾力臂)的计算
62
二、初稳性高与静稳性曲线
三、船舶稳性横准的基本思想
稳性曲线只是表示了船舶本身所具有的抵抗 外力矩的能力,或者说,只表示了船舶本身 所具有的稳性能力。 至于船舶受到的力矩究竟有多大,以及是否 经受得住,这要看外力矩的作用情况而定。
33
5、静稳性曲线下的面积越大,船舶所具有可 抵抗横倾力矩的位能就越大,即船舶的稳性 就越好。
34
§4-6 动稳性
• 一、基本概念
35
1、船舶在倾斜和复原过程中的运动情况
36
2、倾斜过程中船舶的往复摆动
37
3、动倾角
只有当外力矩 所作的功完全 由复原力矩所 作的功抵消时 ,船的角速度 才变为零而停 止倾斜。根据 这个原理,确
2)如果选外力矩为定值,则用动稳性曲线求解 比用静稳性曲线方便。
3)如果选外力矩为变值,则用静稳性曲线求解 比用动稳性曲线方便。
54
四、进水角与进水角曲线
1)进水角:船舶倾斜时,使船舶最先进水的那 个非水密开口处的倾斜角度,称为进水角。
55
2、进水角曲线
1)船舶的进水角随排水体积的变化而变化,进 水角随排水体积变化的曲线称为进水角曲线。
31
3、船舶在恒定静横倾力矩作用下一般有两个 平衡位置,分别处于横倾力矩与静稳性曲线 的上升段和下降段的交点。在上升段的交点 为稳定平衡位置,在下降段的交点为不稳定 平衡位置。
32
4、复原力矩等于零的点D对应的横倾角称为 稳性消失角,原点到D的距离称为稳矩。在稳 矩范围内,复原力矩为正值;超出稳矩范围 ,复原力矩为负值,使船无复原可能而继续 倾斜至倾覆;
定动倾角。
38
4、静稳性和动稳性的特点
回复力矩是衡量船舶静稳性的重要指标。 船舶静稳性是以回复力矩来表达的。
回复力矩所做的功是衡量船舶动稳性的重 要指标。船舶动稳性是以回复力矩所做的 功来表达的。
39
二、动稳性曲线
复原力矩所 作的功:
40
复原力矩所 作的功又可 写成:
41
动稳性曲 线与静稳 性曲线的 关系:动 稳性曲线 是静稳性 曲线的积 分曲线。
56
2)有进 水角时 ,船舶 最小倾 覆力矩 的确定 方法。
57
§4-7 船舶稳性校核计算
• 一、稳性衡准数K • 稳性衡准数K是对船舶稳性重要基本的要求
之一。规则规定:船舶在所核算的各种装 载情况下的稳性,应满足:
58
1、最小倾覆力矩(最小倾覆力臂)的计算
最小倾覆力矩(最小倾覆力臂)是根据 静稳性曲线或动稳性曲线以及横摇角来 确定的。关键是计算横摇角。
别计算这些水线下的浮心位置,在计算各倾 角下的复原力臂并绘制该排水量时的静稳性 曲线。
• 二、具体计算方法 • 反复试算,以确定某一倾角下的等体积倾斜
水线。
21
§4-4 上层建筑与自由液面对静稳性 曲线的影响
22
23
24
自由液面对静稳性曲线的影响
25
自由液面产生了一个倾斜力矩 船舶的实际复原力矩
7
浮力作用线至轴线N-N的距离:
8
9
的计算:
10
浮力作用线至 重力作用线( 通过假定重心 S)的水平距
离:
11
12
的计算:
13
同理可得:
14
入水小三角形的 面积对N-N轴线 的面积静矩为:
15
沿船长L积分得微楔体对N-N轴线的 体积静矩为:
整个入水楔形对N-N轴体积静矩为:
16
整个出水楔形对N-N轴体积静矩为:
26
27
结论:
在接近满舱或空舱时,自由液面对稳性的影响 很小;但在半舱时,其影响较大。
在稳性计算中,应把影响最大的情况作为进行 修正的依据。
28
§4-5 静稳性曲线的特征
29
一、 静稳性曲线的特征
1、静稳性曲线在原点处的斜率等于初稳性 高。常用此特性来绘制或检验静稳性曲线 的起始阶段。
30
2、静稳性曲线的最高点B的纵坐标值是船 舶在横倾过程中所具有的最大复原力矩( 或复原力臂),表示船舶所能承受的最大 静态横倾力矩。其对应的横倾角(B点的横 坐标值)称为极限静倾角。
式中 为 水线面对 N-N轴的面 积惯性矩 。
17
三、 稳性 插值 曲线
18
四、稳性横截曲线图
19
五、静稳性曲线
计算不同横倾角时的静稳性臂 l,据此可以绘制船舶在某一 排水量(即某一装载情况下) 时的静稳性曲线。
20
§4-3 静稳性曲线的等排水量法
• 一、基本原理 • 首先确定各倾角的等体积倾斜水线,然后分
42
三、静稳性和动稳性曲线的应用
1、动倾角的 确定
43
1)利用静稳性曲线确定
44
2)利用动稳性 曲线确定
当倾角为1 弧度时, 动倾力矩 所作的功 在数值上 与力矩相 等。
45
2、求极限动倾力矩和极限动倾角
1) 利用 静稳 性曲 线确 定
46
2)利用动稳性曲线确定
47
3、风浪联合作用下,极限动倾力矩 和极限动倾角
