第二章 凝固热力学(最新)要点
合集下载
第二章 热力学第一定律

T (B, ,T)
£K r Hm (T)
标准摩尔燃烧焓[变]的定义 在温度 T 物质 B 完全氧化( T)表示 叫标准摩尔燃烧焓 g H2O(l)的 T)计算
£K r Hm £K cHm £K r Hm B
-
)成相同温度下指定产物时的标准摩尔焓[变] 用
£K cHm
(B
指定产物 CO2 由
£K c Hm
物理化学学习指导
第二章 热力学第一定律
第二章 热力学第一定律
一. 基本概念及公式
1 热力学基本概念
(1)系统和环境 系统——热力学研究的对象(是大量分子 外的周围部分存在边界 环境——与系统通过物理界面(或假想的界面)相隔开并与系统密切相关的周围部分 根据系统与环境之间发生物质的质量与能量的传递情况 系统分为三类: 原子 离子等物质微粒组成的宏观集合体) 系统与系统之
H = Qp 适用于真实气体 理想气体 液体
T2 T1
∆H = ∫ nC p ,m dT
T1
T2
固体定压过程 理想气体任意 p
V
T 变化过程
∆U = ∫ nCV ,m dT = nC v ,m (T2 − T1 ) ∆H = ∫ nC p ,m dT = nC p ,m (T2 − T1 )
T1 T2
体积功 功有多种形式 通常涉及的是体积功 它是系统发生体积变化时的功 定义为
δW = − p su dV
式中 psu 为环境的压力
W = ∑ δW = − ∫ p su dV
V2 V1
对恒外压过程
psu = 常数
W = − p su (V2 − V1 ) W = − ∫ pdV
V1 V2
对可逆过程 因 p =psu
第二章 凝固热力学(最新)

第二节 二元合金的稳定相平衡
dF=dFA+dFB =(PA+PB)dVA=0。 但dVA≠0,所以,PA=PB。
当两相在恒温且总体积不变的情况下处于平衡状态时,两相 当两相在恒温且总体积不变的情况下处于平衡状态时, 的压强应相等。 的压强应相等。
假设两相间的接触面是平面,如果接触面 为弯曲界面,如图所示,
化潜热远低于气化潜热。根椐金属汽化潜热与熔化潜热的 比值,可以推出金属在熔时其配位数变化时很小的。 (三)熔化熵 三 熔化熵 表明物质(或系统)内部混乱程度。熵增大 ,混乱程度增加。
第一节
液态金属结构
金属在熔化时熵有较大的增加,说明金属在熔化时虽然原 子间距及配位数变化不大,但是原子排列的有序度却得到 了一定程度的破坏。
相:体系中均匀一致的部分,该部分与其他部分有 明显的分界线。
金属熔体有固 体从熔体中析 出
固体与金属熔体之间有 一个明显的分界面存在 (固/液界面)
体系于两相以上的多相状态
相平衡问题
第二节 二元合金的稳定相平衡
一、热平衡
设将A和B两个相封闭在一 个与环境无热量和物质交 换的体系内,A与B两相间 只有热量交换,即A,B两 相间的隔板完全固定,只 能导热,如图1—1所示。
式1-3与式1-4相加,可得:
第二节 二元合金的稳定相平衡
当TA>TB时,d(SA+SB)>0,即体系处于不平衡状态,热量 由高温传至低温。
当体系处于平衡态时,由热力学可知,其熵应为最大值,也 就是d(SA+SB)=0,于是可以得出δQ(TA-TB)=0, 但∆Q≠0,故有: TA=TB。
两相在互相接触的情况下达到平衡时,温度应该相等。
第一节
液态金属结构
两类凝固反应的区别:一类是突然转变成晶体,另一类 是连续地转变为玻璃质。 原因:具有不同的物质结构(分子结构和晶体结构),液 体中形成结晶相核心的机率不同所造成的。
第二章材料的凝固

正温度梯度
材料科学基础
实际金属结晶主要以树枝状长大。 是因存在负温度梯度,且晶核棱
角处散热好,生长快,先形成一
次轴,一次轴产生二次轴…,树 枝间最后被填充。
负温度梯度
材料科学基础
金属的树枝状结晶
材料科学基础
第三节
金属的同素异构转变
纯铁的同素异构转变
物质在固态下晶体结构随温度变 化的现象称同素异构转变。同素 异构转变属于相变之一—固态相 变。 白锡四方13 灰锡金刚石立方 ⇌ ℃
⑶ 振动、搅拌等: 对正在结晶的金属进行振动或搅动, 一方面可靠外部输入的能量来促进形核,
另一方面也可使成长中的枝晶破碎,使晶核数
目显著增加。
电磁搅拌细化晶粒示意图
材料科学基础
气轮机转子的宏观组织(纵截面)
细晶的熔模铸件(上)
普通铸件(下)
材料科学基础
4、晶粒大小对金属性能的影响
常温下,晶粒越细,晶界面积越 大,因而金属的强度、硬度越高, 同时塑性、韧性也越好,即细晶强 化。
铸件中的气孔
张开的气孔
材料科学基础
四、铸造缺陷的消除与防止
净化
镇静钢与沸腾钢
连续铸造
)
形核前的界面能为:σLCA1 形核后的界面能为:σLSA2+σSCA1 故:ΔGS=(σLSA2+σSCA1)-σLCA1 =2πr2σLS(1-cosθ)+πr2θ(σSC-σLC) 把σLC=σLScosθ+σsc代入上式,得: ΔGS=πr2σLS(2 -3cosθ+(cosθ)3) ΔGS为形核的界面能变化值;
材料科学基础
体积相变吉布斯自由能:
02章_热力学第二定律

①用373 K热源加热系统至373K,用273K热源吸 热使系统复原:
高温热源:-758kJ, 低温热源:+758kJ
②用温度相差无穷小的一系列热源加热系统至373 K, 用该系列热源使系统复原: 。
§2.2 热力学第二定律的语言表述
Clausius 的说法: 不可能从低温物体向高温物体传热而不产生其它 影响。 Kelvin 的说法: 不可能从单一热源吸热使之完全转化为功而不产 生其它影响。
500g水(273.2K)-→500g水(373.2K) 已知水的摩尔等呀热容:Cpm= 75.3 JK-1mol-1
解:(1) 用T环 =373.2K热源加热
Q/T环 = Cp(T2-T1)/T2 = (500/18) ×75.3× (373.2-273.2)/373.2 = 560.5 JK-1 (2) 先用T环1=323.2K的热源加热到323.2K,
1kgH2O(s) ———————→ 1kg H2O (l) 已知:水的比熔化焓为333.3J/g,求:△S
解:ΔS = ΔH相变/T =1000×333.3/273.2 = 1220.0 J/K
例2.4.4: 101.3kPa 90.18K O2 (l) ———————→O2 (g) ΔvapHm=6.820 kJmol-1
(2) 等压变温过程
S T2 nCp,mdT
T1
T
若Cpm与T无关:ΔS = nCpm ln(T2/T1)
例题:1 mol N2气在等容下用723.2K热源由298.2K 加热到723.2K,求过程的ΔS、ΔS环。
解:
等容,T环=723.2K
1molN2(298.2K)————→1molN2(723.2K)
例题:500g水在常压下用373.2K热源由273.2K加
高温热源:-758kJ, 低温热源:+758kJ
②用温度相差无穷小的一系列热源加热系统至373 K, 用该系列热源使系统复原: 。
§2.2 热力学第二定律的语言表述
Clausius 的说法: 不可能从低温物体向高温物体传热而不产生其它 影响。 Kelvin 的说法: 不可能从单一热源吸热使之完全转化为功而不产 生其它影响。
500g水(273.2K)-→500g水(373.2K) 已知水的摩尔等呀热容:Cpm= 75.3 JK-1mol-1
解:(1) 用T环 =373.2K热源加热
Q/T环 = Cp(T2-T1)/T2 = (500/18) ×75.3× (373.2-273.2)/373.2 = 560.5 JK-1 (2) 先用T环1=323.2K的热源加热到323.2K,
1kgH2O(s) ———————→ 1kg H2O (l) 已知:水的比熔化焓为333.3J/g,求:△S
解:ΔS = ΔH相变/T =1000×333.3/273.2 = 1220.0 J/K
例2.4.4: 101.3kPa 90.18K O2 (l) ———————→O2 (g) ΔvapHm=6.820 kJmol-1
(2) 等压变温过程
S T2 nCp,mdT
T1
T
若Cpm与T无关:ΔS = nCpm ln(T2/T1)
例题:1 mol N2气在等容下用723.2K热源由298.2K 加热到723.2K,求过程的ΔS、ΔS环。
解:
等容,T环=723.2K
1molN2(298.2K)————→1molN2(723.2K)
例题:500g水在常压下用373.2K热源由273.2K加
二 凝固热力学
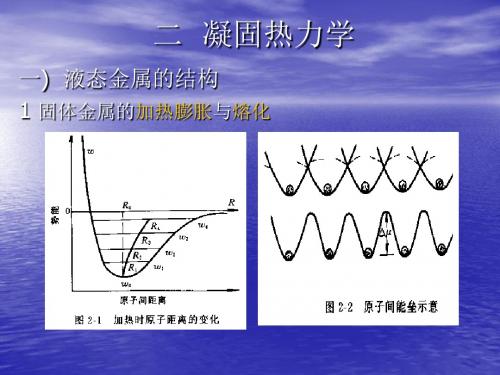
二 凝固热力学
一) 液态金属的结构 1 固体金属的加热膨胀与熔化
2 液态金属结构 1)液态金属与固体金属的差别 与气体相比,液体与固体的结构有相似性:
① 汽化潜热与熔化潜热的比值很大。 ② 金属从固态转变到液态其熵值变化不大。 ③ 物质的固态和液态在其熔点附近有很多相似之处
液态和固态之间的差别:
① 固体熔化时,体积膨胀3%。 ② 液态合金中的溶质扩散系数比固体合金中的溶质
3 液态金属的遗传性
①炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影响;
②在液态合金中加入合金元素后,改变了合金中元素与元素之间
的相互作用,进而影响凝固后铸件或毛坯的组织;
液态金属或合金的结构对凝固后铸件或毛坯的组织有影响,这 些影响液态金属或合金熔体结构进而影响凝固后铸件或毛坯的 组织与性能称为液态金属或合金的遗传性。
dG V dp S dT dG V dp S dT
2-1 2-2
由: dG dG 得:
S dp S S V dT V V
2-3
由
G H TS
G H TS
平衡时, G G G H T S 0
1 xS
其中
为组元A的摩尔分数,故上式变为:
V k V k k 1 1 k0 RTm (1 xS ) RTm
' 0 S m, B S m, B
2-26
从上式可以看出,曲率半 径越小,即曲率K越大, 在xs为定值的情况下,则 xL值越小,这就意味着, 曲率半径小的晶体,其固 液界面前沿富集起来的液 相浓度要比曲率半径大的 晶体小。
的扩散系数通常大1000倍。
2)液态金属的研究方法
一) 液态金属的结构 1 固体金属的加热膨胀与熔化
2 液态金属结构 1)液态金属与固体金属的差别 与气体相比,液体与固体的结构有相似性:
① 汽化潜热与熔化潜热的比值很大。 ② 金属从固态转变到液态其熵值变化不大。 ③ 物质的固态和液态在其熔点附近有很多相似之处
液态和固态之间的差别:
① 固体熔化时,体积膨胀3%。 ② 液态合金中的溶质扩散系数比固体合金中的溶质
3 液态金属的遗传性
①炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影响;
②在液态合金中加入合金元素后,改变了合金中元素与元素之间
的相互作用,进而影响凝固后铸件或毛坯的组织;
液态金属或合金的结构对凝固后铸件或毛坯的组织有影响,这 些影响液态金属或合金熔体结构进而影响凝固后铸件或毛坯的 组织与性能称为液态金属或合金的遗传性。
dG V dp S dT dG V dp S dT
2-1 2-2
由: dG dG 得:
S dp S S V dT V V
2-3
由
G H TS
G H TS
平衡时, G G G H T S 0
1 xS
其中
为组元A的摩尔分数,故上式变为:
V k V k k 1 1 k0 RTm (1 xS ) RTm
' 0 S m, B S m, B
2-26
从上式可以看出,曲率半 径越小,即曲率K越大, 在xs为定值的情况下,则 xL值越小,这就意味着, 曲率半径小的晶体,其固 液界面前沿富集起来的液 相浓度要比曲率半径大的 晶体小。
的扩散系数通常大1000倍。
2)液态金属的研究方法
第二章 焊接熔池凝固

系统总自由能变化△G由 两部分组成,即体积自由 能(由△Gv引起)和阻碍 相变的表面自由能。
r*为临界晶核半径. 只有r> r*的晶核才 可成为稳定晶核.
液相中形成球形晶胚时自由 能变化
4
§2-1-1 晶核形成—自发形核
也称为均质形核,是指形核前液相金属或合金中 无外来固相质点,而从液相自身发生形核的过程。
§2-3 结晶形态与成分过冷
纯金属的结晶形态 (右图所 示)
合金的结晶形态
平面结晶 planar 胞状晶 cellular 胞状树枝晶 cellular dendritic 柱状树枝晶 columnar dendritic 等轴晶 equi-axed dendritic
合金的结晶形态除了受“热 过冷”影响外,还受“成分 过冷”的影响,且后者往往 更重要。
焊接速度一定时,随焊接电流增加,G减小 (G/R减小),结晶形态从胞状晶向树枝晶转变。
焊接速度㎜/S 150A
300A
450A
0.85 1.69 3.39
胞状晶 胞状晶 细胞状晶
6.77
很细胞状晶
Source:From Savage et al.
胞状树枝晶
粗大胞状树枝晶
细胞状树枝晶 粗大胞状树枝晶
动力学过冷
热过冷
△T
纯金属的结晶形态 11
§2-3-1 成分过冷
(Constitutional Supercooling)
凝固过程的溶质再分配引 起固-液界面前沿的溶质富 集(b图),导致界面前沿 熔体液相线温度发生改变 的改变(c图)。
当界面前沿液相的实际温 度梯度小于界面处液相线 的斜率时,则出现过冷 (如图中“G2实际”)。
熔池在运动状态下结晶 结晶前沿随热源同步运动 液态金属受到力的搅拌运动 熔池金属存在对流运动
r*为临界晶核半径. 只有r> r*的晶核才 可成为稳定晶核.
液相中形成球形晶胚时自由 能变化
4
§2-1-1 晶核形成—自发形核
也称为均质形核,是指形核前液相金属或合金中 无外来固相质点,而从液相自身发生形核的过程。
§2-3 结晶形态与成分过冷
纯金属的结晶形态 (右图所 示)
合金的结晶形态
平面结晶 planar 胞状晶 cellular 胞状树枝晶 cellular dendritic 柱状树枝晶 columnar dendritic 等轴晶 equi-axed dendritic
合金的结晶形态除了受“热 过冷”影响外,还受“成分 过冷”的影响,且后者往往 更重要。
焊接速度一定时,随焊接电流增加,G减小 (G/R减小),结晶形态从胞状晶向树枝晶转变。
焊接速度㎜/S 150A
300A
450A
0.85 1.69 3.39
胞状晶 胞状晶 细胞状晶
6.77
很细胞状晶
Source:From Savage et al.
胞状树枝晶
粗大胞状树枝晶
细胞状树枝晶 粗大胞状树枝晶
动力学过冷
热过冷
△T
纯金属的结晶形态 11
§2-3-1 成分过冷
(Constitutional Supercooling)
凝固过程的溶质再分配引 起固-液界面前沿的溶质富 集(b图),导致界面前沿 熔体液相线温度发生改变 的改变(c图)。
当界面前沿液相的实际温 度梯度小于界面处液相线 的斜率时,则出现过冷 (如图中“G2实际”)。
熔池在运动状态下结晶 结晶前沿随热源同步运动 液态金属受到力的搅拌运动 熔池金属存在对流运动
凝固热力学

通过对金属固、液、气态转变的热化学数据分析和X 射线衍射分析,得到如下 结论: (1)液态金属中的平均原子间距比固态稍大; (2)液态金属中的配位数一般在8—11之间,配位数 变化不大; (3)液态金属中原子排列规则性降低,呈短程有序。
液态金属中的结构起伏 液态金属中的原子并非完全混乱,在要达到结晶温度 时,在液体内部存在许多在很短距离内有序排列的原 子集团,称为近程有序原子集团或晶坯。 结构起伏(相起伏):近程有序原子集团大小不等, 取向不同,时有时无,此起彼伏的现象。 结构起伏的晶坯尺寸与温度有关:温度低,晶坯的尺 寸大。
三、液态金属的遗传性
体现在以下几方面: (1)炉料的组织和缺陷对凝固后铸件或毛坯的组织、 缺陷有影响; (2)液态合金中加入合金元素后,改变了合金中元素 之间的相互作用,进而影响凝固后铸件或毛坯的组织; (3)液态金属或合金的结构不同(如:过冷度、净化 程度等),对凝固后铸件或毛坯组织有影响。 ——这些影响液态金属或合金熔体结构进而影响凝固后 铸件或毛坯的组织与性能现象称为液态金属或合金的遗 传性。 组织遗传性 炉料组织对铸锭组织有遗传性: 铝合金回炉料中含铁针片状化合物的组织对铝合金铸锭 组织的影响:
将纯铁片加入含0.4%Fe的ZL108,熔化保温,在 700C°浇铸,制成含1.26%Fe的ZL108—3合金。 组织:细小针状含铁化合物; 可见:回炉料组织中含铁相的形态对所配合金中含铁相 的形态具有明显的遗传性。 原因:含铁相是高熔点化合物,在铝合金熔体中难彻底 溶解,凝固时,新析出含铁相依附在原未溶含铁相上生 长,从而保留了原有含铁相的形态。
3、熔化熵 熔化温度定义为:液、固两相自由能相等的温度。 金属熔化时熵是增加的,但增加不大。考虑到金属熔化 时配位数和原子间距变化不大,则熵的增加主要增加了 原子排列的无序度。 4、热容量 可以作为判断原子运动特性的依据。实验发现,金属液 固两态的热容量差别不大。 证明:液固两态中原子运动状态也是相近的,与气态差 别较大。 5、导电性 大多数金属熔化后电阻增加近一倍,并且随温度的升高 继续增大,即:具有正的电阻温度系数。 说明:液体金属仍然是电子导电,具有金属键结合;气 体金属则和一般气体一样,完全失去了金属特性。
金属凝固热力学与动力学

ms ml
常数
K0
CS* Cl*
(Tm T *) / ms (Tm T *) / ml
ml ms
常数
❖ 当K0<1时,固相线、液相线张角向下, K0↓,成分偏析严重 当K0>1时,固相线、液相线张角向上, K0↑,成分偏析严重 常将∣1- K0 ∣称为“偏析系数”
❖ (二) K0的热力学意义
❖ 根据物理化学中相平衡热力学条件推导:
第1节 凝固热力学
❖ 一、液-固相变驱动力
❖ 相变驱动力:根据热力学原 理,相变是系统自由能由高 向低变化的过程,新相与母 相的体积自由能之差△GV。
GV
HmT Tm
❖ 液态金属的结晶过 程:
❖ 金属原子在相变驱动力 的驱使下,不断借助起 伏作用克服能量障碍, 并通过生核和生长方式 而实现转变的过程。
❖ 结晶过程中克服的两种不同的能障:
❖ 热力学能障:它由被迫于高能态过渡状态下的界面 原子所产生,能直接影响到体系自由能的大小。 (界面能属此种情况,对生核影响较大)
❖ 动力学能障:由金属原子穿越界面,原则上与驱动 力的大小无关而仅取决于界面的结构性质。(激活 能属此种情况,对晶体生长影响较大)
二、曲率及压力对合金熔点的影响
G非 V冠GV LC SLC ( CS LS )SC S
[
4 r3
3
GV
4
r
2
LC
][
2
3
cos
4
cos3
]
G均 f ( )
❖ 非均质形核的临界晶核半径为
r非*
2 SC
GV
2 LCTm
H T
❖ 将r*值代入△G非式,求得非均质形核的临界形核 功△G非*为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节
二、两种类型的凝固
液体具有高
液态金属结构
根据物质的
液体状态
的流动性
流动性
固体状态
如:0℃时,在盛有冰和水混合物的容器中,由于水很
容易流动,而冰却保持一定的形状,因此可以容易地辨 别出该混合物中的固相和液相。根据流动性辨别液体和 固体是可行的。
第一节
液态金属结构
在某些场合下,这一标准是不充分的,例如胶的水溶液在 100℃时具有良好的流动性,冷到室温时溶液就不能自由 流动了,但是低于零度时也不从溶液中析出冰来。这一类
平衡位置停留时间少于10-11秒。
在室温时为105秒,在熔点时约为 10-4秒。
第一节
液态金属结构
对液体金属衍射和计算可以知道液体金属中原子间距离和 配位数。在表1-4中比较了由衍射所得到的液体和固体结构 的数据,从表中可以得出下述重要的结论:
第一节
液态金属结构
1.在液体金属中平均原子间距略大于固体中的原子间距 (指大多数金属,下同); 2.在液体金属中的配位数比在固体中的小,通常在8~11
式1-3与式1-4相加,可得:
第二节 二元合金的稳定相平衡
当TA>TB时,d(SA+SB)>0,即体系处于不平衡状态,热量
由高温传至低温。
当体系处于平衡态时,由热力学可知,其熵应为最大值,也 就是d(SA+SB)=0,于是可以得出δQ(TA-TB)=0, 但ΔQ≠0,故有: TA=TB。 两相在互相接触的情况下达到平衡时,温度应该相等。
第一节
液体金属结构理论:
液态金属结构
1、液体中原子堆积是密集的,但排列不是那么规则的;
2、虽然大范围原子排列是不规则的,局部的微小区域来看, 原子可以偶然地在某一瞬间内出现规则的排列,然后又散开。 3、瞬时间内存在的微小区域内的原子规则排列称为“近程有 序”。而大小不一的近程有序排列的此起彼伏就构成了液体 金属的动态图象; 4、近程有序排列的原子集团就是晶胚。在具备一定条件后, 大于一定尺寸的晶胚就会成为晶核。
第二节 二元合金的稳定相平衡
dF=dFA+dFB =(PA+PB)dVA=0。 但dVA≠0,所以,PA=PB。 当两相在恒温且总体积不变的情况下处于平衡状态时,两相 的压强应相等。 假设两相间的接触面是平面,如果接触面 为弯曲界面,如图所示,
第二节 二元合金的稳定相平衡
假使A相是球体时,则应加入表面能项,还有σdαA项,σ 为比表面能,αA为A相的表面积。于是有: dFA=-SAdTA-pAdVA+σdαA dFB=-SBdTB-pBdVB 将dVA用-dVB替换,则由dVA+dVB=0可得: 故:
物质在冷却过程中是逐渐变硬或被固定的,在冷却到“固
态”过程中不发生物理性质的突然变化。 但是,水冷到0℃时(在一个大气压下)会结冰,出现物理性 质和物质状态的突变。
第一节
液态金属结构
存在两种截然不同的凝固反
物质由液态变成固态时(水
和液体金属或合金),流动 性和其他物理性质会发生突 然的变化(见图),在凝固过 程中,从液体中分离出一定
在固态,而低于该数值,则认为它们是处在液态。
玻璃质转变的连续性,所以这一数值纯粹是人为规定的。然而, 在大多数场合下它还是有意义的。
第一节
液态金属结构
两类凝固反应的区别:一类是突然转变成晶体,另一类 是连续地转变为玻璃质。 原因:具有不同的物质结构(分子结构和晶体结构),液 体中形成结晶相核心的机率不同所造成的。 凝固 形核
第二章 凝固热力学
考虑晶体生长情况时,必须确定究竟是与达到的平衡状态有
关,还是与各种过程进行的速率有关。
如果晶体生长或晶体的形态取决于过程的速率,如在表面
上的成核速率,就必须用适当的速率理沦来分析,这时热
力学就没有什么价值了。
如果过程进行非常接近于平衡状态,如在高温时常常可以看
到有准平衡状态,那么热力学对于预测生长量,以及成分 随温度、压力和实验中其他变数而改变的情况,就有很大
第一节
液态金属结构
抑制结晶,一般需要的冷却速度达106~108K/秒数量级。
具有玻璃质转变的物质(如二
氧化硅)在一定条件下也可以 发生第一类凝固反应,得到 晶体的固体。在图中表示了 二氧化硅两种可能的凝固类
型。但是应该说,在这类液
体中形成复杂结构的晶核是 极其困难的。
第二节 二元合金的稳定相平衡
第一节
液态金属结构
金属在熔化时熵有较大的增加,说明金属在熔化时虽然原
子间距及配位数变化不大,但是原子排列的有序度却得到 了一定程度的破坏。
第一节
液态金属结构
(四)液体金属结构的衍射研究 衍射研究表明:液体金属在温度
略高于其熔化温度时原子之间是
相当紧密接触的,而原子的局部 排列在不断变化着,原子在一定
第二节 二元合金的稳定相平衡
二 、力学平衡 若两相均为流体时,将它们放置在一个恒温恒容的箱子内,根 据自由能判据可得出,平衡状态时应有dF=dFA+dFB=0; 设两相间无物质交换,但体积可变,则:
由于是恒温状态,所以 dTA=dTB=0; 由于总体积不变,故:dV=dVA+dVB=0 即dVA=-dVB
范围内,值得注意的是由衍射实验直接测定的液体金属结
构的数据与前面根据热化学数据所作出的间接的定性的推 论是一致的。
第一节
三、液体金属结构的理论
液态金属结构
理论主要有三种;凝聚理论、点阵理论、几何理论。几何理 论提出的模型比较成熟,但是,也还不能说是令人满意的。
(一)凝聚理论 凝聚理论 (Condensation theories) 把液体看作 稠密的气体 (Dense-gas) , 由气体的动力学理论:在稠密气体中由原子或分子极为接近引起它们之间 力的作用,通过修正状态方程式(例如范德荷夫方程式),以描述液体金属
第一节 (三)几何理论
液态金属结构
衍射研究已确认在大多数液体金属中原子间距略大于固体金属 中原子间距,配位数比固体金属的配位数小,但是还不能提出
液体金属中原子排列的模型,为此,进行了几何学分析。
假定液体金属是宏观上均匀、互相密合的和大体上无规则的原 子或分子的聚合体,而且其中不含有结晶区域,也没有大空穴。 在这些假定条件下建立几何模型。
第二章 凝固热力学
二晶体生长:它关系到凝固后金属组织组成物的形态,金属
材料的晶体形态直接与金属材料的性能有关,如何控制晶
体生长,已经成为控制金属材料性能的一个重要手段。 晶体生长是一个动态过程,不可能在平衡状态下进行,而热 力学所处理的问题一般都是属于平衡问题,这两者结合到一
起似乎有些矛盾。
在研究任何过程的动力学问题之前,对其平衡问题有所了 解,则可以预测过程中所遇到的问题(偏离平衡状态的程 度),以及说明或提出解决问题的途径。
铝原子的配位数是12,而在气相中其配位数是零。
第一节
液态金属结构
固体气体时,必须破坏12个最邻近的金属键,而气化潜热
就提供破坏结合键所需要的能量。
固体液体时,只需要破坏不到一半的最邻近的键,所以熔
化潜热远低于气化潜热。根椐金属汽化潜热与熔化潜热的
比值,可以推出金属在熔时其配位数变化时很小的。 (三)熔化熵 表明物质(或系统)内部混乱程度。熵增大 ,混乱程度增加。
的实际意义。
第一节
(一)熔化时体积的变化
液态金属结构
一、液体金属的实验结果及其分析
不常见晶体结构的金属在熔化时有小量的收缩,大多数金属在 熔化时,体积膨胀3~5%,表明金属在固态和液态的原子间
距相差不大。
第一节
(二) 熔化潜热
液态金属结构
气化潜热与熔化潜热的比值是大的。例如对具有面心立方晶 体结构的铝:28倍
第一节
液态金属结构
第二类凝固反应在冶炼和凝固过程中也会碰到。例如在黑色金 属中所观察到的非金属夹杂物大多数是玻璃质。它们多为含硅 的渣粒,在冶炼和铸造过程中进入液体金属,在随后冷却中经
历玻璃质转变。
对于具有玻璃质转变的物质:液态或固态的区分,选定一个粘 度值,η(η是流动性φ的倒数),当η>1015泊时认为该玻璃质处
第一节
液态金属结构
办法:在气球内堆放数千个钢球, 并压紧和振动以达到最大密度的 无序密集堆积。为了防止规则、 密集堆积区域的出现,应该使气
球外表面呈无规则形状。并为了
便于随后分析起见,把油漆之类 物质灌注到气球内,油漆干后, 把部分钢球胶合在一起,取出钢 球进行分析。
第一节
液态金属结构
分析表明:相互接触的或近于接触的钢球,在油漆表面张力 作用下,才沾有油漆并胶合在一起,而其他钢球没有沾附油
配,还有理论认为熔化是一个典型的有序-无序反应。
液体中,原子继续被限制在点阵位置的附近,允许原子作无序 地和独立地振荡。根据这些理论得出许多实际的答案。 但是认为在液体金属中存在有一定程度的长程有序,实验证明 在液体金属中不存在这种结构,也就是说,点阵理论低估了由 熔化引起的熵变化(见表1—3),所以该理论受到损害。
第二节 二元合金的稳定相平衡
设此时从A相有微量的热量传到B相内,则由热力学可
知,A,B两相的内能变化为:
式中,U为内能,T为温度;S为熵;P为压力;V为体积, 下角标A,B表示A相与B相。
由于隔板固定,故A,B两相的体积也不会发生变化,故:
第二节 二元合金的稳定相平衡
体系内能的变化只表现为热量的改变 即:δQ=-dUA=dUB。 因:假定热量由A传至B时,对B相来说,δQ为正,反之 δQ为负。
的结构。提出一系列适合于液体的动力理论阐述的分子分布函数。这些公
式阐述在数学上是复杂的,但是,几乎没有得到在实际方面的答案。
第一节
(二)点阵理论
液态金属结构
引进各种缺陷来描述液体金属的结构。例如空洞或游离体积 理论把液体金属当作具有大量空穴位置的伪点阵来对待,有 效结构理论认为液体状态涉及晶体状和气体状分量之间的分
