1 电力系统各元件数学模型
电力系统各元件的数学模型

推导过程:从1-1’,2-2’之间等值,将导纳支路拿出去
ZT 1:k
I1 1 I2 k
U2
k
U1
I1
ZT
1 I1
U1
ZT
1:k I2
2 U2
I1
U1 ZT
U2
1’
ZT k
U1 (y10
y) 12
2’
U2
y 12
I2
U1 ZT k
U2 ZT k2
U1 y12
U2 (y20
y) 12
§2.5 电力系统的等值电路
一些常用概念
1. 实际变比 k
k=UI/UII UI、UII :分别为与变压器高、低压绕组实际 匝数相对应的电压。 2. 标准变比kN
• 有名制:归算参数时所取的变比 • 标幺制:归算参数时所取各基准电压之比
3. 非标准变比 k* k*= k /kN=UIIN UI /UII UIN
U
U UB
I S Z
I IB S SB Z ZB
P jQ SB
R jX ZB
P SB R ZB
j
Q SB
P
jQ
j
X ZB
R
jX
§2.5 电力系统的等值电路
2、基准值的选取 1) 基准值的单位与对应有名值的单位相同 2) 各种量的基准值之间应符合电路的基本关系
SB 3 UB IB UB 3 IB ZB
§2.5 电力系统的等值电路
四、电力系统的等值电路制订
1、决定是用有名值,还是用标幺值
容量不相同时 2、变压器的归算问题
电压等级归算
采用Γ型和T型 采用π型—不归算
3、适当简化处理
第二章电力系统各元件的数学模型

试验时小绕组不过负荷,存在归算问题,归算到SN
2) 对于(100/50/100)
2
Pk (12)
P' k (12)
IN 0.5IN
P 4 ' k (12)
2
Pk ( 23)
P' k (23)
IN 0.5IN
P 4 ' k ( 23 )
3) 对于(100/100/50)
2
Pk (13)
P' k (13)
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
一次整循环换位:
A B
C
换位的目的:为了减 少三相参数的不平衡
§2.3 电力线路的参数和数学模型
Xd
§2.1 发电机的数学模型
受限条件
定子绕组: IN为限—S园弧
转子绕组: Eqn ife 励磁电流为限—F园弧 Xd
原动机出力:额定有功功率—BC直线
其它约束: 静稳、进相导致漏磁引起温升—T弧
进相运行时受定 子端部发热限制 受原动机出力限制
定子绕组不超 过额定电流
励磁绕组不超 过额定电流 留稳定储备
2、由短路电压百分比求XT(制造商已归算,直接用)
U U U U 1 k1(%) 2
k(12) (%) k(13) (%) (%) k(23)
XT1
Uk
1(%
)U2 N
100SN
U U U U 1 k2 (%) 2
k(12) (%) k(23) (%) (%) k(13)
第2章 电力系统稳态分析_电力系统各元件的特性和数学模型

第二节 变压器的参数和数学模型
两绕组变压器的 Γ 型等值电路与参数计算公式
2 2 Pk U N Uk % UN ,X T RT 2 SN 100 S N P0 I0 % SN GT 2 ,BT 2 U 100 U N N k U 1 N / U 2 N
~ S (U d jU q )(I d jI q ) (U d I d U q I q ) j(U q I d U d I q )
P U d I d U q I q Q U q I d U d I q
从而
第一节 发电机组的运行特性和数学模型
P0 GT 2 1000 UN
第二节 变压器的参数和数学模型
3. 变比 k 定义为一次额定电压与二次空载电压之比,可由 空载试验测得或由变压器铭牌查得。 安装在高压绕组上; 对应于额定电压的抽头为主抽头,其余抽头的 电压相对额定电压偏离一定值;
变压器的实际变比=对应于实际 抽头位置的一 次电压与二次电压之比。
一型
第二节 变压器的参数和数学模型
特点:
增加传输能力 减少功率损耗
S 3UI
S L 3I 2 Z ZS 2 / U 2
减少电压降落
3ZI Z S/ U dU
类型:
单相、三相 两绕组、三绕组 普通、自耦 普通、有载调压、加压调压
第二节 变压器的参数和数学模型
一、双绕组变压器的参数和数学模型
1 U 1ZT 1 NhomakorabeaYT
ZT 2
2
ZT 3
3
U 3
U 2
第二节 变压器的参数和数学模型
电力系统各元件的特性和数学模型课件

变压器的主要参数
额定电压
变压器能够长期正常工作的电压值。
额定容量
变压器的最大视在功率,表示变压器的输出 能力。
额定电流
变压器能够长期通过的最大电流值。
效率
变压器传输的功率与输入的功率之比,表示 变压器的能量转换效率。
变压器数学模型
变压器数学模型通常采用传递函数的 形式来表示,可以描述变压器在不同 工作状态下的输入输出关系。
THANKS FOR WATCHING
感谢您的观看
配电系统是电力系统的重要组成部分,主要负责将电能从发电厂或上级电网分配给 终端用户。
配电系统的工作原理包括电压变换、电流变换和功率传输等过程,通过变压器、开 关设备和输配电线路等设备实现。
配电系统通常分为高压配电、中压配电和低压配电三个层次,以满足不同用户的需 求。
配电系统的主要参数
电压
配电系统的电压等级通常在1kV至35kV之间,其 中1kV以下为低压配电,35kV以上为高压配电。
电力系统的控制策略
电力系统的控制策略包括发电机的励磁控 制、调速控制等,这些控制策略对电力系
统的稳定性起着至关重要的作用。
电力系统的运行状态
电力系统的运行状态对稳定性有直接影响 ,如负荷的大小和分布、发电机的出力、 电压和频率等。
外部环境因素
外部环境因素包括自然灾害、战争、恐怖 袭击等,这些事件可能导致电力系统受到 严重干扰,影响其稳定性。
04
负荷:消耗电能的设备或设施。
电力系统元件的分类
一次元件
包括发电机、变压器、输电线路等,是构成电力系统的主体 部分。
二次元件
包括继电器、断路器、测量仪表等,用于控制、保护和监测 电力系统。
电力系统正序、负序、零序网络画法
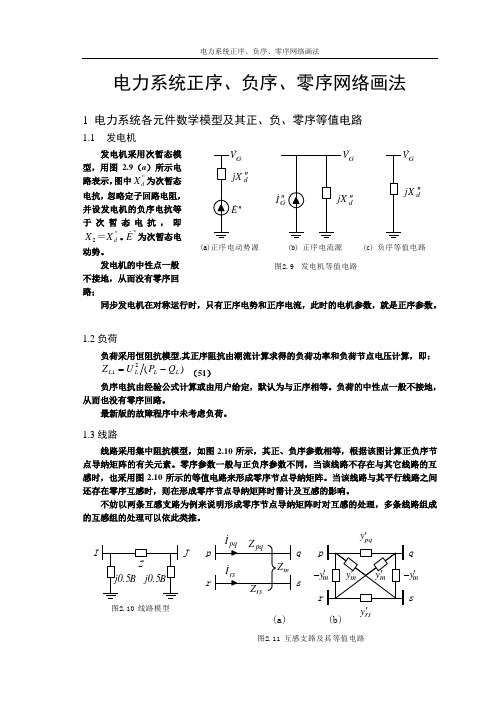
电力系统正序、负序、零序网络画法1 电力系统各元件数学模型及其正、负、零序等值电路1.1 发电机发电机采用次暂态模型,用图2.9(a )所示电路表示,图中X d ''为次暂态电抗,忽略定子回路电阻,并设发电机的负序电抗等于次暂态电抗,即X X d 2=''。
''E为次暂态电动势。
发电机的中性点一般不接地,从而没有零序回路;同步发电机在对称运行时,只有正序电势和正序电流,此时的电机参数,就是正序参数。
1.2负荷负荷采用恒阻抗模型,其正序阻抗由潮流计算求得的负荷功率和负荷节点电压计算,即:Z U P Q L L L L 12=-() (51)负序电抗由经验公式计算或由用户给定,默认为与正序相等。
负荷的中性点一般不接地,从而也没有零序回路。
最新版的故障程序中未考虑负荷。
1.3线路线路采用集中阻抗模型,如图2.10所示,其正、负序参数相等,根据该图计算正负序节点导纳矩阵的有关元素。
零序参数一般与正负序参数不同,当该线路不存在与其它线路的互感时,也采用图2.10所示的等值电路来形成零序节点导纳矩阵。
当该线路与其平行线路之间还存在零序互感时,则在形成零序节点导纳矩阵时需计及互感的影响。
不妨以两条互感支路为例来说明形成零序节点导纳矩阵时对互感的处理,多条线路组成的互感组的处理可以依此类推。
IJ 图2.10 线路模型p q rs(a)pqrs(b)y 'rsy '-my'图2.11 互感支路及其等值电路E'' d X j ''G (a)正序电动势源d''G (b) 正序电流源dX j ''G(c) 负序等值电路图2.9 发电机等值电路由图2.11(a )得两支路的电压-电流方程为:⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--s r qp rs m m pq rs pq rs pq rs m m pq s r q p V V V V y y y y I I I I Z Z Z Z V V V V'''' (52) 由此得消互感后的等值电路如图2.11(b )所示,根据该图即可按照无互感的情况计算零序节点导纳矩阵的有关元素。
电力系统各元件的特性和数学模型

E q
Ixd cos
P ,Q
Eq sin
Q
Ixd
Ixd cos
U
I
Ixd
sin
Eq
cos
U
I I
cos sin
Eq sin
xd
Eq cos
xd
U
P
UI
cos
由此,
Q UI sin
EqU sin
xd
EqU cos
xd
U 2
EqU cos
xd
U2
xd
(2-2)
(2-3)
按每相的绕组数目
双绕组:每相有两个绕组,联络两个电压等级
三绕组:每相有三个绕组,联络三个电压等级,三个绕 组的容量可能不同,以最大的一个绕组的容量为变压器 的额定容量。
类别 普通变 自耦变
高 100% 100% 100% 100%
中 100% 50% 100% 100%
低 100% 100% 50% 50%
1.3 凸极机的稳态相量图和数学模型
11
第一节 发电机组的运行特性和数学模型
12
第一节 发电机组的运行特性和数学模型
13
第一节 发电机组的运行特性和数学模型
稳态分析中的发电机模型
发电机简化为一个节点 节点的运行参数有:
U U G
节点电压:U U u 节点功率:S~ P jQ
S~ P jQ
19
第二节 变压器的参数和数学模型
2.1 变压器的分类:有多种分类方法
按用途:升压变、降压变 按电压类型:交流变、换流变 按三相的磁路系统:
单相变压器、三相变压器 按每相绕组的个数:双绕组,三绕组 按绕组的联结方式:
电力系统各元件的特性和数学模型

电力系统各元件的 特性和数学模型
复功率的规定
•
• 国际电工委员会(IEC)的规定 S U I
j U
•
S U I Ue ju Ie ji UIe j(u i ) UIe j
UI cos j sin
I
u
i
S cos j sin
P jQ
“滞后功率因数 运行”的含义
符号 S φ P Q
电力系统各元件的特性和数学模型
18
双绕组变压器和三绕组变压器
• 双绕组变压器:每相两个绕组,联络两个电压等级
2020/9/7
电力系统各元件的特性和数学模型
6
2.1节要回答的主要问题
• 功角的概念是什么?与功率因数角的区别? • 隐极机的稳态功角特性描述的是什么关系?(由此可
以引申出高压输电网的什么功率传输特性?) • 发电机的功率极限由哪些因素决定?对于隐极机,这
些因素如何体现在机组的运行极限图中?发电机的额 定功率与最大功率有什么关系?发电机能否吸收无功 功率? • 稳态分析中所采用的发电机的数学模型是怎样的?
• 负荷以超前功率因数运行时所吸收的无功功率为 负。——容性无功负荷(负)
• 发电机以滞后功率因数运行时所发出的无功功率为 正。——感性无功电源(正)
• 发电机以超前功率因数运行时所发出的无功功率为 负。——容性无功电源(负)
2020/9/7
ห้องสมุดไป่ตู้
电力系统各元件的特性和数学模型
3
目录
2.1 发电机组的运行特性和数学模型 2.2 变压器的参数和数学模型 2.3 电力线路的参数和数学模型 2.4 负荷的运行特性和数学模型 2.5 电力网络的数学模型 本章小结 习题
电力系统正序、负序、零序网络画法

电力系统正序、负序、零序网络画法1 电力系统各元件数学模型及其正、负、零序等值电路发电机发电机采纳次暂态模型,用图(a )所示电路表示,图中X d''为次暂态电抗,忽略定子回路电阻,并设发电机的负序电抗等于次暂态电抗,即X X d 2=''。
''E为次暂态电动势。
发电机的中性点一样不接地,从而没有零序回路;同步发电机在对称运行时,只有正序电势和正序电流,现在的电机参数,确实是正序参数。
负荷负荷采纳恒阻抗模型,其正序阻抗由潮流计算求得的负荷功率和负荷节点电压计算,即:Z U P Q L L L L 12=-() (51)负序电抗由体会公式计算或由用户给定,默以为与正序相等。
负荷的中性点一样不接地,从而也没有零序回路。
最新版的故障程序中未考虑负荷。
线路线路采纳集中阻抗模型,如下图,其正、负序参数相等,依照该图计算正负序节点导纳矩阵的有关元素。
零序参数一样与正负序参数不同,当该线路不存在与其它线路的互感时,也采纳图所示的等值电路来形成零序节点导纳矩阵。
当该线路与其平行线路之间还存在零序互感时,那么在形成零序节点导纳矩阵时需计及互感的阻碍。
不妨以两条互感支路为例来讲明形成零序节点导纳矩阵时对互感的处置,多条线路组成的互感组的处置能够依此类推。
IJ 图2.10 线路模型p q rs(a)p qrs(b)y 'rsy -my '图2.11 互感支路及其等值电路E'' d X j ''G (a)正序电动势源d''G (b) 正序电流源I dX j ''G(c) 负序等值电路图2.9 发电机等值电路由图(a )得两支路的电压-电流方程为:⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--s r qp rs m m pq rs pq rs pq rs m m pq s r q p V V V V y y y y I I I I Z Z Z Z V V V V'''' (52) 由此得消互感后的等值电路如图(b )所示,依照该图即可依照无互感的情形计算零序节点导纳矩阵的有关元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 电力系统各元件数学模型1.1 发电机组参数及数学模型发电机组在稳态运行时的数学模型(图1所示)极为简单,通常由两个变量表示,即发出的有功功率P 和端电压U 的大小或发出的有功功率P 和无功功率Q 的大小。
以第一种方式表示时,往往还需伴随给出相应的无功功率限额,即允许发出的最大、最小无功功率max Q 、min Q 。
图 1 发电机数学模型1.2 变压器参数及数学模型1.2.1双绕组变压器Γ型等值电路模型TjX 图2 双绕组变压器Γ型等值电路模型双绕组变压器Γ型等值电路模型如图2所示,电路参数通过以下公式计算。
注意,公式中N U 取不同绕组的额定电压,表示将参数归算到相应绕组所在的电压等级(所得所得阻抗/导纳参数都是等值为Y/Y 接线的单相参数);公式中各参数由变压器厂家提供,采用实用单位。
22020210001001000%100k N T Nk NT N T NN T N P U R S U U X S P G U I S B U ⎧∙=⎪⎪⎪%∙=⎪⎪⎨⎪=⎪⎪⎪=∙⎪⎩(1-1) 其中,k P 为短路损耗,k U %为短路电压百分数,0P 为空载损耗,0%I 为空载电流百分数,N U 为归算侧的额定电压,N S 为额定容量 该电路模型一般用于手算潮流中。
1.2.2 双绕组变压器T 型等值电路模型1jX '图 3 双绕组变压器T 型等值电路模型其中,1R 和1X 为绕组1的电阻和漏抗,'2R ,'2X 为归算到1次侧的绕组2 的电阻和漏抗,m R 和m X 为励磁支路的电阻和电抗。
该电路模型一般用于电机学中加深对一二次侧和励磁支路电阻电抗的理解以及手算潮流计算中。
1.2.2 三绕组变压器Z 图4三绕组变压器的等值电路三绕组变压器的等值电路如图3所示,图中,变压器的励磁支路也以导纳表示。
该电路模型一般用于手算潮流计算中。
三绕组变压器的参数计算如下: 电阻:由短路损耗计算()()()1(12)(31)(23)2(23)(12)(31)3(31)(23)(12)121212k k k k k k k k k P P P P P P P P P P P P ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-2) 211222233100010001000k N T Nk N T Nk NT N P U R S P U R S P U R S ⎧∙=⎪⎪⎪∙⎪=⎨⎪⎪∙⎪=⎪⎩(1-3) 其中,k P 为短路损耗,N U 为归算侧的额定电压,N S 为额定容量对于容量比为100/100/50和100/50/100的变压器,厂家提供的短路损耗是小容量绕组达到自身额定电流()/2N I 时的试验数据,计算时应首先将短路损耗折算为对应于变压器额定电流()N I 的值例如,对于100/100/50型变压器,厂家提供的是未经折算的短路损耗'(23)k P -,'(31)k P -,'(12)k P -首先应进行容量归算'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩(1-4) 按新标准,厂家仅提供最大短路损耗max k P ,按以下公式计算电阻:2max (100%)2(50%)(100%)20002k N T N T T P U R S RR ⎧=⎪⎨⎪=⎩(1-5) 其中max k P 为最大短路损耗,N U 为归算侧的额定电压,N S 为额定容量 电抗:由短路电压百分数计算()()()1(12)(31)(23)2(12)(23)(31)3(23)(31)(12)1%%%%21%%%%21%%%%2k k k k k k k k k k k k U U U U U U U U U U U U ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-6) 211222233100100100k N T Nk N T N k NT N U U X S U U X S U U X S ⎧%=⎪⎪⎪%⎪=⎨⎪⎪%⎪=⎪⎩(1-7) 其中,k U %为短路电压百分数,N U 为归算侧的额定电压,N S 为额定容量 注意,厂家提供的短路电压是经过额定电流折算后的数据。
导纳:由空载损耗和空载电流百分数计算02021000%100T NNT N P G U I S B U ⎧=⎪⎪⎨⎪=∙⎪⎩(1-8) 其中,0P 为空载损耗,0%I 为空载电流百分数,N U 为归算侧的额定电压,NS 为额定容量1.2.3自耦变压器等值电路与普通三绕组变压器相同。
若容量为100/100/50按旧标准,厂家提供的短路损耗和短路电压百分数均为未经折算的数据,因此计算阻抗时,需首先进行容量折算:'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩(1-9) '(23)(23)'(31)(31)%2%%2%k k k k U U U U ----⎧=⎪⎨=⎪⎩(1-10) 其中,k P 为短路损耗,k U %为短路电压百分数按新标准,则提供最大短路损耗max k P 和折算后的短路电压百分数。
1.3 电力线路数学模型1.3.1 电力线路的物理现象:电阻:载流导体的发热效应(有功损耗)电抗:电力线路通过交流电流时的磁场效应(导体中产生感应电动势) 电导:高电压作用下导线表面电场强度过高而产生的电晕损耗;绝缘不完善产生的泄漏电流(有功损耗)电钠:交流电压施加在电力线路上而产生电场效应(导线之间、导线与大地之间产生位移电流)100km l ≤的架空线路或10kV 以下的电缆线路Z图5电力线路短线模型()11Z R jX r x l =+=+(1-11)其中,1r 为线路单位长度的电阻,1x 为线路单位长度的电抗,l 为线路长度。
1.3.3 中长线模型100km 300km l ≤≤的架空线路或100km l ≤的电缆线路π型等值电路如下:图6电力线路中长线模型()()1111Z R jX r x lY G jB g b l=+=+⎧⎪⎨=+=+⎪⎩(1-12) 其中,1r 为线路单位长度的电阻,1x 为线路单位长度的电抗,1g 为线路单位长度的电导,1b 为线路单位长度的电钠,l 为线路长度。
稳态分析中一般用给定的P、Q来表示负荷(恒定功率负荷模型)1.5电力网络数学模型1.5.1标幺值=有名值(任意单位)标幺值基准值(单位与有名值相同)三相系统基准值一般取法:①取线电压基准值BU,一般取电网额定电压②取三相功率基准值BS,一般取100MV A,1000MV A ③根据约束关系计算其他基准值:22,B BB B BB BU SI Z YS U===(1-13)其中,BS为基准功率,BU为基准电压,BI为基准电流,BZ为基准阻抗,BY 为基准导纳标幺值的电压等级归算:①参数归算法②基准值归算法1.5.2 等值变压器模型为什么引入等值变压器模型?①采用变压器Γ型等值电路建立多级电网等值电路时,需要用变压器实际变比进行电压归算。
若分接头发生变化,相关的一大批参数都需要重新归算②环网中变压器变比不匹配时,电压归算有困难。
''图 7双绕组变压器原电路''图 8等值双绕组变压器模型其中121020211,,T T T Y k k z y Y y Y k k k--===(1-14) 注意:① 模型中1/T T Y Z =,不是变压器励磁导纳② 由于低压侧通常只有一个分接头,建议将变压器参数归算到低压侧 ③ 理想变压器都串联在高压绕组端点,不串联在低压绕组端点,考虑励磁支路时,通常将其接到远离理想变压器的一侧,即连接在低压端为宜 该电路模型一般用于计算潮流中。
1.5.3 等值变压器模型的应用1、有名制,线路参数为实际值,变压器参数归算到低压侧理想变压器变比k =变压器实际变比(1-15)2、有名制,线路参数与变压器参数已按额定变比归算到高压侧理想变压器变比*=N k k k =实际变比额定变比(1-16) 3、标幺制,线路和变压器参数已按选定基准电压IB U 、IIB U (一般为额定电压或平均额定电压)归算为标幺值(就地标幺法)理想变*=B k k k =实际变比基准变比(1-17) 1.5.4 三绕组变压器的π型模型三绕组变压器原始网络如下,1、2、3分别代表高、中、低压绕组高压1中压2低压3图 9三绕组变压器原电路三绕组变压器的等值多电压级网络如下图所示,两台理想变压器分别串联在高、中压绕组的端点,相应的理想变压器变比分别取12/;/I III II III k U U k U U ==(1-18)其中,I U ,II U ,III U 分别为一、二、三次侧基准电压II'图 10接入理想变压器后的等值电路进一步可将等值电路等效为'3图 11π型等值电路以导纳形式表示其中,11111010121112222202022222211,,11,,T c T c T T c T c T Y k k y y Y y Y k k k Y k k y y Y y Y k k k --⎧===⎪⎪⎨--⎪===⎪⎩(1-19) 其中,1/T T Y Z =该电路模型一般用于机算潮流中。
1.5.5 改进的三绕组变压器等值模型i图12中所有参数按标准电压1N U 、2N U 、3N U 归算到基本级,当变压器实际运行的分接头电压为1U 、2U 、3U 时,为不改变已归算的参数,可以在三个绕组等值电抗前各串联一个理想变压器。
各侧理想变压器的变比按下式计算:111222333///NN N k U U k U U k U U=⎧⎪=⎨⎪=⎩(1-20)2Z 2:1k图 12 三绕组变压器的3π等值电路模型查阅文献可知,负阻抗所在绕组的理想变压器的变比越大,则潮流计算越容易收敛。
在同一运行条件下,3π等效电路串联变压器的变比总是比2π等值电路对应绕组的串联变压器变比高。
采用3π等效电路更容易收敛。
1.5.6 各类变压器模型的适用范围表1 各类变压器模型适用范围i 林褀蓉等,潮流计算中变压器模型的选择及改进分析[J]. 电气工程与自动化。
