2017—2018学年第一学期八年级数学期中复习要点
广东省东莞市翰林学校2017-2018学年八年级上学期数学期中考试试卷及参考答案

三、解答题
22. 计算: +( ﹣1)0﹣|﹣3|.
23. 计算:|﹣2|+
﹣(﹣1)2017 .
24. 计算:( ﹣ )2+( +3)( ﹣3).
25. 把下列各数分别填入相应的集合里. ﹣5,﹣2.626 626 662…,0,π,﹣ ,0.12,|﹣6|.
(1)正数集合:{
…};
(2)负数集合:{
=4.1,则
=________.
18. 的算术平方根是________.
19. 已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为________. 20. 实数4的算术平方根是________. 21. 已知﹣2xm﹣2y2与3x4y2m+n是同类项,则m﹣3n的平方根是________.
A . 1个 B . 2个 C . 3个 D . 4个
二、填空题
13. 当x=2时,二次根式
的值是________
14. 正方形的面积是24,那么它的边长是________.
15. 计算3 ﹣ 的结果是________.
﹣2
0
16. 计算:(﹣ )﹣2+(﹣2017)0=________.
17. 已知
6. 式子
在实数范围内有意义,则x的取值范围是( )
A . x>1 B . x≥1 C . x<1 D . x≤1
7. 下列运Байду номын сангаас正确的是( )
A.
B.
C.
D.
8. 下列实数中,是无理数的为( ) A . 3.14 B . C . D .
9. 在平面直角坐标系中,点P(﹣1,2)的位置在( )
每日一学:河南省信阳市羊山中学2017-2018学年八年级上学期数学期中考试试卷_压轴题解答

每日一学:河南省信阳市羊山中学2017-2018学年八年级上学期数学期中考试试卷_压轴题解答
答案河南省信阳市羊山中学2017-2018学年八年级上学期数学期中考试试卷_压轴题
~~ 第1题 ~~
(2018信阳.八上期中) 如图,在△ABC 中,∠ACB 是直角,∠B=60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE
相交于点F ,且FG ⊥AB 于G ,FH ⊥BC 于H .
(1) 求证:∠BEC=∠ADC ;
(2) 请你判断并FE 与FD 之间的数量关系,并证明.
考点: 三角形的角平分线、中线和高;三角形内角和定理;全等三角形的判定与性质;角平分线的性质;~~
第2题 ~~
(2018信阳.八上期中) 如图,依据尺规作图的痕迹,计算 ________.
~~ 第3题 ~~
(2018信阳.八上期中) 一个长方形面积是3a -3ab+6a ,一边长为3a ,则它的周长是( )
A . 2a-b+1
B . 4a-b+2
C . 8a-2b+4
D . 10a-2b
河南省信阳市羊山中学2017-2018学年八年级上学期数学期中考试试卷_压轴题解答
~~ 第1题 ~~
答案:2
解析:
答案:
解析:
~~ 第3题 ~~
答案:C
解析:。
湖南省桑植县第四中学2017_2018学年八年级数学上学期期中试题新人教版(附答案)
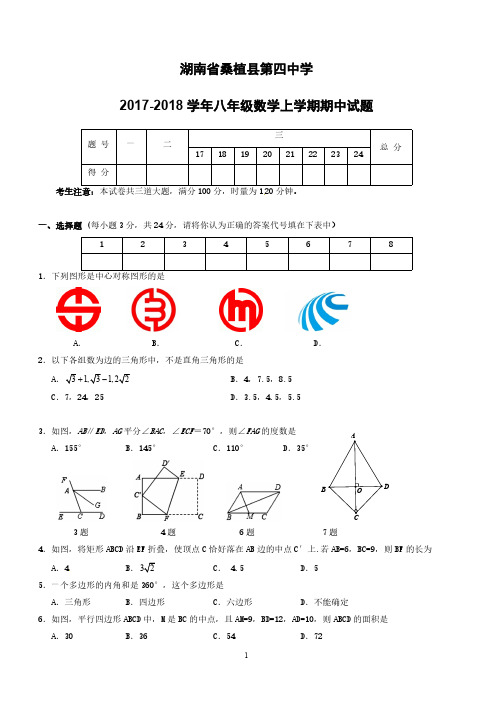
湖南省桑植县第四中学2017-2018学年八年级数学上学期期中试题三题 号一二1718192021222324总 分得分考生注意:本试卷共三道大题,满分100分,时量为120分钟。
一、选择题 (每小题3分,共24分,请将你认为正确的答案代号填在下表中)123456781.下列图形是中心对称图形的是A .B .C .D .2.以下各组数为边的三角形中,不是直角三角形的是A 31,22+-B .4,7.5,8.5C .7,24,25 D .3.5,4.5,5.53.如图,AB ∥ED ,AG 平分∠BAC ,∠ECF =70°,则∠FAG 的度数是A .155°B .145°C .110°D .35° 3题4题 6题 7题4.如图,将矩形ABCD 沿EF 折叠,使顶点C 恰好落在AB 边的中点C′上.若AB=6,BC=9,则BF 的长为A .4B .32C . 4.5D .55.一个多边形的内角和是360°,这个多边形是A .三角形B .四边形C .六边形D .不能确定6.如图,平行四边形ABCD 中,M 是BC 的中点,且AM=9,BD=12,AD=10,则ABCD 的面积是A .30B .36C .54D .72O B D7.如图,四边形ABCD 中,∠BCD=90°,BC=CD ,对角线AC⊥BD 于点O ,若CD AD 2,则∠ADC 的度数为A .100°B .105°C .85°D . 95°8.下列图案中,既是轴对称图形又是中心对称图形的是A .B .C .D .二、简答题 (每小题3分,共18分)9题 11题12题 14题9.Rt△ABC 中,∠C=90°,如图(1),若b=5,c=13,则a =__________;若a=8,b=6,则c=__________.10.在平行四边形ABCD 中,对角线AC 、BD 相交于点O.如果AB=14,BD=8,AC=x ,那么x 的取值范围是 11.如图,在菱形ABCD 中,AB=10,AC=12,则它的面积是 .12.如图,已知正方形ABCD 边长为3,点E 在AB 边上且BE=1,点P ,Q 分别是边BC ,CD 的动点(均不与顶点重合),当四边形AEPQ 的周长取最小值时,四边形AEPQ 的面积是 .13.已知点G 是△ABC 的重心,AD 是中线,如果AG=6,那么AD= .14.如图是“赵爽弦图”,△ABH、△BCG、△CDF 和△DAE 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形.如果AB=10,EF=2,那么AH 等于_______.三、解答题 (共58分)15.你能判断点A (-1-2a ,3+2b )在第几象限?(5分)16.(5分)“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:317.(5分)如图,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.(1)求证:△AED≌△CFB;(2)若∠A=30°,∠DEB=45°,求证:DA=DF.18.(6分)如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)求证:四边形BFDE为矩形.19.(6分)如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD 于F,点G为BC中点,连接EG、AF.(1)求EG的长;(2)求证:CF=AB+AF.20.(6分)我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB CB=,⊥,OF CB=.⊥,垂足分别是E,F.求证:OE OF AD CD=.对角线AC,BD相交于点O,OE AB21.(7分)如下图在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BC=32,且BD︰CD=9:7,求:D到AB边的距离.22.(8分)△ABC 中,CD⊥AB 于D ,AC=4,BC=3,DB=59.(1)求DC 的长;(2分)(2)求AD 的长;(2分)(3)求AB 的长;(2分)(4)求证:△ABC 是直角三角形.(2分)23.(10分)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念理解如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.(2分)(2)问题探究①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
中学2017-2018学年第一学期八年级数学教案整数指数幂

(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解整数指数幂的基本概念。整数指数幂是指底数为整数,指数为整数的情况。它是数学中非常重要的一个概念,广泛应用于科学计算、金融等领域。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了整数指数幂在实际中的应用,以及它如何帮助我们解决问题。
3.理解负整数指数幂的概念,掌握其计算方法,并了解其在数学中的应用。
具体内容包括:
(1)整数指数幂的定义及性质;
(2)正整数指数幂的计算方法;
(3)负整数指数幂的计算方法及其与正整数指数幂的关系;
(4)整数指数幂在实际问题中的应用。
二、核心素养目标
本章节的核心素养目标主要包括以下三个方面:
1.培养学生的数学抽象能力,使其能从具体实例中提炼出整数指数幂的定义和性质,形成数学概念。
中学2017-2018学年第一学期八年级数学教案整数指数幂
一、教学内容
本节课选自中学2017-2018学年第一学期八年级数学教材,主要涉及第三章“指数与指数幂”的第二节“整数指数幂”。教学内容包括以下三个方面:
1.掌握整数指数幂的定义,了解底数、指数和幂的关系。
2.学会计算正整数指数幂,并能熟练运用到实际问题中。
3.重点难点解析:在讲授过程中,我会特别强调整数指数幂的定义和计算方法这两个重点。对于难点部分,如负整数指数幂的计算,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与整数指数幂相关的实际问题。
第一学期初二年级数学期中复习要点梳理知识点总结

第一学期初二年级数学期中复习要点梳理知识点总结
知识点是学习各门课的关键。
我们要对它格外重视。
因此精品小编为大家整理了这篇第一学期初二年级数学期中复习要点总结以供大家参考。
立方根
一般地,如果一个数_的立方等于a,即_3=a那么这个数_就叫做a 的立方根(或三次方根)。
性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
1、实数比较大小:正数大于零,负数小于零,正数大于一切负数;数轴上的两个点所表示的数,右边的总比左边的大;两个负数,绝对值大的反而小。
2、实数大小比较的几种常用方法
(1)数轴比较:在数轴上表示的两个数,右边的数总比左边的数大。
(2)求差比较:设a、b是实数,
a-b0 则ab
a-b≦0 则a≦b
(3)求商比较法:设a、b是两正实数,ab1 则ab ab1 则ab
(4)绝对值比较法:设a、b是两负实数,则|a||b| 则ab
(5)平方法:设a、b是两负实数,。
a2 b2则ab
精品。
江岸区2017—2018学年度上学期期中考试八年级数学试题(含答案与解析)

2017-2018学年湖北省武汉市江岸区八年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3.00分)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,故A符合题意;B、不是轴对称图形,故B不符合题意;C、不是轴对称图形,故C不符合题意;D、不是轴对称图形,故D不符合题意.故选:A.2.(3.00分)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【解答】解:为△ABC中BC边上的高的是A选项.故选:A.3.(3.00分)已知三角形两边长分别为3和8,则该三角形第三边的长可能是()A.5 B.10 C.11 D.12【解答】解:根据三角形的三边关系,得第三边大于:8﹣3=5,而小于:3+8=11.则此三角形的第三边可能是:10.故选:B.4.(3.00分)下列各组条件中,能够判定△ABC≌△DEF的是()A.∠A=∠D,∠B=∠E,∠C=∠F B.AB=DE,BC=EF,∠A=∠DC.∠B=∠E=90°,BC=EF,AC=DF D.∠A=∠D,AB=DF,∠B=∠E【解答】解:如图:A、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误;B、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误;C、符合直角三角形全等的判定定理HL,即能推出△ABC≌△DEF,故本选项正确;D、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误;故选:C.5.(3.00分)如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是()A.SSS B.ASA C.AAS D.SAS【解答】解:在△ADC和△ABC中,,∴△ADC≌△ABC(SSS),∴∠DAC=∠BAC,即∠QAE=∠PAE.故选:A.6.(3.00分)如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=()A.25°B.45°C.30°D.20°【解答】解:∠C=∠C'=30°,则△ABC中,∠B=180°﹣105°﹣30°=45°.故选:B.7.(3.00分)如图,△ABC中,∠A=50°,BD,CE是∠ABC,∠ACB的平分线,则∠BOC的度数为()A.105°B.115°C.125° D.135°【解答】解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=130°,∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=65°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°,故选:B.8.(3.00分)如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为()A.B.C. D.【解答】解:∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β,∵线段AE,AD的中垂线分别交直线DE于B和C两点,∴BA=BE,DA=DC,∴∠BEA=,∠CDA=,∴∠DAE=180°﹣﹣=,故选:A.9.(3.00分)如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m﹣a与b﹣n的大小关系是()A.m﹣a>b﹣n B.m﹣a<b﹣nC.m﹣a=b﹣n D.m﹣a>b﹣n或m﹣a<b﹣n【解答】解:在CM上截取CG=CA,连接DG.∵CD=CD,∠ACD=∠DCG,AC=CG,∴△ACD≌△GCD,∴AD=DG=n,在△BDG中,BD=m,BG=BC+CG=BC+AC=a+b,∴m+n>a+b,∴m﹣a>b﹣n.故选:A.10.(3.00分)如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是()A.β﹣α=60°B.β+α=210°C.β﹣2α=30°D.β+2α=240°【解答】解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,∵∠OQN=180°﹣30°﹣∠ONQ,∠OPM=∠NPQ=30°+∠OQP,∠OQP=∠AQN=30°+∠ONQ,∴α+β=180°﹣30°﹣∠ONQ+30°+30°+∠ONQ=210°.故选:B.二、填空题(每题3分,共18分)11.(3.00分)已知点P关于x轴的对称点P1的坐标是(1,2),则点P的坐标是(1,﹣2).【解答】解:点P关于x轴的对称点P1的坐标是(1,2),则点P的坐标是(1,﹣2).故答案为:(1,﹣2).12.(3.00分)若正多边形的内角和是外角和的4倍,则正多边形的边数为10.【解答】解:设这个多边形的边数是n,根据题意得,(n﹣2)•180°=4×360°,解得n=10,答:这个多边形的边数为10,故答案为:10.13.(3.00分)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是30.【解答】解:作DE⊥AB于E,由基本尺规作图可知,AD是△ABC的角平分线,∵∠C=90°,DE⊥AB,∴DE=DC=4,∴△ABD的面积=×AB×DE=30,故答案为:30.14.(3.00分)如图,在平面直角坐标系中,△ABC是以C为直角顶点的直角三角形,且AC=BC,点A的坐标为(﹣1,0),点B的坐标为(0,4),则点C的坐标为(﹣,).【解答】解:作CE⊥x轴于E,CF⊥y轴于F,则∠ECF=90°,又∠ACB=90°,∴∠ECA=∠FCB,在△ECA和△FCB中,,∴△ECA≌△FCB,∴CE=CF,AE=BF,设AE=BF=x,则x+1=4﹣x,解得,x=,∴CE=CF=,∴点C的坐标为(﹣,),故答案为:(﹣,).15.(3.00分)如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(3,0),则第17次碰到长方形边上的点的坐标为(1,4).【解答】解:根据题意,如下图示:根据图形观察可知,每碰撞6次回到始点.∵17÷6=2…5,∴第17次碰到长方形边上的点的坐标为(1,4),故答案为(1,4).16.(3.00分)如图,△ABC是直角三角形,记BC=a,分别以直角三角形的三边向外作正方形ABDE,正方形ACFG,正方形BCMN,过点C作BA边上的高CH并延长交正方形ABDE的边DE于K,则四边形BDKH的面积为a2.(用含a的式子表示)【解答】解:∵BC⊥AC,CH⊥BA,∴BC2=BH•BA,即BH•BA=a2,∵四边形ABDE是正方形,∴BD=BA,∴四边形BDKH的面积=BH•BD=BH•BA=a2,故答案为:a2.三、解答题(共8道小题,共72分)17.(8.00分)在△ABC中,∠B=∠A+10°,∠C=30°,求△ABC各内角的度数.【解答】解:∵在△ABC中,∠B=∠A+10°,∠C=30°,∴∠B+∠A=150°,∴解得:,故∠A=70°,∠B=80°,∠C=30°.18.(8.00分)如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:BD=AC.【解答】证明:∵AC⊥AD,BC⊥BD,∴∠ADC=∠BCA=90°,在Rt△ABD和Rt△BAC中,,∴在Rt △ABD ≌Rt △BAC (HL ),∴BD=AC .19.(8.00分)如图,已知点E ,C 在线段BF 上,且BE=CF ,AB ∥DE ,AC ∥DF ,AC 与DE 相交于点O ,求证:S 四边形ABEO =S 四边形OCFD .【解答】证明:∵BE=CF ,∴BE +CE=CF +CE即BC=EF .∵AB ∥DE ,AC ∥DF ,∴∠B=∠DEF ,∠C=∠DFE ,在△ABC 和△DEF 中,,∴△ABC ≌△DEF ,∴S △ABC 与S DEF ,∴S △ABC ﹣S △ECO =S DEF ﹣S △ECO ,∴S 四边形ABEO =S 四边形OCFD .20.(8.00分)如图,点E 在AB 上,△ABC ≌△DEC ,求证:CE 平分∠BED .【解答】证明:∵△ABC ≌△DEC ,∴∠B=∠DEC ,BC=EC ,∴∠B=∠BEC ,∴∠BEC=∠DEC,∴CE平分∠BED.21.(8.00分)(1)如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.(2)如图2,若△ABC与△DEF关于直线l对称,请作出直线l(请保留作图痕迹)(3)如图3,在矩形ABCD中,已知点E,F分别在AD和AB上,请在边BC上作出点G,在边CD作出点H,使得四边形EFGH的周长最小.【解答】解:(1)如图1,△AB′C即为所求;(2)如图2,直线l即为所求;(3)如图3,四边形EFGH即为所求.22.(10.00分)如图,四边形ABCD为正方形(各边相等,各内角为直角),E 是BC边上一点,F是CD上的一点.(1)若△CFE的周长等于正方形ABCD的周长的一半,求证:∠EAF=45°;(2)在(1)的条件下,若DF=2,CF=4,CE=3,求△AEF的面积.【解答】(1)证明:延长CF至G,使DG=BE,连接AG,如图所示:∵四边形ABCD是正方形,∴∠BAD=∠ABE=∠ADF=90°,AB=BC=CD=AD,∴∠ADG=90°,∵△CFE的周长等于正方形ABCD的周长的一半,∴CE+CF+EF=CD+BC,∴DF+BE=EF,∴DF+DG=EF,即GF=EF,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∴∠EAG=90°,在△AEF和△AGF中,,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=×90°=45°;(2)解:∵DF=2,CF=4,CE=3,∴AB=AD=CD=BC=2+4=6,BE=BC﹣CE=3,由(1)得:△AEF的面积=△AGF的面积=△ABE的面积+△ADF的面积=×6×3+×6×2=15.23.(10.00分)如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;(2)如图2,连接BF交AC于G点,若=3,求证:E点为BC中点;(3)当E点在射线CB上,连接BF与直线AC交于G点,若=,则=(直接写出结果)【解答】证明:(1)如图1,∵∠FAD+∠CAE=90°,∠FAD+∠F=90°,∴∠CAE=∠F,在△ADF和△ECA中,,∴△ADF≌△ECA(AAS),∴AD=CD,FD=AC,∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;证明:(2)如图2,过F点作FD⊥AC交AC于D点,∵△ADF≌△ECA,∴FD=AC=BC,在△FDG和△BCG中,,∴△FDG≌△BCG(AAS),∴GD=CG,∵=3,∴=2,∴=,∵AD=CE,AC=BC∴=,∴E点为BC中点;(3)过F作FD⊥AG的延长线交于点D,如图3,∵=,BC=AC,CE=CB+BE,∴=,由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,∴CG=GD,AD=CE,∴=,∴=,∴==,∴=.故答案为:.24.(12.00分)如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足(m﹣2n)2+|n﹣2|=0.(1)求点D的坐标;(2)求∠AKO的度数;(3)如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON ⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.【解答】解:(1)∵(m﹣2n)2+|n﹣2|=0,又∵(m﹣2n)2≥0,|n﹣2|≥0,∴n=2,m=4,∴点D坐标为(4,2).(2)如图1中,作OE⊥BD于E,OF⊥AC于F.∵OA=OB,OD=OC,∠AOB=∠COD=90°,∴∠BOD=∠AOC,∴△BOD≌△AOC,∴EO=OF(全等三角形对应边上的高相等),∴OK平分∠BKC,∴∠OBD=∠OAC,易证∠AKB=∠BOA=90°,∴∠OKE=45°,∴∠AKO=135°.(3)结论:BM=MN+ON.理由:如图2中,过点B作BH∥y轴交MN的延长线于H.∵OQ=OP,OA=OA,∠AOQ=∠BOP=90°,∴△AOQ≌△BOP,∴∠OBP=∠OAQ,∵∠OBA=∠OAB=45°,∴∠ABP=∠BAP,∵NM⊥AQ,BM⊥ON,∴∠ANM+∠BAQ=90°,∠BNO+∠ABP=90°,∴∠ANM=∠BNO=∠HNB,∵∠HBN=∠OBN=45°,BN=BN,∴△BNH≌△BNO,∴HN=NO,∠H=∠BON,∵∠HBM+∠MBO=90°,∠BON+∠MBO=90°,∴∠HBM=∠BON=∠H,∴MH=MB,∴BM=MN+NH=MN+ON.。
2018年八年级上学期数学期中复习专题(教师版)
期中复习专题专题1 等腰直角三角形综合探究1.已知,在△ABC 中,CA =CB =10,O 为AB 的中点,点E ,F 分别在直线AC ,BC 上,且∠EOF =2∠A. (1)若∠A=450.①如图①,连接OC ,当E ,F 分别在线段AC ,BC 上时,求证:△COF≌△BOF; ②如图②,当E ,F 分别在AC 延长线上和CB 延长线上时,求CF-CE 的值;(2)如图③,若∠A=30°,且E ,F 分别在AC 延长线上和线段BC 上,试说明CF 与CE 满足怎样的关系式.【解析】(1)①∵CA =CB ,∠A=45°∴∠A=∠B=45°,∠ACB=90°.∵AO =OB ,∴OC =OA =OB ,∠ACO =∠BC0=45°,CO ⊥AB.∵∠EOF=2∠A=90°,∠COB=90°,∴∠EOF=∠COB ,∴∠EOC=∠BOF ,在△EOC 和△FOB 中,∠ECO=∠B ,CO=OB ,∠EOC=∠FOB,∴△EOC≌△FOB (ASA). ②连接CO ,由①易知∠ACO-∠ABC =45°,∴∠ECO=∠OBF =135°.∵∠COB=∠EOF=90°, ∠COE =∠BOF.在△EOC 和△FOB 中,∠ECO=∠F BO ,CO =OB ,∠EOC=∠FOB, ∴△FOC≌△FOB (ASA).∴EC =BF,∴CF-EC =BC +BF-EC =BC =10.(2)CF-CE =5.连接OC,在CF 上截取CM =CO ,连接EF ,OM.∵∠A=∠B=30°,O 为AB 中点, 易得∠ACB =120°,CO ⊥AB.∴∠ACO=∠BCO=60°,∴∠OCE=120°.∵CM =CO ,∴△COM 为等边三角形,∴∠COM =60°,∴∠OMB=120°=∠OCE.∵∠EOF =2∠A =60°,∴∠COM =∠EOF ,∴∠COE =∠MOF .MF EFEFEOCB A 图① 图② 图③ABCOA BCO在△COE 和△MOF 中,∠COE=∠MOF ,CO=MO,∠OCE=∠OMF,∴△COF≌△MOF.∴CE =MF . ∴CF-CE =CF-MF =CM =CO.在Rt△AOC 中,∠A=30°,AC =10,∴C0=5.∠CF-CE =5.2.(2016秋.黄陂区月考)已知在△ABC 中,AC =BC ,∠CAB=∠CBA =45︒,点M 为直线BC 上任意一点,过点C 作CD ⊥AM 交AB 于点D ,在BC 上取一点N ,使CN =BM .连接DN . (1)如图,M ,N 在线段BC 上,求证:∠AMC=∠DNB;(2)若M ,N 分别在CB ,BC 的延长线上,试画出图形,并说明(1)中的结论是否成立?【解析】(1)如图①,作BG 上BC ,交CD 的延长线于G ,设AM 交CD 才0.∵AM ⊥CD ,BG ⊥BC ,∴∠AOC=∠CBG 90°,∴∠ACO+∠CAO=90°∴∠ACO +∠BCG =90°∴∠CAM =∠BCG ∵AC =BC ,易证△ACM≌△CBG (ASA),∴ CM =BG ,∠AMG.∴CN =BM,∴BN =CM =BG.∵∠DBN ≌△DBG ( SAS), ∴ ∠G =∠BND,∠AMC=△DNB(2)(1)中的结论成立.理由:作BG 上BC,交CD 的延长线于G ,设AM 交CD 的延长线于O ,∵AM ⊥CD ,BG ⊥BC ,∴∠AOC=∠CBG=∠ACM =90°,∴∠ACO +∠CAO=90°,∠ACO +∠BCG =90°,∴∠CAM =∠BCG.又∵AC =BC ,∴△ACM ≌△CBG(AAS),∴CM =BG,∠M=∠G.∵CN=BM ,∴CM =BN=BG .∵BD=BD ,∠DBN =∠DBG ==45°,BN =BG ,∴△DBN≌△DBG( SAS),∴∠G =∠N ,∴∠M =∠N .NMDCBA答图图① 图②ONMDC BAGGABCDMN专题2 等腰三角形与全等1.(2017秋·青山区期中)已知,AB =AC ,D ,A ,E 三点在同一直线上,且∠BDA=∠AEC =∠BAC=120°.(1)如图①,求证:BD =AE ;(2)如图②,AF 平分∠BAC,且AF =AB ,连接FD ,FE ,试判断△FDE 的形状,并说明你的结论.【解析】(1)∵∠BDA =∠BAC=120°,∴∠DBA+∠DAB =∠CAE+∠DAB =60°∴∠DBA =∠CAE.在△BAD 和△ACE 中,∠BDA=∠AEC,∠DBA=∠CAE,BA =AC ,∴△ADB≌△CEA(AAS),∴BD =AE.(2)△DEF 为等边三角形.理由:如图②,连接BF,CF.∵AB =AC =AF ,AF 平分∠BAC,∠BAC =120°,∴△ABF 和△ACF 均为等边三角形,∴BF-AF =AB =AC =CF ,∠BAF=∠CAF=∠ABF=60°.由(1)知△ADB ≌ △CEA(AAS),∴BD =AE,∠DBA=∠CAE .∵∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE.在△BDF 和△AEF 中,FB =FA ,∠DBF=∠FAE ,BD =AE ,∴△DBF ≌△EAF (SAS).∴DF =EF ,∠BFD=∠AFE .∴∠DFE=∠DFA+∠AFE=∠DFA +∠BFD=60°,∴△DEF 为等边三角形.2.(2016秋·武昌区期末)已知,在△ABC 中,AC =BC ,(1)如图①,分别过A ,B 做AM ⊥BC ,BN ⊥AC ,垂足分别为点M ,N ,AM 与BN 相交于点P ,求证:AP =BP ;(2)如图②,分别在AC 的右侧,BC 的左侧做等边△ACE 和等边△BCD,AE 与BD 相交于点F ,连接CF 并延长交AB 于点G ,求证:点G 是AB 的中点;(3)在(2)的条件中,当∠ACB 的大小发生变化时,设直线CD 与直线AE 相交于H 点,当∠ACB图① 图②EFEDCBACB等于 时,使得AH =CD .【解析】(1)∵AM ⊥BC,BN ⊥AC ,∴∠AMC 一∠BNC=90°.∴∠C+∠CAM =90°,∠C+∠CBN =90°.∠CAM=∠CBN.∴CA =CB,∴∠CAB=∠CBA,∴∠PAB =∠PBA,∴PA =PB. (2)∵CA =CB ∴∠CAB=∠CBA.∵△AEC 和△BCD 为等边三角形,∴∠CAE =∠CBD.∴∠FAG =∠FBG.∴AF =BF.在△ACF 和△BCF 中,AF =BF ,AC =BC ,CF =CF ,∴△AFC ≌△BFC(SSS), ∴∠ACF =∠BCF.∵AC =BC ,∴AG =BG ,即点G 为AB 的中点.3.(2017秋·黄陂区期中)如图,在△ABC 和△ADE 中,AB =AD ,AC =AE ,∠BAC=∠DAE,BC 交DE 于点O ,∠BAD=a . (1)求证:∠BOD=a ;(2)若AO 平分∠DAC,求证:AC =AD ;(3)若∠C=30°,OE 交AC 于F ,且△AOF 为等腰三角形,则a .【解析】(1)设AD 交OB 于K.在△ABC 和△ADE 中,AB =AD ,∠BAC=∠DAE ,AC=AE ,∴△ABC ≌△ADE (SAS),∴∠B=∠D.∵∠AKB =∠DKO,∴∠BOD=∠BAD=a.(2)过A 作AM ⊥BC 于M ,作AN ⊥DE 于N,∵△ABC ≌△ADE ,∴S △ABC =S △ADE ,BC =DE ,∴12BC ·AM =12DE ·AN ,∴AM =AN .∴AO 平分∠BOE,图① 图②GPABCDA BCE MNABCDOE∴∠AOB=∠AOE.∴AO 平分∠DAC,∴∠DAO=∠CAO.∴∠DAE -∠DAO=∠BAC -∠CAO,即∠BAO =∠EAO.在△ABO 和△AEO 中,∠BAO=∠EAO,AO=AO,∠AOB=∠AOE,∴△ABO ≌△AEO(ASA),∴AB =AE,∵AB =AD ,AC =AE,∴AC =AD.4.如图,在等腰△ABC 中,AB =AC ,点P 为底边BC 上一动点,连接AP ,在AP 左侧作等腰△APD,使PA =PD ,∠APD=∠BAC,连接BD .(1)如图①,若∠APD=∠BAC=60°,求证:△ABD≌△ACP;(2)如图②,若∠APD -∠BAC=90°,AB =2,当点P 由点C 运动到点B 时: ①∠PBD 的大小是否为定值?若为定值,求出其大小,若发生变化,请说明理由; ②求出点D 运动的路径长度,【解析】(1)如图①,∵∠BAC=60º,AB=AC ,∴△ABC 为等边三角形,同理,得△APD 也是等边三角形,∴AD =AP ,∠DAP =∠BAC=60º,∴∠DAB +∠BAP =∠CAP+∠BAP,∴∠DAB =∠CAP,∴△ABD∽△ACP (SAS).(2)①∠PBD 的大小会发生变化.过A 作AF ⊥BC ,交BC 于F ,则F 是BC 的中点, i )当点P 在FC 上运动时,∠PBD=45º,如图②,理由:过点D 作DG ⊥BC 于G ,∵∠APF+∠DPG =90º,∠GDP+∠DPG =90º,∴∠APF=∠GDP.∵∠AFP=∠DGP =90º,AP =PD, ∴△AFP≌△PGD (AAS),∴AF=PG ,PF =GD.∵AF =BF,∴BF=PG ∴BF-FG=PG-FG,即BG=PF . ∴BG =GD ,∴△BGD 是等腰直角三角形,∴∠PBD=45º; ii )当点P 与中点F 重合时,∠PBD=O º;iii )当点P 在BF 上运动时,∠PBD=135º,理由:如图③,过点D 作DG 上BC,交CB 的延长线于点G ,易证:△APF ≌△PDG ,∴AF =PG,PF =DG .又∵AF =BF ,∴PG =BF ,∵BG =PF =DG .∴△BDG 是等腰直角三角形,∴∠GBD=45º,∴∠PBD=135º.图① 图②D CAPP BABCD②如图:D,点D运动的路径是从点D到点E,当点P在点C时,设AD交BC于F,∵△APD 与△ABC都是等腰直角三角形,∴AD⊥BC.当点P运动到点B时,由∠APD=90º得∠ABE=90º,∴∠ABC=45º,∴∠CBD=45º,∠EBD=180º,∴E,B,D在同一直线上.∵△ADE是等腰直角三角形.AB=2,∴ED=2AB=4,∴点D运动的路径长庋为4.专题3 等边三角形综合探究1.(2017秋·青山区期末)已知△ABC 是等边三角形,过点C 作CD ‖AB ,且CD=AB ,连接BD 交AC 于点O .(1)如图①,求证:AC 垂直平分BD ;(2)点M 在BC 的延长线上,点N 在AC 上,且ND=NM ,连接BN , ①如图②,点N 在线段CO 上,求∠NMD 的度数;②如图③,点N 在线段AO 上,求证:NA=MC .【解析】(1)△ABC 是等边三角形,∠ABC=∠ACB =∠CAB=60º.AB∥CD,∠ACD=∠A=60º=∠ACB,又CD=AB=BC ,∵BO=DO,CO ⊥BD ,∴AC 垂直平分BD.(2)①如图②,由①知AC 垂直平分BD , NB=ND,∠CBD =12∠ABC=30º.∴∠1=∠2, ∴∠BND=180º-2∠2.∵ND=NM ,∴NB=NM ,∴∠3=∠4,∠BNM=180º -2∠4,∴∠DNM=360°-(180°-2∠2)一(180°-2∠4)=2(∠2+∠4)=60°,又∵ND=NM ,∴△NMD 为等边三角形,∴∠NMD=60°.②连接AD .如图,由题意知,△ACD 是等边三角形,∴∠ADC=60°,AD=CD .与①同理可证∠1=∠2,∠3=∠NBM,∠BND=180°-2∠2, ∠BNM=180°-2∠NBM,∴∠MND=∠BND -∠BNM=2(∠NBM -∠2)=60°.3214321NMMNODCBA ODCBA ODCB A图① 图② 图③图① 图② 图③AB CDOA BCDOA BCDONMMN∵ND=NM ,∴△MND 是等边三角形.∴DN=DM ,∠NDM 一60°,∠ADC 一∠NDM ,∴∠NDA =∠MDC.在△AND 与∠CMD 中,DN=DM ,∠NDA=∠MDC ,AD=DC,∴△AND ≌△CMD(SAS),∴NA=MC.2.(2017秋·东湖高新区期末模拟)如图,在△ABC 中,∠ACB =900,∠ABC =300,△CDE 是等边三角形,点D 在边AB 上.(1)如图①,当点E 在边BC 上时,求证:DE =EB ;(2)如图②,当点E 在△ABC 内部时,猜想ED 和EB 的数量关系,并加以证明;(3)如图③,当点E 在△ABC 外部时,EH 上。
2017-2018学年第一学期期中考试八年级数学试题及答案
2017-2018学年第一学期八年级 数学(上) 参考答案及评分标准一、选择题(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)二、填空题(本大题共4个小题,每小题3分,共12分,把答案写在题中横线上)17.> 18.3 19.2 20.8三、解答题(本大题共6个小题,共56分.解答应写出相应的文字说明或解题步骤)21.(1)解:原式=yx 2- ……………(4分) 21.(2)解:原式=2)1()1()111(a a a a a a +-∙++-+ ……………(2分) =2)1()1(11a a a +-∙+- =21-a ……………(4分) 21.(3)解:据题意得:x ﹣2=22=4,∴ x =6, ……………(1分)2y ﹣11=(﹣3)3=﹣27,∴ y =﹣8, ……………(2分)则x 2+y 2=62+(﹣8)2=36+64=100, ………………(3分)∴ x 2+y 2的平方根为±10. …………………(4分)22.解:(1)二, …………………(2分)a-24; …………………(4分) (2)由题意得,aa a -++222=2, 即a-24=2, …………………(5分) 解得:a =0, …………………(7分)经检验,a =0是原方程的解,∴ 当a =0时,原代数式的值等于2. …………………(8分)23.如图1,作出∠B =∠β得3分;作出边BC =a 得2分;作出边AC =b 和A ′C =b 共得3分,少一种情况扣1分.24.(1)命题一,命题二; …………………(4分) (2)命题一: 条件是①AB=AC ,②AD=AE ,③∠1=∠2,结论是④BD=CE .证明:∵∠1=∠2∴∠BAD=∠CAE ,又AB=AC ,AD=AE ,∴△ABD ≌△ACE (SAS ) …………………(8分)∴BD=CE .…………………(9分)或:命题二:条件是①AB=AC ,②AD=AE ,④BD=CE ,结论是③∠1=∠2.证明:∵AB=AC ,AD=AE ,BD=CE ,∴△ABD ≌△ACE (SSS ),…………………(8分)∴∠BAD=∠CAE ,∴∠1=∠2.…………………(9分)25.解:(1)设第一次购进衬衫x 件. 根据题意得:48000217600=-xx .…………………(4分) 解得:x =200.…………………(6分)经检验:x =200是原方程的解.答:该服装店第一次购进衬衫一共200件.…………………(7分)(2)盈利;…………………(8分)盈利=58×(200+400)﹣(17600+8000)=9200(元)…………………(9分) 答:该服装店这笔生意一共盈利9200元.26.(1)△ABE ≌△ACE ,△ADF ≌△CDB ………………(2分)(2)CEAF =2 …………………(3分) 证明:如图2,∵AE 平分∠DAC ,图2 A′ β b图1 A C B ba∴∠CAE =∠BAE ,∵AE ⊥CE ,∴∠AEC =∠AEB =90°,在△AEC 和△AEB 中,⎪⎩⎪⎨⎧∠=∠=∠=∠BAECAE AE AE AEBAEC∴△AEC ≌△AEB (ASA ),∴CE =BE ,即CB =2CE ,…………………(5分)∵∠ADC =90°,∴∠ADF=∠CDB =90°,∴∠B +∠DCB =90°,∵∠B +∠DAF =90°,∴∠DAF =∠DCB ,在△ADF 和△CDB 中,⎪⎩⎪⎨⎧∠=∠=∠︒=∠=∠DCBDAF CD AD CDB ADF 90,∴△ADF ≌△CDB (ASA ),∴AF =CB =2CE ,即CE AF=2. …………………(7分)(3)等于; ……………(8分)辅助线如图3, …………………(9分)作法:过点P 作PG ⊥DC 交CE 的延长线于点G ,交DC 于点B . ………………(10分) 或:过点P 作PG ∥AD 交CE 的延长线于点G ,交DC 于点B . 或:延长CE 到点G ,使CE =GE ,连接PG 交DC 于点B . (说明:其它作法正确均给分)D CE 图3 G。
2017-2018学年山东省德州五中八年级(上)期中数学试卷(解析版)
2017-2018 学年山东省德州五中八年级(上)期中数学试卷一、选择题(每题4 分,共48 分)1.(4 分)下列图形中不是轴对称图形的是()A.B.C.D.2.(4分)三角形两边的长分别是4 和10,则此三角形第三边的长可能是()A.5 B.6 C.11 D.163.(4 分)等腰三角形的两边长分别为4cm 和8cm,则它的周长为()A.16cm B.17cm C.20cm D.16cm 或20cm4.(4 分)如图:DE 是△ABC 中AC 边的垂直平分线,若BC=8 厘米,AB=10 厘米,则△EBC 的周长为()厘米.A.16 B.18 C.26 D.285.(4 分)一个多边形的内角和是900°,则这个多边形的边数是()A.4 B.5 C.6 D.76.(4 分)已知:如图,AD 是△ABC 的角平分线,且AB:AC=3:2,则△ABD 与△ACD 的面积之比为()A.3:2 B.9:4 C.2:3 D.4:97.(4 分)△ABC 中,∠ABC 与∠ACB 的平分线相交于I,且∠BIC=130°,则∠A 的度数是()A.40° B.50° C.65°D.80°8.(4 分)如图∠1+∠2+∠3+∠4+∠5+∠6+∠7=()A.540°B.550° C.650° D.180°9.(4 分)如图,在△ABC 和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是()A.BC=B′C′ B.∠A=∠A′ C.AC=A′C′D.∠C=∠C′10.(4 分)如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3 等于()A.90° B.120° C.150°D.180°11.(4 分)如图,等边△ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是AC 边上一点,若A E=2,当EF+CF 取得最小值时,则∠ECF 的度数为()A.15° B.22.5° C.30° D.45°12.(4 分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON 上,点B1、B2、B3…在射线OM 上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7 的边长为()A.6 B.12 C.32 D.64二、填空题(每题4 分,共24 分)13.(4 分)从长度为2cm,3cm,4cm,5cm 四条线段中任意取三条组成三角形,则组成三角形的个数为.14.(4 分)如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入号球袋.15.(4 分)如图,点P 是∠AOB 外一点,点M、N 分别是∠AOB 两边上的点,点P 关于OA 的对称点Q 恰好落在线段MN 上,点P 关于OB 的对称点R 落在线段MN 的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR 的长为.16.(4 分)点P(3a+6,3﹣a)关于x 轴的对称点在第四象限内,则a 的取值范围为.17.(4 分)在△ABC 中AB=AC,中线BD 将△ABC 的周长分为12cm 和15cm,则三角形底边长.18.(4 分)如图,C 为线段AE 上一动点(不与点A、E 重合),在AE 同侧分别作正△ABC 和正△CDE,AD 与BE 交于点O,AD 与BC 交于点P,BE 与CD 交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有.(把你认为正确的序号都填上)三、解答题:(共78 分)19.(8 分)已知一个多边形的内角和与外角和的差为1440°,求这个多边形的边数.20.(10 分)如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)(1)画出格点△ABC 关于直线DE 对称的对称的△A1B1C1;(2)在直线DE 上画出点P,使△PAC 周长最小.21.(10 分)如图,已知AB∥DE,AB=DE,BE=CF,求证:AC∥DF.22.(12 分)如图,O 为码头,A、B 两个灯塔与码头O 的距离相等,OA,OB 为海岸线,一轮船P 离开码头,计划沿∠AOB 的平分线航行.(1)用尺规作出轮船的预定航线OC;(2)在航行途中,轮船P 始终保持与灯塔A、B 的距离相等,试问轮船航行时是否偏离了预定航线?请说明理由.23.(12 分)如图,已知△ABC 中,AB>AC,BE、CF 都是△ABC 的高,P 是BE 上一点且BP=AC,Q 是CF 延长线上一点且CQ=AB,连接AP、AQ、QP,判断△APQ 的形状.24.(12 分)在△ABC 中,∠ACB=90°,AC=BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN 于E.(1)当直线MN 绕点C 旋转到图1 的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN 绕点C 旋转到图2 的位置时,直接写出DE、AD、BE 的关系为:(3)当直线MN 绕点C 旋转到图3 的位置时,试问DE、AD、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.25.(14 分)如图,已知△ABC 中,AB=AC=10cm,BC=8cm,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1s 后,△BPD 与△CQP 是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次在△ABC 的哪条边上相遇?2017-2018 学年山东省德州五中八年级(上)期中数学试卷参考答案与试题解析一、选择题(每题4 分,共48 分)1.(4 分)下列图形中不是轴对称图形的是()A.B.C.D.【解答】解:根据轴对称图形的概念可知:A,B,D 是轴对称图形,C 不是轴对称图形,故选:C.2.(4分)三角形两边的长分别是4 和10,则此三角形第三边的长可能是()A.5 B.6 C.11 D.16【解答】解:设此三角形第三边的长为a,则10﹣4<a<10+4,即6<a<14.故选:C.3.(4 分)等腰三角形的两边长分别为4cm 和8cm,则它的周长为()A.16cm B.17cm C.20cm D.16cm 或20cm【解答】解:等腰三角形的两边长分别为4cm 和8cm,当腰长是4cm 时,则三角形的三边是4cm,4cm,8cm,4cm+4cm=8cm 不满足三角形的三边关系;当腰长是8cm 时,三角形的三边是8cm,8cm,4cm,三角形的周长是20cm.故选:C.4.(4 分)如图:DE 是△ABC 中AC 边的垂直平分线,若BC=8 厘米,AB=10 厘米,则△EBC 的周长为()厘米.A.16 B.18 C.26 D.28【解答】解:∵DE 是△ABC 中AC 边的垂直平分线,∴AE=CE,∴AE+BE=CE+BE=10,∴△EBC 的周长=BC+BE+CE=10 厘米+8 厘米=18 厘米,故选:B.5.(4 分)一个多边形的内角和是900°,则这个多边形的边数是()A.4 B.5 C.6 D.7【解答】解:设该多边形的边数为n则:(n﹣2)•180°=900°,解得:n=7.故选:D.6.(4 分)已知:如图,AD 是△ABC 的角平分线,且AB:AC=3:2,则△ABD 与△ACD 的面积之比为()A.3:2 B.9:4 C.2:3 D.4:9【解答】解:过点D 作DE⊥AB 于E,DF⊥AC 于F.∵AD 为∠BAC 的平分线,∴DE=DF,又AB:AC=3:2,∴S△ABD:S△ACD=(AB•DE):(AC•DF)=AB:AC=3:2.故选:A.7.(4 分)△ABC 中,∠ABC 与∠ACB 的平分线相交于I,且∠BIC=130°,则∠A 的度数是()A.40° B.50° C.65°D.80°【解答】解:∵∠BIC=130°,∴∠EBC+∠FCB=180°﹣∠BIC=180°﹣130°=50°,∵BE、CF 是△ABC 的角平分线,∴∠ABC+∠ACB=2(∠EBC+∠FCB)=2×50°=100°,∴∠A=180°﹣100°=80°.故选:D.8.(4 分)如图∠1+∠2+∠3+∠4+∠5+∠6+∠7=()A.540°B.550° C.650° D.180°【解答】解:如图,∠6+∠7=∠8+∠9,由五边形内角和定理得:∠1+∠2+∠3+∠8+∠9+∠4+∠5=540°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.故选:A.9.(4 分)如图,在△ABC 和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是()A.BC=B′C′ B.∠A=∠A′C.AC=A′C′ D.∠C=∠C′【解答】解:A、若添加BC=BˊCˊ,可利用SAS 进行全等的判定,故本选项错误;B、若添加∠A=∠A',可利用ASA 进行全等的判定,故本选项错误;C、若添加AC=A'C',不能进行全等的判定,故本选项正确;D、若添加∠C=∠Cˊ,可利用AAS 进行全等的判定,故本选项错误;故选:C.10.(4 分)如图,是三个等边三角形随意摆放的图形,则∠1+∠2+ ∠3 等于()A.90° B.120° C.150°D.180°【解答】解:∵图中是三个等边三角形,∴∠1=180°﹣60°﹣∠ABC=120°﹣∠ABC,∠2=180°﹣60°﹣∠ACB=120°﹣∠ACB,∠3=180°﹣60°﹣∠BAC=120°﹣∠BAC,∵∠ABC+∠ACB+∠BAC=180°,∴∠1+∠2+∠3=360°﹣180°=180°,故选:D.11.(4 分)如图,等边△ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是AC 边上一点,若AE=2,当EF+CF 取得最小值时,则∠ECF 的度数为()A.15° B.22.5° C.30° D.45°【解答】解:过E 作EM∥BC,交AD 于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD 是BC 边上的中线,△ABC 是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E 和M 关于AD 对称,连接CM 交AD 于F,连接EF,则此时EF+CF 的值最小,∵△ABC 是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF= ∠ACB=30°,故选:C.12.(4 分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON 上,点B1、B2、B3…在射线OM 上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1 ,则△A6B6A7 的边长为()A.6 B.12 C.32 D.64【解答】解:∵△A1B1A2 是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,∵△A2B2A3 、△A3B3A4 是等边三角形,∴∠11=∠10=60°,∠13=60°,∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,以此类推:A6B6=32B1A2=32.故选:C.二、填空题(每题4 分,共24 分)13.(4 分)从长度为2cm,3cm,4cm,5cm 四条线段中任意取三条组成三角形,则组成三角形的个数为 3 个.【解答】解:任意三条线段组合有:2cm,3cm,4cm;2cm,3cm,5cm;2cm,4cm,5cm;3cm,4cm,5cm.根据三角形的三边关系,可知2cm,3cm,5cm 不能组成三角形.故答案为:3 个14.(4 分)如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入 1 号球袋.【解答】解:如图,该球最后将落入1 号球袋.15.(4 分)如图,点P 是∠AOB 外一点,点M、N 分别是∠AOB 两边上的点,点P 关于OA 的对称点Q 恰好落在线段MN 上,点P 关于OB 的对称点R 落在线段MN 的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR 的长为4.5cm .【解答】解:由轴对称的性质可知:PM=MQ=2.5cm,PN=RN=3cm,QN=MN﹣QM=4﹣2.5=1.5cm,QR=QN+NR=1.5+3=4.5cm.故答案为:4.5cm.16.(4 分)点P(3a+6,3﹣a)关于x 轴的对称点在第四象限内,则a 的取值范围为﹣2<a<3 .【解答】解:∵P 关于x 轴的对称点在第四象限内,∴点P 位于第一象限.∴3a+6>0①,3﹣a>0②.解不等式①得:a>﹣2,解不等式②得:a<3,所以a 的取值范围是:﹣2<a<3.故答案为:﹣2<a<3.17.(4 分)在△ABC 中AB=AC,中线BD 将△ABC 的周长分为12cm 和15cm,则三角形底边长 11cm 或7cm .【解答】解:如图,∵DB 为△ABC 的中线,∴AD=CD.设AD=CD=x,则AB=2x,当x+2x=12,解得x=4,BC+x=15,解得BC=11,此时△ABC 的底边长为11cm;当x+2x=15,BC+x=12,解得x=5,BC=7,此时△ABC 的底边长为7cm.故答案为11cm 或7cm.18.(4 分)如图,C 为线段AE 上一动点(不与点A、E 重合),在AE 同侧分别作正△ABC 和正△CDE,AD 与BE 交于点O,AD 与BC 交于点P,BE 与CD 交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有①②③⑤.(把你认为正确的序号都填上)【解答】解:①∵正△ABC 和正△CDE,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ADC≌△BEC(SAS),∴AD=BE,∠ADC=∠BEC,(故①正确);②又∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,∴∠QPC=∠BCA,∴PQ∥AE,(故②正确);③∵△CDP≌△CEQ,∴DP=QE,∵△ADC≌△BEC∴AD=BE,∴AD﹣DP=BE﹣QE,∴AP=BQ,(故③正确);④∵DE>QE,且DP=QE,∴DE>DP,(故④错误);⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故⑤正确).∴正确的有:①②③⑤.故答案为:①②③⑤.三、解答题:(共78 分)19.(8 分)已知一个多边形的内角和与外角和的差为1440°,求这个多边形的边数.【解答】解:设此多边形的边数为n,则:(n﹣2)•180=1440+360,解得:n=12.答:这个多边形的边数为12.20.(10 分)如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)(1)画出格点△ABC 关于直线DE 对称的对称的△A1B1C1;(2)在直线DE 上画出点P,使△PAC 周长最小.【解答】解:(1)如图所示:从△ABC 各顶点向DE 引垂线并延长相同的长度,找到对应点,顺次连接即可得△A1B1C1;(2)如图所示:利用轴对称图形的性质可得点C 关于直线DE 的对称点C1,连接C1A,交直线DE 于点P 点,P 即为所求,此时△PAC 的周长最小.21.(10 分)如图,已知AB∥DE,AB=DE,BE=CF,求证:AC∥DF.【解答】证明:∵AB∥DE,∴∠ABC=∠DEF,又∵BE=CF,∴BE+EC=CF+EC,即:BC=EF,在△ABC 和△DEF 中∴△ABC≌△DEF(SAS),∴∠ACB=∠DFE,∴AC∥DF.22.(12 分)如图,O 为码头,A、B 两个灯塔与码头O 的距离相等,OA,OB 为海岸线,一轮船P 离开码头,计划沿∠AOB 的平分线航行.(1)用尺规作出轮船的预定航线OC;(2)在航行途中,轮船P 始终保持与灯塔A、B 的距离相等,试问轮船航行时是否偏离了预定航线?请说明理由.【解答】解:(1)如图所示:OC 即为所求.(2)没有偏离预定航行,理由如下:在△AOP 与△BOP 中,,∴△AOP≌△BOP(SSS).∴∠AOC=∠BOC,即点C 在∠AOB 的平分线上.23.(12 分)如图,已知△ABC 中,AB>AC,BE、CF 都是△ABC 的高,P 是BE 上一点且BP=AC,Q 是CF 延长线上一点且CQ=AB,连接AP、AQ、QP,判断△APQ 的形状.【解答】解:△APQ 是等腰直角三角形.∵BE、CF 都是△ABC 的高,∴∠1+∠BAE=90°,∠2+∠CAF=90°(同角(可等角)的余角相等)∴∠1=∠2 又∵AC=BP,CQ=AB,在△ACQ 和△PBA 中,∴△ACQ≌△PBA∴AQ=AP,∴∠CAQ=∠BPA=∠3+90°∴∠QAP=∠CAQ﹣∠3=90°∴AQ⊥AP∴△APQ 是等腰直角三角形24.(12 分)在△ABC 中,∠ACB=90°,AC=BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN 于E.(1)当直线MN 绕点C 旋转到图1 的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN 绕点C 旋转到图2 的位置时,直接写出DE、AD、BE 的关系为:DE=AD﹣BE(3)当直线MN 绕点C 旋转到图3 的位置时,试问DE、AD、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.【解答】(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,而AD⊥MN 于D,BE⊥MN 于E,∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE.在△ADC 和△CEB 中,,∴△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=DC+CE=BE+AD;(2)DE=AD﹣BE,在△ADC 和△CEB 中,,∴△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=CE﹣CD=AD﹣BE;故答案为:DE=AD﹣BE(3)DE=BE﹣AD.易证得△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=CD﹣CE=BE﹣AD.25.(14 分)如图,已知△ABC 中,AB=AC=10cm,BC=8cm,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1s 后,△BPD 与△CQP 是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次在△ABC 的哪条边上相遇?【解答】解:(1)①∵t=1s,∴BP=CQ=3×1=3cm,∵AB=10cm,点D 为AB 的中点,∴BD=5cm.又∵PC=BC﹣BP,BC=8cm,∴PC=8﹣3=5cm,∴PC=BD.又∵AB=AC,∴∠B=∠C,在△BPD 和△CQP 中,∴△BPD≌△CQP(SAS).②∵v P≠v Q,∴BP≠CQ,若△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,∴点P,点Q 运动的时间s,∴cm/s;(2)设经过x 秒后点P 与点Q 第一次相遇,由题意,得x=3x+2×10,解得.∴点P 共运动了×3=80cm.△ABC 周长为:10+10+8=28cm,若是运动了三圈即为:28×3=84cm,∵84﹣80=4cm<AB 的长度,∴点P、点Q 在AB 边上相遇,∴经过s 点P 与点Q 第一次在边AB 上相遇.。
【中小学资料】山东省济宁市邹城市2017-2018学年八年级数学上学期期中复习试题(12)(无答案) 新人教版
八年级数学试卷(12)一、选择题 (每小题3分,共30分)1.下列三条线段,能组成三角形的是( )A 、3,3,3B 、3,3,6C 、3,2,5D 、3,2,62.五边形的内角和是( )A 、180° B、360° C、540° D 、600°3.从n 边形的一个顶点作对角线,把这个n 边形分成三角形的个数是( )A 、n 个B 、(n -1)个C 、(n -2)个D 、(n -3)个4.已知△ABC 中,∠A、∠B、∠C 三个角的比例如下,其中能说明△ABC 是直角三角形的是( )A 、2:3:4B 、1:2:3C 、4:3:5D 、1:2:25.下列图形中有稳定性的是( )A 、正方形B 、直角三角形C 、长方形D 、平行四边形6.能把一个三角形分成两个面积相等的三角形是三角形的( )A 、中线B 、高线C 、角平分线D 、以上都不对7.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A 、锐角三角形B 、钝角三角形C 、直角三角形D 、不能确定8.已知△ABC 中,∠A=80°,∠B、∠C 的平分线的夹角是( )A 、130° B、60° C 、130°或50° D 、60°或120°9.将一副直角三角板如图放置,使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重合,则∠1的度数为( )A 、45° B、60° C、75° D、85°10.用三种不同的正多边形能够铺满地面的是( )A 、正三角形、正方形、正五边形B 、正三角形、正方形、正六边形C 、正三角形、正方形、正七边形D 、正三角形、正方形、正八边形二、填空题 (每小题3分,共24分)11.三角形的内角和是 ,n 边形的外角和是 .12.已知三角形三边分别为1,x ,5,则整数x = .13.一个三角形的周长为81cm ,三边长的比为2︰3︰4,则最长边比最短边长 .14.若三角形三个内角度数的比为2:3︰4,则相应的外角比是 .15.若等腰三角形的两边长分别为3cm 和8cm ,则它的周长是 .16.如图,在Rt △ABC 中,∠ACB=90°,∠A=50°,将其折叠,使点A 落在边CB 上的A' 处,折痕为CD ,则∠A ' DB = . 第9题图第11题图A /第16题图D C BA 17.已知一个多边形的所有内角与它的一个外角之和是2400°,那么这个多边形的边数是 ,这个外角的度数是 .18.用黑白两种颜色的正六边形地板砖按图所示的规律镶嵌成若干个图案:⑴第四个图案中有白色地板砖 块;⑵第n 个图案中有白色地板砖 块.三、解答题 (满分66分)19.(6分)一个多边形的内角和是外角和的2倍,它是几边形?20.(8分)如下图,经测量,B 处在A 处的南偏西57°的方向,C 处在A 处的南偏东15°方向,C 处在B 处的北偏东82°方向,求∠C 的度数.21.(10分)如下图,在直角三角形ABC 中,∠ACB=90°,CD 是AB 边上的高,AB=13cm ,BC=12cm ,AC=5cm ,求(1)△ABC 的面积;(2)CD 的长.22.(10分)如图所示,在△ABC 中,AB=AC ,AC 边上的中线把三角形的周长分为24 cm 和30 cm 的两部分,求三角形各边的长.A BDE23.(10分)如图所示,∠ACD 是△ABC 的外角,∠A=40°,BE 平分∠ABC,CE 平分∠ACD,且BE 、CE 交于点E ,求∠E 的度数.24.(10分)多边形的内角和与某一个外角的度数总和为1350°.(1)求多边形的边数;(2)此多边形必有一个内角为多少度?25.若a ,b ,c 分别为三角形的三边,化简:|a ﹣b ﹣c|+|b ﹣c ﹣a|+|c ﹣a+b|.26.(12分)如下图,四边形ABCD 中,AE 平分∠BAD,DE 平分∠ADC.(1)如果∠B+∠C=120°,则∠AED 的度数= .(直接写出结果)(2)根据(1)的结论,猜想∠B+∠C 与∠AED 之间的关系,并说明理由.27.如图,在△ABC 中,∠B=30°,∠C=50°,AE 是∠BAC 的平分线,AD 是高.(1)求∠BAE 的度数;(2)求∠EAD 的度数;(3)△ABC 中,若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE 与α,βE间的等量关系,并说明理由.28.如图,已知△ABC的周长为24cm,AD是BC边上的中线,AD=AB,AD=5cm,△ABD的周长是18cm,求AC的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017—2018学年第一学期八年级数学期中复习要点本次考试范围:苏科版八上第一章《全等三角形》、第二章《轴对称》、第三章《勾股定理》、第四章《实数》和八下第十二章《二次根式》,期中第一章《全等三角形》是上学期学习第二章 轴对称1、 轴对称图形相对一个图形的对称而言;轴对称是关于直线对称的两个图形而言。
2、 轴对称的性质:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连的线段的垂直平分线; 3、线段的垂直平分线:①性质定理:线段垂直平分线上的点到线段两个端点的距离相等。
②判定定理:到线段两个端点距离相等的点在这条线段的垂直平分线上。
拓展:三角形三条边的垂直平分线的交点到三个顶点....的距离相等 4、角的角平分线:①性质定理:角平分线上的点到角两边的距离相等。
②判定定理:到角两个边距离相等的点在这个角的角平分线上。
拓展:三角形三个角的角平分线的交点到三条边...的距离相等。
5、等腰三角形: ①性质定理:⑴等腰三角形的两个底角相等;(等边对等角)⑵等腰三角形的顶角平分线、底边上的中线、底边上的高线互相重合。
(三线合一) ②判断定理:一个三角形的两个相等的角所对的边也相等。
(等角对等边) 6、等边三角形: ①性质定理:⑴等边三角形的三条边都相等;⑵等边三角形的三个内角都相等,都等于60°;拓展:等边三角形每条边都能运用三线合一....这性质。
②判断定理:⑴三条边都相等的三角形是等边三角形;⑵三个角都相等的三角形是等边三角形;有两个角是60°的三角形是等边三角形; ⑶有一个角是60°的等腰三角形是等边三角形。
7、直角三角形推论:⑴直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半。
⑵直角三角形中,斜边上的中线等于斜边的一半。
例题评析123例1:如图,在△ABC中,DE是AC的垂直平分线.(1)若AC=6,△ABD的周长是13,则△ABC的周长是_______;(2)若△ABC的周长是30,△ABD的周长是25,则AC=_______.例2:如图,在△ABC中,边AB、AC的垂直平分线分别交BC于点E、点D.(1)若BC=8,则△ADE的周长是_______;(2) 若∠BAC=110°,那么∠EAD=______(3) 若∠EAD=100°,那么∠BAC=______4、角的对称轴有条,是5、角平分线上的点到的距离相等∵又∵∴6、角的内部到距离相等的点在角的平分线上∵,又∵∴例3:如图,在△ABC中,∠C=90°,AD平分∠BA C.(1)若CD=5,则点D到AB的距离为.(2) 若BD:DC=3:2,点D到AB的距离为6,则BC的长是.例4:如图,OP平分∠AOB,P A⊥OA,PB⊥OB,垂足分别为A、B.下列结论中,不一定成立的是( ) A.P A=PB B.PO平分∠APBC.OA=OB D.AB垂直平分OP补充:①三角形的三条边的垂直平分线的交点到的距离相等②三角形的三条角平分线的交点到的距离相等。
FEPBAC2.如图,求作点P,使点P同时满足:①P A=PB;②到直线m,n的距离相等.7、等边对等角∵∴8、等角对等边∵∴9、等腰三角形、、重合(三线合一)(有条对称轴)∵∵∵又∵又∵又∵∴∴∴版权所有@蔡老师数学 第4页(共38页)例5:(1)等腰三角形的一边长为5,另一边长为11,则该等腰三角形的周长为(2)等腰三角形的两边长分别为4、5.则该等腰三角形的周长为 (3)已知等腰三角形的一个外角为100°,则这个等腰三角形的顶角为__________. (4)等腰△ABC 中,若∠A =30°,则∠B = . 例6:(1)如图①,在Rt △ABC 中,若AB =AC ,AD =AE ,∠BAD =40°,则∠EDC =_______.(2)如图②,∠ACB =90°,E 、F 为AB 上的点,AE =AC ,BC =BF ,则∠ECF =___ __. (3)如图③, AB =AC =DC ,且BD =AD ,则∠B =___ __.例7:如图,∠ABC 、∠ACB 的平分线相交于点F ,过点F 作DE ∥BC , 交AB 于点D ,交AC 于点E .试说明BD +EC =DE .例8:如图,已知AB =AC ,AD =AE .求证:BD =CE .例9:在△ABC 中,AB =AC ,点D 是BC 的中点,点E 在AD 上. (1)求证:BE =CE ;(2)如图2,若BE 的延长线交AC 于点F ,且BF ⊥AC ,垂足为F ,∠BAC =45°,原题设其它条件不变.求证:△AEF ≌△BCF .10、(1)等边三角形的性质:等边三角形的三条边 ,三个角都是 ,每条边上都有三线合一,有 条对称轴③(2)等边三角形的3个判定方法:三条边都的三角形是等边三角形三个角都的三角形是等边三角形有一个角是的三角形是等边三角形例10:(1)如图①,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE=____.(2)如图②,正方形ABCD,△EAD为等边三角形,则∠EBC=_______.(3)如图③,已知等边△ABC,AC=AD,且AC⊥AD,垂足为A,则∠BEC=_______.①②③例11:如图,C为线段AE上一动点(点C不与点A、E重合),在AE的同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.下列五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°,其中恒成立的有__________(填序号).例12:如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE∥B C.11、直角三角形斜边上的中线等于∵又∵∴12、用等积法求直角三角形斜边上的高SΔABC==13、直角三角形中,30°的角所对的直角边等于∵又∵∴版权所有@蔡老师数学第5页(共38页)例13:(1)在Rt△ABC中,∠C=90°,CD是斜边AB的中线,且CD=4 cm,则AB=_______.(2)在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则AC=_______.(3)在Rt△ABC中,∠C=90°,AC=8,BC=6,则AB边上的高CD=.例14:如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.例15:如图,已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF,求证:(1)△DEF为等腰直角三角形.(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论。
相关练习:1.如图,在△ABC中,BC=8 cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,求△PDE的周长.2.如图,在边长为2等边△ABC中,AD是BC边上的中线,E、F是AD的三等分点,则图中阴影部分的面积是__________cm2.3.如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF//BC交AC于点E.试说明(1) △DCF 为直角三角形;(2)DE=EF.4.如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试找出图中除△ABC外的等腰三角形,并说明你的理由.5.如图,AD是△ABC的角平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F.求证:EC平分∠DEF.6.如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=D C.BE与DF相等吗?请说明理由.7.如图,C为线段AB上任意一点(不与A、B重合),在AB的同侧分别作△ACD和△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接P C.试说明:(1) △ACE≌△DCB;(2) PC平分∠AP B.8.如图,等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.(1)求BE的长;(2)试说明BD=ED。
9.画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.(1)尺规作图(不写作法,保留作图痕迹):作∠AOB的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连接OE、CF、DF.(2)在所画图中,①线段OE与CD之间有怎样的数量关系,并说明理由.②求证:△CDF为等腰直角三角形10.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=C A.(1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证:ME=B D.11.如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.(1)求证:△ABQ≌△CAP;(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.12.如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CD,BD=CF.(1)试说明DE=DF.(2)若∠A=40°,求∠EDF的度数.13.如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 _______.14.如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N,连接MN交OP于点D.则①PM=PN;②MO=NO;③OP⊥MN;④MD=N D.其中正确的有15.如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.(1)当∠DQC=30°时,求AP的长.(2)作PE⊥AC于E,求证:DE=AE+C D.16.如图,在△ABC中,已知BA=BC,∠B=120°,AB的垂直平分线DE交AC于点D.(1)求∠A的度数;(2)若AC=6cm,求AD的长度.17.若直角三角形斜边上的高和中线分别为10 cm、12 cm,则它的面积为__________cm2.18.如图,某市把一块形状为直角三角形废地开辟为生物园,∠ACB=90o.AC=80 m.BC=60 m.(1)若入口E在边AB上,且与A、B距离相等,求从人口E到出口C的最短路线的长;(2)若线段CD是一条水渠,且点D在AB边上,已知水渠造价约为10元/m,则点D在距点A多远处,此水渠的造价最低?最低造价是多少?第三章 勾股定理勾:直角三角形较短的直角边;股:直角三角形较长的直角边;弦:斜边。
