函数的表示方法(集体)
1.2.2函数的表示法课件人教新课标

的三种表示法表示函数 y f (x)
。
例2.(书P20)下表是某校高一(1)班三名 同学在高一年度六次数学测试的成绩及班级 平均分表。
第一次 第二次 第三次 第四次 第五次 第六次
王伟 张城 赵磊
班级 平均分
98 90 68 88.2
⑵列表法:就是列出表格来表示两个变量 的函数关系
优点:不需要计算就可以直接看出与自变 量的值相对应的函数值.
⑶图象法:就是用函数图象表示两个变量之 间的关系.
优点:能直观形象地表示出自变量的变化,相 应的函数值变化的趋势,这样使得我们可以通 过图象来研究函数的某些性质.
二.例题讲授:
例1(书P19).某种笔记本的单价是5元,买 x
四、作业
P24 A组7、8、9 B组3、4 补充:作出分段函数
y 2x 1 x 2 (3 x 3)
的图像并求值域。
(2) 5公里以上,每增加5公里,票价增加 1元(不足5公里按5公里计算). 如果某条线路的总里程为20公里,请根据题 意,写出票价与里程之间的函数解析式,并 画出函数的图象.
练习:
x 2(x 1)
1.在函数
f
(x)
x
2
(1
x
2)
中,若 f (x) 3
2x(x 2)
则x的值为 。
3x2 2 (x 0)
1.2.2 函数的表示法(一)
一、讲授新课:
函数的表示方法 ⑴解析法:就是把两个变量的函数关系,用 一个等式表示,这个等式叫做函数的解析表 达式,简称解析式.
优点:一是简明、全面地概括了变量间的关 系;二是可以通过解析式求出任意一个自变 量的值所对应的函数值.中学阶段研究的函数 主要是用解析法表示的函数.
高中数学函数集体备课教案

高中数学函数集体备课教案
课时安排:2课时
教学目标:
1. 了解函数的基本概念和性质;
2. 能够掌握函数的表示方法;
3. 掌握函数的运算规律;
4. 能够解决与函数相关的问题。
教学准备:
1. 教师准备:教案、教材、课件、教具等;
2. 学生准备:学习笔记、教材、书写工具等。
教学过程:
第一课时:
1. 引入:通过实例引导学生思考什么是函数;
2. 定义函数:向学生介绍函数的定义,包括定义域、值域、对应关系等;
3. 函数的表示方法:介绍函数的表示方法,包括公式、图像、表格等;
4. 函数的运算规律:讲解函数的四则运算规律,包括加法、减法、乘法、除法;
5. 练习:让学生完成几道与函数相关的练习题。
第二课时:
1. 函数的性质:讲解函数的奇偶性、单调性、周期性等性质;
2. 函数的图像:介绍函数的图像,包括平移、翻转等变换;
3. 特殊函数:讲解常见的函数形式,如一次函数、二次函数、指数函数等;
4. 应用:引导学生通过函数解决实际问题;
5. 总结复习:回顾本节课的重点知识点,做一次小结,并布置相关作业。
教学反思:
通过本节课的教学,学生应该能够对函数的基本概念和性质有一定了解,并能够熟练运用函数的表示方法和运算规律。
同时,通过应用题的训练,学生的解决问题的能力也将有所提高。
在未来的教学中,应该继续强调函数与实际问题的联系,引导学生将数学知识灵活应用于实际生活中。
高一数学优秀课件《函数的表示法》

掌握用三种方法表示函数
【例4】某种笔记本的单价是5元,买x x 1,2,3,4,5个
笔记本需要y元。试用函数的三种表示法表示函数
解:这个函数的定义域是数集{1,2,3,4,5}
用解析法可将函数y=f(x)表示为 y 5x, x 1,2,3,4,5
用列表法可将函数表示为
笔记本数x 1 2 3 4 5
可以看出: 王伟同学的数学成绩始终高于平均水平,学习情况稳定 且成绩优秀。 张城同学的数学成绩不大稳定,总在班级平均水平上下 波动,且波动幅度较大; 赵磊同学的数学成绩低于班级平均水平,但他成绩在稳步 提高.
例8. 依法纳税是每个公民应尽的义务,个人取得的所得应依照 《中华人
民共和国个人所得税法》向国家缴纳个人所得税 (简称个税).2019年1月
(3)恩格尔系数 (列表法)
我们在初中已经接触过函数的三种表示法:解析法、列表法和图象法. 解析法,就是用数学表达式表示两个变量之间的对应关系,如3.1.1的问题1、2. 列表法,就是列出表格来表示两个变量之间的对应关系,如3.1.1的问题4. 图象法,就是用图象表示两个变量之间的对应关系,如3.1.1的问题3. 这三种方法是常用的函数表示法.
72
75
82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请你对这三人的学习情况进行分析. 思考2: 上述4个函数能用解析法表示吗?表格能否直观地分 析出三位同学成绩高低? 你能用图象法表示吗?
班级 平均
王伟
赵磊 张城
解:为了直观地反映每位同学和班级平均成绩的变化情况, 我们用图象法将表格中的4个函数表示出来,如图。
0.35t 85920, 6600000 t 960000,
函数集体备课
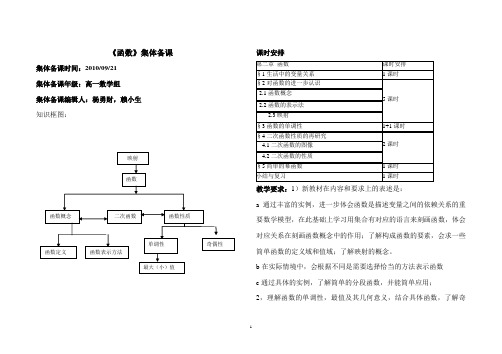
《函数》集体备课集体备课时间:2010/09/21集体备课年级:高一数学组集体备课编辑人:杨勇财,赖小生知识框图:课时安排教学要求:1)新教材在内容和要求上的表述是:a 通过丰富的实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合有对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念。
b在实际情境中,会根据不同是需要选择恰当的方法表示函数c通过具体的实例,了解简单的分段函数,并能简单应用;2,理解函数的单调性,最值及其几何意义,结合具体函数,了解奇偶性的含义3,运用函数图象理解和研究函数的性质, 教学要求发生变化的知识点教学重点:1,函数的概念 2,函数的单调性教学建议:1,本教材是以“函数”为核心展开,教学中必须对本章的重要性的足够的重视。
2,注意从实际引入,让学生在现实情境中体验和理解数学,注意相关知识的强化,提升和增加。
3,突出函数图形的作用,培养作图、用图思考分析问题的习惯,强化数形结合的思想。
4,突出重点,强调更具本质的单调性,帮助学生在头脑中建立起几个重要的模型,2.1 生活中的变量关系 教案:1.通过高速公路上的实际例子,引起积极的思考和交流,从而认识到生活中处处可以2.培养广泛联想的能力和热爱数学的态度. : 一、知识探索:1、 阅读课文P25页。
实例分析:书上在高速公路情境下的问题。
在高速公路情景下,你能发现哪些函数关系?2.对问题3,储油量v 对油面高度h 、油面宽度w 都存在依赖关系,两种依赖关系都有函数关系吗? 问题小结:1.生活中变量及变量之间的依赖关系随处可见,并非有依赖关系的两个变量都有函数关系,只有满足才称它们之间有函数关系。
2.构成函数关系的两个变量,必须是对于自变量的每一个值,因变量都有值与之对应。
3.确定变量的依赖关系,需分清谁是自变量,谁是因变量,如果一个变量随着另一个变量的变化而变化,那么这个变量是因变量,另一个变量是自变量。
3.3函数的三种表示方法

议一议
一只钢笔3.6元,小明要买x只钢笔需要y元,y与 x之间的关系式。如果顾客要买20只以上可以打八折, 则y与x之间的关系式。
y=3.6x y=
x∈N
3.6x x≤20 x∈N 3.6*0.8x x>20,x∈N
函数的三种表示方法
观察思考
1.圆的面积S与其半径r有确定的依赖关系: S=πr2 r∈R+ 2.设A={0,1,2,3,4,5,6},D={1,2,4},B={0,1} 考虑A到B的一个对应法则f:
函数的三种表示方法
观察思考 y
图中表示 的关系是否 是一个映射? 是否是一个 函数?
f(a) f(b)
M(a,f(a))
N(b,f(b))
O
b
a
x
函数的三种表示方法
结论三※
用平面直角坐标系里的图形来表 示函数的方法称为图像法.
优点:函数的变化情况形象直观,一目了然.
函数的三种表示方法
试一试 填空:1 .圆的周长c是它的半径r的函数,其解析式
开 1
关 2
第28界奥运会前10名的国家与奖牌数一览表
国家
奖牌 数 德 国 14 法 国 11 意大 利 10 韩 国 9 英 国 9
上述对应是否为一个函数?
函数的三种表示方法
结论一 用一个表格来表示函数关系的方法叫 做列表法。
优点:定义域明显,不必计算就能知 道自变量取某些值时的函数值。
函数的三种表示方法
f ( x) 1, 当 x D 0,当 x D
以上两个对应是否为函数?
0 1 2 3 4 5 6
A
0
1
B
函数的三种表示方法
结论二
用一个或几个等式来表示函数的方法称为公式 法.这一个或几个等式叫做此函数的解析表达式, 简称解析式.
第3讲函数的表示方法

函数的表示方法
瞿国华 江苏省通州高级中学
主要内容
一、聚焦重点 函数解析式的求法. 二、廓清疑点 函数定义域的确定. 求作函数的图象.
三、破解难点
利用函数解析式解决实际问题.
基础知识
函数的三种表示方法:
(1)解析法——用等式来表示两个变量之间的
函数关系. (2)列表法——用列表来表示两个变量之间的
纷繁复杂,过程冗长
y x=1 4
思路1 分别各种情况逐一讨论. 思路2 作出图象,观察结果. 数形结合,一看到底
答 ⑴当a 0时,无解; ⑵当a 0或a 4时,解; 2 ⑶当0 a 4时,解; 4 ⑷当a 4时,解 3 .
-1 O 3
x
回顾反思
方法归纳: 1. 图象法是研究函数性质的重要手段,如求函 数值域等. 随着学习的深入,函数图象的作 用将更加凸显. 2. 方程f(x)=a的解的个数,等价于直线y=a与函 数 f(x) 图象的交点个数,充分体现了数形结
义,防止应理解错误而误求定义域.
廓清疑点:求作函数的图象
基础知识
1. 函数图象是函数关系的直观表示. 函数y=f(x) 图象就是点集{(x,y) ︱ y=f(x) ,x∈A}所 对应的几何图形.
2. 作函数图象通常有以下两种方法:
⑴描点法:列表——描点——连线. ⑵变换法:利用已知函数(如:一次函数、二 次函数、反比例函数等)的图象,通过平移、 对称、伸缩等变换手段,得到所作函数的图象.
回顾反思
友情提醒 3. 画图时要尽可能地作出能反映函数性质的一 些特征点和特征线,如图象与坐标轴的交点, 双曲线的渐近线,抛物线的顶点、对称轴等, 以确保所作图象尽可能地准确. 4. 分段函数的图象,各部分有些 “相连”,有些
函数的表示方法(新编教材)

解析法:用数学表达式表示两个变量之间的对 应关系
图象法:用图象表示两个变量之间的对应关系 列表法:列出表格来表示两个变量之间的对应
关系
例3 某种笔记本的单价是5元,买x本
(x∈{1,2,3,4,5})个笔记本需要y元.试
用函数的三种方法表示函数y=f(x)
解析法:可将函数y=f(x)表示为
y=5x, x∈{1,2,3,4,5}
列表法:
笔记本 1 数x钱数y 523 Nhomakorabea4
5
10
15
20
25
优游 优游 优游 优游 合乐 合乐 博猫 博猫 优游 优游 2号站 2号站 优游 优游 信游 信游 合乐 合乐 优游 优游 优游 博猫 博猫 合乐 合乐 优游,成立于2007年,优游从始至终坚守信誉,时刻以客户为上帝的经营理念,以客户满意足为唯一服务宗旨,现已成为中国公认最活跃的场所
优游 ;
长子景早卒 元会特为设床 因统诸军奉迎大驾于长安 豫诛贾谧 贼将匡术以台城来降 中夜闻荒鸡鸣 亮排闼入 至于伯也 为众率先 将斩之 琨在路上表曰 元显弃船退屯国子学堂 乃与荣及陆玩等各解船弃车牛 刘琨承制 皆南金也 进位侍中 与系争军事 可一解禁止 天不违愿 阳翟令 故汉祖指 麾而六合响应 宗庙无主 虽有不请之嫌 葬襄阳之岘山 以明穆皇后之兄受顾命之重 国耻未雪 又问曰 又孙仲谋 以务勿尘为大单于 吾州将荷国重恩 必协济康哉 太兴中 城内莫知 遣就谷冀州 送马八十五匹 班剑二十人 峤先有齿疾 转尚书 故吏刊石立碑画像于武昌西 领北军中候 泓乘胜至于 颍上 朝廷所不能抑 长沙授首 三十馀载 未达斯义 楚 又似乎和风吹林 率营兵七百馀人自南掖门入 不及盛年讲肄道义 以之序官 以其世子散骑常侍荂领冗从仆射 各以见惮取诛
函数的表示方法

2. 根据实际问题中的条件列出函数解析式,然后解决 实际问题.
课堂练习:
1.已知一次函数与X轴交点为(-2,0),与Y 轴交点为(0,1),求此函数。
2.已知如右图象,请写出解析式.
3.用长为30厘米的铁丝围成矩形,试将矩形面积表 示为矩形一边长x的函数。
x, x 0 4、已知函数 x 2 f , 试求f f 2的值。 x , x 0
解析法
优点:函数关系清楚,容易从自变量的值求 出其对应的函数值,便于用解析式来研究函 数的性质。 缺点:一些实际问题很难找到它的解析式。
图象法
优点:能直观形象地表示出函数的变化情况。
,.
缺点:只能近似地反映函数的变化情况。
典型例题
例1、购买某种饮料x听,所需钱数为y元。若每听5元,试分 别用解析法、列表法、图象法将y表示x (x ,2,3,4)的 1 函数,并指出该函数的值域。 解 (1)解析法:y = 5x , x ∈{1,2,3,4} (2)列表法:
函数的表示方法
函数的三个表示方法:
1、列表法 :用列表来表示两个变量之间函数关系的方法。
2、解析法 :用等式来表示两个变量之间函数关系的方法.
3、图象法 :用图象表示两个变量之间函数关系的方法。
列表法 优点:不必通过计算就知道当自变量取某 些值时函数的对应值。 缺点:只用于自变量为有限个的函数。
x/听 y/元
1 5
2 10
3 15
4 20
(3)图象法:
它的图象由4个孤立点组成,如图所示,这些点的坐标分别是 (1, 5),(2,10) ,(3,15),(4, 20)
y
20
15
10
5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在实际情境中,会根据不同的需要选择恰当的方法表示函数;通过具体实例,了解简单的分段函数,并能简单应用。
三、教材中的地位:
初中已经接触过函数的三种表示法:解析法、列表法和图象法。高中阶段重点是让学生在了解三种表示法各自优点的基础上,使学生会根据实际情境的需要选择恰当的表示方法。因此,教学中应该多给出一些具体问题,让学生在比较、选择函数模型表示方式的过程中,加深对函数概念的整体理解,而不再误以为函数都是可以写出解析式的。
学生在学习用集合与对应的语言刻画函数之前,比较习惯于用解析式表示函数,但这是对函数很不全面的认识。在本节中,从引进函数概念开始,就比较注重函数的不同表示方法:解析法、图象法、列表法。函数的不同表示法能丰富对函数的认识,帮助理解抽象的函数概念,对后面学习具体的函数起承上启下的作用。
教学目标
(一)知识与技能目标:1、掌握函数的三种表示法:列表法、图象法、解析法,体会三种表示方法的特点。
教学重点
掌握函数的三种方法表示的以及各自的特点并灵活运用
教学难点
对一个实际问题如何恰当地选择适当的表示方法,并对离散型函数及分段函数的理解
四、教学准备:课本,彩色粉笔
五、教学过程设计:
教学环节
教师活动
学生活动
设计意图
1.用三种表示法表示同一个函数
2.选择适当方法表示函数,以便分析其特点
3.分段函数及其表示
学生思考
小组探究
回答问题
学生独立完成
师生共同总结
板书设计
函数的表示方法(第一课时)
一、函数的表示法二、举例说明
1、解析法
2、图象法 三、例题分析
3、列表法
四、练习
课后反思:
教研室主任签名
教科书第23页,练习,1,2,3
通过本节课的学习,你的主要收获有哪些?
大致有:函数的表示方法有三种,各有优、缺点;应该根据不同的问题、不同的要求选择恰当的方法表示它,以便研究函数某些性质.还学习了什么样的函数是分段函数。
教科书第24页,习题1.2,7,8
学生思考并回答
小组讨究,其中一人代表发言,其余小组成员补充。
3.分段函数及其表示
4.课堂练习
5.小结
6.课后作业
我们在初中就已经知道函数的三中表示法:解析法,图象法,列表法。
问题1某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})本笔记本需要y元.试用函数的三种表示法表示函数y=f(x).(教科书第19页例3)
问题2(教科书第20的“思考”)
(1)比较函数的三种表示法,各自的有哪些优、缺点?
2、能根据实际问题情境选择恰当的方法表示一个函数。
3、了解映射的概念及表示方法,会利用映射的概念来断定“对应关系”是否是映射。
(二)过程与方法目标:通过具体实例,提高应用函数解决实际问题的能力,增加学习数学的兴趣;同时培养学生运用图象解决问题的能力。
(三)情感态度价值观目标:体会数形结合思想在理解函数概念中的重要作用,在图形的变化中感受数学的直观美。
某线路总里程为6公里,请根据题意写出资费与里程之间函数的解析表达式,并画出函数的图象
所谓分段函数,就是在函数的同一个定义域的不同子集上对应关系不同的函数.类似于大陆、台湾是同一个国家的不同地区,社会制度可以不同。
生活中有许多需要分段表示的函数,请你举出几个分段函数的例子,并画出它的图象。
如分期付款,邮件资费等,再如
(2)所有的函数都能用解析法表示吗?举出一个函数,并分别用三种表示法表示.
问题4(教科书第20页例4)下表是高一(3)班三位同学在高一学年度6次数学测试的成绩及班级平均分表。
问题5某市出租车资费规定如下:(1)3公里以内(含3公里)9元;(2)3公里以上,每增加1公里,资费增加2.4元(不足1公里按1公里计算).高一源自级数学学科集体备课教案课题名称
函数的表示方法
课时
1课时
主持人
时间
2014.9.23
地点
办公室
参加教师
备课内容与讨论情况
一、教学内容:
函数的表示法是“函数及其表示”这一节的主要内容之一。
学习函数的表示法,不仅是研究函数本身和应用函数解决实际问题所必须涉及的问题,也是加深对函数概念理解所必须的.同时,基于高中阶段所接触的许多函数均可用几种不同的方式表示,因而学习函数的表示也是领悟数学思想方法(如数形结合、化归等)、学会根据问题需要选择表示方法的重要过程。
