指数函数和对数函数公式(全)
指数函数与对数函数知识总结及练习
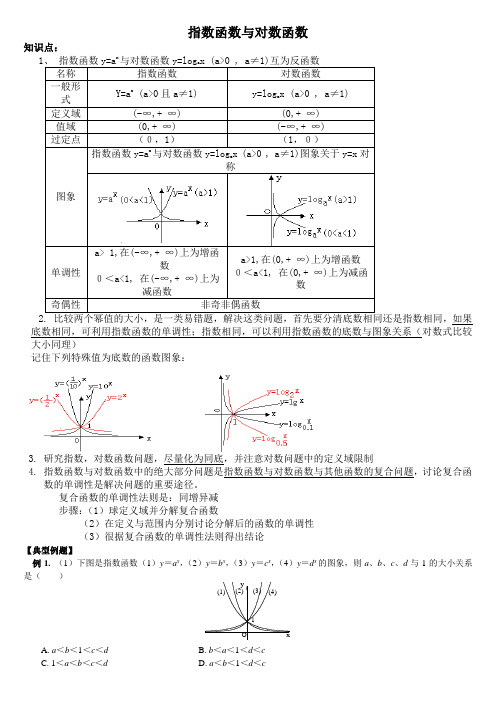
指数函数与对数函数知识点:x比较两个幂值的大小,是一类易错题,解决这类问题,首先要分清底数相同还是指数相同,如果底数相同,可利用指数函数的单调性;指数相同,可以利用指数函数的底数与图象关系(对数式比较大小同理)记住下列特殊值为底数的函数图象:3. 研究指数,对数函数问题,尽量化为同底,并注意对数问题中的定义域限制4. 指数函数与对数函数中的绝大部分问题是指数函数与对数函数与其他函数的复合问题,讨论复合函数的单调性是解决问题的重要途径。
复合函数的单调性法则是:同增异减 步骤:(1)球定义域并分解复合函数(2)在定义与范围内分别讨论分解后的函数的单调性 (3)很据复合函数的单调性法则得出结论【典型例题】例1. (1)下图是指数函数(1)y =a x ,(2)y =b x ,(3)y =c x ,(4)y =d x 的图象,则a 、b 、c 、d 与1的大小关系是( )y x1O(4)(3)(2)(1)A. a <b <1<c <dB. b <a <1<d <cC. 1<a <b <c <dD. a <b <1<d <c剖析:可先分两类,即(3)(4)的底数一定大于1,(1)(2)的底数小于1,然后再从(3)(4)中比较c 、d 的大小,从(1)(2)中比较a 、b 的大小。
解法一:当指数函数底数大于1时,图象上升,且底数越大,图象向上越靠近于y 轴;当底数大于0小于1时,图象下降,底数越小,图象向右越靠近于x 轴.得b <a <1<d <c 。
故选B 。
解法二:令x =1,由图知c 1>d 1>a 1>b 1,∴b <a <1<d <c 。
例2. 已知2x x +2≤(41)x -2,求函数y =2x -2-x 的值域。
解:∵2x x +2≤2-2(x -2),∴x 2+x ≤4-2x , 即x 2+3x -4≤0,得-4≤x ≤1。
又∵y =2x -2-x 是[-4,1]上的增函数,∴2-4-24≤y ≤2-2-1。
对数函数与指数函数的相互关系

指数函数的性质
定义域:所有实数 值域:正实数集 函数图像:在第一象限内单调递增 函数值永远大于0
对数函数与指数函数的图像
对数函数图像:以10为底的对数函数图像是单调递增的,随着x的增大,y值也增大。 指数函数图像:以2为底的指数函数图像是单调递减的,随着x的增大,y值减小。 对数函数与指数函数图像关系:对数函数和指数函数互为反函数,它们的图像关于直线y=x对称。 图像性质:对数函数和指数函数的图像都是连续的,并且在定义域内是单调的。
对数函数与指数函数的 相互关系
汇报人:XX
目录
对数函数与指数函数的定 义
01
对数函数与指数函数的性 质
02
对数函数与指数函数的相 互转换
03
对数函数与指数函数的应 用
04
对数函数与指数函数的比 较
05
对数函数与指数 函数的定义
对数函数的定义
定义:对数函数是指数函数的反函数,即以底数为自变量,指数为因变量的函数。
对数函数与指数 函数的相互转换
指数函数转换为对数函数
公式:a^x = y 可以转换为 log(a,y) = x
意义:将指数函 数的形式转换为 对数函数的形式, 可以更好地理解 和分析函数的性 质和变化规律
应用:在数学、 物理、工程等领 域中,经常需要 将指数函数转换 为对数函数进行 计算和分析
注意:转换时需 要注意函数的定 义域和值域,以 及选择合适的底 数和真数
实际应用:在实际应用中,对数函数和指数函数可以相互转化,通过对数运算或指数运算进行计算 和分析。
感谢您的观看
汇报人:XX
对数函数与指数函数的表示方法
对数函数表示为 y = log_a(x),其中 a 是底数, x 是自变量
指数函数与对数函数知识点总结

指数函数与对数函数知识点总结一、指数函数1、指数函数的定义一般地,函数\(y = a^x\)(\(a > 0\)且\(a ≠ 1\))叫做指数函数,其中\(x\)是自变量,函数的定义域是\(R\)。
需要注意的是,底数\(a\)的取值范围,当\(a = 1\)时,函数就变成了\(y = 1^x = 1\),是一个常函数,不符合指数函数的定义;当\(a < 0\)时,对于某些\(x\)的值,\(a^x\)无意义,比如\((-2)^{\frac{1}{2}}\)就没有实数解。
2、指数函数的图象当\(a > 1\)时,指数函数\(y = a^x\)的图象是上升的,经过点\((0, 1)\),在\(R\)上单调递增;当\(0 < a < 1\)时,指数函数\(y = a^x\)的图象是下降的,经过点\((0, 1)\),在\(R\)上单调递减。
我们可以通过几个特殊的点,比如\((0, 1)\)、\((1, a)\)、\((-1, \frac{1}{a})\)等来大致描绘指数函数的图象。
3、指数函数的性质(1)定义域:\(R\)(2)值域:\((0, +∞)\)(3)恒过定点\((0, 1)\)(4)单调性:当\(a > 1\)时,在\(R\)上单调递增;当\(0 <a < 1\)时,在\(R\)上单调递减(5)函数值的变化情况当\(a > 1\)时,若\(x > 0\),则\(a^x > 1\);若\(x = 0\),则\(a^x = 1\);若\(x < 0\),则\(0 < a^x < 1\)。
当\(0 < a < 1\)时,若\(x > 0\),则\(0 < a^x < 1\);若\(x = 0\),则\(a^x = 1\);若\(x < 0\),则\(a^x > 1\)。
4、指数运算的性质(1)\(a^m × a^n = a^{m + n}\)(2)\(\frac{a^m}{a^n} = a^{m n}\)(\(a ≠ 0\))(3)\((a^m)^n = a^{mn}\)(4)\((ab)^n = a^n b^n\)这些运算性质在化简指数表达式和进行指数运算时经常用到。
对数函数指数函数幂函数

对数函数指数函数幂函数 LELE was finally revised on the morning of December 16, 2020真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于等于零,底数则要大于0且不为1对数函数的底数为什么要大于0且不为1【在一个普通对数式里 a<0,或=1 的时候是会有相应b的值的。
但是,根据对数定义: logaa=1;如果a=1或=0那么logaa就可以等于一切实数(比如log1 1也可以等于2,3,4,5,等等)第二,根据定义运算公式:loga M^n = nloga M 如果a<0,那么这个等式两边就不会成立(比如,log(-2) 4^(-2) 就不等于(-2)*log(-2) 4;一个等于4,另一个等于-4)】通常我们将以10为底的对数叫常用对数(common logarithm),并把log10N记为lgN。
另外,在科学技术中常使用以无理数e=···为底数的对数,以e为底的对数称为自然对数(natural logarithm),并且把loge N 记为In N. 根据对数的定义,可以得到对数与指数间的关系:当a 〉0,a≠ 1时,a^x=N→X=logaN。
由指数函数与对数函数的这个关系,可以得到关于对数的如下结论:负数和零没有对数;loga 1=0 loga a=1 (a为常数)对数的定义和运算性质一般地,如果a(a大于0,且a不等于1)的b次幂等于N,那么数b 叫做以a为底N的对数,记作log(a)(N)=b,其中a叫做对数的底数,N叫做真数。
底数则要大于0且不为1 真数大于0对数的运算性质:当a>0且a≠1时,M>0,N>0,那么:(1)log(a)(MN)=log(a)(M)+log(a)(N);(2)log(a)(M/N)=log(a)(M)-log(a)(N);(3)log(a)(M^n)=nlog(a)(M) (n∈R)(4)换底公式:log(A)M=log(b)M/log(b)A (b>0且b≠1)(5) a^(log(b)n)=n^(log(b)a) 证明:设a=n^x 则a^(log(b)n)=(n^x)^log(b)n=n^(x·log(b)n)=n^log(b)(n^x)=n^(log(b)a)(6)对数恒等式:a^log(a)N=N;log(a)a^b=b对数与指数之间的关系当a>0且a≠1时,a^x=N x=㏒(a)N右图给出对于不同大小a所表示的函数图形:可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形,因为它们互为反函数。
高数积分公式大全

高数积分公式大全高等数学中的积分是数学分析的重要内容之一,它是求函数面积、定积分、不定积分等的方法,被广泛应用于科学和工程领域。
下面是高等数学中常用的积分公式大全,供大家参考和学习。
一、基本积分公式:1. 常数函数积分公式:∫c dx = cx + C(其中c为常数,C为积分常数)2. 幂函数积分公式:∫x^n dx = (1/(n+1)) * x^(n+1) + C(其中n不等于-1,C 为积分常数)3. 指数函数积分公式:∫e^x dx = e^x + C4. 三角函数积分公式:∫sin(x) dx = -cos(x) + C∫cos(x) dx = sin(x) + C5. 乘方函数积分公式:∫(a^x) dx = (1/log(a)) * (a^x) + C(其中a为正数且不等于1,C为积分常数)6. 对数函数积分公式:∫(1/x) dx = ln|x| + C二、常用积分公式:1. 三角函数的复合积分:∫sin(ax) dx = - (1/a) * cos(ax) + C∫cos(ax) dx = (1/a) * sin(ax) + C2. 反三角函数的积分:∫1/(√(1-x^2)) dx = arcsin(x) + C∫1/(1+x^2) dx = arctan(x) + C3. 指数函数的积分:∫e^(ax) dx = (1/a) * e^(ax) + C4. 对数函数的积分:∫(1/x) dx = ln|x| + C5. 分式函数的积分:∫(1/(x-a)) dx = ln|x-a| + C(其中a不等于0)∫(1/(x^2+a^2)) dx = (1/a) * arctan(x/a) + C(其中a不等于0)6. 三角函数的积分:∫sin^n(x) cos^m(x) dx7. 部分分式的积分:∫(p(x)/q(x)) dx8. 具体函数的特殊积分:∫e^x sin(x) dx∫e^x cos(x) dx∫(sin(x))^n (cos(x))^m dx(其中n和m为正整数)三、数列求和公式:1. 等差数列求和公式:S_n = (n/2)(a_1 + a_n)(其中S_n为前n项和,a_1为首项,a_n为末项)2. 等比数列求和公式:S_n = (a_1(1-q^n))/(1-q)(其中S_n为前n项和,a_1为首项,q为公比)以上是高等数学中一些常见的积分公式,通过掌握和灵活运用这些公式,可以帮助我们更好地解决数学中的问题。
函数公式大全

函数公式大全在数学中,函数是描述自变量和因变量之间关系的一种数学工具,它是数学中的一个重要概念,也是解决问题的重要工具。
函数公式则是用来表示函数关系的具体表达式,通过函数公式我们可以更加清晰地了解函数的特性和性质。
下面将介绍一些常见的函数公式,希望能对大家有所帮助。
1. 线性函数公式。
线性函数是一种最简单的函数形式,它的函数公式通常表示为,y = kx + b,其中k和b分别代表斜率和截距。
线性函数的图像是一条直线,斜率决定了直线的倾斜程度,截距则表示了直线与y轴的交点。
2. 二次函数公式。
二次函数的一般形式为,y = ax^2 + bx + c,其中a、b、c为常数且a不为0。
二次函数的图像是一个抛物线,开口的方向由a的正负决定,抛物线的顶点坐标为(-b/2a, -Δ/4a),其中Δ=b^2-4ac称为二次函数的判别式。
3. 指数函数公式。
指数函数的一般形式为,y = a^x,其中a为底数,x为指数。
指数函数的图像是一条逐渐增长或逐渐减小的曲线,底数a大于1时曲线逐渐增长,底数a在0和1之间时曲线逐渐减小。
4. 对数函数公式。
对数函数的一般形式为,y = loga(x),其中a为底数,x为真数。
对数函数的图像是一条渐近于x轴的曲线,底数a大于1时曲线在一、三象限递增,底数a在0和1之间时曲线在一、三象限递减。
5. 三角函数公式。
三角函数包括正弦函数、余弦函数、正切函数等,它们的一般形式分别为,y = sin(x)、y = cos(x)、y = tan(x)。
三角函数的图像是周期性的波动曲线,正弦函数和余弦函数的振幅为1,而正切函数的图像有无数个渐近线。
6. 绝对值函数公式。
绝对值函数的一般形式为,y = |x|,表示x的绝对值。
绝对值函数的图像是一条以原点为对称中心的V形曲线,曲线在原点处转折。
7. 指数增长函数公式。
指数增长函数的一般形式为,y = a^x + b,其中a为底数,b为常数。
指数增长函数的图像是一条逐渐增长的曲线,随着x的增大,y的增长速度越来越快。
指数函数和对数函数知识点总结

指数函数和对数函数知识点总结一、指数函数:1.基本概念:指数函数是形如y=a^x(a>0,且a≠1)的函数,其中a称为底数,x 称为指数,a^x称为底数a的x次幂。
2.基本性质:(1)a^0=1,任何数的0次幂等于1;(2)a^x*a^y=a^(x+y),相同底数的指数幂相乘,底数不变,指数相加;(3)a^x÷a^y=a^(x-y),相同底数的指数幂相除,底数不变,指数相减;(4)(a^x)^y=a^(x*y),指数幂的乘积再乘方,指数相乘;(5)a^(-x)=1/(a^x),任何数的负指数满足倒数规律。
3.常见指数函数:(1)指数函数y=2^x:以2为底的指数函数,可以用来描述2的x 次幂关系,是一种常见的指数型增长函数,图像逐渐向上凸起。
二、对数函数:1.基本概念:对数函数是指y=loga(x),其中a>0,且a≠1,a称为底数,x称为真数,y称为以a为底x的对数。
2.基本性质:(1)loga(1)=0,底数为任何正数时,1的对数都是0;(2)loga(a)=1,底数为任何正数时,底数的对数都是1;(3)loga (x*y) = loga(x) + loga(y),对数相乘,真数取乘积,对数相加;(4)loga (x/y) = loga(x) - loga(y),对数相除,真数取商,对数相减;(5)loga(x^k) = k * loga(x),对数乘方,真数取底数的k次方,对数乘以指数。
3.常见对数函数:(1)常用对数函数:y=log10(x),其中底数为10,对数函数可以简写为y=log(x)。
常用对数函数是以10为底的对数函数,输入一个正实数x,输出满足10^y=x的y值。
(2)自然对数函数:y=ln(x),其中底数为e。
自然对数函数是以e 为底的对数函数,输入一个正实数x,输出满足e^y=x的y值。
三、指数函数与对数函数的关系:四、指数函数与对数函数的应用:1.科学中的指数增长:指数函数常常用于描述原子衰变、细胞分裂和放射性物质的衰变等过程。
对数函数运算法则公式

对数函数运算法则公式一、什么是对数函数对数函数,又称为指数函数,是一类常见的数学函数,它可以用来表达不同系数的多次方之间的关系。
它的基本形式为y=loga x (a>0, a≠1),其中 a 为底数,x 为真数,y 为对数。
二、对数函数运算法则1. 同底数相加/减法则:若 y1=loga x,y2=loga m,则有:y1+y2=loga x+loga m =loga (xm)y1-y2=loga x-loga m =loga (x/m)2. 同底数乘/除法则:若 y1=loga x,y2=loga m,则有:y1*y2=loga x*loga m =loga (x^m)y1/y2=loga x/loga m =loga (x^(1/m))3. 相乘/除法则:若 y1=loga x,y2=logb m,则有:y1*y2=loga x*logb m =loga (x^b)y1/y2=loga x/logb m =loga (x^(1/b))4. 幂函数的对数运算法则:若 y=ax,则有:loga y=x*loga a5. 指数函数的对数运算法则:若 y=a^x,则有:loga y=x*loga a6. 反函数的对数运算法则:若 y=f-1(x),则有:loga y=loga f-1(x)=loga x7. 同余式的对数运算法则:若y=a^x ≡ b^x mod c,则有:loga y=x*loga a ≡ x*loga b mod c三、总结以上就是关于“对数函数运算法则公式” 的详细介绍,它是一类常见的数学函数,可以用来表达不同系数的多次方之间的关系,它有 7 种运算法则,即同底数相加/减法、同底数乘/除法、相乘/除法、幂函数的对数运算法则、指数函数的对数运算法则、反函数的对数运算法则以及同余式的对数运算法则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数和对数函数
重点、难点:
重点:指数函数和对数函数的概念、图象和性质。
难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数
y a x ,y log a x 在
a 1及 0 a 1两种不同情况。
1、指数函数:
y
x
且a
叫指数函数。
定义:函数
aa
0 1
定义域为 R ,底数是常数,指数是自变量。
为什么要求函数 y
a x 中的 a 必须 a
0且a
1 。
因为若 a
0时, y
4 x ,当 x
1
时,函数值不存在。
4
a
0 , y 0x ,当 x
0 ,函数值不存在。
a 时, y
1 x
x 虽有意义,函数值恒为
1,但
1
对一切 y
1x 的反函数不存在,
因 为 要 求 函 数 y
a x 中 的
a
0且 a 1 。
x
1、对三个指数函数
y
2 x , y
1 ,y
10x 的图象的
2
认识。
图象特征与函数性质:
图象特征
函数性质
( 1)图象都位于
x 轴上方;
( 1) x 取任何实数值时,都有 a
x
0 ;
2
0 1 ); ( 2)无论 a 取任何正数, x 0
时, y 1 ;
( )图象都经过点( ,
( 3) y
2x , y 10 x 在第一象限内的纵坐
( 3)当 a
x 0,则 a x 1
1 时,
0,则 a x
1
标都大于 1,在第二象限内的纵坐标都小于
1,
x
1 y
2
x
x 0,则 a x
1
当 0
的图象正好相反;
a 1时,
0,则 a x 1
x
( 4) y
2x , y 10 x 的图象自左到右逐渐
( 4)当 a 1 时, y
a x 是增函数,
上升, y 1
2
x a 1时,y a x是减函数。
当 0
的图象逐渐下降。
对图象的进一步认识,(通过三个函数相互关系的比较):
①所有指数函数的图象交叉相交于点( 0,1),如y2x和 y10 x相交于(0,1),当x0 时,y 10x 的图象在 y 2 x的图象的上方,当x 0,刚好相反,故有 10222及102 2 2。
1x
② y 2 x与y的图象关于 y 轴对称。
2
③通过 y 2x,y10 x,y1
2x
三个函数图象,可以画出任意一个函数y a x(a0且a 1 )的
示意图,如y 3x的图象,一定位于 y 2 x和 y 10 x两个图象的中间,且过点(0,1) ,从而 y 1
3x
也由
1关于 y 轴的对称性,可得y
3
2、对数:x
的示意图,即通过有限个函数的图象进一步认识无限个函数的图象。
定义:如果b(
a 01)
,那么数 b 就叫做以 a 为底的对数,记作
b log a N
( a 是底数, N 是
aN且a 真数, log a N 是对数式。
)
由于 N a b
0故
log a N
中 N必须大于。
当N为零的负数时对数不存在。
( 1)对数式与指数式的互化。
由于对数是新学的,常常把不熟悉的对数式转化为指数式解决问题,如:
求 log 0.3252
4
log
52
分析:对于初学者来说,对上述问题一般是束手无策,若将它写成0.32x ,再改写为指数式就
4
比较好办。
解:设 log
52
0 .32x
4
则 0.32 x
5
2
4
8x
8 即
25
25
∴ x 1
2
即 log
5 2
0.32
4
1 2 1 2
评述: 由对数式化为指数式可以解决问题,反之由指数式化为对数式也能解决问题,因此必须因题而异。
如求 3x
5中的 x ,化为对数式 x log 3 5即成。
( 2)对数恒等式:
由 a b
N (1) b log a N
(2)
将( 2)代入( 1)得 a log a N
N
运用对数恒等式时要注意此式的特点,不能乱用,特别是注意转化时必须幂的底数和对数的底数相同。
log 1 2
计算:
3
3
1
l og 1 2 2
解:原式
3
3
( 3)对数的性质:①负数和零没有对数; ② 1 的对数是零;③底数的对数等于 1。
( 4)对数的运算法则:
1
3
lo g 1 2 2
3。
① log a MN
log a M l og a N M , N R
②
log a M
log a M log a N M ,
N R
N
③
log a N n
n l og a N N
R
④ log a
n
N
1
log a NNR
n
3、对数函数:
定 义 : 指 数 函 数 y a x
( a 且 a 1)
的反函数
y log a x x (0, ) 叫做对数函数。
1、对三个对数函数 y
log 2 x , y l og 1 x ,
2
y lg x 的图象的认识。
图象特征与函数性质:
图象特征函数性质
( 1)图象都位于y 轴右侧;( 1)定义域:R+,值或:R;
( 2)图象都过点(1, 0);
( 2)x1时,y0。
即 log a 10 ;
( 3)y l og2x , y lg x 当x
( 3 )当a 1 时,若x 1 ,则y0 ,若1时,图象
x1,则y 0;
在 x 轴上方,当0x0 时,图象在x轴下当
0a 1 时,若 x0 ,则y0 ,若
方, y log 1x 与上述情况刚好相反;0x1时,则y0 ;
2
( 4)y log2x, y lg x 从左向右图象是上( 4)a1时,y log a x
是增函数;
升,而 y log 1 x 从左向右图象是下降。
0 a1
时, y log a x 是减函数。
2
对图象的进一步的认识(通过三个函数图象的相互关系的比较):
( 1)所有对数函数的图象都过点( 1,0 ),但是y log2 x 与 y lg x 在点(1,0)曲线是交叉的,即当 x0时, y log 2x 的图象在 y lg x 的图象上方;而0x1时,y l og2 x 的图象在 y lg x 的图象的下方,
故有: log.l g .
l g 01.。
2 1515 ; log 2 01.
( 2)y log2 x 的图象与y log 1 x 的图象关于x轴对称。
2
( 3)通过y l og 2 x , y lg x ,y log 1x 三个函数图象,可以作出任意一个对数函数的示意图,如
2
作 y log3 x 的图象,它一定位于 y log2x 和 y lg x 两个图象的中间,且过点(1,0),x 0时,在 y lg x 的上方,而位于y log 2 x 的下方,0 x1时,刚好相反,则对称性,可知 y log 1x 的示意图。
3因而通过课本上的三个函数的图象进一步认识无限个函数的图象。
4、对数换底公式:
log b N log a N log a b
LN n log e N (其中
e 2.71828
⋯称为的自然对数
)N
LN g log10 N 称为常数对数由换底公式可得:
L n N l g N lg N
2.303lg N l g e0.4343
由换底公式推出一些常用的结论:
( 1)log a b
1
或 l og a b· log b a 1 l og b a
( 2)log n b m m
log a b
a n
( 3)log a n b n log a b
( 4)log a n a m m
n
5、指数方程与对数方程*
定义:在指数里含有未知数的方程称指数方程。
在对数符号后面含有未知数的方程称对数方程。
由于指数运算及对数运算不是一般的代数运算,故指数方程对数方程不是代数方程而属于超越方程。
指数方程的题型与解法:
名称题型解法
基本型
a f x b取以 a 为底的对数f x log a b
同底数型
不同底数型a f ( x)a( x)取以 a 为底的对数f x x
需代换型
a f x
b x
fx· l g a x · lgb
F a x0
取同底的对数化为
换元令 t a x转化为t的代数方程
对数方程的题型与解法:
名称题型解法
基本题
log a f x b对数式转化为指数式f x a b 同底数型
log a x转化为 f x x
log a fx(必须验根)
需代换型
F
(log a0换元令 t log a x 转化为代数方程
x)。
