精度设计理论-6
合集下载
第三章 仪器设计的精度理论

粗大误差
是超出在规定条件下预期的误差,此误差值 较大,明显歪曲测量结果。 一般是由于疏忽或错误,在 测得值中出现的误差,在测量过程中,一旦出现这类误差, 应予以剔除。
精度
精度含义
精度与误差概念相反;精度高、低用误差来衡量。 误差大,精度低;误差小,精度高。
精度分为:
准确度:它是系统 误差大小的反映;
线性化
ห้องสมุดไป่ตู้z f tan
物镜
实际上为了减少工艺上的困 难,分划板是等间隔刻划的,即 形成如下关系:
z f
(tg )
f'
自准直仪的原理误差
z
原理误差来源分析
这样不可避免地要产生原理误差z
z z z f tan f 3 f ( ) f 3 1 f 3 3
s 2 sin 0.2666 0.2705rad a 7.5 1 1 3 3 s a 7.5 0.2705 0.023686mm 于是原理误差为 6 6
原理误差分析方法举例
即原理误差几乎等于允许的示值误差,并大于 0.01mm 的刻度值,当然这是不允许的。因此,在这种情况下,对示 值范围应加以限制。 3 a s 1 3 s a 6a 6 在结构允许的条件 a s 下应尽量加大臂长a s一定
随机误差的大小,决定仪器示值的分散性,即精密度。 随机误差按其误差的分布规律,又分为:正态分布和非正态 分布两种。
正态分布
随机误差每次出现的情况虽无规律,但在相同测量 或工艺条件下,其误差值是按统计规律变化的。并且, 在大多数情形下,是服从正态分布的。
误差
非正态分布
大部分随机误差是服从正态分布的,但是大量的实践证明, 也有一部分随机误差的分布会偏离正态性,也就是产生了 非正态分布的随机误差,故在误差理论中,除了要讨论正 态分布的误差外,还要研究非正态分布的随机误差。
精度设计理论-8

例
在图所示的圆柱形轴系中,主轴 的圆柱度误差为△tz, 轴套的圆 柱度误差为△tk,则由此引起的 主轴角运动误差可由下式算得
垂直度误差
• 零件平面对轴线的垂直度误差对圆柱形轴 系、半运动式圆柱形轴系和平面轴系的定 向精度和轴向回转精度都有影响。
•例如,在图所示的平面轴 系中,与钢球接触的主轴上 盖承导平面对轴线有垂直度 误差△z。它在轴系配合间 隙较小时,会使主轴转动发 滞,甚至卡住,而在配合间 隙大时,它会导致主轴角运 动误差的增大。
回转速度与轴系摩擦阻力的关系
• 摩擦阻力(或摩擦系数)在某种程度上与运动速度
有关系(参见图),当主轴回转速度增大时,轴系 开始从半干摩擦变为湿摩擦。
磨损对轴系精度的影响
•
• • • •
轴系在长期使用后,由于机械和化学作用产生的磨损,对于 轴系零件的形状、尺寸和相互位置都有不同程度的影响,一 般会出现以下几种情况: 1)主轴轴颈直径缩小,轴套孔径变大,因此轴系配合间隙增 大 2)破坏主轴轴颈和轴套配合表面的形状,引起主轴轴心径向 晃动轨迹的变化 3)轴系中支承元件(滚珠和顶针)的磨损以及滚珠滚道平面 (或锥面)的磨损会引起轴系中关键零件相对位置的改变。 由于上述元件的磨损,将导致主轴径向晃动误差,角运动误 差以及轴向窜动误差的增大,使轴系的回转精度明显下降。
α,β与制造主轴的材料有关的系数
改善措施
• 温度对轴系配合间隙的影响可能很大,只有适当 的选择轴系零件的材料 才能减小温度变化的影响。 • 为此我们希望选用相同膨胀系数的材料来制造轴 和轴套,但这 种条件也不是随便可以达到的。 因为同样材料制造的零件,其配合表面间将产生 很大的摩 擦和磨损,当压力很大时,甚至将配 合表面磨坏。 • 轴系用于测量仪器时,旋转困难一般发生在低 温时,在这种条件下,选择材料应使轴 套材料 的线膨胀系数比主轴的线膨胀系数小。
精度设计理论-6

• 例如。在实现函数的运动规律 的凸轮机构中,为了减少 磨 损,常需将从动杆的端头设计 成半径为r的圆球头
原理误差
• 原理误差是仪器在原理上固有的误差。原理误差 的存在使仪器的示值对被测量的真值始终存在一 定范围的偏离。它属于仪器中的未定系统误差 • 对于那些因设计不当而带来的原理误差,应当坚 决于以避免。 • 在多数情况下,设计中所以允许有原理误差的存 在是因为它可以换得简化测量、简化结构、简化 工艺、简化算法的好处。即使如此我们也应注意 把由此而引起的原理误差控制在允许的范围之 内,并尽力使其减小。
为了方便,先就集中参数独立பைடு நூலகம்统的精度方程进行讨论。为了 确定一个产品技术参数的精度,设计者必须全面了解影响输出 参数不确定度的各主要有贡献的不确定度分量,为此先用符号 将各类影响分量表征如下
开环精度系统和闭环精度系统
• 按是否有精度反馈和补偿可以分为开环精度设计 和闭环精度设计。 • 开环精度设计 仅研究系统结构参数波动对精度 的影响,本身不带有精度反馈和补偿功能。开环 精度设计是系统基本结构上的精度设计。 • 闭环精度设计 在开环精度设计基础上研究精度 反馈和补偿。带有精度反馈和补偿装置。
性变形在许多情况下,将引起另一种空程——弹 性空程,也会影响精度。
减小空程误差的方法
• ①使用仪器时,采用单向运转,把间隙和弹性变 形预先消除,然后再进行使用; • ②采用间隙调整机构,把间隙调到最小; • ③提高构件刚度,以减少弹性空程; • ④改善摩擦条件,降低摩擦力,以减少由于摩擦 力造成的空程。
应力变形引起误差
• 零件虽然经过时效处理,内应力仍可能不平衡, 金属的晶格处于不稳定状态,使零件产生变形, 在运行时产生误差。
减小或消除应力变形
原理误差
• 原理误差是仪器在原理上固有的误差。原理误差 的存在使仪器的示值对被测量的真值始终存在一 定范围的偏离。它属于仪器中的未定系统误差 • 对于那些因设计不当而带来的原理误差,应当坚 决于以避免。 • 在多数情况下,设计中所以允许有原理误差的存 在是因为它可以换得简化测量、简化结构、简化 工艺、简化算法的好处。即使如此我们也应注意 把由此而引起的原理误差控制在允许的范围之 内,并尽力使其减小。
为了方便,先就集中参数独立பைடு நூலகம்统的精度方程进行讨论。为了 确定一个产品技术参数的精度,设计者必须全面了解影响输出 参数不确定度的各主要有贡献的不确定度分量,为此先用符号 将各类影响分量表征如下
开环精度系统和闭环精度系统
• 按是否有精度反馈和补偿可以分为开环精度设计 和闭环精度设计。 • 开环精度设计 仅研究系统结构参数波动对精度 的影响,本身不带有精度反馈和补偿功能。开环 精度设计是系统基本结构上的精度设计。 • 闭环精度设计 在开环精度设计基础上研究精度 反馈和补偿。带有精度反馈和补偿装置。
性变形在许多情况下,将引起另一种空程——弹 性空程,也会影响精度。
减小空程误差的方法
• ①使用仪器时,采用单向运转,把间隙和弹性变 形预先消除,然后再进行使用; • ②采用间隙调整机构,把间隙调到最小; • ③提高构件刚度,以减少弹性空程; • ④改善摩擦条件,降低摩擦力,以减少由于摩擦 力造成的空程。
应力变形引起误差
• 零件虽然经过时效处理,内应力仍可能不平衡, 金属的晶格处于不稳定状态,使零件产生变形, 在运行时产生误差。
减小或消除应力变形
精度设计理论-5

1≤ i 〈 j
m
简单的合成公式
当 xi 和 x j 相互独立时, ρij = 0
标准不确定度传播公式
⎛ ∂F ⎞ 2 uc ( y ) = ∑ ⎜ ⎟ u ( xi ) i =1 ⎝ ∂xi ⎠
m 2
【例1】
解:
常见的间接测量函数模型
(1)设 Y = ∑ ai X i , 各 X i之间互不相关,则有 i
【例】
解
直径.高度和质量不确定度
测量结果
使用合成标准不确定度
• 适用范围
• 基础计量学研究; • 基本物理常量测量; • 复现国际单位制的同际比对.
• 应包括的内容
• 明确说明被测量的定义; • 给出被测量的估计值、合成标准不确定度及其单 位,必要时还应给出自由度。 • 必要时也可给出相对标准不确定度.
重复测量分量的自由度为 ν 2 = 3 − 1 = 2 则有效自由度
0.0154 v= ≈8 4 4 0.001 0.015 + 2 8
( 扩展不确定度 U 99 = t99 8)uc = 3.355 × 0.015 = 0.049
扩展不确定度的计算
简易法
取 k = 3 ,有
U = kuc = 0.045
【解】
根据合成标准不确定度的计算公式,得
uc ( y ) = y ⎛ u ( xi ) ⎞ ∑⎜ x ⎟ i =1 ⎝ i ⎠
3 2
= (0.25%) 2 + (0.57%) 2 + (0.82%) 2 = 1.03%
计算
由于 则根据有效自由度计算
veff
∂f y u ( xi ) = u ( xi ) ∂xi xi
为 Y = Y1 + Y2 + + Ym ,当各分量 Yi 均服从正态分 布,且相互独立时,可根据韦尔奇-萨特思韦特 (Welch- Satterthwaite)公式来计算其合成标 准不确定度的有效自由度。 4
m
简单的合成公式
当 xi 和 x j 相互独立时, ρij = 0
标准不确定度传播公式
⎛ ∂F ⎞ 2 uc ( y ) = ∑ ⎜ ⎟ u ( xi ) i =1 ⎝ ∂xi ⎠
m 2
【例1】
解:
常见的间接测量函数模型
(1)设 Y = ∑ ai X i , 各 X i之间互不相关,则有 i
【例】
解
直径.高度和质量不确定度
测量结果
使用合成标准不确定度
• 适用范围
• 基础计量学研究; • 基本物理常量测量; • 复现国际单位制的同际比对.
• 应包括的内容
• 明确说明被测量的定义; • 给出被测量的估计值、合成标准不确定度及其单 位,必要时还应给出自由度。 • 必要时也可给出相对标准不确定度.
重复测量分量的自由度为 ν 2 = 3 − 1 = 2 则有效自由度
0.0154 v= ≈8 4 4 0.001 0.015 + 2 8
( 扩展不确定度 U 99 = t99 8)uc = 3.355 × 0.015 = 0.049
扩展不确定度的计算
简易法
取 k = 3 ,有
U = kuc = 0.045
【解】
根据合成标准不确定度的计算公式,得
uc ( y ) = y ⎛ u ( xi ) ⎞ ∑⎜ x ⎟ i =1 ⎝ i ⎠
3 2
= (0.25%) 2 + (0.57%) 2 + (0.82%) 2 = 1.03%
计算
由于 则根据有效自由度计算
veff
∂f y u ( xi ) = u ( xi ) ∂xi xi
为 Y = Y1 + Y2 + + Ym ,当各分量 Yi 均服从正态分 布,且相互独立时,可根据韦尔奇-萨特思韦特 (Welch- Satterthwaite)公式来计算其合成标 准不确定度的有效自由度。 4
机械精度设计及检测19第11章尺寸链的精度设计基础
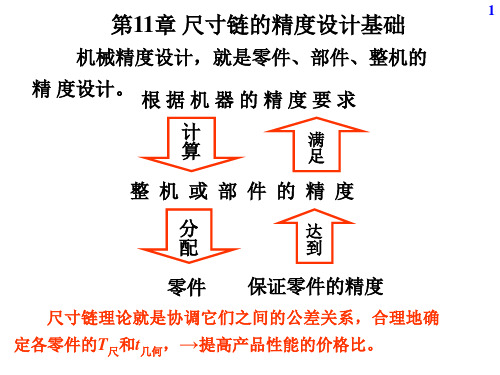
偏差 为
A1
101
0.35 0
A2
50
0.25 0
A3
A5
50 0.048
⑤ 用中间计算方法计算A4的上、下偏差 ES0 ESA1() ESA2() 2EIA3() EI A4()
EIA4() ESA1() ESA2() 2EI A3() ES0
0.35 (0.25) 2(0.048) (0.75)
A3
(4) 校核计算结果
19
∵ ES0=-0.01 , EI0=-0.08 (A1=Φ70 ,
T0 ES0 EI0 = 0.07
41
Ti TA1 TA2 TA3
i 1
2
2
= 0.02+0.03+0.02 = 0.07
3
T0 Ti 0.07
1
∴ 计算无误,则壁厚
A2/2 A0
A2=Φ60 A3=0±0.01)
Ai 的方向与封闭环A0
的方向相同为Ai (-) 。
图11.4尺寸链图
由图可见: A1为A1() , A2、A3为A2()、A3()
例11.2 加工顺序(见图11.5):
9
(1)镗孔A1,(2)插键槽A2,(3)磨内孔A3。 解:(1)按加工顺序画尺寸链图。oA3/2 A1/ Nhomakorabea A2 A0
(2)
判断
对包容面(即孔): 下偏差为零(EI=0)。
如
Φ30
对被包容面(轴): 上偏差为零(es=0)。
Φ30
29
例11.7 图11.10为对开齿轮箱的一部分。 A0=1~1.75, A1=101、A2=50、A3=A5=5、A4=140。 计算各组成环的公差和上、下偏差。
检测技术 仪器精度理论

2.相对误差 :绝对误差与被测量真值的比值
∆ δ = x0
特点:无量纲
表示方法
•引用误差 绝对误差的最大值与仪器示值范围的比值。 •额定相对误差 示值绝对误差与示值的比值。
二、精度
1)正确度 它是系统误差大小的反映,表征测量结果稳定地接近真值
的程度。
2)精密度 它是随机误差大
小的反映,表征测量结果的 一致性或误差的分散性。
∆ (t ) = y (t ) − x (t )
反映仪器的瞬态响应品质。 如果已知仪器的数学模型,可以由传递函数与输入信号拉氏变换 的乘积的拉氏反变换获得对特定激励 x (t ) 的响应 y (t ) 。 也可用实验测试的方法得到输出信号 y (t ) 的样本集合 Y (t ) ,将均 值与被测量信号之差作为测量仪器的动态偏移误差,即
第二章 仪器精度理论
意义:精度分析和精度设计是仪器设计的重要内涵
仪器误差来源与特性 误差计算与评定
•内容:
误差传递及相互作用的规律 误差合成与分配原则和方法 对仪器精度的测试过程
第二章 仪器精度理论
第一节 第二节 第三节 第四节 第五节 第六节 仪器精度理论中的若干基本概念 仪器误差的来源与性质 仪器误差的分析 仪器误差的综合 仪器误差的分析合成举例 仪器精度设计
r r sin 2 α ∆ h = OA − OB ≈ − r cos α = cos α cos α = r tan α sin α ≈ r α 2
图2—8
凸轮机构原理误差
•正弦机构 测杆位移与摆杆转角的关
摆杆
1 3 ∆s = aϕ − a sin ϕ ≈ aϕ 6 (四)测量与控制电路
系是非线性的,但将其视为线性关系 时就引起了原理误差 :
机械制造基础第三章形状和位置精度设计

■ 平行度
■ 线对线平行度
公差带是距离为公差值t且 平行于基准线,位于给定方 向上的两平行面之间的区域
被测轴线必须位于距离为公 差值0.1且在给定方向上平行 于基准轴线的两平行平面之间
■ 线对线平行度
▲如公差值前加注Φ,公差带 是直径为公差值t且平行于基准 线的圆柱内的区域
被测轴线必须位于直径为公 差值0.03且平行于基准轴线 的圆柱面内
■ GB /T1182-1996《形状和位置公差 通则、定义、符 号和图样表示法》
■ GB/T 1184-1996《形状和位置公差 未注公差值》 ■ GB/T 4249-1996《公差原则》 ■GB/T 1667l-1996《形状和位置公差最大实体要求,最
小实体要求和可逆要求》 ■ GB 1958-1980《形状和位置公差检测规定》
3.2 形状和位置公差
3.2.1 基本概念
■形状和位置误差的研究对象是机械零件的几何要素
△概念:几何要素是构成零件几何特征的点、线、面 的统称
△从不同角度对几何要素的分类
1.按存在的状态分类 ■实际要素:零件上实际存在的要素,通常用测量得到的
要素来代替。 ■理想要素:仅具有几何学意义的要素,即几何的点、线、
(0.03×0.05) ,且平行于基准要素的四棱柱的 区域。
A
■ 垂直度
■ 线对线垂直度
▲公差带是距离为公差值t且垂直于基准 面的两平行平面之间的区域
■ 线对面垂直度 ▲在给定方向上,公差带是距离为公差 值t且垂直于基准面的两平行平面之间 的区域
■ 线对面垂直度 ▲如公差值前加注Φ,则公差带是 直径为公差值t且垂直于基准面的 圆柱面内的区域
距离为t的两平行面。
2、测量方法Βιβλιοθήκη 不同 测量圆跳动时,零件绕基准轴线回转,零件和指
仪器精度理论

为什么会产生原理误差?
1)采用近似的理论和原理进行设计是为了简化设 计、简化制造工艺、简化算法和降低成本。
2)有些情况是由于理想的原理在设计中难以实现。
设计仪器时首先应分析原理误差。
分析原理误差的途径:
将仪器各个组成环节之间的实际关系与设计、计 算时采用的理论关系进行比较,如有差异,则存在原 理误差。
仪器的静态特性:当输入量不随时间的变化而变化或变
化十分缓慢时,输出Y与输入f(x)之间的关系。
希望呈线性关系
实际为非线性关系
仪器的线性度:
2、示值误差与示值重复性
•示值误差 •示值重复性
3、灵敏度与分辨力
•灵敏度 •分辨力 4、仪器的稳定性与漂移 •稳定性
•漂移
5、滞差
(二)仪器的动态特性与精度指标
•随机误差
•系统误差
• 粗大误差
一个正确的测量不应包含粗大误差,在误差分析时, 主要分析系统误差和随机误差,并应剔出粗大误差。
(2)按被测参数的时间特性区分
•静态参数误差 •动态参数误差 (3)按误差间的关系区分 •独立误差 •非独立误差
3、误差的表示方法
•绝对误差 Δi=xi-xo
能反映出误差的大小和方向
电场 磁场 湿度 压力
2-3 仪器误差的分析与计算
仪器误差分析
是为了寻找影响仪器精度根源及其规律。
仪器误差计算
是确定其对总精度的影响程度,以便正确地选择仪器设 计方案,合理地确定结构和技术参数,合理地设置误差 补偿环节----得到满足要求的总精度。
误差分析: •寻找仪器的误差源; •计算分析各个源误差对仪器精度的影响;
C2 仪器精度理论
主要内容: 分析影响仪器精度的各项误差来源及特性 研究误差的评定和计算方法(重点) 研究误差的传递、转化和相互作用的规律 (难点) 仪器误差的分析与合成(重点) 仪器误差的设计与分配(重点)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精度设计理论-6
—精度理论的基本知识
主要内容
☆系统静态精度特性 ☆如何提高精度 ☆影响精度的主要因素 ☆精度设计的基本原则
精度理论应用
• 误差处理是研究在各种测量方式及测量条件下, 以最经济简便的方法得到最优的测量结果,它是 测试技术、仪器仪表及工程实验等领域不可缺少 的重要理论基础。 精度理论主要研究影响系统精度的各项误差来源 及特性,研究误差的评定和估计方法,掌握误差 的传递、转化和相互作用的规律,误差合成与分 配原则,从而为精度设计提供可靠的科学依据。
应力变形引起误差
• 零件虽然经过时效处理,内应力仍可能不平衡, 金属的晶格处于不稳定状态,使零件产生变形, 在运行时产生误差。
减小或消除应力变形
• 减小或消除内应力的一般方法是充分地进行时效 处理,切除表面应力层,用氮化代替淬火,锻造 代替轧制等。
制造误差成本控制
☆例如,螺旋副传动机构中,螺杆的螺距误差,螺
为了方便,先就集中参数独立系统的精度方程进行讨论。为了 确定一个产品技术参数的精度,设计者必须全面了解影响输出 参数不确定度的各主要有贡献的不确定度分量,为此先用符号 将各类影响分量表征如下
开环精度系统和闭环精度系统
• 按是否有精度反馈和补偿可以分为开环精度设计 和闭环精度设计。 • 开环精度设计 仅研究系统结构参数波动对精度 的影响,本身不带有精度反馈和补偿功能。开环 精度设计是系统基本结构上的精度设计。 • 闭环精度设计 在开环精度设计基础上研究精度 反馈和补偿。带有精度反馈和补偿装置。
原理误差-近似数据处理带来的
• 数据处理方法上的近似带来的原理误差。
• 用近似计算公式进行运算带来的原理误差。 • 数值舍位带来的原理误差。
例如 用激光干涉方法测量位移
• 位移量可以表达 为脉冲当量q与其脉冲个数n的乘积。 设激光波长0.63281984um。当激光测量系统在经过光学 和电学的64倍细分之后,则一个脉冲当量为q=0.63281984 /64=0.00988781/um。 用这个数作为脉冲当量,再乘以脉冲数进行读数,是不方 便的。因为,通常分辨率以0.1um、0.01um计比较方便。 这样,对激光干涉测量读数,就需要进行数据上的处理, 由此产生了相应的原理误差。
开环系统静态参数方程
开环系统静态精度方程
闭环系统静态参数方程
闭环系统静态精度方程
闭环系统静态精度方程
如何提高精度?
☆在精密工程发展初期,提高精度水平的主要途
径是完善传统技术. ☆ 随着精度水平的进一步提高、如果继续提高精 度水平,除采用新技术外,必须考虑各误差源 的影响方式及如何消除其影响。
运动特性
• 精密测试仪器运动装置的精度除取决于运动机 构结构设计和形状特性外,还取决于运动机构 之间由于相对运动产生的变形、运动速度及惯 性。
运动装置变形对测量误差的影响
• 影响仪器精度的因素是仪器运动装置的自重及由 于运动引起重量移动造成的变形的影响
运动惯性和支承点位置的影响
• 在连续接触式动态测量中,测量头的质量及支点 的位置会影响动态测量的响应特性.
般振幅达到1~5um,频率5~30Hz。
• 高精度的测量必须考虑环境灰尘的影响,清洁度的 控制对精密仪器是非常重要的。
减小振动影响的办法
• 在高精度计量仪器中,尽量避免采用间歇运动机 构,而用连续扫描或匀速运动机构; • 零部件的自振频率要避开外界振动频率; • 采取各种防振措施,如防振墙、防振地基、防振 垫等; • 通过柔性环节使振动不传到仪器主体上。
原理误差-简化机构带来的
• 一种情况是用简单 的机构来代替复杂 的机构,用简单的 运动关系来表达复 杂的运动关系,另 一种情况是利用具 有单一主动件的简 单机构实现多元函 数作用方程。
原理误差-测量原理和方法不完善
• 有些仪器的测量原理,没 有遵守按被测参数定义进 行测量的原则进行设计, 则仪器在测量原理或方法 上便存在原理误差。
原理误差-参数理论值与实际值不符
• 系统特性方程中参数理论值与实际值不符假定测试系统 的理论特性方程式为
而测试系统的实际方程式为
可见,特性方程中各物理参数都有误差 系统原理误差为
【例 1】
气压式高度表在对流层内的理论特性方程式为
则它们引起的原理误差为
原理误差-近似方程式
在实际应用中,也经常会遇到系统特性方程采用 近似方程式的情况。 假定特性方程理论方程式为 y 0= f0 ( x ) ,而近 似方程式为 y = f ( x ) ,则原理误差为
重心位置变化产生的变形
• 工作台沿导轨移动,重心位置随着改变,使仪器 产生变形。
环境温度变化对精度的影响
• 测量温度变化会导致测量误差的出现。
在精密测量时,如检定块规,必须规定偏离标准温度的 公差和在一定的时间内温度的允许变化范围。在测量过 程中,物体内部没有热源,偏离标准温度产生的长度误 差△可由下式给出,即
温度引起误差
• 在使用过程 中,由于温度 变化使仪器零 部件尺寸、形 状和物理参数 改变,可能影 响精度.如光学
仪器中温度对像面 的影响
例:工具显微镜
噪声,振动与灰尘干扰
• 噪声的影响是降低劳动效率1.0一25%
• 环境振动的影响主要来自两个方面;其一是大自然 和地壳内部变化因素产生的,一般振幅较小,大约 0.1um,其二也是对精密仪器影响较大的振动来 源,是人的走动,汽车行驶;机器运转等因素产生的,一
避免和减小原理误差的方法
• 尽力遵守按被测参数定义进行设计仪器和数据处
理的原则和正确的结构设计 • 原理误差进行实时修正 • 非线性刻度特性线性化原理误差的补偿 • 利用计算机技术减小原理误差 • 正确的数据处理方法
特性方程中参数变化(解决)
• 对于特性方程中参数变化产生的原理误差,如例 1 ,可分别对各参数进行实测,然后将实测结果 作为补偿信号传入测试系统中进行处理。 • 参数理论值,可以完全消除参数变化带来的原理 误差种消除取决于参数实测结果的精度。
性变形在许多情况下,将引起另一种空程——弹 性空程,也会影响精度。
减小空程误差的方法
• ①使用仪器时,采用单向运转,把间隙和弹性变 形预先消除,然后再进行使用; • ②采用间隙调整机构,把间隙调到最小; • ③提高构件刚度,以减少弹性空程; • ④改善摩擦条件,降低摩擦力,以减少由于摩擦 力造成的空程。
磨损引起误差
• 由于零件加工表面轮廓微观形状不规则,配合面有少数顶 峰接触,因而单位面积的摩擦力很大,使顶峰很快磨平, 从而迅速扩大了接触面积,磨损速度随之变慢 .
精度设计的基本原则
• 阿贝原则 ,布莱恩原则 • 最小变形原则 • 基准面选择原则 • 测量链最短原则 • 粗精分离原则
阿贝原则
• 为了使测量仪器设计所产生的误差对测量精度影 响最小,德国蔡氏厂创始人阿贝于1890年提出了 关于计量仪器设计的一个重要原则,称为阿贝原 则,在精密计量仪器设计中,阿贝原则得到广泛 应用。 • 所谓阿贝原则,即被测尺寸与标准尺寸必须在测 量方向的同一直线上,或者说,被测量轴线只有 在基准轴线的延长线上,才能得到精确的测量结 果。
旋副在其啮合范围内的螺距累积误差直接影响螺 旋副传动机构的精度。螺距误差或螺距累积误差 产生于加工过程中。采用精密螺纹磨进行精加工 可以提高零件的加工精度,但从经济的观点来分 析,精度愈高,误差愈小,制造成本也愈高。
运行误差
• 在工作过程中也会产生误差,是指外力、 自重、 力及温度变化引起的变形误差问题,振动和灰尘 的干扰误差等。 • 为了保持稳定状态,一般都采用三点定位支承。 但是,由于受外部力和变形的干扰,会影响仪器 的测量精度。
【例2】
例 绕线电位计可以通过位移的变化引起电阻变化
来实现位移的测量,在设计时的理想化特性方程为
电位计的理想化特性方程为线性直线,但在实际测 量时,电位计电刷只特性线性化
• 在一些机械、电学、气动原理的测微仪或传感器 中,由于其中存在非线性转换传动环节,使其输 入量与输出量之间的关系呈非线性. • 非线性刻度即其理论刻度特性是非线性的,但非 线性度盘难以刻划,而且工作时,还要求被测量 值的零位与度盘的零位同步,使用不便。因此, 一般希望仪器做成线性刻度,这样便带来原理误 差。
【例3】
正弦机构时,从杠杆与量杆的运动形 式表明,把直线运动转换为转动,其 传动规律为
当仪器采用正弦机构时.如果设计采用均匀刻度,由于不能满足线性传动的 要求,将产生理论误差,即杠杆接触点的弧位移aθ与量杆直线位移差
采用近似理论的原则:原理误差和仪器的各原始误差应当具有 相同的数量级。当原理误差远远大于仪器的原始误差时,一般 不可采用这种近似方案。
影响精度的主要因素
☆为了获得所需求的精度,必须对影响系统精度的各
项误差源进行分析,找出影响精度的主要因素加以 控制,设法减少其对系统精度的影响。
☆影响精度的因素也来源于设计、研制、使用过程, 原理误差 制造误差 运行误差 因素决定精度。
原理误差
☆原理误差可以分为理论误差、方案误差、技术原 理误差、机构原理误差、零件原理误差和电路控制 系统的原理误差等。 ☆产生原理误差的原因很多,如:所选测量方法的 不完善,对测试系统的特性方程作了某些近似处 理,或特性方程中的某些参数与实际情况有所不同 等。针对误差产生原因的不同有不同的处理方法, 下面讨论几种典型情况.
•
静态特性和精度
• 静态特性和精度是精密机械系统和测量控制系统 (以下简称系统)的基本特性,是产品的主要质量 指标. • 系统静态精度分析是机械学、测试学和制造学的 重要内容。 • 设计中的精度分配、制造中的精度获得、测量中 的精度确认,都必须以统一的理论、概念和术语 来描述。
系统静态精度基本方程
测量方法自身的不完善(解决)
• 在测试系统的设计过程中,所选测量方法自身的 不完善也会带来原理误差。 • 这种原理误差与系统采用近似方程式的不同地方 在于,采用近似方程式导致的原理误差主要由实 现测量方法过程中的某些因素所引起,而测量方 法自身并没有问题。
—精度理论的基本知识
主要内容
☆系统静态精度特性 ☆如何提高精度 ☆影响精度的主要因素 ☆精度设计的基本原则
精度理论应用
• 误差处理是研究在各种测量方式及测量条件下, 以最经济简便的方法得到最优的测量结果,它是 测试技术、仪器仪表及工程实验等领域不可缺少 的重要理论基础。 精度理论主要研究影响系统精度的各项误差来源 及特性,研究误差的评定和估计方法,掌握误差 的传递、转化和相互作用的规律,误差合成与分 配原则,从而为精度设计提供可靠的科学依据。
应力变形引起误差
• 零件虽然经过时效处理,内应力仍可能不平衡, 金属的晶格处于不稳定状态,使零件产生变形, 在运行时产生误差。
减小或消除应力变形
• 减小或消除内应力的一般方法是充分地进行时效 处理,切除表面应力层,用氮化代替淬火,锻造 代替轧制等。
制造误差成本控制
☆例如,螺旋副传动机构中,螺杆的螺距误差,螺
为了方便,先就集中参数独立系统的精度方程进行讨论。为了 确定一个产品技术参数的精度,设计者必须全面了解影响输出 参数不确定度的各主要有贡献的不确定度分量,为此先用符号 将各类影响分量表征如下
开环精度系统和闭环精度系统
• 按是否有精度反馈和补偿可以分为开环精度设计 和闭环精度设计。 • 开环精度设计 仅研究系统结构参数波动对精度 的影响,本身不带有精度反馈和补偿功能。开环 精度设计是系统基本结构上的精度设计。 • 闭环精度设计 在开环精度设计基础上研究精度 反馈和补偿。带有精度反馈和补偿装置。
原理误差-近似数据处理带来的
• 数据处理方法上的近似带来的原理误差。
• 用近似计算公式进行运算带来的原理误差。 • 数值舍位带来的原理误差。
例如 用激光干涉方法测量位移
• 位移量可以表达 为脉冲当量q与其脉冲个数n的乘积。 设激光波长0.63281984um。当激光测量系统在经过光学 和电学的64倍细分之后,则一个脉冲当量为q=0.63281984 /64=0.00988781/um。 用这个数作为脉冲当量,再乘以脉冲数进行读数,是不方 便的。因为,通常分辨率以0.1um、0.01um计比较方便。 这样,对激光干涉测量读数,就需要进行数据上的处理, 由此产生了相应的原理误差。
开环系统静态参数方程
开环系统静态精度方程
闭环系统静态参数方程
闭环系统静态精度方程
闭环系统静态精度方程
如何提高精度?
☆在精密工程发展初期,提高精度水平的主要途
径是完善传统技术. ☆ 随着精度水平的进一步提高、如果继续提高精 度水平,除采用新技术外,必须考虑各误差源 的影响方式及如何消除其影响。
运动特性
• 精密测试仪器运动装置的精度除取决于运动机 构结构设计和形状特性外,还取决于运动机构 之间由于相对运动产生的变形、运动速度及惯 性。
运动装置变形对测量误差的影响
• 影响仪器精度的因素是仪器运动装置的自重及由 于运动引起重量移动造成的变形的影响
运动惯性和支承点位置的影响
• 在连续接触式动态测量中,测量头的质量及支点 的位置会影响动态测量的响应特性.
般振幅达到1~5um,频率5~30Hz。
• 高精度的测量必须考虑环境灰尘的影响,清洁度的 控制对精密仪器是非常重要的。
减小振动影响的办法
• 在高精度计量仪器中,尽量避免采用间歇运动机 构,而用连续扫描或匀速运动机构; • 零部件的自振频率要避开外界振动频率; • 采取各种防振措施,如防振墙、防振地基、防振 垫等; • 通过柔性环节使振动不传到仪器主体上。
原理误差-简化机构带来的
• 一种情况是用简单 的机构来代替复杂 的机构,用简单的 运动关系来表达复 杂的运动关系,另 一种情况是利用具 有单一主动件的简 单机构实现多元函 数作用方程。
原理误差-测量原理和方法不完善
• 有些仪器的测量原理,没 有遵守按被测参数定义进 行测量的原则进行设计, 则仪器在测量原理或方法 上便存在原理误差。
原理误差-参数理论值与实际值不符
• 系统特性方程中参数理论值与实际值不符假定测试系统 的理论特性方程式为
而测试系统的实际方程式为
可见,特性方程中各物理参数都有误差 系统原理误差为
【例 1】
气压式高度表在对流层内的理论特性方程式为
则它们引起的原理误差为
原理误差-近似方程式
在实际应用中,也经常会遇到系统特性方程采用 近似方程式的情况。 假定特性方程理论方程式为 y 0= f0 ( x ) ,而近 似方程式为 y = f ( x ) ,则原理误差为
重心位置变化产生的变形
• 工作台沿导轨移动,重心位置随着改变,使仪器 产生变形。
环境温度变化对精度的影响
• 测量温度变化会导致测量误差的出现。
在精密测量时,如检定块规,必须规定偏离标准温度的 公差和在一定的时间内温度的允许变化范围。在测量过 程中,物体内部没有热源,偏离标准温度产生的长度误 差△可由下式给出,即
温度引起误差
• 在使用过程 中,由于温度 变化使仪器零 部件尺寸、形 状和物理参数 改变,可能影 响精度.如光学
仪器中温度对像面 的影响
例:工具显微镜
噪声,振动与灰尘干扰
• 噪声的影响是降低劳动效率1.0一25%
• 环境振动的影响主要来自两个方面;其一是大自然 和地壳内部变化因素产生的,一般振幅较小,大约 0.1um,其二也是对精密仪器影响较大的振动来 源,是人的走动,汽车行驶;机器运转等因素产生的,一
避免和减小原理误差的方法
• 尽力遵守按被测参数定义进行设计仪器和数据处
理的原则和正确的结构设计 • 原理误差进行实时修正 • 非线性刻度特性线性化原理误差的补偿 • 利用计算机技术减小原理误差 • 正确的数据处理方法
特性方程中参数变化(解决)
• 对于特性方程中参数变化产生的原理误差,如例 1 ,可分别对各参数进行实测,然后将实测结果 作为补偿信号传入测试系统中进行处理。 • 参数理论值,可以完全消除参数变化带来的原理 误差种消除取决于参数实测结果的精度。
性变形在许多情况下,将引起另一种空程——弹 性空程,也会影响精度。
减小空程误差的方法
• ①使用仪器时,采用单向运转,把间隙和弹性变 形预先消除,然后再进行使用; • ②采用间隙调整机构,把间隙调到最小; • ③提高构件刚度,以减少弹性空程; • ④改善摩擦条件,降低摩擦力,以减少由于摩擦 力造成的空程。
磨损引起误差
• 由于零件加工表面轮廓微观形状不规则,配合面有少数顶 峰接触,因而单位面积的摩擦力很大,使顶峰很快磨平, 从而迅速扩大了接触面积,磨损速度随之变慢 .
精度设计的基本原则
• 阿贝原则 ,布莱恩原则 • 最小变形原则 • 基准面选择原则 • 测量链最短原则 • 粗精分离原则
阿贝原则
• 为了使测量仪器设计所产生的误差对测量精度影 响最小,德国蔡氏厂创始人阿贝于1890年提出了 关于计量仪器设计的一个重要原则,称为阿贝原 则,在精密计量仪器设计中,阿贝原则得到广泛 应用。 • 所谓阿贝原则,即被测尺寸与标准尺寸必须在测 量方向的同一直线上,或者说,被测量轴线只有 在基准轴线的延长线上,才能得到精确的测量结 果。
旋副在其啮合范围内的螺距累积误差直接影响螺 旋副传动机构的精度。螺距误差或螺距累积误差 产生于加工过程中。采用精密螺纹磨进行精加工 可以提高零件的加工精度,但从经济的观点来分 析,精度愈高,误差愈小,制造成本也愈高。
运行误差
• 在工作过程中也会产生误差,是指外力、 自重、 力及温度变化引起的变形误差问题,振动和灰尘 的干扰误差等。 • 为了保持稳定状态,一般都采用三点定位支承。 但是,由于受外部力和变形的干扰,会影响仪器 的测量精度。
【例2】
例 绕线电位计可以通过位移的变化引起电阻变化
来实现位移的测量,在设计时的理想化特性方程为
电位计的理想化特性方程为线性直线,但在实际测 量时,电位计电刷只特性线性化
• 在一些机械、电学、气动原理的测微仪或传感器 中,由于其中存在非线性转换传动环节,使其输 入量与输出量之间的关系呈非线性. • 非线性刻度即其理论刻度特性是非线性的,但非 线性度盘难以刻划,而且工作时,还要求被测量 值的零位与度盘的零位同步,使用不便。因此, 一般希望仪器做成线性刻度,这样便带来原理误 差。
【例3】
正弦机构时,从杠杆与量杆的运动形 式表明,把直线运动转换为转动,其 传动规律为
当仪器采用正弦机构时.如果设计采用均匀刻度,由于不能满足线性传动的 要求,将产生理论误差,即杠杆接触点的弧位移aθ与量杆直线位移差
采用近似理论的原则:原理误差和仪器的各原始误差应当具有 相同的数量级。当原理误差远远大于仪器的原始误差时,一般 不可采用这种近似方案。
影响精度的主要因素
☆为了获得所需求的精度,必须对影响系统精度的各
项误差源进行分析,找出影响精度的主要因素加以 控制,设法减少其对系统精度的影响。
☆影响精度的因素也来源于设计、研制、使用过程, 原理误差 制造误差 运行误差 因素决定精度。
原理误差
☆原理误差可以分为理论误差、方案误差、技术原 理误差、机构原理误差、零件原理误差和电路控制 系统的原理误差等。 ☆产生原理误差的原因很多,如:所选测量方法的 不完善,对测试系统的特性方程作了某些近似处 理,或特性方程中的某些参数与实际情况有所不同 等。针对误差产生原因的不同有不同的处理方法, 下面讨论几种典型情况.
•
静态特性和精度
• 静态特性和精度是精密机械系统和测量控制系统 (以下简称系统)的基本特性,是产品的主要质量 指标. • 系统静态精度分析是机械学、测试学和制造学的 重要内容。 • 设计中的精度分配、制造中的精度获得、测量中 的精度确认,都必须以统一的理论、概念和术语 来描述。
系统静态精度基本方程
测量方法自身的不完善(解决)
• 在测试系统的设计过程中,所选测量方法自身的 不完善也会带来原理误差。 • 这种原理误差与系统采用近似方程式的不同地方 在于,采用近似方程式导致的原理误差主要由实 现测量方法过程中的某些因素所引起,而测量方 法自身并没有问题。
