第二章 逻辑函数及逻辑门
第2章 逻辑代数基础
A B
冗余律: AB A C BC AB A C
证明: AB A C BC
AB A C ( A A) BC
AB A C ABC A BC
互补率A+A=1 分配率 A(B+C)=AB+AC 0-1率A+1=1
AB(1 C) A C(1 B)
1、并项法
利用公式A+A=1,将两项合并为一项,并消去一个变量。 运用分配律 变并 相 和 包 量成 同 反 含 Y1 ABC A BC BC ( A A ) BC BC 的一 时 变 同 若 因项 , 量 一 两 BC BC B(C C ) B 子, 则 , 个 个 。并 这 而 因 乘 运用分配律 消两其子积 去项他的项 Y2 ABC AB AC ABC A( B C ) 互可因原中 ABC ABC A( BC BC) A 为以子变分 反合都量别 运用摩根定律
(2)反演规则:对于任何一个逻辑表达式Y,如果将表达式 中的所有“·”换成“+”,“+”换成“·”,“0”换成“1”, “1”换成“0”,原变量换成反变量,反变量换成原变量,那么 所得到的表达式就是函数Y的反函数Y(或称补函数)。这个规 则称为反演规则。例如:
Y AB CD E
Y A B C D E
A A B A 吸收率: A ( A B) A
A ( A B) A B A A B A B
证明: A A B ( A A)(A B)
分配率 A+BC=(A+B)(A+C)
1 ( A B)
互补率A+A=1
第2章 逻辑门电路-习题答案
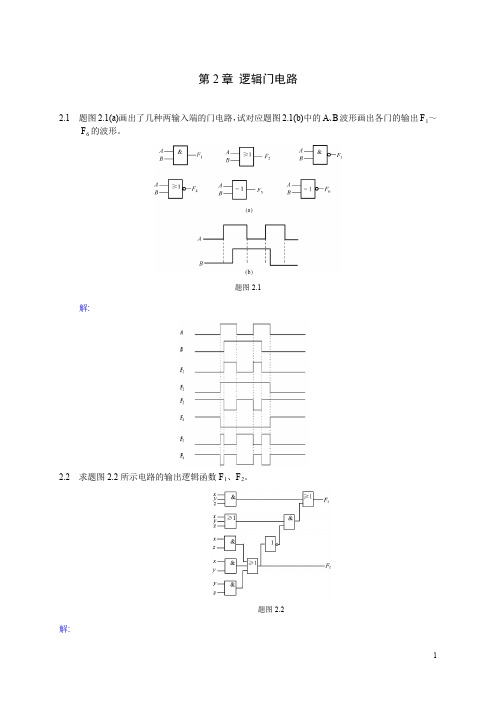
第2章逻辑门电路2.1 题图2.1(a)画出了几种两输入端的门电路,试对应题图2.1(b)中的A、B波形画出各门的输出F1~F6的波形。
题图2.1解:2.2 求题图2.2所示电路的输出逻辑函数F1、F2。
题图2.2解:2.3 题图2.3中的电路均为TTL门电路,试写出各电路输出Y1~Y8状态。
题图2.3解: Y1=0, Y2=0, Y3=Hi-Z, Y4=0, Y5=0, Y6=0, Y7=0, Y8=0.2.4 题图2.4中各门电路为CMOS电路,试求各电路输出端Y1、Y2和Y的值。
题图2.4解: Y1=1, Y2=0, Y3=0.2.5 6个门电路及A、B波形如题图2.5所示,试写出F1~F6的逻辑函数,并对应A、B波形画出F1~F6的波形。
题图2.5解:2.6 电路及输入波形分别如题图2.6(a)和2.6(b)所示,试对应A、B、C、x1、x2、x3波形画出F端波形。
题图2.6解:2.7 TTL与非门的扇出系数N是多少?它由拉电流负载个数决定还是由灌电流负载决定?解: N≤8 N由灌电流负载个数决定.2.8 题图2.8表示三态门用于总线传输的示意图,图中三个三态门的输出接到数据传输总线,D1D2、D3D4、…、D m D n为三态门的输入端,EN1、EN2、EN n分别为各三态门的片选输入端。
试问:EN信号应如何控制,以便输入数据D1D2、D3D4、…、D m D n顺序地通过数据总线传输(画出EN1~EN n 的对应波形)。
题图2.8解:用下表表示数据传输情况2.9 某工厂生产的双互补对称反相器(4007)引出端如题图2.9所示,试分别连接成:(1)反相器;(2)三输入与非门;(3)三输入或非门。
题图2.9解: (1) 反向器(2)与非门 (3)或非门2.10 按下列函数画出NMOS 电路图。
123()()()F AB CD E H G F A B CD AB CD F A B=+++=+++=⊕解:(1)(2) (3)2.11 将两个OC门如题图2.11连接,试写出各种组合下的输出电压u o及逻辑表达式。
数字电路 第二章 逻辑代数与逻辑函数化简

= A+ B+ A+ C
或与式转换为与或非式
F = (A + B)(A + C)
= A+ B+ A+ C
= AB + AC
§2.4.3 逻辑函数的代数法化简
化简的意义:将逻辑函数化成尽可能简单的形式,以减少逻辑门 化简的意义:将逻辑函数化成尽可能简单的形式,
电路的个数,简化电路并提高电路的稳定性。 电路的个数,简化电路并提高电路的稳定性。
A + AB = A + B
E = A+ B+ C+ BCD+ BC = A + B + C+ C(BD+ BE) = AB + C+ BE+ BD
§2.5.1 逻辑函数的最小项表达式 公式化简法评价:
优点:变量个数不受限制。 缺点:目前尚无一套完整的方法,结果是否最简有时不 易判断。
卡诺图是按一定规则画出来的方框图,是逻辑 函数的图解化简法,同时它也是表示逻辑函数 的一种方法。 利用卡诺图可以直观而方便地化简逻辑函数。 它克服了公式化简法对最终化简结果难以确定 等缺点。
__
__________ __________ _
A + B + C+⋯ = ABC⋯
逻辑代数的基本定律: 逻辑代数的基本定律: P21,熟记 ,
§2.3.2 逻辑代数的基本规则
代入规则
AB = A + B
____
A ↔F = AC
反演规则
____
⇒ ACB = AC + B
F = AC+ BCD+ 0
第二章-逻辑函数及其简化

A 0 0 1 1
B 0 1 0 1
Y 1 0 0 1
例2 有X、Y、Z三个输入变量,当其中两个或两个以上取值 为1时,输出F为1;其余输入情况输出均为0。试写出描述此 问题的逻辑函数表达式。 解:三个输入变量有23=8种不同组合,根据已知条件可得真值表 如 下:
由真值表可知,使F=1的输入变量组合有4个,所以F的与—或 表达式为:
F XYZ X Y Z XY Z XYZ
2)逻辑函数的表示方法
(1)真值表 逻辑函数的真值表具有唯一性。逻辑函数有n个变量时, 共有2n个不同的变量取值组合。在列真值表时,变量取值 的组合一般按n位二进制数递增的方式列出。用真值表表 示逻辑函数的优点是直观、明了,可直接看出逻辑函数值 和变量取值之间的关系。
对偶关系
A(A+B)=AB
4)包含律
证明:
AB+AC+BC=AB+AC
AB+AC+BC =AB+AC+(A+A)BC =AB+AC+ABC+ABC =AB(1+C)+AC(1+B) =AB+AC
对偶关系
5) 关于异或和同或运算
对偶数个变量而言, 有 A1A2... An=A1 A2 ... An
对奇数个变量而言, 有 A1A2... An=A1 A2 ... An
异或和同或的其他性质:
A 0= A 1= A A= A (B C)=(A B ) C A (B C)=AB AC
A 1=A A 0 =A A A= 1 A (B C)=(A B) C A+(B C )=(A+B) (A+C)
2009数字[第二课 逻辑函数和逻辑门]
![2009数字[第二课 逻辑函数和逻辑门]](https://img.taocdn.com/s3/m/cb2e2c18f18583d049645926.png)
4 〉 逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的,可以有多 种形式,并且能互相转换。 例如:
其中,与—或表达式是逻辑函数的最基本表达形式。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
5 〉 表 达 式 → 电 路 图
(1)用与非门实现(Y=AB)
•非:Y=A=AA
•与:Y=AB=AB •或:Y=A+B=A+B=A B
L=A+B
4 、 其 他 常 用 逻 辑 运 算
3〉异或: A
B = AB + AB 相同为0 A A=0 相异为1 A A=1
A 1=? A A 0=? A
4〉同或: A⊙ B = A B=AB + AB 相同为1 相异为0
@ Copyright 杭州电子科技大学 电子信息学院 张珣
二、逻辑函数及其表示方法
* 表 示 方 式
逻辑变量、逻辑函数、真值表、逻辑电路等。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
一、与或非代数系统基本逻辑关系
1、与: Y=X1^X2=X1.X2=X1X2 (逻辑乘) X1 X2 Y
全1为1
有0则0
例: 1^1=? 1^0=? 0^1=? 0^0=?
1 0 0 0
在应用反演规则求反函数时要注意两点: (1)保持运算的优先顺序不变,必要时加括号表明。 (2)变换中,几个变量(一个以上)的公共非号保持不变。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
2 、逻辑规则
4〉展开规则: Y=f(X1,X2,X3,…,Xk) =X1f(0,X2,…,Xk)+X1f(1, X2,…,Xk) =[X1+f(0,X2,…,Xk)][X1 + f(1, X2,…,Xk)]
数字电路知识点总结(精华版)

数字电路知识点总结(精华版)数字电路知识点总结(精华版)第一章数字逻辑概论一、进位计数制1.十进制与二进制数的转换2.二进制数与十进制数的转换3.二进制数与十六进制数的转换二、基本逻辑门电路第二章逻辑代数逻辑函数的表示方法有:真值表、函数表达式、卡诺图、逻辑图和波形图等。
一、逻辑代数的基本公式和常用公式1.常量与变量的关系A + 0 = A,A × 1 = AA + 1 = 1,A × 0 = 02.与普通代数相运算规律a。
交换律:A + B = B + A,A × B = B × Ab。
结合律:(A + B) + C = A + (B + C),(A × B) × C = A ×(B × C)c。
分配律:A × (B + C) = A × B + A × C,A + B × C = (A + B) × (A + C)3.逻辑函数的特殊规律a。
同一律:A + A = Ab。
摩根定律:A + B = A × B,A × B = A + Bc。
关于否定的性质:A = A'二、逻辑函数的基本规则代入规则在任何一个逻辑等式中,如果将等式两边同时出现某一变量 A 的地方,都用一个函数 L 表示,则等式仍然成立,这个规则称为代入规则。
例如:A × B ⊕ C + A × B ⊕ C,可令 L = B ⊕ C,则上式变成 A × L + A × L = A ⊕ L = A ⊕ B ⊕ C。
三、逻辑函数的化简——公式化简法公式化简法就是利用逻辑函数的基本公式和常用公式化简逻辑函数,通常,我们将逻辑函数化简为最简的与或表达式。
1.合并项法利用 A + A' = 1 或 A × A' = 0,将二项合并为一项,合并时可消去一个变量。
数字电路第2章逻辑代数基础及基本逻辑门电路

(5)AB+A B = A (6)(A+B)(A+B )=A 证明: (A+B)(A+B )=A+A B+AB+0 A( +B+B) = 1 JHR A =
二、本章教学大纲基本要求 熟练掌握: 1.逻辑函数的基本定律和定理; 门、 2.“与”逻辑及“与”门、“或”逻辑及“或”
“非”逻辑及“非”门和“与”、“或”、“非” 的基本运算。 理解:逻辑、逻辑状态等基本概念。 三、重点与难点 重点:逻辑代数中的基本公式、常用公式、 基本定理和基本定律。
JHR
难点:
JHR
1.具有逻辑“与”关系的电路图
2.与逻辑状态表和真值表
JHR
我们作如下定义: 灯“亮”为逻辑“1”,灯“灭”为逻辑“0” 开关“通”为逻辑“1”,开关“断”为逻辑 “0” 则可得与逻辑的真值表。 JHR
3.与运算的函数表达式 L=A·B 多变量时 或 读作 或 L=AB L=A·B·C·D… L=ABCD… 1.逻辑表达式 2.逻辑符号
与非逻辑真值表
Z = A• B
3.逻辑真值表
逻辑规律:有0出1 全1 出0
JHR
A 0 0 1 1
B 0 1 0 1
Z 1 1 1 0
二、或非逻辑 1.逻辑表达式 2.逻辑符号
Z = A+ B
先或后非
3.逻辑真值表
JHR
三、与或非逻辑 1.逻辑表达式 2.逻辑符号
1.代入规则 在任一逻辑等式中,若将等式两边出现的同 一变量同时用另一函数式取代,则等式仍然成立。
JHR
代入规则扩大了逻辑代数公式的应用范围。例如摩 根定理 A+B = A ⋅ B 若将此等式两边的B用B+C 取代,则有
高二通用技术---逻辑门

00
1
01 4
6
14
11
10
9
(2) 四个相邻最小项合并可以消去两个因子
CD AB 00 01 11 10
00 0
32
01 4
11 12
10 8
11 10
CD AB 00 01 11 10
00 0
2
01
57
11
13 15
10 8
10
(3) 八个相邻最小项合并可以消去三个因子
CD AB 00 01 11 10
[例] 证明: 德 摩根定理
A+A=A
A B AB
A B A B 00 0 1 01 0 1 10 0 1 11 1 0
AB
A B
11 1 0 1 1
10 1 1 0 0
01 1 1 0 0
00 0 1 0 0
相等
相等
五、关于等式的三个规则
1. 代入规则: 等式中某一变量都代之以一个逻 辑函数,则等式仍然成立。
A BC ( A B) ( A C)
[例 ] 证明公式 [解] 方法一:公式法
右式 ( A B)( A C) A A A C A B B C A AC AB BC A(1 C B) BC A BC 左式
证明公式 方法二:真值表法(将变量的各种取值代入等式
(2) 或非逻辑
(NOR)
A ≥1
B
Y2 A B
(3) 与或非逻辑
A
(AND – OR – INVERT) B
Y3 AB CD
C D
Y1、Y2 的真值表
Y1
A B Y1 Y2
00 11
01 10
Y2 1 0 1 0 11 00
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2)A+AB=B+BA=A+B 证明: A+AB
= A(B+B)+AB =AB+AB+AB
= AB+AB+AB +AB =A+B
*逻辑规则
1)代入规则: 指在一个逻辑等式中,如将其中某个变量,都代之 以另一个逻辑函数,则该等式依然成立 在摩根律AB=A+B中用BC代替B,得:
代数法化简函数
例8:试简化函数F AC AD BD BC
利用反演律
解: F AC AD BD BC
AC配项BC加ADB (A B)
AC BC DAB消因律 AC 消B项CABAB DAB
AC BC AB D
F(或与式)求对偶式 F(与或式)简化 F
AC BC(最D简与或式)求对偶式 F(最简或与式)
表 输入
输出
A
B
L
A
=1
0
0
0
0
1
1
B
1
0
1
1
1
0
L=A + B
4)同或(异或非)
AB F 00 1 01 0 10 0 11 1
“⊙”同或逻辑
逻辑表达式 运算符 F=A B= AB
逻辑符号
A
=1
F
B
二、逻辑函数的运算定律及规则
常用公式: 1)摩根公式:
AB=A+B A+B=A B
推广:ABC=ABC=A+B+C A+B+C=A+B+C=A B C
3)、未完全描述函数的真值表及表达式
完全描述的逻辑函数:真值表中各行的输出都是明确的, 非0即1
符所构成的表达式。
3.逻辑图——由逻辑符号及它们之间的连线而构成的图形。
C合,A、B中 均
有一断个,合F,灭F亮 C开,F灭 A B C F 断“0” 0 0 0 0 00 1 0
合“1” 0 1 0
0
01 1 亮“1” 1 0 0
1 0
10 1 1
灭“0” 1 1 0
0
11 1 1
输入变量取值为1用原变量表
A.(BC)=A+BC=A+B+C
2)对偶规则 一个逻辑函数Y,如将其中的与换成或,或 换成与,0换成1,1换成0,而变量及反变量 本身保持不变,经这样置换后的新函数Y*, 便是原函数Y的对偶函数。
Y=AB+BC(A+BC)
Y*=(A+B )[B+C+A(B+C)]
与或互换、0和1互换,变量和反变量不变,非不变。
的对应最大项
• 然后将这些项逻辑乘
F(A、B、C)
A B C mi Mi F
000 0 001 1 010 2 011 3 100 4 101 5 110 6 111 7
00 10 20 31 40 51 61 71
( A B C)( A B C)( A B C)( A B C)
M 0M1M 2M 4 M (0,1,2,4) Nhomakorabea即:
mi = Mi Mi = mi
• 若干个最小项之和表示的表达式F,其反函数F可 用等同个与这些最小项相对应的最大项之积表示。
例: F m1 m3 m5 m7
F m1 m3 m5 m7
= m1• m3 • m5 • m7 = M1 • M3 • M5 • M7
2)、逻辑函数的标准形式 式中的每一个乘
2
M2
3
M3
4
M4
5
M5
6
M6
7
M7
最大项的性质:
• 任意一组变量取值,只有一个最大 项 的值为0,其它最大项的值均为1
• 同一组变量取值任意两个不同最大项 的和为1。即Mi+Mj=1 (i≠j) 2n 1
• 全部最大项之积为0,即 Mi 0 i0
• 最小项与最大项的关系
• 相同编号的最小项和最大项存在互补关系
2)或运算
A
B
V
L
A
≥1
L=A+B
B
或逻辑表达式:
L=A+B
A
不闭合 不闭合
闭合 闭合
B
不闭合 闭合 不闭合 闭合
灯L
不亮 亮 亮 亮
或逻辑真值表
输入
输出
A
B
L
0
0
0
0
1
1
1
0
1
1
1
1
或逻辑——当决定一件事情的几个条件中,只要有一个 或一个以上条件具备,这件事情就发生。
3)非运算
R
V
A
A
灯L
闭合
• 或与表达式的简化
2、用卡诺乘积图项化简和项函数
1)、 最小项和最大项
最小项: n个变量的逻辑函数中,包最括小全项部编n号个i变-各量输入变 的乘积项(每个变量必须量而取且值只看能成以二原进变制数, 量或反变量的形式出现一次)对应的十进制数
n个变量有2n个最小项,记作mi 3个变量有23(8)个最小项
逻辑函数式
• 挑出函数值为1的项
示;反之,则用反变量表示 ABC、ABC、ABC
• 每个函数值为1的输入变量取值组合写成一个乘积项
• 这些乘积项作逻辑加 F= ABC+ABC+ABC
例1. 三个人表决一件事情,结果按“少数服从多数”的
原则
决定,试建立该逻辑函数。
解:第一步:设置自变量和因变量。 第二步:状态赋值。 对于变量A、B、C设: 同意为逻辑“1”, 不同意为逻辑“0”。
010 2 2 0 011 3 3 1
100 4 4 0
ABC ABC ABC ABC 1 0 1 5 5 1
m3 m5 m6 m7
110 6 6 1 111 7 7 1
m(3、5、6、7)
• 最大项(标准和)之积表达式
例11:已知函数的真值表,写出该函数的最大项之积表达式
解: • 从真值表找出F为0
A B C
000
0
M0
A B C
001
1
M1
ABC
010
2
M2
ABC
011
3
M3
ABC
100
4
M4
ABC
101
5
M5
ABC
110
6
M6
ABC
111
7
M7
最大项 二进制数 十进制数 编号
A B C
000
A B C
001
ABC
010
ABC
011
ABC
100
ABC
101
ABC
110
ABC
111
0
M0
1
M1
AB(C C) A BC ABC ABC A BC
m3 m2 m1 m(1、2、3)
例10:已知函数的真值表,写出该函数的标准积之和表达式
解: • 从真值表找出F为1
的对应最小项
A B C mi Mi F
• 然后将这些项逻辑加
000 0 0 0 001 1 1 0
F(A、B、C)
1
0
1
1
1
0
& L=A·B
2)或非 —— 由或运算和 非运算组合 而成。
“或非”真值
表 输入
输出
A
B
L
A
≥1
0
0
1
0
1
0
B
1
0
0
1
1
0
L=A+B
3)异或
异或是一种二变量逻辑运算,当两个变量取值相同时, 逻辑函数值为0;当两个变量取值不同时,逻辑函数值为1。
异或的逻辑表达式为: L A B
“异或”真值
m5
m6
m7
2n-1
F mi
ABC ABC ABC
i0
00 0
1
00 0
1
00 0
1
00 0
1
00 0
1
10 0
1
01 0
1
00 1
1
• 最大项
最大项:n个变量的逻辑函数中,包括全部n个变量 的和项(每个变量必须而且只能以原变量
或反变量的形式出现一次)
n个变量有2n个最大项,记作i
最大项 二进制数 十进制数 编号
1
0
四、逻辑函数的简化
函数的简化依据
• 逻辑电路所用门的数量少 • 每个门的输入端个数少 • 逻辑电路构成级数少 • 逻辑电路保证能可靠地工作
降低成本
提高电路的工作 速度和可靠性
返回
1、代数法化简函数 • 实现电路的与门少 • 下级最或简门式输的入标端准个数少
• 与或表达式的简化
与• 门首的先输是入式端中个乘数积少项最少
00 1
1
01 1
1
10 1
1
11 0
0
1
1
0
0
0
0
0
0
A• B= A+B A+ B=AB
例7、试用真值表证明 AB AB AB AB
A B AB AB AB AB AB+AB AB+AB AB+AB
001 0 0 0 0
1
0
010 1 0 0 1
0
1
100 0 1 0 1
