材料热力学练习三:各种热力学性质的计算
3.4 热力学性质的计算

P
Ml (T1,P1) C
Mv (T2,P2) t
T
22:48:09
纯物质的热力学性质计算
对于均相纯物质,当给定两个强度性质(通常是p,V,T中的 任意两个)后,其他的热力学性质就能计算了,所用模型主 要是状态方程。 纯物质的热力学性质计算,主要计算偏离焓、偏离熵以及逸度 系数等,可借助计算软件ThermalCal进行。 例题3-8(陈新志P46例3-4) 计算异丁烷在400K,2.19MPa 时的压缩因子、偏离焓、偏离熵、逸度系数。
解 : 三 元 均 相 混 合 物 体 系 的 自 由 度 为 4 , 给 定 了 T=310.8K , P=15.2MPa , y1 = 0.82, y2 = 0.10, y3 = 0.08 后 体 的 质 确 下 了 , 系 性 就 定 来
计算PR方程常数需要临界参数和偏心因子,查得
临界温度、临界压力和偏心因子 组分(i) 甲烷(1) 氮气(2) 乙烷(3) 计算过程如下:
例题3-9(陈新志P46例3-5 )试用PR方程计算在200℃、7MPa 下丁烯-1蒸汽的V、H、S。假设0℃的丁烯-1饱和液体的H、S 为零,已知:Tc=419.6K,Pc=4.02MPa,ω=0.187;0℃时丁 烯-1的饱和蒸汽压是Ps=0.1272MPa;
ig CP R =1.967 + 31.63×10−3T − 9.837 ×10−6T 2
T2
∫
1
ig CP P dT − Rln 2 ≈ 22.15J mol-1K-1 (熵 R ) RT P 1 T
T2
∫
1
V2 = 286.41cm 3 mol-1
S(T2 , P ) = 8.314× (−1.6236) − 8.314× (− 9.6202) + 22.15 = 88.63J mol-1K-1 2
3.2 热力学性质的计算

k
1 ∂V =− V ∂P 。 T
提示:设V=V(T,P), 求出dV表达式。
解:设V=V(T,P), ∂V 则dV= ∂T • dT +
P
∂V • dP ∂P T
而β
1 =V
∂V , ∂T P
②第二dS方程 ②第二dS方程 当S=S(T,P)时, 则dS= + , 压,不做非体积功W’时, W’ 有 =dH=CpdT, 又由CpdT=TdS+VdP=TdS
而等
(dP=0)
∴dS= 又 =-
,即
=
,
(马氏)
(由dG=-SdT+VdP得到),故有: dS= 第二dS方程
积分有: S-S0=△S= 当为理想气体时: ∵ = =
,而
V ∂T P
,
∴dS= - βVdP (第二dS) dH= CpdT + V (1 − βT )dP (第二dH) 由于k 和β 对于液体而言受压力影响 很小,故常设其为常数,积分时该 常数可以取区间的算术平均值。
CpdT T
3.2.2 剩余(多余)性质法
前面介绍了直接从热力学函数的导 数关系式计算热力学性质,还可使用 多余性质法计算(更为方便)。 (剩)多余性质:气体在真实状态下 的热力学性质与在同样温度、压力下 假设气体处于理想状态下热力学性质 之间的差额。
由Cv=
= ,等容时, 不做W’),
(由dU= + =0,有dU=
又由dU=TdS-PdV= TdS (∵dV=0)
∴Cv= 即 又
= = Cv/T =
=T
,
材料热力学习题集

问:1)当混合气体(97%H2O + 3%H2, 体积)在 1000 K 是否能将 Ni 氧化? 2)现有 Ni-Au 固溶体(XNi = 0.1)。已知在 1000 K 时, 与此合金平衡的氢气体体积
例题 6-8 右图所示是铜和铜铝合金(18 at.% Al)在 700℃温度下扩散退火 38.4 天的浓度分
布曲线。求当 Al 的浓度为 4 at%时,Al 在 Cu 中的扩散系数。
18
Cu - Al
Cu
16
A
14
C , at.% Al
12
k
Matano interface
10
8 mark interface
.
材料热力学上课题目
例 1-1 已知液体铅在 1 个大气压下的热容量 Cp(l)为 Cp(l)=32.43-3.10×10-3T J/(mol·k),固 体铅的热容量 Cp(s)为 Cp(s)=23.56+9.75×10-3T J/(mol·k),已知液体铅在熔点(600 K)凝固为固 体时放热 4811.60 J/mol,求液体铅过冷至 590K 凝固为固体时焓的变化。
6
4
2
A
1
0 -10 -8 -6 -4 -2 0 2 4 6 8 10
x
六大 板块
第一章 第二章 第三章 第四章 第五章 第六章
物理化学复习纲要
热力学定律(热力学第一定律、热力学第二定律) 自由能(ΔF、ΔG) 热力学状态函数、关系式及应用 相变热力学 溶液 扩散
.
材料热力学练习题

1、由5个粒子所组成的体系,其能级分别为0、ε、2ε及3ε,体系的总能量为3ε。
试分析5个粒子可能出现的分布方式;求出各种分布方式的微观状态数及总微观状态数。
2、有6个可别粒子,分布在4个不同的能级上(ε、2ε、3ε及4ε),总能量为10ε,各能级的简并度分别为2、2、2、1,计算各类分布的Ωj 及Ω总。
3、振动频率为ν的双原子分子的简谐振动服从量子化的能级规律。
有N 个分子组成玻耳兹曼分布的体系。
求在温度T 时,最低能级上分子数的计算式。
4、气体N 2的转动惯量I =1.394⨯10-46kg ⋅m 2,计算300K 时的Z J 。
5、已知NO 分子的Θυ=2696K ,试求300K 时的Z υ。
~J υ7、计算300K 时,1molHI 振动时对内能和熵的贡献。
8、在298K 及101.3kPa 条件下,1molN 2的Z t 等于多少?9、在300K 时,计算CO 按转动能级的分布,并画出分子在转动能级间的分布曲线。
10、计算H 2及CO 在1000K 时按振动能级的分布,并画出分子在振动能间的分布曲线;再求出分子占基态振动能级的几率。
11、已知HCl 在基态时的平均核间距为1.264⨯10-10m ,振动波数ν~=2990m -1。
计算298K 时的Θm S 。
12、证明1mol 理想气体在101.3kPa 压力下Z t =bLM 3/2(T /K )5/2 (b 为常数)13、计算1molO 2在25︒C 及101.3kPa 条件下的Θm G 、Θm S 及Θm H 。
设Θ0U 等于零。
14、已知300K 时金刚石的定容摩尔热容C V ,m =5.65J ⋅mol -1⋅K -1,求ΘE 及ν。
15.已知300K 时硼的定容摩尔热容C V ,m =10.46J ⋅mol -1⋅K -1,求(1) ΘD ;(2) 温度分别为30K 、50K 、100K 、700K 、1000K 时的C V ,m 值;(3) 作C V ,m 值− T 图形。
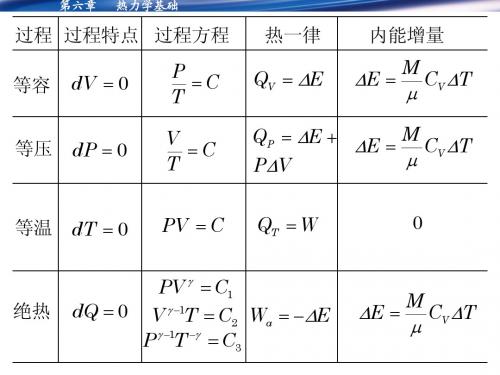
热力学小结与习题
= 0,∴∆E = 0
Q = ∆ E + W = W = 1 .25 × 10 J
第六章
热力学基础
双原子分子理想气体经过如图的过程, 例 1mol 双原子分子理想气体经过如图的过程,其 为绝热过程、 中1— 2 为直线过程 、2— 3 为绝热过程、3— 1 为等温 过程.已知 T1, T2 = 2T1 , V3 = 8V1 .求:1)各过程的功、 过程 已知 求 )各过程的功、 热量和内能变化; )此循环热机效率. 热量和内能变化;2)此循环热机效率 p 解 1): 1— 2
第六章
热力学基础
例:讨论理想气体下图过程中,各过程 讨论理想气体下图过程中,
P A* 1 O 2 绝热 *B V
Q 的正负。
A— B
QAB = 0
WAB = −∆E AB > 0
A— 1— B
QA1B = ∆EAB + WA1B = WA1B −WAB ∵W A1B < W AB ∴ Q A1B < 0
p
A
p=C
解
B
QAB = ∆EAB + WAB
Q AC = W AC
T =C
C
QAD = 0
∵ W AB > W AC > W AD
dQ = 0
D
∆EAB > 0 , ∆EAD < 0
o VA
VB V
∴ Q AB > Q AC > Q AD = 0
第六章
热力学基础
例 一定量理想气体的 图所示, 循环过程如 P-V 图所示, 请填写表格中的空格. 请填写表格中的空格
P A 等温 B
绝热
o
内能增量ΔE/J Δ 0 A→B 过程 B→C C→D D→A ABCD -50 -100 150 50 50 -50 0
热力学练习题全解

热力学练习题全解热力学是研究热能转化和热力学性质的科学,它是物理学和化学的重要分支之一。
在热力学中,我们通过解决一系列练习题来巩固和应用所学知识。
本文将为您解答一些热力学练习题,帮助您更好地理解和应用热力学的基本概念和计算方法。
1. 练习题一题目:一个理想气体在等体过程中,吸收了50 J 的热量,对外界做了30 J 的功,求该气体内能的变化量。
解析:根据热力学第一定律,内能变化量等于热量和功之和。
即ΔU = Q - W = 50 J - 30 J = 20 J。
2. 练习题二题目:一摩尔理想气体从A状态经过两个等温过程和一段绝热过程转变为B状态,A状态和B状态的压强和体积分别为P₁、P₂和V₁、V₂,已知 P₂ = 4P₁,V₁ = 2V₂,求这个过程中气体对外界做的总功。
解析:由两个等温过程可知,气体对外界做的总功等于两个等温过程的功之和。
即 W = W₁ + W₂。
根据绝热过程的特性,绝热过程中气体对外做功为零。
因此,只需要计算两个等温过程的功即可。
根据理想气体的状态方程 PV = nRT,结合已知条件可得:P₁V₁ = nRT₁①P₂V₂ = nRT₂②又已知 P₂ = 4P₁,V₁ = 2V₂,代入式①和式②可得:8P₁V₂ = nRT₁③4P₁V₂ = nRT₂④将式③和式④相减,可得:4P₁V₂ = nR(T₁ - T₂) ⑤由于这两个等温过程温度相等,即 T₁ = T₂,代入式⑤可得:4P₁V₂ = 0所以,这个过程中气体对外界做的总功 W = 0 J。
通过以上两个练习题的解答,我们可以看到在热力学中,我们通过应用热力学第一定律和理想气体的状态方程等基本原理,可以解答各种热力学问题。
熟练掌握这些计算方法,有助于我们更深入地理解热力学的基本概念,并应用于实际问题的解决中。
总结:本文对两道热力学练习题进行了详细解答,分别涉及了等体过程和等温过程。
通过这些例题的解析,读者可以理解和掌握热力学的基本计算方法,并将其应用于实际问题的求解中。
高中物理热力学问题中的热容和热功的计算方法

高中物理热力学问题中的热容和热功的计算方法热力学是物理学中的一个重要分支,研究物质在热平衡状态下的性质和相互关系。
在高中物理中,热力学是一个重要的考点,其中热容和热功的计算方法是学生们经常遇到的难点。
本文将详细介绍热容和热功的计算方法,并通过具体题目举例,帮助读者更好地理解和应用这些知识。
一、热容的计算方法热容是物质吸收或释放单位温度变化时所吸收或释放的热量。
具体计算方法如下:1. 对于固体和液体物质,热容可以通过以下公式计算:Q = mcΔT其中,Q是物质吸收或释放的热量,m是物质的质量,c是物质的比热容,ΔT是温度变化。
2. 对于气体物质,热容的计算方法略有不同。
在等压条件下,热容可以通过以下公式计算:Q = nCpΔT其中,Q是物质吸收或释放的热量,n是物质的摩尔数,Cp是物质的摩尔热容,ΔT是温度变化。
举例说明:假设有一块质量为0.5kg的铁块,其初始温度为20℃,加热后的最终温度为80℃。
已知铁的比热容为450J/(kg·℃),求铁块吸收的热量。
解析:根据热容的计算方法,可以使用公式Q = mcΔT来计算。
代入已知条件,得到:Q = 0.5kg × 450J/(kg·℃) × (80℃ - 20℃) = 13500J因此,铁块吸收的热量为13500J。
二、热功的计算方法热功是物质通过热量传递做的功。
具体计算方法如下:1. 对于等容过程,热功可以通过以下公式计算:W = 02. 对于等压过程,热功可以通过以下公式计算:W = PΔV其中,W是热功,P是压强,ΔV是体积变化。
3. 对于绝热过程,热功可以通过以下公式计算:W = Q其中,W是热功,Q是吸收或释放的热量。
举例说明:假设有一摩尔的理想气体,初始体积为V1,初始压强为P1,最终体积为V2,最终压强为P2。
已知该过程是等压过程,求气体所做的热功。
解析:根据热功的计算方法,可以使用公式W = PΔV来计算。
3.4 热力学性质的计算

T2
∫
1
ig CP P dT − Rln 2 ≈ 22.15J mol-1K-1 (熵 R ) RT P 1 T
T2
∫
1
V2 = 286.41cm 3 mol-1
S(T2 , P ) = 8.314× (−1.6236) − 8.314× (− 9.6202) + 22.15 = 88.63J mol-1K-1 2
性 质
V v / cm3mol −1
T = 400 K,P = 2.19 MPa, 气相 PR 方 程 三参 数对 态原 应 理 6 a =1461372 MPa cm mol-2, = 72.35675 cm mol-1 b 3 ( 例题5)
1080.85 0.7117 -0.9107 -0.6497 -0.2610
∫
22:48:11
例题3-5(续)
= S(T2 , P ) − Sig (T2 , P ) − S(T , P ) − Sig (T , P ) + Sig (T2 , P ) − Sig (T , P ) 2 2 1 1 1 1 2 1 1
T
S(T2 , P ) = S(T2 , P ) − S(T , P ) 2 2 1 1
T
H(T2 , P ) = H(T2 , P ) − H(T , P ) 2 2 1 1
[
] [
] [
]
2 ig H(T2 , P ) − Hig (T2 ) H(T , P ) − Hig (T ) CP 2 1 1 1 = RT2 − RT dT +R 1 RT2 RT R 1 T 1
22:48:11
例题3-10(陈新志P49例3-6) 混合物性质计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新型材料设计及其热力学与动力学
The excess Gibbs energies of bcc solid solution of (Fe,Cr) and fcc solid solution of (Fe,Cr) is represented by the following expressions:
G ex(bcc)/J=x Cr x Fe (25104-11.7152T);
G ex(fcc)/J=x Cr x Fe (13108-31.823T+2.748T log e T)
For the bcc phase, please do the following calculations using one calculator.
(a) Calculate the partial Gibbs energy expressions for Fe and Cr
(b) Plot the integral and partial Gibbs energies as a function of composition at
873 K
(c) Plot the activities (a Cr and a Fe) as a function of composition at 873K
(d) What are the Henry’s law constants for Fe and Cr?
For the fcc phase, please do the calculations (a) to (b) by using your own code 翻译:
BCC(Fe,Cr)固溶体的过剩吉布斯自由能和fcc固溶体(Fe,Cr)的吉布斯自由能表达式如下:
G ex(bcc)/J=x Cr x Fe (25104-11.7152T);
G ex(fcc)/J=x Cr x Fe (13108-31.823T+2.748T ln T) G ex/J
对于体心立方相,请使用计算器做下面的计算。
(a)计算Fe和Cr的局部吉布斯能量表达式;
(b)画出873K时局部吉布斯自由能和整体吉布斯自由能的复合函数图。
(c)画出873K时Fe和Cr反应的活度图。
(d)F e和Cr亨利定律常数是什么?
对于fcc,请用你自己的符号计算a和b。
(a )由ex
G j = ex G m +
ex
G m / x j - x i
ex
G m / x i 可得
ex
G Fe =Xc r X Fe ex
G (bcc)+X Cr ex
G m (bcc)-[X Fe X Cr ex
G+X Cr X Fe ex
G ]
=Xc r X Fe (25104-11.7152T ) +X Cr (25104-11.7152T ) -[X Fe X Cr (25104-11.7152T )
+X Cr X Fe (25104-11.7152T ) ]
=X 2
Cr (25104-11.7152T ) 同理;可得;
ex
G Cr =X 2
Fe (25104-11.7152T )
(b)当T=873K 时,
G ex
(bcc)=x Cr x Fe (25104-11.7152T )= x Cr x Fe 14876.6304 J 设x Cr =X ,则X Fe =1-X
ex G Fe=X 2
·14876.6304 J (T=873K ) ex
G Cr =(1-X )2
·14876.6304 J (T=873K )
0.0
0.2
0.4
0.6
0.8
1.0
-2000
02000
40006000800010000
120001400016000e x G F e (J )
X
exGFe
0.0
0.2
0.4
0.6
0.8
1.0
-2000
0200040006000800010000120001400016000
图一 ex
G Fe -X 图
0.0
0.2
0.4
0.6
0.8
1.0
-2000
02000
40006000800010000
1200014000
16000e x G F e (J )
X
0.0
0.20.40.60.8-2000
0200040006000800010000120001400016000
图二 ex
G cr -X 图
0.0
0.3
0.6
0.9
1000
200030004000
e x G
x
0.0
0.2
0.4
0.6
1000
1500
2000
2500
3000
3500
4000
图三 ex
G-X 图
(C )a m =X m ·f m a B = x B exp[X 2
·o
L /(RT)]
ex
G (bcc)/J =x Cr x Fe o
L
o
L=25104-11.7152T
因而
a Fe = (1-X)· exp[X 2
·(25104-11.7152T ) /(RT)](T=873K ) a Cr = X · exp[(1-X)2·(25104-11.7152T ) /(RT)] (T=873K )
0.00.5
1.0
a F e
x
图三 a Cr –X 图
a C r
x
图五 a Fe –X 图
(d)
f b =
exp[o
L /RT] 所以:
f Fe =f Cr = exp[25104-11.7152T /RT] fcc:
ex
G Fe = X 2
Cr (13108-31.823T +2.748T In T ) ex
G Cr = X 2
Fe (13108-31.823T +2.748T ln T )
设x Cr =X,则X Fe=1-X
2(13108-31.823T+2.748T In T)
ex G
Fe = X
2(13108-31.823T+2.748T ln T) ex G
Cr = (1-X)
感谢您的支持与配合,我们会努力把内容做得更好!。
