第三章多变量回归分析(计量经济学南开大学)
合集下载
南开大学计量经济学课件回归方程的变量和形式
检验判断1994年之前和之后两段时期消费函数是否产生显著的
差异。
7.2 模型的稳定性检验
2、Chow预测检验
Chow预测检验是先对包含前T1个观察值的子样本 建立模型，然后用这个模型对后T2个观察值的自变量 进行预测，如果实际值与预测值有很大变动，就可以 怀疑模型中存在结构性变化。T1 和T2的相对大小，没 有确定的规则，可能根据如战争、石油危机、经济改 革等明显的转折点来确定，如果不存在这样明显的转 折点，常用的方法是用85%-90%的数据进行估计，剩 余的数据进行检验。
7.2 模型的稳定性检验
1、Chow断点（Breakpoint）检验
实例一：估计C-D函数 log(Y ) 0 1 log(L) 2 log(K )
（1）1929－1967年数据估计如下 log(Y ) 3.938 1.451log(L) 0.384log(K )
R 2 0.9946 , R 2 0.9943 , RSS 0.0434 （2）分1929-1948和1949－1967两段数据估计如下 log(Y ) 4.058 1.617log(L) 0.220log(K )
3、冗余（Redundant)变量检验
检验一部分变量的统计显著性，通过判断方程中一
部分变量系数是否与0没有显著差异，决定是否从方程 中剔除这些变量，检验方法可以通过F检验和似然比 （LR）检验。 冗余变量检验是遗漏变量检验逆过程。
Eviews实现过程：
View－Coefficient Tests－Redundant Variables－
7.2 模型的稳定性检验
1、Chow断点（Breakpoint）检验（邹至庄断点检验） 思想：对每个子样本单独拟合方程，并与对于全部样本 拟合方程进行比较，来观察每个子样本的估计方程是否 有显著差异，判断是否存在结构变化。 零假设：两个子样本拟合的方程无显著差异。即结 构没有发生变化。 如果拒绝零假设，则代表有显著差异，意味着模型 中存在结构变化。
南开计量经济学课件 (3)
以下非线性回归模型是无法用最小二乘法估计参数的。 可采用非线性方法进行估计。估计过程非常复杂和困难，计 算机的出现大大方便了非线性回归模型的估计。专用软件使 这种计算变得非常容易。但本章不是介绍这类模型的估计。
下面介绍几种典型的可以做线性化处理的非线性模型。
(1)多项式函数模型(1)
多项式方程
（第3版教材第90页）
案例4 ：钉螺存活率曲线（file:nonli3）（生长曲线模型）
100
Y 80
60
40
20
T
0
0
2
4
6
8
10
12
案例4：钉螺存活率曲线（file:nonli3）（生长曲线模型）
钉螺存活率样本值与拟合值。
100 Y YF
80
60
40
20
T
0
2
4
6
8
10
12
点预测：当t = 6.5月时
yˆt
101 1 e4.310.76536.5
还原，Lny = Ln(7.33) + 104.5 (1/x) 104.5( 1 )
y 7.33e x
(6) 幂函数模型(全对数模型)
(b > 1)
(b = -1) (b < -1)
(0<b <1)
(0 > b > -1)
yt axt b eut
b取不同值的图形分别见上图。对上式等号两侧同取对数，得
(4) 生长曲线 (logistic) 模型（与教材中的模型稍异，称S曲线）
Y k
Y k
k/2
0
0
(lnb)/a
t
t
下面介绍几种典型的可以做线性化处理的非线性模型。
(1)多项式函数模型(1)
多项式方程
（第3版教材第90页）
案例4 ：钉螺存活率曲线（file:nonli3）（生长曲线模型）
100
Y 80
60
40
20
T
0
0
2
4
6
8
10
12
案例4：钉螺存活率曲线（file:nonli3）（生长曲线模型）
钉螺存活率样本值与拟合值。
100 Y YF
80
60
40
20
T
0
2
4
6
8
10
12
点预测：当t = 6.5月时
yˆt
101 1 e4.310.76536.5
还原，Lny = Ln(7.33) + 104.5 (1/x) 104.5( 1 )
y 7.33e x
(6) 幂函数模型(全对数模型)
(b > 1)
(b = -1) (b < -1)
(0<b <1)
(0 > b > -1)
yt axt b eut
b取不同值的图形分别见上图。对上式等号两侧同取对数，得
(4) 生长曲线 (logistic) 模型（与教材中的模型稍异，称S曲线）
Y k
Y k
k/2
0
0
(lnb)/a
t
t
第三章多变量回归分析(计量经济学南开大学)
根据残差的平方和最小化的原理，解出参数的估计量。 ˆ ˆ X ˆ X )2 ˆ i2 (Yi 残差平方和RSS u 1 2 2i k ki
ˆ 'u u ˆ u ˆ Y Xβ ˆ ˆ Y Xβ u ˆ )' ( Y Xβ ˆ) ˆ i2 u ˆ ' u ( Y Xβ RSS u ˆ ' X' Y β ˆ ' X' Xβ ˆ Y' Y β ˆ ' X' Y Y ' Y 2β
ˆ 2代替 2，则 如果 2未知，以 2 1 ˆ )的估计量为： ˆ（ Var Cov(β X' X）
2 1 1 ˆ 的标准差Se(β ˆ )为 ˆ（ ˆ β X' X） （X' X）
ˆ 的性质： 四、OLS估计量 β
1 、线性 1 ˆ （ β [ X' X） X' ]Y 2、无偏性 ˆ] β E[β 3、最小方差性 ˆ 具有Var (β ˆ )最小。 OLS估计量β
X X X X
2i 2 2i 3i
2i
X X X X
3i 2i 2
3i
3i
X X X X X
ki
X ki X 2i 1 X 22 X 32 X k2 1 X 23 X 33 X 3k
X ki X 3i
ˆ 1 ˆ 2i ki ˆ2 3i ki 3 2 ˆ X ki k
二、 的估计量
2 ˆ u i
ˆ ' X' Y β ˆ ' X' Xβ ˆ ˆ Y' Y 2β u ˆ u ˆ 0 2 X' Y 2 X' Xβ
第二章 双变量回归分析(计量经济学,南开大学)
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
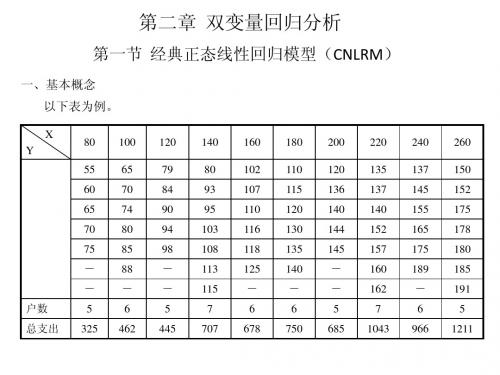
6、样本回归函数（SRF） 由于在大多数情况下，我们只知道变量值得一个样本，要用样本信息的基础 上估计PRF。(表） 样本1
X（收入） Y（支出） 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ： 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差：VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量（Estimator）：一个估计量又称统计量(statistic)，是指一个规则、公式 或方法，以用来根据已知的样本所提供的信息去估计总体参数。在应用中，由估 计量算出的数值称为估计（值）（estimate)。 样本回归函数SRF的随机形式为：
南开大学计量经济学练习题(含答案)
第1章绪论习题一、单项选择题1．把反映某一总体特征的同一指标的数据，按一定的时间顺序和时间间隔排列起来，这样的数据称为（）A. 横截面数据B. 时间序列数据C。
面板数据 D. 原始数据2．同一时间、不同单位按同一统计指标排列的观测数据称为（）A．原始数据 B．截面数据C．时间序列数据 D．面板数据3．用计量经济学研究问题可分为以下四个阶段( ）A．确定科学的理论依据、建立模型、模型修定、模型应用B．建立模型、估计参数、检验模型、经济预测C．搜集数据、建立模型、估计参数、预测检验D．建立模型、模型修定、结构分析、模型应用4．下列哪一个模型是计量经济模型（ )A。
投入产出模型 B.数学规划模型C.包含随机变量的经济数学模型D.模糊数学模型二、问答题1．计量经济学的定义2．计量经济学的研究目的3．计量经济学的研究内容习题答案一、单项选择题1．B 2．B 3．B 4．C二、问答题1．答：计量经济学是统计学、经济学、数学相结合的一门综合性学科，是一门从数量上研究物质资料生产、交换、分配、消费等经济关系和经济活动规律及其应用的科学2．答:计量经济学的研究目的主要有三个：（1） 结构分析。
指应用计量经济模型对经济变量之间的关系作出定量的度量。
（2） 预测未来。
指应用已建立的计量经济模型求因变量未来一段时期的预测值。
（3） 政策评价。
指通过计量经济模型仿真各种政策的执行效果，对不同的政策进行比较和选择。
3．答：计量经济学在长期的发展过程中逐步形成了两个分支：理论计量经济学和应用计量经济学。
理论计量经济学主要研究计量经济学的理论和方法.应用计量经济学将计量经济学方法应用于经济理论的特殊分支，即应用理论计量经济学的方法分析经济现象和预测经济变量。
2一元线性回归模型习 题一、单项选择题1．最小二乘法是指（ ） A 。
使()∑=-nt ttYY 1ˆ达到最小值 B 。
使ˆmin i iY Y -达到最小值 C. 使tt Y Y ˆmax -达到最小值 D. 使()21ˆ∑=-nt t t Y Y 达到最小值2． 在一元线性回归模型中，样本回归方程可表示为（ ） A. 01i i i Y X u ββ=++ B.01ˆˆˆi i i Y X e ββ=++ C ． 01ˆˆˆi i Y X ββ=+ D. ()01i iE Y X ββ=+3．线设OLS 法得到的样本回归直线为01ˆˆi i i Y X e ββ=++，以下说法不正确的是（ ）A ．0=∑i e B ．0),(≠i i e X COVC ．Y Y =ˆD ．),(Y X 在回归直线上4．对样本的相关系数γ,以下结论错误的是( ）A. γ越接近0， X 与Y 之间线性相关程度高B.γ越接近1，X 与Y 之间线性相关程度高C. 11γ-≤≤D 、0γ=,则X 与Y 相互独立二、多项选择题1．最小二乘估计量的统计性质有（ ）A. 无偏性B. 线性性 C 。
第3章_双变量回归模型： 计量经济学-古扎拉蒂 教学课件_834
的 – 假定3:干扰项ui的均值为零 – 假定4:同方差性或ui的方差相等
vauir|(Xi)E[ui E(ui)|Xi]2
E(ui2|Xi)2
f(u)
0
Y
X1
X2
X3
X4
X 同方差性：Var(ui|Xi)= Var(uj|Xj)，i≠j
3.2经典线性回归模型
• 最小二乘法的基本假定
– 假定5:各个干扰之间无自相关
E (Yi X i ) 0 1 X i Var (Yi | X i ) 2
Cov (Yi , Y j ) 0 (i j )
Yi ~ N ( 0 1 X i , 2 )
3.3最小二乘估计的精度或标准 误差
方差:
var(ˆ2)
2
xi2
var( ˆ1 ) n
X
2 i
x
2 i
2
标准误:
3.2经典线性回归模型
• 最小二乘法的基本假定
– 假定7:观测次数n必须大于待估计的参数个 数.即观测次数n必须大于解释变量的个数
– 假定8:X值要有变异性 – 假定9:正确地设定了回归模型. – 假定10:没有完全的多重共线性.
3.2经典线性回归模型
• 由于被解释变量 Yi分布的性质决 定于ui ，因而对 ui的各项假定也 适用于 Yi，从而 有：
se(ˆ2)
xi2
se ( ˆ1 )
n
X
2 i
x
2 i
3.4最小二乘法回归线性质
• 回归线的性质
1. 它是通过Y和X的样本均值的一条直线. 2. 估计的Y(即 Yˆi )的期望值等于实测的Y的期望值. 3. 残差的期望值为零. 4. 残差和预测的Yi值不相关. 5. 残差和Xi不相关.
vauir|(Xi)E[ui E(ui)|Xi]2
E(ui2|Xi)2
f(u)
0
Y
X1
X2
X3
X4
X 同方差性：Var(ui|Xi)= Var(uj|Xj)，i≠j
3.2经典线性回归模型
• 最小二乘法的基本假定
– 假定5:各个干扰之间无自相关
E (Yi X i ) 0 1 X i Var (Yi | X i ) 2
Cov (Yi , Y j ) 0 (i j )
Yi ~ N ( 0 1 X i , 2 )
3.3最小二乘估计的精度或标准 误差
方差:
var(ˆ2)
2
xi2
var( ˆ1 ) n
X
2 i
x
2 i
2
标准误:
3.2经典线性回归模型
• 最小二乘法的基本假定
– 假定7:观测次数n必须大于待估计的参数个 数.即观测次数n必须大于解释变量的个数
– 假定8:X值要有变异性 – 假定9:正确地设定了回归模型. – 假定10:没有完全的多重共线性.
3.2经典线性回归模型
• 由于被解释变量 Yi分布的性质决 定于ui ，因而对 ui的各项假定也 适用于 Yi，从而 有：
se(ˆ2)
xi2
se ( ˆ1 )
n
X
2 i
x
2 i
3.4最小二乘法回归线性质
• 回归线的性质
1. 它是通过Y和X的样本均值的一条直线. 2. 估计的Y(即 Yˆi )的期望值等于实测的Y的期望值. 3. 残差的期望值为零. 4. 残差和预测的Yi值不相关. 5. 残差和Xi不相关.
南开大学计量经济学期末复习重点
ˆ 1
( xt x )( y t y ) ， ( xt x ) 2
ˆ y ˆ x 0 1
第2章 一元线性回归模型
2.3 OLS 回归函数的性质
ˆt = 0 (1) 残差和等于零， u
ˆ + ˆ xt 过（ x , y ）点。 ˆt = (2) 估计的回归直线 y 0 1 ˆt = y 。 (3) yt 的拟合值的平均数等于其样本观测值的平均数， y ˆ 和 ˆ 的特性 2.4 最小二乘估计量 0 1
（1）线性特性， （2）无偏性， （3）最小方差性， （4）一致性。 Gauss-Marcov 定理：若 ut 满足 E(ut) = 0，D(ut) = 2，那么用 OLS 法得到的估计量就具有最佳线性无偏性。估计量称最佳线 性无偏估计量。
第2章 一元线性回归模型
分清 4 个式子的关系。 (1) 真实的统计模型，yt = 0 + 1 xt + ut
第2章 一元线性回归模型
2.1 一元线性回归模型 yt = 0 + 1 xt + ut 模型分为两部分。 （1）回归函数部分，E(yt) = 0 + 1 xt,（2）随机部分 ut 。 对模型解释变量和误差项 ut 做出如下假定。 (14) ut N (0,
)。(5) ui 非自相关。(6) xi 是非随机的。
1 T 1 T
T
=
Cov( x t , y t ) D( x t ) D( y t )
。
=
t 1 ( xt x )( y t y )
T
t 1 ( xt x ) 2
1 n -1
1 T
n
四计量经济学多变量回归分析模型
i 1
n
2
Min[Yi ( 0 1 X 1i ... p X pi )]
i 1
n
^
^
^
2
• 根据最 小二乘原 理，参数 估计值应 该是右列 方程组的 解
ˆ 0 ˆ 1 ˆ 2 ˆ k
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki Ki
2 ˆ Q e (Yi Yi ) i 1 2 i i 1 n n
i=1,2…n
其 中
ˆ ˆ X ˆ X ˆ X )) (Yi ( 0 1 1i 2 2i k ki
1 Y1 X 1n Y2 Y X kn n
0 1 β 2 k
X 11 X 12 X 1n
X 21 X X kn n ( k 1 )
( k 1 )1
1 μ 2 n n 1
用来估计总体回归函数的样本回归函数为：
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki ki
ˆ ˆ X ˆ X ˆ X e 其随机表示式: Yi 0 1 1i 2 2i ki ki i
ei称为残差或剩余项(residuals)，可看成 是总体回归函数中随机扰动项i的近似替代。
表示：各变量X值固定时Y的平均响应。
j也被称为偏回归系数，表示在其他解释变
量保持不变的情况下，X j每变化1个单位时，Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响。
n
2
Min[Yi ( 0 1 X 1i ... p X pi )]
i 1
n
^
^
^
2
• 根据最 小二乘原 理，参数 估计值应 该是右列 方程组的 解
ˆ 0 ˆ 1 ˆ 2 ˆ k
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki Ki
2 ˆ Q e (Yi Yi ) i 1 2 i i 1 n n
i=1,2…n
其 中
ˆ ˆ X ˆ X ˆ X )) (Yi ( 0 1 1i 2 2i k ki
1 Y1 X 1n Y2 Y X kn n
0 1 β 2 k
X 11 X 12 X 1n
X 21 X X kn n ( k 1 )
( k 1 )1
1 μ 2 n n 1
用来估计总体回归函数的样本回归函数为：
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki ki
ˆ ˆ X ˆ X ˆ X e 其随机表示式: Yi 0 1 1i 2 2i ki ki i
ei称为残差或剩余项(residuals)，可看成 是总体回归函数中随机扰动项i的近似替代。
表示：各变量X值固定时Y的平均响应。
j也被称为偏回归系数，表示在其他解释变
量保持不变的情况下，X j每变化1个单位时，Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可得到如下正规方程组：
nˆ1 ˆ2 X 2i ˆk X ki Yi
ˆ1
X 2i ˆ2
X
2 2i
ˆk
X 2i X 3i ˆk
X 2i X ki
X 2iYi
ˆ1
X 3i ˆ2
X 3i X 2i ˆ2
X2 3i
ˆk
X 3i X ki
X 3iYi
ˆ1
如果根据理论，因变量Y与k-1个变量X2，X2，…，Xk 有因果关系，我 们要建立的回归模型要在这些变量中选择正确的解释变量，要根据变量的 边际贡献大小，把贡献大的变量纳入回归模型。分析边际贡献并选择变量 的过程，实际上是一个逐步回归的过程。
首先，分别建立Y与k-1个变量X2，X2，…，Xk 的回归模型：
X ki ˆ2
X ki X 2i ˆk
X ki X 3i ˆk
X2 ki
X kiYi
写成矩阵形式：
n
X 2i
X 3i
X 2i
X 3i
X2 2i
X 3i X 2i
X 2i X 3i X2
3i
X ki
X ki X 2i
X ki X 3i
1
1
1
X 21 X 22 X 23
（2）计算统计量：
t
ˆi Se(ˆi )
（3）查t分布表，找出t (n k)。 2
（4）判断：
t 若
t
t 2 (n k )，则接受H0 , 参数i显著异于0
t
2
(n
k
)，则拒绝H
0
,
接受H1
,
参数
不
i
显著异于0
如果根据理论或常识，i 非负，则可做单侧检验，比较 t 与tα。
若 t t (n k)，则接受H0,参数i不显著异于0 t t (n k)，则拒绝H0 , 接受H1,参数i显著异于0
选择其中ESS最大并通过F检验的变量作为首选解释变量，假定是X2 。
m n-(k+m)
U1/(k-1) U2/(k+m-1) (U2-U1)/m Q/( n-k-m)
TSS
n-1
定义统计量： F (ESS'ESS) / m RSS' /(n k m)
并检验其显著性。
在新引入变量的系数为0的原假设下，
统计量 F (ESS'ESS) / m ~ F (m, n k m) RSS' /(n k m)
βˆ ' X' y nY 2 Y' Y nY 2
1 RSS 1 TSS
uˆi2 yi2
yi2与解释变量X的个数无关，而 uˆi2则可能随着解释变量的增加
而减少（至少不会下降），因而，不同的SRF，得到的R2 就可能不同。
必须消除这种因素，使R2 即能说明被解释的离差与总离差之间的关系， 又能说明自由度的数目。定义校正的样本决定系数 R 2 ：
二、回归的总显著性检验： 检验回归系数全部为零的可能性。
原假设H0 : 1 2 k 0 备择假设H1 : i (i 1,2, , k)不同时为零
方差分析表（ ANOVA)
平方和
df
ESS
(Yˆi Yˆ)2 Y' Y βˆ ' X' Y
k-1
RSS
uˆ2 βˆ ' X' Y nY 2 i
X
31
X 32
X 33
X
k1
Xk2
X 3k
1 Y1
X 2n Y2
X 3n
Y3
X kn Yn
即： (X'X)βˆ X'Y
βˆ (X'X)1 X'Y
X ki ˆ1
X X
2i 3i
X X
ki ki
ˆ2 ˆ3
X2 ki
ˆk
如果直接用矩阵微分，则
uˆ 2 Y' Y 2βˆ ' X' Y βˆ ' X' Xβˆ i
成立。
5、u ~ N (0, 2I)
随机干扰项服从正态分布。
三、多 变量线性回归模型的SRF
SRF :
Yi ˆ1 ˆ2 X 2i ˆ3 X 3i ˆk X ki uˆi
或 Y Xβˆ uˆ
其中βˆ 和uˆ分别为回归系数的OLS估计量的列向量和残差列向量。
第二节 多变量回归模型的OLS估计
n-k
TSS
(Yi Y )2 Y'Y nY2
n-1
均方差
(Y' Y βˆ ' X' Y) /(k 1) (βˆ ' X' Y nY 2 ) /(n k )
如果假定：1 2 k 0，则统计量
ESS /(k 1) (βˆ ' X' Y nY 2 ) /(k 1) F RSS /(n k ) (Y' Y βˆ ' X' Y) /(n k ) ~ F (k 1, n k )
2
n
u2
un
或： Y Xβ u
Y为因变量观测值列向量
在
Y Xβ u 中，X为数据矩阵。
β 为待估计参数列向量
u为随机扰动项列向量
二、多 变量线性回归模型的基本假定
1、 Eu 0
随机干扰项的期望值为0。
u1
2、
E
u
u
'
u2 un
u1
u2
2 0 0 0
0 0
ESS TSS ESS Y'Y nY 2 Y' Y βˆ ' X' y βˆ ' X' Y nY 2
方差分析表（ ANOVA)
平方和
df
ESS
(Yˆi Yˆ)2 Y' Y βˆ ' X' Y
k-1
RSS
uˆ2 βˆ ' X' Y nY 2
i
n-k
TSS
(Yi Y )2 Y'Y nY2
R 2 1 ESS /(n k ) 1 (1 R2 ) n 1
TSS /(n 1)
nk
1
ˆ 2
Se(Yˆ )
三、R2 与 R 2的性质
0 R2 1,
0 R2 1
R 2 R2 , 当k 时，R 2 R2
第四节 显著性检验
一、单参数的显著性检验：
根据假定，u ~ N (0, 2I)，因此ˆ ~ N ( , 2 (X' X)1)
标准差为
(X' X)1
如果 2未知，以 ˆ 2代替 2，则 Var Cov(βˆ )的估计量为：ˆ（ 2 X' X）1
βˆ 的标准差Se(βˆ )为 ˆ（ 2 X' X）1 （X' X）1ˆ
四、OLS估计量 βˆ 的性质：
1、线性 βˆ （ [ X' X）1X' ]Y
2、无偏性 E[βˆ ] β
第三章 多变量回归分析
第一节 多变量线性回归模型
一、多变量线性回归模型的PRF
如果假定对因变量Y 有k-1个解释变量：X2，X3，…，Xk，k 变量总 体回归函数为：
其中PR1为F 常: 数项Y，i 2 ~1 2为2 X解2i释变3量XX3i 2~Xk的系k X数ki ， uui为, i随 1机,2干,扰,项k 。
uˆ 2 i
βˆ
2X' Y 2X' Xβˆ
0
βˆ (X' X)1 X' Y
二、 的估计量
ˆ
uˆ 2 uˆ 'uˆ i
nk nk
ˆ为的无偏估计量：E[ˆ ] 。
三、βˆ 的方差-协方差矩阵
βˆ (X' X)1 X' y (X' X)1 X' (Xβ u) (X' X)1 X' Xβ (X' X)1 X'u β (X' X)1 X'u
Yi a 2 X 2i ui Yi 1 2 X 3i ui
Yi 1 2 X ki ui
回归后， TSS( X 2 ) ESS( X 2 ) RSS( X 2 )
得到各 回归方
TSS( X 3) ESS( X 3) RSS( X 3)
程的平
方和
TSS( X k ) ESS( X k ) RSS( X k )
n-1
均方差
(Y' Y βˆ ' X' Y) /(k 1) (βˆ ' X' Y nY 2 ) /(n k )
判定系数：
二、校正的R2 ：
R2
ESS TSS
βˆ ' X' y nY 2 Y' Y nY 2
由R2的计算式可看出， R2 随解释变量的增加而可能提高（不可能降
低）：
R2
ESS TSS
根据R2 ESS ，F ESS /(k 1) ,TSS ESS RSS
TSS
RSS /(n k)
可得到F
R2 /(k 1) (1 R2 ) /(n
k)
显然，R2 越大，F越大，当R2 =1时，F 无限大。
选择显著水平α ，计算F统计量的值，与F分布表中的临界值进行比
较：
若 F F (k 1, n k)，则接受H0 ,不显著 F F (k 1, n k)，则拒绝H0 , 接受H1,显著
决定一个变量是否引入回归模型，就要先研究它的边际贡献，以正确 地建立模型。如果变量的边际贡献较小，说明改变量没有必要加入模型。
分析变量的编辑贡献，可以使用方差分析表为工具，根据变量引入前、 后的RSS的变化量及其显著性检验（扣除原来引入模型的解释变量的贡 献），确定该变量的边际贡献是否显著。