11-4毕萨定律(新)
毕萨定律(解读
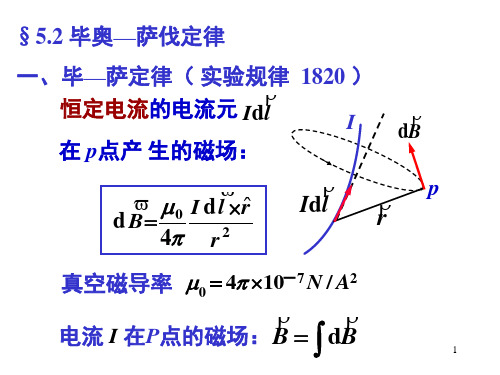
0 I d l r ˆ d B 4 r 2
dB
Idl
r
p
真空磁导率 0 4 10 7 N / A2
电流 I 在P点的磁场: B dB
2 32
圆电流中心的磁场
无限长直电流的磁场Fra bibliotek I 0 B
2R
0 I B 2 r
8
圆电流的磁场
I
【例】密绕长直螺线管轴线上的磁场
计算各匝圆电流在 p 点磁场的矢量积分 n, I 内部轴线上的磁场 p
B 0 nI
端口中心处的磁场
B 1 0nI 2
(教材P249例8.3)
10
通电螺线管的磁场
1
运动点电荷磁场公式 毕—萨定律: P r r ˆ S Idl dB
v n,q dl dl dl v v
点电荷q在p点的磁场(v<<c): q ˆ B0 0 2 v r 4 r 电流元磁场 dB (n Sdl )B0
2
dB ( nSdl ) B0
S2 S1
L
?
原因:物理上,恒定电流一定闭合!
17
3、安培环路定理是基本的规律,而毕—萨定律 只是磁场的定义。 4 、包括非恒定情况的安培环路定理将在 §8.5 介绍。 5、安培环路定理的微分形式—磁场的旋度 B 0 j
其中,j 为恒定电流的电流密度矢量。 Bdl B dS 0 j dS
0 4 10 7 N / A2
I1 B2
I2
11-4 毕奥-萨伐尔定律
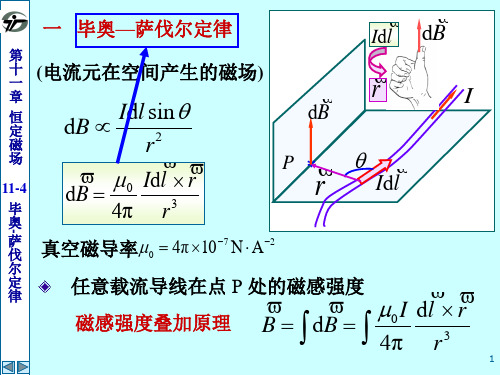
如图所示,有一长为l , 半径为R的载流密 绕直螺线管,螺线管的总匝数为N,通有电流I. 设把螺线管放在真空中,求管内轴线上一点处 的磁感强度.
o * p
R
dx
x
x
++ ++++ ++ +++ ++ +
解 由圆形电流磁场公式 B
例 判断下列各点磁感强度的方向和大小.
1
8
2
d 1、5 点 : B 0
7
Id l
R
6
3、7点 :d B 3
0 Id l
4π R
2
2、4、6、8 点 :
dB
4
5
0 Id l
4π R
2
sin 45
0
2
二 毕奥---萨伐尔定律应用举例
第 十 一 章 恒 定 磁 场 11-4 毕 奥 萨 伐 尔 定 律 -
(1)P点位于管内轴线中点
cos 1 cos 2
cos 2
1 π 2
l/2
l / 2
2
R
2
18
第 十 一 章 恒 定 磁 场 11-4 毕 奥 萨 伐 尔 定 律 -
1
x1
x2 o 2 p 2 x1 2 ++ + + + + + + + + + + + + + R csc d + + +x+ + + + + + + + + + + +
大学物理磁场与毕萨定理new解读

2
O
x
在螺线管上的 x 处截取一小段
d I Ind x
dB 0 R2nIdx
2 (R2 x2 )3 2
B dB x2 0 R2nIdx
x1 2 (R 2 x 2 )3 2
dx R csc2 d
B 2 0nI sin d
1 2
R
1 2
0nI(cos
2
cos
1)
无限长螺线管:
它所产生的圆电流的电流强度为:
I q ve
T 2 r
v
r
o
e
B
0I
2r
0 4
ev r2
解法二:用运动电荷的磁场公式
B
0 4
ev r2
b
B dB ab 0Idx 0 I ln a b
b 2ax 2a b
dI
I
dx x
a
例:在半径R 的“无限长”半圆柱形金属片中,有
电流I 从下而上地通过,如图,试求圆柱轴线上一
点P的磁感强度。
y
解:将金属片分划成许多细
长条 dI I Rd R
dB
0dI 2R
0 Id 2 2 R
x
3/ 2
讨论:
(1)载流圆环环心处的磁场
Bo0 I2RR NhomakorabeaB
I o xP
x
B R I o
(2)载流圆弧导线在圆心处产生的磁场
I
0 • O
B
dB
0 Il 4r 2
0 I 0 4r
r
方向:右手法则
例:一根无限长导线通有电流I,中部弯成圆弧形, 如图所示。求圆心o点的磁感应强度B。
解:直线段ab在o点产生 a
毕萨奥伐尔定律

毕萨奥伐尔定律
摘要:
1.毕萨奥伐尔定律的简介
2.毕萨奥伐尔定律的公式及含义
3.毕萨奥伐尔定律在现实生活中的应用
4.毕萨奥伐尔定律的局限性及改进方法
5.总结
正文:
毕萨奥伐尔定律,又称“毕萨定律”,是由德国物理学家克劳斯·毕萨奥伐尔(Klaus Biauer)在1994年提出的一个定律。
该定律主要用于描述在固定压力下,流体通过管道时的流量与管道长度、管道直径之间的关系。
毕萨奥伐尔定律的公式为:Q = π/8 * d * √(2gh) ,其中Q表示流量,d 表示管道直径,g表示重力加速度,h表示管道长度。
在现实生活中,毕萨奥伐尔定律广泛应用于液体和气体的输送系统设计、优化及运行管理。
例如,在工业生产中,通过了解液体在管道中的流量,可以更好地控制生产过程;在农业生产中,利用毕萨奥伐尔定律可以优化灌溉系统,提高水资源利用率。
然而,毕萨奥伐尔定律也有其局限性。
首先,该定律适用于稳态流动,而在非稳态流动中,液体的流速与管道长度、直径的关系可能会发生改变。
其次,毕萨奥伐尔定律未考虑流体的黏性对流动的影响,因此在处理粘性流体时,需要对其进行修正。
为了解决这些问题,研究人员对毕萨奥伐尔定律进行了改进。
例如,引入了考虑流体黏性的修正系数,使得该定律在处理粘性流体时具有更好的准确性。
此外,还有一些研究者提出了基于毕萨奥伐尔定律的改进公式,以适应非稳态流动的计算需求。
总之,毕萨奥伐尔定律是一个具有广泛应用价值的定律,但在实际应用中也需要注意其局限性。
毕萨定律实验报告

毕萨定律实验报告一、噪声的来源噪声的种类很多,因其产生的条件不同而异。
地球上的噪声主要来源于自然界的噪声和人为活动产生的噪声。
自然界形成的这些噪声是不以人们的意志为转移,因此,人们是无法克服的。
我们所研究的噪声主要是指人为活动所产生的噪声,它的来源分为以下几种情况。
⑴交通噪声在我国,道路交通噪声在城市中占的比重通常为40%以上,有的甚至在75%以上,随着城市车辆的拥有量不断增加,道路交通噪声的危害也将不断加剧。
系由各种交通运输工具产生的振动声、喇叭声、汽笛声、刹车声、排气声、防盗报警鸣笛声、穿越而过的铁路(包括地上、地下)和飞机起落时的噪声等。
⑵工业噪声系由工业生产活动中的机械设备和动力装置产生的噪声。
工业噪声在我国城市环境噪声中所占的比重约为20%左右,在我国城市中,居民与厂矿的混杂情况甚多,厂矿噪声的强度大,作用时间长,使得居民对厂矿声的反应特别强烈。
⑶建筑施工噪声建筑工地地打桩声能传到数公里以外,且工期大都在一年以上,因而对周围居民地干扰是很大的。
⑷社会生活噪声泛指人们因生活(商业文化、娱乐等)活动所产生的噪声。
二、噪声的危害噪声污染已成为城市四大公害之一,其危害主要表现在一下及格方面:⑴阻碍和侵害听力。
噪声污染可引起耳鸣耳痛、听力损伤等听力损害。
另外,噪声会干扰听力,掩鼻需要的声音,使人不易察觉一些危险的信号,从而容易造成重大事故。
⑵引发心血管系统、内分泌系统、消化系统、呼吸系统等方面的疾病。
⑶对心理、睡眠、神经系统、工作和生活产生影响。
噪声会使人心烦意乱、负面情绪增加;使感知判断能力、智力思维、瞬时记忆、视听反应速度和验收调能力下降。
人长时间在噪声刺激下就会患“神经衰弱症”。
⑷对妇女、孕妇、胎儿、儿童产生影响。
长期弱噪声可以引致女性月经不调、性机能失调;在噪声环境下生活的儿童,智力发育水平必须比安静条件下的儿童高20%。
⑸对视觉的影响。
长时间处于噪声环境中,很容易发生眼疲劳、眼痛、眼花和流泪等,同时还会使色觉、视野发生异常。
毕奥-萨伐尔定律公式

毕奥-萨伐尔定律公式
毕奥-萨伐尔定律公式是描述电磁感应现象的重要公式之一,它是由法国物理
学家毕奥和英国物理学家萨伐尔分别独立提出的,因此也被称为毕萨定律。
该定律表述了当一个闭合电路中的磁通量发生变化时,该电路内会产生电动势。
具体来说,如果一个电磁感应器中的磁通量Φ发生变化,那么在该感应器两端就
会产生一个电动势E,其大小与磁通量变化率的绝对值成正比。
毕奥-萨伐尔定律公式可以用一个简单的公式来表达:
E = -dΦ/dt
其中,E是感应电动势的大小,Φ是穿过感应电路的磁通量,t是时间,d/dt表示对时间的导数运算。
公式中的负号表示感应电动势的方向与磁通量变化的方向相反。
需要注意的是,该定律只适用于闭合电路中的感应电动势。
对于非闭合电路,根据法拉第电磁感应定律,产生的感应电动势大小与闭合电路中的相同,但方向可能不同。
总的来说,毕奥-萨伐尔定律公式是电磁学中一个非常重要的公式,广泛应用
于各种电磁感应现象的分析和设计中。
11-4 毕奥-萨伐尔定律
判断下列各点磁感强度的方向和大小. 例 判断下列各点磁感强度的方向和大小
8 2
d 1,5 点 : B = 0 ,
3,7点 :dB , 点 +3
+
=
0 Id l
4π R
2
7
Idl
R
6 5
2,4,6,8 点 : , , ,
+4
dB =
0 Idl
4π R
sin 450 2
第十一章 恒定磁场
毕奥11 – 4 毕奥-萨伐尔定律 毕奥---萨伐尔定律应用举例 二 毕奥 萨伐尔定律应用举例 载流长直导线的磁场. 例1 载流长直导线的磁场
∫β
β2
1
sin β d β
第十一章 恒定磁场
毕奥11 – 4 毕奥-萨伐尔定律
物理学教程 第二版) (第二版)
讨 论
B=
0 nI
2
(cos β 2 cos β1 )
β1 = π β 2
l/2
点位于管内轴线中点 (1)P点位于管内轴线中点 ) 点位于管内
cos β1 = cos β 2
cos β2 =
0
r
2
第十一章 恒定磁场
毕奥11 – 4 毕奥-萨伐尔定律
物理学教程 第二版) (第二版)
B=
0 I
4 π r0
∫θ
θ2
1
sin θ d θ =
(cosθ1 cosθ 2) 4π r0
0 I
B 的方向沿 x 轴的负方向. 轴的负方向
无限长载流长直导线的磁场 无限长载流长直导线的磁场. 载流长直导线的磁场
第十一章 恒定磁场
毕奥11 – 4 毕奥-萨伐尔定律 (1) ) I (2 ) R o (3) I ) R o
毕萨定律演示文稿
O l
x
θ
θ
1
⊗
P
µ0I = (cosθ1 −cosθ2) 4x π
I dl
r
讨论
µ0I B= (cosθ1 −cosθ2) 4x π
∞ ( x<<L) 0 θ2 π
θ2
1、无限长载流直导线 、
当 L θ1
比较无限长带电 直导线附近场强
λ E= 2πε 0 x
µ0I B= 2x π
l O
x
θ
I dl
y
设圆电流在yz平面内 设圆电流在 平面内
I z
R o
x.
P
x
y
Id l r 组成的平面
Idl r0 ˆ
I z R
o
r
dB
x
.
P
x
第一步: 解:第一步:在圆电流上任取一电流元 Idl 由毕-萨定律知其在场点P 由毕-萨定律知其在场点P产生的磁感强度
dB =
ˆ µ0 Idl × r 0 4πr
2
第二步: 第二步:分析各量关系 明确 dB的方向和大小
毕奥- §11-2 毕奥-萨伐尔定律及其应用
要解决的问题是: 要解决的问题是: 真空中电流与其激发的磁场之间的定量关系 真空中电流与其激发的磁场之间的定量关系 电流与其激发的磁场 方法: 方法:将电流分割成无穷多电流元 Idl 求出电流元产生的磁感强度 应用叠加原理 可得到任一电流所激发的磁场
一 毕奥 – 萨伐尔定律
(4)通电均匀密绕螺线管轴线上 注意: 注意:a、分析B的对称性,建立坐标系,变矢量积分为标量 分析B的对称性,建立坐标系, 积分进行计算; 统一积分变量,给出正确的积分上下限。 积分进行计算;b、统一积分变量,给出正确的积分上下限。 5、用已知典型电流的磁场迭加求出未知磁场的分布
毕萨定律
p
真空磁导率 0 4 10 7 N / A2
0 Idl sin 磁感的 dB 大小: 4 r2
磁感的方向: 线电流:
分量式(直角坐标系):
0 Idl r ˆ B dB r2 4
由I d l 转向 r 的右手螺旋方向。
B x d Bx , B y d B y , Bz d Bz
圆电流的 磁感线
通电螺线管的 磁感线
I
I
I
I
2、磁通量—穿过任意曲面的磁感线数(单位:韦伯)
S
B
B
B ds
(符号:Wb)
S
Байду номын сангаас n
B
B BS
B B S BS cos
S
ds
n
S
B
ds
n
B
B B ds B cos ds
α
Idl
B
dB
L
L
0 Idl r 4 r 3
(下一页)
• 运动电荷的磁场
导体中的电流是大量自由电子的定向运动。因 此,电流磁场的本质是这些运动电荷产生的磁 场的宏观表现。
dB的大小为
由毕 — 萨定律,电流元Idl 产生的磁感应强度
0 Idl sin Idl , r dB 2 4 r
3、磁场的高斯定理 穿过任意闭合曲面的磁通量如何?
B ds 0
比较
S
B
穿过任意闭合曲面的磁通量 等于零, 称为磁场的高斯定理
?
1 E ds qi s 0
11-4磁场的高斯定理和安培环路定理
闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场, 安培环路定理的存在说明磁场不是保守场,不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线, 做 PO 垂线,取对称的长直 电流元,其合磁场方向平行于电流平面。 电流元,其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大, 电流平面无限大,故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零: 同理可求得在螺绕管外部的磁场为零:
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
右手螺旋前进法则
I
r
dB
二. 运动电荷的磁场
dB = 4 π
=4 π
μ
o
I dl sina r
2 2
S +
dl
+
μ
o
n qv S dl sina r
<
I
v
+
r r ) dB μ qv sin( v 、 B= = r π dN 4
μ qv dN sin( v 、 r =
π 4
o 2 o
I = n qvS
o 2 2 o 2 2
μ
dB
a
μ I cosβ dβ = πa
o
4
电流元的dB已经有了,接 下去对整体载流导线产生 磁感应强度量值的积分。
μ I cosβ dβ dB = π a
o
4
电流元的dB已经有了,接 下去对整体载流导线产生 磁感应强度量值的积分。
dl
I dl
B = dB = β
o
β2
讨论:
当螺线管为无限长时:
B =μ o n I
作为经验公式记住!
β1
π
、
β2
0
归纳总结
利用毕奥 萨伐尔 (Biot-savart) 解题思路: 定律求磁感应强度的分布
1.将载流导线无限分割成电流元Idl ,任一电流 元在空间某点处产生磁感应强度用dB 表示。 2.由磁场的叠加原理求得整根载流导线所产生的 磁感应强度B = dB
比例系数
dB ∝ I dl sin a r
2 o 2
a 表示电流元和
矢径之间的夹角 ∨
可写为
真空磁导率
μ I dl sin a dB = r π 4
a = ( I dl 、r )
dB = 4 π
μ
o
I dl sina r
2
μ
o
真空中的磁导率
7
1
此数据加以 适当记忆!
1
μ o =4 π ×10 ( H . m
当直线电流为“无限长”时:
I
β
π
1
取
o
2
β
2
取 2
π
β2 β1
μ I B=
dB
sin β ( 2 - sinβ 1) a π 4 πa 4
o
o
a 作为经验 公式记住
μ I =
×2
μ I = 2π a
μ B = πI 2 a
o
无限长载流直导线外任意一点 处的磁感应强度的量值公式。
注意:这里的a是考察点到无限长直线电流的垂直距离
2.
载流圆线圈轴线上的磁场
研究载流圆线圈轴线上P点处 的磁感应强度B 大小和方向 攫取载流圆线圈上的电 流元Idl,并设定电流元 到P 的矢径为r
I dl
R
90
0
r
θ
dB
根据右手螺旋前进法则
I
·
I dl
x
·
P
I dl × r
可以确定电流元Idl 在P点 处磁感应强度dB 的方向
dB
其中电流元和矢径的夹角
半无限长载流螺线管轴线上
P点处的磁感应强度B:
(5)一段圆弧在圆心处产生的磁场
μ I θ B= 4 πR
o
0
θ
0
一段圆弧所对 应的圆心角。
上面的计算结果可作为经验公式使用,必须牢 记!对某些形状比较复杂的载流导线或导体, 可看作这些简单电流的组合。
I dl
a
β
I
l
90
0
r
β
dB
的方向: I dl × r
右手螺旋前进法则
dB
a
· P
dB 的大小:
dB = 4 π
μ
o
I dl sina r
2
1. 载流直导线的磁场
dB 的方向: dB 的大小:
I dl × r
右手螺旋前进法则
o
dB = 4 π
μ
I dl sina r
2
以下是数学关 系的变化过程
▲
如果按照本教材 (P82图11-9中角度的取向)
β2
分析的思路基本相同,就 是积分角度不同。
I
β1
μ I B=
o
cosβ 1 - cosβ 2) ( a π 4
取 0 ,β 2 取π
o
当直线电流为“无限长”时:
dB a
β
1
μ I B = πa 2
作为经验公式记住!
如果是半无限长,则:
μoI 1 × μoI B= = 4π a 2 2π a
毕奥
萨伐尔定律
(历史上曾经称:毕奥-萨伐尔.拉普拉斯定律)
Law of Biot-Savartg
一个用于计算载流导线和运动电荷周围磁 感应强度B 的大小和方向的重要工具
m
m S
en
S
I
+ I
dl
+
I
+
v
....................
× × × × × × × × × × × × × × × × × × × ×
解题步骤: (1)用定律写出载流导线上任一电流元
在空间某点产生的磁感应强度:
。
dB = 4 π
μ I dl × r
o
r
3
并判别其方向。
(2)由磁场叠加原理计算载流导线在空间某点产生的 B
B = dB = 4 π
化为分量式 。
μ I dl × r
o
r
3
(3)选取适当的坐标系,把矢量积分式
B = dB
1 E= 4 π ε
0
q r ( r r )
2
此式表明运动电荷激发的电场和磁场是紧 密相关的,从而加速奠定了电磁场的理论。
§11-4 毕奥
萨伐尔定律的应用
1. 载流直导线的磁场
求载流导线外任意一点P的 磁感应强度B(已知P点与 载流导线的垂直距离为a)
在载流导线上攫 取电流元 I dl
▲
dl
电流元 I dl 到 P点的矢径为r
P
l ctgβ = l = R ctgβ R 2 β dβ csc = dl R
.
β1
β
R
β2
dl
l
R
× × × × × × × ×× × × × × × × ×× × × ×
μ n I dl R dB =
o 2 2 o
2 3 2 2
P β
2( R + l )
2 2
·
R
dl
μ n I ( R csc β dβ =
3
2 2
1 2
3
μ IR
o
2 3 2
2( x 2+ R 2 )
=(x + R )
2 2
3 2
B=
μ IR
o
2 3 2
讨论:
(1)在圆心处,x = 0
R
2( x 2+ R 2 )
B= 2 R
o
μ I
I
·
P
x
·
作为经验公式记住! 如果是载流半圆环圆心处,则: (2)引入磁场中新的物理量:磁矩m
1 × μ oI B = 2 2R
β2
I
β1
a
dB a
如果按照本教材 (P82图11-9中角度的取向)
μ I B=
o
cos β ( a π 4
1
- cos β 2)
(2)无限长直线电流的磁场
(2)无限长直线电流的磁场
μ I B = πa 2
o
a 是考察点到无限长直 线电流的垂直距离 如果是半无限长,则:
(3)载流圆线圈轴线上P 点处的磁感应强度B
o 2 o
μ
2
o
2
o
2
μ I sin d l θ B = dB x = 4 πr
o 2
I dl
R
90
0
r
θ
dB
sin θ =R r
I
·
I dl
x
·
P
μ I =
o
πr r 4
2 o
R
d l
3 2
dB
dl = 2π R
2π R
= =
μ IR
4π ( x + R )
2 2
r = (x + R )
N
线圈的匝数
S
线圈所包围的面积
已知:
B=
μ IR
o 2
2 3 2
2( x + R )
2
m=N I S e n
(2)引入磁矩后,圆电流轴线 处的磁感应强度可表示为:
B= =
μ IR
o 2
2 3 2
2( x + R ) μ oI R 2
2
m × IS
2( x + R )
2 2
3 2
m × Iπ R
磁矩
dB 的大小
dB = 4 π
μ
a = 90
o
0
o
I dl sina μ I dl =4 π r r
2
2
再在载流圆线圈的下端攫取电流元Idl,并确定dB的方向
再在载流圆线圈的下端攫取电流元Idl,并确定dB的方向 建三维坐标: I dl R
90
0
r
θ
y dB
注意到 dB矢量在三维 坐标上分量的对称性:
用矢量形式表示的毕奥
