有限元模态分析实例
SAMCEF有限元分析 耦合分析典型实例
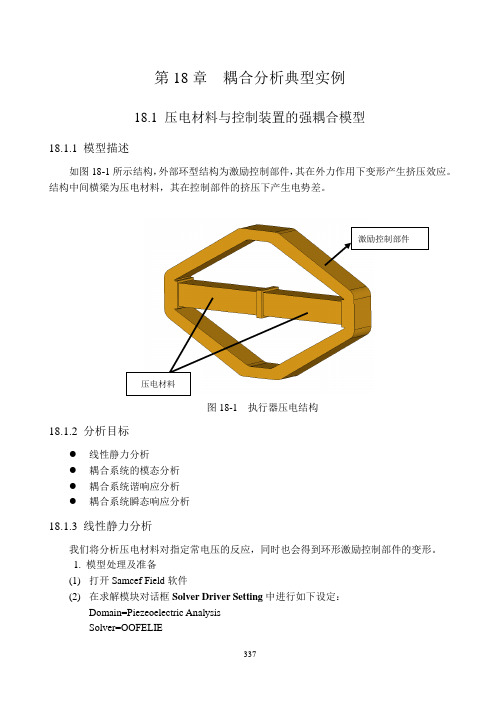
第18章耦合分析典型实例18.1 压电材料与控制装置的强耦合模型18.1.1 模型描述如图18-1所示结构,外部环型结构为激励控制部件,其在外力作用下变形产生挤压效应。
结构中间横梁为压电材料,其在控制部件的挤压下产生电势差。
18.1.2 分析目标●线性静力分析●耦合系统的模态分析●耦合系统谐响应分析●耦合系统瞬态响应分析18.1.3 线性静力分析我们将分析压电材料对指定常电压的反应,同时也会得到环形激励控制部件的变形。
1. 模型处理及准备(1)打开Samcef Field软件(2)在求解模块对话框Solver Driver Setting中进行如下设定:Domain=Piezeoelectric AnalysisSolver=OOFELIEAnalysis type=Linear Static(3)点击工具菜单中File\Import geometry,在出现的Input对话框中,直接进入samceffield安装路径下的example文件夹,选择brep\piezoelectrics\Actuator.brep,点击<Open>导入模型。
(4)点击工具菜单中的File\Save As将文件另存到一新的工作路径中。
2. 建立分析数据点击按钮<Analysis Data>进入分析数据定义模块。
(1)几何属性和材料属性我们先来定义两个非压电部分的属性,对于本例来说就是外部的环和两个压电体中间的连接部分。
1)在数据树或3D显示区域选择”Actuator”,点击工具栏中的<Behavior>几何属性定义按钮,在几何属性定义对话框中,几何类型(behavior)选择体,对象选择类型(place on)选择<solid>。
几何属性(type)选择柔体<Flexible>,在3D显示区域选择以下两个高亮显示部分作为Flexible part(如图18-2)。
挖掘机动臂有限元模态分析

中 图分 类 号 :H1 ,U 2 文 献标 识码 : T 6T 6 1 A
挖掘机工作装置的传统设计多采用静力计算确定工作装置
当系统的 自由度很大时对这样一组耦合方程进行求解将非 模态分析方法就是以无阻尼的各阶主振型所对应的模态 的受力 ,依靠 安全系数的选取保证其强度及 可靠性的经验方法 , 常困难 。 1解耦 , 变成各个独立的微分方程 。 对 而未能充分考虑其工作 过程 中所受动态载荷带来 的冲击与振动 坐标来 代替物理坐标使式( ) 问题 。挖掘机作业过程中工作装置时刻处于振动之 中, 且其振动 式() 1 进行拉氏变换后得到: 怕【] ) ()_ ) () s c+ { s }( } 2 陶 x 5
r dotntos e w i r asltfens adpat a rs i i .tatte o e 5moe r i u i w t s hc ae boue rees n r i etco A s. r1 dsae e t a h c c l rtn l h f aotdadetn e.sihrn eunyadm i ir i oeirve e.h td rvdsi— dpe n xeddI n eetrqec n anv a o m d s eiw dTes y poie m— t f b tn u p r t oe p a eefr ayio m cv o, dipoiefu dt no eaa s — ot dl a m tro l sf a o e aa ra t rvds on ai t l i o d n a m r n a s r f x t n o f h n y sf y n ip r r neadot i i rcua ya i caat ii frt m o cv o dte m f a c e omac i z o o s utr dn c hr esc o ea e aa ra n p m a nf t t l m c r ts h r f x t n h
有限元模态分析实例

ANSYS模态分析实例5.2ANSYS建模该课题研究的弹性联轴器造型如下图5.2:在ANSYS中建立模型,先通过建立如5.2所式二分之一的剖面图,通过绕中轴线旋转建立模拟模型如下图5.35.3单元选择和网格划分由于模型是三给实体模型,故考虑选择三维单元,模型中没有圆弧结构,用六面体单元划分网格不会产生不规则或者畸变的单元,使分析不能进行下去,所以采用六面体单元。
经比较分析,决定采用六面体八结点单元SOLID185,用自由划分的方式划分模型实体。
课题主要研究对象是联轴器中橡胶元件,在自由划分的时候,中间件2网格选择最小的网格,smart size设置为1,两端铁圈的smart size设置为6,网格划分后模型如图5.4。
5.4边界约束建立柱坐标系R-θ-Z,如5-5所示,R为径间,Z为轴向选择联轴器两个铁圈的端面,对其面上的节点进行坐标变换,变换到如图5.5所示的柱坐标系,约束节点R,Z方向的自由度,即节点只能绕Z轴线转5.5联轴器模态分析模态分析用于确定设计中的结构或者机器部件振动特性(固有频率和振型),也是瞬态变动力学分析和谐响应分析和谱分析的起点。
在模态分析中要注意:ANSYS模态分析是线性分析,任何非线性因素都会被忽略。
因此在设置中间件2的材料属性时,选用elastic材料。
5.5.1联轴器材料的设置材料参数设置如下表5-1:表5.1材料参数设置表5.1材料参数设置5.5.2联轴器振动特性的有限元计算结果及说明求解方法选择Damped方法,频率计算结果如表5-2,振型结果为图5.6:表5.2固有频率(l)一阶振型频率为40.199Hz,振型表现为大铁圈和中间件顺时针旋转(从小铁圈观察),小铁圈逆时针旋转。
(2)二阶振型频率为73.632Hz, 振型表现为大铁圈,中间件和小铁圈同时顺时针旋转(从小铁圈观察)。
(3)三阶振型频率为132.42Hz,振型表现为大铁圈和小铁圈同时逆时针旋转(从小铁圈看),中间件顺时针旋转,由上图我们可以发现,在这个频率下是联轴器最容易发生断裂。
复合材料风机叶片有限元模态分析

料 和结构 性能. 态性 能 对其 疲 劳 和 可靠 性 有很 大 动
影响. 为了减少 动态性能 的影 响 , 振动 研究常用 于避
{ , , 和 { — — 分 别 表 示 有 限 元 节 点 } { { ) ) F)
免共振 , 叶 片 的 激振 频 率 远 离 本 身 固 有 频率 . 使 因 此, 研究 叶片 的固有 频率 显 得尤 为 重要 . 目前 , 多 很
价值 的理论 参考.
关 键 词 : 叶 片 ; 合 材 料 ; 态仿 真 ; 力 刚 化 复 模 动 中 图 分 类 号 :TK8 3 文 献 标 识 码 :A 文 章 编 号 :l 7 — 1 9 2 1 ) 1 0 2 — 0 6 1 1 X( 0 1 O — 0 8 3
统啪对 复合 材料 叶片进行 模 态仿 真 , 研究其 振 动频
机技 术[ 的 方 法 , 用 大 型 非 线 性 a a u 3 采 b q s仿 真 系
收稿 日期 :0 O O — 1 2 1— 9 3 基金 项 目 ; 湖南 省 教 育厅 科 研 资 助 项 目( 0 0 5 ) 1 c 5 2 作 者 简 介 : 建 华 ( 96 李 1 7 一) 男 , 士 , 程 师 , 究 方 向 : 拟 样 机技 术 与 仿 真 。 , 硕 工 研 虚
叶 片 由有 限 元离 散化 处理 后 , 应用 瞬时 最小 势
能 原 理 [ 可 导 出结 构 运 动 微 分 方 程 5
[ { +[ ] ) K] 1 一{ £ ) M] } c { +[ { ) F() 1
量 、 尼和刚 度矩阵 ; 阻
() 1
式 中[ 、c 和[ —— 分别为 叶片 结构 的整体 质 M] [ ] K]
城市地铁车车体强度有限元分析及模态分析

城市地铁车车体强度有限元分析及模态分析随着我国城市化的发展,城市轨道交通的地位变得越来越重,具有高效、快捷、舒适、客运量大等优点的地铁已经成为城市轨道交通中最常见的一种。
然而,任何事物都是一把双刃剑,地铁为人们提供了方便,但一旦发生安全事故,其后果是无法想象的。
历史上有很多次地铁安全事故都源于车体强度问题和振动问题。
因而,对新设计的车体结构进行强度校核和模态分析具有显著的社会意义和经济意义。
地铁是城市轨道交通的一种,一般由车体、转向架、制动装置、风源系统、电气传动控制、辅助电源、通风、采暖与空调、内部装修及装备、车辆连接装置、受流装置、照明、自动监控系统等组成。
地铁车型往往被分为A、B、C三种型号,三种车型的主要区分是车体宽度,A型地铁列车:长22.8米,宽3米;B型地铁列车:长19米,宽2.8米;C型地铁列车:长19米,宽2.6米。
一般A型、B型车最常见,C型车一般比较少见,因其运输能力有限,在交通比较拥挤的城市无法容纳高峰客流。
本文的目的是在现有几何模型的基础上建立该地铁车车体的有限元模型并对车体进行强度分析和模态分析,了解在工况下车体的变形及应力情况,为检验设计是否符合标准提供依据。
通过模态分析可以了解车体部件的固有频率以确定出车体振动频率的危险频率段,从而可以确定车体在什么样的载荷下工作不会发生共振。
标签:地铁;车体强度;有限元分析1 引言本课题拟根据某城市地铁车车体的实际几何结构,在HyperMesh软件环境下建立与几何结构相符的中面模型,并在中面模型上进行网格划分,建立完整的有限元模型,然后根据相应的技术规范中的要求,在ANSYS软件中进行强度分析和模态分析计算。
结果显示,车体在相应静强度工况下应力分布较合理,最大应力不超过材料屈服极限,满足设计要求;模态分析得到车体一阶垂向振动频率为13.5575Hz,一阶扭振频率为18.1975Hz。
所得计算结果可以为工程设计人员提供理论指导。
2 计算模型本课题研究的某城市地铁车体是钢铝混合结构:车顶、侧墙、底架、端墙采用以型材为主要结构形式的铝合金材料,牵引梁、缓冲梁、枕梁采用高强度钢结构,钢结构与铝合金结构间通过铆钉相连。
武汉轻轨箱形梁的有限元模态分析

作者简介 :马伟东 (9 2 ) 男 , 16 . , 广东省广州市人 , 工程师。
维普资讯
维普资讯
7 4
武
汉
工
业
学
院
学
报
20 0 7钲
H apoeA pie a na[ . ea edhn m l rD t Maul Z] Txs i f a Isu ns20 . nt met,02 r
[ ] 李双 勋 , 4 欧建 平.L 30 I2 T C 2 AC 3在 音频 处 理 中 的应 用 [ ] 国外 电子元器件 ,04,1 ) J. 20 (0 .
THE I MPL M E A ON OF MP C0DER E NT TI 3 DE
S YSTE B M ASED ON F XED. OI I P NT DSP
关 键词 :箱形 梁; 态分析 模
中图分 类号 :U4 15 4 . 文 献标识 码 : A
模型。
0 引言
武汉 市 轨道 交通 一 号线 位 于京 汉 大道 上 , 程 工 全 长约 2 k 分 两期实施 。一 期工 程 由宗关 至 黄浦 7 m, 路, 已完工 并 投入 正 常 商 业 运 行 , 长 1.4 m, 全 O2 k 设 1 O座车 站 , 总投 资 约 2 2亿 元 。高 架 桥 桥 梁 采 用 箱 形结 构形 式 , 主要 为单箱单 室形 式 , 在交叉线 与折 返 线处 采用 双箱双 室和单箱 双 室形式 。本文 主要研 究 了单 室单 箱 2 5m跨 长 的箱 形 梁 结 构 的振 动 模 态 。
5I 1l 【 28 5 5 01 05
2 05 8
I5 _
有限元Comsol-Multiphysics的输电杆塔模态分析

有限元Comsol-Multiphysics的输电杆塔模态分析本科毕业设计(论文)基于Comsol Multiphysics的输电杆塔模态分析摘要随着社会的发展,输电线路作为电网的大动脉,其安全稳定的运行关乎着国民经济的稳定。
作为支撑输电线的骨骼,输电铁塔的安全可靠运行是电网安全稳定运行的重要保证。
但近年来,在各种极端情况下,倒塔断线事故时有发生,严重危害了电网安全。
因此,研究输电塔架在各种复杂极端情况下的静动力特性对提高输电线路的安全可靠性有着重要的研究以及工程价值。
本文以有限软软件COMSOL Multiphysics为研究平台,根据已有的设计资料,研究了输电塔架的有限元模型的建立方法,建立了酒杯型直线塔的有限元分析模型,并提出了塔架在风载荷、覆冰载荷、基础沉降等工况下的研究处理办法。
根据设计规程,通过分析计算得出了输电塔架在大风作用下的风载荷,并分段施加在输电塔架以实现风载荷的准确施加。
风载荷下,最大的位移出现在塔身。
然后研究了输电塔架在覆冰、基础沉降等工况下的静力学特性。
最后重点研究了输电塔架的动力特性,对有限元模型进行了模态分析,得到了输电塔架的前10 阶振型以及相对应的自振频率,通过研究发现在塔腿和塔身部分容易过早的出现局部模态。
关键词:输电杆塔;输电塔线体系;静力特性;动力特性AbstractWith the development of society, the security an stability of electric transmission line system is important to national economy. As the artery of electric network, electric transmission line is a vital implement. Recently, the happening of the collapsing accidents of tower-line system threatened the security of electric network. Therefore, the study of static and dynamic characteristics of the transmission tower has important value both in theory and engineering to improve the safety and reliability of power system.The finite software COMSOL Multiphysics is used as the analyzing platform in this paper. Based on design information,transmission tower as the glass-shaped tangent tower for analyses is established. In the meantime, the paper advanced the processing methods of different loading cases, such as in wind , ice, foundation settlement.According to the design standards, the subsection wind load of solo tower under maximum wind design are calculated and loaded. The maximum displacement appears in the windward side of tower body.Then the paper studied the mechanical property of transmission tower under extreme cases such as ice, foundation settlement and other working conditions.Moreover, the mode analyses are carried out considering tangent tower, obtaining its former ten self vibration frequency and vibration mode correspondingly. According to the frequency and vibration mode, finding that part of tower leg and body are tend to appear partial mode.Key words:Transmission tower; Transmission line system;Static characteristic; Dynamic characteristic;目录第一章绪论 (1)1.1 选题的意义和目的 (1)1.2 输电杆塔在国内外的发展与研究 (2)1.3 论文研究主要内容 (3)第二章输电杆塔体系的建模及分析 (5)2.1 输电杆塔概况 (5)2.2 有限元分析软件Comsol Multiphysics (6)2.1.1 有限元理论概述 (6)2.1.2 Comsol Multiphysics软件的主要功能和分析过程实现 (7)2.1.3 有限元建模要求 (7)2.2 输电杆塔体系模型的建立 (8)2.2.1 仿真模块的选取 (8)2.2.2 输电杆塔模型的建立 (8)101112121214151516161717 3.3 基础沉降作用下的静力学分析 (18)3.3.1 基础沉降 (18)3.3.2 输电单塔基础沉降作用下的静力学分析 (18)3.3.3 输电塔线在基础沉降作用下的静力学分析 (20)3.4 本章小结 (20)第四章基于COMSOL Multiphysics输电杆塔模态分析 (21)4.1 输电杆塔模态分析理论 (21)4.1.1 输电单塔的自振模态分析 (22)4.2 模态分析在COMSOL Multiphysics中的实现 (23)4.3 输电塔线体系的模态分析 (26)4.3.1输电塔塔模态分析 (26)4.3.2输电塔线耦合模态分析 (29)4.4 本章小结 (30)结论和展望 (31)总结 (31)展望 (31)参考文献 (32)致谢 ....................................................... 错误!未定义书签。
有限元模态分析实例

有限元模态分析实例有限元模态分析是一种用数学方法对结构物的振动特性进行分析的工程方法。
在设计和优化结构时,对结构的模态进行分析是十分重要的。
通过模态分析可以获得结构的固有频率、模态形态以及模态阻尼等信息,为结构的设计和工程优化提供依据。
下面将介绍一个有限元模态分析的实例。
工程项目中有一座长桥,设计要求对该桥进行模态分析,以评估其振动特性和优化设计。
桥梁的整体结构是由主梁和横梁构成。
在进行模态分析之前,首先进行了有限元建模。
主梁和横梁的几何尺寸、材料性质和截面形状被纳入有限元模型中。
通过有限元分析软件对桥梁进行了静力分析,确定了主梁和横梁的应力分布和变形情况。
在静力分析的基础上,进行了模态分析。
在模态分析中,首先得到了桥梁的固有频率。
固有频率是结构在没有外部激励作用下自发振动的频率,也可以理解为结构的固有振动频率。
通过固有频率的计算,可以得到结构的自由振动周期。
接下来,得到了桥梁的模态形态。
模态形态是固有振动状态下结构各个节点的振型。
通过模态形态的计算,可以了解结构在不同频率下的振动模式,进一步评估结构的振动特性。
最后,得到了桥梁的模态阻尼。
模态阻尼是结构在振动过程中能量耗散的程度。
结构的阻尼特性对于振动特性的评估和结构的设计优化具有重要影响。
对模态分析的结果进行评估,发现一些模态频率较接近结构的主要激励频率,存在共振现象。
为了消除共振现象,采取了一些优化措施,如增加结构的刚度、改变材料性质等。
通过有限元模态分析,得到了桥梁的固有频率、模态形态和模态阻尼等信息,为结构的设计和工程优化提供了依据。
基于模态分析的结果,进行了优化设计和改进措施,提高了结构的振动特性和抗震能力。
总之,有限元模态分析是一种重要的工程分析方法,通过模态分析可以评估结构的振动特性,并为结构的设计和工程优化提供依据。
符合桥梁的模态分析在设计和改进中的实践,对于确保工程质量和结构的稳定性具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS模态分析实例5.2ANSYS建模该课题研究的弹性联轴器造型如下图5.2:在ANSYS中建立模型,先通过建立如5.2所式二分之一的剖面图,通过绕中轴线旋转建立模拟模型如下图5.35.3单元选择和网格划分由于模型是三给实体模型,故考虑选择三维单元,模型中没有圆弧结构,用六面体单元划分网格不会产生不规则或者畸变的单元,使分析不能进行下去,所以采用六面体单元。
经比较分析,决定采用六面体八结点单元SOLID185,用自由划分的方式划分模型实体。
课题主要研究对象是联轴器中橡胶元件,在自由划分的时候,中间件2网格选择最小的网格,smart size设置为1,两端铁圈的smart size设置为6,网格划分后模型如图5.4。
5.4边界约束建立柱坐标系R-θ-Z,如5-5所示,R为径间,Z为轴向选择联轴器两个铁圈的端面,对其面上的节点进行坐标变换,变换到如图5.5所示的柱坐标系,约束节点R,Z方向的自由度,即节点只能绕Z轴线转5.5联轴器模态分析模态分析用于确定设计中的结构或者机器部件振动特性(固有频率和振型),也是瞬态变动力学分析和谐响应分析和谱分析的起点。
在模态分析中要注意:ANSYS模态分析是线性分析,任何非线性因素都会被忽略。
因此在设置中间件2的材料属性时,选用elastic材料。
5.5.1联轴器材料的设置材料参数设置如下表5-1:表5.1材料参数设置表5.1材料参数设置铁圈1中间件2铁圈3泊松比0.30.49970.3弹性模量Mpa2E5 1.274E32E5密度kg/m7900100079005.5.2联轴器振动特性的有限元计算结果及说明求解方法选择Damped方法,频率计算结果如表5-2,振型结果为图5.6:表5.2固有频率SET TEME/FREQ LOAO STEP SUBSTEP CUMULATIVE 140.199111173.6321223132.421334197.34144(l)一阶振型频率为40.199Hz,振型表现为大铁圈和中间件顺时针旋转(从小铁圈观察),小铁圈逆时针旋转。
(2)二阶振型频率为73.632Hz, 振型表现为大铁圈,中间件和小铁圈同时顺时针旋转(从小铁圈观察)。
(3)三阶振型频率为132.42Hz,振型表现为大铁圈和小铁圈同时逆时针旋转(从小铁圈看),中间件顺时针旋转,由上图我们可以发现,在这个频率下是联轴器最容易发生断裂。
(4)四阶振型频率为197.34Hz,振型表现为大铁圈,中间件和小铁圈同时逆时针旋转(从小铁圈观察)。
5.6 联轴器瞬态动力学分析为了简化计算方法和节省计算用时,首先对联轴器的模型进行简化。
因为铁圈上的螺孔的存在会大大的影响计算的复杂程度和时间,但对计算结果的影响却微乎其微,所以决定建模时省略螺孔。
简化后的模型网格划分后如下图5.7:由于橡胶的特殊机械性能,在进行计算机模拟时,必需把非线性因素考虑进去。
5.6.1 非线性分析的基本信息ANSYS程序应用NR(牛顿-拉斐逊)法来求解非线性问题.在这种方法中,载荷分成一系列的载荷增量.载荷增量施加在几个载荷步.图5.8说明了非线性分析中的完全牛顿-拉斐逊迭代求法,共有2个载荷增量。
在每次求解前,NR方法估算出残差矢量,这个矢量回复力(对应于单元应力的载荷)和所加载和的差值,程序然后使用不平衡载荷进行线性求解,且检查收敛性.如果不满足收敛准则,重新估算非平衡载荷,修改刚度矩阵,获得新的解答.持续这种迭代过程直到问题收敛。
ANSYS程序提供了一系列命令来增强问题的收敛性,如线性搜索,目动载荷步,二分等,可被激活来加强问题的收敛性,如果得不到收敛,那么程序试图用一个较小的载荷增量来继续计算。
非线性求解被分成三个操作级别:载荷步,子步和平衡迭代.(1)顶层级别由在一定“时间”范围内用户明确定义的载荷步组成.假定载荷在载荷步内线性地变化。
(2)在每一个载荷步内,为了逐步加载,可以控制程序来多次求解(子步或者时间步)。
(3)在每一子步内,程序将进行一系列的平衡迭代以获得收敛的解。
下图5.9说明了一段用于非线性分析的典型的载荷历史。
5.6.2非线性材料的模拟材料非线性包括塑性,超弹性,蠕变等,非线性应力应变关系是非线性结构行业的普通原因,如图5.10:橡胶是高度非线性的弹性体,应力应变关系较为复杂,在本课题中采用工程中广泛采用Mooent-Rivlin2参数模型进行橡胶材料的模拟,参数包括C10和C01。
5.6.2.1Mooey-Rivlin常数测量的理论基础超弹性材料是指具有应变能函数的一类材料数,对应变分量的导数决定了对应的应力量。
应变能函数W为应变或变形张量的纯量函数,W对应变分量的导数决定了对应的应力量,即:式中S ij——第二类Piola-Kirchhoff应力张量的分量W——单位未变形体积的应变能函数E ij——Green应变张量的分量C ij——变形张量的分量式(5-1)为超弹性材料的本构关系,可以看出,建立本构关系就是要建立应变能函数的表达式。
Mooney-Rivlin模型是1940看由Mooeny提出,后由Rivlin发展的。
其中一般形式为式中C rs——材料常数I1,I2——Cauchy变形张量的不变量超弹性不可压缩材料的本构方程可表示为:式中σij——Cauchy(真实)应力张量的分量P——静水压力δij——Korneker算符下面假设取变形的主方向为坐标轴方向,则Cauchy变形张量用矩阵形式表示为:式中λ1——i方向的主伸长比式中εi——i方向工程应变主值所以C ij的不变量表示为由不可压缩条件:,考虑薄式片受简单拉伸的情况,即试片一个方向受拉力,另两个方向自由,假设受拉方向为1,则有:给定伸长比λ2=λ,则:由式(5-13)解出P代入式(5-12)得:根据所取W的具体形式,可求出的表达式,其中含有材料常数,由试验数据求得各伸长比及对应的应力,将多个试验点的λ和σ11代入式(5-14),可求得这些材料常数值。
5.6.2.2试验测试实验采用长的薄式片作为拉伸试样,通过拉伸计算伸长比λ和应力σ。
按式(5-14)进行回归分析,求解回归系数,将式(5-14)中的应力理论值σ11表示为σi(C jk)(下标i表示数据点序号),用最小二乘法求回归系数C jk。
残差平方和为:通过对R最小化,求Mooney—Rivlin常数C10,C01。
可求得最小二乘意义下的Mooney-Rivlin常数C10,C01。
5.6.2.3橡胶材料的硬度与C10和C01,的关系G或E与材料常数的关系为文献给出了橡胶硬度Hr(IRHD硬度)与弹性模量E的试验数据,经拟合得:通过硬度利用式(3-38),(5-20)得出G,E,将G,E代入(5-18),(5-19)求出C10和C01。
橡胶的硬度为70,通过计算确定C10和C01分别为1.14Mpa和0.023Mpa。
ANSYS中参数设置如图5.11和5.12所示,其中式中d—橡胶材料的不可压缩比v—像胶材料的泊松比,0.49975.6.3施加载荷在小铁圈端施加205-105cis314t的动载荷,为了能够清楚地看到动态变化的过程,我们取两个周期。
在0.001秒施加第一个载荷,T1=100,迅速达到电动机工作状态。
对于正纺载荷,将每四分之一周期划分成五小段,每一个小段作为1个载荷步,一共可分为20个载荷步。
载荷点和施加过程如图5.13和图5.14所示:考虑到计算的精确性和计算时间,每个载荷步分成5个子步。
5.6.4计算结果及说明ANSYS常用的求解器有:波前求解器、稀疏矩阵直接求解器、雅克比共扼梯度求解器(JCG),不完全乔列斯基共扼梯度求解器(ICCG)、前置条件共扼梯度求解器(PCG)前两种为直接求解器,后二种为迭代求解器。
本课题采用JCG求解器。
计算结果如下图5.15所示:(1)为大小铁圈的相对转角,之所以振幅越来越小是因为理论值中的齐次方程的解随着时间越来越接近于0。
(2)为大小铁圈的相对角速度;(3)为相对角加速度。
速度和加速度都以类似于正弦曲线发生改变,之所以没有完全按照正弦,是由于阻尼的存在,大大缓解了激励载荷对联轴器的影响。
弹性联轴器的使用状况直接关系到机械设备的安全及寿命问题,尤其是一些重要场合,弹性联轴器的失效会引起巨大的经济损失和人员伤亡事故。
弹性联轴器的工作状态涉及多个方面,其中重要的一个方面是弹性联轴器在工作过程中的扭振现象。
因此,对于联轴器的扭振研究有着巨大的实际意义。
6.1 本文总结本文所做的主要工作为分析弹性联轴器,建立了弹性联轴器动力学力学模型并对其进行了仿真计算,同时,对其进行了有限元分析。
现将本文的结论归纳如下:1 引起弹性联轴器扭转振动的原因主要归结于两个方面:即由柴油机引起的机械扰动和由发电机引起的电气扰动,电气扰动的频率较稳定,力矩较小。
2 弹性联轴器的动刚度与静刚度比值为1.3-1.5之间。
3 阻尼对于弹性联轴器的固有特性的影响很小,计算固有频率时,可以近似认为阻尼为O:对于非圆轴的旋转零件的固有频率的计算,可以通过将转动惯量等效分布到圆轴上的方法进行计算。
4 在联轴器的设计过程中,可以通过控制两端的转动惯量,或者通过改变联轴器本身的尺寸来控制它的扭转刚度,力求使弹性联轴器的临界阻尼系数尽可能的接近联轴器本身的阻尼系数,从而减少产生的剪切力,提高联轴器的工作状态和延长联轴器的使用寿命。
5 采月Moony 一rivlin模型参数来模拟超弹性的橡胶材料时,可以通过式(3-37) ,(5-18), (5-19)利用橡胶材料的硬度求出C10和CO1,具有较高的准确性。
6 采用ansys件进行计算机模拟,得出弹性联轴器的固有频率以及干扰正弦激励下的动态特性。
6.2 创新点国内外对扭振进行了大量的研究,但是研究内容大多局限于传动轴系,很少涉及具有大阻尼特性材料的旋转零件的扭振研究。
本课题的研究对象是橡胶弹性联轴器,橡胶是一种典型的非线性材料,具有很大的阻尼特性,本文通过理论方面和计算机方面进行研究,得出了如上的结论。
6.3不足和展望本课题没有引入试验装置,得出的理论结论和试验结论没有试验结果作对比,缺少一定的说服力和信服力;在今后的工作中,引入适当的实验装置,采用合适的实验模拟方法.采集实验数据并进行分析,验证上述结论的正确性。
(注:本资料素材和资料部分来自网络,仅供参考。
请预览后才下载,期待您的好评与关注!)。
