高中数学函数图象及其变换专题
高中数学各类函数图像规律及变换规律和练习-(修复的)

指数函数图像规律对数函数图像规律y=a x在第一象限内的图像随着 a 值的增加由下向上扬起,a<io rn为减函数,a>i0时是增函数。
丫=占与y=a-x=(1)x的a图像关于y轴对称以下为对数函数图像:从第一象限看从左4 X幕函数图像规律到右依次是昏皿yTogi 藍2从第一象限内的图像随着a的增加由左向右偏移,a< 0时是减函数,a>0时是增函数。
y = y = logi x = —log fi x的图像关于x轴对称y(x) = x3y(x)= x23-y(x) = x24■ *f / ~“"八⑷=x5 y(x) = x 54g i(x) = xa> 1陡a< 1缓y(x)f1(x) = x0a> 0增a< 0减y(x) = X 2x1在直线x=1的右侧,随着a值I增大,函数图像从下到上逐渐仰起,且图像总过点(1,1 )。
根据第一象限图像规律再结|合奇偶性即可容易的画出任/一幂函数图像。
把a化成/口形式,n为偶非奇非偶;n为犬m为奇则奇平移变换…a>0向左平移a个单位绝对值变换函数图像变换规律负>下正上下f(x) + b他+e+b左右左负右-ab> 0向上平移b个单位x在以下坐标系内画出各自对应的函数示意图h(x)=(7)[ Lyg(x)=(訓f(x)=(述二7321112丄aQ 一-1 o 1 X2、xy!321-2 -1 o 1 2-1x-2y i321-2 -1 o 1 2 -1x-2f[x) = Cfco=?x321-2 -1 o 1 2 -1f(x) = 2XF(x) = 3XL321-2 -1 o 1 2-1xx1321-2 -1 o 1-1-22 xf(x) =(ll)xf(x)二(1321-2 -1o 1-1 2x1f(x) = log! X2f(x) = 10g3x1________ f(x) = log2xf⑴=log2 Xyy l-2 -1 o 1 2-1-2 -1 o 1 2 -1-2 f(x) = x~ 2 f(x) = x~ 1y l-21f(x) = x 2f(x) = Xy l-2 -1 o 1 2 -1 -2 -1 -2 o 1 2-1-21x2f(x) = log] X] ____________f(x) = log] X y*5I321-2 -1 o 1 2-1-2“ 2f(x) = X3f(x) —x2-2 -1 o 1 2-1-2。
高中数学函数图象及其变换专题(完整资料).doc

【最新整理,下载后即可编辑】专题 函数图象及其变换考点精要1.理解指数函数的概念、图象及性质. 2.理解对数函数的概念图象和性质. 3.理解幂函数y=x ,y=x 2,y=x3,1y x=,12y x =的图象及其性质.4.掌握一次函数、正比例函数、二次函数、反比例函数的图象及其性质. 5.理解图象的平移变换、伸缩变换、对称变换.热点分析函数的图象是函数的一种重要表示方法,利用函数的图像可以帮助我们更好地理解函数的重要性质.基本初等函数的图像及其变换,是考查的热点;利用变换作图,也是考查的重点,利用形数结合的数学思想解题,看图想性质,数形转化灵活解题.知识梳理函数的图象及其变换 基础知识:1.图象法:就是用函数图象表示两个变量之间的关系 优点:能直观形象地表示出函数的变化情况. 体现:映射与反演、形数结合的数学思想. 2.基本初等函数图象y=x n y=a x y=log a x y=sin x y=cos x y=tan x 初等函数图像:y=kx y=kx+b y=ax 2+bx+ck y x=b y ax x=+3.作图基本方法(1)利用描点法作图:①确定函数的定义域:图象沿x 轴展布范围及渐近线; ②化简函数解析式:等价变形; ③讨论函数的性质:奇偶性:关于图象对称性 单调性:关于图象升降性 周期性:关于图象重要性极值、最值:关于图象最高点、最低点 截距:与x 轴、y 轴交点坐标④画出函数的图象(2)利用基本初等函数的图象的变换作图:①平移变换0,0,||()h hh h y f x ><=−−−−→右移左移y=f (x h )0,0,()k k k k y f x ><=−−−−−→上移下移||y=f (x )+k②伸(放)缩变换: 沿x 轴: ()y f x ω=()0ω>沿y 轴: y = A f (x ) (A >0)③对称变换:y=f (x ) y= f (x ) y=f (x ) y= f (x ) y=f (x ) y=f (2a x )y=f (x ) y=f 1(x )y=f (x ) y=f (x )y=f (x ) y=f (|x |) y=f (x )y=|f (x )|④几种基本变换的合成. y=f (x )−−−−→()y A f x k ωφ=++ 待三角函数的复习中再集中进行研究.例题精讲:例1 作出函数211x y x +=+的图像,并指出函数的单调区间,图象的对称中心.例2 作出函数的图像: (1)223y xx =--(2)|1|12x y -⎛⎫= ⎪⎝⎭(3)3x y x=(4)21x y x +=- (5)2log 1y x =- (6)lg y x =(7)22x y +=例3 已知函数f (x )和g (x )的图像关于原点对称、且f (x )=x 2+2x . (1)求函数g (x )的解析式; (2)解不等式()()|1|g x f x x ≥--.例4、若不等式2log 0a x x -<对1(0,)2x ∈恒成立,则实数a 的取值范围是A 、01a <<B 、1116a ≤< C 、1016a <≤D 、1a >例6、若直线y x m =-与曲线y x =-12有两个不同的交点,则实数m 的取值范围是___________。
高中数学必修一函数图像变换

(专题一)函数图像变换函数图像画法的基本原理变换作图法 1 平移)()(a x f y x f y -=→= 方法:向右平移a 个单位长度 b x f y x f y +=→=)()( 方法:向上平移b 个单位长度2 对称)()(x f y x f y -=→= (关于y 轴对称) )()(x f y x f y -=→= (关于x 轴对称) )()(x f y x f y --=→= (关于原点对称)3 其他)()(x f y x f y =→= 先画)(x f y =图,保留x 轴上方部分,再把x 轴下方图沿x 轴对折到上方)()(x f y x f y =→= 先画)(x f y =图,保留y 轴右方图像,再把y 轴右方图像沿y 轴对折典型题型1 做出822-+=x x y 的图像变式练习,当m 为怎样的实数时,方程822-+=x x m 有四个互不相等的实数根,三个互不相等的实数根,二个互不相等的实数根,没有实数根?2 作出542+-=x x y 的图像变式练习,当m 为怎样的实数时,方程542+-=x x m 有四个互不相等的实数根,三个互不相等的实数根,二个互不相等的实数根,没有实数根? 直线1=y 与曲线a x x y +-=2有四个交点,求a 的取值范围有关双绝对值的图像问题(方法零点分段法) 典型题型3 作出21-++=x x y 图像通过作出图像观察值域可以得到[)+∞,3 然后可以得到一个重要结论b a b x a x -≥-+- 变式练习如果m x x ≥-++23恒成立,求m 的取值范围 4作出21--+=x x y 图像通过作出图像观察值域可以得到[]3,3- 然后可以得到一个重要结论b a b x a x b a -≤-+-≤--(1)如果m x x ≥--+23恒成立,求m 的取值范围 (2)如果m x x ≥--+23解集是空集,求m 的取值范围 典型习题已知函数)1(2)(+-=x x x f(1) 作出)(x f 的图像判断关于x 的方程)1(2+-=x x a 的解的个数函数图像变换习题试讨论方程|x2-x+3|=a的解的个数(a∈R).例9.已知f(x)当x∈R时恒满足f(2+x)=f(2-x),若方程f(x)=0恰有5个不同的实数根,求各根之和。
高一必修1-函数图象的变换ppt课件.ppt

练习: 将直线y=2x+1向左平移5个单位,
得到的函数为__y_=_2_x+_1_1_______
左右平移时,发生变化的仅是x本身,如果x的系 数不是1时,需要把系数提出来,再进行变换.
(6)y=f(|x|)的图象:可先作出y=f(x)当x≥0 时的图象,再利用_偶__函__数__的__图__象__关__于__y_轴__对__称, 作出y=f(x)(x≤0)的图象.
函数y=|log2x|的图象是( A )
解析
f
(x)
|
lo g2
x
|
lo g2
lo
g1
2
x, x x,0
1, x
课前练习:
当a>2时,函数 y ax和y (a 1)x2 的图 象只可能是( )
y
y
y
y
0
x
A
0
x
B
0x
C
0x
D
知识回顾:基本初等函数及图象(大致图象)
函数 一次函数 y=kx+b
图象
二次函数
y=ax2+bx+ c
指数函数 y=ax
对数函数 y=logax
知识回顾:
下列二次函数的图象,是由 抛物线y=x2通过怎样的平移变换得 到的?
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
设奇函数 f(x) 的定义域为[-5, 5], 若当x∈[0, 5]时, f(x)的图象如右图所
示. 则不等式 f(x)<0 的解集
是 (-2, 0)∪(2, 5]
高中数学-函数图象变换及经典例题练习

高中数学-函数图象变换1、平移变换(左加右减上加下减):y=f(x)h 左移→y=f(x+h); y=f(x)h 右移→y=f(x -h); y=f(x)h 上移→y=f(x)+h; y=f(x)h 下移→y=f(x)-h.2、对称变换:y=f(x) 轴x →y= -f(x); y=f(x)轴y →y=f(-x); y=f(x) 原点→y= -f(-x). y=f(x) a x =→直线y=f(2a -x); y=f(x) x y =→直线y=f -1(x);3、翻折变换:(1)函数|()|y f x =的图像可以将函数()y f x =的图像的x 轴下方部分沿x 轴翻折到x 轴上方, 去掉原x 轴下方部分,并保留()y f x =的x 轴上方部分即可得到;(2)函数(||)y f x =的图像可以将函数()y f x =的图像右边沿y 轴翻折到y 轴左边替代原y 轴左 边部分并保留()y f x =在y 轴右边部分即可得到.4、伸缩变换:y=f(x)ω⨯→x y=f(ωx ); y=f(x)ω⨯→y y=ωf(x). 经典题型:作已知函数的图像、知式选图或知图选式、图像应用例1.函数111--=x y 的图象是( ) 答案B例2.如图所示,)(),(),(),(4321x f x f x f x f 是定义在]1,0[上的四个函数,其中满足性质:“对]1,0[中任意的1x 和2x ,)]()([21)2(2121x f x f x x f +≤+恒成立”的只有( ) 答案A例3、利用函数x x f 2)(=的图象,作出下列各函数的图象:(1))1(-x f ;(2)|)(|x f ;(3)1)(-x f ;(4))(x f -;(5).|1)(|-x f例4已知0>a ,且≠a 1,函数x a y =与)(log x y a -=的图象只能是图中的( ) 答案B例5函数)(x f y =与函数)(x g y =的图象如右上,则函数)(x f y =·)(x g 的图象是( ) 答案A例6 已知函数y =f (x )的周期为2,当x ∈[-1,1]时f (x )=x 2,那么函数y =f (x )的图象与函数y =|lg x |的图象的交点共有( ).A .10个B .9个C .8个D .1个解析:画出两个函数图象可看出交点有10个.答案 A例7.y =x +cos x 的大致图象是( )解析 当x =0时,y =1;当x =π2时,y =π2;当x =-π2时,y =-π2,观察各选项可知B 正确. 例8.函数cos622x xx y -=-的图象大致为( )例9.函数y =11-x的图象与函数y =2sin πx (-2≤x ≤4)的图象所有交点的横坐标之和为( ). A .2 B .4 C .6 D .8解析 此题考查函数的图象、两个函数图象的交点及函数的对称性问题.两个函数都是中心对称图形.如右图,两个函数图象都关于点(1,0)成中心对称,两个图象在[-2,4]上共8个公共点,每两个对应交点横坐标之和为2,故所有交点的横坐标之和为8.例10.函数21log 1x y x+=-的图象( ) A . 关于原点对称 B. 关于主线y x =-对称C. 关于y 轴对称D. 关于直线y x =对称解析 设21()log 1x f x x +=-,则21()log 1x f x x --=+=()f x -,所以函数21log 1x y x+=-是奇函数,其图象关于原点对称,故选A.例11. 若方程2a =|a x -1|(a >0,a ≠1)有两个实数解,求实数a 的取值范围.解:当a >1时,函数y =|a x -1|的图象如图①所示,显然直线y =2a 与该图象只有一个交点,故a >1不合适; 当0<a <1时,函数y =|a x -1|的图象如图②所示,要使直线y =2a 与该图象有两个交点,则0<2a <1,即0<a <12.综上所述,实数a 的取值范围为(0,12).函数图像及图像变换练习(带答案)1. 函数)1(||>⋅=a a x x y x 的图象的基本形状是 ( ) 答案A2.方程lg x =sin x 解的个数为( )。
高三数学专题教案函数图像的变换及应用_

芯衣州星海市涌泉学校2021届高三数学专题教案:函数图像的变换及应用一.知识梳理复习函数图像的变换:(1)、奇偶函数图象的对称性;(2)、假设f(x)满足f(a+x)=f(b -x)那么f(x)的图象以2a b x+=为对称轴;特例:假设f(a+x)=f(a -x)那么f(x)的图象关于x=a 对称。
(3)、假设f(x)满足f(a+x)=-f(b -x)那么f(x)的图象以(,0)2a b +为对称中心;特例:假设f(a+x)=-f(a -x)那么f(x)的图象以点〔a,0〕为对称中心。
(4)、假设f(x)满足f(a+x)+f(b-x)=c 那么f(x)的图象关于点(,)22a b c +中心对称。
二.例题讲解例1、求函数y=f 〔1-x 〕与函数y=f 〔x-1〕的图象对称轴方程?〔1〕.对于定义在R 上的函数)(x f ,有下述命题: ①假设)(x f 是奇函数,那么)1(-x f 的图像关于点)0,1(A 对称;②假设对R x ∈,恒有)1()1(-=+x f x f ,那么)(x f 的图像关于直线1=x 对称; ③假设函数)1(-x f 的图像关于直线1=x 对称,那么)(x f 为偶函数; ④函数)1(x f +与函数)1(x f -的图像关于直线1=x 对称.其中正确命题的序号为______________________.例2、设f(x)=x+1,求f(x+1)关于直线x=2对称的曲线的解析式。
例3、设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,求f(x)的解析式。
例3、设定义域为R 的函数⎩⎨⎧=≠-=1,01,||1|lg |)(x x x x f ,那么关于x 的方程0)()(2=++c x bf x f有7个不同实数解的充要条件是〔〕(A)0<b 且0>c(B)0>b 且0<c (C)0<b 且0=c (D)0≥b 且0=c 例4.函数)(x f 的图像与函数21++=x x y 的图像关于点)1,0(A 对称. 〔1〕求)(x f 的解析式;〔2〕假设xa x f x g +=)()(且)(x g 在区间]2,0(上为减函数,求正数a 的取值范围. 例5、函数4(1)|1|()2(1)x x f x x ⎧≠⎪-=⎨⎪=⎩〔1〕作出函数()y f x =的大致图像. 〔2〕〔考虑题〕假设关于x 的方程2()()0f x bf x c ++=有三个不同的实数解123x x x 、、,求222123x x x ++的值.三、课后习题:1、设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,求f(x)的解析式。
高一数学(必修1)专题复习二函数的图像变换

高一数学(必修1)专题复习二函数的图象变换一.平移变换:(1)函数)(h x f y )0(h 的图象是把)(x f y 的图象向左平移h 个单位得到的;(2)函数)(h x f y )0(h 的图象是把)(x f y 的图象向右平移h 个单位得到的;(3)函数k x f y )()0(k 的图象是把)(x f y 的图象向上平移k 个单位得到的;(4)函数k x f y)()0(k的图象是把)(x f y的图象向下平移k 个单位得到的.练习:1.将下列变换的结果填在横线上:(1)将函数xy 3的图象向右平移2个单位,得到函数的图象;(2)将函数)13(log 2x y的图象向左平移2个单位,得到函数的图象.2.函数)32(x f 的图象,可由)32(xf 的图象经过下述变换得到()A .向左平移6个单位B .向右平移6个单位C .向左平移3个单位D .向右平移3个单位3.讨论函数xx y3132的图像是由哪个反比例函数的图像通过哪些变换而得到?二.对称变换1.同一函数的对称性(自对称)若函数)(x f y对定义域内一切x(1))(x f =)(x f 函数)(x f y图象关于y 轴对称;(2)函数)(x f y的不可能关于x 轴对称(除0)(x f 外);(3))(x f =-)(x f 函数)(x f y 图象关于原点对称;(4))()(1x f x f函数)(x f y 图象关于直线x y对称;(5))()(x f x f 函数)(x f y图象关于直线y 轴对称;(6))()2(x f x af 函数)(x f y 图象关于直线a x对称;(7))()(x a f x a f 函数)(x f y 图象关于直线a x 对称;(8))()(x a f a x f 函数)(x f y 图象关于y 轴对称;(9))()(x b f x af 函数()yf x 的图象关于直线2a b x对称;(10))(2)2(x f bx a f 即bx f x af 2)()2(函数)(x f y 图象关于点),(b a 成中心对称.2.不同函数对称性(互对称)给出函数)(x f y (1)函数)(x f y 与)(x f y 的图象关于y 轴对称;(2)函数)(x f y 与)(x f y 的图象关于x 轴对称;(3)函数)(x f y 与)(x f y 的图象关于原点对称;(4)函数)(1x fy 与)(x f y的图象关于直线x y 对称;(5)函数)(x f y的图象可以看作)(x f y的图象去掉y 轴左边部分,保留y 轴右边部分,并在y 轴左方作右方关于y 轴对称的图象(注意)(x f y为偶函数);(6)函数)2(x a f y 与)(x f y 的图象关于直线a x对称;(7)函数)(x a f y 与)(x a f y 的图象关于y 轴对称;(8)函数)(a x f y 与)(x a f y 图象关于直线a x 对称;(9)函数)(x af y与)(x bf y的图象关于直线2ab x 对称;(10)函数)(x f y 与)2(2x a f b y (即)2(2x af yb)的图像关于点),(b a 成中心对称.三.训练题目1.已知函数)(x f y 的定义域为R ,则下列命题中:①若)2(x f 是偶函数,则函数)(x f 的图象关于直线2x对称;②若)2()2(xf x f ,则函数)(x f 的图象关于原点对称;③函数)2(x f y 与函数)2(x f y 的图象关于直线2x ④函数)2(xf y与函数)2(x f y的图象关于直线2x其中正确的命题序号是.2.已知函数x f 是定义域为R 的偶函数,且x f x f 2.若x f 在0,1上是减函数,则x f 在3,2上是()A .增函数B .减函数C .先增后减的函数D .先减后增的函数3.设实数集R 上定义的函数)(x f ,对任何R x 都有)(x f +)(x f =1,则这个函数的图象()A .关于原点对称B .关于y 轴对称C .关于点)21,0(对称D .关于点)1,0(对称4.函数)1(x f y 与)1(1x fy 的图像关于()对称A .直线x y B .直线1xy C .直线1x yD .直线xy5.设定义域为R 的函数)(x f y 、)(x g y 都有反函数,并且)1(x f 和)2(1x g 的函数图像关于直线x y 对称,若2002)5(g ,那么)4(f ()A .2002 B .2003C .2004D .20056.已知函数1)22(x f y 是定义在R 上的奇函数,函数)(x g y 的图象与函数)(x f y的图象关于直线0yx对称,若221x x ,则)()(21x g x g ()A .2B .2C .4D .47.已知函数)(x f y 满足:①是偶函数)1(x f y;②在,1上为增函数.若0,021x x ,且221x x ,则)(1x f 与)(2x f 的大小关系是()A .)()(21x f x fB .)()(21x f x f C .)()(21x f x f D .不能确定8.函数11xy 的图象与x 轴围成封闭区域的面积是.9.函数(21)yf x 是偶函数,则函数(2)y f x 的对称轴是.10.设)(x f 是定义在R 上的偶函数,且)1()1(x f x f ,当01x 时,x x f 21)(,则)6.8(f __.11.设)(x f 是定义在R 上的奇函数,且图象关于直线21x ,则)5()4()3()2()1(f f f f f __ ___.12.函数)(x f y 对一切实数x 都满足)21()21(x f x f 并且方程0)(x f 有三个实根,这三个实根的和.13.定义在R 上的函数)(x f 满足)()(x a f x f ,(a 是大于1的整数),若方程0)(x f 有n 个实根,它们的和为2001,N n,则a ,n 的值可能有___种.14.若函数)(x f y 的图象关于直线2x 对称,当2x 时,21)(x x f ,则当2x 时,则)(x f .15.已知曲线C 与抛物线142x xy 关于点(2,-1)对称,函数)(x f y的图象与曲线C 关于x 轴对称,则)(x f y的函数关系式为.16.定义在R 上的函数)(x f 满足)1(1)1(1)1(x f x f x f ,则)2000()3()2()1(f f f f 的值为_ _.。
高中函数图像及其平移与变换
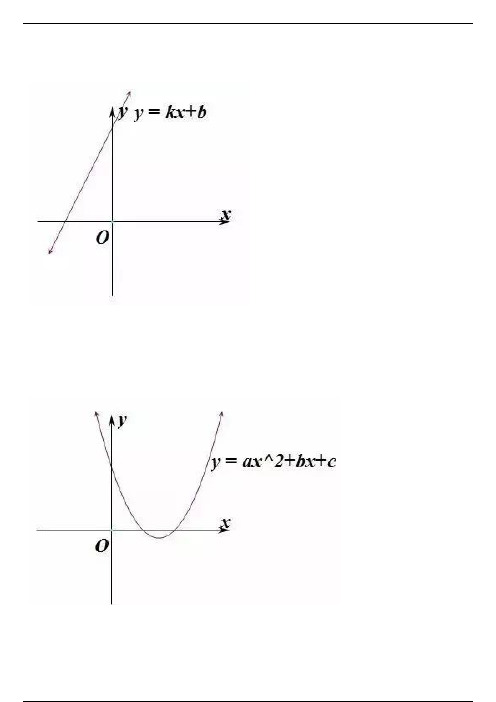
基本初等函数的图像1.一次函数性质: 一次函数图像是直线,当k>0时,函数单调递增;当k<0时,函数单调递减 2.二次函数性质:二次函数图像是抛物线,a决定函数图像的开口方向,判别式b^2-4ac决定了函数图像与x轴的交点,对称轴两边函数的单调性不同。
3.反比例函数性质:反比例函数图像是双曲线,当k>0时,图像经过一、三象限;当k<0时,图像经过二、四象限。
要注意表述函数单调性时,不能说在定义域上单调,而应该说在(-∞,0),(0,∞)上单调。
4.指数函数当0<a<b<1<c<d时,指数函数的图像如下图不同底的指数函数图像在同一个坐标系中时,一般可以做直线x=1,与各函数的交点,根据交点纵坐标的大小,即可比较底数的大小。
5.对数函数当底数不同时,对数函数的图像是这样变换的6.对勾函数对于函数y=x+k/x,当k>0时,才是对勾函数,可以利用均值定理找到函数的最值。
7. 幂函数性质:先看第一象限,即 x>0 时,当 a>1 时,函数越增越快;当0<a<1 时,函数越增越慢;当 a<0 时,函数单调递减;然后当x<0 时,根据函数的定义域与奇偶性判断函数图像即可。
8. 正弦函数、余弦函数、正切函数函数图像的变换 1 平移变换(1)水平平移: 函数 y = f(x + a)的图像可以把函数 y =f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到; (2)竖直平移: 函数 y = f(x) + a 的图像可以把函数 y =f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到。
2 对称变换(1)函数 y = f(-x) 的图像可以将函数 y = f(x)的图像关于y轴对称即可得到; (2)函数 y = - f(x) 的图像可以将函数 y =f(x)的图像关于x轴对称即可得到;(3)函数 y = - f(-x) 的图像可以将函数 y =f(x)的图像关于原点对称即可得到;3 翻折变换(1)函数 y =| f(x)| 的图像可以将函数 y =f(x)的图像的x轴下方部分沿x轴翻折到x轴上方,去掉x轴下方部分,并保留 y =f(x)的x轴上方部分即可得到;(2)函数 y = f(|x|) 的图像可以将函数 y =f(x)的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y =f(x)在y轴右边部分即可得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y=f(xh)
y=f(x)+k
②伸(放)缩变换:
沿x轴:
沿y轴: y=A f(x) (A>0)
③对称变换:
y=f(x) y=f(x)
y=f(x) y=f(x)
y=f(x) y=f(2ax)
y=f(x) y=f1(x)
y=f(x) y=f(x)
y=f(x) y=f变换的合成.y=f(x)
待三角函数的复习中再集中进行研究.
例题精讲:
例1作出函数 的图像,并指出函数的单调区间,图象的对称中心.
例2作出函数的图像:
(1) (2)
(3) (4) (5) (6)
(7)
例3已知函数f(x)和g(x)的图像关于原点对称、且f(x)=x2+2x.
(1)求函数g(x)的解析式;(2)解不等式 .
知识梳理
函数的图象及其变换
基础知识:
1.图象法:就是用函数图象表示两个变量之间的关系
优点:能直观形象地表示出函数的变化情况.
体现:映射与反演、形数结合的数学思想.
2.基本初等函数图象
y=xny=axy=logaxy=sinxy=cosxy=tanx
初等函数图像:
y=kxy=kx+by=ax2+bx+c
5(08山东)函数f(x)=axb的图象如右图,其中a,b为常数,则下列结论正确的是
A.a>1,b<0B.a>1,b>0
C.0<a<1,b>0D.0<a<1,b<0
答案1 A 2A324B5D
7.函数 的图像是
8.“a=1”是函数f(x)=|xa|在区间 上为增函数的
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
9.已知定义域为R的函数f(x)在区间 上为减函数,且函数y=f(x+8)为偶函数,则
A.f(6)>f(7)B.f(6)>f(9)C.f(7)>f(9)D.f(7)>f(10)
3.作图基本方法
(1)利用描点法作图:
①确定函数的定义域:图象沿x轴展布范围及渐近线;
②化简函数解析式:等价变形;
③讨论函数的性质:
奇偶性:关于图象对称性
单调性:关于图象升降性
周期性:关于图象重要性
极值、最值:关于图象最高点、最低点
截距:与x轴、y轴交点坐标
④画出函数的图象
(2)利用基本初等函数的图象的变换作图:
针对训练
1.C2.B3.C4.A5.B6.A7.B8.A9.D10.D11.A12.D13.B14.D15.3
高考链接
1(06北京理)在下列四个函数中,满足性质:“对于区间 上的任意 , 恒成立”的只有
(A) (B)
(C) (D)
2(全国)若0<a<1,b<1,则函数y=f(x)=ax+b的图象不经过
10.函数f(x)=axb的图象如右图,其中a,b为常数,则下列结论正确的是
A.a>1,b<0B.a>1,b>0
C.0<a<1,b>0D.0<a<1,b<0
11.若0<a<1,b<1,则函数y=f(x)=ax+b的图象不经过
A.第一象限B.第二象限C.第三象限D.第四象限
12.函数y=f(x)的图像与函数g(x)=log2x(x>0)的图象关于原点对称,则f(x)的表达式为
A. B.
C. D.
13.向高为h的水瓶注水,注满为止,若注水量v与水深h的函数关系如右图所示,那么水瓶的形状是
14.函数y=e|lnx||x1|的图像大致是
15.函数 的图像和函数g(x)=log2x的图象的交点个数是_________
答案:
例1. 对称中心(1, 2)增区间
例2.(1) (2)
例3.(1)g(x)=x2+2x(2)
A.第一象限B.第二象限C.第三象限D.第四象限
3(08北京)如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=;
4(全国)函数y=lg|x|
A.是偶函数,在区间 上单调递增B.是偶函数,在区间 上单调递减
C.是奇函数,在区间 上单调递增D.是奇函数,在区间 上单调递减
3.设a<b,函数y=(xa)2(xb)的图像可能是
4.与曲线 关于原点对称的曲线为
A. B. C. D.
5.函数y=lg|x|
A.是偶函数,在区间 上单调递增B.是偶函数,在区间 上单调递减
C.是奇函数,在区间 上单调递增D.是奇函数,在区间 上单调递减
6.当a>1时,在同一坐标系中,函数y=ax与y=logax的图像是
专题函数图象及其变换
考点精要
1.理解指数函数的概念、图象及性质.
2.理解对数函数的概念图象和性质.
3.理解幂函数y=x,y=x2,y=x3, , 的图象及其性质.
4.掌握一次函数、正比例函数、二次函数、反比例函数的图象及其性质.
5.理解图象的平移变换、伸缩变换、对称变换.
热点分析
函数的图象是函数的一种重要表示方法,利用函数的图像可以帮助我们更好地理解函数的重要性质.基本初等函数的图像及其变换,是考查的热点;利用变换作图,也是考查的重点,利用形数结合的数学思想解题,看图想性质,数形转化灵活解题.
例4、若不等式 对 恒成立,则实数 的取值范围是
A、 B、 C、 D、
例6、若直线 与曲线 有两个不同的交点,则实数 的取值范围是___________。
针对训练
1.函数 的图像关于
A.y轴对称B.直线y=x对称
C.坐标原点对称D.直线y=x对称
2.函数y=1+cosx的图像
A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线 对称
