820高等代数考试大纲
801《高等代数》考试大纲

801 《高等代数》考试大纲一、考试要求1.掌握基本的代数运算方法,包括:行列式的计算,矩阵运算(乘法、求秩、判别方阵的可逆性及求逆、求方阵的特征值及特征向量),线性方程组解的判定及求解,多项式运算(带余除法,辗转相除法,综合除法)等.2.掌握基本的代数分析技巧,包括:向量的线性相关和线性无关性,向量空间的基与维数,线性方程组解的结构, 线性变换和矩阵的关系,方阵可相似对角化的判定,对称矩阵与二次型,一元多项式的整除性及因式分解.3.掌握代数的基本几何背景,理解代数与几何的关系,包括:欧氏空间和酉空间,正交变换与正交矩阵, 对称变换与对称矩阵, 主轴定理, 利用二次型理论化简二次曲面方程.二、考试内容第一部分多项式1.一元多项式的定义和基本运算;2.多项式的带余除法与综合除法,多项式整除性的常用性质;3.多项式的最大公因式概念及性质,辗转相除法;4.不可约多项式的概念及性质,多项式的唯一因式分解定理,多项式的重因式;5.多项式函数与多项式的根的概念及性质;6.代数基本定理,复数域和实数域上多项式的因式分解定理,Vieta定理;7.整系数多项式的有理根,Eisenstein判别法;8.多元多项式概念及字典排列法,对称多项式.第二部分行列式1. 线性方程组和行列式的关系,排列、n阶行列式及其子式和代数余子式;2. 行列式的性质及行列式的基本计算方法;3. 克拉默法则.第三部分线性方程组1.线性方程组求解的消元法;2.矩阵的秩的概念,用矩阵的初等变换求秩;3.线性方程组可解的判别法;4.两个多项式的结式和多项式的判别式.第四部分矩阵1. 矩阵的线性运算、乘法、转置及其运算法则;2.逆矩阵概念,矩阵可逆的判定条件及可逆矩阵的性质,求可逆矩阵的逆矩阵的方法;3.矩阵的分块法,分块矩阵的运算法则.第五部分向量空间1. 向量空间及子空间的定义;2.向量组线性相关、线性无关的定义,向量组线性相关性的判定条件和性质,向量组的极大无关组;3.向量空间的基与维数,过渡矩阵及坐标变换式;4.向量空间的同构及其性质;5.齐次线性方程组的解空间与基础解系;线性方程组的结构式通解.第六部分线性变换1. 向量空间线性映射概念及其相关性质;2.线性变换的运算和矩阵的相似关系;3.不变子空间及其性质;4.方阵的特征值和特征向量;5.可以对角化的矩阵.第七部分欧氏空间和酉空间1. 向量空间中向量的内积、长度、夹角的定义及性质,规范正交基,Schmidt正交化方法;2. 正交变换与正交矩阵的定义和性质;3. 对称变换与实对称矩阵,实对称矩阵的正交相似对角化;4.酉空间的定义及其基本性质,酉变换和酉矩阵.第八部分二次型1. 二次型与对称矩阵,矩阵的合同关系;2.复数域和实数域上的二次型,用正交变换化实二次型为标准形的方法;3.正定二次型与正定矩阵,实对称矩阵正定的判定条件和性质;4.主轴定理, 利用二次型理论化简二次曲面方程.参考文献1.张禾瑞,郝鈵新《高等代数》(第四版)高等教育出版社 19992.北京大学数学系《高等代数》(第三版)高等教育出版社 20033.丘维声《高等代数》(第二版)高等教育出版社 2003。
《高等代数》考试大纲

五邑大学2021年硕士学位研究生招生《高等代数》课程考试大纲一、课程的性质,目的和任务高等代数是数学(数学与应用数学,数学教育)专业的一门重要基础课程。
通过本课程的教学,应培养学生良好的数学素养,打下较扎实的代数学理论基础,提高学生的抽象思维的能力和逻辑推理能力,并掌握较系统的代数基础知识,为学习后继课程服务。
二、基本要求这门课程大致分为两部分:多项式理论和线性代数。
前者以数域上一元多项式的因式分解理论为中心内容;后者主要讲授线性方程组的理论,向量空间和线性变换。
本课程应着重于基本理论的讲授和基本技能的培养和训练,不适求内容上的完备和全面.三、考试范围(一)多项式理论1. 数域 (A)2. 整除的概念 (A)3. 最大公因式. (A)4. 因式分解定理. (A)5. 重因式. (A)6. 多项式函数. (A)8. 复系数与实系数多项式的因式分解. (A)9. 有理系数多项式. (A)*10.多元多项式. (B)*11.对称多程式. (B)(二) 行列式1. 排列. (A)2. n阶行列式的定义和性质. (A)3. 行列式的依行和依列展开. (A)4. 行列式的计算. (A)5. Crammer法则(克莱姆法则). (A)6. Laplace(拉普拉斯)定理. 行列式的乘法规则. (A)(三)线性方程组1. 线性方程组的消元法. (A)2. n维向量空间 (A)3. 线性相关性. (A)4. 矩阵的秩. (A)5. 线性方组有解的判定定理. (A)6. 线性方程组解的结构. (A)7. 二元高次方程. (B)(四) 矩阵1. 矩阵的概念与运算. (A)2. 矩阵乘积的行列式与秩. (A)3. 矩阵的逆. (A)4. 矩阵的分块. (A)5. 初等矩阵. (A)(五) 二次型1. 二次型的矩阵表示. (A)2. 标准形. (A)3. 唯一性. (A)4. 正定二次型. (A)(六) 线性空间1. 线性空间的定义与简单性质. (A)2. 维数.基与坐标. (A)3. 基变换. (A)4. 线性子空间 (A)5. 子空间的交与和. (A)6. 子空间的直和. (A)7. 线性空间的同构. (A)(七) 线性变换1. 定义和例子 (B)2. 线性变换的运算. (A)3. 线性变换的矩阵. (A)4. 特征值与特征向量. (A)5. 对角矩阵. (A)6. 线性变换的值域与核. (A)7. 不变子空间. (A)8. Jordan标准形介绍. (B)(八) 入一矩阵1. 入一矩阵. (A)2. 入一矩阵在初等变换下的标准形. (A)3. 不变因子. (A)4. 矩阵相似条件. (A)5. 初等因子. (A)*6.Jordan标准形的理论推导. (C)(九) 欧几里得空间1. 定义与基本性质. (A)2. 标准正交基. (A)3. 同构. (A)4. 正交变换. (A)5. 子空间. (A)6. 对称矩阵的准形. (A)四、主要教材和参考书1. 北京大学数学力学系,高等代数(第二版),高教出版社。
华南理工大学820有机化学2021年考研专业课
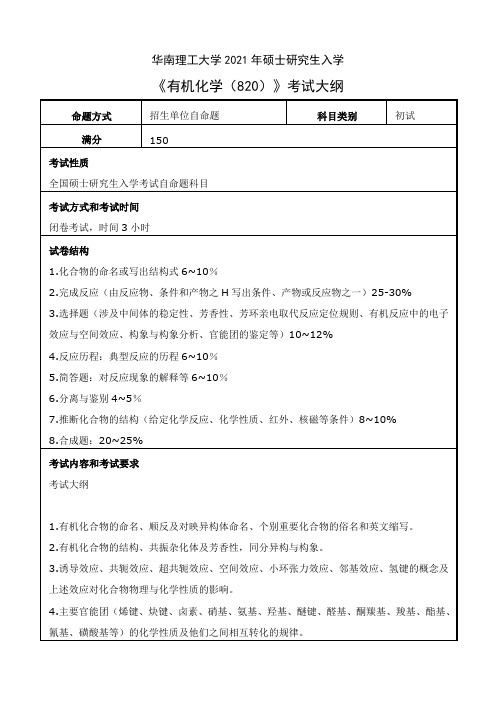
华南理工大学2021年硕士研究生入学《有机化学(820)》考试大纲
5.烷烃、脂环烃、烯烃、炔烃、卤代烃、醇、酚、醚、醛、酮、不饱和醛酮、羧酸、羧酸及其衍生物、丙二酸酯、β-丙酮酸酯、氨基酸、硝基化合物、胺、腈、偶氮化合物、磺酸、简单杂环化合物、单糖等的制备、分离、鉴定、物理性质、化学性质及在合成上的应用。
6.常见有机化合物的波谱(红外、核磁)
7.饱和碳原子上的自由基取代,亲核取代,芳环上的亲电与亲核取代,碳碳重键的亲电、自由基及亲核加成,消除反应,氧化反应(烷烃、烯烃、炔烃、醇、醛、芳烃侧链的氧化、烯炔臭氧化及Cannizzaro反应),还原反应(不饱和烃、芳烃、醛、酮、羧酸、羧酸衍生物、硝基化合物、腈的氢化还原及选择性还原反应),缩合反应(羟醛缩合、Claisen缩合、Caisen-Schmidt缩合、Perkin缩合),降级反应(Hofmann降解,脱羧),重氮化反应,偶合反应,重排反应(频那醇重排、Beckmann重排、Hofmann重排)的历程及在有机合成中的应用。
8.碳正离子、碳负离子、自由基、苯炔的生成与稳定性及其有关反应的规律。
能够从中间体稳定性来判断产物结构。
备注
选读书目
《有机化学》(第四版)天津大学高鸿宾主编,高等教育出版社2004年;
《有机化学》古练权、汪波、黄志纡、吴云东编著,高等教育出版社2008年。
2023年研究生招生《高等代数》考试大纲

佛山科学技术学院2023年硕士研究生招生考试大纲科目名称:高等代数一、考查目标高等代数是大学数学系本科学生的最基本课程之一,它的主要内容包括多项式理论、行列式、线性方程组、矩阵、二次型、线性空间、线性变换、欧几里得空间、双线性函数。
要求考生比较系统地理解高等代数的基本概念和基本理论,掌握高等代数的基本思想和方法。
二、考试形式与试卷结构考试采用闭卷笔试形式,试卷满分为150分,考试时间为180分钟,其中简答题(40分),计算与解答题(60分),证明题(50分)。
三、考查范围(一)多项式1.一元多项式的因式、带余除法公式及互素的概念及判别;2.复根存在定理;3.根与系数关系;(二)行列式1.行列式的置换、对换、置换奇偶性;2.行列式的定义,基本性质及计算;3.范德蒙得行列式;4.行列式的代数余子式。
(三)矩阵1.矩阵基本运算、分块矩阵运算;2.初等矩阵、初等变换和矩阵的秩;3.矩阵的逆、伴随阵、线性方程组的矩阵形式;4.行列式乘积定理;5.矩阵和转置6.对角阵、三角阵、三对角阵;7.矩阵的迹、方阵多项式;(四)线性方程组求解1.线性方程组有解的充分必要条件;2.消元法;(五)线性空间和线性变换;1.向量的线性相关和线性无关;2.线性空间的定义及性质;3.向量组的秩、线性空间的基及坐标;4.线性变换的矩阵表示;5.矩阵相似;6.不变子空间;7.子空间的直接和、维数公式;8.线性空间的同构。
(六)特征值和特征向量1.特征值和特征多项式;2.特征向量、特征子空间、度数和重数;(七)内积空间1.欧几里得空间的标准正交基,施密特正交化;2.正交变换及其矩阵表示;(八)二次型和对称矩阵1.二次型及其标准形、惯性定理;2.实对称矩阵正定的充分必要条件;四、掌握重点(一)行列式乘积定理及其应用(二)分块矩阵运算及其应用(三)矩阵三角分解及其应用(四)矩阵的秩及其应用(五)线性空间的概念及性质(六)线性变换下的不变子空间及其矩阵表示(七)二次型的标准形(八)实对称矩阵及其性质参考书目:[1]北京大学数学系前代数小组,王萼芳,石生明编,《高等代数》(第五版),高等教育出版社.。
高代知识点

《高等代数》复习参考提纲一、总体要求高等代数是数学各专业的一门重要基础理论课。
要求学生掌握高等代数的基本概念,基本理论,基本方法和基本技巧;熟练掌握矩阵和线性变换的关系,学会线性方程组,矩阵,线性变换问题的相互转化;理解具体与抽象、特殊与一般、有限与无限等辨证关系。
并善于应用这些理论和方法,具有较强的分析问题与解决问题的能力。
二、课程考试内容(一)多项式数域,整除的概念与性质,最大公因式,因式分解,重因式,多项式函数,有理系数多项式,多元多项式,对称多项式。
(二)行列式排列,n阶行列式的概念,n阶行列式的性质,行列式的计算,行列式按一行(列)展开,拉普拉斯(Lap lace)定理,克兰姆法则。
(三)线性方程组消元法,矩阵,矩阵的秩,线性方程组的初等变换等概念及性质,线性方程组有解判别定理。
n维向量的概念及运算;向量组的线性组合、线性表示、线性相关、线性无关等概念;向量组的线性相关性的判定;两个向量组的等价;向量组的极大无关组、秩的概念及性质;向量组的秩与矩阵的秩的关系。
线性方程组解的结构。
(四) 矩阵矩阵的概念,矩阵的运算,矩阵乘积的行列式与秩,矩阵的逆,矩阵的分块,初等矩阵,分块矩阵的初等变换及应用。
(五)二次型二次型的矩阵表示,标准形,唯一性,惯性定律,正定二次型。
(六)线性空间线性空间的概念与性质,维数,基,坐标,基变换,坐标变换,子空间,子空间的和与交,子空间的直和,线性空间的同构。
(七)线性变换线性变换的概念与性质,线性变换的运算,线性变换的矩阵,特征值与特征向量,矩阵相似对角矩阵的各种条件,线性变换的值域和核,不变子空间,Jordan标准形,最小多项式。
(八)λ-矩阵λ-矩阵的标准形,行列式因子,不变因子,初等因子,矩阵相似的条件,矩阵的有理标准形。
(九)欧几里得空间欧几里得空间的概念与性质,标准正交基,欧几里得空间的子空间与同构,正交变换与对称变换,Schimidt正交化方法,实对称矩阵的标准形,最小二乘法,酉空间。
820考研考试大纲

820考研考试大纲考研,即全国硕士研究生招生考试,是中国高等教育体系中选拔研究生的重要途径。
每年的考研考试大纲是考生们复习备考的重要参考。
820考研考试大纲,即2020年的考研大纲,虽然已经过去,但仍然可以为考生们提供一些参考和借鉴。
# 820考研考试大纲概述考研考试大纲主要包括公共课和专业课两部分。
公共课一般包括政治理论、外国语(英语、日语、俄语等)、数学等科目,而专业课则根据考生报考的专业方向而定。
# 政治理论政治理论是考研的必考科目,主要测试考生对马克思主义哲学、政治经济学、科学社会主义、中国特色社会主义理论体系等基本理论的掌握程度。
考试内容通常涵盖以下几个方面:- 马克思主义哲学基本原理- 政治经济学基础- 科学社会主义与国际共产主义运动- 中国特色社会主义理论体系- 当代中国政治、经济、文化、社会等方面的发展# 外国语外国语考试通常以英语为主,测试考生的英语阅读、翻译、写作等能力。
考试内容包括:- 阅读理解:考察考生对文章主旨、细节信息的把握能力- 完形填空:测试考生对文章结构和逻辑的理解- 翻译:包括英译汉和汉译英,考察语言转换能力- 写作:通常包括短文写作和图表作文,测试考生的表达和论述能力# 数学数学考试分为数学一、数学二和数学三,不同专业对数学的要求不同。
数学考试主要测试考生的数学基础知识和解决问题的能力,内容包括:- 高等数学:函数、极限、微积分、级数等- 线性代数:矩阵、向量空间、线性变换等- 概率论与数理统计:随机事件、概率分布、统计推断等# 专业课专业课考试内容因专业而异,通常包括专业基础知识和专业综合能力测试。
考生需要根据自己报考的专业方向,熟悉相关课程的考试大纲和要求。
# 考试形式与评分标准考研考试通常采用闭卷笔试的形式,部分科目如外国语的听力部分可能采用机考。
评分标准通常以百分制计算,不同科目的分值比重不同。
# 备考建议1. 熟悉大纲:考生应仔细阅读考试大纲,了解考试内容和要求。
考研《高等代数》(学术学位)考试大纲

(3)初等矩阵与初等变换
掌握矩阵的初等变换和初等矩阵的概念,明确二者关系。能熟练进行矩阵的初等变换,能利用初等变换求解线性方程组,并能进行有关证明。
(4) 相似矩阵与矩阵合同
三、主要参考书目
1、《高等代数》(第三版),北京大学数学系几何与代数教研室前代数小组著,高等教育出版社 2003 或之后版本
2、《高等代数(上下册)》(第二版),丘维声著,高等教育出版社,1999 或之后版本
硕士研究生入学考试自命题科目考试大纲
科目代码、名称:
专业类别:
■学术学位□专业学位
适用专业:
数学
一、基本内容
1、多项式
本部分要求掌握一元多项式及其整除问题、多项式函数、最大公因式、重因式和因式分解定理等有关概念和基本结论,能够进行多项式的有关计算和有关问题的证明。
2、行列式
(1)定义与性质
要求熟悉排列、逆序、对换等概念;理解行列式的定义;掌握行列式的性质。
9、欧几里得空间
掌握欧几里得空间的定义与性质,掌握内积、正交性、标准正交基的概念及有关计算方法,能证明有关性质和结论。
二、考试要求(包括考试时间、总分、考试方式、题型、分数比例等)
考试时间:180分钟
总分:150分
考试方式:笔试,闭卷
题型:填空题,计算与证明题
分数比例:填空题(60分)占40%,计算与证明题(90分)占60%。
(3)线性方程组解的结构
掌握线性方程组解的判定定理,会求有解的线性方程组的通解,熟练掌握线性方程组常用的解
法,并能证明有关结论。
4、矩阵
820高等代数知识点总结

820高等代数知识点总结一、环与域环是代数学中一个非常重要的概念,它是一种代数结构,具有加法和乘法两种运算。
一个集合R满足以下条件时,我们称它为一个环:1. 对于R中的任意两个元素a和b,都有a + b和a × b也属于R;2. 对于R中的任意两个元素a、b和c,有结合律:(a + b) + c = a + (b + c)和(a × b) × c = a × (b × c);3. 对于R中的任意两个元素a、b和c,有分配律:a × (b + c) = a × b + a × c和(b + c) × a =b × a +c × a;4. 存在一个元素0,对于任意元素a,有a + 0 = a;5. 对于任意元素a,存在一个元素-b,使得a + (-b) = 0。
域是环的一个推广,它是一种具有加法、乘法和除法三种运算的代数结构。
一个集合F满足以下条件时,我们称它为一个域:1. 对于F中的任意两个元素a和b,都有a + b和a × b也属于F;2. 对于F中的任意两个元素a、b和c,满足交换律:a + b = b + a和a × b = b × a;3. 对于F中的任意两个非零元素a和b,有除法运算a/b也属于F,并且满足结合律和分配律。
二、群与环群是代数学中的一种抽象代数结构,它是一个集合G加上一个满足封闭性、结合律、单位元素和逆元素的二元运算构成的代数结构。
满足以下条件时,我们称它为一个群:1. 对于G中的任意两个元素a和b,都有a • b属于G;2. 对于G中的任意三个元素a、b和c,有结合律:(a • b) • c = a • (b • c);3. 存在一个元素e,对于任意元素a,有a • e = a和e • a = a;4. 对于任意元素a,存在一个元素a^-1,使得a • a^-1 = e和a^-1 • a = e。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑龙江大学硕士研究生入学考试大纲
考试科目名称:高等代数考试科目代码:[820]
一、考试内容及要求
一、行列式
1.内容:行列式概念及性质,行列式按行(列)展开。
2.要求:
①理解数域的概念,掌握常见的数域和最小数域。
②理解n阶行列式的定义,掌握行列式性质。
③能用行列式定义、性质(包括按行(列)展开的性质)递推及归纳法等计算行列式。
二、矩阵
1.内容:矩阵的概念,矩阵运算,逆矩阵和克莱姆法则,分块矩阵,初等变换和初等阵,矩阵的等价分解,矩阵的秩,初等块矩阵及等价分解的应用。
2.要求:
①理解矩阵概念及相关运算法则,能熟练地进行矩阵的相关运算,掌握行列式乘法定理。
②理解逆矩阵的概念,掌握伴随矩阵求逆方法,掌握矩阵可逆充要条件并用于判别,理解克莱姆法则并用于求解线性方程组。
③了解分块矩阵的运算法则,准确用于计算。
④理解三种初等变换及相应的初等阵,了解初等阵是可逆阵的乘法生成元。
⑤理解矩阵的等价分解,理解矩阵秩的定义,能用初等变换求矩阵秩及逆矩阵。
⑥能利用等价分解、分块矩阵、初等矩阵及归纳法等解决一些矩阵分解,求秩相关的计算和证明问题。
三、n维向量与线性方程组
1.内容:n维向量,向量的线性相关性,向量组的秩,消去法解线性方程组,线性方程组解的判定,线性方程组解的结构。
2.要求:
①掌握n维向量线性表出,线性相关,线性无关的概念,能进行判别及相关的证明。
②理解向量组的秩,矩阵的三秩相等定理,掌握向量组的秩以及极大无关组的概念,会求极大无关组以及向量组的秩。
③能用消去法解线性方程组,特别能对带参数的方程组进行解的情况的讨论。
④掌握齐次方程组基础解系定理,一般线性方程组解的结构定理,并能用于解决有关问题。
四、特征值与特征向量
1.内容:特征值与特征向量,相似矩阵,R n空间内积,正交阵,实对称阵的正交对角化。
2.要求:
①掌握特征值与特征向量的概念及求法。
②理解矩阵相似的概念,理解矩阵相似于对角阵的充要条件及充分条件,会进行相关的计算和证明。
③掌握施密特正交化方法并能用于将实对称阵正交对角化。
④理解正交阵的概念及等价条件,利用实对称阵正交对角化定理解决一些论证问题。
五、二次型
1.内容:实二次型,正定二次型,半正定二次型,惯性定理,一般数域上的二次型。
2.要求:
①掌握一般二次型的概念,用矩阵和内积分别表示二次型的方法。
②理解实二次型的惯性定理,掌握实数域及一般数域上二次型的标准形及其求法。
③理解正定二次型,半正定二次型的概念及若干等价条件并能用于相关计算与证明。
六、多项式
1.内容:一元多项式,整除,最大公因式,因式分解定理,重因式,多项式函数,复系数及实系数多项式因式分解,有理系数多项式。
2.要求:
①掌握数域上一元多项式的概念及相关运算(包括带余除法)。
②理解多项式整除及最大公因式等概念,会用辗转相除法求最大公因式。
③理解因式分解定理及其唯一性的含义,掌握有重因式的充要条件,并能用于判别。
④理解多项式恒等与多项式函数相等的关系,能利用恒等或判别恒等解决相关问题。
⑤掌握整系数多项式的有理根判别法以及关于不可约的Eisenstein判别法解决某些问题。
⑥了解复系数多项式的代数基本定理,理解实系数多项式的虚根成对定理,并能用于简单证明。
七、线性空间
1.内容:线性空间定义及简单性质,维数,基底与坐标,基变换与坐标变换,线性子
空间,子空间的交与和,子空间的直和,线性空间的同构。
2.要求:
①理解线性空间的公理化定义,掌握其简单性质。
②掌握线性空间维数,基底,坐标等概念,掌握基变换及坐标变换公式进行有关计算。
③掌握线性子空间,交子空间,和子空间的概念及交与和的维数公式。
④理解子空间直和的概念,掌握直和的几个充要条件并能用于相关证明和计算。
⑤理解线性空间的同构概念,掌握有限维线性空间同构的条件。
八、线性变换
1.内容:线性变换及其运算,线性变换的矩阵,哈密顿-凯莱定理,线性变换的值域与核,不变子空间,若当标准形介绍,最小多项式,矩阵相似与λ-矩阵。
2.要求:
①掌握线性变换概念并能用于判别,理解线性变换的加法,数乘,乘法运算。
②掌握线性变换的矩阵表示及其求法,了解哈密顿-凯莱定理。
③理解线性变换的值域与核的概念,并了解其与线性方程组基础解系定理之间关系。
④理解线性变换不变子空间的概念,掌握空间分解为不变子空间直和与矩阵相似于准对角阵之关系。
⑤了解复矩阵若当标准形的结构,能用λ-矩阵方法求一个复矩阵的若当标准形。
⑥了解最小多项式的概念,会求简单阵的最小多项式。
⑦了解用λ-矩阵表述的矩阵相似的几个充要条件。
九、欧氏空间
1.内容:欧氏空间定义及其基本性质,标准正交基,同构,正交变换,子空间,对称变换,最小二乘法,酉空间。
2.要求:
①掌握抽象欧氏空间的定义及其基本性质。
②理解标准正交基及欧氏空间同构的概念,会求一个欧氏空间的标准正交基。
③掌握有限维欧氏空间的正交变换的定义及其等价条件并能用于证明。
④理解欧氏空间子空间及其正交补的概念,会进行相关计算与证明。
⑤了解对称变换及其矩阵表示,了解最小二乘法的思想。
⑥了解酉空间的概念及与欧氏空间相平行的结论。
二、试卷结构
1.考试时间:180分钟
2.试卷分值:150分
3.题型结构:(1)多项选择与填空(约占20-30分)
(2)计算题(约占50-60分)
(3)证明题(约占60-70分)
三、参考书目
1.曹重光, 线性代数, 内蒙古科学技术出版社, 1999.
2.北京大学数学系几何与代数教研室前代数小组, 高等代数(第三版), 高等教育出版社, 2003.。
