第四章 弯曲
合集下载
《材料力学》课程讲解课件第四章弯曲内力

x
∴ 弯曲构件内力:Fs -剪力,M -弯矩。
若研究对象取m - m 截面的右段:
Y 0, Fs F FBY 0.
mC 0,
FBY
FBY (l x) F(a x) M 0.
Fs
F (l a) l
,
M F (l a) x 18 l
1. 弯矩:M 构件受弯时,横截面上
存在垂直于截面的内力偶矩 (弯矩)。
由 Fy 0, 得到:
A
FAy
a
Mc
C FSc
FAy q 2a FSc 0
FSc FAy q 2a qa
(剪力FS 的实际方向与假设方
向相反,为负剪力)
由 MC 0, 得到:
MC FAy 2a 2qa a M1 0
MC FAy 2a 2qa a M1 2qa2
F
M (x) FAY x M A
F(x L) (0 x l)
x
③根据方程画内力图
FL
x
41
§4-4 剪力方程和弯矩方程 剪力图和弯矩图
q
例题4-2
悬臂梁受均布载荷作用。
x
试写出剪力和弯矩方程,并
q
l
x
FS
M x
FS x
画出剪力图和弯矩图。
解:任选一截面x ,写出
剪力和弯矩方程
ql FS x=qx
变形特点——杆轴线由直线变为一条平面的曲线。
P
主要产生弯曲变形的杆--- 梁。
q
M
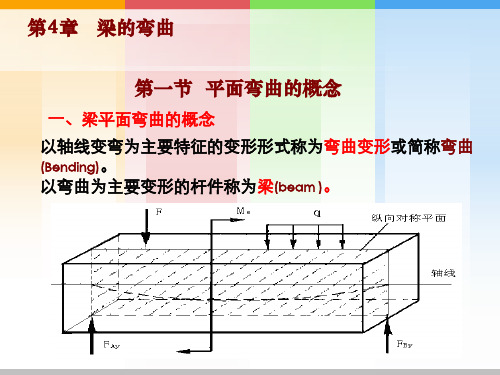
二、平面弯曲的概念:
RA
NB
3
F1
q
F2
M
纵向对称面
平面弯曲 受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在
《材料力学》第四章 弯曲内力

ql FS = R A-qx= -qx 2 x qlx qx 2 M = R A x-qx ⋅ = - 2 2 2
M FS
F S
(3)画出FS图与M图。 画出F 图与M 剪力图为一斜直线, 剪力图为一斜直线, x=0,FS=ql/2;x=l,FS=-ql/2; ; 弯矩图为一抛物线, 弯矩图为一抛物线, 由三点来确定: 由三点来确定: x=0及x=l时,M=0; x=l/2, M=ql2/8。 。
M x = a, M = O a AC段 x=0, AC段:x=0,M=0 ; l
CB段 CB段:x=a, x=l, M= x= , M=0
MO M =- b l
试作轴的简力图和弯矩图
补例1 补例1
解
(1)求支反力。 求支反力。
1 ql 2
R A = RB =
(2)用截面法求剪力和弯矩方程。 用截面法求剪力和弯矩方程。
∑ mA = 0 ∑m
B
=0
l -m-P ⋅ + YB ⋅ l = 0 2 l -YA ⋅ l-m+P ⋅ = 0 2
YA-FSC=0 , 3 FSC=- P 2
5 P B 2 3 Y A =- P 2 Y =
m
(2)计算C截面的内力。 计算C截面的内力。
∑Y = 0 ,
P
l 13 mC=0 , YA ⋅ -m+M C=0 , M C= Pl ∑ 4 8
求反力: 解 (1)求反力:
∑ X = 0, X = 0 ∑ Y = 0, P - Y =0 ∑ m =0, m - Pa =0
C C C C
YC= P m C= Pa
(2)列弯矩和轴力方程。 列弯矩和轴力方程。 AB段 AB段:M(x)= Px, N(x)=0 , BC段 BC段:M(y)=mC=Pa, N(y)=P ,
M FS
F S
(3)画出FS图与M图。 画出F 图与M 剪力图为一斜直线, 剪力图为一斜直线, x=0,FS=ql/2;x=l,FS=-ql/2; ; 弯矩图为一抛物线, 弯矩图为一抛物线, 由三点来确定: 由三点来确定: x=0及x=l时,M=0; x=l/2, M=ql2/8。 。
M x = a, M = O a AC段 x=0, AC段:x=0,M=0 ; l
CB段 CB段:x=a, x=l, M= x= , M=0
MO M =- b l
试作轴的简力图和弯矩图
补例1 补例1
解
(1)求支反力。 求支反力。
1 ql 2
R A = RB =
(2)用截面法求剪力和弯矩方程。 用截面法求剪力和弯矩方程。
∑ mA = 0 ∑m
B
=0
l -m-P ⋅ + YB ⋅ l = 0 2 l -YA ⋅ l-m+P ⋅ = 0 2
YA-FSC=0 , 3 FSC=- P 2
5 P B 2 3 Y A =- P 2 Y =
m
(2)计算C截面的内力。 计算C截面的内力。
∑Y = 0 ,
P
l 13 mC=0 , YA ⋅ -m+M C=0 , M C= Pl ∑ 4 8
求反力: 解 (1)求反力:
∑ X = 0, X = 0 ∑ Y = 0, P - Y =0 ∑ m =0, m - Pa =0
C C C C
YC= P m C= Pa
(2)列弯矩和轴力方程。 列弯矩和轴力方程。 AB段 AB段:M(x)= Px, N(x)=0 , BC段 BC段:M(y)=mC=Pa, N(y)=P ,
第四章 梁弯曲变形与内力

18
中性层:梁内纵向长度既没有伸长也没有缩短的纤 维层。 中性轴:中性层与横截面的交线 。
19
中性层将梁分成受压和受拉区,即中性层一侧作 用拉伸应力,另一侧作用压缩应力,中性层上正应 力为零,梁横截面的偏转就是绕其中性轴旋转的。
20
根据弯矩的定义:
M A y dA
σ:横截面上距中性轴为y处的正应力 dA:横截面上距中性轴为y处的一微面积 y:正应力到中心轴的距离
弯矩的符号约定
M M
+
M
-
M
上压下拉为正
上拉下压为负
29
计算弯矩法则:梁在外力作用下,其任意指定截面 上的弯矩等于该截面一侧所有外力对该截面中性轴取 矩的代数和;凡是向上的外力,其矩取正;向下的外 力,其矩取负值。
30
三 剪力图和弯矩图
梁的剪力方程和弯矩方程:
以坐标 x 表示横截面位置,则剪力和弯矩可表 示为x的函数:Q = Q(x), M = M(x) 剪力图和弯矩图:为了形象地表示梁各个横截面上 弯矩的大小与正负,将剪力方程和弯矩方程用图 表示 。
33
分段列剪力方程:
AC段 CD段 DE段 EB段 0<x≤0.25m, Q=RA=935N=Q1 0.25m≤x≤0.5m, Q=RA - P1=935 -500 = 435N = Q2 0.5m≤x<0.8m, Q=RA-P1-P2 = 935-500-1000 = - 565N=Q3 0.8m≤x<1m, Q = RA -P1 -P2 -P3= 935 - 500 -1000 -300 = -865N=Q4
剪力图和弯矩图的作法:按选定的比例,以横截 面上的剪力或弯矩为纵坐标,以横截面位置为横 坐标,把Q=Q (x), M=M(x) 的图线表示出来。
第四章梁的弯曲详解
FQ
F yi
若外力使选取研究对象绕所求截面产生顺时针 方向转动趋势时,等式右边取正号;反之,取 负号。此规律可简化记为“顺转剪力为正”, 或“左上,右下剪力为正”。相反为负。
第4章 梁的弯曲 第二节 梁的内力计算
(2)横截面上的弯矩M,在数值上等于截面一 侧(左侧或右侧)梁上所有外力对该截面形心 的力矩的代数和。即:
例题4 简支梁受均布荷载作用,如图示, 作此梁的剪力图和弯矩图。
解:1.求约束反力由对称关系,可得:
FAy
FBy
1 2
ql
第4章 梁的弯曲 第二节 梁的内力计算
2.列剪力方程和弯矩方程
FQ (x)
FAy
qx
1 2
ql
qx
M (x)
FAy x
1 9x2 2
第4章 梁的弯曲 第二节 梁的内力计算
三、剪力方程和弯矩方程 在一般情况下,则各横截面上的剪力和弯矩都可 以表示为坐标x的函数
梁的剪力方程 FQ=FQ (x) 梁的弯矩方程 M=M(x)
第4章 梁的弯曲 第二节 梁的内力计算
四、剪力图和弯矩图
以梁横截面沿梁轴线的位置为横坐标,以垂直于 梁轴线方向的剪力或弯矩为纵坐标,分别绘制表 示FQ (x)和M(x)的图线。这种图线分别称为剪力 图和弯矩图,简称FQ图和M图。绘图时一般规定 正号的剪力画在x轴的上侧,负号的剪力画在x轴 的下侧;正弯矩画在x轴下侧,负弯矩画在x轴上 侧,即把弯矩画在梁受拉的一侧。
第4章 梁的弯曲 第二节 梁的内力计算
例题3 图所示,悬臂梁受集中力F作用, 试作此梁的剪力图和弯矩图
解: 1.列剪力方程和弯矩方程
FQ (x) F (0 ≤ x ≤ l )
M (x) Fx (0≤x ≤ l)
《材料力学》第4章弯曲内力 课后答案

0 ; FS−C
= b F, a+b
M
− C
=
ba a+b
F
FS+C
=
−a a+b
F
,
M
+ C
=
ba a+b
F ; FSB
=
−A a+b
F
,MB
=
0
d解
图(d1), ∑ Fy
=
0,F
=
1 2
ql
,
∑
M
A
= 0,M A
=
− 3 ql 2 8
仿题 a 截面法得
FSA
=
1 2
ql
,MA
=
−
3 8
ql
2
;
FS−C
FS (x) = −F
⎜⎛ 0 < x < l ⎟⎞
⎝
2⎠
M (x) = −Fx ⎜⎛0 ≤ x ≤ l ⎟⎞
⎝
2⎠
FS (x) = F
⎜⎛ l < x < l ⎟⎞
⎝2
⎠
45
M (x) =
FA x +
FB
⎜⎛ ⎝
x
−
l 2
⎟⎞ ⎠
,
FB
= 2F
M (x) = Fx − Fl ⎜⎛ l ≤ x ≤ l ⎟⎞
( ) 解
∑MB
=
0 , FA
⋅l
+
ql 2
×
3l 4
− ql 2
=
0
, FA
=
5 ql 8
↑
( ) ∑ Fy
= 0 , FB
第四章(弯曲挠度3-Lu)

§4-9 用积分法计算梁旳挠度与转角
对于等截面梁,EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M (x)dx]dx Cx D
式中C, D 由梁支座处旳已知位移条件即位 移边界条件拟定。
HOHAI UNIVERSITY
EIw EI M ( x )dx C
C wc2(q)
c 2 (q)
HOHAI UNIVERSITY
3o 求 c、wc
A
c c (F ) c1(q) c2 (q)
F
C (F)
C (F )
B
C
qa 3 qa 3 qa 3
4 EI 6 EI 3EI
qa 3 4 EI
(b)
q
B
(d)
C
wc1(q) c1 (q )
wc wc (F ) wc1(q) wc2 (q)
EI 2
Fb 2l
x2
F 2
(
x
a
)2
C2
EIw2
Fb 6l
x3
F 6
(x
a)3
C2 x
D2
HOHAI UNIVERSITY
F
边界条件:x = 0 ,w1= 0。 x = l ,w2= 0。
a
b
A
CD
Bx
x
y
l
连续条件:x = a ,w1′= w2′, w1= w2
由连续条件,得:C1= C2, D1= D2
EIw [ M ( x)dx]dx Cx D
如:
p
A
B
p A
边界条件: wA=0 wB=0
边界条件: wA=0 θA=0
对于等截面梁,EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M (x)dx]dx Cx D
式中C, D 由梁支座处旳已知位移条件即位 移边界条件拟定。
HOHAI UNIVERSITY
EIw EI M ( x )dx C
C wc2(q)
c 2 (q)
HOHAI UNIVERSITY
3o 求 c、wc
A
c c (F ) c1(q) c2 (q)
F
C (F)
C (F )
B
C
qa 3 qa 3 qa 3
4 EI 6 EI 3EI
qa 3 4 EI
(b)
q
B
(d)
C
wc1(q) c1 (q )
wc wc (F ) wc1(q) wc2 (q)
EI 2
Fb 2l
x2
F 2
(
x
a
)2
C2
EIw2
Fb 6l
x3
F 6
(x
a)3
C2 x
D2
HOHAI UNIVERSITY
F
边界条件:x = 0 ,w1= 0。 x = l ,w2= 0。
a
b
A
CD
Bx
x
y
l
连续条件:x = a ,w1′= w2′, w1= w2
由连续条件,得:C1= C2, D1= D2
EIw [ M ( x)dx]dx Cx D
如:
p
A
B
p A
边界条件: wA=0 wB=0
边界条件: wA=0 θA=0
第四章 弯曲

A By B Ay y
F=3kN C
q=2kN/m
M0 6kN m
A
D
B
1m
FAy
4m
1m
FBy
2、由微分关系判断各段的Q、M形状。
CA AD DB
载荷
q0
qC 0
q0
Q 图
M 图
斜直线
FAy 7.2kN FBy 3.8kN
斜直线
F=3kN
q=2kN/m
M0 6kN m
外伸梁 Beam with an overhang (overhangs)
三、剪力和弯矩
求弯曲内力(剪力和弯矩)的基
本方法——截面法
设有一简支梁AB,受集中力F 作用。现分 析距A端为x 处的横截面m-m上的内力。
解:1、根据平衡条件求支座反力
a m A x
m
F
b B
FAy
Fb Fa , FBy L L
控制截面的概念:外力规律发生变化的截面— 集中力、集中力偶作用点、分布载荷的起点和终 点处的横截面。
M0 8kN m
P=2kN q=2kN/m
A
F
E
1m 1m 2m
B
D
1m
FBy
1m
FAy
◆因此,必须分段列出梁的剪力方程和弯矩方程, 各段的分界点为各段梁的控制截面。
剪力图和弯矩图——用图示方法形象地表示 剪力和弯矩沿梁轴线的变化情况。
F=qa C a
q
A
FAy
3 qa 2
xE
3 a 2
B x
FBy
2a
(+) E
Q 图
1 2 qa 8
F=3kN C
q=2kN/m
M0 6kN m
A
D
B
1m
FAy
4m
1m
FBy
2、由微分关系判断各段的Q、M形状。
CA AD DB
载荷
q0
qC 0
q0
Q 图
M 图
斜直线
FAy 7.2kN FBy 3.8kN
斜直线
F=3kN
q=2kN/m
M0 6kN m
外伸梁 Beam with an overhang (overhangs)
三、剪力和弯矩
求弯曲内力(剪力和弯矩)的基
本方法——截面法
设有一简支梁AB,受集中力F 作用。现分 析距A端为x 处的横截面m-m上的内力。
解:1、根据平衡条件求支座反力
a m A x
m
F
b B
FAy
Fb Fa , FBy L L
控制截面的概念:外力规律发生变化的截面— 集中力、集中力偶作用点、分布载荷的起点和终 点处的横截面。
M0 8kN m
P=2kN q=2kN/m
A
F
E
1m 1m 2m
B
D
1m
FBy
1m
FAy
◆因此,必须分段列出梁的剪力方程和弯矩方程, 各段的分界点为各段梁的控制截面。
剪力图和弯矩图——用图示方法形象地表示 剪力和弯矩沿梁轴线的变化情况。
F=qa C a
q
A
FAy
3 qa 2
xE
3 a 2
B x
FBy
2a
(+) E
Q 图
1 2 qa 8
冲压工艺学4弯曲课件

越小越有利于弯曲成形。
第四章 弯曲
第三节 最小弯曲半径
最小弯曲半径的近似计算:
断面收缩率可表示为:
弯曲最外侧的拉伸应变
=
1+
t
2
1 2 r 1
t
r=( 1 1)t
2
r =( 1 1)
t 2
实际应用: 最小弯曲半径rmin =t Kmin
其中,最小弯曲系数Kmin
1
2max
1,
不必计算,查表4-1可得。
第四章 弯曲
第四节 弯曲卸载后的回弹
二、回弹值的确定(续)
1.大半径自由弯曲( 弯曲系数K r / t 10 )时的回弹值
K>10时,弯曲半径较大,弯曲变形程 度较小,弹性变形的影响较大,回弹 明显。
凸模工作部分的圆角半径可按下式
进行计算:
卸载前弯曲半径,
rp
即凸模圆角半径
卸载后弯曲半径
rp
1
r
第四章 弯曲
第三节 最小弯曲半径
2.提高弯曲极限变形程度的方法 (1)经冷变形硬化的材料,可热处理后再弯曲。 (2)清除冲裁毛刺,或将有毛刺的一面处于弯曲受压的内缘。 (3)对于低塑性的材料或厚料,可采用加热弯曲。 (4)采取两次弯曲的工艺方法,中间加一次退火。 (5)对较厚材料的弯曲,如结构允许,可采取开槽后弯曲。
三、影响回弹值的因素
1.材料的力学性能 S / E 越大,回弹越大。
材料的力学性能对回弹值的影响 1、3-退火软钢 2-软锰黄铜 4-经冷变形硬化的软钢
第四章 弯曲
第四节 弯曲卸载后的回弹
三、影响回弹值的因素(续)
2.弯曲系数 K r / t
K越大,弹性变形在总变形 的比例越大,回弹就越大。
第四章 弯曲
第三节 最小弯曲半径
最小弯曲半径的近似计算:
断面收缩率可表示为:
弯曲最外侧的拉伸应变
=
1+
t
2
1 2 r 1
t
r=( 1 1)t
2
r =( 1 1)
t 2
实际应用: 最小弯曲半径rmin =t Kmin
其中,最小弯曲系数Kmin
1
2max
1,
不必计算,查表4-1可得。
第四章 弯曲
第四节 弯曲卸载后的回弹
二、回弹值的确定(续)
1.大半径自由弯曲( 弯曲系数K r / t 10 )时的回弹值
K>10时,弯曲半径较大,弯曲变形程 度较小,弹性变形的影响较大,回弹 明显。
凸模工作部分的圆角半径可按下式
进行计算:
卸载前弯曲半径,
rp
即凸模圆角半径
卸载后弯曲半径
rp
1
r
第四章 弯曲
第三节 最小弯曲半径
2.提高弯曲极限变形程度的方法 (1)经冷变形硬化的材料,可热处理后再弯曲。 (2)清除冲裁毛刺,或将有毛刺的一面处于弯曲受压的内缘。 (3)对于低塑性的材料或厚料,可采用加热弯曲。 (4)采取两次弯曲的工艺方法,中间加一次退火。 (5)对较厚材料的弯曲,如结构允许,可采取开槽后弯曲。
三、影响回弹值的因素
1.材料的力学性能 S / E 越大,回弹越大。
材料的力学性能对回弹值的影响 1、3-退火软钢 2-软锰黄铜 4-经冷变形硬化的软钢
第四章 弯曲
第四节 弯曲卸载后的回弹
三、影响回弹值的因素(续)
2.弯曲系数 K r / t
K越大,弹性变形在总变形 的比例越大,回弹就越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 拉弯
一、拉弯的基本原理
1.拉弯的定义:型材零件在弯曲过程中施加一定的拉力,使其产生拉伸 弯曲变形,简称拉弯。 2.拉弯的过程
(a)预拉夹紧毛料
(b)沿拉弯模弯曲毛料 图1-18 拉弯的过程
(c)补拉成形
第三节 拉弯
一、拉弯的基本原理
3.拉弯的基本原理:是在毛料弯曲的同时,加以切向拉力,改变了毛料 断面内的应力状态,减小或基本消除弯曲回弹,从而提高零件的准确度。
(1)压弯时,材料产生外拉内压,中间不受拉也不受压。
(2)弯曲变形受最小弯曲半径的限制和回弹的影响。
第一节 压弯
一、压弯原理及变形特点
3.弯曲力的计算 弯曲力与下列因素有关: (1)金属的力学性能。 (2)毛料的厚度和宽度。 (3)弯曲时的变形程度。 (4)其他因素。
第一节 压弯
一、压弯原理及变形特点
机械弯管的方法、芯棒的作用。
第一节 压弯
一、压弯原理及变形特点
弯曲的定义 把板料、管材或型材等弯成一定曲率或角度,并得到一定形状零件的 冲压工序称为弯曲。 弯曲零件种类很多,如汽车纵梁、自行车车把、仪表电器壳等。 最常见的弯曲是在压力机上用弯曲模压弯,此外还有折弯机上的折弯、
拉弯机上的拉弯、辊弯机上的辊弯以及辊压成形等。
弯曲模、圆管形件弯曲模、Z形件弯曲模。
4.自动弯曲机上的弯曲成形。
第二节 滚弯
一、滚弯设备
概述 1.滚弯定义:通过旋转的滚轴,使毛料弯曲的方法叫滚弯。 2.滚弯的实质:连续不断的弯曲。 3.应用:用于板材、型材的弯曲。 1.三轴滚弯机:分为对称式和不对称式两类。
图1-13 三轴滚弯机 1—上滚轮;2—下滚轮;3—手柄;4—导轮
步减小,板料与凸模三点接触: r1→r2,
板料直边部分向与以前相反的方向变形; 到时行程终了时,凸、凹模对弯
曲件进行校正,使其直边、圆角与模具全
部靠紧。 图1-4 弯曲过程
第一节 压弯
一、压弯原理及变形特点
变形后工件侧壁坐标网及断面的变化:
图1-5 弯曲前后坐标网的变化 (1) 圆角部分的下方形网格变成扇形,远离圆角的两直边处网格没有变 化。说明:变形区主要在圆有部分。靠近圆有的直边,仅有少量的变形。
1.机械弯曲:是将板料、条料、型材等,用机械的方法在塑性变形的范 围内沿直线弯成一定的角度或一定的弧度的操作。
2.机械弯曲的方法:压弯、滚弯、拉弯。
第一节 压弯
一、压弯原理及变形特点
1.压弯原理:由于板料具有一定的塑性,能用弯曲的方法将其弯成所需 的各种形状。在板料上加压产生弯矩,而使其弯曲成形的方法。 (1)自由弯曲阶段; (2)接触弯曲阶段; (3)矫正弯曲阶段。 2.压弯变形特点
第三节 拉弯
五、拉弯常见质量故障、原因分析与排除方法
表1-1
第四节 管子弯曲
一、管子弯曲受力分析
1.管子外侧受到拉力易变薄或开裂。 2.管子内侧收到压力易起皱。 3.管子截面发生压扁成椭圆形。 4.回弹。
二、常用弯管方法
1.手工弯管
(1)弯曲小直径管子
(2)手工装砂热弯
第四节 管子弯曲
二、常用弯管方法
第一节 压弯
一、压弯原理及变形特点
9.窄板弯曲时应力-应变状态 板料弯曲时,其变形主要表现在内、外层金属纤维的缩伸,就绝对值 来看,切向应变为最大主应变,切向应力为最大主应力。 变形区的应力应变状态主要与板材的相对弯曲半径r/t、相对宽度b /t 等因素有关。
第一节 压弯
一、压弯原理及变形特点
切向的外层应变为正、内层为负; 宽向和径向的外层应变为负、内层 为正。 切向的外层应力为正、内层为负;
旋转。
第三节 拉弯
四、拉弯工艺
1.一次拉弯 (1)一次拉弯适用于变形较小的中小型型材零件的拉弯。 (2)工艺过程 下料→淬火→在淬火后材料的时效期内预拉→保持拉力不变,将型材 毛料弯曲至贴合模具外形→补拉→检验。
2.两次拉弯
(1)两次拉弯用于变形程度大的大中型型材零件的拉弯。 (2)工艺过程
下料→退火→预拉→不变预拉力绕拉弯模弯曲→淬火→弯至贴膜后进
图1-16 板材滚弯
2.型材滚弯:型材滚弯使用 的多为四轴滚弯机。 图1-17 型材滚弯
1,2—导轮;3—弯曲轮;4—支承轮
第二节 滚弯
三、滚弯的特点
1.通用性好。 2.零件的回弹可通过调整滚轮的位置的方法加以补偿。 3.滚弯机床结构简单,使用和维护方便。 4.滚弯成形效率低,精度不高。
第二节 滚弯
第二节 滚弯
一、滚弯设备
2.四轴滚弯机
图1-14 四轴滚弯机 1—上滚轮;2—侧滚轮;3—下滚轮;4—侧滚轮;5、6、7—手柄;
8—机座;9—制动手柄
3.多轴滚弯机
图1-15 多轴滚弯机
第二节 滚弯
二、滚弯基本原理
1.板材滚弯:板料滚弯时,毛料在滚轴作用力和摩擦力的连续加载下, 通过滚轴产生塑性弯曲变形。
图1-19 拉弯的应力状态 (a)简单弯曲时板料中产生的应力状态 (b)拉伸时板料中产生的应力
状态
第三节 拉弯
二、拉弯的特点
1.回弹小、精度高,可拉制相对弯曲半径大的零件。 2.模具结构简单,不用修回弹角。
三、拉弯设备
1.转台式拉弯机:台面连同模具在工作过程中旋转,而拉伸作动筒固定 不动。 2.转臂式拉弯机:台面固定不动,由两侧转臂连同拉伸作动筒环绕模具
第一节 压弯 第二节 滚弯 第三节 拉弯 第四节 管子弯曲
第四章 弯曲
【教学目标】 知道机械弯曲的定义、方法;知道管子弯曲时的受力情 况;掌握手工弯管方法;掌握机械弯管的方法、芯棒的作用;知道弯管常 见质量故障、原因分析及排除方法。 【教学重点】 压弯的原理、定义、弯曲力的计算;板材、型材的滚弯 原理;拉弯的定义、设备与原理;手工弯管的方法。 【教学难点】 压弯方法;板材、型材的滚弯工艺方法;拉弯工艺方法;
图1-3 V形弯曲 图为V形弯曲时板料的受力情况,在板料A处,凸模1施加外力2F,在 凹模2支承点B处,则产生反力并与这外力构成了弯曲力矩M=F×L,该弯曲
力矩使板料产生弯曲变形。
第一节 压弯
一、压弯原理及变形特点
板材在V形模内的校正弯曲过程: 凸模下压,直边与凹模V形表面逐 渐靠近,曲率径的弯曲力臂逐步变小: r0→r1,l0 →l1; 凸模继续下压,弯曲变形区进一
4. 板料弯曲变形过程 (1)自由弯曲阶段; (2)接触弯曲阶段; (3)矫正弯曲阶段。
图1-1 弯曲变形过程 (a)(b)自由弯曲;(c)接触弯曲;(d)矫整弯曲
第一节 压弯
一、压弯原理及变形特点
5.弯曲工件的加工形式
图1-2 弯曲工件的加工形式
第一节 压弯
一、压弯原理及变形特点
6. 弯曲变形过程分析
机械弯管 (1)绕弯 ①芯棒的作用:从管材内部支撑管壁,预防管材截面畸变和管壁起皱。 ②防皱块的作用:插在弯管模胎和管子之间,前端应紧靠管壁和弯管 模胎相切处,有效地填补了弯管模胎和管子内侧之间的空隙,起着从外面
支撑管壁,防止起皱的作用。
(2)滚弯 (3)冲模压弯
(4)拉弯
(5)热弯 (6)推弯
第四节 管子弯曲
飞机钣金工岗位基础理论与实践
主讲教师:汉锦丽、贺磊
目录
第一章 金属变形基本理论 第二章 模线样板 第三章 钣金分离工艺 第四章 弯曲 第五章 拉深成形 第六章 橡皮成形 第七章 拉形成形 第八章 旋压成形
第九章 落压成形
第十章 其他钣金成形工艺方法
第四章 弯曲
一、压弯原理及变形特点
7.弯曲变形特点 (1)中性层位置内移 应变中性层 – 既不伸长也不缩短的板料纵截面纤维层。 应力中性层 – 应力发生突然变化或不连续的板料纵截面纤维层。 区变形
中弹性部分的恢复所导致的弯曲件形状和尺寸与模具不一致的现象。 (3)变形区板厚的减小
第一节 压弯
一、压弯原理及变形特点
(4) 变形区横截面的畸变
图1-6 材料弯曲后的畸变 当相对宽度b/t ≤3时,弯曲厚板料横截面变为梯形且有微小翘曲;当
相对宽度b/t >3时,横截面形状变化不大,仅在端部可能出现翘曲和不平,
同时板料外侧易出现拉裂,且相对弯曲半径愈小,拉裂愈容易出现。
第一节 压弯
图1-9 弯曲中的偏移
第一节 压弯
一、压弯原理及变形特点
采用压料装置,使坯料在压紧的状态下逐渐弯曲成形,从而防止坯料 的滑动,而且能得到较平整的制件。
图1-10 压料装置
第一节 压弯
一、压弯原理及变形特点
利用坯料上的孔或设计工艺孔,用定位销插入孔内再弯曲,使坯料无 法移动.
图1-11 定位销
第一节 压弯
四、滚弯工艺
1.板材滚弯 (1)等曲度零件的滚弯。 在滚弯过程中,保持上滚轴上下不动,三根滚轴相互平行。 (2)变曲度零件的滚弯。 在滚弯过程中,三根滚轴保持相互平行,并随时改变上滚轴的上下位
置。
(3)锥形零件滚弯。 采用分段滚弯的方法。
2.型材滚弯
(1)滚轮的典型结构 (2)型材滚弯常见质量故障、原因分析和排除方法
相对弯曲半径r/t < 4时,中性层内移,外层受拉减薄量大于内层受
压增厚量,弯曲变形区板料厚度总体变薄;r/t 愈小,变薄程度愈大。
第一节 压弯
一、压弯原理及变形特点
8.纯塑性弯曲时应力-应变状态 板料弯曲时,其变形主要表现在内、外层金属纤维的缩伸,就绝对值 来看,切向应变为最大主应变,切向应力为最大主应力。 变形区的应力应变状态主要与板材的相对弯曲半径r/t、相对宽度b /t 等因素有关。
一、压弯原理及变形特点
将不对称形状的弯曲件组合成对称弯曲件弯曲,然后再切开,使坯料 弯曲时受力均匀,不容易产生偏移。
