河南省高一3月月考数学试题

合集下载

河南省洛阳市新安一高-高一数学3月月考试题(含解析)新人教A版

高一（下）3月月考数学试卷参考答案与试题解析一、选择题1．（5分）设A，B为两个事件，且P（A）=0.3，则当（）时一定有P（B）=0.7．2．（5分）计算机执行如图的程序段后，输出的结果是（）3．（5分）（2011•宁波模拟）某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如右图所示，则中位数与众数分别为（）4．（5分）为了了解某校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第1小组的频数为6，则报考飞行员的学生人数是（）0.125=（5分）在面积为S的△ABC的边AB上任取一点P，则△PBC的面积不小于的概率是（）5．的面积不小于的面积大于等于；则由三角形的相似性AP=6．（5分）为了在运行下面的程序之后得到输出16，键盘输入x应该是（）INPUT xIF x＜0 THENy=（x+1）（x+1）ELSEy=（x﹣1）（x﹣1）END IFPRINT y7．（5分）如图，程序运行后输出的结果为（）8．（5分）若某程序框图如图所示，则该程序运行后输出的值是（）9．（5分）函数f（x）=x2﹣x﹣2，x∈[﹣5，5]，在定义域内任取一点x0，使f（x0）≤0P=10．（5分）将参加夏令营的600名学生编号为：001，002，…，600．采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区．三个营区被抽中=，12．（5分）两人约定在20：00到21：00之间相见（两人出发是各自独立，且在20：00到21：00各时刻相见的可能性是相等的），并且先到者必须等迟到者40分钟方可离去，则两，进而根据几何概率模型的计算公式可得答案．=﹣2×××=．则两人在约定时间内能相见的概率是二、填空题13．（5分）从1，2，3，4，5这5个数中任取两个，则这两个数正好相差1的概率是．=，故答案为：14．（5分）在Rt△ABC中，∠A=60°，∠C=90°，过点C做射线交斜边AB于P，则CP＜CA 的概率是．=故答案为：．15．（5分）（2008•湖南）从某地区15000位老人中随机抽取500人，其生活能否自理的情则该地区生活不能自理的老人中男性比女性约多60 人．解：由表得16．（5分）执行如图所示的程序，输出的结果为48，则判断框中应填入的条件为i＞3？（或者i＞=4？）．三、解答题17．（10分）已知有一列数，设计框图实现求该列数前20项的和．，画出程序框图．S=S+18．（12分）不透明袋中有3个白球，3个黑球，从中任意摸出3个，求下列事件发生的概率：（1）摸出1个或2个白球；（2）至少摸出1个白球．个白球的摸球方法有+•，从而求得至少=20+•=，﹣=19．（12分）根据下面的要求，求满足1+2+3+…+n＞500的最小的自然数n．（1）画出执行该问题的程序框图；（2）以下是解决该问题的一个程序，但有3处错误，请找出错误并予以更正．（2）①S＜=50020．（12分）设函数f（x）=x2+2ax+b2（1）将一枚骰子抛掷两次，若先后出现的点数分别为a、b，求函数f（x）无零点的概率．（2）若a是从区间[0，2]任取的一个数，b是从区间[0，3]任取的一个数，求函数f（x）有零点的概率．=21．（12分）为了分析某个高二学生的学习状态，对其下一阶段的学习提供指导性建议．现x、物理成绩y进行分析．下面是该生7次考试的成绩．（2）已知该生的物理成绩y与数学成绩x是线性相关的，若该生的物理成绩达到115分，请你估计他的数学成绩大约是多少？并请你根据物理成绩与数学成绩的相关性，给出该生在学习数学、物理上的合理建议．）=142==0.522．（12分）若a是从1，2，3三个数中任取的一个数，b是从2，3，4，5四个数中任取的一个数，（1）有序数对（a，b）共有多少个？将结果列举出来．（2）求成立的概率．（3）设函数，求f（x）＞b恒成立的概率．）验证条件“利用基本不等式可得：为“P=．=成立．。

河南省高一下学期数学3月月考试卷

河南省高一下学期数学 3 月月考试卷姓名:________班级:________成绩:________一、选择题（本大题共 12 小题，共 60 分）， (共 12 题；共 60 分)1.（5 分）在中，角 A,B,C 所对的边分别为 a,b,c，若，则等于（）A.B.C . -1D.12. （5 分） (2019 高一下·成都月考) 在斜已知，若中，设角，，是角的角平分线，且的对边分别为，，，，则（）A.B.C.D.3. （5 分）已知等比数列中，各项都是正数，且 A.成等差数列，则（）B.C.D.4. （5 分） (2020 高二下·南宁期中) 已知等差数列的前 n 项和为第 1 页共 16 页，若，则一定成立的是（）A.B.C.D.5. （5 分） (2018 高一下·芜湖期末) 在，，若的面积，则中，角，，的对边分别为，，，已知的外接圆直径为（）A. B.C.D.6. （5 分） (2020·吉林模拟) 设的内角 A，B，C 的对边分别是 a，b，c．已知，，则（）A.B. C.D.7. （5 分） (2018·孝义模拟) 问题“今有女子不善织布，逐日所织的布以同数递减，初日织五尺，末一日织一尺，计织三十日，问共织几何？”源自南北朝张邱建所著的《张邱建算经》，该问题的答案是（）A. 尺第 2 页共 16 页B. 尺 C. 尺 D. 尺 8. （5 分） (2020 高二上·夏津月考) 已知三棱锥底面是边长为 1 的等边三角形，侧棱长均为 2，则侧棱与底面所成角的余弦值为（）A. B.C.D.9. （5 分） (2018·恩施模拟) 已知等差数列则（）的前项和为，公差A.B.C.D.10. （5 分）在的值为（）中，分别是角的对边，已知成等比数列，且A.，且，，则B.C.D.第 3 页共 16 页11. （5 分） (2018·大新模拟) 设椭圆，若的外接圆和内切圆的半径分别为的焦点为，是椭圆上一点，且，当时，椭圆的离心率为（）A.B.C.D.12. （5 分） (2019·乌鲁木齐模拟) 公差不为零的等差数列等比中项，，则（）的前项和为，若是与的A.B.C.D.二、填空题（本大题共 4 小题，共 20 分） (共 10 题；共 90 分)13. （5 分） (2018 高一下·上虞期末) 在中，面积，则角的大小为________．14. （5 分） (2020 高一下·吉林期中) 如图，设两点在河的两岸，在 A 所在河岸边选一定点 C，测量的距离 50m，，则可以计算两点间的距离是________15. （5 分） (2019·昌平模拟) 等差数列满足第 4 页共 16 页，则 a5=________；若，则n=________时，{an}的前 n 项和取得最大值．16. （5 分） (2015 高一下·太平期中) 在等差数列{an} 中，已知公差 a1+a2+a3+…+a100=________．，且 a1+a3+a5+…+a99=60，则17. （10 分） (2019 高二上·郾城月考) 已知数列满足，，数列满足.（1）证明数列是等差数列并求数列的通项公式；（2）求数列的前 n 项和 .18. （12 分） (2019 高二上·林州月考) 已知是等差数列，，.（1）求的通项公式；（2）设的前项和，求的值.19. （12 分） (2020 高一下·萍乡期末) 设△ ，（1）求角的大小；的内角的对边分别为，且（2）若△的面积为，其外接圆半径，求的值.20. （12 分） (2017 高一下·东丰期末) 等差数列的前 n 项和为，已知（1）求通项；（2）若，求 n 。

河南省高一数学3月月考试题(有答案)

河南省高一数学3月月考试题一. 选择题：（本大题共12小题,每小题5分，共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.）1. 在①160°；②480°；③﹣960°；④1530°这四个角中，属于第二象限角的是（）A．① B．①② C．①②③ D．①②③④2．某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=（）A．9 B．10 C．12 D．133. 在某项体育比赛中，七位裁判为一选手打出的分数如下：90，89，90，95，93，94，93去掉一个最高分和一个最低分后，所剩数的平均值和方差分别为（）A．92，2 B．92，2.8 C．93，2 D．93，2.84. 下列说法正确的是（）A．抛一枚硬币10次，一定有5次正面向上B．明天本地降水概率为70%，是指本地下雨的面积是70%C．互斥事件一定是对立事件，对立事件不一定是互斥事件D．若A与B为互斥事件，则P（A）+P（B）≤15. 从1，2，3，5这四个数字中任意选出两个数字，则这两个数字之和是偶数的概率为（）A．23B．12C．13D．166.用“辗转相除法”求得459和357的最大公约数是：（）A．51 B．9 C．17 D．37. 已知变量x，y之间的线性回归方程为ˆy=﹣0.7x+10.3，且变量x，y之间的一组相关数据如表所示，则下列说法错误的是（）A．变量x，yB．m=4C．可以预测，当x=11时，y=2.6D．由表格数据知，该回归直线必过点（9，4）8. 如图所示，矩形长为6，宽为4，在矩形内随机的撒2400颗黄豆，数得落在椭圆外的黄豆数为516颗，依据此实验数据可以估计出椭圆的面积约为( )A.17.84B. 5.16C. 18.84D.6.169. 已知角a的终边经过点P（-4，m），且3sin5α=，则m等于 ( )A ．3 B.35 C.-3 D. 35- 10. 如图左图是某高三学生进入高中三年来的数学考试成绩的茎叶图，图中第1次到14次的考试成绩依次记为A 1，A 2，…A 14．右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（） A ．8 B ．9 C ．10 D ．1111. 《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验方式为：弧田面积=12（弦×矢+矢2），弧田（如图）由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为32π，半径等于4米的弧田，按照上述经验公式计算所得弧田面积约是（） A ．6平方米B ．9平方米C ．12平方米D ．15平方米C ．第一、二、四象限角 D.第一、三、四象限角二、填空题：(本大题共4小题，每小题5分，共20分，把答案填在答题纸横线上.) 13. 已知x 为第二象限角，且2tan 3tan 40x x +-=，则sin cos 2sin cos x xx x+=- .14. 一只口袋内装有大小相同的5只球，其中3只白球，2只黑球，从中一次性随机摸出2只球，则摸到同色球的概率为．15. 已知2sin(),63πα+=则cos()3πα-= . 16. 一个几何体的三视图如图所示，则该几何体的体积为 .三、解答题：（本大题共6小题，共70分。

2022-2023学年河南省郑州市高一年级下册学期3月月考数学试题【含答案】

2022-2023学年河南省郑州市高一下学期3月月考数学试题一、单选题1．PA BC BA +-=（）A ．PBB ．CPC ．ACD ．PC【答案】D【分析】根据平面向量的线性运算法则，即可求解.【详解】根据向量的线性运算法则，可得PA BC BA PA AC PC +-=+=.故选：D.2．已知向量a ，b 的夹角为π3，3a b ⋅=，2b = ，则a = （）A ．2B ．3C ．6D ．12【答案】B【分析】直接利用向量的数量积运算即可求解．【详解】依题意，π1cos 2332a b a b a a ⋅=⋅⋅=⋅⋅==.故选：B.3．已知向量a 与b 的方向相反，()2,3b =-r ，213a =，则a = （）A ．()6,4-B ．()4,6-C ．()4,6-D ．()6,4-【答案】C【分析】根据共线定理，可得两向量的数乘关系，设出向量坐标，建立方程，可得答案.【详解】∵a 与b的方向相反，∴a b λ= （0λ<）．设(),a x y = ，则()(),2,3x y λ=-，于是2,3.x y λλ=-⎧⎨=⎩由213a = ，得2252x y +=，即222491352λλλ+==，∴24λ=，∴2λ=-，∴()4,6a =-．故选：C.4．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，43a =，12b =，60B =︒，则A =（）A ．30°B ．45°C ．150°D ．30°或150°【答案】A【分析】运用正弦定理，结合三角形大边对大角的性质进行求解即可.【详解】因为43a =，12b =，60B =︒，所以由正弦定理可得343sin 12sin 122a B A b⨯===，所以30A =︒或150°．因为b a >，所以B A >，所以30A =︒．故选：A5．已知在ABC 中，5AB =，4BC =，4cos 5B =，则cos A =（）A ．35B ．34C ．32D ．25【答案】A【分析】直接利用余弦定理可解得3AC =，由此可知ABC 为直角三角形，所以3cos 5AC A AB ==.【详解】由余弦定理可得2222cos AC AB BC AB BC B =+-⋅⋅，解得3AC =，所以222AB AC BC =+，所以ABC 为直角三角形，则在Rt ABC △中，3cos 5AC A AB ==．故选：A.6．如图，在ABC 中，π3ABC ∠=，E 为AB 边的中点，F 为BC 边上的点，且34BF BC = ，2AB =，4BC =，则AC EF ⋅=（）A ．6B ．9C ．10D ．19【答案】B【分析】运用向量运算法则将AC EF ⋅ 转化为51224AC EF BA BC ⋅-⋅+=，再代入向量数量积公式πcos 3BA BC BA BC ⋅⋅⋅= 即可求解.【详解】依题意，()()()3142AC EF BC BA BF BE BC BA BC BA ⎛⎫⋅=-⋅-=-⋅- ⎪⎝⎭223131512242424BC BA BC BA BC BA BA BC =-⋅-⋅+=-⋅+5π5114cos 142494342BA BC =-⋅⋅=-⨯⨯⨯= ．故选：B.7．如图，在矩形ABCD 中，E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，且线段EF 交AC 于点P ．若AB a=，AD b = ，则AP = （）A ．3344a b+ B ．331313a b +C ．51142a b+ D ．19416a b+ 【答案】B【分析】AP AC λ= ，将AP 用,AE AF表示，再根据E ，F ，P 三点共线，求得λ，从而可的答案.【详解】∵E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，∴13AE AD = ，34AF AB = ，设()433AP AC AB AD AF AE λλλ⎛⎫==+=+ ⎪⎝⎭，∵E ，F ，P 三点共线，∴4313λλ+=，解得313λ=，于是()()333131313AP AB AD AB AD a b λ=+=+=+ ．故选：B.8．已知锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．若()2cos cos cos 3sin A B C B +=，7a =，6bc =，则b c +=（）A ．9B ．8C ．5D ．4【答案】C【分析】利用诱导公式、两角和的余弦公式化简已知条件，求得A ，利用余弦定理求得b c +.【详解】∵()2cos cos cos 3sin A B C B +=，πA B C ++=，∴()2cos cos 2cos π3sin A B A B B +--=，()2cos cos 2cos 3sin A B A B B -+=，∴2sin sin 3sin A B B =．∵ABC 为锐角三角形，∴sin 0B ≠，∴3sin 2A =．而π0,2A ⎛⎫∈ ⎪⎝⎭，∴π3A =．由余弦定理可得222π2cos 3a b c bc =+-，∴2276b c =+-，∴2213b c +=，则()222213125b c b c b c bc +=+=++=+=．故选：C二、多选题9．已知向量()()2,1,2,4a b ==- ，则（）A ．5a =B ．1//()4a ab +C ．a b⊥ D ．a b a b+=+ 【答案】AC【分析】根据平面向量的坐标表示与运算，结合向量的平行坐标表示和数量积的坐标运算公式，逐项判定，即可求解.【详解】由()2,1a =r，可得5a = ，所以A 正确；由()()2,1,2,4a b ==- ，可得13(,2)42a b += ，因为322102⨯-⨯≠，所以a 与14a b + 不共线，所以B 错误；由2(2)140a b ⋅=⨯-+⨯=r r ，所以a b ⊥，故C 正确；由()()2,1,2,4a b ==- ，可得241(2)0⨯-⨯-≠，可得a 与b 的方向不相同，所以a b a b +≠+，故D 错误．故选：AC.10．下列说法中正确的有（）A ．若AB与CD 是共线向量，则点A ，B ，C ，D 必在同一条直线上B ．若向量()1,3a = ，()1,3a b -=--，则a b∥C ．若平面上不共线的四点O ，A ，B ，C 满足320OA OB OC -+=，则2AB BC=D ．若非零向量a ，b 满足a b a b ==- ，则a 与a b + 的夹角是π3【答案】BC【分析】对于A ，根据向量共线的定义，可得其正误；对于B ，利用向量共线定理，可得其正误；对于C ，根据向量减法，结合共线定理，可得其正误；对于D ，根据向量模的求解以及夹角公式，可得答案.【详解】AB与CD 是共线向量，也可能是AB CD ，故A 错误；设(),b x y = ，∵()1,3a = ，()1,3a b -=--，∴11,33,x y -=-⎧⎨-=-⎩解得2,6,x y =⎧⎨=⎩∴()2,6b = ，又∵16320⨯-⨯=，∴a b∥，故B 正确；由已知得()()220OA OB OC OB BA BC -+-=+= ，∴2AB BC =，∴2AB BC=，故C 正确；由()22a a b =- 整理可得22b a b =⋅，设a 与a b + 的夹角是θ，则()22222213322cos 232a b a a a b a a b a a a b a bθ+⋅+====⋅+⋅++⋅ ，∴a 与a b + 的夹角是π6，故D 错误．故选：BC.11．已知向量a ，b的夹角为π6，3a = ，1= b ，R t ∈，则（）A ．b 在a 方向上的投影向量的模为32B ．3a b + 在a 方向上的投影向量的模为32C ．ta b + 的最小值为14D ．ta b +取得最小值时，()a ta b⊥+ 【答案】AD【分析】AB 选项，利用投影向量的定义求解判断；CD 选项，利用数量积的运算律求解判断.【详解】因为b 在a 方向上的投影向量的模为π3cos 62b = ，故A 正确；因为3a b + 在a 方向上的投影向量的模为()22π3331cos 339632a b a a b a a a +⨯⨯⨯+⋅+⋅=== ，故B 错误；22222223331292193319264ta b t a ta b b t t t t t ⎛⎫+=+⋅+=+⨯+=++=++ ⎪ ⎪⎝⎭，当36t =-时，ta b + 取得最小值12，此时()233333990262a ta b ta a b t ⎛⎫⋅+=+⋅=+=⨯-+= ⎪ ⎪⎝⎭，所以()a tab ⊥+，故C 错误，D 正确．故选：AD.12．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且()sin sin sin sin a A B c C b B -=-，则下列说法正确的是（）A ．π6C =B ．若ABC 的面积为3，则c 的最小值为2C ．若1a =，5π12B =，则ABC 的面积为338+D ．若3b =，7c =，则满足条件的ABC 有且仅有一个【答案】BC【分析】由正、余弦定理及已知得π3C =，再根据选项综合应用正、余弦定理和三角形面积公式求解．【详解】∵()sin sin sin sin a A B c C b B -=-，∴由正弦定理可得22()a a b c b -=-，即222a b c ab +-=，对于A 选项，由余弦定理可得2221cos 22a b c C ab +-==，∵0πC <<，∴π3C =，故A 错误；对于B 选项，由题可知13sin 324ab C ab ==，∴4ab =，由余弦定理可得222222cos 24c a b ab C a b ab ab ab ab =+-=+-≥-==，∴2c ≥，当且仅当2a b ==时等号成立，故c 的最小值为2，故B 正确；对于C 选项，由题可知π4A =，由正弦定理得sin sin a c A C =，∴3sin 62sin 222a C c A ===∴ABC 的面积为1165π6ππsin 1sin sin()22212446ac B =⨯⨯=+66233448++=⨯=，故C 正确；对于D 选项，由余弦定理可得2222cos c a b ab C =+-，即2793a a =+-，2320a a -+=，解得1a =或2a =，故D 错误．故选：BC ．三、填空题13．已知向量()1,3a =- ，(),0b x =，()2,1c = ，若()c a b ⊥+ ，则实数x 的值为．【答案】12-/0.5-【分析】利用平面向量的坐标运算，结合向量垂直的坐标表示求解作答.【详解】因为向量()1,3a =- ，(),0b x = ，则()1,3a b x +=-，又()2,1c = ，且()c a b ⊥+ ，因此2(1)30x -+=，解得12x =-，所以实数x 的值为12-.故答案为：12-14．已知14AB BC = ，且BA mAC =，则实数m =．【答案】15-/-0.2【分析】利用平面向量的线性运算求解.【详解】解：∵()1144BA AB BC BA AC =-=-=-+，∴15BA AC mAC =-=，∴15m =-．故答案为：15-15．如图所示，向量OA 与OB 的夹角为5π6，向量OP 与OB 的夹角为π6，2OA OP == ，4OB = ，若OP mOA nOB =+ ，（m ，n R ∈），则m n +=．【答案】312+【分析】建立直角坐标系，利用共线向量坐标表达公式进行求解即可.【详解】以O 为坐标原点，OB 所在直线为x 轴，垂直于OB 且向上的方向为y 轴建立平面直角坐标系，则()4,0B ．设()11,P x y ，()22,A x y ，于是1π2cos36x ==，1π2sin 16y ==，且25π2cos36x ==-，25π2sin 16y ==．由OP mOA nOB =+得()()()3,13,14,0m n =-+，∴334,1,m n m ⎧=-+⎪⎨=⎪⎩解得1,3,2m n =⎧⎪⎨=⎪⎩∴312m n +=+．故答案为：312+16．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，π4A =，22222b a c =+，则sin C =．【答案】255【分析】综合运用正、余弦定理求解即可．【详解】由22222b a c =+得2222c a b =-，而π4A =，由余弦定理可得222222cos 2a b c bc A b c bc =+-=+-，即222222c b b c bc -=+-，整理可得324b c =，所以222222952828c c a b c c =-=-=，于是522a c =，由正弦定理可得sin 5sin 22a A c C ==，所以22π25sin sin 455C ==，故答案为：255．四、解答题17．已知向量()1,2a =r，()1,b t = （R t ∈）．(1)若()()a b a b +-，求t 的值；(2)若1t =，a与a mb + 的夹角为锐角，求实数m 的取值范围．【答案】(1)2t =(2)()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭【分析】（1）根据平面向量共线的坐标表示即可求t 值；（2）根据平面向量夹角的定义及其坐标表示即可求m 的取值范围．【详解】（1）由题可知(1,2)(1,)(2,2)a b t t +=+=+ ，(1,2)(1,)(0,2)a b t t -=-=-∵()()a b a b +- ，∴2(2)0t -=，∴2t =．（2）若1t =，则()1,1b = ，(1,2)a mb m m +=++，∵a与a mb + 的夹角为锐角，∴()0a a mb ⋅+> ，且a与a mb + 不共线，∴12(2)02(1)2m m m m+++>⎧⎨+≠+⎩，解得53m >-且0m ≠，∴m 的取值范围是()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭．18．已知1e 、2e 为单位向量，且1e 、2e 的夹角为120 ，向量122a e e =+，21b e e =-．(1)求a b ⋅ ；(2)求a 与b的夹角．【答案】(1)32-(2)120【分析】（1）利用平面向量数量积的定义求出12e e ⋅的值，再利用平面向量数量积的运算性质可求得a b ⋅的值；（2）求出a r 、b ，设a 与b的夹角为θ，求出cos θ的值，结合向量夹角的取值范围可得出θ的值.【详解】（1）解：因为1e 、2e 为单位向量，且1e 、2e 的夹角为120，则12121cos1202e e e e ⋅=⋅=- ，又因为122a e e =+，21b e e =-，则()()221221112213222122a b e e e e e e e e ⋅=+⋅-=-+⋅+=--+=- .（2）解：由已知条件可得()222121211222244a e e e e e e e e =+=+=+⋅+144132⎛⎫=+⨯-+= ⎪⎝⎭，()222212121*********b e e e e e e e e ⎛⎫=-=-=-⋅+=-⨯-+= ⎪⎝⎭，设向量a 、b的夹角为θ，则0180θ≤≤ ，因为()2312cos 23a b a b θ-⋅===-⋅ ，故120θ= ，因此，向量a 、b的夹角为120 .19．已知在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，sin 2sin B B =．(1)求B ；(2)若a c >，且3a c b +=，证明：2a c =．【答案】(1)π3B =(2)证明见解析【分析】（1）由正弦二倍角公式进行求解即可；（2）根据余弦定理，结合已知进行运算证明即可.【详解】（1）因为sin 2sin B B =，即2sin cos sin B B B =，所以1cos 2B =．因为()0,πB ∈，所以π3B =；（2）由余弦定理得222cos 2a c b B ac+-=，所以222122a c b ac +-=，即222ac a c b =+-．①因为3a c b +=，所以3a cb +=．②将②代入①，得()2222123ac a c a ac c =+-++，整理得()()220a c a c --=．因为a c >，所以2a c =．20．已知ABC 的外心为点O ，且()CO CA CB λ=+（R λ∈），P 为边AB 的中点．(1)求证：CP AB ⊥；(2)若514λ=，求ACB ∠的余弦值．【答案】(1)证明见及解析(2)25【分析】（1）连接OB ，OC ，OP ，CP ，由ABC 的外心为点O ，P 为边AB 的中点，得到OP AB ⊥，再由()CO CA CB λ=+ ，得到C ，O ，P 三点共线即可；（2）由（1）知CP AB ⊥，P 为边AB 的中点，得到CA CB =，结合OB OC =，得到2POB PCB ACB ∠=∠=∠．再由cos OP OP POB OB OC ∠==，514λ=求解.【详解】（1）如图，连接OB ，OC ，OP ，CP ．∵ABC 的外心为点O ，P 为边AB 的中点，∴OP AB ⊥．∵2CA CB CP += ，∴()2CO CA CB CP λλ=+= ，∴C ，O ，P 三点共线，∴CP AB ⊥．（2）由（1）知CP AB ⊥．又P 为边AB 的中点，∴CA CB =，∴PCA PCB ∠=∠．∵OB OC =，∴PCB OBC ∠=∠，∴2POB PCB ACB ∠=∠=∠．∵cos OP OP POB OB OC ∠==，514λ=，∴()5577CO CP CO OP ==+ ，∴2577CO OP = ，即25CO OP = ，∴25OP OC =，即2cos 5ACB ∠=．21．已知E 为ABC 内一点，F 为AC 边的中点．(1)若30EA EB EC ++= ，求证：52BE BF = ；(2)若230EA EB EC ++= ，EBC ，ABC 的面积分别为S '，S ，求证：6S S ='．【答案】(1)证明见解析(2)证明见解析【分析】（1）利用平面向量的加减数乘运算的几何意义，结合三角形中几何性质，可得答案；（2）利用三角形线段的比例关系，结合三角形面积的等积变换，可得答案.【详解】（1）∵30EA EB EC ++= ，∴3EA EC EB +=- ．又F 为AC 边的中点，∴233EF EB BE =-= ．∵BE EF BF += ，∴32BE BE BF += ，∴52BE BF = ．（2）如图，设BC 边的中点为P ，连接EF ，EP ．∵230EA EB EC ++= ，∴()2EA EC EB EC +=-+ ，∴24EF EP =- ，即2EF EP =- ，∴F ，E ，P 三点共线．设点E ，F 到BC 的距离分别为1d ，2d ，则12:1:3d d =．设点A 到BC 的距离为3d ．∵F 是AC 的中点，∴23:1:2d d =，∴13:1:6d d =，∴13::1:6S S d d =='，即6S S ='．22．如图，已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，22223sin sin sin sin sin sin 3A CB A BC +-=-⋅．(1)求B ；(2)若2223a c c b ++=，152BA BC ⋅=- ，点D 在边AC 上，且BD 在BC 和BA 上的投影向量的模相等，求线段BD 的长．【答案】(1)2π3B =(2)158【分析】（1）综合运用正、余弦定理即可求解；（2）由（1）及已知可求得5c =，7b =，又由BD 在BC 和BA 上的投影向量的模相等，知BD 为ABC∠的平分线，由角平分线定理得358AD =，再在ABC 和ABD △中应用正弦定理求解即可．【详解】（1）∵22223sin sin sin sin sin sin 3A B C A C B -+-=，∴由正弦定理可22223sin 3a cb ac B =+--，由余弦定理可得222cos 2a c b B ac+-=，∴232cos s 3ac B ac inB =-即tan 3B =-，∵()0,πB ∈，∴2π3B =．（2）由（1）知2π3ABC ∠=，∴2222cos ac ABC ac a c b ∠=-=+-又2223a c c b ++=，∴2222(3)ac a c a c c -=+-++，解得3a =．∵152BA BC ⋅=- ，∴15cos 22ac ac ABC ∠=-=-，可得5c =，由2223a c c b ++=可得292515b ++=212559b ++=，解得7b =．∵BD 在BC 和BA 上的投影向量的模相等，∴BD 为ABC ∠的平分线，由角平分线的性质知AD c b AD a =-，即573AD AD =-，解得358AD =，在ABC 中，由正弦定理可得143sin sin 3a b A ABC ==∠，∴33sin 14A =，在ABD △中，π3ABD ∠=，由正弦定理可得sin sin BD AD A ABD =∠，即358333142BD =，解得158BD =．。

河南省高一下学期3月份月考数学试题(解析版)

一、单选题1．如图，在四边形ABCD 中，若，则图中相等的向量是（）AB DC =A ．与B ．与C ．与D ．与AD CBOB OD AO OC AC BD 【答案】C【分析】利用向量相等的定义即可判断出图中相等的向量.【详解】由，可得四边形ABCD 为平行四边形. AB DC =选项A ：与互为相反向量，判断错误；AD CB选项B ：与互为相反向量，判断错误；OB OD选项C ：与满足向量相等的定义，判断正确；AO OC选项D ：与方向不同不满足向量相等的定义，判断错误. AC BD故选：C2．下列关于向量的命题正确的是（） A ．若，则B ．若，则||||a b = a b =||||a b = //a bC ．若，，则D ．若，，则a b = b c =a c = //ab //b c//a c 【答案】C【分析】利用平面向量的知识对每一个选项逐一分析判断得解．【详解】选项A ，向量的长度相等，方向不一定相同，从而得不出，即该选项错误； a b =选项B ，长度相等,向量可能不平行，该选项错误；∴选项C ，显然可得出，该选项正确；,a b b c ==a c = ∴选项D ，得不出，比如不共线，且，该选项错误. //,//ab bc //a c ,a c 0b = ∴故选：C .3．已知向量，，则（）()1,2a =-()3,1b = ()a ab ⋅-= A ．2 B ．4 C ．6 D ．-6【答案】C【分析】首先根据平面向量的坐标运算得到，再根据平面向量数量积的运算进行计算即可得出a b -答案.【详解】，.()=4,1a b --()()14126a a b ⋅-=-⨯-+⨯= 故选：C.4．在中，已知，，，则角的大小为（） ABC A =2b 3c =1sin 3B =C A ．B ．C ．或D ．或6π3π6π56π3π23π【答案】C【分析】根据正弦定理理解三角形，根据边角关系，可得答案. 【详解】由正弦定理，可得，则，由，则， sin sin b cB C =311sin sin 232c C B b ==⨯=>c b C B >由，则或. ()0,C π∈6C π=56π故选：C.5．在△中，为边上的中线，为的中点，则ABC AD BC E AD EB =A ．B ．3144AB AC -1344AB AC -C ．D ．3144+AB AC1344+AB AC【答案】A【分析】分析：首先将图画出来，接着应用三角形中线向量的特征，求得，之后1122BE BA BD =+应用向量的加法运算法则-------三角形法则，得到，之后将其合并，得到BC BA AC =+，下一步应用相反向量，求得，从而求得结果.3144BE BA AC =+3144EB AB AC =- 【详解】根据向量的运算法则，可得，()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC=++=+所以，故选A.3144EB AB AC =-【点睛】该题考查的是有关平面向量基本定理的有关问题，涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题，在解题的过程中，需要认真对待每一步运算.6．平面向量与的夹角为，，，则（） a b60︒1a = 2b = 2a b -= A B ．2C ．4D ．12【答案】B【分析】根据向量模的公式直接计算结果.【详解】2a = ，，，21a = 24b = cos 601⋅==a b a b. 22a ∴= 故选：B【点睛】本题考查向量数量积，向量的模，重点考查计算，属于基础题型,.7．已知向量，（其中，），若与共线，则的最小值为()3,a m n =-()2,1b =-r 0m >0n >a b 412m n +（） A ．B ．C ．D ．94346159【答案】B【分析】本题首先可以根据与共线得出，然后将转化为，通过a b 23n m +=412m n +18532n m m n ⎛⎫++ ⎪⎝⎭基本不等式即可得出结果.【详解】因为与共线，，， a b()3,a m n =-()2,1b =-r 所以，即，()32m n --=23n m +=则， ()411411812553232323n m n m m n m n m n ⎛⎫⎛⎫⎛⎫+=⨯+⨯+=++≥= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭当且仅当、时等号成立， 12n =2m =故的最小值为， 412m n+3故选：B.8．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且，若，222b c a bc +=+2sin sin sin B C A =则△ABC 的形状是（） A ．等腰三角形 B ．直角三角形C ．等边三角形D ．等腰直角三角形【答案】C【分析】先依据条件求得，再利用可以求得，从而判断222b c a bc +=+π3A =2sin sin sinBC A =b c =△ABC 的形状是等边三角形【详解】△ABC 中，，则222b c a bc +=+2221cos 222b c a bc A bc bc +-===又，则0πA <<π3A =由，可得，代入 2sin sin sinBC A =2a bc =222b c a bc +=+则有，则，则 222b c bc bc bc +=+=()20b c -=b c =又，则△ABC 的形状是等边三角形 π3A =故选：C二、多选题9．下列能使成立的是（） //a bA ．B ．C ．与方向相反D ．或a b = a b = a b0a =0b = 【答案】ACD【解析】根据向量共线的定义判断可得；【详解】解：对于A ，若，则与大小相等且方向相同，所以；对于B ，若，则a b =a b //a b r r a b =r r与的大小相等，而方向不确定，因此不一定有；对于C ，方向相同或相反的向量都是平行a b //a b r r向量，因此若与方向相反，则有；对于D ，零向量与任意向量平行，所以若或a b //a b r r0a = 0b = ，则. //a b r r故选：ACD 【点睛】本题考查平行向量共线的定义的理解，属于基础题. 10．下列各组向量中，可以作为基底的是（）A ．B ． 2130,2(0),2e e →→⎛⎫⎪⎝⎭＝,＝()()12120,0e e →→-＝，＝,C ． D ．()()121,326e e →→--＝，＝,()()123,5,5,3e e →→＝＝【答案】AD【分析】不共线的两个向量才可作为基底，从而判断每个选项的两个向量是否共线，这样即可找出能作为基底的向量.【详解】对于A ，，可以作为基底； 300202⨯-⨯≠12,e e →→对于B,，共线，不能作为基底；120e e →→=⋅12,e e →→对于C,，共线，不能作为基底；1212e e →→=-⋅12,e e →→对于D ，，可以作为基底. 33550⨯-⨯≠12,e e →→故选:AD.11．已知点，，，，则下列结论正确的为（） ()0,0O ()1,3A ()3,1B (),OP OA OB R λμλμ=+∈A ．当时， 2λμ=OP AB ⊥ B ．当时，点P 在直线AB 上1λμ+=C ．当时，λμ=OP AP OB =+D ．当时，在1λμ-=OP AB【答案】BD【分析】对A ，计算出即可判断；对于B ，由条件得可判断；对于C ，用反证法OP AB ⋅ BP BA λ=证明；对于D ，根据投影向量的模计算即可.【详解】由已知， (2,2),(1,3),(3,1),(2,2)AB OA OB BA =-===-对于A ，由，得，所以， 2λμ=2(0)λμμ=≠2(5,7)OP OA OB μμμμ=+= 所以，不正确，故A 不正确； (5,7)(2,2)101440OP AB μμμμμ⋅⋅-===--≠ OP AB ⊥对于B ，当时，由，1λμ+=OP OA OB λμ=+得,从而可知点三点共线，因此点()(1)OP OA OB OP OB OA BP BA OB λλλλ⇒-==+--⇒=,,A B P P 在直线AB 上，故B 正确；对于C ，若成立，则有，这显然不成立，故C 不正OP AP OB =+ OP OP OA OB OA OB =-+⇒=确；对于D ，当时，，1λμ-=()(43,411))(OP OA OB OA OB OB λλλλλ=+-==+---则在方向上的投影向量的模为D 正OP AB ||O P 确. 故选：BD12．在中，角的对边分别为.根据下列条件，判断三角形解的情况，其中正确的ABC A ,,A B C ,,a b c是（）A ．，有唯一解 5,7,8a b c ===B ．，无解 18,20,60b c B ===°C ．，有两解 8,45a b B ===︒D ．，有唯一解 30,25,150a b A ===︒【答案】AD【分析】根据三边确定可判断A 选项；由正弦定理，在结合大边对大角可判断B ，C ，D 选项. 【详解】解：选项A ，，已知三边三角形确定，有唯一解，A 正确；5,7,8a b c ===选项B ，由正弦定理得：，则，再由大边对大角可得sin sin b c B C=sin sin 1c B C b ==<，故可以为锐角，也可以为钝角，故三角形有两解，B 错误；C B >C选项C ，由正弦定理得：，则，且，由大边对大角sin sin a b A B=sin 1sin 12a B A b ===<a b <可得，则只能为锐角，故三角形有唯一解，C 错误； A B <A 选项D ，由正弦定理得：，，由于，则是sin sin a bA B =sin 25sin1505sin 13012b A B a ︒===<150A =︒B 锐角，有唯一解，D 正确. 故选：AD.三、填空题13．已知，点P 在直线上，且，则点P 的坐标是_____．()()2,5,10,3A B --AB 13PA PB =-【答案】(1,3)【分析】由题意可知，三点共线，且有，设出点的坐标，利用向量相等的条,,A B P 13PA PB =-P 件建立方程求出点P 的坐标【详解】解：设(),P x y ，点P 在直线上()()2,5,10,3A B -- AB ，(,)PA x y ∴=--- 25(,)PB x y =---103，则有PA PB =- 1312(10)315(3)3x x y y ⎧--=--⎪⎪⎨⎪-=---⎪⎩解得 13x y =⎧⎨=⎩()1,3P ∴【点睛】本题考查向量共线的坐标表示，向量相等的条件.解题的关键是由题设条件得出两向量的数乘关系，再利用向量相等的条件得出坐标的方程求出P 的坐标.14．设，是不共线的两个非零向量，若，，，且点a b 12OA ka b =+ 45OB a b =+ 10OC ka b =-+ A ，，在同一直线上，则__________． B C k =【答案】.23-【分析】根据向量共线得方程，解得k 的值.【详解】由题得 ()()47,45,AB OB OA k a b CB OB OC k a b =-=--=-=+-因为点，，在同一直线上，所以 A B C 472,.453k k k --=∴=-+-故答案为23-【点睛】本题考查向量共线，考查基本求解能力15．已知向量，．若向量与垂直，则________．(1,2)a =- (,1)b m =r a b +a m =【答案】7【分析】首先求出的坐标，再根据两个向量垂直的性质得到，根据向量数量积的a b +()0a b a +⋅= 坐标运算得到方程，即可求得实数的值．m 【详解】解：因为，，所以，因为向量与垂直，所以(1,2)a =- (,1)b m =r ()1,3a b m +=- a b +a ，解得，()()1230a b a m +⋅=--+⨯=7m =故答案为：7．16．在中，角A ，B ，C 所对的边分别为a ，b ，c ．且，，ABC A sin A B =6C π=ac ______．=a【分析】先由正弦定理及已知条件得出a ，b，c 之间的关系，再由余弦定理求出即可．【详解】∵，根据正弦定理得，sin A B =a∴，又∴， b =acc=π6C =再根据余弦定理得∴，解得222cos 2b a c C ab +-===a =四、解答题17．已知向量，，，且，． (1,2)a = (3,)b x = (2,)c y = //a b a c ⊥(1)求向量、；b c(2)若，，求向量，的夹角的大小.2m a b =- n a c =+m n 【答案】(1)， (3,6)b = (2,1)c =-(2) 34π【分析】（1）由题意结合向量平行及垂直的坐标表示可求，，进而可求；x y （2）设向量，的夹角的大小为．先求出，，然后结合向量夹角的坐标公式可求． m n θmn 【详解】（1）解：因为，，，且，，(1,2)a = (3,)b x = (2,)c y = //a b a c ⊥所以，， 230x -⨯=220a c y ⋅=+=所以，，6x =1y =-所以，；(3,6)b = (2,1)c =-（2）解：设向量，的夹角的大小为．mn θ由题意可得，，，()()()22,43,61,2m a b =-=-=--(3,1)n a c =+= 所以cos ||||m n m n θ⋅= 因为，所以． 0θπ≤≤34πθ=18．在中，、、所对的边分别为、、，，． ABC A A B C a b c π3B =57a b =(1)求的值； sin A (2)若，求．7b =c【答案】(2) 8c =【分析】（1）由正弦定理可得，又因为，代入即可求出．sin sin a B A b=π3B =sin A （2）首先得到，再由余弦定理，可得边． a 2222cos b c a ca B =+-c 【详解】（1）因为，， π3B =57ab =所以由正弦定理得sin 5sin 7a B A b ===（2）因为，，所以．7b =57a b =5a =由余弦定理得， 2222cos b c a ca B =+-222755c c =+-解得或（舍）．8c =3c =-19．已知、是非零向量，，且、．a b()a ab ⊥- a = 4b = (1)求与的夹角；a bθ(2)求． 32a b - 【答案】(1)6π(2)【分析】（1）依题意可得，根据数量积的运算律求出，再根据计算可()0a a b ⋅-= a b ⋅cos a b a bθ⋅=⋅得；（2）根据32a b -=【详解】（1）解：因为，所以，即，即，()a ab ⊥- ()0a a b ⋅-= 20a a b -⋅=212a b a ⋅== 所以，所以；cosa b a b θ⋅⋅===[]0,θπ∈6πθ=（2）解：32a b-=====20．如图，在中，D ，F 分别是BC ，AC 的中点，，，． ABC A 23AE AD =AB a =AC b =(1)用，分别表示向量，；a b AE BF (2)求证：B ，E ，F 三点共线．【答案】(1)，()13A a b E += 12=-+BF a b (2)证明见解析【分析】（1）由，得到，()()1122AD AB AC a b =+=+()2133AE AD a b ==+ 由，得到． 1122== AF AC b 12BF AF AB a b =-=-+（2）由（1）知，，得到即可．12=-+ BF a b 21213332BE AE AB a b a b ⎛⎫=-=-+=-+ ⎪⎝⎭ 23BE BF = 【详解】（1）∵，()()1122AD AB AC a b =+=+∴，∵， ()2133AE AD a b ==+1122== AF AC b ∴．12BF AF AB a b =-=-+ （2）由（1）知，12=-+BF a b ，21213332BE AE AB a b a b ⎛⎫=-=-+=-+ ⎪⎝⎭∴．∴与共线．23BE BF = BEBF 又BE ，BF 有公共点B ，所以B ，E ，F 三点共线．21．在中，内角A ，B ，C 对应的边分别为a ，b ，c ，已知. ABC A cos sin a B b A =(1)求B ；(2)若，求b 的值. a =3c =【答案】(1)；4B π=(2). b =【分析】（1）利用正弦定理，将边化角转化，即可求得；cos sin a B b A =B（2）利用余弦定理，结合（1）中所求，即可求得.b 【详解】（1）在中，由正弦定理得，ABC A sin cos sin sin A B B A =因为，所以，所以，0A π<<sin 0A ≠tan 1B =又因为，所以.0B π<<4B π=（2）在中，由余弦定理得，ABC A 2222cos b a c ac B =+-代入数据解得， 229235b =+-=所以b 22．如图，在矩形中，，，点为的中点，点在上，且． ABCD 4AB =3AD =P CD Q BC 2BQ =（1）求；AP AQ ⋅ （2）若（，），求的值. AC AP AQ λμ=+ λμ∈R λμ【答案】（1）14；（2）. 23λμ=【分析】分别以边，所在的直线为轴，轴，点为坐标原点，建立平面直角坐标系，利AB AD x y A 用向量坐标的线性运算以及数量积的坐标运算即可求解.【详解】解：如图，分别以边，所在的直线为轴，轴，AB AD x y 点为坐标原点，建立平面直角坐标系，A 则，，，，.()0,0A ()2,3P ()4,0B ()4,3C ()4,2Q（1）∵，，()2,3AP = ()4,2AQ = ∴.243214AP AQ ⋅=⨯+⨯= （2）∵，，，()4,3AC = ()2,3AP = ()4,2AQ = 由，得，AC AP AQ λμ=+ ()()4,324,32λμλμ=++∴解得 244,323,λμλμ+=⎧⎨+=⎩1,23,4λμ⎧=⎪⎪⎨⎪=⎪⎩∴. 23λμ=【点睛】本题考查了向量坐标的线性运算、向量数量积的坐标运算，考查了基本运算求解能力，属于基础题.。

河南省焦作市第一中学2022-2023学年高一下学期3月月考数学试题

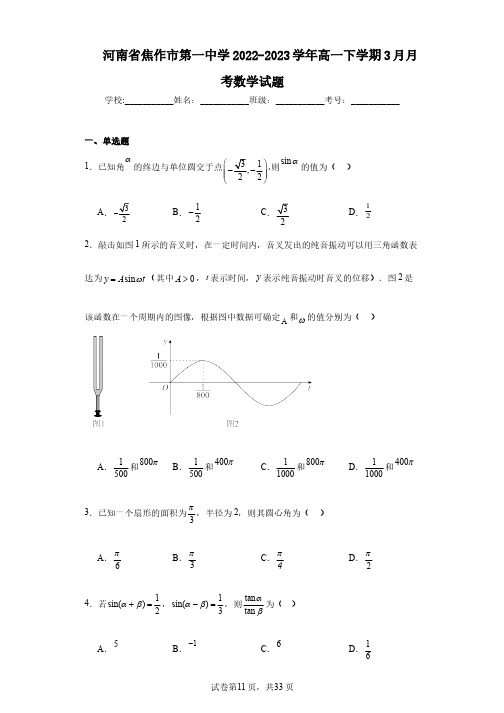
r a
=
ur 3e1
+
uur 3e2
，
r b
=
ur e1
+
uur e2
C．
r a
=
ur e1
-
ur 2e2
，
r b
=
ur e1
+
uur e2
D．
r a
=
ur e1
-
ur 2e2
，
r b
=
ur 2e1
-
uur 4e2
7．在
DABC
中，
G
为
DABC
的重心，
M
为
AC
上一点，且满足
uuuuv MC
=
uuuuv 3AM
cr
，求
cr
×
(ar
+
r b)
的值.
21．已知向量
av
与向量
v b
的夹角为
45°，其中
av
=
2
，
v b
=1.
（1）求
av
+
v 2b
的值；
（2）若向量
2av
-
v lb
与
lav
-
v 3b
的夹角是锐角，求实数
l
的取值范围.
22．设函数
f
(x)
=
cos
x
×
cos
æ çè
x
-
p 6
ö ÷ø
+
3
sin2
x
-
33 4
试卷第11 页，共33 页
D． 1 6
5．设非零向量

河南高一下学期3月月考数学试题(解析版)

一、单选题1．已知，则（）3i(i)(2i)(,R)a b a b -=-∈a b +=A ．B ．9C ．7D ．9-7-【答案】B【分析】根据题意，利用复数的运算法则，得到，求得的值，即可求解.1i 8i a b +=+,a b 【详解】由，根据复数的运算法则，可得，3i(i)(2i)a b -=-1i 8i a b +=+所以，所以.8,1a b ==9a b +=故选：B.2．已知等边三角形，则与的夹角为（） ABC A AB BC A ．B ．C ．D ．120︒60︒30︒60-︒【答案】A 【分析】根据向量夹角的定义求解即可.【详解】因为等边三角形，故与的夹角为，与的夹角和与的夹角ABC A BA BC 60︒AB BC BA BC 互补，为.120︒故选：A3．已知向量，若，则实数的值是（）()()8,2,,1a b m =-= a b λ= m A ．-4B ．-1C ．1D ．4【答案】A【分析】根据向量共线列方程，化简求得的值.m 【详解】由于， a b λ= 所以，解得. 82m λλ=⎧⎨-=⎩4m =-故选：A4．在中，角的对边分别为，已知则（） ABC A ,,A B C ,,a b c 60a b B ===︒，A =A ．45°或135°B ．135°C ．45°D ．60°或120° 【答案】C【分析】根据正弦定理求解即可.【详解】由正弦定理得：得： sin sin a b A B =sin sin a A B b ===因为，所以，所以.a b <0A B << 45A =o 故选：C5．若复数满足，则在复平面内对应的点的坐标为（）z (2i)(1i)=i z -+z A ． B ． C ． D ． 13,22⎛⎫-- ⎪⎝⎭15,22⎛⎫- ⎪⎝⎭13,22⎛⎫- ⎪⎝⎭15,22⎛⎫ ⎪⎝⎭【答案】D【分析】利用复数的四则运算解出，得到对应的点坐标即可求解. 15i 22z =+【详解】由得， (2i)(1i)=i z -+()()()()1i i i 1i 152i 2i 2i i 1i 1i 1i 222z -+=+=+=+=++-+所以z 在复平面内对应的点为. 15(,)22故选：D.6．已知的内角的对边分别是，则“是钝角三角形”是 “ABC A A B C ，，a b c ，，ABC A 2220a b c +-<” 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【分析】先举出反例，得到充分性不成立，再由余弦定理得到必要性成立.【详解】若△ABC 中B 为钝角，则C 为锐角，，即有，故充分性不成立； cos 0C >2220a b c +->若，由余弦定理得即C 为钝角，故必要性成立. 2220a b c +-<222cos 02a b c C ab +-=<，故选：B.7．已知向量的夹角为且|，，则在上投影向量的坐标为（） ,a b π3||2a = (1,1)= b a bA ．B ．C ．D ．11,22⎛⎫ ⎪⎝⎭(1,1)【答案】C【分析】根据给定条件，利用投影向量的定义，结合向量坐标运算求解作答.【详解】依题意，在上投影向量为，其中， a b (||cos )||b a b θ ,a b θ=〈〉所以在上投影向量的坐标为. a b π(2cos 3=故选：C8．在平行四边形中，，，，，且，则平行ABCD 4AB =3AD =13AE EB = 2DF FC = 6BF CE ⋅=- 四边形的面积为（）ABCDA B C ． D ． 245125【答案】A【分析】根据条件，利用基底向量表示，即可求，再利用同角三角函数,CB CD BF CE ⋅ cos BCD ∠函数表示，最后根据平行四边形面积求解.sin BCD ∠【详解】因为，，所以13AE EB = 2DF FC = ()()BF CE CF CB CB BE ⋅=-⋅+= ，1334CD CB CB CD ⎛⎫⎛⎫-⋅+ ⎪ ⎪⎝⎭⎝⎭2215||412CB CD CB CD =-+-⋅ 22153434cos 55cos 6412BCD BCD ∠∠=-+⨯-⨯⨯=--=-解得：，则 1cos 5BCD ∠=sin BCD ∠=所以sin 43ABCD S CB CD BCD =⋅⋅∠=⨯=A 故选：A.二、多选题9．对于任意的平面向量，下列说法错误的是（）,,a b c A ．若，则与不是共线向量a b ≠ a b B ．()a b c a c b c +⋅=⋅+⋅ C ．若，且，则a b a c ⋅=⋅ 0a ≠ b c = D ．()()a b c b c a ⋅⋅=⋅⋅ 【答案】ACD【分析】根据共线向量的定义即可判断A ；根据数量积的运算律即可判断B ；举反例即可判断C ；根据数量积的定义即可判断D.【详解】对于A ，当时，，但是共线向量，故A 错误；a b =- a b ≠ ,a b 对于B ，根据数量积的分配律得，故B 正确； ()+⋅=⋅+⋅ a b c a c b c 对于C ，若，且，则，a b a c ⋅=⋅ 0a ≠ cos ,cos ,b a b c a c =r r r r r r不妨取，此时，故C 错误； π,,1,,023,b a b c a c ==== b c ≠ 对于D ，表示的是与共线的向量，表示的是与共线的向量， ()a b c ⋅ c ()b c a ⋅ a 而向量的方向不确定，所以无法确定与是否相等，故D 错误. ,a c ()a b c ⋅ ()b c a ⋅ 故选：ACD.10．若复数为纯虚数，则（）z A ．为实数B ．为实数 z z +z z -C ．为实数D ．为实数2z i z ⋅【答案】ACD【分析】根据题意，设且，得到，结合复数的运算法则，逐项判定，即i(R z m m =∈0)m ≠i z m =-可求解.【详解】因为为纯虚数，设且，则，z i(R z m m =∈0)m ≠i z m =-由，所以A 正确；0z z +=由，所以B 错误；2i z z m -=由为实数，所以C 正确；22z m =-由为实数，所以D 正确.i i i z m m =⋅=-⨯=故选：ACD.11．下列说法正确的是（） A ．若两个非零向量共线，则必在同一直线上,AB CD ,,,A B C D B ．若向量与平行，与平行，则，方向相同或相反a b b c a c C ．若非零向量与是共线向量，则它们的夹角是0°或180°AB CD D ．平行向量就是共线向量，共线向量就是平行向量【答案】CD【分析】根据平面向量平行的概念和夹角的概念依次判断选项即可.【详解】对选项A ，若两个非零向量共线，则与平行或在一条直线上，故A 错误.,AB CD AB CD 对选项B ，若，与不平行，则满足向量与平行，与平行，故B 错误.0b = a c a b b c 对选项C ，若非零向量与是共线向量，则它们的夹角是0°或180°，故C 正确.AB CD 对选项D ，平行向量就是共线向量，共线向量就是平行向量，故D 正确.故选：CD12．在中，内角A ，B ，C 所对的边分别为a ，b ，c ，则下列结论正确的是（）ABC AA ．若a >b ，则sin sin A B >B ．若，则A >Bsin sin A B >C ．若，则是等腰三角形cos cos a A b B =ABC A D ．若为锐角三角形，则ABC A sin cos A B >【答案】ABD【分析】根据三角形的基本性质及正弦定理，正弦函数的单调性，逐项分析得出结果即可．【详解】对于选项A ，在中，大边对大角，若，则，ABC A a b >A B >根据正弦定理可得，选项A 正确；sin sin A B >同理，选项B 正确；对于选项C ，若，由正弦定理可得，cos cos a A b B =sin cos sin cos A A B B =即，所以即或即， sin 2sin 2A B =22A B =A B =22πA B +=π2A B +=所以为等腰角三角形或直角三角形，选项C 错误；ABC A 对于选项D ，若为锐角三角形，则， ABC A πππ0222A B A B +>∴>>->又正弦函数在上为单调增函数，π02⎛⎫ ⎪⎝⎭，，即，选项D 正确． πsin sin 2A B ⎛⎫∴>- ⎪⎝⎭sin cos A B >故选：ABD ．三、填空题13．设复数z 满足，则___________.i 1z z +=||z =【分析】根据复数的四则运算可求得，进而可求共轭复数以及模长. 1122z i =+【详解】∵，则， i 1z z +=()111i 11i i 11i 1i (1i)22z -+====+---+∴，故1122z i =-z ==. 14．在中，角的对边分别为，且，，则 ABC A A B C ，，a b c ，，cos sin b C c B a +=6b = _________. 2sin 2sin a b A B+=+【答案】【分析】利用正弦定理及得到，求出，再利用正弦定理得到()sin sin A B C =+sin cos B B =π4B =，代入得到答案. ,a A b B ==【详解】由正弦定理得，sin cos sin sin sin B C C B A +=即，()sin cos sin sin sin sin cos cos sin B C C B B C B C B C +=+=+ ，sin sin cos sin C B B C ∴=∵，()0,πC ∈∴，sin 0C ≠，，sin cos B B ∴=tan 1B =，()0,πB ∈ ∴，π4B =由正弦定理得sin sin sina b c AB C ==== a A b B∴==，，所以. 2sin 2sin ab A B +==+故答案为：15．已知平面向量，，若与的夹角为锐角，则的取值范围为()1,2a =-r ()4,b y = a a b + y ____________.【答案】 ()9,88,2⎛⎫-∞-⋃- ⎪⎝⎭【分析】已知条件可转化为，且与不共线，利用平面向量数量积的坐标公式以()0a a b +> A a a b + 及共线公式列不等式，解出的取值范围．y 【详解】因为与的夹角为锐角，所以，且与不共线， a a b + ()0a a b +> A a a b + ，，即，且，()1,2a =-r ()5,2a b y +=- ()15220y ⨯-->()1225y ⨯-≠-⨯解得且 92y <8y ≠-故答案为： ()9,88,2⎛⎫-∞-⋃- ⎪⎝⎭16．如图，中华中学某班级课外学习兴趣小组为了测量某座山峰的高气度，先在山脚A 处测得山顶C 处的仰角为60°，又利用无人机在离地面高400m 的M 处（即），观测到山顶C 处的仰400MD =角为15°，山脚A 处的俯角为45°，则山高___________m.BC =【答案】600【分析】确定，，在中，利用正弦定理计算得到AM =45ACM ∠=︒75MAC ∠=︒MAC △答案.【详解】，则，,， 45AMD ∠=︒AM ==451560CMA ∠=︒+︒=︒60CAB ∠=︒故，，18060MAC ∠=︒-︒4575-︒=︒180756045ACM ∠=︒-︒-︒=︒在中，由正弦定理得，即， MAC △sin sin AC MA AMC ACM =∠∠sin60AC =︒解得.AC =sin60600BC AC =︒=故答案为：600四、解答题17．已知虚数z .(1)求证：在复平面内对应的点在直线上； 5i z z+y x =(2)若是方程的一个根，求与.z 2240(R)x x k k ++=∈k z 【答案】(1)证明见解析(2)， 10k =12i z =-±【分析】（1）由题设可得，应用代数运算化简并确定点坐标，即可证结论； 5i i z z z z+=+（2）将复数代入方程求参数即可.i z a b =+【详解】（1）设， i z a b =+(,R,0)a b b ∈≠5zz =所以， 5i i i (i)i ()()i z z z a b a b a b a b z +=+=++-=+++所以在复平面内对应的点为，在直线上. 5i z z+(,)a b a b ++y x =（2）同（1）设复数，因为z 是方程的一个根， i(,R,0)z a b a b b ∈≠=+2240(R)x x k k ++=∈所以，即，22(i)4(i)0a b a b k ++++=22224(44)i 0a b a k ab b -++++=所以且，得，222240a b a k -++=440ab b +=1a =-因为，所以，225a b +=2b =±把代入得：，1,2a b =-=±222240a b a k -++=10k =所以，.10k =12i z =-±18．已知向量满足，，且.2= a 3b = (3)(2)16a b a b +⋅-=- (1)若，求实数的值；()()a b a b λ-⊥+ λ(2)求与的夹角的余弦值.a 2ab - 【答案】(1)27【分析】（1）利用数量积的运算律及向量垂直的充要条件即可求解；（2）先数量积知识求出，的值，然后利用数量积的夹角公式求解即可.2a b - (2)a a b ⋅- 【详解】（1）因为，所以，(3)(2)16a b a b +⋅-=- 2235216a a b b -⋅-=- 即，解得，若，223252316a b ⨯-⋅-⨯=- 2a b ×= ()()a b a b λ-⊥+ 则，()()0a b a b λ-⋅+= 即，即，解得. 22(1)0a a b b λλ+-⋅-=2222(1)30λλ+--⨯=27λ=（2）因为2a b -==== 又，22(2)22226a a b a ab ⋅-=-⋅=⨯-= 所以 (2)cos ,22a a b a a b a ab ⋅--===⋅- 即与a 2a b - 19．已知内角的对边分别为，且.ABC A A B C ，，a b c，，2cos cos cos c A a B b A =+(1)求角；A (2)若的周长为外接圆的半径为1，判断的形状，并求的面积.ABC A ABC A ABC A ABC A【答案】(1) π3(2) 【分析】（1）由正弦定理及三角形的性质即可求角；（2）利用正弦定理求出边长a ，然后再根据周长和余弦定理列式解出b 和c ，从而判断性质和求解面积.【详解】（1）由题意，2cos cos cos c A a B b A =+由正弦定理得，2sin cos sin cos sin cos C A A B B A =+因为，sin cos sin cos sin()sin A B B A A B C +=+=所以，因为，所以，所以， 2sin cos sin C A C =()0,πC ∈sin 0C ≠1cos 2A =又，所以. ()0,πA ∈π3A =（2）设外接圆的半径为，则，由正弦定理得，ABC A R 1R =2sin a R A ==因为的周长为ABC A b c +=由余弦定理得，即，所以， ()2222π2cos 33a b c bc b c bc =+-=+-3123bc =-3bc =由为等边三角形，3b c bc ⎧+=⎪⎨=⎪⎩b c ⎧=⎪⎨=⎪⎩ABC A所以的面积 ABC A 11sin 322S bc A ==⨯=20．如图，在等腰梯形中，，，，E 是边的中点． ABCD AB CD ∥22AB DC == π3BAD ∠=BC(1)试用，表示，；AB AD AE BC (2)求的值．DB AE ⋅ 【答案】(1)， 3142AE AB AD =+ 12BC AD AB =- (2)94【分析】（1）利用几何图形，结合平面向量基本定理，利用基底表示向量；（2）以向量为基底，表示向量，结合向量数量积的运算律和定义，即可求解.,AD AB ,DB AE 【详解】（1）， 12AC AD DC AD AB =+=+ ， ()1113122242AE AB AC AB AD AB AB AD ⎛⎫=+=++=+ ⎪⎝⎭ ． 1122BC AC AB AD AB AB AD AB =-=+-=- （2）由题意可知，，， ()11221π1cos 32AB DC AD -=== DB AB AD =- 所以 ()221331124424DB AE AB AD AD AB AB AD AB AD ⎛⎫⋅=-⋅+=--⋅ ⎪⎝⎭ 22311πcos 4243AB AD AB AD =--⋅⋅ ． 31119412142424=⨯-⨯-⨯⨯⨯=21．如图，在平面四边形中，，设.ABCD90AB ADC CAB =∠=∠= DAC ∠θ=(1)若，求的长度；60,2AB CD θ== BD (2)若，求.30ADBABC ∠=∠= tan θ【答案】【分析】（1）根据题意求得，在中，利用余弦定理，即可求得的长；1AD =ABD △BD （2）根据题意求得，得到，在中，利用正弦定理求得2AC =2cos ,60AD ABD θθ=∠=- ABD △的值. 2cos sin(60)θθ=- tan θ【详解】（1）解：由题意得且，90AB CD ADC CAB ==∠=∠= 60DAC ∠= 可得， 1tan 60CD AD ==在中，，ABD △150,1DAB AB AD ∠===由余弦定理可知：， 222222cos 60121(19BD AB AD AB AD =+-⋅=+-⨯⨯=所以BD =（2）解：因为，所以， 90,30CAB ABC ∠=∠= tan 2AC AB ABC =⋅∠==又因为且，可得,90ADC ∠= DAC ∠θ=2cos ,60AD ABD θθ=∠=- 在中，由正弦定理知， ABD △si n si n AD AB ABD ADB=∠∠所以， 2cos sin(60)θθ=- 2cos )6cos θθθθ=-=-可得，即. 4cos θθ=tan θ=22．记的内角所对的边分别为，已知.ABC A A B C ，，a b c ，，sin sin a A c C b +=(1)求证： 222sin cos 1ac B B a c+=+；(2)若的面积，求的最大值，并证明：当取最大值时，为直角三角形. ABC A 20S kb k =>（）k k ABC A 【答案】(1)证明见解析(2)，证明见解析 14【分析】(1)利用正弦定理边角互化结合余弦定理即可求解；(2)利用三角形的面积公式结合基本不等式即可求解. 【详解】（1）证明：由， sin sin sin a b c A B C ==得， sin sin sin sin a B c B A C b b==代入，得， sin sin a A c C b +=22sin sin a B c B b b b+=所以， 222sin b B a c=+由余弦定理，得，2222cos b a c ac B =+-所以， 2222222cos 2sin 1cos a c ac B ac B B a c a c +-==-++所以. 222sin cos 1ac B B a c+=+（2）由(1)知， 222sin b B a c=+所以的面积， ABC A 222211sin 22b S ac B ac kb a c==⋅=+所以， 221112224ac ac k a c ac =⋅≤⋅=+当且仅当时取等号，所以的最大值为. a c =k 14下面证明当，即时，为直角三角形.14k =a c =ABC A 把代入，得， a c =222sin cos 1ac B B a c +=+sin cos 1B B +=两边平方，得，所以， 22sin 2sin cos cos 1B B B B ++=sin cos 0B B =因为，所以，即，0sin 0B B π<<≠，cos 0B =2B π=所以为直角三角形. ABC A。

河南省名校联考2024-2025学年高一上学期第一次月考数学试题(含解析)

河南省名校联考2024-2025学年上期高一第一次月考数学注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

4.本试卷主要考试内容：人教A版必修第一册前两章。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符题目要求的.1.下列关系式正确的是A.3∈QB.—1∈NC. Z⊆ND. Q⊆R2.关于命题q:∀a<b,|a|≤|b|,下列结论正确的是A. q是存在量词命题，是真命题B. q是存在量词命题，是假命题C. q是全称量词命题，是假命题D. q是全称量词命题，是真命题3.已知集合A={x∈Z|3x―1∈Z},则用列举法表示A=A.{—2,0,2,4}B.{—2,0,1,2,4}C.{0,2,4}D.{2,4}4.已知a>0,b>0,c>0,则“a+b>c”是“a,b,c可以构成三角形的三条边”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知正数a，b满足1a +2b=1,则a+2b的最小值为A.9B.6C.4D.36.已知集合A={(x,y)|y=x²+ ax+1},B={(x,y)|y=2x-3},C=A∩B,若C恰有1|真子集，则实数a=A.2B.6C.2或6D.—2或67.某花卉店售卖一种多肉植物，若每株多肉植物的售价为30元，则每天可卖出25株；若每株肉植物的售价每降低1元，则日销售量增加5株.为了使这种多肉植物每天的总销售额不于1250元，则每株这种多肉植物的最低售价为A.25元B.20元C.15元D.10元【高一数学第1页(共4页)】 ·A18.学校统计某班45名学生参加音乐、科学、体育3个兴趣小组的情况，其中有20名学生参加了音乐小组，有21名学生参加了科学小组，有22名学生参加了体育小组，有24名学生只参加了1个兴趣小组，有12名学生只参加了2个兴趣小组，则3个兴趣小组都没参加的学生有A.5名B.4名C.3名D.2名二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.下列各组对象能构成集合的有A.郑州大学 2024 级大一新生B.我国第一位获得奥运会金牌的运动员C.体型庞大的海洋生物D.唐宋八大家10.已知a>b>0,则使得a+ca >b+cb成立的充分条件可以是A. c=-2B. c=-1C. c=1D. c=211.已知二次函数y=ax²+bx+c(a,b,c为常数，且a≠0)的部分图象如图所示，则A. a+b>0B. abc>0C.13a+b+2c>0D.不等式bx²―ax―c>0的解集为{x|-2<x<1}三、填空题：本题共3小题，每小题5分，共15分.12.已知a=10―6,b=6―2,则a ▲ b.(填“◯”或“<”)13.已知a∈R,b∈R,集合{,则(a―b)³=.14.已知m<n<0,则8nm+n ―2mm―n的最大值为▲ .四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知全集U=R,集合A={x|-2<x<3},B={x|a-1<x<2a}.(1)若a=2,求A∪B,C∪B;(2)若B⊆A,求a 的取值范围.【高一数学第2页(共4页)】 A116.(15分)给出下列两个结论：①关于x的方程.x²+mx―m+3=0无实数根；②存在0≤x≤2,使(m+1)x―3=0.(1)若结论①正确，求m 的取值范围；(2)若结论①，②中恰有一个正确，求m的取值范围.17.(15分)已知正数a,b,c 满足 abc=1.(1)若c=1,求2a +3b的最小值；(2)求a2+b2+2c2+8ac+bc的最小值.A11918.(17分)已知a∈R,函数y=ax²+(3a+2)x+2a+3.(1)当a=1时,函数y=ax²+(3a+2)x+2a+3的图象与x轴交于A(x₁,0),B(x₂,0)两点，求x31+x32;(2)求关于x的不等式y≥1的解集.19.(17分)设A是由若干个正整数组成的集合，且存在3个不同的元素a，b，c∈A，使得a-b=b-c，则称A 为“等差集”.(1)若集合A=1,3,5,9,B⊆A,且B是“等差集”，用列举法表示所有满足条件的B；(2)若集合.A=1,m,m²―1是“等差集”，求m的值；(3)已知正整数n≥3,证明:{x,x²,x³,…,x"}不是“等差集”.【高一数学第4 页(共4 页)】 A1·数学参考答案1. D 3₃∉Q,-1∉N,N ⊆Z,Q ⊆R2. C 由-2<1,|-2|>|1|,知q 是假命题,且q 是全称量词命题.3. A 因为3=1×3=(--1)×(-3),所以A={-2,0,2,4}.4. B 取a=5,b=3,c=1,满足a+b>c,此时b+c<a,a,b,c 不可以构成三角形的三条边.由a,b,c 可以构成三角形的三条边,得a+b>c.故“a+b>c”是“a,b,c 可以构成三角形的三条边”的必要不充分条件.5. A 因为 1a +2b =1,所以 a +2b =(1a +2b)(a +2b )=5+2b a+2a b.又a>0,b>0,所以 2ba + 2ab ≥22b a⋅2ab =4,当且仅当a=b=3时，等号成立，故a+2b 的最小值为9.6. D 因为C 恰有1个真子集，所以C 中只有1个元素.联立方程组 {y =x 2+ax +1,y =2x ―3,整理得 x ²+(a ―2)x +4=0,则 (a ―2)²―16=0,解得a=-2或6.7. D 设每株多肉植物的售价降低x(x∈N)元，则这种多肉植物每天的总销售额为(30-x)(25+5x)元.由(30-x)(25+5x)≥1 250,得5≤x≤20,故每株这种多肉植物的最低售价为30-20=10元.8. B 如图，由题可知 {a +b +9m +x ―20,a +c +m +z ―21,b +c +m +s ―21,a +b +c +1>22,a +b +z ―12,x +9z +z =24,则 3m=63-2(a+b+c)-(x+y+z)=15,则m=5,从而3个兴趣小组都没参加的学生有45-(a+b+c)-(x+y+z)-m=4名.9. ABD 由题可知，A ，B ，D 中的对象具有确定性，可以构成集合，C 中的对象不具有确定性，不能构成集合.10. AB 由a +c a>b +c b,得 a +c a ―b +cb=b (a +c )―a (b +c )ab=c (b ―a )ab>0.因为a>b>0,所以c<0.11. BCD 由图可知a>0,二次函数 y =ax ²+bx +c 的图象与x 轴相交于(--1,0),(2,0)两点，则 {a ―b +c =0,4a +2b +c =0,整理得 {b =―a ,c =―2a ,则 a+b=0, abc>0,A 不正确,B 正确. 由【高一数学·参考答案第 1页(共4 页)】 ·A1·{4a―2b+c>0,9a+3b+c>0,得13a+b+2c>0,C正确.因为{b=―a,c=―2a,所以bx²―ax―c=―ax²―ax+2a>0,即x²+x―2<0,,解得-2<x<1,D正确.12.<a―b=10+2―26,因为( 10+2)2=12+45,(26)2=24,45<12(所以(10+2)2<(26)2,则10+2<26,从而a<b.13.8 由a+b,a,2=a²,2,0,得a=0或a=a².若a=0,则a²=0,，不符合集合元素的互异性.若a=a²,则a=0(舍去)或a=1,所以a+b=0,即b=-1,从而((a―b)³=8.14.―18nm+n ―2mm―n―4(m+n)―4(m―n)m+n―(m+n)+(m―n)m―n=3―[4(m―n) m+n +m+nm―n].因为m<n<0,所以4(m―n)m+n >0,m+nm―n>0,则4(m―n)m+n+m+nm―n≥24(m―n)m+n⋅m+nm―n=4，当且仅当m=3n时，等号成立，故的最大值为-（1）由a=2,得B={x|1<x<4}, ... 1分 (1)则或x≥4}. ... 3分 (3)因为A={x|-2<x<3},所以A∪B={x|-2<x<4}................................................5分（2）若B=∅,则a-1≥2a,解得a≤-1,满足B⊆A (7)若B≠∅,则由B⊆A,得分 (9)解得 (11)综上所述，a的取值范围为 (13)16.解:（1）由结论①正确,得分 (3)解得-6<m<2 (5)故当结论①正确时，m的取值范围为{m|-6<m<2}....................................6分（2）若m=-1,则原方程转化为-3=0,恒不成立. ... 7分 (7)若m≠-1,则由（m+1）x-3=0,得分 (8)从而解得 (10)当结论①正确，结论②不正确时， (12)当结论②正确,结论①不正确时,m≥2 (14)综上所述，当结论①，②中恰有一个正确时，m的取值范围为或m≥2}..........15 17.解分 (1)则 (4)当且仅当时，等号成立，故的最小值为₆ (6)（2）因为, (8)当且仅当a=b=c=1时,等号成立,... 9分 (9)所以分 (10) (12)当且仅当 ac+ bc=2时,等号成立,此时a=b=c=1, ... 14分 (14)所以的最小值为8………………………………………………………………………………15分18.解:(1)当a=1时,y=x²+5x+5.由题可知x₁,x₂;是方程x²+5x+5=0的两个实数根， (2)由{x21+5x1+5=0, x22+5x2+5=0,得{x 31=―5x21―5x1,x32=―5x22―5x2, 4分则x i+x32=―5(x21+x22)―5(x1+x2)=―5[(x1+x2)2―2x1x2]+25=―75+25=―50.6分(2)由y≥1,得ax²+(3a+2)x+2a+2≥0.当a=0时，不等式整理为………………………………………………………………………………………………………………………………………………………………………7分当a≠0时,令ax²+(3a+2)x+2a+2=(x+1)( ax+2a+2)=0,得x=---1或x=...............................................................................................................9分当a>0时,则原不等式的解集为或3x≥-1} (11)当--2<a<0时,―1<―2a+2a,则原不等式的解集为{x|―1≤x≤―2a+2a};当a=-2时,则原不等式的解集为{-1}；...............................................................15分当a<-2时,则原不等式的解集为 (17)【高一数学·参考答案第3页(共4页)】 ·A1·…13分1,3,5或1,5,9,………………………………………………………………………… (1)故满足条件的B可能是{1,3,5},{1,5,9},{1,3,5,9}...........................................4分（2）解:由A 是“等差集”,得, ... 5 分 (5)且m≥2,则 (6)（舍去）或m=2 (8)当m=2时,A={1,2,3}是“等差集”,故m=2 (9)（3）证明:假设{x,x²,x³, (10)则存在1≤i<j<k≤n,其中i,j,k∈N*,使得 (11)即则分 (12)因为1≤i<j<k≤n,所以k-i>j-i,从而k-i≥j-i+1,... 13分 (13)则2xʲ⁻ⁱ=1+xᵏ⁻ⁱ≥1+xʲ⁻ⁱ⁺¹, ……………………14分则分 (15)因为x≥2，所以从而2-x>0,即x<2, (16)不是“等差集” (17)【高一数学·参考答案第 4 页(共4页)】。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

河南省高一3月月考数学试题
姓名:________ 班级:________ 成绩:________
一、单选题 (共10题；共20分)
1. （2分） (2020高一下·忻州月考) 下列角位于第三象限的是（）
A .
B .
C .
D .
2. （2分） (2019高一上·涟水月考) 点是角的终边与单位圆的交点，则的值为（）
A .
B .
C .
D .
3. （2分） (2020高一上·滁州期末) 已知，(0, π)，则 =（）
A . 1
B .
C .
D . 1
4. （2分）等于（）
A . -
B .
C . -
D .
5. （2分） (2020高一上·宿州期末) 已知函数，则下列正确的是（）
A . 是周期为1的奇函数
B . 是周期为2的偶函数
C . 是周期为1的非奇非偶函数
D . 是周期为2的非奇非偶函数
6. （2分） (2019高一下·上海期中) 的值等于（）
A .
B .
C .
D .
7. （2分）给出以下命题：
①若、均为第一象限角，且，且；
②若函数的最小正周期是，则；
③函数是奇函数；
④函数的周期是；
⑤函数的值域是[0,2].
其中正确命题的个数为（）
A . 3
B . 2
C . 1
D . 0
8. （2分）函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜）的部分图象如图，且过点A(,0),B(0,-1)，则以下结论不正确的是（）
A . f（x）的图象关于直线x=- 对称
B . f（x）的图象关于点(.0)对称
C . f（x）在[- ,-]上是增函数
D . f（x）在[ ,]上是减函数
9. （2分）(2018·南阳模拟) 已知，则（）
A . 2
B .
C . -2
D . -
10. （2分）已知函数，下面结论错误的是（）
A . 函数的最小正周期为
B . 函数在区间上是增函数
C . 函数的图像关于直线x=0对称
D . 函数是奇函数
二、填空题 (共5题；共5分)
11. （1分）(2020·上海模拟) 在中，，则面积的最大值是________
12. （1分） (2019高一下·内蒙古期中) 的内角的对边分别为，已知
.则 ________
13. （1分）设扇形的周长为8cm，面积为4cm2 ，则扇形的圆心角的弧度数是________
14. （1分） (2019高一下·顺德期末) 一船自西向东匀速航行,上午10时到达一座灯塔的南偏西距塔64海里的处,下午2时到达这座灯塔的东南方向的处,则这只船的航行速度为________海里/小时．
15. （1分）设命题p：将函数f（x）=sin2x的图象向右平移个长度单位，所得图象经过点（，0）；
命题q：将函数f（x）=sin（2x+ ）的图象向左平移个单位，得到一个偶函数的图象，
则下列命题正确的序号是________．
①¬p为真；②q为假；③p∧q为假；④p∨q为真．
三、解答题 (共6题；共60分)
16. （5分）已知，求的值．
17. （10分） (2016高一下·龙岩期中) 已知函数f（x）=2sin（ωx+φ）（ω＞0，﹣＜φ＜）的部分图象如图所示；
（1）求ω，φ；
（2）将y=f（x）的图象向左平移θ（θ＞0）个单位长度，得到y=g（x）的图象，若y=g（x）图象的一个对称点为（，0），求θ的最小值．
（3）对任意的x∈[ ， ]时，方程f（x）=m有两个不等根，求m的取值范围．
18. （10分）已知sinα=，α∈（0，）．sinβ=，β是第二象限角．
（1）cos（α﹣β）；
（2）tan2α；
（3）sin（+β）的值．
19. （10分）(2019·安徽模拟) 已知函数的图象关于直线对称．
（1）求的最小正周期；
（2）求在上的单调递增区间；
（3）若，求．
20. （10分） (2019高一下·延边月考) 已知函数在区间
上单调，当时，取得最大值5，当时，取得最小值-1.
（1）求的解析式
（2）当时，函数有8个零点，求实数的取值范围。

21. （15分） (2020高三上·福建月考) 已知向量，向量，函数
.
（1）求函数在区间上的最大值和最小值以及取得最值时的值；
（2）求证：存在大于的正实数，使得不等式在区间有解.（其中为自然对数的底数）
参考答案一、单选题 (共10题；共20分)
答案：1-1、
考点：
解析：
答案：2-1、
考点：
解析：
答案：3-1、
考点：
解析：
答案：4-1、考点：
解析：
答案：5-1、考点：
解析：
答案：6-1、考点：
解析：
答案：7-1、考点：
解析：
答案：8-1、考点：
解析：
答案：9-1、考点：
解析：
答案：10-1、
考点：
解析：
二、填空题 (共5题；共5分)答案：11-1、
考点：
解析：
答案：12-1、
考点：
解析：
答案：13-1、考点：
解析：
答案：14-1、考点：
解析：
答案：15-1、
考点：
解析：
三、解答题 (共6题；共60分)
答案：16-1、
考点：
解析：
答案：17-1、
答案：17-2、
答案：17-3、
考点：
解析：
答案：18-1、
考点：
解析：
答案：19-1、答案：19-2、
答案：19-3、考点：
解析：
答案：20-1、
答案：20-2、考点：
解析：
答案：21-1、
答案：21-2、考点：
解析：。