二面角的求法(精华版)分享资料
二面角的求法公式

二面角的求法公式
二面角的求法有多种,以下是其中的一些:
1. 一般求法:先找到二面角的平面角,然后用量角器直接测量。
2. 法向量法:利用向量的数量积来求二面角。
设两个法向量分别为
$\mathbf{a}$ 和 $\mathbf{b}$,则二面角的大小为
$\arccos(\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \times
\mathbf{b}})$。
3. 平行向量法:利用向量的平行性质来求二面角。
设两个平行的向量分别为$\mathbf{a}$ 和 $\mathbf{b}$,则二面角的大小为
$\arccos(\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \times
\mathbf{b}})$。
4. 方程方法:利用空间几何的知识,建立二面角的方程,然后求解。
这些方法各有优缺点,具体使用哪种方法需要根据具体的情况来决定。
二面角的求法

P F A B E C D
规范训练三:
过正方形ABCD的顶点A作PA 平面ABCD,设 PA=AB=a,求平面PAB和平面PCD所成的二面角的大 小。
则∠ACB即为该二面角的平面角。
探 究 三
探究四:
例4:如图:直四棱柱ABCDA1B1C1D1,底面ABCD是菱形, AD=AA1 ,∠DAB=600,F为棱AA1 的中点。求:平面BFD1与平 面ABCD所成的二面角的大B
C
解法一:
如图:延长D1F交DA的延长线于点P, 连接PB,则直线PB就是平面BFD1与 平面ABCD的交线。 ∵ F是AA1的中点,∴可得A也是PD 的中点,∴AP=AB, 又∵∠ DAB=600,且底面ABCD是菱 形,∴可得正三角形ABD, 故 ∠DBA=600, ∵∠P=∠ABP=300, ∴∠DBP=900,即PB⊥DB; 又因为是直棱柱,∴DD1 ⊥ PB, ∴PB⊥面DD1B, 故 ∠DBD1就是二面角D1-PB-D的平 面角。 显然BD=AD=DD1, ∴∠DBD1=450。即 为所求.
D1 A1 F D A P B B1
C1
C
解法二:
如图:延长D1F交DA的延长线 于点P,连接PB,则直线PB就 是平面BFD1与平面ABCD的交 线; 因为是直棱柱,所以AA1 ⊥ 底面ABCD,过A做AE⊥PB,垂足 为E,连接EF, 由三垂线定理可知,EF⊥PB, ∴∠AEF即为二面角D1-PB-D的 平面角; 同解法一可知,等腰△APB, ∠P=300, Rt△APB中,可求 得AE= 1 ,(设四棱柱的棱长为 2)又AF= 1, ∴∠AEF=450,即 为所求。
一、忆一忆:
二面角是指从一条直线出发的 1、二面角的概 两个半平面所组成的图形; 念 平面角是指以二面角的棱上一 点为端点,在两个半平面内分别 二面角的平面角 做垂直于棱的两条射线,这两条 的概念 射线所成的角就叫做该二面角的 平面角。
二面角的多种求法

二面角的多种求法1.概念法例1:如图所示,在四面体ABCD 中,1AC AB ==,2CD BD ==,3AD =。
求二面角A BC D --的大小。
分析:四面体ABCD 的各个棱长都已经给出来了,这是一个典型的根据长度求角度的问题。
解:设线段BC 的中点是E ,接AE 和DE 。
根据已知的条件1AC AB ==,2CD BD ==,可以知道AE BC ⊥且DE BC ⊥。
又BC 是平面ABC 和平面DBC 的交线。
根据定义,可以得出:AED ∠即为二面角A BC D --的平面角。
可以求出32AE =,3DE =3AD =。
根据余弦定理知:22222233)372cos 243232AE DE ADAED AE DE+-+-∠==-⨯⨯⨯即二面角A BC D --的大小为7arccos4π-。
例2:如图所示,ABCD 是正方形,PB ABCD ⊥平面,1PB AB ==,求二面角A PD C --的大小。
解:作辅助线CE PD ⊥于点E ,连接AC 、AE 。
由于AD CD =,PA PC =,所以PAD PCD ≅三角形三角形。
即AE PD ⊥。
由于CE PD ⊥,所以AEC ∠即为所求的二面角的大小。
通过计算可以得到:2PC =3PD =,又1CD =,在三角形PCD 中可以计算得到63CE =。
由此可以得到:63AE CE ==,又2AC =。
由余弦定理:222222133cos 22223AE CE AC AEC AE AC +-+-∠===-⋅⋅即:23AEC π∠=。
2.空间变换法空间变换法指的是基本的空间方法,包括三垂线法、补角法、垂面法、切平面法等方法。
下面用例3介绍三垂线法、补角法和垂面法。
例3:如图所示,现有平面α和平面β,它们的交线是直线DE ,点F 在平面α内,点C 在平面β内。
求二面角F DE C --的大小。
分析:过点C 作辅助线CA 垂直于DE ,作CB 垂直于平面β于点B 。
二面角公式

高中数学二面角公式是:θ=π-α。
二面角一般都是在两个平面的相交线上,取恰当的点,经常是端点和中点。
过这个点分别在两平面做相交线的垂线,然后把两条垂线放到一个三角形中考虑。
有时也经常做两条垂线的平行线,使他们在一个更理想的三角形中。
由公式S射影=S斜面cosθ,作出二面角的平面角直接求出。
运用这一方法的关键是从图中找出斜面多边形和它在有关
平面上的射影,而且它们的面积容易求得。
也可以用解析几何的办法,把两平面的法向量n1,n2的坐标求出来。
然后根据n1·n2=|n1||n2|cosα,θ=α为两平面的夹角。
这里需要注意的是如果两个法向量都是垂直平面,指向两平面内,所求两平面的夹角θ=π-α。
二面角的通常求法:
1、由定义作出二面角的平面角;
2、作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角;
3、利用三垂线定理(逆定理)作出二面角的平面角;
4、空间坐标求二面角的大小。
二面角的三种求法

1 2 = 2 ,PO 2
2 ∴所求的二面角P-AB-C 的正切值为 2 所求的二面角 20:33
E
O
二面角的计算: 二面角的计算:
1、找到或作出二面角的平面角 、 2、证明 1中的角就是所求的角 、 3、计算出此角的大小 、
计算” 一“作”二“证”三“计算”
20:33
16
二面角
练习1:已知Rt△ 在平面α内 斜边AB在 练习 :已知 △ABC在平面 内,斜边 在30º的二 在平面 的二 面角α-AB-β的棱上,若AC=5,BC=12,求点 到平面 的棱上 面角 的棱 , ,求点C到平面 β的距离 。 的距离CO。 的距离
20:33
C
B
β
B
p α
O
ι
A
二面角
如图, 是二面角α棱上一点, 例 1.如图, 已知 P是二面角 AB-β棱上一点, 过 P分 如图 棱上一点 别 在 α 、 β 内 引 射 线 PM 、 PN , 且 ∠ MPN=60º ∠BPM=∠BPN=45º ,求此二面角的度数。 ∠ 求此二面角的度数。 C 在 α 解: PB上取不同于P 的一点O, M 在α内过O作OC⊥AB交PM于C, O P A 在β内作OD⊥AB交PN于D, B 连CD,可得 D N ∠COD是二面角α-AB-β的平面角 β 设PO = a ,∵∠BPM =∠BPN = 45º ∴CO=a, DO= a , PC = 2 a , PD 2 a C = 又∵∠MPN=60º ∴CD=PC = 2 a
C O
α β
B
A
D
O
练习2: 已知棱长为1正方体 正方体ABCD-A1B1C1D1, 求二面 练习 : 已知棱长为 正方体 的大小。 角C1-BD-B1的大小。
二面角的求法(总结)

2、三垂线定理、平面的 法向量。
探究准备: 答
二、想一想:
1、怎样做出二面 角的平面角?
:1、做二面角的平面角主 要有3种方法:
(1)、定义法:在棱上取一 点,在两个半平面内作垂直于 棱的2 条射线,这2条所夹 的 角; (2)、垂面法:做垂直于棱 的一个平面,这个平面与2个 半平面分别有一条交线,这2 条交线所成的角; (3)、三垂线法:过一个半 平面内一点(记为A)做另一 个半平面的一条垂线,过这个 垂足(记为B)再做棱的垂线, 记垂足为C,连接AC,则 ∠ACB即为该二面角的平面角。 α C α β
2 2
S
E A D C
B
议一议:刚才的证明过
程中,是用什么方法找到 二面角的平面角的? 请各小组讨论交流一下。
2
2
2
2
探究二:
试一试 例二:如图:直四棱柱ABCDA1B1C1D1,底面ABCD是菱形, AD=AA1 ,∠DAB=600,F为棱AA1的中 点。 求:平面BFD1与平面ABCD所 成的二面角的大小。
1D1C1B1A1(θ是所求二面角的平面角) 以下求面积略。
F
D
A B
C
点评:这种解法叫做“射影面积法”
在选择和填空题中有时候用起来会很 好
总一总:求二面角的方法你都
学会了哪些?每一种方法在使用 上要注意什么问题?
请同学们先自己思考,然后小 组内交流学习一下。
二面角的几种主要常用的求法:
1、垂面法。见例一和例二的解法一; 2、三垂线法。见例二的解法二; 3、射影面积法。见例二的解法三; 4、法向量夹角法。见例二的解法四。
A1 F A D1 B1 C1
D
B
C
要求:1、各人思考;2、小组讨论;
二面角的求法

解:以A为原点,如图 建立空间直角坐标系。
则:S 0, 0,1 , C 1,1, 0 , 1 D 0, , 0 , B 1, 0, 0 2
x
y
设平面SCD的法向量为n x, y, z
n SC , n SD n SC 0, n SD 0 1 SC 1,1, 1 , SD 0, , 1 2 x y z 0 xz y n 1, 2,1 z0 y 2z 2 1 平面SAB的法向量为AD 0, , 0 2
1 .确定F的位置,使得DF1 平面AB1F; 2 .当D1E 平面AB1F时,求二面角C1 EF A的大小。
z
A1 D1 B1 C1
A D F B
y
x
E
C
解:以A为坐标原点,建立空间直角坐标系A xyz
1 .设DF x, 则A 0, 0, 0 , B 1, 0, 0 , C 1,1, 0, D 0,1, 0 , A1 0, 0,1 ,
a
O B
于B,作AC⊥ 于C,面 过二面角内一点A作AB⊥ ABC交棱a于点O,则∠BOC就是二面角的平面角。 A A
C
a
A
B
O
a
O
B
二面角的求解步骤:
1、找到或作出二面角的平面角
2、证明 1中的角就是所求的角
3、计算出此角的大小
一“作”二“证”三“计算”
16
例1:已知正三角形ABC,PA⊥面ABC,且 PA=AB=a, 求二面角A-PC-B的正切值的大小。
1、定义法: 以二面角的棱a上任意一点O为端点,在两个面内
二面角的五种求法.doc
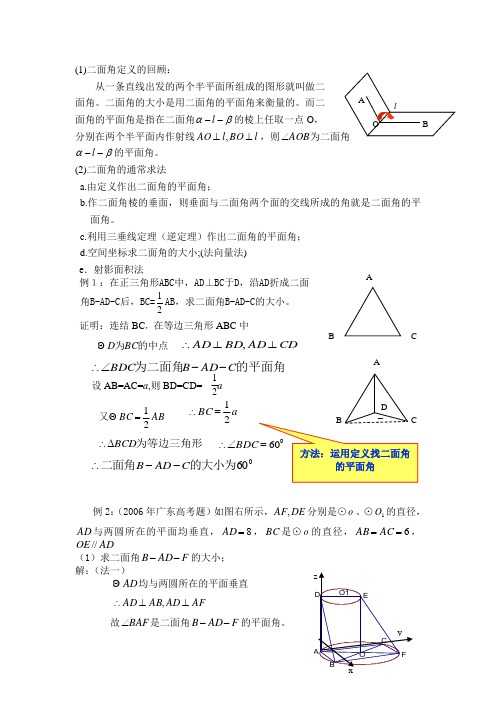
(1)二面角定义的回顾:从一条直线出发的两个半平面所组成的图形就叫做二 面角。
二面角的大小是用二面角的平面角来衡量的。
而二 面角的平面角是指在二面角βα--l 的棱上任取一点O , 分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠βα--l 的平面角。
(2)二面角的通常求法a.由定义作出二面角的平面角;b.作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角。
c.利用三垂线定理(逆定理)作出二面角的平面角;d.空间坐标求二面角的大小;(法向量法)e .射影面积法例1:在正三角形ABC 中,AD ⊥BC 于D ,沿AD 折成二面角B-AD-C 后,BC=21AB ,求二面角B-AD-C 的大小。
证明:连结BC ,在等边三角形ABC 中设AB=AC=a ,则BD=CD= a例2:(2006年广东高考题)如图右所示,DE AF ,分别是⊙o 、⊙1O 的直径,AD 与两圆所在的平面均垂直,8=AD ,BC 是⊙o的直径,6==AC AB ,AD OE //(1)求二面角F AD B --的大小; 解:(法一)AD 均与两圆所在的平面垂直AF AD AB AD ⊥⊥∴,故BAF ∠是二面角F AD B --的平面角。
ABCA的中点为BC D CDAD BD AD ⊥⊥∴,为二面角C AD B BDC --∠∴21ABBC 21= 又a BC 21=∴为等边三角形BCD ∆∴∠∴060的大小为二面角C AD B --∴BC 是⊙o 的直径,AB=AC∴ BC AO ⊥又AF 是⊙o 的直径∴四边形ABCF 是正方形∴BAF ∠=450即二面角F AD B --的大小为450(法二)运用空间向量坐标运算以A 为原点建立空间直角坐标系A-XYZ ,如图所示: 由(法一)可知:四边形ABCF 是正方形 则A (0,0,0),D (0,0,8) ,B (6,0,0),C (0,6,0),F (6,6,0))0,6,6(),0,6,0(-==∴→→BC AC O DA 圆⊥ ,AC DA ⊥∴又AB AC ⊥ ,→∴AC 是面DAB 的法向量 同理,O DA 圆⊥ , BC DA ⊥∴ 又BC AF ⊥ →∴BC 是面DAF 的法向量2226636||||,cos =⨯=⋅⋅>=<∴→→→→→→BC AC BCAC BC AC∵二面角F AD B--所成的角为锐角 ∴二面角F AD B --的大小为450***(法三)以A 为原点建立空间直角坐标系A-XYZ ,如图所示: 由(法一)可知:四边形ABCF 是正方形 则A (0,0,0),D (0,0,8) ,B (6,0,0),C (0,6,0),F (6,6,0))0,6,6(),8,0,0(),0,0,6(===∴→→→AF AD AB ,设),,(z y x n =→为面DAB 的法向量,则0,0=⋅=⋅→→→→AB n AD n即⎩⎨⎧==⇒⎩⎨⎧==00608y z y z ,令1=x ,则)0,0,1(=→n同理:设),,(z y x m =→为面DAF 的法向量,则)0,1,1(-=→m22211||||,cos =⨯=⋅⋅>=<∴→→→→→→m n mn m n ∵二面角F AD B --所成的角为锐角 ∴二面角F AD B --的大小为450***例3:射影面积法如图5,二面角l αβ--为锐二面角, △ABC 在半 平面α内, △ABC 在平面β内的射影为△A 1B 1C 1,那么二面角l αβ--的大小111 cos A B C ABCS S θθ∆∆=应满足.(思考例题2用射影面积法)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习1:正方体ABCD-A1B1C1D1中, E为棱AA1的中点,求平面EB1C和平面 ABCD所成的二面角。
D
cos SA1B1C 1
注意: 二面角的平面角必须满足:
1)角的顶点在棱上 (与顶点位置无关) 2)角的两边分别在两个面内 3)角的两边都要垂直于二面角的棱
二面角的平面角的范围: 0180
3
一、几何法:
1、定义法: 以二面角的棱a上任意一点O为端点,在两个面内
分别作垂直于a 的两条射线OA,OB,则∠AOB就 是此二面角的平面角。
S EB1C
A
C B
E D1
C1
A1
B1
练习2:在正方体AC1中,E,F分别是中 点,求截面A1ECF和底面ABCD所成的锐 二面角的大小。
D1 A1
E
C1
B1
G
DH
C
A
FB
DG C H
A FB
练习2:在正方体AC1中,E,F分别是中
点,求截面A1ECF和底面ABCD所成的锐
二面角的大小。
DG C
AD=
1 2
SA=AB=BC=1,
求面SCD与面SBA所成的二面角的大小.
z
解:以A为原点,如图 建立空间直角坐标系。
则:S0,0,1,C1,1,0,
D0, 12,0, B1,0,0
x
y 15
设 平 面 S C D 的 法 向 量 为 n x , y , z
nSC,nSD n•SC0,n•SD0
C1
∴ A1O⊥BD,C1O⊥BD
∴
OA1,OC1
即为二面角A1-BD-C1
A1
B1
的平面角。
cosO A 1,O C 1 O A 1O C 1
1 3
D
y
C
OA 1 OC1
A
O
∴
二面角A1-BD-C1的大小为 arccos
1 3
x
B
12
2、平面法向量法:
求二面角的大小,先求出两个半平面的法向 量的夹角,然后根据二面角与其大小相等或 互补求出二面角的大小。
2、三垂线法:在一个平面 内选一点A向另一平面 作垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足 为O, 连结AO,则∠AOB就是二面角的平面角。
3、垂面法: 过二面角内一点A作AB⊥于B,作AC⊥于C,面
ABC交棱a于点O,则∠BOC就是二面角的平面角。
a
A
A
O B
A
B
a O
C
O a
B
例1:已知正三角形ABC,PA⊥面ABC,且 PA=AB=a, 求二面角A-PC-B的大小。
m n
如图:二面角的大小等于-<m ,n>
13
2、平面法向量法:
求二面角的大小,先求出两个半平面的法向 量的夹角,然后根据二面角与其大小相等或 互补求出二面角的大小。
αm
n
β
如图:二面角的大小等于<m ,n>
14
例4:在底面是直角梯形的四棱锥S—ABCD
中,∠ABC=90°,SA⊥面ABCD,
D1 E
C1
A1
B1
A FEB
G
A1
C
D
A
F
C
B
cos SAFCG
S A1FCE
F
练习3:三棱锥P-ABC中,PA ⊥平面 ABC,PA=3,AC=4,PB=PC=BC (1)求二面角P-BC-A的大小; (2)求二面角A-PC-B的大小。
P D
cos SABC
SPBC
AE
C
B
二、向量法:
1、方向向量法:
三垂线法: 过B作BE⊥AC于E,过E作ED⊥PC于D,连结BD,
则∠BDE就是此二面角的平面角。
P
∵△ABC为正△,∴ BE=
3a 2
在Rt△PAC中,E为AC中点,
则DE= 2 a
D
4
E
在Rt△DEB中
A
C tan
∠
BDE=
BE DE
6
B
∴∠ BDE=arctan 6
几点说明:
⑴定义法是选择一个平面内的一点(一般为这个面的一个 顶点)向棱作垂线,再由垂足在另一个面内作棱的垂线。 此法得出的平面角在任意三角形中,所以不好计算,不是 我们首选的方法。
⑵三垂线法是从一个平面内选一点(一般为这个面的一个 顶点)向另一个面作垂线,再由垂足向棱作垂线,连结这 个点和棱上垂足。此法得出的平面角在直角三角形中,计 算简便,所以我们常用此法。
⑶垂面法需在二面角之间找一点向两面作垂线,因为这 一点不好选择,所以此法一般不用。
⑷以上三种方法作平面角都需写出作法、证明、指出平面角。
将二面角转化为二面角的两个面 的方向向量(在二面角的面内垂 直于二面角的棱且指向该面方向 的向量)所成的角。
D
B C l
A
二面角l 中,B、Cl, AB,CDD
BA,CD arccosBA•CD BA CD
11
例 3 : 在 正 方 体 A C 1 中 , 求 二 面 角 A 1 B D C 1 的 大 小 。
解:建立如图所示的空间直角坐标系D-xyz,
不妨设正方体的棱长为2,BD的中点为O,则
B(2,2,0),A1(2,0,2),C1(0,2,2),O(1,1,0)
DB2,2,0,
O1 A 2,0,21 ,1 ,01 , 1 ,2,
O C1 1,1,2
D D B B • • O O C A 1 1 2 2 1 ( 1 2 ) ( 2 1 1 ) 0 0 2 2 = 0 0D1 z
S C x 2y y1 z,1 z, 010 , SD y x 02z,z1 2 ,n1 1,2,1
平 面 S A B 的 法 向 量 为 A D 0 ,1 2,0
cosn,ADn•AD010 6
n•AD 61 3
1、掌握二面角的定义法; 2、掌握二面角的三垂线法; 3、掌握二面角的垂面法; 4、掌握二面角的射影面积法; 5、掌握二面角的向量法。
1
复 习: 二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角-AB-
A
C
B
二面角- l-
D
l
B
A
二面角C-AB- D
F
E
A
B
D
C
二面角C-AB-2E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
l
P
B
A
P1
B1
A1
二面角的大小用它的平面角的大小来度量 ∠APB= ∠A1P1B1
