+用户材料子程序实例-Johnson-Cook+金属本构模型
Johnson-Cook 材料模型及失效模型

;1.0E+06 3.0E+09 4.1+09 8.2E+09 4.3E+10 1.0
$ D1 D2 K1 K2 K3 FS 1 L7 b3 X/ ^6 z2 c# w" ?$ S
;0.01 1.0 1.6E+11 2.6E+11 3.6E+11 -0.1 % l) V& @; J/ g* d9 t
[2] G. Kay. Failure modeling of titanium 6Al-4V and aluminum 2024-T3 with the Johnson-Cook material model. Tech. Rep. DOT/FAA/AR-03/57. US department of Transportation, Federal Aviation Administration, September, 2003.
D = Σ (Δε/εf) (4)
式中
εf = [D1 + D2exp(D3σ*)][1+D4lnε*][1+D5T*] (5)
Δε - increment of effective plastic strain during an increment in loading
σ* - mean stress normalized by the effective stress
D1, D2, D3, D4, D5 - constants
当D = 1时发生失效。失效应变εf和损伤的累积,是平均应力、应变率和温度的函数。
材料 Ti-6Al-4V TitaMQUIST_CERAMICS
johnson—cook模型参数

《探寻Johnson-Cook模型参数的深度与广度》1. 引言在材料科学和工程领域中,Johnson-Cook模型是一种常用的材料本构模型,用于描述金属材料在高应变率和高温条件下的本构行为。
该模型的参数对于模拟和预测材料的力学性能至关重要。
本文将围绕Johnson-Cook模型参数展开讨论,深入探究其深度与广度。
2. Johnson-Cook模型简介Johnson-Cook模型是由Johnson和Cook在1983年提出,用于描述金属材料在动态加载和高温条件下的本构行为。
该模型基于实验数据,并考虑了材料的应变率、温度和应变硬化效应。
在Johnson-Cook模型中,参数包括A、B、n、C和m等,它们分别代表了材料的流动应力、应变硬化指数、热软化指数和材料的温度敏感性等重要性质。
3. 参数A的理解和研究3.1 参数A表示了材料的流动应力,在Johnson-Cook模型中具有重要的意义。
对于不同金属材料,参数A的取值不同,反映了材料的强度特征。
通过实验测试和数值模拟,研究人员可以获得不同条件下参数A的数值,从而深入理解材料的力学性能和变形行为。
3.2 个人观点:对于参数A的研究需要综合考虑材料的微观结构和宏观性能,通过建立参数A与其他参数的关联模型,可以更深入地理解材料的强度特征和动态响应。
4. 参数B、n的相关性研究4.1 参数B和n分别代表了材料的应变硬化指数和变形行为。
它们的取值对于描述材料的塑性变形过程至关重要,而且彼此之间存在一定的相关性。
通过实验测试和数值模拟,研究人员可以探究参数B、n 与材料微观结构和塑性变形特征之间的关联,以期深入地理解材料的本构行为。
4.2 个人观点:参数B和n的研究不仅需要考虑材料的单调拉伸试验数据,还需要结合压缩试验、扭转试验等多种试验数据,以全面、深入地评估材料的塑性变形特征和本构行为。
5. 参数C、m的温度敏感性研究5.1 参数C和m代表了材料的热软化指数和温度敏感性。
部分JOHNSON-COOK的材料本构参数(精)
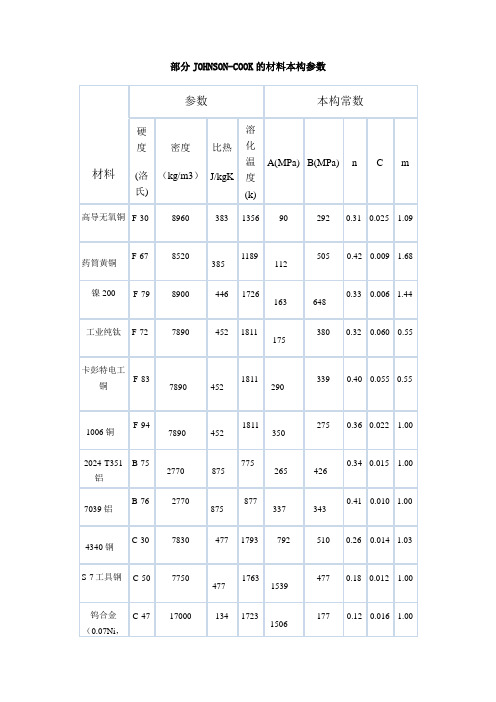
部分JOHNSON-COOK的材料本构参数0.03Fe )DU-75Ti C-45186004471473107911200.250.007 1.00•3#大中小发表于2007-9-24 14:30 只看该作者材料 2024-T3 Aluminum 的本构及失效参数材料2024-T3 AluminumA:369 MPa (53.517 ksi)B:684 MPa (99.202 ksi)n:0.73C:0.0083m:1.7D1:0.112D2:0.123D3:1.500D4:0.007D5:0.0本帖最近评分记录•wswu 贡献积分+1 感谢2007-9-27 07:44yema82811初级会员•个人空间•发短消息4#大中小发表于2007-9-24 14:49 只看该作者一些论文提及的JOHNSON COOK的参数一些论文提及的JOHNSON COOK的参数附件45号钢的动态力学性能研究.pdf (322.69 KB) 2007-9-24 14:49, 下载次数: 126本帖最近评分记录•加为好友•当前离线•wswu 贡献积分+1 感谢2007-9-27 07:45引用使用道具报告回复 TOPyema82811初级会员•个人空间•发短消息•加为好友•当前离线5#大中小发表于2007-9-24 14:51 只看该作者材料 Ti-6Al-4V Titanium材料Ti-6Al-4V TitaniumA:1098 MPa (159.246 ksi)B:1092 MPa (158.376 ksi)n:0.93C:0.014m:1.1D1:-0.090D2:0.270D3:0.480D4:0.014D5:3.870。
johnson-cook力学本构模型

johnson-cook力学本构模型约翰逊-库克力学本构模型是一种描述固体材料的非线性变形和失效行为的力学模型,广泛应用于机械工程、材料科学、爆炸动力学等领域。
约翰逊-库克力学本构模型是由美国犹他大学的两位研究人员约翰逊和库克于1983年提出的。
它是一种经验性本构模型,适用于金属等大变形材料的失效特点研究。
该模型的优点是描述了材料的很多失效行为,如塑性、蠕变、断裂等。
缺点是需要较多的材料实验数据,且选取参数较困难。
该本构模型的核心在于使用一个修正的强度函数,该函数可以反映材料的动态增强和动态软化特性。
其中,强度函数表示为:σ=ε[(A+Bεp)(1-Clnεp)+Dln(εp/εp0)](1+ε˙/ε˙0)^n其中,σ为应力,ε为应变,εp为塑性应变,A、B、C、D、n、ε˙0、εp0均为本构模型参数。
该强度函数的特点如下:1.描述了动态增强和动态软化特性。
随着应变率的增加,材料的强度增加,但塑性应变也随之增加,达到一定程度后,材料变脆并出现软化。
2.考虑了材料的压缩和拉伸特性。
A和B参数控制材料在拉伸和压缩下的应力响应。
3.考虑了材料的应变率效应。
n参数表示应变率对材料强度的影响程度。
在该本构模型中,还引入了力学损伤参数D和反应率参数C。
D表示材料的累积剪切变形量对材料强度降低的影响,C则描述了材料在应变程度超过某一界限时出现的软化过程。
该本构模型的参数选择需要依据材料实验数据,通过拟合实验结果来确定,要求较高的实验技术和分析能力。
同时,该本构模型适用于大变形材料的研究,对于其他类型材料的研究需要进一步改进和完善。
abaqus中johnson-cook本构模型理解 -回复

abaqus中johnson-cook本构模型理解-回复ABAQUS是一种常用的有限元分析软件,广泛应用于工程领域中的结构和材料分析。
在ABAQUS中,材料模型非常重要,因为它决定了结构或部件的力学行为。
本文将重点介绍ABAQUS中的Johnson-Cook本构模型,解释其原理和应用。
一、Johnson-Cook本构模型的基本原理Johnson-Cook本构模型是一种广泛用于金属材料的本构模型,特别适用于高速冲击、爆炸、冲压等工况下的材料行为分析。
该模型基于强化塑性理论并考虑了材料的塑性变形、热软化和应变速率效应。
1. 强化塑性理论:Johnson-Cook本构模型基于强化塑性理论,该理论假设材料的变形主要由两个独立的部分组成:塑性变形和硬化。
塑性变形是由材料中的晶格滑移和形变所引起的,而硬化则是由位错运动和相互作用引起的。
强化塑性理论提供了描述材料行为的基础。
2. 热软化效应:Johnson-Cook本构模型考虑了材料在高温条件下的热软化效应。
在高温下,材料的塑性变形会导致局部温度升高,从而引起局部软化。
这种软化效应可以通过引入热软化参数来描述。
3. 应变速率效应:Johnson-Cook本构模型还考虑了材料的应变速率效应,即材料的塑性行为会随着应变速率的增加而发生变化。
这是因为在高应变速率下,材料的塑性变形速率超过了晶格中位错的运动速度,从而导致材料的变形行为变得复杂。
二、Johnson-Cook本构模型的参数含义与确定方法Johnson-Cook本构模型的参数包括强度系数、表面硬化系数、形变硬化指数、热软化参数和应变速率敏感指数等。
这些参数的确定非常重要,直接影响着本构模型的准确性和预测能力。
一般来说,可以通过实验测试和数值拟合来确定这些参数。
1. 强度系数和表面硬化系数:强度系数表示材料的杨氏模量和屈服强度之间的关系,是描述材料硬度的参数;表面硬化系数用于描述材料的初始硬化过程。
这两个参数可以通过单轴材料拉伸试验获得,并使用试验数据进行拟合来确定。
abaqus中johnson-cook本构模型理解 -回复

abaqus中johnson-cook本构模型理解-回复Abaqus中Johnson-Cook本构模型理解引言:材料的本构模型是描述材料力学行为的数学方程。
在有限元分析中,本构模型可以用于模拟材料的变形和损伤行为,从而预测材料在不同加载条件下的响应。
Johnson-Cook本构模型是一种常用的本构模型,广泛应用于材料科学和工程领域。
本文将从基本原理开始,逐步解释和理解Abaqus 中Johnson-Cook本构模型。
1. 弹塑性本构模型首先需要了解的是,弹塑性本构模型是最基本的材料模型之一。
它基于线弹性理论,假设材料在小应变范围内具有弹性行为,而在大应变范围内表现出塑性行为。
弹塑性本构模型可以描述材料的应力-应变关系,并预测材料的弹性变形和塑性变形。
2. 材料的温度效应在考虑Johnson-Cook本构模型之前,还需要考虑材料的温度效应。
温度对材料力学行为的影响是复杂而重要的。
温度的增加可以引起材料的软化、蠕变和断裂等现象。
因此,在模拟材料行为时,必须考虑材料的温度效应,并选择适当的本构模型来描述。
3. Johnson-Cook本构模型的基本原理Johnson-Cook本构模型是一种经验模型,用于描述材料的塑性行为和温度效应。
它采用以下形式的应力-应变关系:σ= (A + B ε^n) (1 + C ln(ε˙/ε˙_0))^m (1 - T/T_m)^p其中,σ是材料的应力,ε是应变,ε˙是应变速率,T是材料的温度,A、B、C、n、m、p和T_m是需要通过实验来确定的材料参数。
4. 材料参数的确定为了使用Johnson-Cook本构模型,需要通过实验来确定材料参数。
这些参数通常由材料的拉伸实验和冲击实验等得到。
拉伸实验可以提供材料的应力-应变曲线,以及材料的屈服强度和断裂应变等信息。
冲击实验可以提供材料的应变率敏感性和断裂韧性等信息。
根据实验数据,可以使用不同的方法来确定Johnson-Cook本构模型的参数。
基于Johnson_Cook模型的TC16钛合金动态本构关系_杨扬
1 实验
实 验 材 料 是 钛 合 金 TC16 , 成 分 为 Ti-3%Al5%Mo-4.5%V(质量分数),组织类型为马氏体型α+β 态。8032型Instron液压实验机用于温度为293 K、应变 速率为0.001 /s的准静态下拉伸实验,试样参照国标 GB6397—86制备。
利用分离式Hopkinson压杆系统[13−14]在变形温度 范围为293~773 K、应变速率范围为4 623~15 550 /s内 冲击压缩加载;试样为圆柱型,应变速率为103数量级 时,试样尺寸为直径2 mm,高4 mm;应变速率为104 数量级时,试样直径和高都为2 mm。在较高应变速率 实验中,采用小尺寸试样可以在不大幅提高杆的速度 情况下,提高试样的应变,从而提高试样的应变速率。 该系统可以控制应变速率和应变,并可进行高达 900 ℃的高温实验。同时它可以消除紧随拉伸波后的 第二个压缩入射波,避免试样受到多次冲击压缩。在 做高温实验时,入射杆和透射杆远离试样,仅对试样 加温。由于没有附加的第二次冲击压缩,该系统同样 可以进行在高应变速率和不同温度下的等温实验。
图 2 不同条件下 TC16 的真应力—真应变曲线 Fig.2 True stress—true strain curves for TC16 under different conditions
2.2 本构模型的确立及参数获取 2.2.1 确立本构模型
目 前 常 用 的 热 - 粘 塑 性 本 构 模 型 主 要 有 [15] : Johnson-Cook模型、Zerrilli-Armstrong模型、FollansbeeKocks模型及Bodner-Paton模型等。其中Bodner-Paton 本构模型将总应变张量分为弹性和塑性两部分,弹性
JOHNSONCOOK资料及一些材料参数
JOHNSONCOOK资料及一些材料参数Johnson Cook模型是一种常用的材料本构模型,广泛应用于模拟高速冲击和爆炸等复杂加载条件下的材料行为。
下面将介绍Johnson Cook模型的相关资料和一些材料参数。
Johnson Cook资料:Johnson Cook模型由Johnson、Cook等人在1983年提出,主要用于预测材料在高应变率和高温条件下的本构行为。
该模型可以描述材料的弹塑性行为、变形硬化和动态效应。
材料参数:1. 体积塑性应变(Volumetric Plastic Strain):材料在加载过程中发生塑性变形的体积分数。
2. 动态变形硬化参数(Dynamic Strain Hardening Coefficient):描述材料在动态加载下的硬化行为。
3. 温度变形硬化参数(Temperature Strain Hardening Coefficient):描述材料在高温下的变形硬化行为。
4. 动态变形软化参数(Dynamic Strain Softening Coefficient):描述材料在动态加载下的软化行为。
5. 温度软化参数(Temperature Softening Coefficient):描述材料在高温下的软化行为。
6. 强化系数(Strain-Rate Hardening Exponent):描述材料的强化行为。
7.常数A和B:用于描述材料的流动应力曲线。
以上的材料参数需要通过试验数据或其他可靠途径进行测量或者估算。
一般来说,可以使用高速拉伸、压缩或者冲击试验来获得涉及材料的动态和高应变率加载条件下的数据。
除此之外,还需要在模型中输入材料的温度和应变率等参数,以准确描述材料的行为。
Johnson Cook模型的应用广泛,包括高速碰撞、爆炸冲击、金属成型等领域。
通过合理地选择和确定材料参数,可以准确地模拟材料在复杂加载条件下的变形行为和破坏过程,为工程设计和分析提供参考依据。
+用户材料子程序实例-Johnson-Cook+金属本构模型
根据这一估计,选择输入应力脉冲的持续时间 Ts = 2.0 × 10−4 s,上升时间 tr = 3.0 ×10−5 s。 经过若干次试算, 对输入应力脉冲的波形进行了适当的调整, 使试件中产生较均匀的应变率。 最后输入应力脉冲的波形如图 3 所示:
PROPS ( NPROPS )
材料常数矩阵,矩阵中元素的数值对应于关键字“*USER MATERIAL”下面的数据行。
SSE , SPD , SCD
分别定义每一增量步的弹性应变能,塑性耗散和蠕变耗散。它们对计算结果没有影响,仅仅
-3-
Back
作为能量输出。 其他变量:
STRAN ( NTENS ) :应变矩阵; DSTRAN ( NTENS ) :应变增量矩阵;
σ = ( A + Bε n ) 1 + C ln 1 +
& ε *m (1 − T ) &0 ε
并使参考应变率 ε&0 = 1 ,这样公式中的 A 即为材料的静态屈服应力。公式中包含 A, B, n, C , m 五个参 数,需要通过实验来确定。 2 ABAQUS 用户材料子程序 用户材料子程序( User-defined Material Mechanical Behavior ,简称 UMAT )通过与 ABAQUS 主求解程序的接口实现与 ABAQUS 的数据交流。在输入文件中,使用关键字“*USER MATERIAL”表示定义用户材料属性。 子程序概况与接口 UMAT 子程序具有强大的功能,使用 UMAT 子程序: (1) 可以定义材料的本构关系,使用 ABAQUS 材料库中没有包含的材料进行计算,扩充程序 功能。
-6-
C
M
2.7×103
johnson-cook本构方程
johnson-cook本构方程Johnson-Cook本构方程是一种用于描述材料塑性行为的经验模型,在机械材料力学分析中被广泛应用。
本构方程用于描述材料的应力-应变关系,特别适用于高温下变形和失效行为的描述,如金属加工过程中的塑性变形、冲击、爆炸以及动态加载等。
Johnson-Cook方程可以用以下形式表示:$$\sigma = (A + B \cdot \varepsilon^n) \cdot (1 + C \cdot\ln(\dot{\varepsilon_{\text{p}}})) \cdot \left(1 - T^n\right)$$其中,$\sigma$ 是材料的真实应力,$\varepsilon$ 是真实应变,$\dot{\varepsilon_\text{p}}$ 是有效塑性应变速率,$T$ 是材料的温度,$A$、$B$、$C$、$n$ 是方程的参数。
$A$、$B$、$C$是与材料性质相关的常数,可以通过实验测试来确定。
$n$是描述材料的硬化指数,表示应力与应变之间的关系。
$T$是描述温度对材料塑性行为的影响的参数。
在Johnson-Cook方程中,$B \cdot \varepsilon^n$ 部分表示材料的弹性行为,$A$ 是材料的流动应力,$C \cdot\ln(\dot{\varepsilon_{\text{p}}})$ 部分表示材料的动态增强或软化行为,$1 - T^n$ 部分表示材料在高温下的流变特性。
该方程的提出是基于大量试验数据的统计分析,通过拟合实验数据来确定其参数。
Johnson-Cook本构方程具有一定的适用范围,通常适用于金属材料的高速塑性变形行为,并在许多实际应用中取得了良好的结果。
在实际应用中,需要根据具体材料和试验数据来确定Johnson-Cook方程的参数。
可以通过实验测试如拉伸实验、压缩实验和冲击实验来获取材料的应力-应变数据,然后对实验数据进行曲线拟合来确定方程的参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cd =
E
ρ
其中 E 为材料弹性模量, ρ 为材料密度。由此可以计算输入应力波在压杆中的传播速度为 Cd = 5048 m/s。 要求在入力杆应力波的输入端不能出现入射波和反射波的重叠,也就是说在输入应力脉冲的 时间内,应力波的传播距离不应超过两倍的杆长,即:
Ts <
2L 2 = ≈ 4.0 ×10−4 ( s ) Cd 5048
-5-
1 杨氏模量 1-6 弹性应变
2 泊松比
3 塑性耗散比 7-12 塑性应变
4 A
5 B
6 n 13
7 C
8 M
等效塑性应变
Back
ABAQUS 软件 2003 年度用户年会论文集
图2
二维轴对称有限元模型 表 2 模型信息
模 二维 模 型 性 质 数 值
型 入力杆 试件 出力杆
尺寸[mm] (Φ ×L) 25×1000 18×22 25×100件 2003 年度用户年会论文集
(2) 几乎可以用于力学行为分析的任何分析过程, 几乎可以把用户材料属性赋予 ABAQUS 中 的任何单元; (3) 必须在 UMAT 中提供材料本构模型的雅可比(Jacobian)矩阵,即应力增量对应变增量 的变化率。 (4) 可以和用户子程序“USDFLD”联合使用,通过“USDFLD”重新定义单元每一物质点上传 递到 UMAT 中场变量的数值。 由于主程序与 UMAT 之间存在数据传递,甚至共用一些变量,因此必须遵守有关 UMAT 的 书写格式,UMAT 中常用的变量在文件开头予以定义,通常格式为: SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD, 1 RPL,DDSDDT,DRPLDE,DRPLDT, 2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME, 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT, 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,KSTEP,KINC) C INCLUDE 'ABA_PARAM.INC' C CHARACTER*80 CMNAME DIMENSION STRESS(NTENS),STATEV(NSTATV), 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS), 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1), 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3)
σ = ( A + Bε n ) 1 + C ln 1 +
& ε *m (1 − T ) &0 ε
并使参考应变率 ε&0 = 1 ,这样公式中的 A 即为材料的静态屈服应力。公式中包含 A, B, n, C , m 五个参 数,需要通过实验来确定。 2 ABAQUS 用户材料子程序 用户材料子程序( User-defined Material Mechanical Behavior ,简称 UMAT )通过与 ABAQUS 主求解程序的接口实现与 ABAQUS 的数据交流。在输入文件中,使用关键字“*USER MATERIAL”表示定义用户材料属性。 子程序概况与接口 UMAT 子程序具有强大的功能,使用 UMAT 子程序: (1) 可以定义材料的本构关系,使用 ABAQUS 材料库中没有包含的材料进行计算,扩充程序 功能。
-4-
Back
ABAQUS 软件 2003 年度用户年会论文集
图 1 UMAT 流程图 表 1 UMAT 材料常数 PROPS 物理性质 STATEV 变量意义 3 SHPB 实验的有限元模拟 模型的简化与有限元网格 为了不使模型过于庞大,对模型进行了一些简化。首先,改变入力杆和出力杆的尺寸,长度 由原来的 3040mm 减小为 1000mm,直径增加到 25mm,试件的长度和直径也分别变化为 22mm 和 18mm。这样不仅优化了网格的质量,还成倍地减小了模型的规模,其带来的负面影响就是试 件能达到的应变将降低。另外,由于撞击杆仅仅起到产生应力脉冲的作用,在数值模型中没必要 考虑撞击杆,取代的方法是直接在入力杆的输入端施加均布的应力脉冲。 考虑到实验装置的对称性,也做了一些简化。整个实验装置以及载荷等都是关于杆的中心线 轴对称的,所以可以使用轴对称单元进行二维分析。 二维轴对称模型如图 2 所示。在模型中,对试件以及入力杆,出力杆和试件接触的部分进行 了局部网格加密,这样的网格划分可以取得比较经济的结果。
单元类型 CAX4 CAX4 CAX4
单元个数 530 160 530
总节点 数
总单元数
1475
1220
材料定义 入力杆和出力杆使用线弹性材料,弹性模量和泊松比分别为 200GPa 和 0.3,密度为 7.85×103 kg/m3。试件采用用户在 UMAT 中自定义材料,材料参数如表 3 所示,其中 Johnson-Cook 模型 中参数的数值来源于前面的数值拟合程序。 表 3 试件的材料定义 密度 [Kg/m3 ] 杨氏模 量 [MPa] 泊 松 比 Johnson-Cook 模型参数 A [MPa ] 66.56 2 B [MPa] 108.85 3
是一个 NTENS 维的方阵, 称作雅可比矩阵,∂∆σ / ∂∆ε ,∆σ 是应力的增量,∆ε 是应变的增量,
DDSDDE ( I , J ) 表示增量步结束时第 J 个应变分量的改变引起的第 I 个应力分量的变化。 通常雅可
比是一个对称矩阵,除非在“*USER MATERIAL”语句中加入了“UNSYMM”参数。
STRESS ( NTENS )
应力张量矩阵,对应 NDI 个直接分量和 NSHR 个剪切分量。在增量步的开始,应力张量矩阵 中的数值通过 UMAT 和主程序之间的接口传递到 UMAT 中,在增量步的结束 UMAT 将对应力 张量矩阵更新。对于包含刚体转动的有限应变问题,一个增量步调用 UMAT 之前就已经对应力 张量的进行了刚体转动,因此在 UMAT 中只需处理应力张量的共旋部分。UMAT 中应力张量的 度量为柯西(真实)应力。
Back
ABAQUS 软件 2003 年度用户年会论文集
ABAQUS/Standard 用户材料子程序实例
-Johnson-Cook 金属本构模型 卢剑锋 庄茁* 张帆 清华大学工程力学系 北京 100084
摘要:用户材料子程序是 ABAQUS 提供给用户定义自己的材料属性的 Fortran 程序接口,使用 户能使用 ABAQUS 材料库中没有定义的材料模型。 ABAQUS 中自有的 Johnson-Cook 模型只能应用于显式 ABAQUS/Explicit 程序中,而我们 希望能在隐式 ABAQUS/Standard 程序中更精确的实现本构积分,而且应用 Johnson-Cook 模型 的修正形式。这就需要通过 ABAQUS/Standard 的用户材料子程序 UMAT 编程实现。在 UMAT 编程中使用了率相关塑性理论以及完全隐式的应力更新算法。 1 Johnson-Cook 强化模型简介 Johnson-Cook(JC)模型用来模拟高应变率下的金属材料。JC 强化模型表示为三项的乘积, 分别反映了应变硬化,应变率硬化和温度软化。这里使用 JC 模型的修正形式:
STATEV ( NSTATEV )
用于存储状态变量的矩阵, 在增量步开始时将数值传递到 UMAT 中。 也可在子程序 USDFLD 或 UEXPAN 中先更新数据,然后增量步开始时将更新后的数据传递到 UMAT 中。在增量步的结 束必须更新状态变量矩阵中的数据。 和应力张量矩阵不同的是:对于有限应变问题,除了材料本构行为引起的数据更新以外,状 态变量矩阵中的任何矢量或者张量都必须通过旋转来考虑材料的刚体运动。 状态变量矩阵的维数,等于关键字 “*DEPVAR” 定义的数值。状态变量矩阵的维数通过 ABAQUS 输入文件中的关键字“*DEPVAR”定义,关键字下面数据行的数值即为状态变量矩阵的 维数。 材料常数的个数,等于关键字“*USER MATERIAL”中“CONSTANTS”常数设定的值。
根据这一估计,选择输入应力脉冲的持续时间 Ts = 2.0 × 10−4 s,上升时间 tr = 3.0 ×10−5 s。 经过若干次试算, 对输入应力脉冲的波形进行了适当的调整, 使试件中产生较均匀的应变率。 最后输入应力脉冲的波形如图 3 所示:
user coding to define DDSDDE, STRESS, STATEV, SSE, SPD, SCD and, if necessary, RPL, DDSDDT, DRPLDE, DRPLDT, PNEWDT
RETURN END UMAT 中的应力矩阵、应变矩阵以及矩阵 DDSDDE , DDSDDT , DRPLDE 等,都是直接分
-2-
Back
ABAQUS 软件 2003 年度用户年会论文集
量存储在前,剪切分量存储在后。直接分量有 NDI 个,剪切分量有 NSHR 个。各分量之间的顺序 根据单元自由度的不同有一些差异,所以编写 UMAT 时要考虑到所使用单元的类别。下面对 UMAT 中用到的一些变量进行说明:
DDSDDE ( NTENS , NTENS )
-6-
n
C
M
2.7×103
68.0×103
0.33
0.23 8
0.029
0.5
Back
边界条件
ABAQUS 软件 2003 年度用户年会论文集
为了保证 SHPB 实验的要求,在二维模型中施加了必要的边界条件。在对称轴上施加了对称 性边界条件,同时保证压杆和试件可以沿轴线方向自由无约束的运动。压杆和试件之间的接触为 硬接触,光滑无摩擦。 为了确定输入应力脉冲的时间,进行了简单的计算。弹性材料中纵波波速的计算公式为:
