材料力学ch3-拉压变形
合集下载
材料力学第3章 轴向拉压变形
Fy 0 :FN1 sin 30 FN3 sin 30 F
(2) 变形协调方程
Δl2 Δl1 Δl3 Δl2 tan30 sin 30 sin 30 tan30
秦飞 编著《材料力学》 第3章 轴向拉压变形
31
3.4 拉压杆静不定问题的解法
例题3-5
(3) 利用物性关系，用力表示变形协调方程
切
B点水平位移：
线 代
圆
Fa
弧
Bx BB1 l1 EA ()
B点铅垂位移：
By
BB'
l2 sin 45
l1
tan
45
(1
2
2) Fa EA
()
秦飞 编著《材料力学》 第3章 轴向拉压变形
19
3.3 桁架的节点位移
例题3-3
图示托架，由横梁AB与斜撑杆CD所组成，并承受集中载荷
2
3.1拉压杆的轴向变形与横向变形
轴向应变: l 胡克定律： FN
l
E EA
所以得到： l FNl EA
（拉压杆胡克定律）
l FNl EA
EA为拉压刚度，只与材料和横截面面积有关。
秦飞 编著《材料力学》 第3章 轴向拉压变形
3
3.1拉压杆的轴向变形与横向变形
(2)补充方程-变形协调方程(compatibility equation)
l1
tan
l2
sin
l3
秦飞 编著《材料力学》 第3章 轴向拉压变形
25
3.4 拉压杆静不定问题 解法
（3）物性（物理）关系
l1
FN1l1 E1 A1
(2) 变形协调方程
Δl2 Δl1 Δl3 Δl2 tan30 sin 30 sin 30 tan30
秦飞 编著《材料力学》 第3章 轴向拉压变形
31
3.4 拉压杆静不定问题的解法
例题3-5
(3) 利用物性关系，用力表示变形协调方程
切
B点水平位移：
线 代
圆
Fa
弧
Bx BB1 l1 EA ()
B点铅垂位移：
By
BB'
l2 sin 45
l1
tan
45
(1
2
2) Fa EA
()
秦飞 编著《材料力学》 第3章 轴向拉压变形
19
3.3 桁架的节点位移
例题3-3
图示托架，由横梁AB与斜撑杆CD所组成，并承受集中载荷
2
3.1拉压杆的轴向变形与横向变形
轴向应变: l 胡克定律： FN
l
E EA
所以得到： l FNl EA
（拉压杆胡克定律）
l FNl EA
EA为拉压刚度，只与材料和横截面面积有关。
秦飞 编著《材料力学》 第3章 轴向拉压变形
3
3.1拉压杆的轴向变形与横向变形
(2)补充方程-变形协调方程(compatibility equation)
l1
tan
l2
sin
l3
秦飞 编著《材料力学》 第3章 轴向拉压变形
25
3.4 拉压杆静不定问题 解法
（3）物性（物理）关系
l1
FN1l1 E1 A1
工程材料力学第四章轴向拉压杆的变形
§4-5 轴向拉(压)杆的变形·胡克定律
拉(压)杆的纵向变形 （轴向变形） 基本情况下(等直杆，两端受轴向力)：
纵向总变形Δl = l1-l （反映绝对变形量）
l 纵向线应变 （反映变形程度） l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响，则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律，即
ν
亦即
- n
低碳钢(Q235)：n = 0.24~0.28。
7
思考：等直杆受力如图，已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB，ΔlBC，ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系？
uB L1
22
作业：4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式： l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下，当应力不超过材料的比例极限时，
拉(压)杆的纵向变形 （轴向变形） 基本情况下(等直杆，两端受轴向力)：
纵向总变形Δl = l1-l （反映绝对变形量）
l 纵向线应变 （反映变形程度） l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响，则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律，即
ν
亦即
- n
低碳钢(Q235)：n = 0.24~0.28。
7
思考：等直杆受力如图，已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB，ΔlBC，ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系？
uB L1
22
作业：4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式： l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下，当应力不超过材料的比例极限时，
《材料力学》第2章轴向拉(压)变形习题解答
其方向。 解：斜截面上的正应力与切应力的公式为：
ασσα20cos = αστα2sin 2 = 式中，MPa mm N A N 1001001000020===σ，把α的数值代入以上二式得：
[习题 2-7] 一根等直杆受力如图所示。已知杆的横截面面积 A 和材料的弹性模量 E 。试作轴力图，并求杆端点 D 的位移。 解： （1）作轴力图
[习题 2-9] 一根直径 mm d 16=、长 m l 3=的圆截面杆，承受轴 向拉力 kN F 30=，其伸长为 mm l 2.2=?。试求杆横截面上的应 力与材料的弹性模量 E 。 解：（1）求杆件横截面上的应力 MPa mm N A N 3.1491614.34 110302 23=???==σ （2）求弹性模量 因为：EA Nl l = ?， 所以：GPa MPa l l l A l N E 6.203)(9.2035902 .23000 3.149==?=??=???=σ。 [习题 2-10] （1）试证明受轴向拉伸（压缩）的圆截面杆横截 面沿圆周方向的线应变 s ε等于直径方向的线应变 d ε。 （2）一根直径为 mm d 10=的圆截面杆，在轴向力 F 作用下，直 径减小了 0.0025mm 。如材料 的弹性模量 GPa E 210=，泊松比 3.0=ν，试求该轴向拉力 F 。 （3）空心圆截面杆，外直径 mm D 120=，内直径 mm d 60=，材 料的泊松比 3.0=ν。当其轴向拉伸时，已知纵向线应变 001.0=， 试求其变形后的壁厚。 解：（1）证明 d s εε= 在圆形截面上取一点 A ，连结圆心 O 与 A 点，则 OA 即代表直 径方向。过 A 点作一条直线 AC 垂直于 OA ，则 AC 方向代表圆周方向。νεεε-==AC s（泊
第一章 拉压变形
应力的国际单位为N/m2 （帕斯卡） 1N/m2=1Pa 1MPa=106Pa＝1N/mm2
1GPa=109Pa
轴向拉伸实验:
P P
P
P
平截面假设：原为平面的横截面在杆变形后仍为平面
杆内纵向纤维的伸长量是相同的，或者说横截面 上每一点的伸长量是相同的
根据前面的实验，我们可以得出结论：
即横截面上每一点存在相同的拉力
压缩——压应力，为负值，方向指向所在截面。 公式的使用条件 (1) 轴向拉压杆 (2) 除外力作用点附近以外其它各点处。 （范围：不超过杆的横向尺寸）
圣维南原理（Saint-Venant's principle ）
对于作用在物体边界上一小块表面上的外力系 可以用静力等效（主矢量、主矩相同）并且作用于 同一小块表面上的外力系替换，这种替换造成的区 别仅在离该小块表面的近处是显著的，而在较远处 的影响可以忽略。
注意
E
----胡克定律
①当各段的轴力为常量时——
FNi Li DL DL1 DL2 DL3 EA i
②当轴力为x的函数时 N=N(x)——
DL dDL1 dDL2 dDL3
L
FN ( x)dx EA
使用公式的时，轴力一定要代入其正、负号。 （3）、使用条件：轴向拉压杆，弹性范围内工作。
例
作图示杆件的轴力图，求杆件的应力。
1 30 60kN 2 20 40kN 2 60 3 4 35 30kN
FN1 0
50kN
FN 2 60kN FN 3 20kN FN4 50kN
1
3
4 50
FN kN
+
材料力学 杆件的变形计算
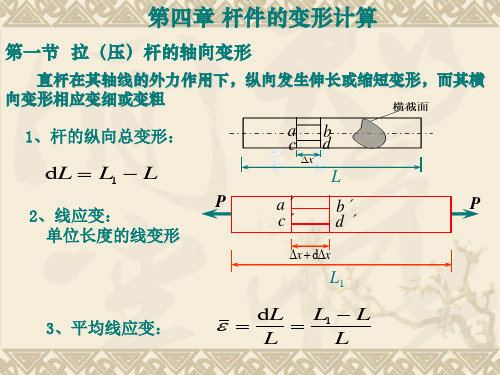
例题4-2: 已知：l = 54 mm ，di = 15.3 mm，E＝200 GPa， ν = 0.3，拧紧后，△l ＝0.04 mm。 试求：(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解：1) 求横截面正应力 ：
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ，di = 15.3 mm， E＝200 GPa， ν = 0.3， △l ＝0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N（x） N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移： 点总位移：
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段， 综合两段，最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆， 图示一等直圆杆，已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2）ϕ AC
材料力学课件-第三章-轴向拉压变形
Δ
F
f
o
d
A
d
•弹性体功能原理：Vε W ,
f df
• 拉压杆应变能
2 FN l V ε 2 EA
Page28
BUAA
MECHANICS OF MATERIALS
*非线性弹性材料
F
f
•外力功计算
W fd
0
F W 2
•功能原理是否成立? •应变能如何计算计算?
dx
dz
dy
x
•单向受力体应变能
V v dxdydz dxdydz 2E
2
z
单向受力
Page30
BUAA
MECHANICS OF MATERIALS
2 dxdydz •单向受力体应变能 V v dxdydz 2E FN ( x ) •拉压杆 (x)= , dydz A A 2 FN ( x ) V dx （变力变截面杆） y 2 EA( x ) l 2 FN l dx （常应力等直杆） V dz 2 EA •纯剪应变能密度 dy dxdz dy dxdydz dVε 2 2 2 1 2 z v G 纯剪切
BUAA
MECHANICS OF MATERIALS
第三章
§3-1 §3-2 §3-3 §3-4
§3-5 §3-6
轴向拉压变形
引言 拉压杆的变形与叠加原理 桁架的节点位移 拉压与剪切应变能
简单拉压静不定问题 热应力与预应力
Page1
BUAA
MECHANICS OF MATERIALS
本章主要研究:
Page7
材料力学组合变形的强度计算第2节 拉压与弯曲的组合变形
=
+
=
1
F1 A
+
2
M max Wz
4）强度计算
因危险点的应力是单向应力状态，所以其强度
条件为：
max
F1 A
M max Wz
[ ]
若为F1 压力，则危险截面上、下边缘处的正应
力分别为：
max
F1 A
M max Wz
，
m
in
F1 A
M max Wz
此时，危险截面的下边缘上的各点是危险点，
查附表，选两 根 18a 槽钢
注意 检验： max 144 MPa [ ] 140 MPa
虽然最大应力大于许用应力，但其值不超过许 用应力的5%，在工程上是允许的。
补充例 如图所示的钩头螺栓中，若已知螺纹内径 d =10mm，偏心距e =12mm，载荷F =1kN，许用应力
[ ]=140MPa 。试校核螺栓杆的强度。
为压应力。它的强度条件为：
max min
F1 A
Mmax Wz
[ ]
例9-1 夹具如图示，已知 F 2.0 kN ，l 60 mm ， b 10 mm，h 22 mm。材料许用正应力[ ] 160 MPa 。
试校核夹具竖杆的强度。
解：（1）外力分析
竖
夹具竖杆所受载荷是偏心载荷， 杆
F e Wz
135MPa
[ ]
b=1.0m，F=36.0kN，AB梁材料的许用应力[ ]=140
MPa。试确定AB梁槽钢的型号。
解： 1）外力分析
n
《材料力学》第2章 轴向拉压变形 习题解
第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a ）解：（1）求指定截面上的轴力 FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。
（b ）解：（1）求指定截面上的轴力 FN 211=-2222=+-=-F F N （2）作轴力图FF F F N =+-=-2233 轴力图如图所示。
（c ）解：（1）求指定截面上的轴力 FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=- 轴力图如图所示。
（d ）解：（1）求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图 中间段的轴力方程为： x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
2400mm A =解：（1）求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
21200mm A =22300mm A =23400mm A =解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FN2 F2
F2 ( l1 l2 ) F1l1 ( l )分段 EA EA
2. 分解载荷法
F2 ( l1 l2F ) ( lF1 l1 l ) F l 1 1 )分段 l 2 1 2 lF1( l F2 EA EA EA EA
( l )分解载荷 lF1 lF2
FN2 F ( 压缩)
FN1 l1 2F 2l 2Fl ( 伸长) l1 EA E1 A1 EA
FN2 l2 Fl l 2 (缩短) E2 A2 EA
2. 作图法求节点位移 圆弧法 作圆弧A1A’、A2A’ 切线代圆弧法 将圆弧A1A’用 其切线A1A3代替 3. 节点位移计算
l
A1
B
A
l f A l cos a l tg a sin a AA cos a
(l l ) A1 B A1 A
切线代圆弧
节点位移分析
图示桁架，试求节点 A 的水平与铅垂位移， 已知 ：E1A1= E2A2=EA，l2=l
1. 轴力与变形分析
FN1 2F ( 拉伸)
横截面内任一点， 任意面内方向上的应变
横向变形与泊松比 泊松比
'
试验表明：在比例极限内，’ ，并异号
－泊松比 (横向变形系数）
Poisson’s Ratio
0 0.5
• 对于绝大多数各向同性材料
• 弹性理论证明： 等温下各向同性线弹性材料 1 0.5
线弹性杆的拉压应变能V来自ε WF l V ε 2 EA
2 N
拉压与剪切应变能密度
拉压应变能密度
dV ε
dxdz dy
2
2
dxdydz
2
单位体积内应变能－应变能密度
vε
dV ε
2
2E
2
2
剪切应变能密度
dxdz dy
2
dxdydz
vε
16 3Fl 2 l AA' 2CC ' EA cos 60
( )
§3 拉压与剪切应变能
应变能概念 轴向拉压应变能 拉压与剪切应变能密度 例题
应变能概念 应变能与功能原理
构件在载荷作用点、沿载荷方向的位移－相应位移 弹性体因变形而储存的能量－应变能 V 外力在变形过程中所作之功－外力功 W 根据能量守恒定律，弹性体因变形所储 存的应变能 ，数值上等于外力所作的功
例 题
例 2-1 F1 = F2 / 2 = F ，求截面 A 的位移
刚体
EA
解：1. 计算 FN与 l
0 M B＝
2F1 F2 FN 6F sin 30
l 6F 4 3Fl sin 60 l EA EA
2. 画变形图
刚性杆不变形
3. 位移计算
Ay
i 1
n
FNi li Ei Ai
FN ( x )dx EA(x )
FNi－杆段 i 轴力（设正） n－总段数，l—伸长为正
变截面变轴力杆 取微段dx, 微段变形
FN ( x ) l dx l EA( x )
横向变形与泊松比 拉压杆的横向变形
横向变形
b b1 b
横向应变
b ' b
2. 螺拴横向变形 横截面内任一点、 在任一方向上的应变
4
' 2.22 10
d ' di 0.0034 mm
螺拴直径缩小 0.0034 mm
例 1-2 图示涡轮叶片，单位体积的质量为r ，求叶片横 截面上的正应力与轴向变形 解：1. 叶片外力
处的向心加速度：
E1 A1 FN1 ＝ cos 2a FN3 －用内力表示的变形协调方程 E3 A3
联立求解平衡与补充方程
Fcos 2a FN1 FN2 E3 A3 2cos 3a E1 A1
综合考虑三方面
F FN3 E1 A1 1 2 cos 3a E3 A3
综合考虑静力、几何与物理三方面
例 题
例 1-1 长度 l = 54 mm ，内径 di = 15.3 mm，E＝200 GPa，
0.3。经预紧后，轴 向变形 l ＝0.04 mm。试求： (a) 螺拴横截面上的正应力
(b) 螺拴的横向变形 d
解：1. 横截面正应力
l -4 7.41 10 l
E 148.2 MPa
2
2G
例 题
例 3-1 用能量法计算节点 B 的铅垂位移 By
解：1. 轴力分析
FN1 ＝ 2F （拉）
FN2 ＝FN3 ＝F （压）
2. 应变能计算
V ε
2 N1
i 1
2
3
2 FN i li 2 Ei Ai
2 N2 2 N3
F 2l F l F l V ε 2 EA 2 EA 2 EA
0
l FN1 ( FN2 F ) 2l 0 2
3. 建立补充方程
l2 2CC' l2 2 2l1
解：1. 应力分析
Fy 0, 2rh F 0
F 2rh
2. 应变能计算
2 F2 dV 2rhdr ＝ dr ε 2G 4rhG
F2 V 4hG
D/ 2 d/2
1 dr r
F (lnD lnd ) 4hG
2
3. 位移计算
FΔ F (lnD lnd ) 2 4hG
外力与 FNi 之间满足静力平衡方程 各 li 之间满足变形协调方程 li 与FNi 之间满足给定物理关系（例如胡克定律） 静不定问题的内力特点
内力分配与杆件刚度有关 一般讲，EiAi ，FNi
例 4-1 求两端固定杆的支反力
解：1. 静力学方面 支反力－2，平衡方程－1，1 度静不定
静不定问题
静不定度 未知力数与有效平衡方程数之差
静不定问题分析
分析方法
求解思路
变形协调条件
建立平衡方程 分析变形，建立补充方程
f ( l1 , l2 , l3 ) 0 li ~ FNi ( i 1,2,3) F ( FN1 , FN2 , FN3 ) 0
补充方程
3. 位移计算
F l ( 2 1) EA
F By W＝ W V 由 ε 2 可得 FBy F 2 l ( 2 1) 2 EA
2Fl ( 2 1) By EA
(解析) 求节点A的位移? B B
a
A P C
A
C
例 3-2 图示隔振器，钢杆与钢套视为刚体，橡皮的 切变模量为 G 。求橡皮管内的应力 与钢杆的位移
各杆变形间满 足一定关系
变形与受力关系 一度静不定
E1A1= E2A2
平衡方程
FN2 sina - FN1sina 0
FN1cosa FN2 cosa FN3 F 0
变形几何关系
l1 l3cosa
变形协调方程
保证结构连续性所应 胡克定律 满足的变形几何关系 F l FN3 l1cosa l1 N1 1 l3 E1 A1 E3 A3 补充方程
E
'
E
E、 G、 之间的关系
E G 2(1 )
理论与实验均已证实
叠加原理
算例 试分析杆 AC 的轴向变形 l
1.分段解法
FN1l1 FN2l2 ( F2 F1 )l1 F2 l2 ( l )分段 EA EA EA EA
FN1 F2 F1
叶片
ar
2
作用在 d 微段上的离心力：
dF 2 dm 2 rAd
dF rAd
2
2. 叶片轴力与应力
2. 叶片轴力与应力
x 截面的轴力：
FN ( x )
Ro x
2 rAd
( Ro2 x 2 )
2 rA
2
x 截面的应力：
注意受力图与变形图协调： 伸长～拉力；缩短～压力 先画变形图，判断轴力正负
解：1. 问题分析 未知力－4，平衡方程－3，一度静不定
2. 画变形与受力图 3. 建立平衡方程
注意受力图与变形图协调： 伸长～拉力；缩短～压力 一度静不定
先画变形图，判断轴力正负
1. 画变形与受力图
2.建立平衡方程
M
B
FAx l1 FBx l2 0 F FAx FBx 0
5. 支反力计算
联立求解平衡方程（a）与补充方程（b），得
Fl2 FAx l1 l2
Fl1 FBx l1 l2
例 4-2 已知：F = 50 kN，[1] = 160 MPa，[2 ] = 120 MPa ，A1= A2。试问：A1=? A2=?
Ax AA2 l2 ( )
l1 l 2 ( ) Ay AA5 cos 45
小变形概念 小变形：与结构原尺寸相比为很小的变形
应 用：在小变形条件下，通常即可： 按结构的原有几何形状与尺寸，计算约束 反力与内力——刚性假定； 采用切线代圆弧的方法确定节点位移； 内力、应力与载荷成线性 位移与应变成线性
f A AB (l l )cos b l cos a
l aa A F
b
l
cos b cos(a ) cos a sin a ( )2 cos a