专题01 平行线知识讲义(原卷版)
《平行线》复习讲义.

《平行线》复习讲义一、教学内容:1. 了解对顶角的概念,掌握其性质,并会用它们进行推理和计算.2. 了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义.3. 知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线.4. 知道两直线平行同位角相等,并进一步探索平行线的特征.5. 知道过直线外一点有且仅有一条直线平行于已知直线.会用三角尺和直尺过已知直线外一点画这条直线的平行线.6. 掌握平行线的三个判定方法,并会用它们进行直线平行的推理.二、知识要点:1. 两条直线的位置关系(1)在同一平面内,两条直线的位置关系有两种:相交与平行.(2)平行线:在同一平面内,不相交的两条直线叫平行线.2. 几种特殊关系的角(1)余角和补角:如果两个角的和是直角,称这两个角互为余角.如果两个角的和是平角,称这两个角互为补角.(2)对顶角:①定义:一个角的两边分别是另一个角两边的反向延长线,这两个角叫对顶角.②性质:对顶角相等.(3)同位角、内错角、同旁内角两条直线分别与第三条直线相交,构成八个角.①在两条直线之间并且在第三条直线的两旁的两个角叫做内错角.②在两条直线的同一侧并且在第三条直线同旁的两个角叫做同位角.③在两条直线之间并且在第三条直线同旁的两个角叫做同旁内角.3. 主要的结论(1)垂线①过一点有且只有一条直线与已知直线垂直.②直线外一点与直线上各点连结的所有线段中,垂线段最短.简称:垂线段最短.(2)平行线的特征及判定平行线的判定平行线的特征同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补经过直线外一点,有且只有一条直线与已知直线平行4. 几个概念(1)垂线段:过直线外一点,作已知直线的垂线,这点和垂足之间的线段.(2)点到直线的距离:从直线外一点到这条直线的垂线段的长度.5. 几个基本图形(1)相交线型.①一般型(如图①);②特殊型(垂直,如图②).ABC DOABCD O ①②(2)三线八角.①一般型(如图①);②特殊型(平行,如图②).A BCDEFABCDEF①②三、重点难点:重点有两个:一方面要掌握关于相交线和平行线的一些基本事实,另一方面学会借助三角尺上的直角或量角器画已知直线的垂线,用移动三角尺的方法画平行线.难点是是利用对顶角的性质、平行线的特征、两直线平行的条件等进行推理和计算.四、考点分析:考查(1)对顶角的性质;(2)平行线的识别方法;(3)平行线的特征,其中依据平行线的识别与特征解决一类与平行线有关的几何问题是历届中考命题的重要考点.常见题型有填空题、选择题和解答题,单纯考查一个知识点的题目并不难,属于中低档题,将平行线的特征与其他知识综合起来考查的题目难度较大,属高档题.【典型例题】例1. 如图所示,已知FC ∥AB ∥DE ,∠α∶∠D ∶∠B =2∶3∶4,求∠α、∠D 、∠B 的度数.ABC DEF12α分析:由条件∠α∶∠D ∶∠B =2∶3∶4.可以分别设出∠α、∠D 、∠B ,再根据题目给出的条件建立方程求解.解:设∠α=2x ,∠D =3x ,∠B =4x . ∵FC ∥AB ∥DE ,∴∠2+∠B =180°,∠1+∠D =180°, ∴∠2=180°-4x ,∠1=180°-3x , 又∵∠1+∠α+∠2=180°,∴180°-3x +2x +180°-4x =180°,∴5x =180°,x =36°,∴∠α=2x =72°,∠D =3x =108°,∠B =4x =144°.评析:解答这类计算题不仅要熟悉图形的性质,还要善于进行等量转化,把待求的角逐步和已知条件建立起联系来,当待求结论要经过复杂过程才能求得时,一定要思路清晰、叙述表达严密.例2. 如图所示,直线a ∥b ,则∠A =__________.AB C Ea b28°50°ABCDEa b28°50°分析:已知条件a ∥b 能转化为三线八角,过A 作AD ∥a ,那么已知的两个角可转换到顶点A (都用内错关系转化),可求∠A. 由AD ∥a ,a ∥b ,可知AD ∥b ,由两直线平行内错角相等得:∠DAB =∠ABE =28°,∠DAE =50°,∴∠EAB =50°-28°=22°.解:22°评析:用平行线三线八角把已知角转化成以A 为顶点的角即可.例3. 已知:如图所示,DF ∥AC ,∠1=∠2.试说明DE ∥AB.ABC DEF 12分析:要说明DE ∥AB ,可以证明∠1=∠A ,而由DF ∥AC ,有∠2=∠A ,又因为∠1=∠2,故有∠1=∠A ,从而结论成立.解:∵DF ∥AC (已知),∴∠2=∠A (两直线平行,同位角相等). ∵∠1=∠2(已知), ∴∠1=∠A (等式性质),∴DE ∥AB (同位角相等,两直线平行).评析:说明两直线平行的方法有:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一条直线的两条直线互相平行;⑤垂直于同一条直线的两条直线互相平行.例4. 试说明:两条平行线被第三条直线所截,一对内错角的平分线互相平行. 分析:先根据题意画出图形,标注字母,找出已知条件和问题,再进行说明.ABCDG HMN EF12解:已知:如图所示,AB ∥CD ,EF 分别交AB 、CD 于G 、H ,GM 、HN 分别平分∠BGF 、∠EHC. 说明GM ∥HN .∵GM 、HN 分别平分∠BGF 、∠EHC (已知), ∴∠1=∠BGF ,∠2=∠EHC (角平分线定义). ∵AB ∥CD ,∴∠BGF =∠EHC (两直线平行,内错角相等). ∴∠1=∠2.∴GM ∥HN (内错角相等,两直线平行). 评析:(1)上题把内错角平分线改为同位角平分线,原结论也成立,请同学们自己试着解一解.(2)此题为文字题,首先应根据题意画出图形,再根据已知条件和结论结合图形写出解题过程.例5. 如图所示,已知CE ∥DF ,说明∠ACE =∠A +∠ABF .ABCDEFG分析:结论中∠ACE ,∠A 与∠ABF 在三个顶点处,条件CE ∥DF 不能直接运用,结论形式启示我们用割补法,即构造一个角等于∠A +∠ABF ,因此想到在点A 处补上一个∠GAB =∠ABF ,只要GA ∥DF 即可,同时可得GA ∥CE ,∠GAC =∠ACE ,结论便成立.解:过A 作AG ∥DF ,∴∠GAB =∠ABF (两直线平行,内错角相等) 又∵AG ∥DF ,CE ∥DF (已知)∴AG ∥CE (平行于同一直线的两条直线互相平行) ∴∠GAC =∠ACE (两直线平行,内错角相等) 又∵∠GAC =∠BAC +∠GAB (已知) ∴∠ACE =∠BAC +∠ABF (等量代换). 评析:(1)割补法是一种常用方法.(2)此题还可以过点C 作一条直线与AB 平行,把∠ACE 分成两个角后,分别说明这两个角与∠A 、∠ABF 相等.例6. 解放战争时期,有一天江南某游击队在村庄A 点出发向正东行进,此时有一支残匪在游击队的东北方向B 点处(如图所示,残匪沿北偏东60°角方向,向C 村进发.游击队步行到A ’处,A ’正在B 的正南方向上,突然接到上级命令,决定改变行进方向,沿北偏东30°方向赶往C 村.问游击队进发方向A ’C 与残匪行进方向BC 至少是多少角度时,才能保证C 村村民不受伤害?A BCA'北东A BCA'北东D E分析:如图可知A ’C 与BC 的夹角最小值是∠BCA ’.本题关键是引辅助线,延长A ’B 到D ,过C 作CE ∥A ’D ,通过平行线特征来求解.解:根据题意∠DBC =60°,∠BA ’C =30°.过点C作CE∥A’B,则∠BCE=∠DBC=60°,∠A’CE=∠BA’C=30°.∴∠BCA’=∠BCE-∠A’CE=60°-30°=30°.夹角至少为30°时才能保证C村村民不受伤害.评析:本题较综合地运用了角、方位角、平行线的有关知识.【方法总结】1. 方程的思想几何图形中常见一些已知线段、角,而要求未知线段和角,我们可以把它们分别视为已知量、未知量,用方程的思想方法求解.2. 比较的思想方法利用比较这一思想方法,分清易混概念和性质,加深对概念性质的理解和认识.例如平行线的性质是理解判定定理时最易混淆的,学习时,可通过比较其异同弄清它们的区别和联系.3. 推理的方法推理是一个思维形式,它是从一个或几个判断得出新判断的思维形式.推理时要时刻明确最终目标,最后推出结论,推理过程要步步有根据,不能“想当然”,推理的根据,可以是已知条件、定义、性质、基本事实等.【模拟试题】(答题时间:60分钟)一. 选择题1. 如图所示,下列说法中正确的是()A. 图中没有同位角、内错角、同旁内角B. 图中没有同位角和内错角,但有一对同旁内角C. 图中没有内错角和同旁内角,但有三对同位角D. 图中没有同位角和内错角,但有三对同旁内角AB C2. 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图),如果第一次转弯时的∠B =140°,那么,∠C应是()A. 140°B. 40°C. 100°D. 180°140°AB CD3. 如图所示,下列说法正确的是()A. 若AB∥CD,则∠B+∠A=180°B. 若AD∥BC,则∠B+∠C=180°C. 若AB∥CD,则∠B+∠D=180°D. 若AD∥BC,则∠B+∠A=180°AB CD4. 如图所示,要得到DE ∥BC ,需要条件( )A. CD ⊥AB ,GF ⊥ABB. ∠DCE +∠DEC =180°C. ∠EDC =∠DCBD. ∠BGF =∠DCBABC D EF G5. 如图所示,AB ⊥AC ,AD ⊥BC ,DE ∥AB ,则∠CDE 与∠BAD 的关系是( ) A. 互余 B. 互补 C. 相等 D. 不能确定ABCDE6. 如图所示,已知AB ∥CD ,CE 平分∠ACD ,∠A =110°,则∠ECD 的度数等于( ) A. 110° B. 70° C. 55° D. 35°C ABED*7. 两条平行线被第三条直线所截,角平分线互相垂直的是( )A. 内错角B. 同旁内角C. 同位角D. 内错角或同位角**8. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)):P(1)P(2)P(3)P(4)从图中可知,小敏画平行线的依据有:( )①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.( )A. ①②B. ②③C. ③④D. ①④ 二. 填空题1. 如图所示,A 、B 之间是一座山,一条铁路要通过A 、B 两地,在A 地测得B 地在北偏东70°,如果A 、B 两地同时开工修建铁路,那么在B 地应按__________方向开凿,才能使铁路在山腹中准确接通.AB北70°北2. 如图所示,A 、C 、B 在同一直线上,DC ⊥CE 于C ,∠ACD =53°,则∠BCE =_______.ABCDE3. 如图所示,四边形ABCD 中,∠1=∠2,∠D =72°,则∠BCD =__________.ABCD12*4. 如图所示,AB ∥CD 、BEFD 是AB 、CD 之间的一条折线,则∠1+∠2+∠3+∠4=__________.ABCDE F12345. 如图所示,a ∥b ,∠1=3∠2,则∠1=__________,∠2=__________.a b 12*6. 已知,如图,AD 与BC 相交于点O ,AB ∥CD ,如果∠B =20°,∠D =40°,那么∠BOD 为__________度.ABCD O7. 如图所示,若AE ∥BD ,那么相等的角有__________;若AB ∥EC ,那么互补的角有__________.A CDB1234567E**8. 设a 、b 、c 为平面内三条不同的直线.(1)若a ∥b ,c ⊥a ,则c 与b 的位置关系是__________;(2)若c ⊥a ,c ⊥b ,则a 与b 的位置关系是__________;(3)若a ∥b ,则c 与b 的位置关系是__________.三. 解答题1. 如图所示,已知AB ⊥BC ,BC ⊥CD ,∠1=∠2,试判断BE 与CF 的关系,并说明理由.ABCD12EF2. 如图所示,已知AB ∥CD ,直线EF ⊥CD 于F ,∠1=2∠2,求∠2的度数.C DEF AB12G*3. 如图所示,已知AB ∥DE ,∠ABC =60°,∠CDE =140°,求∠BCD 的度数.AB CDE4. 如图所示,小刚准备在C 处牵牛到河边AB 饮水.(1)请用三角板作出小刚的最短路线(不考虑其他因素);(2)如图乙,若小刚在C 处牵牛到河边AB 饮水,并且必须到河边D 处观察河水的水质情况,请作出小刚行走的最短路线(不写作法,保留作图痕迹).甲ABC乙ABCD典型例题例1 如图2-45是梯形的有上底的一部分,已知量得∠A =115°,∠D=100°,梯形另外两个角各是多少度?图2-45分析:已知是梯形,可知它的上、下两底平行,要求另外两个角的度数,直接应用平行线的特征即可求出.解:因为梯形上、下两底平行,所以,∠A与∠B互补,∠D与∠C互补,于是∠B=180°-115°=65°,∠C=180°-100°=80°梯形的另外两个角分别是65°、80°.例2 已知,如图2-46,直线a∥b,c∥d,∠1=70°,求∠2、∠3的度数.图2-46分析:这是平行线的特征的应用的计算题,要注意格式.解:∵a∥b(已知),∴∠2=∠1=70°(两直线平行,内错角相等) ∵c∥d(已知),∴∠3=∠2=70°(两直线平行,同位角相等)参考例题[2.2.1探索直线平行的条件(一)][例1]若∠1=52°,如图2-18,问应使∠C为多少度时,能使直线AB∥CD?图2-18分析:要使直线AB∥CD,则需使同位角相等,即∠1=∠C.这样即可求出.解:若∠1=52°,当∠C=52°时,直线AB∥CD.[例2]如图2-19,若∠1=∠4,∠1+∠2=180°,则AB、CD、EF的位置关系如何?图2-19分析:由已知∠1=∠4, 可知:AB ∥EF ,∴可猜想:AB ∥CD ∥EF .由图中可知:∠2+∠3=180°, 而已知:∠1+∠2=180°.∴由同角的补角相等可得∠1=∠3, 这样得到AB ∥CD .由“两条直线都与第三条直线平行,则这两条直线平行”可得:AB ∥CD ∥EF .解:⎪⎭⎪⎬⎫→∠=∠→∠=∠→⎭⎬⎫︒=∠+∠︒=∠+∠EF||CD||AB AB 41311802318021 →AB ∥CD ∥EF . 二、参考练习1.如图2-20,∠1=45°,∠2=135°,则l 1∥l 2吗?为什么? 解:平行.∵∠1+∠3=180°,∠1=45°. ∴∠3=135°,又∵∠2=135°. ∴∠2=∠3,因此l 1∥l 2.图2-20 图2-212.如图2-21,∠1=120°,∠2=60°,问直线a 与b 的关系? 解:直线a 与b 平行.∵:∠2+∠3=180°,∠2=60°, ∴∠3=120°, 又∵∠1=120°.∴∠1=∠3,因此a ∥b .3.在三角形ABC 中,∠B =90°,D 在AC 边上,DF ⊥BC 于F ,DE ⊥AB 于E ,则线段AB 与DF平行吗?BC与DE平行吗?为什么?图2-22解:线段AB与DF平行.线段BC与DE也平行.∵:DF⊥BC于F,则∠DFC=90°,又∵∠B=90°,∴∠B=∠DFC,因此AB∥DF.BC与ED平行的理由同上.【试题答案】一. 选择题1. D2. A3. D4. C5. A6. D7. B8. C二. 填空题1. 南偏西70°2. 37°3. 108°4. 540°分别过点E、F作AB的平行线.5. 135°,45°6. 607. ∠1=∠3,∠5=∠6;∠B与∠BCE,∠BAE与∠68. 垂直,平行,平行或相交三. 解答题1. ∵AB⊥BC,BC⊥CD,∴∠ABC=∠BCD=90°,又∵∠1=∠2,∴∠ABC-∠1=∠BCD -∠2,即∠EBC=∠BCF,∴BE∥CF.2. ∵AB∥CD,∴∠1=∠CFG=2∠2,∵EF⊥CD,∴∠CFE=∠CFG+∠2=2∠2+∠2=3∠2=90°,∴∠2=30°.3. 延长ED交BC于点G,过点C作CF∥AB,则∠BCD=∠BCF-∠DCF=∠ABC-∠GDC=60°-(180°-∠CDE)=20°.4. (1)甲:过C作AB的垂线,垂足与C点之间的线段为最短路线,根据是:垂线段最短.(2)乙:连结CD得线段CD就是最短线段,根据是:两点之间线段最短.《二元一次方程组》复习讲义【学习目标】1.了解二元一次方程(组)的有关概念,会解简单的(数字系数);能根据具体问题中的数量关系,列出二元一次方程组解决简单的实际问题,并能检验解的合理性.2.了解解二元一次方程组的“消元”思想,从而初步理解化“未知”为“已知”和化复杂问题为简单问题的划归思想.【知识网络】【要点梳理】要点一、二元一次方程组的相关概念1. 二元一次方程的定义定义:方程中含有两个未知数(x 和y ),并且未知数的次数都是1,像这样的方程叫做二元一次方程.要点诠释:(1)在方程中“元”是指未知数,“二元”就是指方程中有且只有两个未知数.(2)“未知数的次数为1”是指含有未知数的项(单项式)的次数是1.(3)二元一次方程的左边和右边都必须是整式.2.二元一次方程的解定义:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解. 要点诠释:二元一次方程的每一个解,都是一对数值,而不是一个数值,一般要用大括号联立起来,即二元一次方程的解通常表示为⎩⎨⎧ba ==y x 的形式.3. 二元一次方程组的定义定义:把具有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组. 此外,组成方程组的各个方程也不必同时含有两个未知数.例如,二元一次方程组3452x y x +=⎧⎨=⎩. 要点诠释:(1)它的一般形式为111222a xb yc a x b y c +=⎧⎨+=⎩(其中1a ,2a ,1b ,2b 不同时为零). (2)更一般地,如果两个一次方程合起来共有两个未知数,那么它们组成一个二元一次方程组.(3)符号“{”表示同时满足,相当于“且”的意思.4. 二元一次方程组的解定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解. 要点诠释:(1)方程组中每个未知数的值应同时满足两个方程,所以检验是否是方程组的解,应把数值代入两个方程,若两个方程同时成立,才是方程组的解,而方程组中某一个方程的某一组解不一定是方程组的解.(2)方程组的解要用大括号联立;(3)一般地,二元一次方程组的解只有一个,但也有特殊情况,如方程组⎩⎨⎧=+=+6252y x y x 无解,而方程组⎩⎨⎧-=+-=+2221y x y x 的解有无数个.要点二、二元一次方程组的解法1.解二元一次方程组的思想转化消元一元一次方程二元一次方程组2.解二元一次方程组的基本方法:代入消元法、加减消元法和图像法(1)用代入消元法解二元一次方程组的一般过程:①从方程组中选定一个系数比较简单的方程进行变形,用含有x (或y )的代数式表示y (或x ),即变成b ax y +=(或b ay x +=)的形式; ②将b ax y +=(或b ay x +=)代入另一个方程(不能代入原变形方程)中,消去y (或x ),得到一个关于x (或y )的一元一次方程;③解这个一元一次方程,求出x (或y )的值;④把x (或y )的值代入b ax y +=(或b ay x +=)中,求y (或x )的值;⑤用“{”联立两个未知数的值,就是方程组的解.要点诠释:(1)用代入法解二元一次方程组时,应先观察各项系数的特点,尽可能选择变形后比较简单或代入后化简比较容易的方程变形;(2)变形后的方程不能再代入原方程,只能代入原方程组中的另一个方程;(3)要善于分析方程的特点,寻找简便的解法.如将某个未知数连同它的系数作为一个整体用含另一个未知数的代数式来表示,代入另一个方程,或直接将某一方程代入另一个方程,这种方法叫做整体代入法.整体代入法是解二元一次方程组常用的方法之一,它的运用可使运算简便,提高运算速度及准确率.(2)用加减消元法解二元一次方程组的一般过程:①根据“等式的两边都乘以(或除以)同一个不等于0的数,等式仍然成立”的性质,将原方程组化成有一个未知数的系数绝对值相等的形式;②根据“等式两边加上(或减去)同一个整式,所得的方程与原方程是同解方程”的性质,将变形后的两个方程相加(或相减),消去一个未知数,得到一个一元一次方程;③解这个一元一次方程,求出一个未知数的值;④把求得的未知数的值代入原方程组中比较简单的一个方程中,求出另一个未知数的值;⑤将两个未知数的值用“ ”联立在一起即可.要点诠释:当方程组中有一个未知数的系数的绝对值相等或同一个未知数的系数成整数倍时,用加减消元法较简单.(3)图像法解二元一次方程组的一般过程:①把二元一次方程化成一次函数的形式.②在直角坐标系中画出两个一次函数的图像,并标出交点.③交点坐标就是方程组的解.要点诠释:二元一次方程组无解<=>一次函数的图像平行(无交点)二元一次方程组有一解<=>一次函数的图像相交(有一个交点)二元一次方程组有无数个解<=>一次函数的图像重合(有无数个交点)利用图像法求二元一次方程组的解是近似解,要得到准确解,一般还是用代入消元法和加减消元法解方程组.相反,求两条直线的交点坐标可以转化为求这两条直线对应的函数表达式联立的二元一次方程组的解.要点三、实际问题与二元一次方程组要点诠释:(1)解实际应用问题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的解应该舍去;(2)“设”、“答”两步,都要写清单位名称;(3)一般来说,设几个未知数就应该列出几个方程并组成方程组.要点四、三元一次方程组1.定义:含有三个未知数,并且含有未知数的项的次数都是1的方程叫做三元一次方程;含有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.412,325,51,x y z x y z x y z +-=⎧⎪++=-⎨⎪-+=⎩ 273,31,34a b a c b c +=⎧⎪-=⎨⎪-+=⎩等都是三元一次方程组.要点诠释:理解三元一次方程组的定义时,要注意以下几点:(1)方程组中的每一个方程都是一次方程;(2)如果三个一元一次方程合起来共有三个未知数,它们就能组成一个三元一次方程组.2.三元一次方程组的解法解三元一次方程组的基本思想仍是消元,一般的,应利用代入法或加减法消去一个未知数,从而化三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.解三元一次方程组的一般步骤是:(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;(2)解这个二元一次方程组,求出两个未知数的值;(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;(4)解这个一元一次方程,求出最后一个未知数的值;(5)将求得的三个未知数的值用“{”合写在一起.要点诠释:(1)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求比较简单的解法.(2)要检验求得的未知数的值是不是原方程组的解,将所求得的一组未知数的值分别代入原方程组里的每一个方程中,看每个方程的左右两边是否相等,若相等,则是原方程组的解,只要有一个方程的左、右两边不相等就不是原方程组的解.3. 三元一次方程组的应用列三元一次方程组解应用题的一般步骤:(1)弄清题意和题目中的数量关系,用字母(如x ,y ,z)表示题目中的两个(或三个)未知数;(2)找出能够表达应用题全部含义的相等关系;(3)根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;(4)解这个方程组,求出未知数的值;(5)写出答案(包括单位名称).要点诠释:(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.(3)一般来说,设几个未知数,就应列出几个方程并组成方程组.【典型例题】类型一、二元一次方程组的相关概念1.下列方程组中,不是二元一次方程组的是( ).A.⎩⎨⎧+==-13032x y y xB.⎩⎨⎧=-=+211z y xC.⎩⎨⎧=+-=+63222y x y x x x D.⎩⎨⎧-=+=6352x x y【思路点拨】利用二元一次方程组的定义一一进行判断.【答案】B.【解析】二元一次方程组中只含有两个未知数,并且含有未知数的次数都是1,方程组⎩⎨⎧=+-=+63222y x y x x x 中,y x x x 3222-=+可以整理为y x 32-=.【总结升华】准确理解二元一次方程组和二元一次方程的定义是解本题的关键. 举一反三:【变式】若32225a b a b x y --+-=是二元一次方程,则a = ,b = .【答案】1, 0.2.以⎩⎨⎧-==11y x 为解的二元一次方程组是( ). A.⎩⎨⎧=-=+10y x y x B.⎩⎨⎧-=-=+10y x y x C.⎩⎨⎧=-=+20y x y x D.⎩⎨⎧-=-=+20y x y x【答案】C.【解析】通过观察四个选项可知,每个选项的第一个二元一次方程都是0=+y x ,第二个方程的左边都是y x -,而右边不同,根据二元一次方程的解的意义可知,当⎩⎨⎧-==11y x 时,211)1(1=+=--=-y x .【总结升华】不满足或不全部满足方程组中的各方程的选项都不是方程组的解.举一反三:【变式】若⎩⎨⎧==12y x 是关于y x 、的方程032=+-k y x 的解,则=k . 【答案】 -1.类型二、二元一次方程组的解法3.解方程组15(2)3(25)4(34)5x y x y +=+⎧⎨--+=⎩【思路点拨】由于本题结构比较复杂,不能直接消元,应先将方程组化为一般形式,再看如何消元,即用加减或代入消元法.【答案与解析】解:将原方程组化简得5926x y x y -=⎧⎨-=⎩①-②得:-3y =3,得y =-1,将y =-1代入①中,x =9-5=4.故原方程组的解为41x y =⎧⎨=-⎩.【总结升华】消元法是解方程组的基本方法,消元的目的是把多元一次方程组逐步转化为一元一次方程,从而使问题获解.举一反三:【变式】已知方程组35x y x y +=⎧⎨-=⎩的解是二元一次方程m(x+1)=3(x-y)的一个解,则m= .【答案】3.类型三、实际问题与二元一次方程组4. 2001年以来,我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003、2007年相关数据. 已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中的信息,求2003年和2007年的药品降价金额. 年份2002 2003 2004 2005 2007 降价金额(亿元) 54 35 40 【思路点拨】本题的两个相等关系为:(1)五年的降价金额一共是269亿元;(2)2007年药品降价金额=6×2003年的药品降价金额.【答案与解析】解:设2003年和2007年药品降价金额分别为x 亿元、y 亿元.根据题意,得⎩⎨⎧=++++=2694035546y x x y ,解方程组得⎩⎨⎧==12020y x .答:2003年和2007年的药品降价金额分别为20亿元和120亿元.【总结升华】列方程(组)解实际问题的关键就是准确地找出等量关系,列方程(组)求解. 举一反三:【变式】(山东济南)如图所示,教师节来临之际,群群所在的班级准备向每位辛勤工作的教师献一束鲜花,每束由4支鲜花包装而成,其中有象征母爱的康乃馨和象征尊敬的水仙花两种鲜花,同一种鲜花每支的价格相同,请你根据第一、二束鲜花提供的信息,求出第三束鲜花的价格.【答案】解:设康乃馨每支x 元,水仙花每支y 元.根据题意,可列方程组3192218x y x y +=⎧⎨+=⎩,解得54x y =⎧⎨=⎩. 所以第三束鲜花的价格是x+3y =5+3×4=17(元).答:第三束鲜花的价格是17元.类型四、三元一次方程组7.解方程组312,23,3716.x y z x y z x y z ++=⎧⎪--=-⎨⎪+-=-⎩①②③ 【思路点拨】先用加减法消去y ,变为x 、z 的二元一次方程组.【答案与解析】解:①+②,得329x z +=.②+③,得5819x z -=-.解方程组329,5819,x z x z +=⎧⎨-=-⎩得1,3.x z =⎧⎨=⎩把13x z =⎧⎨=⎩,代入①,得2y =. 所以方程组的解是1,2,3.x y z =⎧⎪=⎨⎪=⎩【总结升华】因为y 的系数为1+或1-,所以先消去y 比先消去x 或z 更简便.。
1第一章 平行线 讲义

学员姓名:辅导课目:数学年级:八年级学科教师:汪老师授课日期及时段课题第一章《平行线》复习学习目标1、理解平行线的性质及其判定2、知道如何求两平行线间的距离教学内容第一章《平行线》复习1.1、同位角、内错角、同旁内角:1、先看图中∠1和∠5,这两个角分别在直线AB、CD的上方,并且都在直线EF的右侧,像这样位置相同的一对角叫做同位角。
在图(1)中,像这样具有类似位置关系的角还有吗?如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角。
变式图形:图中的∠1与∠2都是同位角。
图形特征:在形如字母“F”的图形中有同位角。
2、再看∠3与∠5,这两个角都在直线AB、CD之间,且3在直线EF左侧,∠5在直线EF右侧,像这样的一对角叫做内错角。
同样,∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。
变式图形:图中的∠1与∠2都是内错角。
图形特征:在形如“Z”的图形中有内错角。
3、在图(1)中,∠3和∠6也在直线AB、CD之间,但它们在直线EF的同一旁像这样的一对角,我们称它为同旁内角。
具有类似的位置特征的还有∠4与∠5,因此它们也是同旁内角。
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“n ”的图形中有同旁内角。
与两直线的位置关系 与截线的位置关系 同位角 两直线同侧 截线的同旁 内错角 两直线之间 截线异侧 同旁内角两直线之间截线同侧1.2、平行线的性质:性质1:两条直线被第三条直线所截,如果两条直线平行,那么同位角相等。
简单说成:两直线平行,同位角相等。
几何语言:∵ AB//CD ∴ ∠PMA=∠MNC性质2:两条直线被第三条直线所截,如果两条直线平行,那么内错角相等。
简单说成:两直线平行,内错角相等。
几何语言:∵ AB//CD ∴ ∠BMN=∠CNM性质3:两条直线被第三条直线所截,如果两条直线平行,那么同旁内角互补。
简单说成:两直线平行,同旁内角互补。
几何语言:∵ AB//CD∴ ∠AMN+∠CNM=180°1.3、平行线的判定:几何符号语言:ABE 1 3 4(1)∵ ∠3=∠2 ∴ AB ∥CD (同位角相等,两直线平行) (2)∵ ∠1=∠2 ∴ AB ∥CD (内错角相等,两直线平行)(3)∵ ∠4+∠2=180° ∴ AB ∥CD (同旁内角互补,两直线平行)1.4、两条平行线的距离如图,直线AB ∥CD ,EF ⊥AB 于E ,EF ⊥CD 于F ,则称线段EF 的长度为两平行线AB 与CD 间的距离。
平行线构造和应用讲义(含答案)
二、平行线中构造平行线
5. 已知 AB ∥ CD,点 P 为平面内一点,连接 AP、CP. (1) 探究:如图 (1)∠PAB = 145°,∠PCD = 135°,则 ∠APC 的度数是; 如图 (2)∠PAB = 45°,∠PCD = 60°,则 ∠APC 的度数是. (2) 在图 2 中试探究 ∠APC ,∠PAB,∠PCD 之间的数量关系,并说明理由. (3) 拓展探究:当点 P 在直线 AB ,CD 外,如图 (3)、(4) 所示的位置时,请分别直接写出 ∠APC ,∠PAB,∠PCD 之间的数量关系.
·2·
6. (1) 如图①,∠CEF = 90°,点 B 在射线 EF 上,AB ∥ CD,若 ∠ABE = 130°,求 ∠C 的度数; (2) 如图②,把 “∠CEF = 90°” 改为 “∠CEF = 120°”,点 B 在射线 EF 上,AB ∥ CD. 猜想 ∠ABE 与 ∠C 的数量关系,并说明理由.
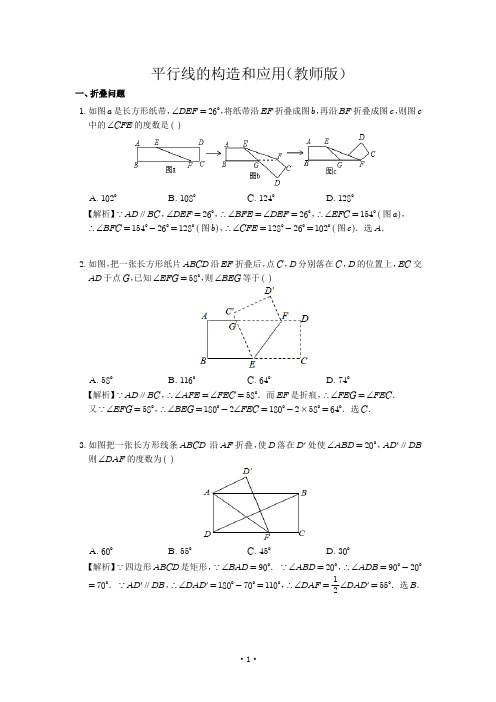
3. 如图把一张长方形线条 ABCD 沿 AF 折叠,使 D 落在 D′ 处使 ∠ABD = 20°,AD′ ∥ DB 则 ∠DAF 的度数为 ( )
A. 60°
B. 55°
C. 45°
D. 30°
【解析】∵ 四边形 ABCD 是矩形,∵ ∠BAD = 90°. ∵ ∠ABD = 20°,∴ ∠ADB = 90° - 20° = 70°. ∵ AD′ ∥ DB,∴ ∠DAD′ = 180° - 70° = 110°,∴ ∠DAF = 21 ∠DAD′ = 55°.选 B.
【解析】(1) 如图 1,分别过点 E,F 作 EM ∥ AB,FN ∥ AB, ∴ EM ∥ AB ∥ FN ,∴ ∠ B = ∠ BEM = 30 ° ,∠ MEF = ∠EFN ,又 ∵ AB ∥ CD,AB ∥ FN ,∴ CD ∥ FN , ∴ ∠D + ∠DFN = 180°,又 ∵ ∠D = 120°,∴ ∠DFN = 60°, ∴ ∠BEF = ∠MEF + 30°,∠EFD = ∠EFN + 60°, ∴ ∠EFD = ∠MEF + 60° ∴ ∠EFD = ∠BEF + 30° = 90°; (2) 如图 1,分别过点 E,F 作 EM ∥ AB,FN ∥ AB, ∴ EM ∥ AB ∥ FN ,∴ ∠ B = ∠ BEM = 30 ° ,∠ MEF = ∠EFN ,又 ∵ AB ∥ CD,AB ∥ FN ,∴ CD ∥ FN , ∴ ∠D + ∠DFN = 180°,又 ∵ ∠D = 120°,∴ ∠DFN = 60°, ∴ ∠BEF = ∠MEF + 30°,∠EFD = ∠EFN + 60°, ∴ ∠EFD = ∠MEF + 60°,∴ ∠EFD = ∠BEF + 30°;
专题01 平行线中的拐点模型之猪蹄模型(M型)与锯齿模型(原卷版)

专题01 平行线中的拐点模型之猪蹄模型(M型)与锯齿模型平行线中的拐点模型在初中数学几何模块中属于基础工具类问题,也是学生必须掌握的一块内容,熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题就平行线中的拐点模型(猪蹄模型(M型)与锯齿模型)进行梳理及对应试题分析,方便掌握。
拐点(平行线)模型的核心是一组平行线与一个点,然后把点与两条线分别连起来,就构成了拐点模型,这个点叫做拐点,两条线的夹角叫做拐角。
通用解法:见拐点作平行线;基本思路:和差拆分与等角转化。
模型1:猪蹄模型(M型)与锯齿模型【模型解读】图1 图2 图3如图1,①已知:AM∥BN,结论:∠APB=∠A+∠B;②已知:∠APB=∠A+∠B,结论:AM∥BN.如图2,已知:AM∥BN,结论:∠P1+∠P3=∠A+∠B+∠P2.如图3,已知:AM∥BN,结论:∠P1+∠P3+...+∠P2n+1=∠A+∠B+∠P2+...+∠P2n.【模型证明】(1)∠APB=∠A+∠B这个结论正确,理由如下:如图1,过点P作PQ∥AM,∵PQ∥AM,AM∥BN,∴PQ∥AM∥BN,∴∠A=∠APQ,∠B=∠BPQ,∴∠A+∠B=∠APQ+∠BPQ=∠APB,即:∠APB=∠A+∠B.(2)根据(1)中结论可得,∠A+∠B+∠P2=∠P1+∠P3,故答案为:∠A+∠B+∠P2=∠P1+∠P3,(3)由(2)的规律得,∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1故答案为:∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1A.55°B.65例2.(2023春·安徽蚌埠·九年级校联考期中)太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线Ð=°,88ABO46Ð=°,则OCDA.116°例3.(2023下·湖北黄冈A.α+β=180°例4.(2023春·河南驻马店Ð=°,则FE66Ð为(例6.(2023下·湖北恩施·七年级统考期中)如图,若BAE CPF Ð=Ð,1202E a°Ð=+,210F aÐ=-例7.(2023下·江苏南通·式.例8.(2023下·江西赣州CD有怎样的位置关系以证明.(3)如图3已知证明.例9.(2023上·黑龙江哈尔滨·七年级校考期中)已知:直线AB 与直线CD 内部有一个点P ,连接BP .(1)如图1,当点E 在直线CD 上,连接PE ,若B PEC P Ð+Ð=Ð,求证:AB CD P ;(2)如图2,当点E 在直线AB 与直线CD 的内部,点H 在直线CD 上,连接EH ,若ABP PEH P EHD Ð+Ð=Ð+Ð,求证:AB CD P ;(3)如图3,在(2)的条件下,BG 、EF 分别是ABP Ð、PEH Ð的角平分线,BG 和EF 相交于点G ,EF 和直线AB 相交于点F ,当BP PE ^时,若10BFG EHD Ð=Ð+°,36BGE Ð=°,求EHD Ð的度数.课后专项训练1.(2023下·江苏无锡·七年级校联考期中)如图,a b ∥,370Ð=°,1210°Ð-Ð=,则1Ð的度数是( )A . 30°B . 40°C . 50°D . 60°2.(2023下·江苏镇江·七年级统考期末)将一副三角尺(厚度不计)如图摆放,使AB 边与CD 边互相平行,则图中1Ð的大小为( )A .120°B .115°C .110°D .105°3.(2023下·安徽马鞍山·七年级校考期末)如图,直线12l l ∥,130Ð=°,则23Ð+Ð=( )A .150°B .210°C .230°D .240°4.(2022下·广东七年级期中)如图AB CD P ,CD EF ∥,^BG GF ,DH 是CDF Ð的平分线,50B G D F Ð=°,,,三点在一条直线上,则GDH Ð的度数为( )A .110°B .140°C .80°D .100°5.(2023·江苏·七年级假期作业)如图,AB CD ∥,点E 在AC 上,11015A D Ð=°Ð=°,,则下列结论正确的个数是( )A.1个B.2个6.(2023下·辽宁铁岭·七年级校考阶段练习)如图,直线()A.a b+7.(2023下·山东德州Ð+Ð=°,M,N1290A.①④B8.(2022下·湖北省直辖县级单位∠西45°方向,则ACB=9.(2023下·江苏扬州于.10.(2023下·江苏连云港上.若165Ð=°,则2Ð等于11.(2023下·江苏扬州·九年级阶段练习)如图,已知:12.(2023下·江苏镇江·七年级统考期中)探照灯、汽车灯及其他很多灯具都与抛物线形状有关,如图是一13.(2023上·江苏常州·八年级统考期中)则2Ð= °.14.(2022下·江苏宿迁·七年级统考期末)如图,直线15.(2023下·江苏苏州Ð=Ð,则AEC m AFC16.(2023下·江苏淮安B C BECÐ+Ð=Ð.求证:_________________)14ECD Ð.知识回顾](1)如图1,点E 在两平行线之间,试说明:BED ABE EDC Ð=Ð+Ð.知识应用](2)如图2,BP 、DP 分别平分ABE Ð、EDC Ð,利用()1中的结论,试说明:12BPD BED Ð=Ð;(1)如图①,求证:AEB DAE CBE Ð=Ð+Ð;(2)如图②,若AE 平分DAC Ð,CAB Ð=①请动动你聪明的头脑,你会发现:ABE AEB ÐÐ+=______°;②如图③,若ACD Ð的平分线与BA 的延长线交于点F ,与AE 交于点P ,且55F Ð=数.23.(2023下·江苏苏州·七年级校考期中)如图1,由线段,,,AB AM CM CD 组成的图形像英文字母M ,称为“M 形BAMCD ”.(1)如图1,M 形BAMCD 中,若//,50AB CD A C Ð+Ð=°,则M Ð=______;(2)如图2,连接M 形BAMCD 中,B D 两点,若150,B D AMC a Ð+Ð=°Ð=,试探求A Ð与C Ð的数量关系,并说明理由;(3)如图3,在(2)的条件下,且AC 的延长线与BD 的延长线有交点,当点M 在线段BD 的延长线上从左向右移动的过程中,直接写出A Ð与C Ð所有可能的数量关系.。
平行线判定及性质复习讲义1

板块一平行线平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线a与直线b互相平行,记作a∥b。
平行线的性质:平行线之间的距离处处相等.两条直线的位置关系在同一平面内,两条直线的位置关系只有两种:⑴相交;⑵平行。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)注意:判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:①有且只有一个公共点,两直线相交;②无公共点,则两直线平行;③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)平行线的画法:平行线的画法是几何画图的基本技能之一,在以后的学习中,会经常遇到画平行线的问题.方法为:一“落”(三角板的一边落在已知直线上),二“靠”(用直尺紧靠三角板的另一边),三“移”(沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点),四“画”(沿三角板过已知点的边画直线).板块二平行公理――平行线的存在性与惟一性经过直线外一点,有且只有一条直线与这条直线平行平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行平行线的判定两直线平行的判定方法方法一两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行简称:同位角相等,两直线平行方法二两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行简称:内错角相等,两直线平行方法三两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行简称:同旁内角互补,两直线平行方法四垂直于同一条直线的两条直线互相平行方法五(平行线公理推论)如果两条直线都与第三条直线平行,那么这两条直线也互相平行方法六(平行线定义)在同一平面内,不相交的两条直线平行板块三.平行线的性质:性质一:两条平行线被第三条直线所截,同位角相等简称:两条直线平行,同位角相等性质二:两条平行线被第三条直线所截,内错角相等简称:两条直线平行,内错角相等性质三:两条平行线被第三条直线所截,同旁内角互补简称:两条直线平行,同旁内角互补2. 两条平行线间的距离:同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度叫做这两条平行线的距离。
七年级下平行线讲义(

平行关系教学目标1、会在简单的图形中辨认同位角、内错角、同旁内角。
2、会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算。
3、理解平行线的判定方法;4、学会用进行简单的几何推理;5、体会用实验的方法得出几何性质(规律)的重要性与合理性.重点、难点1、同位角、内错角、同旁内角的概念与判定 方法2各对关系角的辨认,复杂图形的辨认是本节教学3、推理过程的正确表达.教学内容知识瞭望 1、“三线八角”:如图:直线 a1 , a2 被直线 a3 所截,构成了八个角。
a1a2a3876543212、平行线的判定公理:同位角相等,两直线平行.∵ ∠1=∠2, ∴ a ∥b.判定定理1:内错角相等,两直线平行.∵ ∠1=∠2, ∴ a ∥b.判定定理2:同旁内角互补,两直线平行.∵∠1+∠2=180, ∴ a ∥b.典例剖析例1、∠1的内错角是 ,它们是由直线 和直线 被直线所截而成的,若这两个角相等,那么 ∥∠5的内错角是 ,它们是由直线 和直线 被直线所截而成的,若这两个角相等,那么 ∥∠8的内错角是 ,它们是由直线 和直线 被直线 所截而成的,若这两个角相等,那么 ∥∠3的内错角是 ,它们是由直线 和直线 被直线 所截而成的,若这两个角相等,那么 ∥24865731OBC DAabc21例2、如图,直线AB 、CD 被直线EF 所截,交点分别为点O 、P ,OM 平分∠EOB 、PN 平分∠OPD.如果∠1=∠2,(1)OM ∥PN 吗?为什么?(2)AB ∥CD 吗?为什么? 解:(1)OM ∥PN因为∠1=∠2( )所以 ∥ ( ) (2) AB ∥CD因为OM 平分∠EOB ,PN 平分∠OPD ( ) 所以∠ =21∠EOB, ∠ =21∠OPD( )又∵∠1=∠2(已知)∴∠ =∠ ( )∴ ∥ ( ) 例3、如图,∠E +∠B =∠D ,判断AB 与CD 是否平行点将练兵一.判断题:1.两条直线被第三条直线所截,只要同旁内角相等,则两条直线一定平行。
第一讲 平行线

第一讲 第一章 平行线一、平行线知识点1、平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线a 与直线b 互相平行,记作________. 知识点2、两条直线的位置关系在同一平面内,两条直线的位置关系只有两种:⑴______;⑵_______。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们______;反过来也一样(这里,我们把重合的两直线看成一条直线)判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定: ①有且只有一个公共点,两直线______; ②无公共点,则两直线______; ③两个或两个以上公共点,则两直线______(理由:________________) 知识点3、平行公理――平行线的存在性与惟一性经过直线外一点,___且_____一条直线与这条直线平行 知识点4、*平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相_______二、同位角、内错角和同旁内角知识点5、三线八角两条直线被第三条直线所截形成八个角,它们构成了_______、________与__________。
如图,直线b a ,被直线l 所截① 同位角(位置相同)有_____对, 分别是:② 内错角(位置在内且居截线两侧)有______对,分别是:③ 叫做同旁内角(位置在内且居截线同旁)有______对,分别是: ④三线八角也可以成模型中看出。
同位角是“F”型;内错角是“Z”型;同旁内角是“U”型。
知识点6、如何判别三线八角判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,也可用模型(FZU 型)判断。
【例】1.∠1与∠B 是直线____和直线____被直线_____所截而成的_________角;2.∠2与∠A 是直线____和直线____被直线_____所截而成的_________角; 3.∠3与∠B 是直线____和直线____被直线_____所截而成的_________角;思考:∠2与∠B 是同位角、内错角还是同旁内角?为什么?【练】1.如右图,按各角的位置,下列判断错误的是( )(A )∠1与∠2是同旁内角 (B )∠3与∠4是内错角a b l 1 2 3 4 5 6 7 8B E 12348(C)∠5与∠6是同旁内角(D)∠5与∠8是同位角2.下列4个图中,∠1与∠2不是同位角的是()(A) (B)(C )(D)三、平行线的判定与性质知识点7、平行线的判定与性质平行线的性质与判定是互逆的关系:两直线平行同位角相等;两直线平行内错角相等;两直线平行注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”。
平行线讲义

平行线知识总结1、平行线的概念在同一个平面内,不相交的两条直线叫做平行线。
平行用符号“∥”表示,如“AB∥CD”,读作“AB平行于CD”。
同一平面内,两条直线的位置关系只有两种:相交或平行。
注意:(1)平行线是无限延伸的,无论怎样延伸也不相交。
(2)当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
2、平行线公理及其推论平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
3、平行线的判定平行线的判定公理:两条直线被第三条直线所截,如果同位角相等,那么两直线平行。
简称:同位角相等,两直线平行。
平行线的两条判定定理:(1)两条直线被第三条直线所截,如果内错角相等,那么两直线平行。
简称:内错角相等,两直线平行。
(2)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。
简称:同旁内角互补,两直线平行。
补充平行线的判定方法:(1)平行于同一条直线的两直线平行。
(2)垂直于同一条直线的两直线平行。
(3)平行线的定义。
4、平行线的性质(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
5、认识三角形(1)三角形构成的条件:两边之和大于第三边;(2)推论:两边之差小于第三边;(3)三角形的中线、角平分线、高的定义。
6、多边形的内角和与外角和(1)用平行线的性质定理证明三角形的内角和是180°;(2)n边形的内角和等于(n-2)·180°;(3)多边形的外角和等于360°。
一、选择题1.下列各组角中,∠1与∠2是对顶角的为( )2如图,描述同位角、内错角、同旁内角关系不正确的是()A.∠1与∠4是同位角B.∠2与∠3是内错角C.∠3与∠4是同旁内角D.∠2与∠4是同旁内角3.如图,OB⊥OD,OC⊥OA,∠BOC=32°,那么∠AOD等于(A)A.148°B.132°C.128°D.90°4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数(B)A.65°B.55°C.45°D.35°5.下列命题中,真命题的个数是(D)①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③图形平移的方向一定是水平的;④内错角相等.A.4 B.3 C.2 D.16.如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD.其中能使AD∥BC的条件为(C)A.①②B.③④C.②④D.①③④12.如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则从C岛看A,B两岛的视角∠ACB=70°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题01 平行线知识讲义【技能一】两条直线的位置关系两条直线的位置关系有三种:(1)平行——没有公共点,在同一平面内;(2)相交——有且只有1个公共点,在同一平面内;(3)异面——没有公共点,不在同一平面内.(如下图所示,直线a与b异面)【技能二】与相交线有关的知识点1. 邻补角互补;2. 对顶角相等;3. 垂直是相交的特殊情况.判断两直线垂直的方法:两直线相交形成的四个角中,①一个为直角;②邻补角相等;③对顶角互补.4. 垂线段最短;5. 从直线外一点到直线的垂线段的长度,叫做点到直线的距离.6. 直角三角形斜边上的高等于直角边的乘积除以斜边的长.由S△=ab÷2=ch÷2得:h=ab÷c【技能三】三线八角1. 同位角近似“F” 【★同位角不一定相等】2. 内错角近似“Z” 【★内错角不一定相等】3. 同旁内角近似“U” 【★同旁内角不一定互补】【技能四】平行线的知识点同一平面内,永远不相交的两条直线互相平行,直线a与直线b平行,记作a∥b.【技能五】令人“烦恼”的前提前提:“同一平面内”,“直线外”在哪些情况下添加?过直线外一点,有且只有一条直线与已知直线平行;同一平面内,过一点有且只有一条直线与已知直线垂直;同一平面内,同垂直于一条直线的两条直线互相平行;【技能六】平行线的判定六法1. 定义——同一平面内,不相交的两条直线平行2. 同位角相等,两直线平行3. 内错角相等,两直线平行4. 同旁内角互补,两直线平行5. 平行线传递性6. 同一平面内,同垂直于一条直线的两条直线互相平行【技能七】平行线的性质及命题两直线平行,同位角相等,内错角相等,同旁内角互补.命题组成:题设、结论.形式:如果……,那么……分类:真命题,假命题★若两个角的两组边分别平行(垂直),则这两个角相等或互补.【如下图所示】【技能八】平移性质两条线段平移前后,长度不变,位置共线或平行.考点一:相交线题型一、基本概念例1.(2020·江阴市长泾月考)下列说法错误的是()A.对顶角相等B.两点之间所有连线中,线段最短C.等角的补角相等D.过任意一点P,只能画一条直线【变式1-1】(2020·右玉县期中)下列说法中正确的有( )①对顶角相等;②一个角的补角大于这个角;③互为邻补角的两个角的平分线互相垂直;④若两个实数的和是正数,则这两个实数都是正数.A .1个B .2个C .3个D .4个题型二、求角度例2-1.(2021·江西赣州期末)北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道AB 在点O 南偏东70°的方向上,则这条跑道所在射线OB 与正北方向所成角的度数为( )A .160°B .110°C .70°D .20°例2-2.(2020·浙江嘉兴期末)将一把直尺和一块三角板如图叠放,直尺的一边刚好经过直角三角板的直角顶点且与斜边相交,则1∠与2∠一定满足的数量关系是( )A .221∠=∠B .21180∠+∠=︒C .221180∠+∠=︒D .2190∠-∠=︒【变式2-1】.(2021·山东济南期中)如图,直线m 和n 相交于点O ,若∠1=40°,则∠2的度数是( )A .40°B .50°C .140°D .150°【变式2-2】.(2019·河北邢台期末)小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC ,并将边AC 延长至点P ,第二步将另一块三角板CDE 的直角顶点与三角板ABC 的直角顶点C 重合,摆放成如图所示,延长DC 至点F ,PCD ∠与ACF ∠就是一组对顶角,若30ACF ∠=,则PCD ∠=__________,若重叠所成的∠BCE =n °(0<n <90),则∠PCF 的度数为__________.【变式2-3】(2020·广东阳江期末)如图,两条直线AB,CD交于点O,射线OM是∠AOC 的平分线,若∠BOD=80°,则∠BOM的度数是.题型三、综合题例3.(2021·湖北十堰期末)如图,直线AB,CD相交于点O,OE平分∠AOD,OF∠OC,(1)图中∠AOF的余角是________ (把符合条件的角都填出来);(2)如果∠AOC=140°,那么根据________,可得∠BOD=________;(3)如果∠1=31°,求∠2和∠3的度数.【变式3-1】(2021·辽宁抚顺期末)如图,已知O 为直线AD 上一点,OB 是AOC ∠内部一条射线且满足AOB ∠与AOC ∠互补,OM ,ON 分别为AOC ∠,AOB ∠的平分线.(1)COD ∠与AOB ∠相等吗?请说明理由;(2)若30AOB ∠=︒,试求MON ∠的度数;(3)若MON α∠=,请直接写出AOC ∠的度数.(用含α的式子表示)考点二:垂线题型一、基础概念例1-1.(2021·山东临沂期末)下列四个生活、生产现象:∠用两枚钉子就可以把木条固定在墙上;∠植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;∠体育课上,老师测量某同学的跳远成绩;∠把弯曲的公路改直,就能缩短路程,其中可用基本事实“两点确定一条直线”来解释的现象有( )A .∠∠B .∠∠C .∠∠D .∠∠例1-2.(2021·北京顺义期末)如图,点P 在直线l 外,点A 、B 在直线l 上,若4PA =,7PB =,则点P 到直线l 的距离可能是( )A .3B .4C .5D .7例1-3.(2020·湖南湘潭月考)下列命题中,其中正确的有( ).∠两条相交直线组成的四个角相等,则这两直线垂直.∠两条相交直线组成的四个角中,若有一个直角,则四角都相等.∠两条直线相交,一角的两邻补角相等,则这两直线垂直.∠两条直线相交,一角与其邻补角相等,则这两直线垂直.A .1个B .2个C .3个D .4个【变式1-1】(2019·山西月考)如图,在三角形ABC 中,90ACB ∠=︒,CD AB ⊥于点D ,则图中能表示点B 到直线AC 的距离的是( )A .CD 的长度B .BC 的长度 C .BD 的长度 D .AD 的长度【变式1-2】(2020·福建三明期中)如图所示,某工程队计划把河水引到水池A 中,他们先过A 点作AB CD ⊥,垂足为B ,然后沿AB 开渠,可以节约人力、物力和财力,这样设计的数学依据是( )A .两点之间线段最短B .经过两点有且只有一条直线C .垂直定义D .垂线段最短【变式1-3】(2020·广西贺州期末)下列语句错误..的是( ). A .直线外一点到这条直线的垂线段叫做点到直线的距离.B .在直线外一点与直线上各点的线段中,垂线段最短.C .同一平面内,过一点有且只有一条直线垂直于已知直线.D .经过直线外一点,有且只有一条直线平行于这条直线.题型二、相关计算例2-1.(2020·河南省淮滨县第一中学七年级期末)如图,OA OC ⊥,OB OD ⊥,且150AOD ∠=︒,则BOC ∠的度数是( )A .60︒B .30C .50︒D .40︒例2-2.(2019·浙江杭州)已知60BOC ︒∠=,OF 平分BOC ∠.若AO BO ⊥,OE 平分AOC ∠,则EOF ∠的度数是( )A.45︒B.15︒C.30︒或60︒D.45︒或15︒例2-3.(2021·江苏泰州期末)如图,直线AB、CD相交于点O,OE平分∠BOD,OF∠CD,若∠BOC比∠DOE大75o.求∠AOD和∠EOF的度数.∠,【变式2-1】(2019·四川绵阳期末)如图,若直线AB与CD相交于点O,OD平分BOF ∠=︒,则COE∠的度数为()⊥且29OE OFBODA.116︒B.118︒C.119︒D.120︒【变式2-2】(2020·湖北咸宁期末)如图,直线AB、CD相交于点O,OE平分∠AOC,OF∠OE 于点O,若∠AOD=70°,则∠AOF=______度.【变式2-3】(2020·沭阳县月考)已知如图,直线AB 、CD 相交于点O ,∠COE =90°. (1)若∠AOC =36°,求∠BOE 的度数;(2)若∠BOD :∠BOC =1:5,求∠AOE 的度数;(3)在(2)的条件下,过点O 作OF ∠AB ,请直接写出∠EOF 的度数.【变式2-4】如图,直线BC 、DE 相交于点O ,OA 、OF 为射线,OA OB ⊥,OF 平分BOE ∠,BOF COD ∠+∠=54.求AOE ∠的度数.考点三:三线八角例1.(2020·长汀县月考)如图所示,下列结论中正确的是()A.∠1和∠2是同位角B.∠1和∠4是内错角C.∠2和∠3是同旁内角D.∠3和∠4是对顶角例2.(2019·商水县期末)如图所示,同位角有a对,内错角有b对,同旁内角有c对,则a+b-c的值是____________例3.(2021·河南周口期末)如图,找出标注角中的同位角、内错角和同旁内角.【变式1】.(2020·黑龙江哈尔滨期末)如图,1∠和2∠不是同旁内角的是( ) A .B .C .D .【变式2】.(2019·河南洛阳期中)如图,1∠和2∠是同位角的有( )A .∠∠B .∠∠C .∠∠D .∠∠【变式3】.(2020·河南周口期中)如图,直线AB ,CD 被直线EF 所截,与AB ,CD 分别交于点E,F,下列描述:∠∠1和∠2互为同位角∠∠3和∠4互为内错角∠∠1=∠4 ∠∠4+∠5=180°其中,正确的是()A.∠∠B.∠∠C.∠∠D.∠∠【变式4】(2020·湖北武汉月考)如图所示的图形中,同位角有_____对考点四:平行线例1.(2021·江苏宿迁期末)下列说法错误的是()A.平面内过一点有且只有一条直线与已知直线平行B.平面内过一点有且只有一条直线与已知直线垂直C.两点之间的所有连线中,线段最短D.对顶角相等例2.(2020·四川师范大学附属中学期中)下列说法中不正确的个数为().∠在同一平面内,两条直线的位置关系只有两种:相交和垂直.∠有且只有一条直线垂直于已知直线.∠如果两条直线都与第三条直线平行,那么这两条直线也互相平行.∠从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.∠过一点,有且只有一条直线与已知直线平行.A.2个B.3个C.4个D.5个【变式1】.(2021·陕西宝鸡期末)下列说法中正确的个数为()∠不相交的两条直线叫做平行线;∠平面内,过一点有且只有一条直线与已知直线垂直;∠平行于同一条直线的两条直线互相平行;∠在同一平面内,两条直线不是平行就是相交.A.1个B.2个C.3个D.4个【变式2】.(2020·江苏苏州期中)下列说法中:∠对顶角相等;∠同位角相等;∠平行于同一条直线的两条直线平行;∠垂直于同一条直线的两条直线垂直;其中正确的有()A.1 个B.2 个C.3 个D.4 个内部有一点M,过点M画OA的平行线,这样【变式3】.(2019·山西月考)已知AOB的直线( )A .有且只有一条B .有两条C .有三条D .有无数条考点五:平行线的判定例1. (2020·浙江杭州期中)如图,下列四个图中12∠=∠,不能判断不能判定//a b 的是( ) A . B .C .D .例2.(2021·河南开封期末)如图,下列条件能判断//AD CB 的是( )A .180D DAB ∠+∠=︒ B .12∠=∠C .34∠=∠D .45∠=∠例3.(2021·福建三明期末)如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是()A.同位角相等,两直线平行B.两直线平行,同位角相等C.两直线平行,内错角相等D.内错角相等,两直线平行例4.(2021·浙江绍兴期末)如图,已知CD∠DA,DA∠AB,∠1=∠4.试说明DF∠AE.请你完成下列填空,把证明过程补充完整.证明:∠_________(___________)∠∠CDA=90°,∠DAB=90°(_________).∠∠4+∠3=90°,∠2+∠1=90°.又∠∠1=∠4,∠_____(_____),∠DF∠AE(______).例5.(2020·甘肃张掖期末)已知:如图,1C ∠=∠,2∠和D ∠互余,1∠和D ∠互余,求证://AB CD .例6.(2020·渠县月考)已知:如图,,,,AC AB BD AB CAE DBF ⊥⊥∠=∠且请猜想直线AE 与BF 的位置关系,并说明理由.【变式1】(2020·洛阳市月考)下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )A .∠代表∠FECB .□代表同位角C .▲代表∠EFCD .∠代表AB【变式2】(2020·浙江金华期末)下列说法中:(1)不相交的两条直线叫做平行线;(2)经过一点,有且只有一条直线与已知直线平行;(3)垂直于同一条直线的两直线平行;(4)直线//a b ,//b c ,则//a c ;(5)两条直线被第三条直线所截,同位角相等.其中正确的是________.【变式3】(2019·山西期末)如图1,在探索“如何过直线外一点作已知直线的平行线”时,小颖利用两块完全相同的三角尺进行如下操作:如图 2 所示,(1)用第一块三角尺的一条边贴住直线 l ,第二块三角尺的一条边紧靠第一块三角尺;(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点 A ,沿这边作出直线 AB ,直线 AB 即为所求,则小颖的作图依据是________.【变式4】(2020·江西宜春期末)如图,已知点E 在直线DC 上,射线EF 平分∠AED ,过E 点作EB ∠EF ,G 为射线EC 上一点,连结BG ,且90EBG BEG ︒∠+∠=.(1)求证:DEF EBG ∠=∠;(2)若EBG A ∠=∠,试判断AB 与EF 的位置关系,并说明理由.考点六:平行线的性质题型一、求度数例1-1.(2020·浙江杭州期中)如图,//AB CD ,AD AC ⊥,32ADC ︒∠=,则CAB ∠的度数是( )A .120度B .121度C .122度D .123度例1-2.(2021·山东潍坊期末)一把直尺与30°的直角三角板如图所示,150∠=︒,则2∠=( )A .50°B .60°C .70°D .80°【变式1-1】(2020·浙江金华期中)如图所示,已知AD 与BC 相交于点O ,////CD OE AB .如果40B ∠=︒,30D ∠=︒,则AOC ∠的大小为( )A .60°B .70°C .80°D .120°【变式1-2】如图,∠1=∠2,AC 平分∠DAB ,且∠D :∠DAB =2:1,则∠D 的度数是( )A .120°B .130°C .140°D .150°题型二、方位角 例2.(2021·甘肃白银期末)一条船停留在海面上,从船上看灯塔位于北偏东60°方向,那么从灯塔看船位于灯塔的 方向( )A .南偏西60°B .西偏南60°C .南偏西30°D .北偏西30°【变式】如图,李强和同事驾驶快艇执行巡逻任务,他们从岛屿A 处向正南方向航行到B 处时,向右转60︒航行到C 处,再向左转80︒继续航行,此时快艇的航行方向为( )A .南偏东20︒B .南偏东80︒C .南偏西20︒D .南偏西80︒题型三、综合题型 例3-1.(2020·浙江杭州期中)已知A ∠的两边与B 的两边分别平行,若A ∠的度数比B 的2倍少30°,则B 的度数是( )A .30°B .50°C .30°或70°D .50°或70°例3-2.如图,已知直线AB 、CD 被直线AC 所截,//AB CD ,E 是直线AC 右边任意一点(点E 不在直线AB ,CD 上),设BAE α∠=,DCE β∠=.下列各式:∠αβ+,∠αβ-,∠βα-,∠360αβ︒--,AEC ∠的度数可能是( )A .∠∠∠B .∠∠∠C .∠∠∠D .∠∠∠∠例3-3.(2021·陕西咸阳期末)如图,360ABC C CDE ∠+∠+∠=︒,直线FG 分别交AB 、DE 于点F 、G .若1110∠=︒,则2∠=___________.例3-4.(2021·陕西西安期末)如图,178∠=︒,2102∠=︒,C D ∠=∠.求证://AC DF .【变式3-1】(2021·山东青岛期末)如图,//AB CD ,点E 在AC 上,110A ∠=︒,15D ∠=︒,则下列结论正确的个数是( )(1)AE EC =;(2)85AED ∠=︒;(3)A CED D ∠=∠+∠;(4)45BED ∠=︒A .1个B .2个C .3个D .4个【变式3-2】(2021·广西贵港期末)如图,直线a ,b ,//a b ,点C 在直线b 上,90DCB ∠=︒,若170∠=︒,则2∠的度数为______.【变式3-3】(2020·浙江金华期中)已知A ∠与B (A ∠,B 都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且227A B ∠-∠=︒,则A ∠的度数为_________.【变式3-4】(2020·黑龙江哈尔滨期末)在同一平面内,A ∠与B 的两边分别平行,若50A ∠=︒,则B 的度数为__________︒.【变式3-5】(2021·河南洛阳期末)直线AB 和CD 被直线MN 所截,如图1,EG 平分MEB ∠,FH 平分DFE ∠,当12∠=∠时,小明证明//AB CD 的过程如下:∠EG 平分MEB ∠,FH 平分DFE ∠(已知),∠21MEB ∠=∠,22DFE ∠=∠(角平分线的定义). ∠12∠=∠,(已知),∠MEB DFE ∠=∠(等量代换).∠//AB CD (同位角相等,两直线平行).请你参考上述证明过程解决下列问题:(1)如图2,EG 平分AEF ∠,FH 平分DFE ∠,1∠与2∠满足什么条件时,//AB CD ?说明理由.(2)如图3,若//AB CD ,EG 平分AEM ∠,FH 平分CFN ∠,则1∠与2∠满足怎样的条件?说明理由.【变式3-6】(2021·四川成都期末)完成下面推理过程,在括号内的横线上填空或填上推理依据.如图,已知://AB EF ,EP EQ ⊥,90EQC APE ∠+∠=︒,求证://AB CD证明://AB EFAPE ∴∠=__________(__________)EP EQ ⊥PEQ ∴∠=_________(___________)即90QEF PEF ∠+∠=︒90APE QEF ∴∠+∠=︒90EQC APE ∠+∠=︒EQC ∠=________//EF ∴_______(__________________)//AB CD ∴(________________)考点七:命题例1. 举反例说明 “互为补角的两个角都是直角”为假命题.例2.(2021·浙江绍兴期末)把“同位角相等”写成“如果…那么…”的形式为:为_____.【变式1】判断下列命题的真假,如果是假命题,请举一个反例,真命题不需要举例. (1)钝角的补角是锐角;(2)一个角的余角小于这个角;(3)如果a b =,那么a b =.【变式2】(2021·山东青岛期末)把命题“锐角小于90°”改写成“如果……那么……”的形式:______.考点八:平移例1. (2020·浙江杭州模拟)如图,将ABC 沿AC 方向平移1cm 得到DEF ,若ABC 的周长为10cm ,则四边形ABEF 的周长为( )A .14cmB .13cmC .12cmD .10cm例2.(2021·上海宝山期末)如图,ABC 经过平移后得到DEF ,下列说法:∠//AB DE∠AD BE =∠ACB DFE ∠=∠∠ABC 和DEF 的面积相等∠四边形ACFD 和四边形BCFE 的面枳相等,其中正确的有( )A .4个B .3个C .2个D .1个【变式1】(2021·北京丰台期末)如图,将ABC ∆沿BC 所在的直线平移得到DEF ∆.如果2GC =, 4.5DF =, 那么AG =____.【变式2】(2021·上海浦东新区期末)如图,已知直角三角形ABC ,90A ∠=︒,4AB =厘米,3AC =厘米,5BC =厘米,将ABC 沿AC 方向平移1.5厘米,线段BC 在平移过程中所形成图形的面积为__________平方厘米.。
