离散时间信号处理PPT_第二章 离散时间信号系统
合集下载
离散时间信号处理
– Processing analog signals in a digital way. – Processing digital signals.
• Advantages:
– High reliability（可靠性） – High agility (灵活性好，易于实现系统性能） – High precision（高精度） – Low cost （成本低） –…
•第20页 20
Example: generate the signal with impulse sequence
a3
a3 (n 3)2 -1 0 1 2 3 4 5 n
a6
n 0
a2 (n 2)
a2
n 0
a6 (n 6)
0
x(n) a3 (n 3) a2 (n 2) a6 (n 6)
A convenient notation for the sequence x just is x(n).
•离散时间信号处理
•第12页 12
2.1 Discrete-time signals — graph
• Discrete-time signals are often depicted graphically.
• A discrete-time signal can be represented as
{x(nT), n Z}
where T is time interval between samples. Each sample of sequence x(nT) is determined by the amplitude of signal at instant nT. For example
– Discrete-time signals are those that are defined at discrete times.
• Advantages:
– High reliability（可靠性） – High agility (灵活性好，易于实现系统性能） – High precision（高精度） – Low cost （成本低） –…
•第20页 20
Example: generate the signal with impulse sequence
a3
a3 (n 3)2 -1 0 1 2 3 4 5 n
a6
n 0
a2 (n 2)
a2
n 0
a6 (n 6)
0
x(n) a3 (n 3) a2 (n 2) a6 (n 6)
A convenient notation for the sequence x just is x(n).
•离散时间信号处理
•第12页 12
2.1 Discrete-time signals — graph
• Discrete-time signals are often depicted graphically.
• A discrete-time signal can be represented as
{x(nT), n Z}
where T is time interval between samples. Each sample of sequence x(nT) is determined by the amplitude of signal at instant nT. For example
– Discrete-time signals are those that are defined at discrete times.
Lecture 2_离散时间信号分析,华工数字信号处理课件,DSP
二、离散时间信号的运算
8
基本运算
相乘（product） 相加（addition）
wn xn yn wn xn yn wn Axn wn xn N wn x n
调制、加窗
集合平均
数乘（multiplication）
8 -6 -4 -2 0 2 4 6 10
Q: Can a sample of discrete-time signal take real (continuous) value?
4
离散信号是从哪里来的？
A discrete time sequence x[n] may be generated by periodically sampling a continuous-time signal at uniform intervals of time.
12
采样率的转换（1）
采样率转换：
从给定序列生成采样率高于或低于它的新序列的运算
设原采样率为 FT ，转换后的采样率为 FT
则采样率转换比：
FT R FT
R 1 ：插值（Interpolation）
R 1
抽取（Decimation）
采样率的转换（2）
上采样（up-sampling）
序列
xn 的 Lp 范数定义：
x
L2 范数是 L1范数是
p
( x[n] )
p n
1
p
xn均方根；
xn平均绝对值； xn绝对值的峰值
L范数定义： x x max
有限长序列x的范数MATLAB计算
norm(x); norm(x,2); norm(x,1); norm(x,inf)
第二章(1)时域离散信号和系统的频域分析
第二章 离散时间信号和离 时间系统
2.1 引言
一. FT是重要的变换
1.分析有限长序列的有用工具。 2.在信号处理的理论上有重要意义。 3.在运算方法上起核心作用，谱分析、 卷积、相关都可以通DFT在计算机上 实现。
二、本章主要讨论内容
♦ 付里叶变换的推导 ♦ 付里叶变换的有关性质 ♦ 离散序列付里叶变换逼近连续时间信号的问题 ♦ 序列的Z变换 ♦ Z变换与系统的关系
实部为偶 对称序列 虚部为奇 对称序列
0
n
0
n
（2）定义：若xo(n)满足 xo(n)= -xo*(-n)； （2.2.13）， 则称xo(n)为共轭反对称序列。 将其分成实部和虚部： 用-n取代 n并取共轭：
xo (n) = xor (n) + jxoi (n)
xo*(-n)= xor(-n)-jxoi(-n)
∞
(2.2.8) (2.2.9)
证: FT [ x(n ± n0 )] =
k = n ± n0 → =
n =−∞
∑
x(n ± n0 )e − jω n
k =−∞
∑
∞
x(k )e − jω ( k ∓ n0 ) = e ± jω n0
k =−∞
∑
∞
∞
x(k )e − jω k = e ± jω n0 X (e jω ) x ( n ) e − j (ω ∓ ω 0 ) n = X ( e j (ω ∓ ω 0 ) )
∞
n =−∞
∑
∞
x(n)e− jω n
= ∑ RN (n)e n
n =−∞
− jω n
N-1 ∞ = ∑ e − jω n
n =0
设N＝4其幅度和相 位随ω变化如下图所 示
2.1 引言
一. FT是重要的变换
1.分析有限长序列的有用工具。 2.在信号处理的理论上有重要意义。 3.在运算方法上起核心作用，谱分析、 卷积、相关都可以通DFT在计算机上 实现。
二、本章主要讨论内容
♦ 付里叶变换的推导 ♦ 付里叶变换的有关性质 ♦ 离散序列付里叶变换逼近连续时间信号的问题 ♦ 序列的Z变换 ♦ Z变换与系统的关系
实部为偶 对称序列 虚部为奇 对称序列
0
n
0
n
（2）定义：若xo(n)满足 xo(n)= -xo*(-n)； （2.2.13）， 则称xo(n)为共轭反对称序列。 将其分成实部和虚部： 用-n取代 n并取共轭：
xo (n) = xor (n) + jxoi (n)
xo*(-n)= xor(-n)-jxoi(-n)
∞
(2.2.8) (2.2.9)
证: FT [ x(n ± n0 )] =
k = n ± n0 → =
n =−∞
∑
x(n ± n0 )e − jω n
k =−∞
∑
∞
x(k )e − jω ( k ∓ n0 ) = e ± jω n0
k =−∞
∑
∞
∞
x(k )e − jω k = e ± jω n0 X (e jω ) x ( n ) e − j (ω ∓ ω 0 ) n = X ( e j (ω ∓ ω 0 ) )
∞
n =−∞
∑
∞
x(n)e− jω n
= ∑ RN (n)e n
n =−∞
− jω n
N-1 ∞ = ∑ e − jω n
n =0
设N＝4其幅度和相 位随ω变化如下图所 示
第二章时域离散时间信号与系统1
N个抽样间隔应等于k个连续正弦信号周期
例：
x(n) sin( 3 2 n)
14
0
3 14
2
2 14 N T0 0 3 k T
当14T 3T0时，x(n)为周期为14的周期序列
序列的能量为序列各抽样值的平方和
S x(n) 2 n
x(n)可以表示成单位脉冲序列的移位加权和， 也可表示成与单位脉冲序列的卷积和。
2.1.1信号的采样与采样定理 1.采样的定义：就是利用周期性抽样脉冲序列
pT(t),从连续信号xa(t)中抽取一系列的离散值 ，得到抽样信号（或称抽样数据信号）即离 散时间信号。
抽样是模拟信号数字化的第一环节，再经幅 度量化、编码后即得到数字信号x(n)。
研究内容：
信号经采样后发生的变化（如频谱的变化）
考虑数字正弦序列是由模拟信号 xa (t) Asin t 采样得到，
即
x(n) xa (t) tnT Asin(nT) (2)
数字域频率和模拟信号频率的对应关系
比较(1)、(2)两式得 T
fs
(1.2.9)
ω0=π/8 T=1/16
6.复指数序列 x(n) e( j )n
还可写成
2.序列相乘
是指同序号(n)的 序列值逐项对应 相乘。
x(n) x1(n) x2(n)
3.序列的标乘
A x Ax(n) y(n)
序列的相加和相乘： x1=[0 1 2 3 4 3 2 1 0];ns1=-2; x2=[2 2 0 0 0 -2 -2];ns2=2; nf1=ns1+length(x1)-1; nf2=ns2+length(x2)-1; ny=min(ns1,ns2):max(nf1,nf2); xa1=zeros(1,length(ny)); xa2=xa1; xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1; xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2; ya=xa1+xa2; yb=xa1.*xa2; subplot(2,2,1),stem(ny,xa1);ylabel('x1(n)') subplot(2,2,3),stem(ny,xa2);ylabel('x2(n)') subplot(2,2,2),stem(ny,ya);ylabel('x1(n)+x2(n)') subplot(2,2,4),stem(ny,yb);ylabel('x1(n)*x2(n)')
数字信号处理课件第二章--离散时间信号与系统(ppt文档)
• 2.2.4 因果性（Causality） 系统在n时刻的输出只取决于n时刻以及n时刻以 前的输入，而与n时刻以后的输入无关。 y[n] x[n], x[n-1], x[n-2], … 因果系统---- 物理可实现性 x[n+1], x[n+2], … 非因果系统---- 物理不可实现性
一个非因果系统的例子： y[n]=x[n+1]-x[n]
2.2离散时间系统
离散系统可以定义为一种变换或一个算子，即：
用公式表示为：
y[n] T x[n]
2.2.1 无记忆系统（Memoryless Systems）
y[n]x[n] 例： y[n] x[n]2
2.2.2 线性系统（Linear Systems） 满足叠加原理的系统称为线性系统
y[n] x[k]h[n-k]
k
一个线性时不变（LTI）系统完全可以由它的单位脉冲 响应来表征。
• 卷积和（Convolution）
x1[n] x2[n] x1[k]x2[n k] k
系统输出可表示为：
y[n] x[k]h[n k] x[n] h[n] k
因果序列: x[n] 0, n 0
因果稳定的线性时不变系统：h[n]单边且绝对可和
例：
h[n] anu[n]
a 1
h[n]有限长非零样本-------- 有限冲击响应系统（finite-duration impulse response，FIR）------- 系统总是稳定的
h[n]无限长非零样本-------- 无限冲击响应系统（infinite-duration impulse response，IIR）
第二章 时域离散信号和系统(数字信号处理)
第二章 时域离散信号和系统
6. 复指数序列
x(n)=e(σ+jω0)n 式中ω0为数字域频率，设σ=0，用极坐标和实部虚 部表示如下式： x(n)=e jω0n
x(n)=cos(ω0n)+jsin(ω0n)
由于n取整数，下面等式成立： e j(ω0+2πM)n= e jω0n, M=0,±1,±2…
第二章 时域离散信号和系统
图1.2.5 正弦序列
第二章 时域离散信号和系统
则要求N=(2π/ω0)k，式中k与N均取整数，且k的取
值要保证N是最小的正整数，满足这些条件，正弦序列 才是以N为周期的周期序列。
正弦序列有以下三种情况：
(1)当2π/ ω0为整数时，k=1，正弦序列是以2π/ ω0 为周期的周期序列。例如sin(π/8)n， ω0 =π/8，2π/ ω0 =16,该正弦序列周期为16。
例 设x(n)=R4(n)，h(n)=R4(n)，求y(n)=x(n)*h(n)。
解 按照公式，
y (n )
m
R ( m) R ( n m)
4 4
上式中矩形序列长度为4，求解上式主要是根据矩
形序列的非零值区间确定求和的上、下限，R4(m)的非
令n-k=m，代入上式得到
u( n )
n
( m)
n
第二章 时域离散信号和系统
u(n) 1 „ n 0 1 2 3
单位阶跃序列
第二章 时域离散信号和系统
3. 矩形序列RN(n) 1, RN(n)= 0， 0≤n≤N-1 其它n
上式中N称为矩形序列的长度。当N=4时，R4(n)的
第二章 时域离散信号和系统
第2章 时域离散信号和系统
离散时间信号与离散时间系统
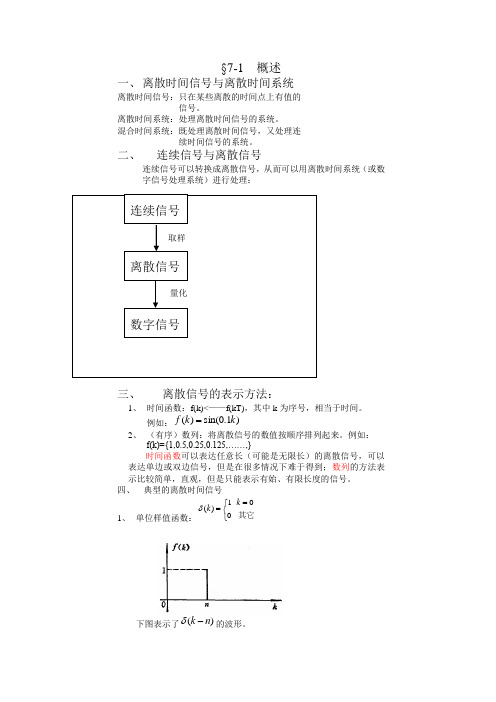
§7-1 概述一、 离散时间信号与离散时间系统离散时间信号：只在某些离散的时间点上有值的信号。
离散时间系统：处理离散时间信号的系统。
混合时间系统：既处理离散时间信号，又处理连续时间信号的系统。
二、 连续信号与离散信号连续信号可以转换成离散信号，从而可以用离散时间系统（或数字信号处理系统）进行处理：三、 离散信号的表示方法：1、 时间函数：f(k)<——f(kT)，其中k 为序号，相当于时间。
例如：)1.0sin()(k k f =2、 （有序）数列：将离散信号的数值按顺序排列起来。
例如：f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长（可能是无限长）的离散信号，可以表达单边或双边信号，但是在很多情况下难于得到；数列的方法表示比较简单，直观，但是只能表示有始、有限长度的信号。
四、 典型的离散时间信号1、 单位样值函数：⎩⎨⎧==其它001)(k k δ下图表示了)(n k -δ的波形。
连续信号离散信号 数字信号 取样量化这个函数与连续时间信号中的冲激函数)(t δ相似，也有着与其相似的性质。
例如：)()0()()(k f k k f δδ=， )()()()(000k k k f k k k f -=-δδ。
2、 单位阶跃函数：⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。
用它可以产生（或表示）单边信号（这里称为单边序列）。
3、 单边指数序列：)(k a k ε比较：单边连续指数信号：)()()(t e t e t a at εε=，其底一定大于零，不会出现负数。
4、 单边正弦序列：)()cos(0k k A εφω+(a) 0.9a = (d) 0.9a =-(b) 1a = (e) 1a =-(c) 1.1a = (f) 1.1a =-双边正弦序列：)cos(0φω+k A五、 离散信号的运算1、 加法：)()()(21k f k f k f +=<—相同的k 对应的数相加。
数字信号处理-第2章第1讲 离散时间信号和离散时间系统
当a>1时 当-1<a<0时 当a< -1时
2.2 常用序列
5、正弦序列
x(n) Asin(n )
x(n) xa (t) tnT Asin(nT ) T / fs 2 f / fs 单位rad, 单位rad / s
6、复指数序列
一阶后向差分： y(n) y(n) y(n 1) 二阶后向差分： 2 y(n) y(n) y(n 1)
y(n) 2 y(n 1) y(n 2) 用延时算子：Dy(n) y(n 1) y(n) y(n) Dy(n) (1 D) y(n) 1 D 2 y(n) y(n) y(n 1) (1 D) y(n) (1 D)Dy(n) (1 D)2 y(n)
卷积和
卷积和的定义
1. 交换律 2. 结合律
y(n) x(k)h(n k) x(n) h(n) k
y(n) h(n)x(n k) h(n) x(n) k
y(n) [x(n) h1(n)]*h2(n)
[x(n) h2(n)]*h1(n) x(n) [h1(n)*h2(n)]
线性非移变系统稳定的充要条件是满足绝对可 和的条件:
S h(n) n
证明:
(1)充分性
当 x(n) M得
y(n) h(k)x(n k) h(k) x(n k)
k
k
M h(k) 得证 k
(2)必要性
x(n) e( j)n
数字频率又叫归一化频率
x(n) en cos(n) jen sin(n)
大学课件浙大数字信号处理课件第二章离散时间信号与系
第二章 离散时间信号与系统
2.0 引言 2.1 离散时间序号：序列 2.2 离散时间系统 2.3 线性时不变系统 2.4 线性时不变系统的性质 2.5 线性常系数差分方程 2.6 离散时间信号与系统的频域表示 2.7 用傅立叶变换表示序列 2.8 傅立叶变换的对称性质 2.9 傅立叶变换定理 2.10 离散时间随机信号（介绍）
连续时间信号、离散时间信号、数字信号
t(s) n
n
数字信号量化表：{-1 –0.5 0 0.5 1}
2.1.1 基本序列和序列运算
序列的基本运算 加法运算：z[n]=x[n]+y[n]={…,x[-1]+y[-1],x[0]+y[0],x[1]+y[1],…}, -∞<n<∞
乘法运算
x[n]*y[n]={…,x[-1]*y[-1],x[0]*y[0],x[1]*y[1],…}, -∞<n<∞
2.2.3 时不变系统
时不变系统是这样一种系统：输入序列的移位将引起输出序列相应的移位。
也就是说，如果T{x[n]}=y[n]，那么T{x[n-n0]}=y[n-n0] for all n0
要证明一个系统是时不变的，必须解出T{x[n-n0]}和 y[n-n0]，看两者是否相等 。
n
例1 y[n] (0.5)ni x[i]
2.1 离散时间信号：序列
连续时间信号： xa(t) 离散时间信号：x[n]=xa(nT), -∞<n<∞ 其中，T是采样周期，f=1/T为采样频率。 注：实际上，离散时间信号未必一定由连续时间信号采样得到，但是 习惯上，将序列值之间的时间间隔都称为采样周期。 同样的，采样周期未必一定是不变的（相同的）周期，但是在课程中， 我们一般只考虑恒定的采样周期。 对于离散时间信号x[n]而言，n是整数，而且是一个无量纲量，与具体 的采样周期无关。 x[n]在n不为整数时没有定义。
2.0 引言 2.1 离散时间序号：序列 2.2 离散时间系统 2.3 线性时不变系统 2.4 线性时不变系统的性质 2.5 线性常系数差分方程 2.6 离散时间信号与系统的频域表示 2.7 用傅立叶变换表示序列 2.8 傅立叶变换的对称性质 2.9 傅立叶变换定理 2.10 离散时间随机信号（介绍）
连续时间信号、离散时间信号、数字信号
t(s) n
n
数字信号量化表：{-1 –0.5 0 0.5 1}
2.1.1 基本序列和序列运算
序列的基本运算 加法运算：z[n]=x[n]+y[n]={…,x[-1]+y[-1],x[0]+y[0],x[1]+y[1],…}, -∞<n<∞
乘法运算
x[n]*y[n]={…,x[-1]*y[-1],x[0]*y[0],x[1]*y[1],…}, -∞<n<∞
2.2.3 时不变系统
时不变系统是这样一种系统：输入序列的移位将引起输出序列相应的移位。
也就是说，如果T{x[n]}=y[n]，那么T{x[n-n0]}=y[n-n0] for all n0
要证明一个系统是时不变的，必须解出T{x[n-n0]}和 y[n-n0]，看两者是否相等 。
n
例1 y[n] (0.5)ni x[i]
2.1 离散时间信号：序列
连续时间信号： xa(t) 离散时间信号：x[n]=xa(nT), -∞<n<∞ 其中，T是采样周期，f=1/T为采样频率。 注：实际上，离散时间信号未必一定由连续时间信号采样得到，但是 习惯上，将序列值之间的时间间隔都称为采样周期。 同样的，采样周期未必一定是不变的（相同的）周期，但是在课程中， 我们一般只考虑恒定的采样周期。 对于离散时间信号x[n]而言，n是整数，而且是一个无量纲量，与具体 的采样周期无关。 x[n]在n不为整数时没有定义。
第二章 离散时间信号与系统
将 x[n] 以纵坐标轴n=0为中心作翻转。
x(n)
3
3
3
2
2
2
…1
1
1
…
-4 -3 -2 -1 0 1 2 3 4 5 6 n
x(-n)
3
3
3
2
2
2
…
1
1
1…
-4 -3 -2 -1 0 1 2 3 4 5 6 n
2.1 离散时间信号
❖ 思考：x(-n+1)和x(-n-1)与x(-n)的移位关系？
作用：表示任意的离散时间序列
任意序列都可以表示成单位抽样序列的移位加权和，即 x(n) x(m) (n m) m
x [n]
3
1 22
n 2 1 0 1 2 3
x[n] 3[n 1] [n] 2[n 1] 2[n 2]
2.1 离散时间信号
➢ 常用典型序列：单位阶跃序列
n ≥0 u1[n] 0 n 0
cos(n) 1（e jn e-jn）；sin(n) 1（e jn - e-jn）
2
2j
x(n)可写成: x(n) rncos(n) jr nsin(n)
由于正弦序列、余弦序列和复指数序列可以相互线性表示，我们统称为正弦类信号。
2.1 离散时间信号
正弦序列：x(n) Asin(n ) 其中，A为幅度；为数字角频率；为起始相位 正弦序列可以由模拟正弦信号xa (t) Asin(2ft )抽样得到 x(n) xa (t) tnT Asin(2ft ) Asin (Tn )，其中 T
R N (n) u(n) - u(n N)
N-1
R N (n) (n m) (n) (n 1) (n 2) (n N) m0
2019-北京邮电大学《数字信号处理》门爱东-dsp02-离散时间系统和离散信号的变换-PPT文档资料-文档资料
北 京
过取样（Oversampling）
邮 电 大
过取样就是用远高于奈奎斯特频率的频率去采样，K×fs/2 好处：
学
简化了抗混叠滤波器设计；
信 息 与
过采样、噪声成形（Noise Shaping） 、数字滤波和抽取（丢点 Decimator）是 ADC 降低噪声，并产生高分辨率输出的重要方法。
11
2. 1.1 取样和取样定理：频域分析
北
京 邮 电 大
p (t)1ejn st T n
且 ej st 2( s)
学
信
息 与 通 信
P()2Tn (ns)
其中
2 s T
工 程 学 院
X ˆa()21Xa()P()T 1Xa()n (ns)
北
京 邮
取样函数定义为:
电 大 学 信 息
p(t)1com b(t)(tnT)
T
T n ------ T ：取样间隔
与 通 信
则：
xˆa(t) xa(t)p(t) xa(t)(t nT)
工
n
程
学 院
xa(nT)(t nT)
多
n
媒
体 中 心 门 爱
若 xa(t) 是一带限函数
邮 电 大 学 信 息 与
Xa()
Xa(),
0,
s
2
s
2
通 信
只要取样频率足够高，当满足以下条件时
工 程 学 院
s
max 2
---------（奈奎斯特定理）
多
媒 体 中 心
第2章 离散时间信号与系统的变换域分析
i 1
bi z i
M
因此，X(z)可以展成以下部分分式形式
r Ak Ck n X ( z ) Bn z 1 1 zk z (1 zi z 1 ) k n 0 k 1 k 1 M N N r
其中，M≥N时，才存在Bn；Zk为X(z)的各单极点， Zi为X(z)的一个r阶极点。而系数Ak，Ck 分别为： A Re s[ X ( z ) ] z z zk k 1 d r k r x( z ) Ck r k [( z zi ) (r k )! dz z zz ,
X ( z)
0
n
0
n2 n
n
x ( n) z
n
n2
n
x ( n) z
x ( n) z
n 1
n2
n
14
第二项为有限长序列,其收敛域 0 z ; 第一项为z的正幂次级数，根据阿贝尔定理, 其收敛域为 0 z Rx ; R x 为最大收敛半径 .
i
k 1, 2r 29
分别求出各部分分式的z反变换（可查 P39 表2-1-1），然后相加即得X(z)的z反变换。
[例2-5]利用部分分式法，求X ( z) 1 (1 2 z 1 ) (1 0.5z 1 ) , z 2 的z反变换。 解：
1 z X ( z) 1 1 (1 2 z )(1 0.5 z ) ( z 2)( z 0.5) X ( z) z A1 A2 z ( z 2)( z 0.5) z 2 z 0.5
对采样信号 进行拉普拉斯变换
x a (t )
n
x (nT ) (t nT )
bi z i
M
因此，X(z)可以展成以下部分分式形式
r Ak Ck n X ( z ) Bn z 1 1 zk z (1 zi z 1 ) k n 0 k 1 k 1 M N N r
其中，M≥N时，才存在Bn；Zk为X(z)的各单极点， Zi为X(z)的一个r阶极点。而系数Ak，Ck 分别为： A Re s[ X ( z ) ] z z zk k 1 d r k r x( z ) Ck r k [( z zi ) (r k )! dz z zz ,
X ( z)
0
n
0
n2 n
n
x ( n) z
n
n2
n
x ( n) z
x ( n) z
n 1
n2
n
14
第二项为有限长序列,其收敛域 0 z ; 第一项为z的正幂次级数，根据阿贝尔定理, 其收敛域为 0 z Rx ; R x 为最大收敛半径 .
i
k 1, 2r 29
分别求出各部分分式的z反变换（可查 P39 表2-1-1），然后相加即得X(z)的z反变换。
[例2-5]利用部分分式法，求X ( z) 1 (1 2 z 1 ) (1 0.5z 1 ) , z 2 的z反变换。 解：
1 z X ( z) 1 1 (1 2 z )(1 0.5 z ) ( z 2)( z 0.5) X ( z) z A1 A2 z ( z 2)( z 0.5) z 2 z 0.5
对采样信号 进行拉普拉斯变换
x a (t )
n
x (nT ) (t nT )
第二章 离散时间序列与系统1
4.序列的周期性
周期序列的概念：如果对所有n存在一个 最小整数N，满足
则称x(n)为周期序列，记为
，最小周期为N。
例： x(n) sin( n) sin[ ( n 8)] 4 4 例： 因此，x(n)是周期为8的周期序列 因此，x(n)是周期为8的周期序列
现在讨论正弦序列的周期性。设
ˆ ( j ) 1 X ( j ) X a T
4.抽样信号的恢复
（a ） ＾a (t) x ya (t)
G(jΩ ) ＾ (jΩ ) Xa
T H ( j ) 0
| |
s 2 s | | 2
（b ）
Ω 0 G(jΩ )
（c ）
Ω －π / T 0 π/ T Xa (jΩ )
（d ）
Ω 0
33
滤波器值允许通过基带频谱，即原信号频谱
因此在滤波器的输出端得到了恢复的原 模拟信号 y(t)=xa(t)
5.取样内插公式
1 h a (t ) 2
H ( j ) e j t d
（a ）
＾a (t) x
G(jΩ ) ＾ (jΩ ) Xa
ya (t)
s sin t T s j t 2 2 d s e s 2 2 t 2
6）正弦序列
x(n) Asin(0n )
模拟正弦信号：
xa (t ) A sin(t )
x(n) xa (t )
t nT
A sin(nT )
：模拟域频率 f s：采样频率
0 T / f s
0：数字域频率
T：采样周期
数字域频率是模拟域频率对采样频率的归一化频率
北京邮电大学《数字信号处理》门爱东-dsp02-离散时间系统和离散信号的变换-PPT精品文档159页
12
2. 1.1 取样和取样定理：频域分析
北
京
X a( )
邮
电
1
Xˆ a ( )
1 T
s 2T
大 学
m
m
信
息
0 m
m
Ω
-Ω s s
0 s Ωs
Ω
与
2
2
通 信
连续信号的频谱和取样信号的频谱 s
工
max 2
程 学 院
然而，当
s
Digital Signal Processing, Men Aidong, Multimedia Technology Centre, BUPT
8
2. 1.1 取样和取样定理：时域分析
北
京 邮
取样函数定义为:
电 大 学 信 息
p(t)1com b(t)(tnT)
T
T n ------ T ：取样间隔
通 信 工 程 学
则映射到频域为：
X ˆa( )21 Xa( )P( )
院
多 因 p(t) 是周期为 T 的函数，可以展开成级数和的形式：
媒
体 中 心 门
p(t)
(tnT)
aejn st m
n
n
其中
2 s T
爱
东
Digital Signal Processing, Men Aidong, Multimedia Technology Centre, BUPT
院
多
媒
体
中
心
门 爱
－B2 －B1
0
B1
B2
东
Digital Signal Processing, Men Aidong, Multimedia Technology Centre, BUPT
离散时间信号处理-因果性稳定性关系34页PPT
离散时间信号处理-因果性稳定性关系
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 反顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚韧何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 反顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚韧何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
数字信号处理(英文版)2-离散时间信号系统
§2.1 Discrete-Time Signals: Time-Domain Representation
Example Amplitude Amplitude Time,t
Time,t
Boxedcar signal
Digital signal
§2.1 Discrete-Time Signals: Time-Domain Representation
-Unit advance x[n]
z
y[n]
y[n]=x[n+1]
§2.2.1 Basic Operations
• Time-reversal (folding) operation: y[n]=x[-n] • Branching operation: Used to provide multiple copies of a sequence
x[n]
Input sequence
Discrete-time system
y[n]
Output sequence
§2.2 Operations on Sequences
• For example, the input may be a signal corrupted with additive noise • Discrete-time system is designed to generate an output by removing the noise component from the input • In most cases, the operation defining a particular discrete-time system is composed of some bame Signals: Time-Domain Representation
精品课件-数字信号处理(第四版)-第2章 时域离散信号和系统的频域分析-3
图2.6.2 H(z)=z－1的频响19特
【例2.6.3】 设一阶系统的差分方程为y(n)=by(n－1)+x(n)
解
由系统差分方程得到系统函H数(为z)
1 1 bz1
z
z b
| z || b |
式中，0<b<1。系统极点z=b，零点z=0，当B点从ω=0逆时针 旋转时，在ω=0点，由于极点向量长度最短，形成波峰；在 ω=π点形成波谷；z=0处零点不影响幅频响应。极零点分布 及幅度特性如图所示。
如果-1<b<0，则峰值点出现在ω=π处，形成高通滤波 器。
20
【例2.6.4】已知H(z)=1－z－N，试定性画出系统的幅频特性。
H(z) 1 zN z N 1 zN
H(z)的极点为z=0，这是一个N阶极点，它不影响系统的幅频响 应。零点有N个，由分子多项式的根决定
z N 1 0 即 z N e j2πk
小结 单位圆附近的零点位置对幅度响应波谷的位置和深度有明
显的影响，零点可在单位圆外。 在单位圆内且靠近单位圆附近的极点对幅度响应的波峰的
位置和高度则有明显的影响，极点在单位圆上，则不稳定。 利用直观的几何确定法，适当地控制零、极点的分布，就
能改变系统频率响应的特性，达到预期的要求，因此它是 一种非常有用的分析系统的方法。
根据其形状，称之为梳状滤波器。
例2.6.4的梳状滤波器的极零点分布及幅频、相频特性
22
2.6.4 几种特殊系统的系统函数及其特点 全通滤波器 梳状滤波器 最小相位系统
23
1 全通系统（全通网络，全通滤波器）
定义：如果滤波器的幅频特性对所有频率均等于常数或1.
| H (ej ) | 1 0 2π
【例2.6.3】 设一阶系统的差分方程为y(n)=by(n－1)+x(n)
解
由系统差分方程得到系统函H数(为z)
1 1 bz1
z
z b
| z || b |
式中，0<b<1。系统极点z=b，零点z=0，当B点从ω=0逆时针 旋转时，在ω=0点，由于极点向量长度最短，形成波峰；在 ω=π点形成波谷；z=0处零点不影响幅频响应。极零点分布 及幅度特性如图所示。
如果-1<b<0，则峰值点出现在ω=π处，形成高通滤波 器。
20
【例2.6.4】已知H(z)=1－z－N，试定性画出系统的幅频特性。
H(z) 1 zN z N 1 zN
H(z)的极点为z=0，这是一个N阶极点，它不影响系统的幅频响 应。零点有N个，由分子多项式的根决定
z N 1 0 即 z N e j2πk
小结 单位圆附近的零点位置对幅度响应波谷的位置和深度有明
显的影响，零点可在单位圆外。 在单位圆内且靠近单位圆附近的极点对幅度响应的波峰的
位置和高度则有明显的影响，极点在单位圆上，则不稳定。 利用直观的几何确定法，适当地控制零、极点的分布，就
能改变系统频率响应的特性，达到预期的要求，因此它是 一种非常有用的分析系统的方法。
根据其形状，称之为梳状滤波器。
例2.6.4的梳状滤波器的极零点分布及幅频、相频特性
22
2.6.4 几种特殊系统的系统函数及其特点 全通滤波器 梳状滤波器 最小相位系统
23
1 全通系统（全通网络，全通滤波器）
定义：如果滤波器的幅频特性对所有频率均等于常数或1.
| H (ej ) | 1 0 2π
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Digital Signal Processor
A kind of microprocessor used to implement digital signal processing algorithm
❖ The foundation of information technology is digitalization.
❖ DSP technology becomes hot front edge and is growing up rapidly.
DSP Solution
Mobile phone
The handset is not only used for voice communication
ADSL
Cruise missile
Smart bomb from F117
Pattern recognization
Fingerprint distinguish
Requirement of DSP Engineers is growing up rapidly
Development of DSP
❖ The kernel of digitalization is digital signal processing
❖ Most of digital signal processing, especially real-time processing are implemented by DSP processor
（Asymmetric Digital Subscriber Line)
ADSL是非对称数字用户线路 （Asymmetric Digital Subscriber Line）的
缩写，有时也作非对称数字用户环路 （Asymmetric Digital Subscriber Loop）。 它是一种在电话铜缆上进行较高速率数据 传输的方法，是DSL 的一种形式。它以普 通电话线路做为传输介质，既在普通双绞 铜线上实现下行高达8Mbit/s传输速度；上 行高达640Kbit/s的传输速度，我们只要在
离散时间信号处理PPT_第二章 离散 时间信号系统
Digital Signal Processing
The College of Electronics and Informatics Zhejiang Sci-Tech University 2005/06
Digital Signal ThPerooryc,emsesthinodg, algorithm
和距离的不同以及上行速率和下行速率 对称性的不同这两个方面
Digital Camera
Digital Camera
HDTV High Definition TV
PDP (Plasma Display)TV
Home Theater
DVD(Digital Video Disc)
GPS(Global Position System)
price ratio ❖ Lower power consumption or
longer battery life
CONTENT
➢ 2.DISCRETE-TIME SIGNAL AND SYSTEMS ➢ 3.THE Z-TRANSFORM ➢ 4.SAMPLING OF CONTINUOUS-TIME SIGNALS ➢ 6.STRUCTURES FOR DISCRETE-TIME SYSTEMS ➢ 7.FILTER DESIGN TECHNIQUES ➢ 8.THE DISCRETE FOURIER TRANSFORM ➢ PUTATION OF THE DISCRETE FOURIER ➢ APPENDIX B CONTINUOUS-TIME FILTERS
普通线路两端加装ADSL设备，既可使用 ADSL提供的高带宽服务，通过一条电话线，
便可以比普通MODEM快一百倍
DSL（数字用户线路，Digital Subscriber Line）是以铜质电话线为传输介质的传输 技术组合，它包括HDSL、SDSL 、VDSL 、 ADSL和RADSL等，一般称之为xDSL。它 们主要的区别就是体现在信号传输速度
Continuous-time signals are defined along a continuum of times and thus are represented by a continuous independent variable. Continuoustime signals are often referred to as analog signals.
.
.
Discrete-time signals are defined at discrete times, and thus, the independent variable has discrete values;
Digital signals are those for both time and amplitude are discrete.
2 Discrete-Time Signals and Systems
2.0 INTRODUCTION
The term signal is generally applied to something that conveys information. The independent variable in the mathematical representation of a signal may be either continuous or discrete.
❖ Higher processing speed ❖ Multi-DSP co-operation ❖ More powerful and convenient
development environment ❖ ASIC based on DSP core ❖ Lower price or higher performance
A kind of microprocessor used to implement digital signal processing algorithm
❖ The foundation of information technology is digitalization.
❖ DSP technology becomes hot front edge and is growing up rapidly.
DSP Solution
Mobile phone
The handset is not only used for voice communication
ADSL
Cruise missile
Smart bomb from F117
Pattern recognization
Fingerprint distinguish
Requirement of DSP Engineers is growing up rapidly
Development of DSP
❖ The kernel of digitalization is digital signal processing
❖ Most of digital signal processing, especially real-time processing are implemented by DSP processor
（Asymmetric Digital Subscriber Line)
ADSL是非对称数字用户线路 （Asymmetric Digital Subscriber Line）的
缩写，有时也作非对称数字用户环路 （Asymmetric Digital Subscriber Loop）。 它是一种在电话铜缆上进行较高速率数据 传输的方法，是DSL 的一种形式。它以普 通电话线路做为传输介质，既在普通双绞 铜线上实现下行高达8Mbit/s传输速度；上 行高达640Kbit/s的传输速度，我们只要在
离散时间信号处理PPT_第二章 离散 时间信号系统
Digital Signal Processing
The College of Electronics and Informatics Zhejiang Sci-Tech University 2005/06
Digital Signal ThPerooryc,emsesthinodg, algorithm
和距离的不同以及上行速率和下行速率 对称性的不同这两个方面
Digital Camera
Digital Camera
HDTV High Definition TV
PDP (Plasma Display)TV
Home Theater
DVD(Digital Video Disc)
GPS(Global Position System)
price ratio ❖ Lower power consumption or
longer battery life
CONTENT
➢ 2.DISCRETE-TIME SIGNAL AND SYSTEMS ➢ 3.THE Z-TRANSFORM ➢ 4.SAMPLING OF CONTINUOUS-TIME SIGNALS ➢ 6.STRUCTURES FOR DISCRETE-TIME SYSTEMS ➢ 7.FILTER DESIGN TECHNIQUES ➢ 8.THE DISCRETE FOURIER TRANSFORM ➢ PUTATION OF THE DISCRETE FOURIER ➢ APPENDIX B CONTINUOUS-TIME FILTERS
普通线路两端加装ADSL设备，既可使用 ADSL提供的高带宽服务，通过一条电话线，
便可以比普通MODEM快一百倍
DSL（数字用户线路，Digital Subscriber Line）是以铜质电话线为传输介质的传输 技术组合，它包括HDSL、SDSL 、VDSL 、 ADSL和RADSL等，一般称之为xDSL。它 们主要的区别就是体现在信号传输速度
Continuous-time signals are defined along a continuum of times and thus are represented by a continuous independent variable. Continuoustime signals are often referred to as analog signals.
.
.
Discrete-time signals are defined at discrete times, and thus, the independent variable has discrete values;
Digital signals are those for both time and amplitude are discrete.
2 Discrete-Time Signals and Systems
2.0 INTRODUCTION
The term signal is generally applied to something that conveys information. The independent variable in the mathematical representation of a signal may be either continuous or discrete.
❖ Higher processing speed ❖ Multi-DSP co-operation ❖ More powerful and convenient
development environment ❖ ASIC based on DSP core ❖ Lower price or higher performance