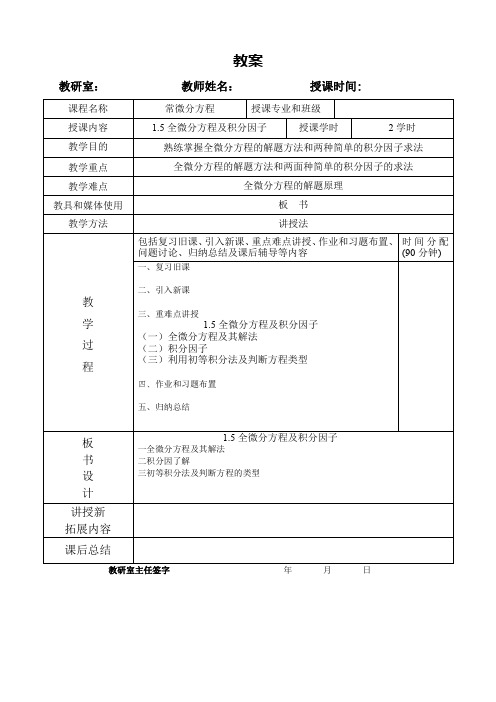
1.5全微分方程及积分因子 .
全微分方程与积分因子法

已构成全微分的项分出再把剩下的项凑成全微分.但这种方法
要求熟记一些简单二元函数的全微分,如
ydx+xdy=d(x,y)
ydx-xdy y2
=d(
x y
)
-ydx+xdy x2
=d(
x y
)
ydx-xdy =d(ιn| x |)
xy
y
ydx-xdy x2+y2
=d(arctg
x y
)
| | ydx-xdy x2-y2
的通解为
μ(x,y)=∫x0xP(x,y)dx+∫y0xQ(x,y)dy=C
(7)
其中点(x0,y0)可在与路径无关的单连通区域 G 内 任 意 取
得.很 多 情 况 下 都 选 (0,0)为 (x0,y0),只 有 当 点 (0,0)不 在 上 述
单连通区域 G 内,才考虑其他点作为曲线积分的始点.
坠p - 坠Q 坠y 坠x
-P
这里 φ 仅为 y 的函数.从而求得方程 (1)的一个积分因子 μ=
e 。 ∫φ(y)dy
例 4 试用公式法解线性微分方程(8)
解 : 将 (8)式 改 写 成 [Q(x)-P(X)Y]DX-DY=0
(10)
这时由公式,μ(x)=e∫p(x)dx.以 μ(x)=e∫p(x)dx 乘上(10)式得到
或 y=e-∫p(x)dx[∫Q(x)e∫p(x)dxdx+C]
2.公 式 法
由同一个方程
ydx-xdy=0
可以有不同的积分因子 1 y2
,
1 x2
,
1和 1 xy x2±y2
.可以证明,只要方程有解,则必有积分因子存在,
并且不是唯一的.因此,在具体解题过程中,由于求出的积分因
微分方程的积分因子

在求解某些类型的微分方程时,可以使用积分因子(integrating factor)来简化方程的求解过程。
积分因子是一个乘法因子,可以乘以微分方程的两边,使其变为可积分的形式。
对于形如dy/dx + P(x)y = Q(x) 的一阶线性常微分方程,其中P(x) 和Q(x) 是已知函数,可以使用积分因子来求解。
积分因子的计算步骤如下:
1.将方程写成标准形式:dy/dx + P(x)y = Q(x)。
2.计算积分因子μ(x) = exp(∫P(x)dx)。
3.将积分因子乘以原方程的两边,得到μ(x)dy/dx + μ(x)P(x)y = μ(x)Q(x)。
4.左侧的第一项可以通过链式法则化简为d(μ(x)y)/dx。
5.整理得到d(μ(x)y)/dx = μ(x)Q(x)。
6.对上述等式两边同时积分,得到μ(x)y = ∫μ(x)Q(x)dx。
7.最后,解出y = (1/μ(x)) ∫μ(x)Q(x)dx。
通过引入积分因子,原本的一阶线性常微分方程可以转化为可积分的形式。
积分因子的选择依赖于方程中的函数P(x) 和Q(x),使得乘以积分因子后,方程的左侧可以写成导数的形式,从而方便求解。
需要注意的是,不是所有的一阶线性常微分方程都可以使用积分因子法求解,这种方法适用于特定类型的方程。
在具体求解时,还需要根据具体方程形式和条件进行判断和处理。
全微分积分因子

全微分积分因子全微分积分因子是微分方程中的一个重要概念,它在解决微分方程的问题时起到了至关重要的作用。
本文将从全微分的定义、积分因子的概念以及如何确定积分因子这三个方面进行阐述。
全微分是微分学的一个重要概念,它是指一个函数在某一点附近的微小变化。
在数学上,全微分可以通过求偏导数来表示。
对于函数f(x,y),它的全微分可以表示为df=f_xdx+f_ydy,其中f_x和f_y 分别表示f对x和y的偏导数,dx和dy表示自变量x和y的微小变化量。
全微分的概念是微分方程求解中的关键,通过对方程进行全微分,可以将其化简为可积分的形式。
积分因子是指用于求解非恰当微分方程的一个乘法因子,通过乘以这个因子,可以将非恰当微分方程转化为恰当微分方程。
对于一个一阶微分方程Mdx+Ndy=0,如果存在一个函数μ(x, y),使得μMdx+μNdy=0是恰当微分方程,那么μ就是这个微分方程的积分因子。
积分因子的作用在于将原方程乘以积分因子后,可以使得新方程满足恰当微分方程的条件,从而利用恰当微分方程的性质来求解。
确定积分因子的方法有很多,常用的方法包括查表法、分离变量法、恰当微分方程的判别法和常数变易法等。
其中查表法是一种快速确定积分因子的方法,通过查表可以找到常见的一些微分方程的积分因子。
分离变量法是一种常用的确定积分因子的方法,通过将方程进行变形,使得方程的两边可以分离变量,从而求得积分因子。
恰当微分方程的判别法是一种判断方程是否是恰当微分方程的方法,如果一个方程满足恰当微分方程的条件,则可以确定它的积分因子。
常数变易法是一种通过引入一个未知函数来确定积分因子的方法,通过求解这个未知函数,可以得到积分因子的表达式。
在实际应用中,确定积分因子是求解非恰当微分方程的关键一步。
通过确定积分因子,可以将非恰当微分方程转化为恰当微分方程,从而利用恰当微分方程的性质来求解。
积分因子的选择不仅要满足方程的形式要求,还要考虑计算的复杂度和求解的效果。
全微分方程与积分因子

全微分方程与积分因子在数学中,微分方程是研究自然现象的一种重要工具,它是描述自然现象变化的一种数学模型。
而全微分方程是其中的一种重要类型,它在物理、工程、经济等领域中都有广泛应用。
全微分方程的定义全微分方程指的是能够写成下面形式的方程:M(x,y)dx+N(x,y)dy=0其中,M(x,y)和N(x,y)是定义在平面区域D上的连续函数。
dx 和dy分别表示x和y的微小变化量,而该式的解y=f(x)就是D中的一个隐函数。
当该式满足以下条件时,被称作全微分方程:∂M/∂y=∂N/∂x换言之,就是该式的两个偏导数相等。
全微分方程的求解对于全微分方程,求解的方法非常简单,只需要对其进行积分,就得到了y=f(x)的通解。
以一个简单的例子来说明:设M(x,y)=3x^2y, N(x,y)=x^3,则上式就变成了:3x^2ydx+x^3dy=0对该式两边同时积分,得到:x^3y+θ=y^2/2其中,θ是一个常数。
积分因子积分因子是用于求解非全微分方程的一种技巧,它能够将非全微分方程转化成全微分方程从而求解。
设非全微分方程为:M(x,y)dx+N(x,y)dy=0称一个与M(x,y)和N(x,y)有关的非零函数μ(x,y)为该非全微分方程的积分因子,当且仅当以下条件成立时:μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0是一个全微分方程。
在实际应用中,常常可以通过以下步骤求解积分因子:1.检查M(x,y)和N(x,y)的偏导数是否满足条件∂M/∂y≠∂N/∂x。
2.令μ(x,y)=exp(Q(x,y)),其中Q(x,y)是希望得到的积分因子。
3.代入μ(x,y)和求导后的积分因子到M(x,y)和N(x,y)的总和中,判断是否为全微分方程,如果是,则可得到积分因子。
例如,考虑非全微分方程:(2y^3 +3x^2y)dx+(3x^2+y^2)dy=0通过检查偏导数条件可知:∂M/∂y=6y^2+3x^2≠∂N/∂x=6x所以该方程不是全微分方程。
全微分方程

1.5.2 积分因子
(2 xy x2 y y3 / 3)dx ( x2 y 2 )dy 0 ex (2xy x2 y y3 / 3)dx ex ( x2 y 2 )dy 0
M N d y x dx N
M N d y x dy M
求 e y dx ( xe y 2 y )dy 0 满足初始条件 y(2) 3 的解。
ห้องสมุดไป่ตู้(2x sin y 3x2 y)dx ( x3 x2 cos y y2 )dy 0
练习1.
( x2 4xy 2 y2 )dx ( y2 4xy 8)dy 0 e y dx ( xe y 3 y 2 )dy 0 ( x3 xy2 )dx ( x2 y y3 )dy 0 y dx ( y 3 ln x)dy 0 x
分组求积分因子
(3x3 y)dx (2x2 y x)dy 0
例12. ( x4 x2 y2 x)dx ydy 0
例13. ydx ( x x2 y y3 )dy 0
例14. 例15.
( x3 y 2 y 2 )dx x4dy 0
( x y)dx ( x y)dy 0
( x)
( y )
例8. 例9. 例10.
xdy ydx 0
(2 xy x 2 y 1 3 y )dx ( x 2 y 2 )dy 0 3
M N d y x dx N
M N d y x dy M
(3x3 y)dx (2x2 y x)dy 0
例11. (3x 6xy 3 y 2 )dx (2x2 3xy)dy 0
1.5全微分方程及积分因子.
②求原函数,按公式 M ( x, y )dx [N
x
x0
M ( x, y )dx N ( x 0 , y )dy u ( x, y ) (10)
y0 x y x0 y0
证明: (略) 问题: (1) 如何判断(1)是恰当微分方程? (2) 如果(1)是恰当微分方程,如何求得函数 u u ( x, y ) ? (3)如果(1)是恰当微分方程,函数 M ( x, y ), N ( x, y ) 应有什么性质? 定理 2:如果(1)中的 M ( x, y ), N ( x, y ) 在矩形区域 R:|x-x0|≤a,|y-y0|≤b 上 连续可微,那么方程(1)是恰当微分方程的充要条件是:
0
1 1 1 即有通解为 x 4 x 2 y 2 x 3 C 4 2 3
2) (2xy4e y 2xy3 y)dx ( x2 y4e y x2 y2 3x)dy 0 解:由于
M N 2 xy 4 e y 8 xy 3e y 6 xy 2 1 y x 2 xy 4 e y 2 xy 2 3 8 xy 3e y 8 xy 2 4 4 M y
M N (5) y x
且此时恰当微分方程(2)的通解是
M ( x, y )dx [N y M ( x, y)dx]dy = c (9)或
x
x0
M ( x, y )dx N ( x, y )dy u ( x, y ) (10)
y0
y
证明: (略) 3、全微分方程的解题方法 ①由
常微分方程Ch1.5

引理2:若M( x, y),N ( x, y)在矩形域G:a x b,c y d
b
内连续可微,则含参量的积分I( y) M( x, y)dx在(c, d )内 a
可微,且
d dy
I( y)
d dy
b a
M ( x,
y)dx
b a
M y(x,
y)dy.
常微分方程
一、恰当方程
M( x, y) N ( x, y)dy 0 是U( x, y)的全微分,即
dU( x, y) M( x, y)dx N( x, y)dy,
则称M ( x, y) N ( x, y)dy 0为恰当方程 或全微分方程。
常微分方程
一、恰当方程
5/25
例如:
xdx ydy 0是恰当方程,可取U ( x, y) x2 y2 ; 2
下面我们在证明M( x, y)dx N( x, y)dy 0为恰当方程的同时,求 出U( x, y)。这种证明方法在数学上称为构造性证明]。
因为所求的U ( x, y)应满足 U M ( x, y),U N ( x, y).
x
y
常微分方程
一、恰当方程
13/25
设( x0 ,
常微分方程
一、恰当方程
18/25
例2. 求方程(3x2 6xy2 )dx (6x2 y 4 y3 )dy 0的通解.
解. 记M ( x, y) 3x2 6xy2,N ( x, y) 6x2 y 4 y3.则
M 12xy, N 12xy.
y
x
因此方程为恰当方程。
取( x0 ,
y0
全微分方程及积分因子

1.5 全微分方程及积分因子一、全微分方程的定义及条件则它的全微分为是一个连续可微的函数设,),(y x U U =dy yU dx x U dU ¶¶+¶¶=如果我们恰好碰见了方程0),(),(=¶¶+¶¶dy yy x U dx x y x U 就可以马上写出它的通积分.),(c y x U=定义1使得若有函数),,(y x U dyy x N dx y x M y x dU ),(),(),(+=则称微分方程)1(,0),(),(=+dy y x N dx y x M 是全微分方程..),()1(c y x U =的通积分为此时如0=+ydx xdy 0)2()3(322=+++dy xy x dx y y x 0)()(=+dy y g dx x f 是全微分方程.=)(xy d =+)(23xy y x d =+òò))()((y d y g x d x f d 1.全微分方程的定义需考虑的问题(1) 方程(1)是否为全微分方程?(2) 若(1)是全微分方程,怎样求解?(3) 若(1)不是全微分方程,有无可能转化为全微分方程求解?2 方程为全微分方程的充要条件定理1则方程偏导数中连续且有连续的一阶域在一个矩形区和设函数,),(),(R y x N y x M )1(,0),(),(=+dy y x N dx y x M 为全微分方程的充要条件是).2(,),(),(x y x N y y x M ¶¶=¶¶)1(,0),(),(=+dy y x N dx y x M证明“必要性”设(1)是全微分方程,使得则有函数),,(y x U dy yU dx x U y x dU ¶¶+¶¶=),(dy y x N dx y x M ),(),(+=故有),,(y x M xU =¶¶),(y x N y U =¶¶从而从而有都是连续的和由于,22y x U x y U ¶¶¶¶¶¶,22y x U x y U ¶¶¶=¶¶¶故.),(),(xy x N y y x M ¶¶=¶¶yx U y N x y U y M ¶¶¶=¶¶¶¶¶=¶¶22,“充分性”,xy x N y y x M ¶¶=¶¶),(),(若解这个方程得看作参数把出发从,,)5(y 满足则需构造函数),,(y x U )4(,),(),(),(dy y x N dx y x M y x dU +=即应满足)5(),,(y x M x U =¶¶)6(),,(y x N yU =¶¶ò+=).(),(),(y dx y x M y x U j,)(的任意可微函数是这里y y j =¶¶y U 因此ò¶¶-=)7(),()(dx y x M y N dy y d j ,)7(无关的右端与下面证明x 的偏导数常等于零即对x 事实上]),([ò¶¶-¶¶dx y x M y N x ]),([ò¶¶¶¶-¶¶=dx y x M yx x N )6(),,(y x N y U =¶¶即同时满足使下面选择),6(),(U y j ò+¶¶dy y d dx y x M y )(),(j N =ò+=).(),(),(y dx y x M y x U j]),([ò¶¶¶¶-¶¶=dx y x M x y x N yM x N ¶¶-¶¶=.0º积分之得右端的确只含有于是,)7(,y ,]),([)(dy dx y x M y N y òò¶¶-=j 故ò=dx y x M y x U ),(),(,]),([dy dx y x M yN òò¶¶-+(8)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(x,y)
(0,0)
u( x, y )
x 0 x
( x, y)
( 0, 0 )
M ( x, y )dx N ( x, y )dy
y 0
M ( x,0)dx N ( x, y)dy 2 xdx (sin x x e 2)dy
y 2 y
0
0
x y sin x x (e 1) 2 y y sin x x 2e y 2 y.
M ( x , y )dx N ( x , y )dy 0, (1)
(2).
4
为恰当方程的充要条件是
M ( x, y ) N ( x, y ) , y x
常微分方程
绵阳师范学院
u 证明 “必要性” 设(1)是恰当方程, 则有函数 ( x, y ), 使得
u u du( x, y ) dx dy M ( x , y )dx N ( x , y )dy x y
故有
u M ( x , y ), x
2 u M , yx y
u N ( x, y ) y
从而
2 u N . xy x
2u 2u , y x x y
2u 2u 由于 和 都 是 连 续 的从 而 有 , yx xy
12
常微分方程
绵阳师范学院
(3 x 2 6 xy2 )dx (6 x 2 y 4 y 3 )dy 0 的通解. 例2 求方程
解:
由于M ( x, y) 3 x 2 6 xy2 , N ( x, y) 6 x 2 y 4 y 3 ,
N ( x , y ) M ( x, y) , 12xy x y
故所给方程是恰当方程. 把方程重新“分项组合”得
3 x 2dx 4 y 3dy (6 xy2dx 6 x 2 ydy) 0
即
dx3 dy4 (3 y 2dx2 3 x 2dy2 ) 0
d( x3 y4 3x2 y2 ) 0
13
或写成
。 故通解为: x 3 y 4 3 x 2 y 2 c, c为任常数
是全微分方程(或恰当方程.) 此 时(1)的 通 解 为 ( x , y ) c . u 如
3
d (xy) xdy ydx 0
2
d ( x y xy ) (3 x 2 y y 2 )dx ( x 3 2 xy)dy 0
d ( f ( x )d x g( y )d y ) f ( x )dx g( y )dy 0
x d ( ), y2 y y ydx xdy d ( ), x x2
ydx xdy
x ydx xdy d (ln | |), y xy ydx xdy x d (arctan ), 2 2 x y y ydx xdy 1 x y d (ln ). 2 2 2 x y x y
u N ( x , y ), (6) y
这 里 ( y )是y的 任 意可 微 函 数 ,
下 面选 择 ( y ), 使u同 时满 足6), 即 ( u d ( y ) M ( x, y )dx N y dy y d ( y) N M ( x, y )dx 因此
20 求u( x, y )
0
M ( x, y )dx ( y ),
u 3 由 N ( x, y )求 ( y ). y
例1 验证方程
(e x y )dx ( x 2 sin y )dy 0
是恰当方程,并求它的通解.
9
常微分方程
绵阳师范学院
解:
由于M ( x, y) e x y, N ( x, y) x 2 sin y.
从而(1)为恰当方程 。
16
常微分方程
绵阳师范学院
x, y
这时, 取( x0 , y0 ) R, 则
x0 , y0
x
x0
M ( x, y0 )dx
从而(1)的通解为
x
x0
M ( x, y0 )dx
y
y0
N ( x, y )dy c, c为任常数 。
17
常微分方程
故所给方程是恰当方程. 把方程重新“分项组合”得
cos x sin xdx ( xy 2dx x 2 ydy ) ydy 0,
即
1 2 1 2 2 1 2 d sin x d x y d y 0, 2 2 2
14
常微分方程
绵阳师范学院
1 2 1 2 2 1 2 d sin x d x y d y 0 2 2 2
是恰当方程.
3
常微分方程
绵阳师范学院
需考虑的问题
M ( x, y)dx N ( x, y)dy 0,
(1)
(1) 方程(1)是否为恰当方程? (2) 若(1)是恰当方程,怎样求解? (3) 若(1)不是恰当方程,有无可能转化为恰当方 程 求解? 方程为恰当方程的充要条件 设 函 数 ( x , y )和N ( x , y )在 一 个 矩 形 区 M 定理1 域R中 连 续 且 有 连 续 的 一 偏 导 数, 则 方 程 阶
故
M ( x, y) N ( x, y) . y x
5
常微分方程
绵阳师范学院
“充分性”
M ( x, y) N ( x, y) 若 , y x
则 需 构 造 函 数( x , y ), 满 足 u
du( x , y ) M ( x , y )dx N ( x , y )dy, ( 4)
或写成
d (sin2 x x 2 y 2 y 2 ) 0, sin2 x x 2 y 2 y 2 c,
故通解为:
由初始条件(0) 2, 得 c 4, y
故所求的初值问题的解为:
sin x x y y 4.
2 2 2 2
15
常微分方程
绵阳师范学院
3 线积分法 定理1充分性的证明也可用如下方法:
y
dy 下 面 证 明7)的 右 端 与 无 关, 即 对x的 偏 导 数 常 等 于 零 ( x
( 7)
事实上
N [N M ( x, y)dx] [ M ( x, y )dx] x y x x y 7
常微分方程
绵阳师范学院
N N M [ M ( x, y )dx] 0. x y x x y
N ( x , y ) M ( x, y ) , 1 x y
故所给方程是恰当方程.
由 于 所 求 函 数( x , y )满 足 u
u e x y, x
u x 2 sin y, y
由偏导数的定义 , 只要将 看作常数将e x y对x积分得 y ,
u( x , y ) (e x y )dx ( y ) e x yx ( y ).
10
常微分方程
绵阳师范学院
u( x, y) e x yx ( y).
对u( x, y )关 于y求偏导数, 得 ( y )应满足的方程为
d ( y) x x 2 sin y dy d ( y) 2 sin y 即 dy 积分后得: ( y ) 2 cos y ,
M ( x , y ) N ( x , y ) 由于 , y x
由数学分析曲线积分与路径无关的定理知:
M ( x, y)dx N ( x, y)dy为某函数 ( x, y)的全微分 u ,
即有函数 ( x, y ), 使 u
du( x , y ) M ( x , y )dx N ( x , y )dy,
于 是, (7)右 端 的 确 只 含 有 积 分 之 得 y,
( y)
[N y
M ( x, y)dx]dy,
(7)
故
u( x , y ) M ( x , y )dx [ N M ( x, y)dx]dy, (8) y 即u( x , y )存 在, 从 而(1)为 恰 当 方 程 。
d ( y ) N M ( x , y )dx dy y
注:若(1)为恰当方程,则其通解为
M ( x , y )dx [ N M ( x , y )dx]dy c, c为任常数 y
8
常微分方程
绵阳师范学院
恰当方程的求解 1 不定积分法
10 判 断M ( x , y )dx N ( x , y )dy 0是 否 为 恰 当 方 程 , 若是进入下一步 .
u M ( x, y ), x
u N ( x, y), y
即应满足
(5)
(6)
从(5)出 发, 把y看 作 参 数 解 这 个 方 程 得 ,
u( x , y )
M ( x, y)dx ( y).
6
常微分方程
绵阳师范学院
u( y )
M ( x, y)dx ( y).
是恰当方程.
20
常微分方程
绵阳师范学院
对一阶线性方程:
dy ( P ( x ) y Q( x ))dx 0,
方程两边同乘以 e
故所给方程是恰当方程.
由 于M ( x , y ), N ( x , y )在 全平面上连续 ,
(x,y)
(0,0)
故取( x0 , y0 ) (0,0), 则
