反应动力学基础
第11章反应动力学基础

• 学习重点: • 1)化学与生物反应的计量学、动力学及其研究方法 • 2)环境工程中常用的各类化学和生物反应器的基本类
型及其操作原理和设计计算方法
反应工程原理
——反应动力学基础
本章主要内容
• 第一节 反应器和反应操作
• 反应器的主要类型与特点、常见的反应器操作方 式及其特点
• 第二节 反应的计量关系
• 反应组分(参与反应的各物质)间的定量关系
• 第三节 反应动力学
• 反应速率与反应条件之间的关系
第一节 反应器和反应操作
• 反应器 (reactor) :进行化学或生物反应的容器的总 称。
• 反应器:实现反应的外部条件。 反应器的操作方式和反应器的结构决定反应
器的特性(包括反应器内物料的流动状态、混合状态 以及质量和能量传递特性)。
A(nn0)nA0nA
• 等分子反应:计量方程中计量系数的代数和等于零, 膨胀因子为0。
• 非等分子反应:计量系数的代数和非为零(可正、可
负),A物质膨胀因子如下 APQAAB
膨胀因子的计算
• 例题:已知某反应反应计量式如下:A+2B=3C+4D B物质的膨胀系数
B342122
r A ( r A m )V r A m
3 .0 1 3 0 1 .2 3 .6 1 3 m 0 c o 3 ) m l/(
反映了一个反应器的强度。(SV=2 h-1表示1h处理2 倍于反应体积的流体。)
空速越大,反应器的负荷越大。
反应器内反应物流动与混合状态
• 理想状态下两种流动状态 1)完全混合流 (complete mixing):亦称全混流、理 想混合,反应物进入反应器后,能瞬间达到完全混合, 反应器内的浓度、温度等处处相同。全混流可以认为 返混为无限大。 2)(平)推流 (plug/ piston flow):亦称活塞流、 挤出流,反应物以相同的流速和一致的方向移动,即反 应物在反应器内齐头并进。在径向充分混合,但不存 在轴向混合,即返混为零。
化学反应动力学及其在化工工艺中的应用

化学反应动力学及其在化工工艺中的应用一、引言化学反应动力学是研究化学反应速率和反应机理的科学,是化学工程和化学工业的重要基础。
化学反应动力学的研究不仅能够揭示反应过程中物质的转化路径和速率规律,还能够指导和优化化工工艺的设计和操作。
二、化学反应动力学基础1. 反应速率反应速率是指单位时间内反应物消失或生成物产生的量,可以通过实验数据计算得出。
反应速率与反应物浓度之间存在一定的关系,常用的反应速率方程为:速率 = k[反应物A]ᵐ[反应物B]ⁿ其中,k为速率常数,m和n为反应物A和B的反应级数,反应级数代表了反应物对于反应速率的贡献程度。
2. 反应机理反应机理是指化学反应按照一定的步骤进行,每一步都有特定的速率常数和反应物。
通过研究反应机理,可以了解反应的分子层面过程,揭示反应物的中间体和过渡态的形成和消失规律。
三、常见的反应动力学模型1. 零级反应在零级反应中,反应速率与反应物浓度无关,常用于描述固体表面催化反应。
2. 一级反应一级反应中,反应速率与反应物浓度成正比,即速率 = k[反应物]。
一级反应多用于描述溶液中的分解反应或放射性衰变等。
3. 二级反应二级反应中,反应速率与反应物浓度的平方成正比,即速率 = k[反应物]²。
二级反应常用于描述分子间反应或双分子碰撞等。
四、反应动力学在化工工艺中的应用1. 反应速率常数的测定通过实验测定不同条件下的反应速率,可以计算出反应速率常数k的数值。
反应速率常数的大小和温度密切相关,可以借此来优化反应条件或选取合适的催化剂。
2. 反应速率方程的推导根据实验数据,可以通过最小二乘法等数学方法推导出反应速率方程。
反应速率方程可以预测反应速率对反应物浓度的依赖关系,从而指导反应工艺的设计和调节。
3. 反应动力学的模拟和优化设计借助计算机模拟和反应动力学模型,可以预测不同反应条件下的反应速率和产物分布。
通过模拟和优化设计,可以降低反应温度、减少副反应或降低能耗。
化工-第七章 化学反应动力学基础

反应速率与转化率:
设A组分:n A0 初始量、t反应时间、n At时刻瞬时量 x At时刻瞬时转化率 反应消耗的A的量 n A0 n A xA 反应初始时A的量 n A0 即: n A n A0 (1 x A ) 若反应前后体积变化不大:c A c A0 (1 xA ) 1 dnA 1 nA0 dx A 则: rA V dt V dt nA0 x A
转化为目的产物的反应物的物质的量 选择性()= 反应物被转化掉的物质的量 收率:
收率()= 转化为目的产物的反应物的物质的量 进入反应器的反应物的物质的量
二、复杂反应的速率方程式
1、平行反应:
k2 A B S dcS dcP a1 b1 a b 则:rp k1c A cB rS k2c A2 cB2 dt dt rp k1 a1 a2 b1 b2 平行反应速率之比为: = c A cB rS k2 k1 A B P
第七章 化学反应动力学基础
内容: 2、简单反应的速率方程式 4、本征动力学和宏观动力学
1、化学动力学基本概念 3、简单反应和复杂反应
重点: 2、简单反应和复杂反应
1、简单反应的速率方程式
§7-1 化学动力学基本概念
一、化学计量方程式
复杂的化学计量方程式: 0= i Bi
n
i : 为组分Bi的计量系数。反应物为负、产物为正。
r f (c, T ) r f (T ) (c) f (T ):反应速率的温度效应、 (c):反应速率的浓度效应 f (T )常表示为反应速率常数k : k A exp( E 对于均相反应:aA bB sS
( c) c cB A
化学反应动力学基础

为了计算各组分的摩尔分率,先计算A、 yA0和A的值:
A = ( -2 – 1 + 2 )/2 = -0.5
yA0= 2/(2+5+1+10)= 0.111
A=AyA0=(-0.5)(0.111) = -0.0555
. 1 + AxA = 1 + (-0.0555)(0.8) = 0.956
2 化学反应动力学基础 2.1 转化率与摩尔分率
nB = nB0 – (b/a)nA0xA = nA0[B – (b/a)xA]
另一方面,每反应1 mol组分A就会生成 (c/a) mol组分C和(d/a) mol组分D。时刻t=t时 两种产物的摩尔量分别为:
nC = nC0 + (c/a)nA0xA = nA0[C + (c/a)xA]
nD = nD0 + (d/a)nA0xA = nA0[D + (d/a)xA]
n A 0 (1 x A )
同样,
CB = CA0 [B - (b/a)xA ]
=(2)[2.5–(1/2)(0.8)]=4.2[kmol· -3] m
CC = CA0 [ C + (c/a)xA ] =(2)[0.5+(2/2)(0.8)]=2.6 [kmol· -3] m
CI = CA0I = (2)(5) = 10 [kmol· -3] m
若出口处的转化率(最终转化率)表示为 xAf:
xAf = ( FA0 – FAf ) / FA0
用FA替代nA,参照间歇反应器中推导出的 关系式可得下列各式:
FA = FA0 – FA0xA = FA0(1- xA) FB = FB0 – (b/a)FA0xA
反应动力学基础复习

第二章反应动力学基础一、化学反应速率的定义1、均相反应单位时间内单位体积反应物系中某一组分的反应量。
恒容反应:连续流动过程:2、多相反应单位时间内单位相界面积或单位固体质量反应物系中某一组分的反应量。
二、反应速率方程1、速率方程(动力学方程):在溶剂及催化剂和压力一定的情况下,定量描述反应速率和温度及浓度的关系。
即:2、反应速率方程的形式主要有两类:双曲函数型和幂级数型。
3、反应级数:速率方程中各浓度项上方的指数分别代表反应对组分的反应级数,而这些指数的代数和称为总反应级数。
反应级数仅表示反应速率对各组分浓度的敏感程度,不能独立地预示反应速率的大小。
4、反应速率常数:方程中的k称为速率常数或比反应速率,在数值上等于是各组分浓度为1时的反应速度。
它和除反应组分浓度以外的其它因素有关,如温度、压力、催化剂、溶剂等。
当催化剂、溶剂等因素固定时,k就仅为反应温度的函数,并遵循阿累尼乌斯Arrhenius方程:可分别用分压、浓度和摩尔分率来表示反应物的组成,则相应的反应速率常数分别用kp,kc,ky来表示;相互之间的关系为:5、化学平衡常数与反应速率常数之间的关系说明:常数称为化学计量数,表示速率控制步骤出现的次数。
(注意不要和化学计量系数相混淆)三、温度对反应速率的影响1、不可逆反应由阿累尼乌斯方程,温度升高,反应速率也升高(例外的极少),而且为非线性关系,即温度稍有变化,反应速率将剧烈改变。
也就是说,反应温度是影响化学反应速率的一个最敏感因素。
2、可逆反应(1)可逆吸热反应反应速率将总是随反应温度的升高而增加(2)可逆放热反应反应速率在低温时将随反应温度的升高而增加,到达某一极大值后,温度再继续升高,反应速率反而下降。
再升高温度,则可能到达平衡点,总反应速率为零。
最优温度与平衡温度关系:四、复合反应1、反应组分的转化速率和生成速率我们把单位之间内单位体积反应混合物中某组分i的反应量叫做该组分的转化速率或生成速率。
第2章 反应动力学基础

温度一定:转化率↑ 可逆放热反应的速率↓ 温度一定:转化率↑,可逆放热反应的速率↓ 可逆放热反应按最佳温度曲线操作, 可逆放热反应按最佳温度曲线操作,反应速率最大
N2+3H2=2NH3 (A) 是在高温高压下采用熔融铁催化剂进行的。 是在高温高压下采用熔融铁催化剂进行的。合成氨反应为可逆 放热反应,故过程应尽可能按佳温度曲线进行。 放热反应,故过程应尽可能按佳温度曲线进行。现拟计算下列 条件下的最佳温度: 25.33MPa下 3:1的氢氮混合气进 条件下的最佳温度:(1)在25.33MPa下,以3:1的氢氮混合气进 行反应, 17%, %,(2) 但氨含量为12 12%, 行反应,氨含量为17%,(2)其他条件同(1),但氨含量为12%, (3)把压力改为32.42MPa,其他条件同(1)。 把压力改为3 MPa, 已知该催化剂的正反应活化能为58 618× J/mol, 58. 已知该催化剂的正反应活化能为58.618×103J/mol,逆 反应的活化能为167.48 167.48× J/mol。平衡常数K 与温度T(K) 反应的活化能为167.48×103J/mol。平衡常数K,与温度T(K) 及总压P(MPa)的关系如下: P(MPa)的关系如下 及总压P(MPa)的关系如下: logKp=(2172.26+19.6478p)/TlogKp=(2172.26+19.6478p)/T-(4.2405+0.02149p) (B) 解:(1)首先求出氨含量为17%时混合气体组成,再利用平衡 (1)首先求出氨含量为17%时混合气体组成, 首先求出氨含量为17 关系式算出Kp Kp值 利用式(B)求得平衡温度Te (B)求得平衡温度Te, 关系式算出Kp值,利用式(B)求得平衡温度Te,最后代入式 (2.37),即为所求。 (2.37),即为所求。
第2章 化学反应动力学基础
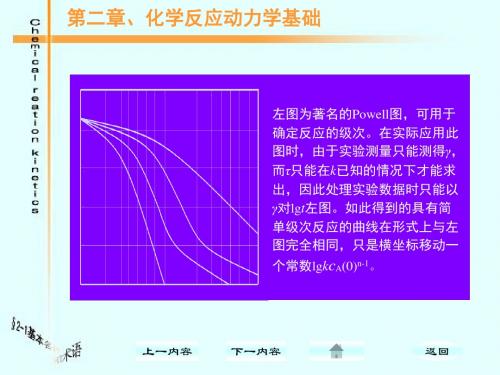
1.3.2 活化能因素: 对于基元反应来说,如果体系中一个组分有两 个以上的基元反应发生,则以活化能最低的发生反 应几率最大,这也是探索历程的一个重要线索依 据,由此因素,我们可以确定基元反应那些反应可 以发生,那些反应的发生可能性最小。
1.3.3 中间物和分子结构因素: 如果能从反应中检验某种中间物,则对反应历 程的确定将起重要作用,某些物质容易捕捉自由 基,反应体系加入这些物质,观察反应速率是否 下降,以判断体系中是否有自由基存在,而自由 基的存在常能导致链反应,此外,所设想的中间 物应与结构化学规律相符合,这就是需要考虑的 结构因素。
cCH3CHO(0)为乙醛的初始浓度。 式中,
上一内容 下一内容 返回
反应级数 当固定乙醛的初始浓度,可见在不同反应时间 测量反应速率时,r与
cCH3CHO 的平方成正比,
即称其时间级数为二级。如果以不同的初始浓
度进行试验,测定反应的初始反应速率,则与 乙醛的初始浓度的一次方成正比,即称为反应 级数为一级。许多反应的时间级数与浓度级数 是相同的,但也有一些不同。
在我们通过考虑三因素后,则基本上对反应的历 程有了某些线索和启发,然后可以进行初步探索 拟定历程,当初步拟定历程后,如何检验所草拟 的历程有一定的正确性和认为可以接受呢? 这就要求我们必须记住服从下面两个一致性:由 拟定的反应历程所得到的反应动力学方程应该和 由实验得到的动力学方程相一致。由拟定的反应 历程所得到的表观活化能应该和由实验测得的活 化能相一致。
t1/2 =
1 n-1-1 ] [ (2) (n-1)αkcA(0)n-1
上一内容 下一内容
[n(≠1)级反应]
返回
八、收率、转化率和选择收率 收率是指一个反应过程的产物量占反应物量的 百分数
反应动力学基础知识点总结

反应动力学基础知识点总结动力学是研究物体运动规律的一个重要学科,在物理学、工程学、生物学等领域都有着广泛的应用。
动力学的基础知识点涵盖了运动学、牛顿力学、静力学、动力学、作用和反作用定律、牛顿三定律等内容。
本文将对动力学的基础知识点进行总结,希望能够帮助读者对动力学有更深入的了解。
一、运动学运动学是动力学的基础,它研究的是物体的运动规律,主要包括位置、速度、加速度和时间等物理量。
在运动学中,我们主要关注的是物体在运动过程中的轨迹和速度加速度的变化规律。
经典力学中的三大定律(牛顿三定律)可以用运动学的知识来进行解释。
1.1 位置、速度和加速度位置是一个物体在空间中的坐标,它可以用矢量来描述。
速度是位置矢量对时间的导数,它描述了物体在单位时间内位移的大小和方向。
加速度是速度矢量对时间的导数,它描述了速度随时间变化的大小和方向。
在运动学中,我们通过对位置、速度和加速度的研究,来了解物体在空间中的运动规律。
1.2 运动学的应用运动学的知识在实际生活和工程中有着广泛的应用。
例如,在交通工程中,我们通过对车辆的运动学参数进行分析,来优化道路设计和交通管理。
在机械工程中,我们通过对机器臂的运动学特性进行研究,来设计和控制机器人的运动。
在航天工程中,我们通过对火箭的运动学特性进行分析,来计算飞行轨迹和着陆位置。
总之,运动学的知识对我们理解和控制物体的运动具有重要的意义。
二、牛顿力学牛顿力学是动力学的重要组成部分,它研究物体的运动规律和受力情况,主要包括牛顿运动定律、牛顿万有引力定律、牛顿的合力原理、牛顿动力学等内容。
牛顿力学是研究物体在受力情况下的运动规律,它是经典力学的基础。
2.1 牛顿三定律牛顿三定律是牛顿力学的核心内容,它包括惯性定律、动量定律和作用和反作用定律。
(1)惯性定律牛顿第一定律也称惯性定律,它阐述了物体静止或匀速直线运动状态不变的规律。
即物体如果不受外力作用,将保持原来的状态,包括保持静止或匀速直线运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一氧化氮氧化动力学方程建立
由于第二步为速率的控制步骤因此有:
r k2C( NO ) 2Co2
2 C K C 1 NO 第一步达到平衡,则 有: ( NO) 2
代入上式得
r k2 K1C Co2 k2C Co2
2 NO 2 NO
因此,当得到的速率方程与由质量作用定律得到的形
r dW
8
空速与接触时间
空速:单位反应体积所处理的混合物的体积流量。因
次为时间的倒数(1/h)。
VS 0 VSP VR
计算空速时的体积流量一般使用标态体积,特殊说明
时可使用操作状态流量。也有使用摩尔流量的,称为 摩尔空速。 是衡量反应器生产强度的重要操作参数。例如:氨合 成反应,压力为10Mpa时,空速为10000(1/h);而当压 力为30Mpa时,空速则为28000-30000(1/h)。
例:NO氧化反应速率方程
对于反应 2 NO O2 2 NO2 得到的速率方程为: r kC 2 C NO O 2 该动力学方程并非是由基元反应的质量
作用定律得出.有学者认为该反应由下列 两步组成 :
NO NO ( NO) 2 ( NO) 2 O2 2 NO2
并且第二步为速率的控制步骤.
式中 A为指前因子,其因次与k相同;E为活化 能;R为气体常数。
30
反应速率常数因次
反应速率常数的因次与反应速率的表示方式,速率方
程的形式以及反应物系组成的表示方式有关。 反应级数(一级、二级)、反应速率的因次(以反应 体积计、以催化剂质量计、以相界面计的反应速率)、 对于气相反应,常用分压、 浓度和摩尔分率 来表示 反应物系的组成, 则 之间有下列关系 k ,k ,k
即r=f(c,T)
14
动力学方程的一般表示形式
影响反应速率的反应主份浓度不限于一个。速率方程
随反应而异,纵使形式相同而参数值也完全不同。对 于同一个反应,所采用催化剂不同,形式和参数都可 能不一样。 对于不可逆反应A+B=· · · · · · ,其动力学方程一般可表 示为:
r kc C C
见正逆反应速率常数与平衡常数之间存在一 定的关系。
24
化学反应平衡
设可逆反应 vAA vB B R R 的速率方程为:
a a a rA kcAA cBB cRR kcAA cB B cR R
平衡时,
a a a kcAA cBB cRR kcAA cB B cR R
对于非基元反应,可以看成是若干基元反应的 综合结果 。反应的速率方程可由反应机理可 以推导得到。
16
与非基元反应速率方程
如果反应 APD 是由下列反应步骤组成:
A A* P A D
这两个反应均为基元反应,其中A* 为反应过程 的中间化合物。由反应机理推导速率方程常 用的方法是假定其中进行较慢的一步为速率 控制步骤,因为它对反应速率起决定性作用。
c
vA / v vB / v vR / v A B R
c
c
K
1/ v c
26
反应速率常数 与化学平衡常数 的关系
比较反映化学反应达到平衡的上述3个
式子可得
A aA vA / v
即
B aB vB / v
1/ v k / k KC
R aR vR / v
V dt
rR=
1 dn R V dt
说明 由于A和B为反应物,其量总是随时间而减少, 故时间导数dnB/dt<0,dnB/dt<0, R为反应产物,情 况则相反,dnB/dt>0。 因此,按反应物反应量来计算反应速率时,需加上 一负号,以使反应速率恒为正值。显然,由于反 应计量系数不同,按不同反应组分计算的反应速 率数值上是不相等的 。
10
多相系统反应速率的换算
均相反应系统一般都是基于反应体积来表示 其反应速率。 多相反应系统,特别是采用固体催化剂进行 反应的系统,以催化剂的体积、催化剂内表 面积、催化剂质量表示的反应速率形式都有。 在实验室进行动力学研究时,第三种形式最
多。 这三种方式表示的反应速率可以进行换算。
rA v r ' A B r
第二章 反应动力学基础
化学反应工程研究的主要对象是工业反应器, 主要研究内容是工业反应动力学。其中宏观 动力学是核心。 宏观反应动力学的基础是本征动力学,即化 学动力学。 本章将在物理化学的基础上,从反应工程学 科的角度阐述一些常用的反应动力学概念和 动力学问题的处理方法,其中包括均相反应 动力学及多相催化剂反应动力学。
或
rA
0
cR c
R aR
aA A A
c
aB B B
k k
25
化学平衡常数 的表示
设A、B及R均为理想气体,A和B为反应物,其 化学计量系数应为负值,当反应达到平衡时, 由热力学可知 :
c c c Kc
vA vB vR A B R
设
v 为正数,上式可改写成:
f 2 (c) c c ....
aA aB A B
22
幂函数型速率方程
幂函数型速率方程形式为:
r kc c .... k c
a A aB A B i 1
N
ai i
式中的浓度级数,对于基元反应为反应计量系数,非
基元反应为实验回归参数。 因为反应物与产物的浓度都会影响反应速率,因此, 式中应包括所有组分浓度的影响,无论是反应物还是 反应产物都包括在内。其有否影响或影响大小要由实 验来判明。
式相同,不能说明该反应一定是基元反应。但基元反 应的速率方程可用质量作用定律来表示。
20
例:反应机理分析
如果所得动力学实验结果与由所设的反应机理推导得到
的速率方程相符合,绝对不能肯定说所设的反应机理是 正确的。只能说明是一个可能的反应机理,因为不同的 反应机理完全可能推导出形式相同的速率方程 。 例如NO的氧化反应,如果机理为:
m A
n B
km ol 3 m s
式中, kc k0e
E RT
以浓度表示的反应速率 常数
15
基元反应与非基元反应
对于基元反应,反应式表示了真正的反应历程, 动力学方程可根据质量作用定律写出.如
A A B B R R
动力学方程为
vA vB rA kcA cB
这一结果可用以检验速率方程推导的正
确性
27
例2.2
28
例题计算结果
29
2.3 温度对反应速率的影响
在幂函数型速度方程中,以反应速率常数k来 体现温度对反应速率的影响。对于一定的温 度,反应速率k为定值。通常用阿累尼乌斯方 程表示反应速率常数与温度的关系。即:
k A exp( E / RT )
23
可逆反应速率方程的幂函数形式
可逆反应的反应速率等于正反应速率与逆反 应速率之差,一般所谓的不可逆反应只是表 明逆反应的反应速率甚小可忽略不计而已。
可逆反应的速率方程可用幂函数表示如下 :
i 1 i 1 当反应达到平衡时,反应速率为 0,因此可
N a N r k ci i k ci i
目前绝大多数化学反应的机理还未弄清 , 仍然 是以实验为基础来确定化学反应的速率方程。 也称经验方程。 经验方程一般为幂函数型速率方程 , 而且往往 将浓度及温度对反应速率的影响分离开来 表
示,即 :r f1 (T ) f 2 (c)
对于一定的温度,则温度函数 f1 (T ) 为常数,以反 应速率常数k表示; 而浓度函数以各反应组成浓度的指数函数
对于恒容过程,V为常数,则有:
dcA r dt
此即为经典化学动力学所常用的反应速率定
义式
6
连续流动的反应速率
连续流动反应器,反 应物A连续地以摩尔 流量FA0通入反应器 进行反应,如果达到 定常态,则反应器内 任何一点处的物系参
数将不随时间而变。 这时, 反应速率表示 一般式为:
dFA r dVr
9
接触时间
接触时间:是一个虚拟时间,不表示真正的反应时
间。 VR 定义:空速的倒数。因次为时间单位。
V0
当体积流量为标态流量时,接触时间为标准接触时间。
如果时操作状态下的流量,则为操作状态下的接触时 间。 如果需要,流动体系的反应速率可通过接触时间表示:
dNA0 (1 x A ) N A0 dxA NT 0 y A0 dxA dNA r dVR d (V0 ) V0 d V0 d
17
非基元反应速率方程的建立
如果第二步较慢,则由质量作用定律速率方程 为: * * A A 2 A
r r k c
K1
第一步达到平衡有:
c* Ac p cA
或
c* A K1 c A / c p
代入上式得到:
rA k2 K1c A / c p kcA / c p
18
7
多相系统反应速率的表示
对于多相反应,也可以用相界面积a代替反应 体积Vr来定义反应速率,反应速率式表示为:
dF A r da 如果系统中采用固体催化剂进行的反应时, 相界面积a催化剂的内表面。 当系统是采用固体催化剂进行的反应时,往 往基于固体的质量W来定义反应速率,此时的 表示式为: dF A
1
2.1 化学反应速率
化学反应速率的一般定义 :单位体积
单位反应时间反应物系中某一反应组 分的反应量或产物的生成量 。 对于反应 A A B B R R 根据反应速率的定义可以分别以反应 组分A、B及R的反应量表示如下:
