八年级数学竞赛讲座平行截割附答案

合集下载

八年级数学竞赛题及答案解析(K12教育文档)

八年级数学竞赛题及答案解析(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学竞赛题及答案解析(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学竞赛题及答案解析(word版可编辑修改)的全部内容。

八年级数学竞赛题(本检测题满分：120分,时间：120分钟）班级：姓名：得分：一、选择题（每小题3分,共30分）1.下列四个实数中，绝对值最小的数是（）A ．－5B ．－2C ．1D ．4 2。

下列各式中计算正确的是（）A 。

9)9(2-=- B.525±= C.3311()-=- D.2)2(2-=-3。

若901k k <<+ (k 是整数)，则k =（）A. 6B. 7C.8D. 9 4。

下列计算正确的是( ) A 。

ab ·ab =2abC.3—=3(a ≥0） D 。

·=(a ≥0，b ≥0）5。

满足下列条件的三角形中，不是直角三角形的是（） A.三内角之比为1∶2∶3 B.三边长的平方之比为1∶2∶3 C 。

三边长之比为3∶4∶5 D 。

三内角之比为3∶4∶56.已知直角三角形两边的长分别为3和4，则此三角形的周长为（） A ．12 B ．7＋7 C ．12或7＋7 D ．以上都不对7。

将一根24 cm 的筷子置于底面直径为15 cm ，高为8 cm 的圆柱形水杯中，设筷子露在杯子外面的长度为h cm,则h 的取值范围是（） A ．h ≤17 B ．h ≥8 C ．15≤h ≤16D ．7≤h ≤168.在直角坐标系中,将点（－2，3)关于原点的对称点向左平移2个单位长度得到的点的坐标是（）A.（4，－3） B 。

初二数学全全等三角形截长补短(讲义及答案)及答案

初二数学全全等三角形截长补短(讲义及答案)及答案一、全等三角形截长补短1．如图，△ABC中，，AD是BC边上的高，如果，我们就称△ABC为“高和三角形”．请你依据这一定义回答问题：（1）若，，则△ABC____ “高和三角形”（填“是”或“不是”）；（2）一般地，如果△ABC是“高和三角形”，则与之间的关系是____，并证明你的结论2．如图，在△ABC中，AB＝AC，∠BAC＝30°，点D是△ABC内一点，DB＝DC，∠DCB＝30°，点E是BD延长线上一点，AE＝AB．（1）求∠ADB的度数；（2）线段DE，AD，DC之间有什么数量关系？请说明理由．3．已知：线段AB及过点A的直线l，如果线段AC与线段AB关于直线l对称，连接BC交直线l于点D，以AC为边作等边△ACE，使得点E在AC的下方，作射线BE交直线l于点F，连接CF．（1）根据题意将图1补全；（2）如图1，如果∠BAD＝α（30°＜α＜60°）．①∠BAE=_______，∠ABE=_______（用含有α代数式表示）；②用等式表示线段FA，FE与FC的数量关系，并证明．（3）如图2，如果60°＜α＜90°，直接写出线段FA，FE与FC的数量关系，不证明．4．已知，90POQ ∠=，分别在边OP ，OQ 上取点A ，B ，使OA OB =，过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C ．点E ，F 分别是射线OP ，OQ 上动点，连接CE ，CF ，EF ．（1）求证：OA OB AC BC ===；（2）如图1，当点E ，F 分别在线段AO ，BO 上，且45ECF ∠=时，请求出线段EF ，AE ，BF 之间的等量关系式；（3）如图2，当点E ，F 分别在AO ，BO 的延长线上，且135ECF ∠=时，延长AC 交EF 于点M ，延长BC 交EF 于点N ．请猜想线段EN ，NM ，FM 之间的等量关系，并证明你的结论．5．问题提出，如图1所示，等边△ABC 内接于⊙O ，点P 是AB 上的任意一点，连结PA ，PB ，PC ．线段PA 、PB 、PC 满足怎样的数量关系?（尝试解决）为了解决这个问题，小明给出这样种解题思路：发现存在条件CA=CB ，∠ACB=60°，从而将CP 绕点逆时针旋转60°交PB 延长线于点M ，从而证明△PAC ≌△MBC ，请你完成余下思考，并直接写出答案：PA 、PB 、PC 的数量关系是；（自主探索）如图2所示，把原问题中的“等边△ABC”改成“正方形ABCD”，其余条件不变，①PC 与PA ，PB 有怎样的数量关系?请说明理由：②PC+PD 与PA ，PB 的数量关系是．（直接写出结果）（灵活应用）把原问题中的“等边△ABC”改成“正五边形ABCDE”，其余条件不变，则PC+PD+PE 与PA+PB 的数量关系是．（直接写出结果）6．如图所示，//AB DC AB AD BE ⊥，，平分ABC CE ∠，平分BCD ∠；（1）求AB CD 、与BC 的数里关系，并说明你的理由．（2）若把AB AD ⊥条件去掉，则（1）中AB CD 、与BC 的数里关系还成立吗?并说明你的理由．7．数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．∠AEF=90°，且EF 交正方形外角∠DCG 的角平分线CF 于点F ，求证：AE=EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM=EC ，易证△AME ≌△ECF ，所以AE=EF ．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．8．如图1，在正方形ABCD 中，点P 为AD 延长线上一点，连接AC 、CP ，过点C 作CF ⊥CP交于C ，交AB 于点F ，过点B 作BM ⊥CF 于点N ，交AC 于点M ．（1）若AP=78AC ，BC=4，求S △ACP ；（2）若CP ﹣BM=2FN ，求证：BC=MC ；（3）如图2，在其他条件不变的情况下，将“正方形ABCD”改为“矩形ABCD”，且AB≠BC ，AC=AP ，取CP 中点E ，连接EB ，交AC 于点O ，猜想：∠AOB 与∠ABM 之间有何数量关系？请说明理由．9．在平行四边形ABCD 中，DE 平分ADC ∠交BC 于点E ，连接AE ．点O 是DE 的中点，连接CO 并延长交AD 于点F ，在CF 上取点G ，连接AG ．（1）若4tan 3B =，5AB =，6BC =，求ABE △的周长．（2）若60B EAG ∠=∠=︒，求证：AF CG =．10．已知平行四边形ABCD 中，N 是边BC 上一点，延长DN 、AB 交于点Q ，过A 作AM ⊥DN 于点M ，连接AN ，则AD ⊥AN ．（1）如图①，若tan ∠ADM ＝34，MN ＝3，求BC 的长；（2）如图②，过点B 作BH ∥DQ 交AN 于点H ，若AM ＝CN ，求证：DM ＝BH +NH ．【参考答案】***试卷处理标记，请不要删除一、全等三角形截长补短1．（1）是（2）；见解析【解析】【分析】（1）在BC上截取，根据，可得△ABE为等边三角形，，问题得解；（2）在△ABC中，在DC上截取，由AD是BC边上的高且，进而证明，△ABD≌△AED（SAS）就可以得到结论.【详解】解：（1）如图，Rt△ABC中，，，，在BC上截取，则△ABE为等边三角形，∴，∵，，∴，∴，∴∵，且△ABE为等边三角形，∴∴，∴是高和三角形．（2）;证明：如上图，在△ABC中，在DC上截取．∵，∴，∵AD是BC边上的高且，∴，△ABD≌△AED（SAS），∴，，∴.【点睛】本题主要考查全等三角形的判定与性质，根据题意构造全等三角形，理解“高和三角形”的定义是解题关键.2．（1）120°；（2）DE＝AD+CD，理由见解析【分析】（1）根据三角形内角和定理得到∠ABC＝∠ACB＝75°，根据全等三角形的性质得到∠BAD ＝∠CAD＝15°，根据三角形的外角性质计算，得到答案；（2）在线段DE上截取DM＝AD，连接AM，得到△ADM是等边三角形，根据△ABD≌△AEM，得到BD＝ME，结合图形证明结论【详解】解：（1）∵AB＝AC，∠BAC＝30°，∴∠ABC＝∠ACB＝12（180°﹣30°）＝75°，∵DB＝DC，∠DCB＝30°，∴∠DBC＝∠DCB＝30°，∴∠ABD＝∠ABC﹣∠DBC＝45°，在△ABD和△ACD中，AB AC DB DC AD AD=⎧⎪=⎨⎪=⎩，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD＝12∠BAC＝15°，∴∠ADE＝∠ABD+∠BAD＝60°，∴∠ADB＝180°﹣∠ADE＝180°﹣60°＝120°；（2）DE＝AD+CD，理由如下：在线段DE上截取DM＝AD，连接AM，∵∠ADE＝60°，DM＝AD，∴△ADM是等边三角形，∴∠ADB＝∠AME＝120°．∵AE＝AB，∴∠ABD＝∠E，在△ABD和△AEM中，ABD EADB AME AB AE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△AEM（AAS），∴BD＝ME，∵BD＝CD，∴CD＝ME．∵DE＝DM+ME，∴DE＝AD+CD．【点睛】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．3．（1）作图见解析；（2）①260α-︒，120α︒-；②FA=FC +FE ，证明见解析；（3）AF=FC-EF ．【分析】（1）先根据轴对称的性质作出线段AC ，再分别以A 、C 为圆心，AC 长为半径画弧，两弧交于点E ，可得等边△ACE ，最后根据题意画出图形即可；（2）①根据轴对称的性质可得∠BAC=2∠BAD=2α，根据等边三角形的性质可知∠EAC=60°，根据角的和差关系即可表示出∠BAE ；根据轴对称的性质和等边三角形的性质可得AB=AE ，根据等腰三角形的性质及三角形内角和定理即可表示出∠ABE ； ②在FA 上截取FG=EF ，连接EG ，利用三角形内角和定理可得∠AFB=60°，即可证明△EFG 是等边三角形，根据角的和差故选可得∠AEG=∠CEF ，利用SAS 可证明△AEG ≌△CEF ，即可得出AG=CF ，根据线段的和差关系即可得结论；（3）由60°＜α＜90°可知点E 在直线l 右侧，根据题意画出图形，在FA 上截取FG=EF ，根据轴对称的性质可得AF ⊥BC ，BF=CF ，根据（2）中结论可得∠FBC=∠FCB=30°，利用三角形外角性质可得∠GFE=60°，可证明三角形EFG 是等边三角形，利用SAS 可证明△AEF ≌△CEG ，可得FA=CG ，根据线段的和差关系即可得答案．【详解】（1）补全图形如下：（2）①260α-︒，120.α︒-①∵AB、AC关于直线l对称，∴∠BAD=∠CAD，AB=AC，∵△ACE是等边三角形，∴∠EAC=60°，AE=AC=EC，∵∠BAD=α，∴∠BAC=BAD+∠CAD=2∠BAD=2α，∴∠BAE=∠BAC-∠EAC=2α-60°．∵AB=AC，AC=AE，∴AB=AE，∴∠ABE=12（180°-∠BAE）=120°-α．故答案为：2α-60°，120°-α②数量关系是FA =FC +FE，证明如下：在FA上截取FG=EF，连接EG，由①得，∠ABE=120°-α，∠BAD=α，∴∠AFB=180°-∠ABE-∠BAD=60°，∴△EFG为等边三角形，∴EG=FE=FG，∠GEF=60°，∵△AEC是等边三角形，∴∠AEC=60°，AE=CE，∴∠AEC=∠GEF=60°，∴∠AEC-∠GEC=∠GEF-∠GEC，即∠AEG=∠CEF，在△AEG和△CEF中，EG EFAEG CEF AE CE=⎧⎪∠=∠⎨⎪=⎩，∴△AEG≌△CEF，∴AG=FC∴FA=AG+FG=FC+FE，（3）AF=FC-EF．∵60°＜α＜90°，∴如图所示，点E在直线l右侧，在FA上截取FG=EF，连接EG，∵AB、AC关于直线l对称，点F在直线l上，∴AF⊥BC，BF=CF，∴∠ABC=∠ACB=90°-α，由（2）可知∠ABE=120°-α，∴∠FBC=∠FCB=120°-α-（90°-α）=30°，∴∠EFG=∠FBC+∠FCB=60°，∴△EFG是等边三角形，∴∠FEG=60°，∵∠AEC=60°，∴∠AEF+∠AEG=∠CEG+∠AEG=60°，∴∠AEF=∠CEG ，在△AEF 和△CEG 中，EF EG AEF CEG AE CE =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△CEG ，∴AF=CG ，∴AF=FC-EF ．【点睛】本题考查轴对称的性质、等边三角形的判定与性质及全等三角形的判定与性质，根据轴对称的性质正确得出对应边并熟练掌握相关性质及判定定理是解题关键．4．（1）见解析；（2）EFAE BF =+；（3）222MN EN FM =+，见解析【分析】（1）连接AB ,通过90POQ ∠=，OA OB =得到AOB 为等腰直角三角形，进而得到45OAB OBA ∠=∠=，根据过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C ，可推出45CBA ∠=，45BAC ∠=，最后通过证明AOB ≌ACB △，可以得出结论；（2）在射线AP 上取点D ，使AD BF =，连接CD ，通过证明CAD ≌CBF ，得到CD CF =，ACD BCF ∠=∠，再结合45ECF ∠=，90ACB ∠=推导证明ECD ≌ECF △，得到ED EF =，最后等量代换线段即可求解；（3）延长AO 到点D ，使得AD BF =，连接CD ，通过证明CAD ≌CBF ，得到CD CF =，ACD BCF ∠=∠，再结合135ECF ∠=，推导证明ECD ≌ECF △，得到D CFM ∠=∠，根据D CFB ∠=∠，等量代换可知CFM CFB ∠=∠，又因为//AC OQ ，推出MCF CFB ∠=∠，进而得到MC MF =，同理可证CN EN =，最后根据勾股定理即可求解．【详解】解：（1）证明：连接AB ．90POQ ∠=，OA OB =，∴AOB 为等腰直角三角形，∴45OAB OBA ∠=∠=，又//BC OP ，且90POQ ∠=，∴BC OQ ⊥，∴90CBF ∠=，∴45CBA ∠=，同理，45BAC ∠=，在AOB 与ACB △中OAB CAB AB ABOBA CBF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴AOB ≌ACB △()ASA ，∴90AOB ACB ∠=∠=，OA OB AC BC ===；（2）如图1，在射线AP 上取点D ，使AD BF =，连接CD ．在CAD 与CBF 中CA CB CAD CBF AD BF =⎧⎪∠=∠⎨⎪=⎩，∴CAD ≌CBF ()SAS ，∴CD CF =，ACD BCF ∠=∠，45ECF ∠=，90ACB ∠=，∴45ACE BCF ∠+∠=，∴45ACE ACD ECD ∠+∠=∠=，∴ECD ECF ∠=∠，在ECD 与ECF △中CD CF ECD ECF CE CE =⎧⎪∠=∠⎨⎪=⎩∴ECD ≌ECF △()SAS ，∴ED EF =，又ED AD AE BF AE =+=+，∴EF AE BF =+．（3）222MN EN FM =+．证明如下：如图2，延长AO 到点D ，使得AD BF =，连接CD ．∴90CAD CBF ∠=∠=，在CAD 与CBF 中CA CB CAD CBF AD BF =⎧⎪∠=∠⎨⎪=⎩，∴CAD ≌CBF ()SAS ，∴CD CF =，ACD BCF ∠=∠，90ACD DCB ∠+∠=，∴90BCF DCB DCF ∠+∠==∠，∴90FCD BCA ∠=∠=，135ECF ∠=，∴36090135135ECD ∠=--=，∴ECF ECD ∠=∠，在ECD 与ECF △中EC EC ECD ECF CD CF =⎧⎪∠=∠⎨⎪=⎩，∴ECD ≌ECF △()SAS ，∴D CFM ∠=∠，CAD ≌CBF ，∴D CFB ∠=∠，∴CFM CFB ∠=∠，//AC OQ ，∴MCF CFB ∠=∠，∴CFM MCF ∠=∠，∴MC MF =，同理可证：CN EN =，∴在Rt MCN △中，由勾股定理得：22222MN CN CM EN FM =+=+．【点睛】本题综合考查了全等三角形的性质和判定,勾股定理以及正方形的有关知识，通过添加辅助线构造全等三角形，通过证明全等三角形得到线段之间的关系是解题的关键．5．【尝试解决】PA+PB=PC ；【自主探索】①PC PA =；理由见解析；②1)()PC PD PA PB +=+；【灵活应用】2)()PC PD PE PA PB ++=+．【分析】尝试解决：利用旋转性质证明△PAC ≌△MBC ，得到PA=BM ，得到PM 等于PB 与PA 的和，再证明△PCM 是等边三角形，得到PM 等于PC ，即可得到结果；自主探索：①在PC 上截取QC=PA ，证出△CBQ 全等于△ABP ，得到△PBQ 是等腰直角三角形，PQ 等于PB 倍，即可得到结果；②同①方法，即可得到PD 与PA 和PB 的关系，即可求出PC+PD 与PA 和PB 的关系；灵活应用：类比（自主探索）中的方法证明PC 与PA 和PB 的关系，再用同样的方法证明PE 与PA 和PB 的关系，构造△CDM 全等于△CBP ，得到PD 与PC 的关系，进一步得到PD 与PA 和PB 的关系，最终求出PD+PE+PC 的和即可得到与PA 和PB 的关系．【详解】尝试解决：PA+PB=PC ；证明：因为∠ACP+∠PCB=60°，∠MCB+∠PCB=60°，∴∠ACP=∠MCB ，又∵CP=CM ，AC=MC ，∴△ACP ≌△BCM ，所以PA=BM ，∠CBM=∠CAP ，∵四边形APBC 内接于圆O ，∴∠CAP+∠CBP=180°，∴∠CBM+∠CBP=180° ，∴P 、B 、M 三点共线，∴△PCM 是等边三角形，∴PM=PC ，∴PC=PM=PB+BM=PB+PA ；自主探索：①PC 与PA 、PB 的数量关系为PC PA =+；理由：截取CQ=PA ，，如图，∵四边形ABCD 是正方形，∴BC=AB ，∠ABC=∠BCD=∠CDA=∠DAB=90°，∵PA=CQ ，∠BCQ=BAP ，BC=AB∴△BCQ ≌△BAP ，∴∠CBQ=∠ABP ，BQ=BP ，∵∠CBQ+∠ABQ=90°，∴90ABP ABQ ∠+∠=︒，∴△PBQ 是等腰直角三角形，∴PQ=2PB ， ∴2PC CQ PQ PA PB =+=+；②(21)()PC PD PA PB +=++证明：在PD 上截取DH=PB ，∵DH=PB ，∠ADH=∠ABP ，AD=AB∴△ADH ≌△ABP∴∠DAH=∠BAP ，AH=AP ，∵∠DAH+∠HAP=90°，∴∠BAP+∠HAP=90°，∴△HAP 是等腰直角三角形，∴PH=2PA ，∴PD=DH+PH=PB+2PA ，∴(21)()PC PD PA PB +=++．灵活应用：(52)()PC PD PE PA PB ++=++．证明：在PC 上截取FC=PA ，∵五边形ABCDE 是正五边形，∴BC=AB=CD=DE=AE ，∠ABC=∠EAB=108°，∵PA=CF ，AB=BC ，∠FCB=∠BAP ，∴△BAP ≌△BCF ，∴BF=PB ，∠CBF=∠ABP ，∵∠CBF+∠FBA=108°，∴∠ABP+∠FBA=108°，∴△FBP 是顶角为108°的等腰三角形，∴PB ，∴PC=PF+FC=12PB+PA ，同理可证PA+PB ，延长PD 至点M 使DM=PB ，∵∠MDC+∠CDP=180°，∠CDP+∠PBC=180°，∴∠CDM=∠CBP又∵CD=BC ，∴△CDM ≌△CBP∴CM=CP ，∠MCD=∠BCP ，又∵∠PCB+∠PCD=108°，∴∠MCD+∠PCD=108°，∴△MCP 是顶角108°的等腰三角形，∴PC ，∴PC-PB ， ∴PC+PD+PE=PC+12+PC-PB+12+PA+PB=32+（12+PB+PA ）+PA=((22PA PB +=(()2PA PB + 【点睛】本题考查旋转性质、圆的有关性质、圆内接四边形、正五边形有关性质、三角形全等的相关性质和判定，综合性强，难度较大是一道好题，属中考压轴题型．6．（1）AB CD BC +=，见解析；（2）成立，见解析【分析】（1）先写出数量关系，过E 作EF BC ⊥于F ，然后证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得结论了．（2）成立, 在BC 上截取CF CD =证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得到结论．【详解】()1AB CD BC +=理由是：过E 作EF BC ⊥于FCE 为角平分线DCE FCE ∴∠=∠//AB DC AB AD ⊥，90D ∴∠=EF BC ⊥D CFE ∴∠=∠CE CE =()CDE CFE AAS ∆≅∆CD CF ∴=同理可证()ABE FBE AAS ∆≅∆AB BF ∴=CF BF AB +=AB CD BC ∴+=()2成立理由：在BC 上截取CF CD =CE 为角平分线DCE FCE ∴∠=∠CE CE =()CDE CFE SAS ∆≅∆CD CF ∴= D CFE ∠=∠//AB DC180D A ∴∠+∠=又180CFE EFB ∠+=A EFB ∴∠=∠又BE是角平分线∴∠=∠ABE FBE=BE BE∆≅∆BAE BFE AAS()∴=AB FB∴CF BF AB+=∴+=AB CD BC7．（1）正确．证明见解析；（2）正确．证明见解析.【分析】=，连接ME，根据已知条件利用ASA判定（1）在AB上取一点M，使AM EC=．AME ECF，因为全等三角形的对应边相等，所以AE EF=，连接NE，根据已知利用ASA判定（2）在BA的延长线上取一点N，使AN CE=．ANE ECF，因为全等三角形的对应边相等，所以AE EF【详解】解：（1）正确．=，连接ME．证明：在AB上取一点M，使AM ECBM BE∴=，∴∠=°，BME45AME，135CF是外角平分线，∴∠=︒，45DCF∴∠=°，135ECFAME ECF ，90AEB BAE ，90AEB CEF ∠+∠=︒， BAE CEF ∴∠=∠， ()AME ECF ASA ，AE EF ∴=．（2）正确．证明：如图示，在BA 的延长线上取一点N ，使AN CE =，连接NE ．BN BE ∴=，45N NEC ， CF 平分DCG ∠，45FCE ，N ECF ，四边形ABCD 是正方形，//AD BE ∴，DAE BEA ，即9090DAE BEA ，NAE CEF ， ()ANE ECF ASA ，AE EF ∴=．【点睛】此题主要考查了正方形的性质，角平分线的性质及全等三角形的判定方法，熟悉相关性质是解题的关键．8．（1）2；（2）证明见解析；（3）∠AOB=3∠ABM ，理由见解析．【分析】（1）由正方形的性质得出AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，由勾股定理求出AC ，得出AP ，即可求出S △ACP ；（2）在CF 上截取NG=FN ，连接BG ，则CF ﹣CG=2FN ，证出∠BCF=∠DCP ，由ASA 证明△BCF ≌△DCP ，得出CF=CP ，证出CG=BM ，由SAS 证明△ABM ≌△BCG ，得出∠AMB=∠BGC ，因此∠BMC=∠BGF ，由线段垂直平分线的性质得出BF=BG ，得出∠BFG=∠BGF，因此∠BMC=∠CBM，即可得出结论；（3）连接AE，先证出∠BCA=2∠PAE，再证明A、D、E、C四点共圆，由圆周角定理得出∠DCP=∠PAE，得出∠BCF=∠PAE，证出∠BCA=2∠ABM，然后由三角形的外角性质即可得出结论．【详解】解：（1）∵四边形ABC是正方形，∴AD∥BC，AB=BC=CD=4，∠ADC=∠CDP=∠ABC=∠BCD=90°，∴，∴AP=78AC=78=2，∴S△ACP=12AP×CD=12×2；（2）在CF上截取NG=FN，连接BG，如图1所示：则CF﹣CG=2FN，∵CF⊥CP，∴∠PCF=90°，∴∠BCF=∠DCP，在△BCF和△DCP中，ABC CDP BC DCBCF DCP∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BCF≌△DCP（ASA），∴CF=CP，∵CP﹣BM=2FN，∴CG=BM，∵∠ABC=90°，BM⊥CF，∴∠ABM=∠BCG，∠BFG=∠CBM，在△ABM和△BCG中，AB BCABI CBG BM CG=⎧⎪∠=∠⎨⎪=⎩，∴△ABM≌△BCG（SAS），∴∠AMB=∠BGC，∴∠BMC=∠BGF，∵GN=FN，BM⊥CF，∴BF=BG，∴∠BFG=∠BGF，∴∠BMC=∠CBM，∴BC=MC；（3）∠AOB=3∠ABM；理由如下：连接AE ，如图2所示：∵AC=AP ，E 是CP 的中点，∴AE ⊥CP ，∠PAE=∠CAE ，∵AD ∥BC ，∴∠BCA=∠PAC=2∠PAE ，∵CF ⊥CP ，∴∠PCF=90°，∴∠BCF=∠DCP ，∵∠ADC=∠AEC=90°，∴A 、D 、E 、C 四点共圆，∴∠DCP=∠PAE ，∴∠BCF=∠PAE ，又∵∠ABM=∠BCF ，∴∠ABM=∠BCF=∠PAE ，∴∠BCA=2∠ABM ，∵∠AOB=∠BCF+∠BCA ，∴∠AOB=3∠ABM ．【点睛】本题是四边形综合题目，考查了正方形的性质、勾股定理、全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质、四点共圆、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要通过作辅助线两次证明三角形全等才能得出结论．9．（1）56；（2）见解析【分析】（1）构建直角三角形，得出AH 、BH ，然后利用角平分线的性质以及平行四边形的性质，进行等量互换，即可得解；（2）首先在AB 上截取BQ BE =，然后判定DOF EOC ≌△△和AEQ GAF ≌△△，进行等量转换，即可得证.【详解】（1）过点A 作AH BC ⊥于点H ，如图所示：4tan 3B ∠=，5AB =， 4AH ∴=，3BH =DE 平分ADC ∠，12∠∠∴=，AD BC ∵∥，13∠∠∴=23∴∠=∠，5DC EC ∴==，1BE ∴=，2EH ∴=，25AE ∴=256ABE C ∴=+△；（2）在AB 上截取BQ BE =，连接EQ ，如图所示：CD CE =，CO DE ⊥，OD DE ∴=①AD BC ∵∥，DFO ECO ∴∠=∠，ADE CED ∠=∠②③ 由①②③得：DOF EOC ≌△△，DF CE ∴=，又AD BC =，AD DF BC CE ∴-=-，即AF BE =60EAG ∠=︒，60BAE FAG ∴∠+∠=︒，60DFC ∠=︒，60FGA FAG ∴∠+∠=︒，CD=CFBAE FGA ∴∠=∠④又120FAG AQE ∠=∠=︒，EQ AF =⑤⑥由④⑤⑥得：AEQ GAF ≌△△，AQ FG ∴=，又AB CF =，AB AQ CF FG ∴-=-，即BQ CG =，AF CG ∴=．【点睛】此题主要考查利用三角函数值构建直角三角形以及全等三角形的判定与性质，熟练掌握，即可解题.10．（1）BC ＝203；（2）见解析. 【分析】（1）如图①中，设AM ＝3k ，DM ＝4k ，则AD ＝5k ，由△ADM ∽△NDA ，可得AD 2＝DM •AN ，由此构建方程即可解决问题．（2）如图②中，连接CH ，在DM 上取一点K ，使得DK ＝BH ．证明△ADK ≌△CBH （SAS ），推出AK ＝CH ，再证明Rt △AMK ≌Rt △CNH （HL ），推出MK ＝HN 即可解决问题．【详解】（1）解：如图①中，∵AM ⊥DN ，∴∠AMD ＝90°，∵tan ∠ADM ＝AII DN ＝34， ∴可以假设AM ＝3k ，DM ＝4k ，则AD ＝5k ，∵AD ⊥AN ，∴∠DAN ＝90°＝∠AMD ，∵∠ADM ＝∠ADN ，∴△ADM ∽△NDA ，∴AD 2＝DM •AN ，∴（5k ）2＝4k （4k +3），解得k＝43，∴AD＝203，∵四边形ABCD是平行四边形，∴BC＝AD＝203．（2）证明：如图②中，连接CH，在DM上取一点K，使得DK＝BH．∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠ADK＝∠BNQ，∵BH∥DQ，∴∠CBH＝∠BNQ，∴∠ADK＝∠CBH，∵DK＝BH，DA＝BC，∴△ADK≌△CBH（SAS），∴AK＝CH，∵AM⊥DQ，AN⊥AD，AD∥BC，∴AN⊥BC，∴∠AMK＝∠CNH＝90°，∵AM＝CN，∴Rt△AMK≌Rt△CNH（HL），∴MK＝NH，∴DM＝DK+MK＝BH+HN．【点睛】本题考查了三角形的综合问题，掌握解直角三角形、相似三角形的性质以及判定定理、全等三角形的性质以及判定定理是解题的关键．。

八年级数学竞赛讲座平行截割附答案

八年级数学竞赛讲座平行截割附答案第十九讲平行截割平行线是初中平面几何中基本而重要的图形，平行线能改变角的位置并传递角，可“送”线段到恰当处，完成等积变形，当一组平行线截两条直线时就得到比例线段，平行线分线段成比例定理是研究比例线段、相似形的重要理论．利用、挖掘、创造平行线，是运用平行线分线段成比例定理解题的关键，另一方面，需要熟悉并善于从复杂图形中分解或构造如下形如“E ”、“A ”型或“X ”型的基本图形：例题求解【例1】如图，已知在平行四边形ABCD 中，M 、N 为AB 的三等分点，DM 、DN 分别交AC 于P 、Q 两点，则AP ：PQ ：QC= ．(河北省初中数学创新与知识应用竞赛试题)思路点拨图中有形如“X ”型的基本图形，建立含AP ，PQ ，QC 的比例式，并把AP ，PQ ，QC 用同一条线段的代数式表示．【例2】如图，已知在△ABC 中，AE ：EB=1：3，BD ：DC=2：1，AD 与CE 相交于F ，则FDAF FC EF 的值为( )A ．21B ．1C ．23D ．2 (江苏省泰州市中考题)思路点拨已知条件没有平行线，需恰当作平行线，构造基本图形，产生含FCEF ，FD AF 的比例线段，并设法沟通已知比例式与未知比例式的联系．【例3】如图，BD 、BA ，分别是∠ADC 与它的邻补角∠ABP 的平分线，AE ⊥BE ，AD ⊥BD ，E 、D 为垂足．(1)求证：四边形AEBD 为矩形；(2)若AD AE =3，F 、G 分别为AE 、AD 上的点，FG 交AB 于点H ，且3=AGAF ，求证：△AHG 是等腰三角形．(厦门市中考题)思路点拨对于(2)，由比例线段导出平行线，证明∠HAG=∠AHG ．【例4】如图，梯形AB CD 中，AD ∥BC ，AB ＝DC ．(1)如果P 、E 、F 分别是BC 、AC 、BD 的中点，求证：AB=PE+PF ；(2)如果P 是BC 上的任意一点(中点除外)，PE ∥AB ，PF ∥DC ，那么AB=PE+PF 这个结论还成立吗?如果成立，请证明；如果不成立，说明理由．(上海市闽行区中考题)思路点拨对于(2)，先假设结论成立，从平行线出发证明AB=PC+PF ，即需证明1=+AB PF AB PE ，将线段和差问题的证明转化为与比例线段有关问题的证明．注若题设条件无平行线，需作平行线．而作平行线要考虑好过哪一点作平行线，一般是由比的两条线段启发而得的，其目的是构造基本图形．平行线分线段成比例定理是证明比例线段的常用依据之一，比例线段丰富了我们研究几何问题的方法，主要体现在：(1)利用比例线段求线段的长度；(2)运用比例线段证明线段相等，线段和差倍分关系、两直线平行等问题．【例5】如图，在四边形ABCD 中，AC 与BD 相交于点O ，直线l 平行于BD ，且与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P ，求证：PM ×PN=PR ×PS(山东省竞赛题)。

部编数学八年级下册专题06特殊平行四边形的两种考法全攻略(解析版)含答案

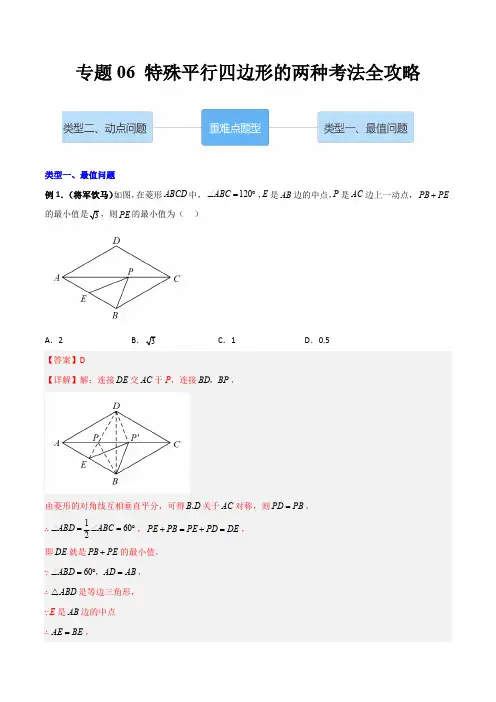
专题06 特殊平行四边形的两种考法全攻略类型一、最值问题例1．（将军饮马）如图，在菱形ABCD 中，120ABC Ð=°，E 是AB 边的中点，P 是AC 边上一动点，PB PE +PE 的最小值为（）A ．2B C ．1D ．0.5由菱形的对角线互相垂直平分，可得B 、∴1602ABD ABC Ð=Ð=°，PE PB PE +=即DE 就是PB PE +的最小值，例2．（中点模型）如图，矩形,2,4ABCD AB BC ==，点A 在x 轴正半轴上，点D 在y 轴正半轴上，当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为（）A ．2B ．2C 1D ．【答案】A 【详解】如图，取AD 的中点H ，连接CH ，OH ，Q 矩形ABCD ，2AB =，4BC =，2CD AB \==，4AD BC ==，例3．（截补模型）如图，在Rt ABC △中，90C =o ∠，2AC BC ==，点D 、E 分别是边BC 、AC 上的动点．且BD CE =，连接AD 、BE ，则AD BE +的最小值为______．∵90ACB Ð=°，AC =∴90FBD ACB Ð=Ð=∵BD CE =，∴(SAS BDF CEB ≌△△AC=，以BC为对角线作正方形BDCE，连例4．（瓜豆模型）如图，平面内三点A，B，C，4AB=，3接AD，则AD的最大值是______．【变式训练1】如图，矩形ABCD 中，84AB AD ==，，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是___________．当点F 与点C 重合时，点P 在1P 当点F 与点E 重合时，点P 在2P ∴PP EC ∥且1PP CE =．【变式训练2】如图，已知线段12AB =，点C 在线段AB 上，且ACD V 是边长为4的等边三角形，以CD 为边的右侧作矩形CDEF ，连接DF ，点M 是DF 的中点，连接MB ，则线段MB 的最小值为_______________．【答案】6【详解】∵ACD V 为等边三角形，∴AC AD =，60DAC Ð=°，∵四边形DCFE 是矩形，点M 是DF 的中点，∴DM ＝CM ，【变式训练3】如图，在正方形ABCD 中，边长2AB =，点Q 是边CD 的中点，点P 是线段AC 上的动点，则DP PQ +的最小值为 _____．【变式训练4】如图，在菱形ABCD 中，10AB =，16AC =，点M ，N 在AC 上，且2MN =，连接BM ，DN ，则BM DN +的最小值为 ______【变式训练5】如图，在Rt ABC △中，90BAC Ð=°，且3BA =，4AC =，点D 是斜边BC 上的一个动点，过点D 分别作DM AB ^于点M ，DN AC ^于点N ，连接MN ，则线段MN 的最小值为_____．类型二、动点问题例1．如图，在正方形ABCD中，E为AB的中点，以A为原点，AB、AD所在直线为x轴、y轴，建立平－向点D运动，面直角坐标系．正方形ABCD的边长是方程28160-+=的根．点P从点B出发，沿BC CDx x-向点C运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个同时点Q从点E出发，沿EB BC△的面积为单位长度．当点P运动到点D时，P、Q两点同时停止运动，设点P运动的时间为t秒，AQPS．(1)求点C的坐标；(2)求S关于t的函数关系式；△是以AP为底边的等腰三角形时，直接写出点P的坐标．(3)当AQP由题意得：EQ t =，2BP t =，∴2AQ AE EQ t =+=+，2BQ t =-，2222222(2)44,(2)(2)AQ t t t PQ BP t t \=+=+++=-+2544t t =-+当AQ PQ =时，22AQ PQ =，∴2244544t t t t ++=-+，解得0=t (舍去)或2，∴4BP =，∴当0t 2££，AQP △是以AP 为底边的等腰三角形时，()44P ，；②24t <£时，如图：由题意得：EB BQ t +=，2BC CP t +=，∴2BQ t BE t =-=-，6CQ BC BE t t =+-=-，224CP t BC t =-=-，282PD BC CD t t =+-=-，22224(2)AQ AB BQ t \=+=+-2420t t =-+2222(6)PQ CQ CP t =+=-22(24)52852t t t +-=-+当AQ PQ =时，22AQ PQ =，∴2242052852t t t t -+=-+，解得2t =(舍去)或4，∴0DP =，∴()04P ，；∴当24t <£，AQP △是以AP 为底边的等腰三角形时，()04P ，，综上所述，当AQP △是以AP 为底边的等腰三角形时，点P 的坐标为()44，或()04，例2.如图，在长方形ABCD 中，4AB =，3BC =，点E 为AD 延长线上一点，且6AE =，点P 从点A 出发，沿A —B —C —D 向终点D 运动．同时点Q 从点B 出发，沿B —C —D —E 向终点E 运动，它们的速度均为每秒1个单位长度．设APQ △的面积为S ，点P 运动的时间为t 秒．(1)当2t =时，S = ；当72t =时，S = ．(2)当07t <£时，用含t 的代数式表示S ．直接写出结果并化简．(3)当点P 在CD 边上，且APQ △为等腰三角形时，直接写出t 的取值或者范围．【变式训练1】如图，在ABCD Y 中，ABC Ð为锐角，5AB =，9BC =，36ABCD S =Y ．动点P 从点A 出发，以每秒2个单位的速度沿A B C D A ®®®®运动．同时，动点Q 从点A 出发，以每秒3个单位的速度沿A D C B A ®®®®运动．当其中一个点到达终点时，另一个点也随之停止运动．设点P 的运动时间为t 秒．(1)点P 在BC 上运动时，CP =_____________；点P 在CD 上运动时，CP =_____________．（用含t 的代数式表示）(2)点P 在CD 上，PQ BC ∥时，求t 的值．(3)当直线PQ 平分ABCD Y 的面积时，求t 的值．(4)若点Q 的运动速度改变为每秒a 个单位．当972t << ，ABCD Y 的某两个顶点与P 、Q 所围成的四边形为菱形时，直接写出a 的值．【变式训练2】如图，长方形ABCD 中，AD BC ∥，90B Ð=°，104AD BC cm AB cm ===，，动点P 从点B 出发，以每秒1cm 的速度沿B A D ®®的方向，向终点D 运动；动点Q 从点B 出发以每秒1cm 的速度沿B C ®的方向向终点C 运动．以PQ 为边向右上方作正方形PQMN ，其中一个动点到达终点时，另一个动点也随之停止运动，设点P Q 、同时出发，运动时间为t 秒0t （＞）．(1)当04t ＜＜时，AP ＝______（用含t 的代数式表示）；(2)当点N 落在AD 边上时，求t 的值；(3)当正方形PQMN 与长方形ABCD 的重叠部分为四边形时，求重叠部分的面积S （用含t 的代数式表示）；(4)请直接写出当t满足什么条件时，正方形PQMN与长方形ABCD的重叠部分为三角形．如图3，当M 点运动到D 点处时，∵10214CQ t CQ PM PM t ===-﹣，，，∴2014t t -=-（1），解得6t =，∴当6t =时，正方形PQMN 与长方形ABCD 的重叠部分为三角形，∴46t ££时，正方形PQMN 与长方形ABCD 的重叠部分为三角形；如图4，当Q 点运动与C 点时，10t =，此时正方形PQMN 与长方形ABCD 的重叠部分为三角形；∴610t ＜＜时，正方形PQMN 与长方形ABCD 的重叠部分为四边形，如图5，【变式训练3】已知在矩形ABCD中，AB＝4，AD＝9，点M在AD上，且AM＝4，动点P从点B出发，以每秒1个单位长度的速度，沿B﹣C﹣D﹣A向终点A运动，运动时间为t秒．(1)当点P在BC边上时，BP＝，CP＝．（用含t的代数式表示）(2)点P在运动过程中，△ABP是直角三角形时，t的取值范围为．(3)点P在运动过程中，△DMP是等腰三角形时，t的值为．(4)连接CM，当点P在线段CM的垂直平分线上时，t的值为．【答案】(1)t，9﹣t(2)0＜t≤9或13≤t＜22(3)1或7或6.5当点P 在线段BC 上时，CP =MP =9-t ，PH =t -4，MH =4，∵△MPH 是直角三角形，∴2222MH PH PM CP +=＝即()()222449t t -=+-，∴t ＝4.9，当点P 在线段AD 上时，同法可得PM ＝CPCP =MP =18-t ，DP =t -13，CD =4∵△CDP 是直角三角形，∴2222CD DP PM CP +=＝即()()22241318t t =+--，∴t ＝13.9．综上所述，满足条件的t 的值为4.9或13.9．故答案为：4.9或13.9．。

八年级数学竞赛讲座图形的折叠、剪拼与分割附答案

第二十七讲图形的折叠、剪拼与分割一页普通的纸，童年时我们用稚气的双手把它折成有趣的动物，民间艺人可以把它剪成美丽的图案．折纸与剪纸是最富于自然情趣而又形象生动的实验，是丰富想象力与心灵手巧的结合．对图形进行折叠与剪拼，是学习几何不可或缺的重要一环，通过折叠与剪拼图形，我们可以发现一些几何结论并知晓这些结论是怎样被证明的．把图形或部分沿某直线翻折叫图形的折叠，对图形通过有限次的剪裁再重新拼接成新的图形叫图形的剪拼．解与图形折叠或剪拼相关的问题，利用不变量解题是关键，在折叠过程中，线段的长度、角的度数保持不变；在剪拼过程中，新图形与原图形的面积一般保持不变．例题求解【例1】如图，有一块直角三角形纸片，两直角边AC=6㎝，BC=8㎝，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于．(南通市中考题)思路点拨设CD=x，由折叠的性质实现等量转换，将条件集中到Rt△BDE中，建立x的方程．注图形折叠与剪拼问题可考壹我们的动手操作能力和分析推理能力，解题时需要把计算、推理与合情想象结合起来．折叠问题可以对称观点认识：(1)折痕两边是全等的；(2)对应点连线被折痕垂直平分．解折叠问题常用到勾股定理、相似形、方程思想等知识与方法．【例2】如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，则重叠部分△AFC的面积为( ) A．12 D10 C．8 D．6 (2004年武汉市选拔赛试题)思路点拨只需求出AF长即可．【例3】取一张矩形的纸进行折叠，具体操作过程如下：第一步：先把矩形ABCD对折，折痕为MN，如图1；第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得Rt△AB'E，如图2；第三步：沿EB'线折叠得折痕EF，如图3．利用展开图4探究：(1)△AEF是什么三角形?证明你的结论．(2)对于任一矩形，按照上述方法是否都能折出这种三角形?请说明理由．(山西省中考题)思路点拨本例没有现成的结论，需经历实验、观察、猜想、证明等数学活动，从而探究得到结论．【例4】如图，是从边长为40cm、宽为30cm的矩形钢板的左上角截取一块长为20cm、宽为10cm的矩形后，剩下的一块下脚料．工人师傅要将它作适当地切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能短的正方形工件．(1)请根据上述要求，设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案(在图2和图3中分别画出切割时所沿的虚线，以及拼接后所得到的正方形，保留拼接的痕迹)；(2)比较(1)中的两种方案，哪种更好一些?说说你的看法和理由．（山东省中考题)思路点拨拼接后正方形的边长为221030 ㎝，它恰是以30cm 和10cm 为两直角边的直角三角形的斜边的长，为此可考虑设法在原钢板上构造两直角边长分别为30㎝和l0cm 的直角三角形，这是解本例的关键．注有效的数学学习过程不能单纯地依赖模仿与记忆，应该通过观察、实验、操作、猜测、验证、推理等数学活动，形成自己对数学知识的理解和有效的学习策略，从而使知识得到内化，形成能力．近年中考中涌现的设计新颖、富有创意的折叠、剪拼与分割等问题，注重对动手实践操作、应用意识、学习潜能的考查．【例5】用10个边长分别为3，5，6，11，17，19，22，23，24，25的正方形，可以拼接成一个矩形．(1)求这个矩形的长和宽； (2)请画出拼接图．思路点拨利用拼接前后图形面积不变求矩形的长和宽；运用矩形对边相等这一性质画拼接图．【例6】如图，已知△ABC 中，∠B=∠C=30°，请设计三种不同的分法，将△ABC 分割成四个三角形，使得其中两个是全等三角形，而另外两个是相似但不全等的直角三角形．请画出分割线段，标出能够说明分法的所得三角形的顶点和内角度数(或记号)．(画图工具不限，不要求证明，不要求写出画法) (温州市中考题)思路点拨充分运用几何计算、推理和作图，综合运用动手操作、空间想象、解决问题．学力训练1．将一张长方形的纸对折，如图所示可得到一条折痕(图中虚线)，继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到条折痕，如果对折n 次，可以得到条折痕．(2002年南宁市中考题)2．一张直角三角形的纸片，像图中那样折叠，使两个锐角顶点A 、B 重合，若∠B=30°，AC=3，则折痕DE 的长等于． (三明市中考题)3．如图，将一块长为12的正方形纸片ABCD 的顶点A 折至DC 边上的点E ，使DE ＝5，折痕为PQ ，则线段PM= ．4．在△ABC 中，已知AB=20，∠A=30°，CD 是AB 边的中线，若将△ABC 沿CD 对折起来，折叠后两个小三角形ACD 与三角形BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的41，有如下结论：①AC 边的长可以等于a ；②折叠前的△ABC 的面积可以等于223a ；③折叠后，以A 、B 为端点的线段AB 与中线CD 平行且相等，其中，正确结论有个． (天津市中考题)5．将四个相同的矩形(长是宽的3倍)，用不同的方式拼成一个大矩形，设拼得大矩形的面积是四个小矩形的面积和，则大矩形周长的值只可能有( )A ．1种B ．2种C ．3种D ．4种 (2003年南昌市中考题)6．如图，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 内部时，则∠A 与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是( ) A ．∠A=∠1+∠2 B ．2∠A ＝∠1+∠2 C ．3∠A ＝2∠1+∠2 D ．3∠A=2(∠l+∠2) (北京市海淀区中考题)7．将一张矩形纸对折再对折(如图)，然后沿着图中的虚线剪下，得到①、②两部分．将①展开后得到的平面图形是( )A ．矩形B ．三角形C ．梯形D ．菱形 (陕西省中考题)8．如图1，小强拿一张正方形的纸，沿虚线对折一次得图2，再对折一次得图3，然后用剪刀沿图3中的虚线剪去一个角，再打开后的形状是( ) (济南市中考题)9．如图，东风汽车公司冲压厂冲压汽车零件的废料都是等腰三角形的小钢板，其中AB=AC，该冲压厂为了降低汽车零件成本，变废为宝，把这些废料再加工成红星农业机械厂粉碎机上的零件，销售给红星农业机械厂，这些零件的形状都是矩形．现在要把如图所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形，每种矩形的面积正好等于该三角形的面积，每次切割的次数最多两次(切割的损失可忽略不计)．(1)请你设计两种不同的切割焊接方案，并用简要的文字加以说明；(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次)，则该三角形需满足什么条件? (十堰市中考题)10．如图，ABCD是矩形纸片，E是AB上一点，且BE：EA＝5：3，EC=155，把△BCE沿折痕EC向上翻折，若点B恰好落在AD边上，设这个点为F，求AB、BC的长．11．如图，在△ABC中，AB＝3，AC＝4，BC=5，现将它折叠，使点B与点C重合，则折痕的长是． (四川省竞赛题)12．如图，一张矩形纸片沿BC折叠，顶点A落在点A，处，第二次过A，再折叠，使折痕DE∥BC，若AB=2，AC=3，则梯形BDEC的面积为．( “宇振杯”上海市竞赛题)13．如图，将矩形ABCD的四个角向内折起，恰好拼成既无缝隙又无重叠的四边形EFGH，若EH＝3，EF＝4，那么线段AD与AB的比等于． ( “希望杯”邀请赛试题)14．要剪切如图l(尺寸单位mm)所示的两种直角梯形零件，且使两种零件的数量相等．有两种面积相等的矩形铝板，第一种长500mm，宽300mm(如图2)；第二种长600mm，宽250mm(如图3)；可供选用．(1)填空：为了充分利用材料，应选用第种铝板，这时一块铝板最多能剪甲、乙两种零件共个，剪出这些零件后，剩余的边角料的面积是 mm2．(2)画图，从图2或图3中选出你要用的铝板示意图，在上面画出剪切线，并把边角余料用阴影表示出来．15．如图，EF为正方形ABCD的对折线，将∠A沿DK折叠使它的顶点A落在EF上的G点，则∠DKG为( ) A．15° B．30° C．55° D．75°16．某班在布置新年联欢会会场时，需要将直角三角形彩纸裁成长度不等的矩形彩条，如图，在Rt△ABC的长都不小于5cm ，则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A ．24B ．25C ． 26D ．27 (山东省济南市中考题)17．如图，若将左边正方形剪成四块，恰能拼成右边的矩形，设a ＝1，则这个正方形的面积为( )A ．2537+ B ．253+ C ．251+ D ．2)21(+ (2003年山东省竞赛题)18．如图，已知Rt △ABC 中，∠C ＝90°，沿过点月的一条直线BE 折叠这个三角形，使点C 落在AB 边上的点为D ，要使点D 恰为AB 的中点，问在图中还需添加什么条件? (1)写出两个满足边的条件； (2)写出两个满足角的条件；(3)写出一个满足除边角以外的其他条件． (黄冈市竞赛题)19．如图，正方形纸片ABCD 中，E 为BC 的中点，折叠正方形，使点A 与点E 重合，压平后，得折痕MN ，设梯形ADMN 的面积为S 1，梯形BCMN 的面积为S 2，求21S S 的值20．已知一个三角形纸片ABC ，面积为25，BC 的长为l0，∠B 、∠C 都为锐角，M 为AB 边上的一动点(M 与A 、B 不重合)，过点M 作MN ∥BC 交AC 于点N ，设MN=x ． (1)用x 表示△AMN 的面积；(2)△AMN 沿MN 折叠，使△AMN 紧贴四边形BCNM(边AM 、AN 落在四边形BCNM 所在的平面内)，设点A 落在平面BCNM 内的点A ′，△A ′MN 与四边形BCNM 重叠部分的面积为y ． ①用的代数式表示y ，并写出x 的取值范围．②当x 为何值时，重叠部分的面积y 最大，最大为多少?。

八年级数学竞赛讲座平行四边形附答案

第十五讲平行四边形平行四边形是一类特殊的四边形，它的特殊性体现在边、角、对角线上，矩形、菱形是特殊的平行四边形，矩形的特殊性体现在有一个角是直角，菱形的特殊性体现在邻边相等，所以，它们既有平行四边形的性质，又有各自特殊的性质．对角线是解决四边形问题的常用线段，对角线本身的特征又可以决定四边形的形状、大小，连对角线后，平行四边形就产生特殊三角形，因此解平行四边形相关问题时，既用到全等三角形法，特殊三角形性质，又要善于在乎行四边形的背景下探索问题，利用平行四边形丰富的性质为解题服务．熟悉以下基本图形、基本结论：例题求解【例1】如图，在矩形ABCD中，已知AD=12，AB=5，P是AD边上任意一点，PE⊥BD于E，PF⊥AC于F，那么PE+PF的值为．(全国初中数学联赛试题)思路点拨分别求出PE、PF困难，△AOD为等腰三角形，若联想“到等腰三角形底边上任一点到两腰距离的和等于腰上的高”这一性质，则问题迎刃而解．注特殊与一般是对立统一的，在一定条件下可以互相转化，相对于一般而言，特殊的事物往往更简单、更直观、更具体．因而人们常常通过特殊去认识一般；另一方面，一般概括了特殊，一般比特殊更为深刻地反映着事物的本质，所以人们也往往通过一般去了解特殊．一般与特殊，是知识之间联系的一种重要形式，知识常常在一般到特殊或特殊到一般的变化过程中，不斩地得到延伸与拓展．【例2】已知四边形ABCD，从下列条件中：(1)AB∠CD，(2)BC∥AD；(3)AB=CD；（4）BC=AD；(5)∠A=∠C；(6)∠B=∠D．任取其中两个，可以得出“四边形ABCD是平行四边形”这一结论的情况有（）A．4种 B．9种 C．13种 D． 15种(山东省竞赛题)思路点拨根据平行四边形的判定方法及新的组合方式判定．【例3】】如图，在△ADC中，∠DAC=90°，AD⊥BC，DC、AF分别是∠ABC、∠DAC的平分线，BE和AD交于G，求证：GF∥AC．(湖北省荆州市中考题)思路点拨从角的角度证明困难，连结CF，在四边形AGFE的背景下思考问题，证明四边形AGFE为特殊平行四边形，证题的关键是能分解出直角三角形中的基本图形．【例4】如图，设P为等腰直角三角形ACB斜边AB上任意一点，PE⊥AC于点E，PF⊥BC于点F，PG ⊥EF于G点，延长GP并在其延长线上取一点D，使得PD＝PC，求证：BC⊥BD，且BC=BD．(全国初中数学联赛试题)思路点拨尽管图形复杂，但证明目标明确，只需证明△CPB≌△DPB，应从图中分离出特殊三角形、特殊四边形，充分运用它们的性质为证题服务．【例5】如图，在等腰三角形ABC中，延长边AB到点D，延长边CA到点E，连结DE，恰有AD=BC=CE=DE．求∠BAC的度数．(北京市竞赛题)思路点拨题设条件给出的是线段的等量关系，要求的却是角的度数，相等的线段可得到全等三角形、特殊三角形，为此需通过构造平行四边形改变它们的位置．注课本中平行四边形的判定定理是从边、角、对角线三个方面探讨的，一般情况是，从四边形边、角、对角线三类元素任意选取两类，任意组合就产生许多判定平行四边形的命题．其中有真命题与假命题，对于假命题，要善于并熟悉构造反例．构造反例是学习数学的一种重要技能，可以帮助我们理解概念．培养推理能力，数学史上就曾有许多著名的论断被一个巧妙的反例推翻的实例．若题设条件中有彼此平行的线段或造成平行的因素，则通过作平行线，构造平行四边形，这是解四边形问题的常用技巧，这是由于平行四边形能使角的位置更理想，送线段到恰当的地方，使线段比良性传递．学力训练1．如图，BD 是平行四边形ABCD 的对角线，点E 、F 在BD 上，要使四边形AECF 是平行四边形，还需要增加的一个条件是 (填上你认为正确的一个即可，不必考虑所有可能情形) (宁波市中考题)2．(1)如图，已知矩形ABCD 中，对角线AC 、BD 相交于O ，AE ⊥BD 于E ，若∠DAE ：∠BAE ＝3：1，则∠CAC ＝； (河南省中考题)(2)矩形的一个角的平分线分矩形一边为lcm 和3cm 两部分，则这个矩形的面积为 cm 2． (武汉市中考题)3．如图，以△ABC 的三边为边在BC 的同一侧分别作三个等边三角形，即△ABD 、△BCE 、△ACF ． (1)四边形ADEF 是；(2)当△ABC 满足条件时，四边形ADEF 为矩形；(3)当△ABC 满足条件时，四边形ADEF 不存在． (2000年贵州省中考题)4．已知一个三角形的一边长为2，这边上的中线为1，另两边之和为1+3，则这两边之积为． (2001年天津市选拔赛试题)5．四边形的四条边长分别是a 、b 、c 、d ，其中a 、c 为对边，且满足cd ab d c b a 222222+=+++，则这个四边形一定是( )A．平行四边形 B．两组对角分别相等的四边形C．对角线互相垂直的四边形 D．对角线相等的四边形6．如图，周长为68的矩形ABCD被分成7个全等的矩形，则矩形ABCD的面积为( )A．98 B．196 C．280 D． 284(湖北省荆州市中考题)7．如图，菱形花坛ABCD的边长为6m，∠B＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长(粗线部分)为( )A．123 m B．20m C． 22m D．24m(吉林省中考题)8．在凸四边形ABCD中，AB∥CD，且AB+BC=CD+DA，则( )A．AD>BC B．AD<BCC．AD=BC D．AD与BC的大小关系不能确定(“希望杯”邀请赛试题)9．如图，△ABC为等边三角形，D、F分别是BC、AB上的点，且CD=BF，以AD为边作等边△ADC．(1)求证：△ACD≌△CNBF；(2)当D在线段BC上何处时，四边形CDEF为平行四边形，且∠DEF=30°?证明你的结论． (南通市中考题)10．如图，在Rt△ABC中，AB=AC，∠A=90°，点D为BC上任一点，DF⊥AB于F，DE⊥AC于C，M为BC的中点，试判断△MEF是什么形状的三角形，并证明你的结论．(黑龙江省中考题)11．如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．(1)求证：CO＝FO；(2)当点O运动到何处时，四边形AECF是矩形?并证明你的结论．(3)当△ABC满足什么条件时，四边形AECF是正方形?12．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中有对四边形面积相等，它们是．(常州市中考题)13．如图，菱形ABCD的对角线AC、BD相交于O，△AOB的周长为3+3，∠ABC＝60°，则菱形ABCD的面积为．14．如图，矩形ABCD的对角线相交于O，AE平分∠BAD交BC于E，∠CAE=15°，则∠BOE= ．15．如图，矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为． (山东省竞赛题)16．如图，平行四边形ABCD中，∠ABC=75°，AF⊥BC于F，AF交BD于E，若DE=2AB，则∠AED的大小是( )A．60° B．65° C．70° D．75° (“希望杯”邀请赛试题)17．如图，正△AEF 的边长与菱形ABCD 的边长相等，点E 、F 分别在BC 、CD 上，则∠B 的度数是( ) A ．70° B ．75° C ．80° D ．95° (重庆市竞赛题)18．如图，正方形ABCD 外有一点P ，P 在BC 外侧，并在平行线AB 与CD 之间，若PA=17，PB=2，PC=5，则PD=( )A ．25B ．19C ．32D ．17 (“五羊杯”竞赛题)19．如图，在平行四边形ABCD 中，BC=2AB ，CZ ⊥AB 于E ，F 为AD 的中点，若∠AEF=54°，则∠B=( )A ．54°B ．60°C ．66°D ．72° (武汉市选拔赛试题)20．如图，在Rt △ABC 中，∠ABC ＝90°，∠C=60°，BC ＝2，D 是AC 的中点，以D 作DE ⊥AC 与CB 的延长线交于E ，以AB 、BE 为邻边作长方形ABEF ，连结DF ，求DF 的长．21．如图，菱形的对角线AC 与BD 交于点O ，延长BA 到E ，使AE=21AB ，连结OE ，延长DE 交CA 的延长线于F ．求证：OE=21DF ． 22．阅读下面短文：如图1，△ABC 是直角三角形，∠C=90°，现将△ABC 补成矩形，使△ABC 的两个顶点为矩形一边的两个端点，第三个便点落在矩形这一边的对边上，那么符合要求的矩形可以画出两个：矩形ACBD 和矩形AEFB(如图2)．解答问题；(1)设图2中矩形ACBD和矩形AEFB的面积分别为S l、S2，则S1 S2(填“>”，“=”或“<”)；(2)如图3，△ABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出个，利用图3把它画出来；(3)如图4，△ABC是锐角三角形且三边满足BC>AC>AB，按短文中的要求把它补成矩形，则符合要求的矩形可以画出个，利用图4把它画出来；(4)在(3)中所画出的矩形中，哪一个的周长最小?为什么?(陕西省中考题)23．如图，在△ABC中，∠C=90°，点M在BC上，且BM＝AC，N在AC上，且AN=MC，AM与BN相交于P，求证：∠BPM=45°．(杭州市“求是杯”竞赛题)24．如图，在锐角△ABC中，AD、CZ分别是BC、AB边上的高，AD、CE相交于F，BF的中点为P，AC的中点为Q，连结PQ、DE．(1)求证；直线PQ是线段DE的垂直平分线；(2)如果△ABC是钝角三角形，∠BAC>90°，那么上述结论是否成立?请按钝角三角形改写原题，画出相应的图形，并给予必要的说明．(“希望杯”邀请赛试题)。

数学竞赛专题讲座----奥赛试题精讲

例1.平面上有n条直线,它们中任意两条都不平行,且任意三条都不交于一点.这n条直线可以把平面分割成多少个局部？此问题的变例〔即特殊情况〕：变例1：十刀最多可以把一张饼分成多少块？变例2：一个圆形纸片,切100刀,最多可以将它分割为多少块？对变例2 ,我们首先猜想其结论：令S1,S2,……,Sn分别表示将圆形纸片切一刀,二刀,……,n刀所得块数,那么有S1=2=1+1S2=4=1+1+2S3=7=1+1+2+3S4=11=1+1+2+3+4……Sn=1+1+2+3+4+……+n=1+(n+1)·n∴当n=100时,有S100=1+〔100+1〕·100=5051〔块〕解：设bn 表示一条直线被n个不同的点分割后所得的分段数,那么有bn=n+1.设an-1为平面被符合条件的n-1条直线分割成的局部数,那么当平面上插入符合条件的第n条直线时,前 n-1条直线与第n 条直线相交于n-1个不同的点,这n-1个点分第n条直线为bn-1段,而每一分段恰分平面上一个已存在的局部为两个局部,于是,有：an =an-1+bn-1〔n＞1,n∈N〕又：bn-1=n∴ an =an-1+n=an-2+( n-1)+ n =……=n+( n-1)+( n-2)+……+2+a1又：a1=2=1+1∴an=n+( n-1)+( n-2 )+ ……+2+1+1例2.有10级台阶,小王从下向上走,假设每次只能跨一级或两级,他走上去共有多少种不同的走法？解：考虑更一般的情况：在同样条件下走n级台阶,情况如何？设an为上n级台阶的所有不同的走法数目.假设第一次走一级,那么余下的n-1级有an-1 种走法；假设第一次走两级,那么余下的 n-2 级有an-2种走法.∴ an =an-1+an-2(n＞2,n∈N)显然a1=1,a2=2∴a3=a1+a2=3a4=a3+a2=5a5=a4+a3=8a6=a5+a4=13a7=a6+a5=21a8=a7+a6=34a9=a8+a7=55a10=a9+a8=89思考题：用8张1×2的方格纸覆盖2×8的方格纸,共有多少种不同的覆盖方式？解题新思路：探究数学问题解决的新思路,对于学生发散性思维和创造性思维的培养是十分有利的.下面一道例题,是从多维度角度出发来探究解题新思路的：例：如图〔1〕在梯形ABCD中,AB∥CD,四边形ACED是平行四边形,延长DC 交BE于F.求证：EF=FB分析：这个题目本身不难,求证也容易,但通过对题设和结论的深入挖掘与探索,我们可以得出许多好的证法,总结如下：证实一：如下图,作BQ∥AD,交DF延长线于Q点,那么四边形ABQD是平行四边形,从而BQ=AD,再由题设可证△CEF≌△QBF, 得证EF=FB.证实二：如左图所示：作FM∥DA交AB于M,那么四边形ADFM是平行四边形,从而FM=DA.再证△CEF≌△MFB,从而结论可得证.证实三：作CN∥EB交AB于N,那么四边形CNBF是□,从而CN=FB.再证：△ANC≌△DFE,可得CN=EF,即EF=FB.证实四：作DP∥FB交AB于P,证实△ADP≌△CEF,从而得出结论.证实五：延长EC交AB于G,那么四边形ADCG是□,∴CE=AD=GC,即C 是EG中点.又CF∥GB,∴F是EB中点,结论得证.证实六：连结AE交CD于O点,那么O 是AE中点,又OF∥AB,∴F是AB 中点,得证.证实七：延长ED交BA延长线于H点,那么HACD是□, ∴CA=DH=ED ∴D是EH中点.又DF∥HB ∴F是EB中点,得证.证实八：作ES∥CD交AD延长线于S,那么CDSE是□∴DS=CE=AD ∴D是AS中点.又SE∥CD∥AB ∴F是EB中点,得证.证实九：在证实一作的辅助线根底上,连结EQ,那么可得ECBQ是□,从而F是□ECBQ对角线EB的中点.总之,上述不同证法的辅助线可归结为以下两种：①作平行线构成平行四边形和全等三角形进行等量代换.②作平行线,由题设产生中点,通过平行线等分线段定理的推论得出结论.这其中,其实蕴含了平面几何的平移变换和旋转变换的数学思想.。

八年级数学平行线等分线段定理及推论; 三角形中位线和梯形中位线华东师大版知识精讲

初二数学平行线等分线段定理及推论；三角形中位线和梯形中位线华东师大版【同步教育信息】一. 本周教学内容：1. 平行线等分线段定理及推论2. 三角形中位线和梯形中位线二. 重点、难点：重点：平行线分线段定理，三角形和梯形中位线定理。

难点：定理的灵活应用。

三. 知识精讲及例题分析（一）知识梳理1. 平行线等分线段定理//////，==若a b c d AB BC CD==则EF FG GH注：此定理与截线l l的位置无关。

12推论1：经过梯形一腰中点与底平行的直线必平分另一腰。

若梯形ABCD ，AD//BC//EF ，AE=EB 则DF=FC若∆ABC 中，DE BC //，AD DB = 则AE EC =2. 三角形中位线定义：连结三角形两边中点的线段叫三角形中位线。

定理：三角形中位线平行于第三边并且等于第三边的一半。

ABC D E ，、为AB 、AC 中点则DE BC //123. 梯形中位线定义：连结梯形两腰中点的线段叫梯形中位线。

梯形面积＝中位线×高【典型例题】例1. 已知：AB BC DC BC ⊥⊥，，E 为AD 中点，且EF BC ⊥ 求证：EF 平分∠BEC证明： AB BC DC BC EF BC ⊥⊥⊥，，∴AB EF DC //// 又 E 是AD 中点 ∴=BF FC∴EF 是BC 的中垂线 ∴=BE EC又 EF 是BC 中线 ∴EF 平分∠BEC例2. 已知M 、N 分别为平行四边形ABCD 的边AB 、CD 的中点求证：BE EF FD ==分析：根据MN 中点及平行四边形ABCD 可得到AN MC //再在∆BFA ，及∆DEC 中用平行线等分线段推论2即可证得BE EF FD ==证明：平行四边形ABCD∴AB DC //又 M 、N 分别为AB 、CD 中点∴==AM AB CN DC 1212∴AM CN //∴四边形AM 为平行四边形 ∴MC AN // 又 M 是AB 中点∴=BE EF 同理DF FE = ∴==BE EF FD例3. 已知∆ABC 中，AD 是BC 边中线，E 是AD 中点，BE 延长线交AC 于F 求证：AF AC =13分析：此题缺平行线因此构造平行线后求证。

初三上竞赛辅导资料1(平行截割)

Q P F E A D CB 初三上竞赛辅导资料1第一讲平行截割赛点归纳相似在竞赛中主要涉及的知识有：1.比例线段（包括比例的性质、平等线分线段成比例定理及推论）；2.相似三角形的性质和判定；3.相似的应用.在熟练掌握相似三角形的概念、性质和判定定理的基础上，要能够灵活地利用已知条件中已有的相似三角形，或善于利用平行线，或适当添加辅助线构造相似形，以利于解决问题.平行线分线段成比例定理及推论是研究比例线段、相似形的重要理论.利用、挖掘、创造平行线，是应用平行线分线段成比例定理解题的关键.解题指导例1、如图7-1-1，已知□ABCD 中，若边AB 上的两点E 、F 满足AE=EF=FB ，CE 分别与DF 、DB 交于点M 、N ，则EM ∶MN ∶NC 等于（）.A.2∶1∶4B. 4∶3∶5C. 5∶3∶12D. 5∶4∶12[思路探究]要求出EM 、MN 、NC 的比，应设法找出这三条线段与某一条线段的关系.此题可由平行线得到一些比例式，再由比例式之间的关系，求出EM ∶MN ∶NC.例2、如图7-1-3，在梯形ABCD 中，AD//BC ，AD ＝a,BC ＝b ，E 、F 分别是AD 、BC 的中点，且AF 交BE 于P ，CE 交DF 于Q ，则PQ 的长为 .[思路探究]欲求PQ 的长，先须应用“平行截割定理”，于是先需发现PQ 与有关线段的平行关系，再由平行线得出比例式. [思维误区]有的学生是这样解答例2的：[解].2121,2121,//b a b a CF ED EC EQ b a b a BE PE BF AE BC AD ======∴ a pQ ba b PQ b a BE PE BC PQ BC PQ EC EQ BE PE =∴=∴==∴∴=∴...//.例3、如图7-1-4，AB//CD 、AD//CE ，F ，G 分别是AC 和FD 的中点，过G 的直线依次交AB 、AD 、CD 、CE 于点M 、N 、P 、Q ，求证：MN+PQ ＝2PN.[思路探究]由已知条件，有两组平行线，能产生多个相关的比例式，而且还可以添加适当的辅助线构造平行四边形，再选取有关的比例式加以组合，不难证明MN+PQ ＝2PN.例4、如图7-1-5，已知M 、N 为△ABC 的边上BC 上的两点，且满足BM ＝MN ＝NC ，一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于D 、E 、F.求证：EF ＝3DE.[思路探究]根据BM ＝MN ＝NC 这一条件，结合要证明的EF ＝3DE ，应考虑添加平行线，应用“平行线分线段成比例定理（推论）”.[拓展题]如图7-1-6，在四边形ABCD 中，AC 与BD 相交于点O ，直线l 平行于BD ，且与AB 、DC 、BC 、AD 及AC 的延长线相交于点M 、民、R 、S 和P.求证：PM •PN ＝PR •PS.例5、如图7-1-7，在□ABCD 中，P 1、P 2、...P n-1是BD 的n 等分点，连结AP 2并延长交BC 于E ，连结AP n-2并延长交CD 于F.（1）求证：EF//BD ；（2）设□ABCD 的面积为S ，若S △AEF =,91S 求n 的值. [思路探究]（1）欲证EF//BD.可先证.2222FP AP E P AP n n --=（2）欲求n 的值，可以由S △AEF =,91S 得出关于n 的方程来求解，则关键是将S △AEF 用含n 的代数式表示.例6、如图7-1-8，在△ABC 中，AB ＝AC ，∠BAC ＝900，BD 是中线，AE ⊥BD ，交BC 于点E.求证：BE ＝2EC.[思路探究]欲证21BE EC ,2==可证EC BE ，则可应用“平行线分线段成比例定理的推论”达到目的，但题中无平行线，故考虑平行线.能力训练1.如图，四边形ABCD 为梯形，一条直线与DA 的延长线、AB 、BD 、AC 、BC 的延长线顺次交于点E 、F 、G 、H 、I 、J.若EF ＝FG ＝GH ＝HI ＝IJ ，则AD ∶BC ＝ .2.（2006，“希望杯”邀请赛）如图，在四边形ABC Ｄ中，Ｅ是对角线BD 上一点，EF//AD ，EM//BC ，那么BC EM DA EF +的值为（）. A.大于1B.等于1C.小于1D.与D 点的位置无关3.（2004，山东竞赛）如图，在△ABC ，点D 、E 分别在边AB 和AV 上，且DE//BC.过点A 作平行于BC 的直线分别交CD 和BE 的延长线于点M 、N.若DE ＝2，BC ＝6，则MN ＝ .4.如图，在△ABC 中，AD 是BC 边上的中线，F 是AD 上一点，且AF ∶FD ＝1∶5，连结CF 并延长交AB 于点E ，则AE ∶EB 等于（）.A. 1∶6B. 1∶8C. 1∶9D. 1∶105.如图，AD 是△ABC 的中线，E 是AD 上一点，且CE AD AE ,31=交AB 于点F ，若AF ＝1.2cm ，则AB ＝ cm.6.如图，在梯形ABCD 中，AB//DC ，点E 、F 分别在AD 、BC 上，EF//DC ，如果,2=EDAE AB ＝7，DC ＝10，那么EF ＝ .7.（2005，重庆中考）如图，DE 是△ABC 的中位线，M 是DE 中点，CM 的延长线交AB 于点N ，则S △DMN ∶S 四边形ANME 等于（）.A.1∶5B. 1∶4C. 2∶5D. 2∶78.如图，ABCD 是正方形，E 、F 是AB 、BC 的中点，连结EC 交DB 、DF 于G 、H ，则EG ∶GH ∶HC ＝ .9.（2003，黄冈竞赛）如图，在△ABC 中，AB ＝AC ，D 在AB 上，E 在AC 的延长线上，BD ＝3CE ，DE 交BC 于F ，则DF ∶FE ＝ .10.已知梯形的上、下底分别为a 和b （a<b ）,直线l 平行于两底，且把腰分成两线段的比值为q p :（自上而下），b a q p ::≠,那么l 夹在梯形两对角线之间的线段长为（）. A.q p aq pb +- B. q p aq pb -- C. q p aq pb ++ D. qp aq pb +-11.（2004.武汉竞赛）如图，在△ABC 中，D 是AC 的中点，E 、F 是BC 的三等分点，AE 、AF 分别交BD 于M 、N 两点，则BM ：MN ：ND ＝（）.A.3：2：1B.4：2：1C.5：2：1D.5：3：212.如图，在△ABC 中，AB ＝73,132=AC ，E 、F 分别是AB 、AC 的中点，且BF ⊥CE ，求BC 的长.13.（2003.河北竞赛）如图，已知正方形ABCD 的边长是5cm ，又EF ＝FG ，FD ＝DG ，求△ECG 的面积.14.（2005，山东竞赛）如图，在△ABC 中，AB ＝1，AC ＝2，D 是BC 的中点，AE 平分∠BAC 交BC 于点E ，且DF//AE.求CF 的长.15.如图，在梯形ABCD 中，AD//BC ，EF 经过梯形对角形的交点O ，且EF//AD.（1）求证：OE ＝OF ；（2）求BC OE AD OE +的值；（3）求证：EFBC AD 211=+.。

八年级几何难题专题讲座十四讲

目录本内容适合八年级学生竞赛拔高使用。

注重中考与竞赛的有机结合，重点落实在中考中难以上题、奥赛方面的基础知识和基本技能培训和提高。

本内容难度适中，讲练结合，由浅入深，讲解与练习同步，重在提高学生的数学分析能力与解题能力。

另外在本次培训中，内容的编排大多大于120分钟的容量，因此在实际教学过程中可以根据学生的具体状况和层次，由任课教师适当的调整顺序和选择内容（如专题复习可以提前上）。

注：有(*) 标注的为选做内容。

本次培训具体计划如下，以供参考：第一讲如何做几何证明题第二讲平行四边形（一）第三讲平行四边形（二）第四讲梯形第五讲中位线及其应用第六讲一元二次方程的解法第七讲一元二次方程的判别式第八讲一元二次方程的根与系数的关系第九讲一元二次方程的应用第十讲专题复习一：因式分解、二次根式、分式第十一讲专题复习二：代数式的恒等变形第十二讲专题复习三：相似三角形第十三讲结业考试（未装订在内，另发）第十四讲试卷讲评第一讲：如何做几何证明题【知识梳理】1、几何证明是平面几何中的一个重要问题，它对培养学生逻辑思维能力有着很大作用。

几何证明有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。

这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。

2、掌握分析、证明几何问题的常用方法：（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题的解决；（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；（3）两头凑法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。

3、掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十九讲平行截割平行线是初中平面几何中基本而重要的图形，平行线能改变角的位置并传递角，可“送”线段到恰当处，完成等积变形，当一组平行线截两条直线时就得到比例线段，平行线分线段成比例定理是研究比例线段、相似形的重要理论．利用、挖掘、创造平行线，是运用平行线分线段成比例定理解题的关键，另一方面，需要熟悉并善于从复杂图形中分解或构造如下形如“E ”、“A ”型或“X ”型的基本图形：例题求解【例1】如图，已知在平行四边形ABCD 中，M 、N 为AB 的三等分点，DM 、DN 分别交AC 于P 、Q 两点，则AP ：PQ ：QC= ．(河北省初中数学创新与知识应用竞赛试题)思路点拨图中有形如“X ”型的基本图形，建立含AP ，PQ ，QC 的比例式，并把AP ，PQ ，QC 用同一条线段的代数式表示．【例2】如图，已知在△ABC 中，AE ：EB=1：3，BD ：DC=2：1，AD 与CE 相交于F ，则FDAFFC EF的值为( ) A ．21 B ．1 C ．23D ．2 (江苏省泰州市中考题)思路点拨已知条件没有平行线，需恰当作平行线，构造基本图形，产生含FCEF，FD AF 的比例线段，并设法沟通已知比例式与未知比例式的联系．【例3】如图，BD 、BA ，分别是∠ADC 与它的邻补角∠ABP 的平分线，AE ⊥BE ，AD ⊥BD ，E 、D 为垂足．(1)求证：四边形AEBD 为矩形； (2)若AD AE =3，F 、G 分别为AE 、AD 上的点，FG 交AB 于点H ，且3=AGAF，求证：△AHG 是等腰三角形．(厦门市中考题)思路点拨对于(2)，由比例线段导出平行线，证明∠HAG=∠AHG ．【例4】如图，梯形AB CD 中，AD ∥BC ，AB ＝DC ．(1)如果P 、E 、F 分别是BC 、AC 、BD 的中点，求证：AB=PE+PF ；(2)如果P 是BC 上的任意一点(中点除外)，PE ∥AB ，PF ∥DC ，那么AB=PE+PF 这个结论还成立吗?如果成立，请证明；如果不成立，说明理由．(上海市闽行区中考题)思路点拨对于(2)，先假设结论成立，从平行线出发证明AB=PC+PF ，即需证明1=+ABPFAB PE ，将线段和差问题的证明转化为与比例线段有关问题的证明．注若题设条件无平行线，需作平行线．而作平行线要考虑好过哪一点作平行线，一般是由比的两条线段启发而得的，其目的是构造基本图形．平行线分线段成比例定理是证明比例线段的常用依据之一，比例线段丰富了我们研究几何问题的方法，主要体现在：(1)利用比例线段求线段的长度；(2)运用比例线段证明线段相等，线段和差倍分关系、两直线平行等问题．【例5】如图，在四边形ABCD 中，AC 与BD 相交于点O ，直线l 平行于BD ，且与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P ，求证：PM ×PN=PR ×PS(山东省竞赛题)思路点拨由于PM 、PN 、PR 、PS 在同一条直线上，所以不能直接应用平行线分线段成比例推得结论，需观察分解图形，利用中间比沟通不同比例式的联系学力训练1．如图，△ABC 中有菱形AMPN ，如果21=MB AM ，则=BCBP． (南通市中考题)2．如图，AD 是BC 边上的中线，F 是AD 上一点，CF 的延长线交AB 于点E ，若31=FD AF ，则=BE AE ；若nFD AF 1=，则=BE AE ．(江苏省镇江市中考题)3．如图，已知点D 为△ABC 中AC 边的中点，AE ∥BC ，ED 交AB 于点G ，交BC 的延长线于点F ，若3=GABG，BC=8，则AE 的长为． (苏州市中考题)4．如图，在平行四边形ABCD 中，AB=4cm ，BC=lcm ，E 是CD 边上一动点，AE 、BC 的延长线交于点F ，设DE=x (㎝)，BF=y(cm)，用x 的代数式表示y 得．(黑龙江省中考题)5．如图，已知DE ∥BC ，EF ∥AB ，现得到下列结论： ①FC BF EC AE =；②BC AB BF AD =；③BC DE AB EF =；④BFEACF CE =．其中正确比例式的个数有( )A ．4个B ．3个C ．2个D ．1个6．如图，BD 、CE 是△ABC 的中线，P 、Q 是BD 、CE 的中点，则BCPQ等于( ) A ．31 B ．41 C ．51 D ．617．如图，已知在平行四边形ABCD 中，O 1、O 2，O 3为对角线BD 上三点，且BO 1=O l Q 2= O 2O 3=O 3D ，连结AO l 并延长交BC 于点C ，连结EO 3延长交AD 于点F ，则AD ：FD 等于( ) A ．19：2 B ．9：1 C ．8：1 D ．7：1(河北省中考题)8．如图，在△ABC 中，AB ＝AC ，D 在AB 上，E 在AC 的延长线上，BD=3CE ，DE 交BC 于F ，则DF ：FE 等于( ) A ．5：2 B ．2：l C ．3：1 D ．4：1 (江苏省竞赛题)9．如图，在梯形ABCD 中，AB ∥CD ，AB=31CD ，E 是AB 上一点，AE=2BE ，M 是腰BC 的中点，连结EM 并延长交DC 的延长线于点F ，连结BD 交EF 于点N 求证：BN ：ND=l ：10． (河南省中考题) 10．如图，梯形ABCD 中，AD ∥BC ，EF 经过梯形对角线的交点O ，且EF ∥AD ． (1)求证：OE=OF ，(2)求BCOEAD OE +的值；（3）求证：EFBC AD 211=+．11．已知如图1，AB ⊥BD ，CD ⊥BD ，垂足分别为B 、D ，AD 和BC 相交于点E ，EF ⊥BD 于F ，我们可以证明EFCD AB 111=+成立．若将图1中的垂直改为斜交，如图2，AB ∥CD ，AD 、BC 相交于点E ，过点E 作EF ∥AB ，交BD 于点F ，则： (1)EFCD AB 111=+还成立吗?如成立，请给出证明；如不成立，请说明理由； (2)请找出S △ABD ，S △BED ，S △BDC 间的关系式，并给出证明． (黄冈市中考题)12．如图，在梯形ABCD 中．AB ∥CD ，AB ＝3CD ，E 是对角线AC 的中点，BE 延长后交AD 于F ，那么FDAF= ． (“祖冲之杯”邀请赛试题)13．如图，平行四边形ABCD 的对角线交于O 点，过O 任作一直线与CD 、BC 的延长线分别交于F 、E 点，设BC=a ，CD=b ，CE=c ，则CF= ． (山东赛区选拔赛试题)14．如图，在梯形ABCD 中，AD ∥BC ，AD= a ，BC= b ，E 、F 分别是AD 、BC 的中点，且AF 交BE 于P ，CE 交DF 于Q ，则PQ 的长为．15．如图，工地上竖立着两根电线杆AB 、CD ，它们相距15m ，分别自两杆上高出地面4m 、6m 的A 、C 处，向两侧地面上的E 、D 、B 、F 点处，用钢丝绳拉紧，以固定电线杆，那么钢丝绳AD 与BC 的交点P 离地面的高度为 m ．(2000年全国初中数学联赛试题)16．如图，在△ABC 中，D 是AC 的中点，E ，F 是BC 的三等分点．AE 、AF 分别交BD 于M 、N 两点，则BM ：MN ：ND=( )A ．3：2；1B ．4：2：lC ．5：2：1D ．5：3：2(2004年武汉市选拔赛试题)17．如图，在梯形ABCD 中，AD ∥BC ，AD=3，BC=9，AB=6，CD ＝4，若EF ∥BC ，且梯形AEFD 与梯形EBCF 的周长相等，则EF 的长为( )A ．745 B ．533 C ．539D ．215(山东省竞赛题)18．如图，平行四边形ABCD 中，F 、F 分别是边AD 、BC 的中点，AC 分别交BE 、DF 于G 、H ，试判断下列结论：①BE=DF ；②AG=GH=HC ；③EG=21BG ； ④S △ABE =3S △AGE ，其中正确的结论有( ) A ．1个 B ．2个 C ．3个 D ．4个19．如图，已知△ABC ，32=DC BD ，43=EC AE ，AD 、BE 交于F ，则FE BF FD AF ⋅的值( ) A ．37 B ．914 C ．1235 D ．135620．如图，已知AB ∥EF ∥CD ，AC+BD=240，BC=100，EC+ED=192，求CF ．(山东省竞赛题)21．如图，已知在平行四边形ABCD 中，F 为AB 边的中点，AF=21FD ，FE 与AC 相交于G ，求证：AG=51AC ． 22．如图，已知M 、N 为△ABC 的边BC 上的两点，且满足BM=MN=NC ，一条平行于AC 的直线分别交AB 、AM和AN 的延长线于点D 、E 和F ，求证：EF=3DE ． (湖北省黄冈市竞赛题)23．在△ABC 中，D 为BC 边的中点，E 为AC 边上的任意一点，BE 交AD 于点O ．某学生在研究这一问题时，发现了如下的事实： (1)当11121+==AC AE 时，有12232+==AD AO (如图甲)；（2）当21131+==AC AE 时，有22242+==AD AO (如图乙)； (3)当31141+==AC AE 时，有32252+==AD AO (如图丙)；在图丁中，当nAC AE +=11时，参照上述研究结论，请你猜想用n 表示AD AO 的一般结论，并给出证明(其中n 是正整数)(山西省中考题)24．如图，在平行四边形ABCD 中，P 1，P 2，…，P n 是BD 的n 等分点，连结AP 2并延长交BC 于点E ，连结AP n-2并延长交CD 于点F ． (1)求证：EF ∥BD ；(2)设平行四边形ABCD 的面积是S ，若S △AEF =83S ，求n 的值． (山东省竞赛题)。