2010年中考数学模拟试题及答案
2010年中考模拟数学卷参考答案

2010年中考模拟试卷 数学参考答案及评分标准三、解答题(本题有8小题,第17~19题每题6分,第20~21题8分,第22~23题每题10分,第24题12分,共66分) 17、(本题满分6分)解:∵方程2233x m x x -=--无解 ∴方程2233x m x x -=--有增根x=3------------2分 ∴方程两边同乘以(x-3),得:26x m -=------------2分∴当x=3时,m =分18、(本题满分6分)解:过C 点作BA 的延长线交于点E ,------------1分∵AB =AC =10,∠B =022.5 ∴∠EAC =045∴△EAC 为等腰直角三角形------------1分设AE =EC =X,则AB =AC =10∴x =∴111022S AB EC ∆=⋅=⨯⨯=35.42m ------------2分 又∵53.610⨯2cm =362m >35.42m ------------1分∴预订草皮够用------------1分19、(本题满分6分) 解:答案不唯一,酌情给分。
20、(本题满分8分)解:(1)18 0.55------------各1分(2)图略--------------共4分(虚设组不设各扣1分)(3)0.55±0.1均为正确------------2分 21、(本题满分8分) 解:(1)正确的结论:①②③------------2分(2)错误理由:当a >0时,只有1x >2x >0或2x <1x <0时,1y <2y 而2x <0<1x 时,1y >2y ------------4分 改正:当a >0时,在同一象限内,函数ay x=,y 随x 增大而减小-----2分22、(本题满分10分)解:(1)如右图------------共6分(030,045角,线段a 各1分,余酌情给分)(2)设AB =x,则Rt △ABC 中,OB =x ,由题意得:6+ x ------------1分得,1)x =≈8米------------2分 答:旗杆高度约为8米。
2010年中考模拟数学试卷和答案

2010年中考模拟试卷数 学考生须知:1.本试卷分试题卷和答题卷两部分,满分120分,考试时间100分钟 .2.答题时,应该在答题卷指定位置内写明校名,姓名和准考证号 .3.所有答案都必须做在答题卷标定的位置上,请务必注意试题序号和答题序号相对应 .4.考试结束后,上交试题卷和答题卷试题卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的 .注意可以用多种不同的方法来选取正确答案 .1. 如果0=+b a ,那么a ,b 两个实数一定是( )A.都等于0B.一正一负C.互为相反数D.互为倒数2. 要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )A.调查全体女生B.调查全体男生C.调查九年级全体学生D.调查七、八、九年级各100名学生 3. 直四棱柱,长方体和正方体之间的包含关系是( )4. 有以下三个说法:①坐标的思想是法国数学家笛卡儿首先建立的;②除了平面直角坐标系,我们也可以用方向和距离来确定物体的位置;③平面直角坐标系内的所有点都属于四个象限 .其中错误的是( )A.只有①B.只有②C.只有③D.①②③ 5. 已知点P (x ,y )在函数x xy -+=21的图象上,那么点P 应在平面直角坐标系中的( )A.第一象限B. 第二象限C. 第三象限D. 第四象限6. 在一张边长为4cm 的正方形纸上做扎针随机试验,纸上有一个半径为1cm 的圆形阴影区域,则针头扎在阴影区域内的概率为( )A.161 B.41 C.16π D.4π 7. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x ,那么x 的值( ) A.只有1个 B.可以有2个 C.有2个以上,但有限 D.有无数个8. 如图,在菱形ABCD 中,∠A=110°,E ,F 分别是边AB 和BC的中点,EP ⊥CD 于点P ,则∠FPC=( ) A.35° B.45° C.50° D.55°9. 两个不相等的正数满足2=+b a ,1-=t ab ,设2)(b a S -=,则S 关于t 的函数图象是( )A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分10. 某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点)(k k k y x P ,处,其中11=x ,11=y ,当k≥2时,⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ,[a ]表示非负实数a 的整数部分,例如[2.6]=2,[0.2]=0 .按此方案,第2009棵树种植点的坐标为( )A.(5,2009)B.(6,2010)C.(3,401) D (4,402)二. 认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案 11. 如图,镜子中号码的实际号码是___________ .12. 在实数范围内因式分解44-x = _____________________ . 13. 给出一组数据:23,22,25,23,27,25,23,则这组数据的中位数是___________;方差(精确到0.1)是_______________ .14. 如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是______________ .15. 已知关于x 的方程322=-+x mx 的解是正数,则m 的取值范围为______________ . 16. 如图,AB 为半圆的直径,C 是半圆弧上一点,正方形DEFG 的一边DG 在直径AB 上,另一边DE 过ΔABC 的内切圆圆心O ,且点E 在半圆弧上 .①若正方形的顶点F 也在半圆弧上,则半圆的半径与正方形边长的比是______________;②若正方形DEFG 的面积为100,且ΔABC 的内切圆半径r =4,则半圆的直径AB = __________ .三. 全面答一答(本题有8个小题,共66分)解答应写出文字说明、证明过程或推演步骤 .如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以 . 17. (本小题满分6分)如果a ,b ,c 是三个任意的整数,那么在2b a +,2c b +,2ac +这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由 .18. (本小题满分6分)如图,,有一个圆O 和两个正六边形1T ,2T .1T 的6个顶点都在圆周上,2T 的6条边都和圆O 相切(我们称1T ,2T 分别为圆O 的内接正六边形和外切正六边形) . (1)设1T ,2T 的边长分别为a ,b ,圆O 的半径为r ,求a r :及b r :的值; (2)求正六边形1T ,2T 的面积比21:S S 的值 .如图是一个几何体的三视图 . (1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程 .20. (本小题满分8分)如图,已知线段a .(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC ,以AB 和BC 分别为两条直角边,使AB=a ,BC=a 21(要求保留作图痕迹,不必写出作法); (2)若在(1)作出的RtΔABC 中,AB=4cm ,求AC 边上的高 .学校医务室对九年级的用眼习惯所作的调查结果如表1所示,表中空缺的部分反映在表2的扇形图和表3的条形图中.(1)请把三个表中的空缺部分补充完整;(2)请提出一个保护视力的口号(15个字以内).22. (本小题满分10分)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .(1)求证:AF=BE;(2)请你猜测∠BPF的度数,并证明你的结论.在杭州市中学生篮球赛中,小方共打了10场球 .他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y 比前5场比赛的平均得分x 要高 .如果他所参加的10场比赛的平均得分超过18分 (1)用含x 的代数式表示y ;(2)小方在前5场比赛中,总分可达到的最大值是多少? (3)小方在第10场比赛中,得分可达到的最小值是多少?24. (本小题满分12分)已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ,又有定点P (2,0) . (1)若0>a ,且tan ∠POB=91,求线段AB 的长; (2)在过A ,B 两点且顶点在直线x y =上的抛物线中,已知线段AB=38,且在它的对称轴左边时,y 随着x 的增大而增大,试求出满足条件的抛物线的解析式; (3)已知经过A ,B ,P 三点的抛物线,平移后能得到259x y =的图象,求点P 到直线AB 的距离 .2010年中考模拟试卷数学参考答案一、仔细选一选(每小题3分,芬30分)二. 认真填一填(本题有6个小题,每小题4分,共24分) 11、326512.)2)(2)(2(2-++x x x 13、23;2.614、14或16或2615、46-≠->m m 或16、①5∶2 ;②21三. 全面答一答(本题有8个小题,共66分) 17、(本题6分)至少会有一个整数 .因为三个任意的整数a,b,c 中,至少会有2个数的奇偶性相同,不妨设其为a ,b , 那么2ba +就一定是整数 . 18、(本题4分)(1)连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点,得以圆O 半径为高的正三角形, 所以r ∶b=3∶2;(2) T 1∶T 2的连长比是3∶2,所以S 1∶S 2=4:3):(2=b a .19、(本题6分)(1) 圆锥; (2) 表面积S=πππππ164122=+=+=+r rl S S 圆扇形(平方厘米)(3) 如图将圆锥侧面展开,线段BD 为所求的最短路程 . 由条件得,∠BAB ′=120°,C 为弧BB ′中点,所以BD =33 .20、(本题8分)(1)作图如右,ABC ∆即为所求的直角三角形;(2)由勾股定理得,AC =52cm , 设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421,所以554=h 21、(本题8分)(1)补全的三张表如下:(表一)(2)例如:“象爱护生命一样地爱护眼睛!”等 . 22、(本题10分)(1)∵BA=AD ,∠BAE=∠ADF ,AE=DF , ∴△BAE ≌△ADF ,∴BE=AF ; (2)猜想∠BPF=120° .∵由(1)知△BAE ≌△ADF ,∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ,而AD ∥BC ,∠C=∠ABC=60°, ∴∠BPF=120° . 23、(本题10分)(1)9191215225++++=x y ;(2)由题意有x x >++++9191215225,解得x <17,所以小方在前5场比赛中总分的最大值应为17×5-1=84分;(3)又由题意,小方在这10场比赛中得分至少为18×10 + 1=181分, 设他在第10场比赛中的得分为S ,则有81+(22+15+12+19)+ S ≥181 .解得S≥29,所以小方在第10场比赛中得分的最小值应为29分 .24、(本题12分)(1)设第一象限内的点B (m,n ),则tan ∠POB 91==m n ,得m=9n ,又点B 在函数xy 1=的图象上,得m n 1=,所以m =3(-3舍去),点B 为)31,3(,而AB ∥x 轴,所以点A (31,31),所以38313=-=AB ;(2)由条件可知所求抛物线开口向下,设点A (a , a ),B (a 1,a ),则AB =a1- a =38, 所以03832=-+a a ,解得313=-=a a 或 .当a = -3时,点A (―3,―3),B (―31,―3),因为顶点在y = x 上,所以顶点为(-35,-35),所以可设二次函数为35)35(2-+=x k y ,点A 代入,解得k= -43,所以所求函数解析式为35)35(432-+-=x y .同理,当a = 31时,所求函数解析式为35)35(432+--=x y ;(3)设A (a , a ),B (a 1,a ),由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为:)2)1()(2(59++--=aa x x y .点A (a , a )代入,解得31=a ,1362=a ,所以点P 到直线AB 的距离为3或136.。
2010年中考模拟卷 数学卷

2010年中考模拟卷 数学参考答案及评分标准题号 选择填空1718192021222324总分得分一.仔细选一选 (本题有10个小题, 每小题3分, 共30分)二.认真填一填(本题有6个小题, 每小题4分, 共24分)11. 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.12. (1,3) 13. =3 14. 215. 3 16. 0或3或4或8 三.全面答一答 (本题有8个小题, 共66分) 17.(本小题满分6分) 解:由题意得120k -≠ 12k ≠..........................................(2) 10k +≥ 1k ≥- (2)△2(21)4(12)(1)k k =-+-⨯-⨯->0k <2 ∴0k ≤<2且12k ≠ (2)18.(本小题满分6分)过点B 作直线BF ∥CD (1)135°105°A BC DFE∵CD ∥AE∴BF ∥CD ∥AE (1)题号 1 2 3 4 5 6 7 8 9 10 答案DBCDDCCBCD∴∠A=∠ABF=105°……………………………………(1) ∴∠CBF=∠ABC-∠ABF=30°………………………….(1) 又BF ∥CD∴∠CBF+∠C=180°..........................................(1) ∴∠C=150° (1)19.(本小题满分6分)(1)5+8+11+16+6=46(人) 一共分成5组。
组距是:65-55=10(分) (2)(2)分布两端虚设的频数为0的是:40─50和100─110两组。
它们的组中值分别是:45分和105分…………(2) (3)80─90一组人数最多。
它的频率是:1684623=…………………………(1) (4)5558651175168569546⨯+⨯+⨯+⨯+⨯77.2≈分 (1)20.(本小题满分8分)作出△ABC 的内心............(3) 作出△ABC 的外心................(3) 作处线段DO2 (1)∴如图所示,线段DO2的长就是△ABC 的内心、外心分别到点A 的距离之差。
2010年中考模拟卷数学参考答案

2010年中考模拟卷数学参考答案二.认真填一填(本题有6个小题,每小题4分,共24分) 11.4(x+3)(x-3) 12.10≠≥x x 且 13.15414.6)1(2+--=x y 15. ︒20 16.)12,1222(22++++n nn n n n P n 三.全面答一答(本题有8个小题,共66分) 17.(本小题满分6分) 解:11)1()1)(1(1----+⨯+=a a a a a a a 原式…………………………………………………2分 =12111--=--a a a …………………………………………………2分 当a=-2时,原式=34…………………………………………………2分18.(本题满分6分) 解:可以做2)1(-n n 条直线…………………………………………………3分 理由如下:平面上有n 个点,两点确定一条直线。
取第一个点A 有n 种取法,取第二个点B(n-1)种取法,所以一共可连成n(n-1)条直线,但AB 和BA 是同一条直线,所以应除以2,得2)1(-n n 条直线 …………………………………………………3分 19.(本题满分6分)解:过点A 作BC 的垂线段,垂足为D ,则由题可知,∠BAD=30°,∠DAC=60° ∵∠BAD=30°,△ABD 为直角三角形, ∴BD=3223663==AD …………………………………………………2分同理可得3663==AD CD …………………………………………………2分∴楼高AB=2.152388≈…………………………………………………2分 20.(本小题6分)(1)21人 …………………………………………………1分(2)众数 90 中位数80…………………………………………………2分(3)从平均数和中位数的角度来比较,一班的成绩比二班好;从平均数和众数的角度来比较,一班的成绩不如二班;从B 级以上(包括B 级)的人数的角度来比较,一班的成绩比二班好。
2010年中考数学模拟试卷 答卷
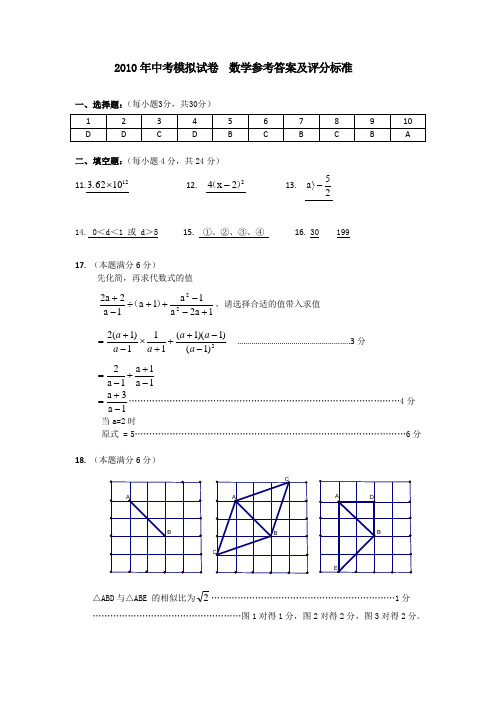
2010年中考模拟试卷 数学参考答案及评分标准一、选择题:(每小题3分,共30分)二、填空题:(每小题4分,共24分)11.12103.62⨯ 12. 22x 4)(- 13. 25a -〉14. 0<d <1 或 d >5 15. ①、②、③、④ 16. 30 19917. (本题满分6分)先化简,再求代数式的值1a 2a 1a 1a 1a 2a 222+--++÷-+)(,请选择合适的值带入求值 2)1()1)(1(111)1(2--+++⨯-+=a a aa a a ………………………………………………..3分 1a 1a 1a 2-++-=1a 3a -+=…………………………………………………………………………………4分当a=2时原式 = 5…………………………………………………………………………………6分18. (本题满分6分)△ABD 与△ABE 的相似比为2………………………………………………………1分 ……………………………………………图1对得1分,图2对得2分,图3对得2分。
19.(本题满分6分)(1)2+22+32+36+28=120,此样本抽取了120名学生才成绩……………………………2分(2)中位数落在80.5 ~90.5这个范围内.……………………………………………4分 (3)4801202836900=+⨯所以该校获得优秀成绩学生的人数约480名。
…………6分 20.(本题满分8分)(1)由△BMC 是等边三角形可知: ∠MBC=∠MCB=60°,BM=MC 又∵ED ∥BC,∴∠EMB=∠MBC;∠DMC=∠MCB ∴∠EMB =∠DMC 又 ∵点M 平分ED, ∴EM = MD则可证△EMB ≌△DMC ………2分 ∴∠EBM =∠ECM 则可得∠EBC =∠DCB∴△ABC 是等腰三角形。
(3)21. (本题满分8分)作AE ⊥y 轴于E∵42AOD S OD ==△,∴21OD.AE=4 ∴AE=4………………………………………………… 1分 ∵AB ⊥OB,且C 为OB 的中点,∴∠DOC =∠ABC =90°,OC =BC, ∠OCD =∠BCA ∴Rt △DOC ≌Rt △ABC∴AB =CD =2…………………………………………………………………………………2分 ∴A(4,2)……………………………………………………………………………………3分 将A(4,2)代入xky 1=中,得k =8∴x8y 1=……………………………………………………………………………………… 4分 将A(4,2)和D(0,-2)代入b kx y 2+=得422a b b +=⎧⎨=-⎩解之得:12a b =⎧⎨=-⎩∴22y x =-…………………………………………………………………………………6分(2)在y 轴的右侧,当21y y 〈时,0<x <2………………………………………………8分22. (本题满分10分)(1)∵半径OD = 5,则直径AB =10∴5310BD AB BD ==,则BD=6∴若设OE=x ,则BE=5-x ,由勾股定理可得:22220E -DO BE -BD =从而列方程:26-2x 5)(-=22x 5-,…………………………………………………3分,得x=524,再由垂径定理可得CD=548…………………………………………………4分 (2) ∵∠ADO:∠EDO=4:1,则可设∠ADO=4x ,∠EDO=x 又∵OA=OD,则∠OAD=∠ODA=4X由AB 垂直CD,得:4x+4x+x=90°∴x=10°……………………………………………6分 ∴∠ADE=50°,则∠AOC=100°……………………7分 (3) ∵弧AC=9251805100=⨯∏⨯∏∴2∏r =∏925,则圆锥底面圆半径为1825 (9)∴侧S =∏=∏⨯=∏1812551825rl ……………………10分23. (本题满分10分)(1)由题意设A 型货箱用了x 节,则B 型货箱用了(50-x )节,则可列不等式组: 35x +25(50-x )≥153015x+35(50-x )≥1150………………………………………………………………2分 解得:28≤x ≤30…………………………………………………………………………3分 ∵x 取整数 ∴ x = 28、29、30……………………………………………………4分 ∴ 有三种方案:当A 型货箱用了28节时,B 型货箱用了22节。
2010年中考数学模拟试题(含答案)
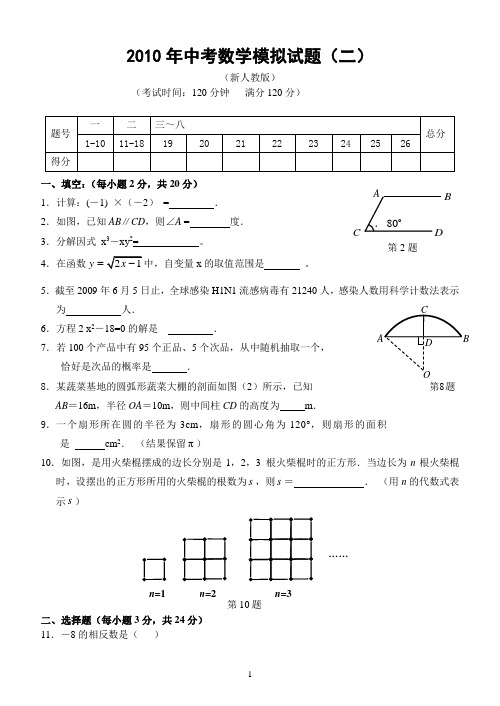
D BAOC 第8题2010年中考数学模拟试题(二)(新人教版)(考试时间:120分钟 满分120分)一、填空:(每小题2分,共20分) 1.计算:(-1) ×(-2) = . 2.如图,已知AB ∥CD ,则∠A = 度. 3.分解因式 x 3-xy 2= 。
4.在函数y =x 的取值范围是 。
5.截至2009年6月5日止,全球感染H1N1流感病毒有21240人,感染人数用科学计数法表示为 人.6.方程2 x 2-18=0的解是 .7.若100个产品中有95个正品、5个次品,从中随机抽取一个,恰好是次品的概率是 .8.某蔬菜基地的圆弧形蔬菜大棚的剖面如图(2)所示,已知 AB =16m ,半径OA =10m ,则中间柱CD 的高度为 m .9.一个扇形所在圆的半径为3cm ,扇形的圆心角为120°,则扇形的面积是 cm 2. (结果保留π)10.如图,是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用n 的代数式表示s )二、选择题(每小题3分,共24分)11.-8的相反数是( )CDB第2题.80A第10题 ……n =1 n =2n =3A .8B .-8C .18 D .18- 12.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( ).A.外离B. 相交C.外切D.内切13.下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )A .①②③B .①②C .①③D .②③14.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,9.1,6.5,7.7,则这四人中,射击成绩最稳定的是( ) A .甲B .乙C .丙D .丁15、tan 30°的值等于( )A. 21B. 22C.23 D.33 16图1中几何体的主视图是( )17.若分式 x 2-1x +1的值为零,则x 的值是( )A .1B .0C .-1D .±118.如图,抛物线y =ax 2+bx +c 的对称轴是x = 13,小亮通过观察得出了下面四条信息:①c <0,②abc <0,③a -b +c >0,④2a -3b =0. 你认为其中正确的有( )A .1个B .2个C .3个D .4 三、解答题:(共76分)19、(本题7分)计算:112sin 602-⎛⎫- ⎪⎝⎭ACBDx第18题20、(本题7分)解方程: 0)3(2)3(2=-+-x x x21.(本题8分)如图,E 是正方形ABCD 的边DC 上的一点,过A 作A F ⊥AE ,交CB 延长线于点F ,求证:△ADE ≌△ABF .22.(本题10分)已知ABC △在平面直角坐标系中的位置如图10所示. (1)分别写出图中点A C 和点的坐标;(2)画出ABC △绕点C 按顺时针方向旋转90A B C '''°后的△; (3)求点A 旋转到点A '所经过的路线长(结果保留π)._F _E _ C _ D _ B _A 第21题 第22题23、(本题10分)右边下面两图是根据某校初三(1)班同学的上学方式情况调查所制作的条形和扇形统计图,请你根据图中提供的信息,解答以下问题: (1) 求该班学生骑自行车的人数有(2)求该班学生人数 人.并将条形统计图补充完整; (3)若该校初三年有600名学生, 试估计该年级乘车上学的人数.24.(本题10分)某冰箱厂为响应国家“家电下乡”号召,计划生产A 、B 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 47500元,不高于48000元,两种型号的冰箱生产成本和售价如下表:(1)冰箱厂有哪几种生产方案?(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?骑自行车20%乘车步行50%第23题25、(本题12分)如图5,在ABC △中,AB AC =,以AB 为直径的O ⊙交BC 于点M ,MN AC ⊥ 于点N .(1)求证MN 是O ⊙的切线;(2)若1202B A C A B ∠==°,,求以直径AB ,弦BC 和⌒AM 围成图形的面积(结果保留π).、第25题26.(本题12分)如图,抛物线21222y x x =-++与x 轴交于A B 、两点,与y 轴交于C 点.(1)求A B C 、、三点的坐标; (2)证明ABC △为直角三角形;(3)在抛物线上除C 点外,是否还存在另外一个点P ,使ABP △是直角三角形,若存在,请求出点P 的坐标,若不存在,请说明理由.参考答案一、1.2 2.120 3.x (x +y )(x -y )4.x≥12 5.2.124×104 6.3和-3 7.1208.4 9.3π 10.2n(n+1)二.11. A 12.C 13.B 14. C 15. D 16.D 17.A18.B19.20.X 1=3,X 2=121.证明:∵ABCD 是正方形 ∴AB AD = ︒=∠=∠=∠90DAB ABF D ∵A F ⊥AE ∴DAE EAB BAF ∠=∠-︒=∠90.在ADE ∆和ABF ∆中∵AE AD BAF DAE ABF D =∠=∠∠=∠,, ∴△ADE ≌△ABF 22.解:(1)()04A ,、()31C ,(2)图略(3)AC =⌒AA' π= 23.解:(1)8 (2)该班学生人数为40%5020=(人) 图画对(略) (3)该年级乘车上学的人数约为1806004012=⨯ 24..解:(1)设生产A 型冰箱x 台,则B 型冰箱为()100x -台,由题意得:47500(28002200)(30002600)(100x x -+-⨯-≤≤解得:37.540x ≤≤ x 是正整 ∴x 取38,39或40.(2)设投入成本为y 元,由题意有: 22002600(100)400260000y x x x =+-=-+4000-< ∴y 随x 的增大而减小∴当40x =时,y 有最小值.即生产A 型冰箱40台,B 型冰箱50台,该厂投入成本最少此时,政府需补贴给农民(280040300060)13%37960()⨯+⨯⨯=元 25.(1)证明:连接OM .∵OM OB =,∴B OMB ∠=∠,∵AB AC =,∴B C ∠=∠. ∴OMB C ∠=∠,∴OM AC ∥.又MN AC ⊥,∴OM MN ⊥,点M 在O ⊙上,∴MN 是O ⊙的切线(2)S =164π+26.解:(1)抛物线21222y x x =-++与x 轴交于A B 、两点,21202x x ∴-++=.即240x -=.解之得:12x x ==∴点A B 、的坐标为(A B ) ,将0x =代入21222y x x =-++, 得C 点的坐标为(0,2)(2)6AC BC AB ===,222AB AC BC ∴=+,则90ACB ∠=°,ABC ∴△是直角三角形.(3)将2y =代入21222y x x =-++,得212222x x -++=,120x x ∴==,P ∴点坐标为.。
2010年中考模拟试卷 数学参考答案及评分标准
2010年中考模拟试卷 数学参考答案及评分标准一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分)二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)11、36b a 12、 2.5 13、a=0或a=2 14、1:5 15、(3,2);(55,358) 16、①②④三. 全面答一答 (本题有8个小题, 共66分) 17.(本小题满分6分)212(2212010))(-+-----π=221211+--+…………………分=227-……………………………2分18.(本小题满分6分)解:原式=x-1 …………………………………4分(从33x -<<的范围内选取一个合适的整数x 代入求值。
其中x ≠±1,0)……2分 19.(本小题满分6分)解:(1)如图所示:……………………………………4分(注:每正确画出1个图且痕迹清晰得2分,)(2)规律:若三角形为锐角三角形,则其最小覆盖圆为该三角形的 外接圆;……………1分 若三角形为直角或钝角三角形, 则其最小覆盖圆是以三角形 最长边(直角或钝角所对的边) 为直径的圆.……………1分20.(本小题满分8分)(1)如图(1).连结AC ,由∠1=∠2,∠APC =∠DPE∴△ACP ∽△DEP .…………………………………2分DEAC DP =∴P A 又AP 25=,∴DE=25221÷⨯=52………………2分(2)如图(2).当Rt Rt ADP QCP △∽△时有得:1QC =.∴Q 与B 重合,0BQ ∴=……………2分 如图(3),当Rt Rt ADP PCQ △∽△时,有QCPD PCAD =,得=QC 41,即43=BQ ………………………2分∴当0BQ =或43=BQ 时,三角形AD P 与以点Q C P ,,为顶点的三角形相似.21.(本小题满分8分)解:(1)1(10%15%30%15%5%)25%a =-++++=. ······································ 1分初一学生总数:2010%200÷=(人). ······················································ 1分 (2)活动时间为5天的学生数:20025%50⨯=(人).活动时间为7天的学生数:2005%10⨯=(人). ········································· 2分频数分布直方图(如图)······················ 1分(3)活动时间为4天的扇形所对的圆心角是36030%108⨯=°°. ························· 1分(4)该市活动时间不少于4天的人数约是6000(30%25%15%5%)4500⨯+++=(人). ························································ 2分(第21题图)人数22.(本小题满分10分) (1)27……………..2分(2)△ABC 如图②所示 ……………2分S △ABC=2a ·4a-21a ·2a-21a ·4a-21×2a ·2a=23a……………….2分(3)构造△ABC 如图③所示(图没有但面积算对不扣分) S △ABC=3m ·4n-21m ·4n-213m ·2n-21×2m ·2n=5mn …………….2分23.(本小题满分10分)⑴ 图略。
2010年中考数学模拟试卷参考答案
2010年中考数学模拟试卷 参考答案及评分标准一. 选择题(每小题3分, 共30分)二. 填空题(每小题4分, 共24分)11. -4,2 12.(3,5) 13.12-14.31 15. n )23( 16. 6S 1≤≤ 三. 解答题(8小题共66分) 17. (本题6分)解:(1)上述两同学回答的均不全面,应该是300 , 1500 , 900 (遗漏一个扣1分) ………3分 (2)答案不唯一.如面对不确定的情况就要考虑进行分类讨论;考虑问题要全面呀等等,只要有这样的意思就得3分. …………………………3分 18. (本题6分)解:900,1350,1800 ,2700, 3600,只要举出其中两个角能够进行三等分, ……………………2分尺规作图正确,每个2分 ………………………4分19、(本题6分)解:(1)第一只 肉 香肠 红枣 红枣第二只 红枣 肉 红枣 红枣 肉 香肠 红枣 香肠 红枣∴P =61122= …………………………3分(2)这样模拟不正确 …………………………1分 理由如下:连续两次掷骰子点数朝上的情况有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4)共16种,而满足条件的情况有4种 …………………………2分 20. (本题8分)解:老板第二次售手链还是赚了. …………………………1分 设第一次批发价为x 元/条,则第二次的批发价为x+0.5元/条 依题意,得: )x1000.5)(10(x ++=150 解之得 5.2x ,2x 21== …………………………3分经检验,5.2x ,2x 21== 都是原方程的根 …………………………1分 由于当x=2.5时,第二次的批发价就是3元/条,而零售价为2.8元,所以x=2.5不合题意,舍去.故第一次的批发价为2元/条.第二次的批发价为2.5元/条第二次共批发手链605.21505.0x 150==+(条) …………………………1分第二次的利润为: 1.2150-5).08.260518.26054(=⨯⨯⨯+⨯⨯ …………………………1分故,老板第二次售手链赚了1.2元 . …………………………1分21.(本题8分)解:(1)如图,由题意得,∠EAD =45°,∠FBD =30°.∴ ∠EAC =∠EAD +∠DAC =45°+15°=60°. ∵ AE ∥BF ∥CD , ∴ ∠FBC =∠EAC =60°. ∴ ∠DBC =30°.又∵ ∠DBC =∠DAB +∠ADB , ∴ ∠ADB =15°.∴ ∠DAB =∠ADB . ∴ BD =AB =2.即B ,D 之间的距离为2km . ……………………………………………4分 (2)过B 作BO ⊥DC ,交其延长线于点O , 在Rt △DBO 中,BD =2,∠DBO =60°. ∴ DO =2×sin60°=2×323=,BO =2×cos60°=1. 在Rt △CBO 中,∠CBO =30°,CO =BO tan30°=33, ∴ CD =DO -CO =332333=-(km ). 即C ,D 之间的距离为332km . …………………………………………………4分 22. (本题10分)解:(1)这个样本的中位数为120(人),众数为100(人),平均数为150(人) ………3分 信息:①这一周每天参观人数不低于100人; ②周末参观人数逐渐增加;金③一周内参观人数在百人左右的天数最多;④星期日参观人数最多;⑤这一周每天参观人数不超过240人;⑥星期五参观人数最接近这一周的平均值;•⑦一周内多数天参观人数低于本周参观人数的平均值等等.…………………………2分(2)①由(1)知样本数据的中位数为120(人),则甲、乙两团共120人,其中甲团有x人,乙团有(120-x)人.∵0<120-x≤50,∴甲团人数超过50人…………………………1分ⅰ)当50<x•≤100,•0<120-x≤50时,W=60x+80(120-x)即W=9600-20x(70≤x≤100)ⅱ)当x>100,0<120-x•≤50时,W=40x+80(120-x)即W=9600-40x(100<x<120)∴当70≤x≤100时,W关于x的函数关系式为W=9600-20x;当100<x<120时,W关于x的函数关系式为:W=9600-40x.…………………………2分②依题意x≤100,∴W关于x的函数关系式应为:W=9600-20x(70≤x≤100)根据一次函数的性质知:当x=70时,W=9600-2×700=8200(元)而两团合起来购票应付费40×120=4800(元),∴两团合起来购票比分开购票最多可节约8200-4800=3400(元).…………………………2分23.(本题10分)证明:(1)连接AM,∵AB是半圆O的直径,∴∠BMA=90°…………………………1分又∵DE⊥AB,∠ABM=∠NBE,∴Rt△ABM∽Rt△NBE∴BN BEBA BM,即BN·BM=BE·BA …………………………2分(2)连接AD,BD(如图2),∵AB是⊙O的直径,∴∠ADB=90°…………………………1分又因∵DE⊥AB,∴BD2=BE·BA …………………………1分∵BC是⊙O1的切线,∴BC2=BN·BM …………………………1分由(1)知BN·BM=BE·BA,∴BC2=BD2,即BC=BD …………………………1分(3)连接O 1N 和OM (如图3),则OM 过点O 1, ∵OB=OM ,O 1N=O 1M ,∴∠MNO 1=∠NMO 1=∠MBO …………………………1分 ∴O 1N ∥OB …………………………1分而DE ⊥OB ,∴OE ⊥O 1N∵O 1N 是 ⊙O 1的半径,∴DE 是⊙O 1的切线.…………………………1分24.(本题12分)解:(1)①法一:由题可知1AO CQ ==.90AOH QCH ∠=∠=,AHO QHC ∠=∠,AOH QCH ∴△≌△.OH CH ∴=,即H 为AQ 的中点. …………………………1分法二:(01)A ,,(01)B -,,OA OB ∴=.又BQ x ∥轴,HA HQ ∴=. …………………………1分 由①可知AH QH =,AHR QHP ∠=∠,AR PQ ∥,RAH PQH ∴∠=∠, RAH PQH ∴△≌△.AR PQ ∴=,又AR PQ ∥,∴四边形APQR 为平行四边形.………………………1分②设214P m m ⎛⎫ ⎪⎝⎭,,PQ y ∥轴,则(1)Q m -,,则2114PQ m =+.过P 作PG y ⊥轴,垂足为G ,在Rt APG △中,2114AP m PQ ===+=.∴平行四边形APQR 为菱形. …………………………2分(2)设直线PR 为y kx b =+,由OH CH =,得,0)2m (H ,214P m m ⎛⎫⎪⎝⎭,代入得: 2021.4m k b km b m ⎧+=⎪⎪⎨⎪+=⎪⎩, 221.4m k b m ⎧=⎪⎪∴⎨⎪=-⎪⎩,∴直线PR 为2124m y x m =-.………………………1分 设直线PR 与抛物线的公共点为214x x ⎛⎫ ⎪⎝⎭,,代入直线PR 关系式得:22110424m x x m -+=,21()04x m -=,解得x m =.得公共点为214m m ⎛⎫ ⎪⎝⎭,. 所以直线PH 与抛物线214y x =只有一个公共点P . …………………………2分 (3)AN ∥GH ,AN 21GH =. …………………………2分由(1)知AP=PQ ,同理知AM=MN.M A N M N A ,A Q P PA Q ∠=∠∠=∠∴ BQ PQ ,BQ M N ⊥⊥∴MN ∥PQ ∴180MPQ NMA =∠+∠ ∵⊿AMN 和⊿APQ 的内角和都为180180MAN MNA AQP PAQ =∠+∠+∠+∠∴ 90MAN PAQ =∠+∠∴ AQ AN 90NAQ ⊥∴=∠∴…………………………2分由(1)知四边形APQR 为菱形,HQ AH PR AQ =⊥∴,PR ∴∥AN为GH ∴⊿ANQ 的中位线.∴AN ∥GH ,AN 21GH = …………………………1分。
2010年中考摸拟试卷数学参考答案及评分标准
2010年中考摸拟试卷数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二.认真填一填(本题有6个小题,每小题4分,共24分) 11. (a-1)(a+1) , x 2+y 2 12. 20 和560 13.52 14.3315.3421或、 16. (3,3);;(3,-2) ;(11,-26)三、解答题(本题有8小题,共66分) 17、(本题6分) (以下给出三种选择方案,其他方案从略) 解答一: Y + Z =(3a 2+3ab )+ (a 2+ab ) =4a 2+4ab ……3分 =4a (a +b ).…………3分 解答二: X- Z = (2a 2+3ab +b 2)-(a 2+ab ) =a 2+2ab +b 2…………3分=(a +b )2 ………3分解答三:Y- X =(3a 2+3ab )- (2a 2+3ab +b 2)=a 2- b 2 …………3分=(a +b )(a -b )……………3分说明:整式计算正确得3分,因式分解正确得3分. 18. (本题6分) 解:(1)设A 市投资“改水工程”年平均增长率是x ,则2600(1)1176x +=.(2分)解得0.4x = 或 2.4x =-(不合题意,舍去)(2分). 所以,A 市投资“改水工程”年平均增长率为40%. (2)600+600×1.4+1176=2616(万元). A 市三年共投资“改水工程”2616万元.(2分)19. (本题6分) 解: 如图:(1)画出△A 1B 1C 1…………..2分 (2)画出△A 2B 2C 2………………………………..2分连结OA ,OA 2,OA =.点A 旋转到A 2所经过的路线长为l=1802……2………….2分20. (本题8分)(1)作图如右---------------------- 4分(2)证明:根据作图知,PQ 是A C的垂直平分线, 所以AO C O =,且E F A C ⊥.因为A B C D是平行四边形,所以O A E O C F ∠=∠ 所以O A E O C F △≌△. 所以A E C F =---------------------- 4分21.(本小题满分8分)解:在R t AD B △中,30A B =米 60ABC ∠=°sin 30sin 6025.9826.0AD AB ABC =∠=⨯=≈≈·°(米) ……2分15D B =米连接BE ,过E 作EN BC ⊥于NAE BC∵∥ ∴四边形AEN D是矩形26N E AD =≈米 ……2分在R t EN B △中,由已知45EBN ∠°≤, 当45EBN ∠=°时26.0BN EN ==米 ……2分26.01511AE AD BN BD ==-=-=∴米 ……1分 答:AE 至少是11米. ……………… 1分22.(本小题满分10分)(1)60306060=-FC,30=FC ;……3分(2)在EF 上任取一点Q ,分别过点Q 作BC ,AB 的垂线,垂足分别是M ,N ,则 CN x +=606030,602-=x CN ,则x BN 2120-=。
2010年中考数学模拟试卷(4)参考答案
2010年中考数学模拟试卷(4)参考答案一、选择题(本大题共10题,每题4分,满分40分)1.D ; 2.C ; 3.D ; 4.B ; 5.A ; 6.D 7.D 8.C 9.D 10.C 二、填空题(本大题共12题,每题4分,满分48分) 11.1x ≠-; 12.12; 13. 略; 14.2000sin α15、4:1 16、(2,4)或(3,4)或(8,4) 三、解答题17、x >-4 画数轴略 18、①原式=11-a 4分 ②如a=2时,原式=1,答案不唯一 2分19、(1)解:树状图:略 P=61 3分(2)两个球上数字之和为6时,概率最大,即3162'==p 6分20、 DF=AB 1分 证明:∵四边形ABCD 是矩形∴∠B=Rt ∠ ∴AD ∥BC∴∠DAF=∠BEA (两直线平行,内错角相等) 3分 又∵DF ⊥AE∴∠DFA=∠B=Rt ∠ ∵AD=AE∴△ADF ≌△EAB(AAS) 5分 ∴DF=AB(全等三角形的对应边相等) 6分 21、解:(1)线段O A 对应的函数关系式为:112s t =(012t ≤≤)线段A B 对应的函数关系式为:1(1220)s t =<≤.(2)图中线段A B 的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟. (3)如图中折线段C D D B -.22、解:(1)设平均每分钟一道正门可以通过x 名学生,一道侧门为y 名学生。
1分 则⎩⎨⎧=+=+22022602y x y x 解得:⎩⎨⎧==60100y x 5分(2)∵(100+60)×80%×4×2=1024 7分 又∵20×50=1000 ∴1024>1000 故学生可以安全撤离 8分 23.解:平移后抛物线的解析式为22(2)1y x =-+. (2)∴A 点坐标为(2,1),……………………………………1分 设直线OA 解析式为y kx =,将A (2,1)代入得12k =,直线OA 解析式为12y x =,将3x =代入12y x =得32y =,∴C 点坐标为(3,32).……1分将3x =代入22(2)1y x =-+得3y =,∴B 点坐标为(3,3)∴A B C 34S = (2)(2)∵PA ∥BC ,∴∠PAB =∠ABC1°当∠PBA =∠BAC 时,PB ∥AC ,∴四边形PACB 是平行四边形,t (分钟)∴32P A B C ==.………………………………………1分∴15(2,)2P .………………………………………………1分2°当∠APB =∠BAC 时,A P AB A BB C=,∴2ABAP BC=.又∵AB ==∴103A P =………………………………………………1分∴213(2,)3P ……………………………………………1分综上所述满足条件的P 点有5(2,)2,13(2,)3.……………………………1分24.解:(1)方法一:由已知得:C (0,-3),A (-1,0) …………………………1分 将A 、B 、C 三点的坐标代入得⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a 解得:⎪⎩⎪⎨⎧-=-==321c b a ……4分所以这个二次函数的表达式为:322--=x x y ……4分方法二:由已知得:C (0,-3),A (-1,0) ………1分 设该表达式为:)3)(1(-+=x x a y ………2分 将C 点的坐标代入得:1=a ………4分 所以这个二次函数的表达式为:322--=x x y ……4分 (注:表达式的最终结果用三种形式中的任一种都不扣分) (2)方法一:存在,F 点的坐标为(2,-3) ……5分 理由:易得D (1,-4),所以直线CD 的解析式为:3--=x y ∴E 点的坐标为(-3,0) ……………6分 由A 、C 、E 、F 四点的坐标得:AE =CF =2,AE ∥CF ∴以A 、C 、E 、F 为顶点的四边形为平行四边形 ∴存在点F ,坐标为(2,-3) …………7分 方法二:易得D (1,-4),所以直线CD 的解析式为:3--=x y∴E 点的坐标为(-3,0) ……………5分 ∵以A 、C 、E 、F 为顶点的四边形为平行四边形∴F 点的坐标为(2,-3)或(―2,―3)或(-4,3) 代入抛物线的表达式检验,只有(2,-3)符合 ∴存在点F ,坐标为(2,-3) ……………7分(3)如图,①当直线MN 在x 轴上方时,设圆的半径为R (R>0),则N (R+1,R ), 代入抛物线的表达式,解得2171+=R …………9分②当直线MN 在x 轴下方时,设圆的半径为r (r>0), 则N (r+1,-r ), 代入抛物线的表达式,解得2171+-=r ………11分∴圆的半径为2171+或2171+-. ……………11分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年中考模拟题数 学 试 卷(四)*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分) 1.sin30°的值为( ) A .21B .23C .33D .222. △ABC 中,∠A=50°,∠B=60°,则∠C =( )A .50°B .60°C .70°D .80°3.如图,直线l 1、l 2、l 3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处.B .两处C .三处.D .四处. 4.点P (-2,1)关于x 轴对称的点的坐标是( )A .(-2,-1)B .(2,-1)C .(1,-2)D .(2,1)5. 若x =3是方程x 2-3mx +6m =0的一个根,则m 的值为 ( )A .1B . 2C .3D .4 6.现有A 、B 两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A 立方体朝上的数字为、小明 掷B 立方体朝上的数字为来确定点P (),那么它们各掷一次所确定的点P 落在已知抛物线上的概率为( )A.118 B.112 C.19 D.167.右图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )A .B .C .D .2138.某超级市场失窃,大量的商品在夜间被罪犯用汽车运走。
三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在A 、B 、C 三人之外;(2)C 作案时总得有A 作从犯;(3)B 不会开车。
在此案中能肯定的作案对象是( )A .嫌疑犯AB .嫌疑犯BC .嫌疑犯CD .嫌疑犯A 和C二、填空题(每小题3分,共24分)9.据中新社报道:2010年我国粮食产量将达到0000千克,用科学记数法表示这个粮食产量为______千克.10.用一个半径为6㎝的半圆围成一个圆锥的侧面,则这个圆锥的侧面积为 ㎝2.(结果保留π)11.△ABC 中,AB =6,AC =4,∠A=45°,则△ABC 的面积为 .12.若一次函数的图象经过反比例函数4y x=-图象上的两点(1,m )和(n ,2),则这个一次函数的解析式是 .13. 某品牌的牛奶由于质量问题,在市场上受到严重冲击,该乳业公司为了挽回市场,加大了产品质量的管理力度,并采取了“买二赠一”的促销手段,一袋鲜奶售价元,一箱牛奶18袋,如果要买一箱牛奶,应该付款 元.14.通过平移把点A(2,-3)移到点A ’(4,-2),按同样的平移方式,点B(3,1)移到点B′, 则点B′的坐标是 ________15.如图,在甲、乙两地之间修一条笔直的公路, 从甲地测得公路的走向是北偏东48°。
甲、乙两地间 同时开工,若干天后,公路准确接通,则乙地所修公 路的走向是南偏西 度。
16.如图,M 为双曲线y =x1上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m 于D 、C 两点,若直线y=-x+m 与y轴交于点A,与x轴相交于点B .则AD ·BC 的值为 .三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)17.求值:计算:()113(2cos301)1-︒-+-18.先化简,再请你用喜爱的数代入求值xx x x x x x x x 42)44122(322-+÷+----+19.已知⊙O 的直径AB 、CD 互相垂直,弦AE 交CD 于F ,若⊙O 的半径为R求证:AE ·AF =2 R 220.据统计某外贸公司2007年、2008年的进出口贸易总额分别为3300万元和3760万元, 其中2008年的进口和出口贸易额分别比2007年增长20%和10%.(1)试确定2007年该公司的进口和出口贸易额分别是多少万元;(2)2009年该公司的目标是:进出口贸易总额不低于4200万元, 其中出口贸易额所占比重不低于60%, 预计2009年的进口贸易额比2008年增长10%, 则为完成上述目标,2009年的出口贸易额比2008年至少应增加多少万元四、(每小题10分,共20分)21.如图,河中水中停泊着一艘小艇,王平在河岸边的A处测得∠DAC=α,李月在河岸边的的B处测得∠DCA=β,如果A、C之间的距离为m,求小艇D到河岸AC的距离.22.某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册元.小军经常来该店租书,若每月租书数量为x册.(1)写出零星租书方式应付金额y1(元)与租书数量x(册)之间的函数关系式;(2)写出会员卡租书方式应付金额y2(元 )与租书数量x(册)之间的函数关系式;(3)小军选取哪种租书方式更合算五、(本题12分)23.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连结AE,点F是AE的中点,连结BF、DF,求证:BF⊥DF六、(本题12分)24.某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:(1)这次共抽调了多少人(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少(3)如果这次测试成绩的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人七、(本题12分)25.在△ABC中,AC=BC,∠ACB=90°,D、E是直线AB上两点.∠DCE=45°(1)当CE⊥AB时,点D与点A重合,显然DE2=AD2+BE2(不必证明)(2)如图,当点D不与点A重合时,求证:DE2=AD2+BE2(3)当点D在BA的延长线上时,(2)中的结论是否成立画出图形,说明理由.八(本题14分)26.如图,已知抛物线y=x2-ax+a2-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形(直接写出答案)&cm=16&tn=ucframework#doc如有需要,可到这里看看,希望对你有帮助2010年中考模拟题(四)数学试题参考答案及评分标准一、选择题(每小题3分,共24分)1.A;2.C; 3.D;4.A;5.C; 6.; 7.A; 8.A二、填空题(每小题3分,共24分)9.×1011;10.18π; 11.62;12.y=-2x-2;13.;14.(5,2);15.48°;16.2三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)17.解:原式22=+++--···················· 3分x x x x44452=-.································ 4分21x当x时,原式2=⨯-21 =··································· 6分318. 解:原式=2)2)(2(])2(1)2(2[2+-+⨯----+x x x x x x x x x ………………3分=x+2-22--x xx ………………5分=24--x x ………………6分当x=6时,原式=21………………8分19.证明:连接BE …………………1分 ∵AB 为⊙O 的直径∴∠AEB =90°…………………2分 ∵AB ⊥CD ∴∠AOF =90° ∴∠AOF =∠AEB =90° 又∠A =∠A∴△AOF ∽△AEB …………………5分AEAOAB AF =∴AE ·AF =AO ·AB ∵AO =R AB =2RAE ·AF =2R 2………………8分20.解:设2007年进口贸易额为x 万元、出口贸易额为y 万元 则:⎩⎨⎧=+++=+3760%)101(%)201(33000y x y x ⎩⎨⎧==20001300y x∴ 2007年进口贸易额为1300万元、出口贸易额为2000万元(2)设2009年的出口贸易额比2008年至少增加z 万元 由2008年的进口贸易额是:1300(1+20%)=1560万元 2008年的出口贸易额是:2000(1+10%)=2200万元则:⎪⎩⎪⎨⎧≥++++≥+++%60)2200(%)101(156022004200)2200(%)101(1560z zz 解得⎩⎨⎧≥≥374284z z所以z ≥374 ,即2009年的出口贸易额比2008年至少增加374万元.……………10分 四.(每小题10分,共20分)21.解:过点D 作DB ⊥AC 于点B,设DB =x………1分在Rt △ADB 中,tan ∠DAB =ABBD∴AB ==∠DAB BD tan αtan x………4分 在Rt △CDB 中,tan ∠DCB =BCBD∴BC =βtan tan xDCB BD =∠∵AB +BC =AC =m ∴αtan x +βtan x =m………8分 解得:x=βαβαtan tan tan tan +m答:小艇D 到河岸AB 的距离为βαβαtan tan tan tan +m ………10分22.解:(1)y1=x..........2分 (2)y2=12+x..........4分(3)当y1=y2时,x=12+x,解得:x=20 当y1>y2时,x>12+x,解得x>20 当y1<y2时,x<12+x,解得x<20综上所述,当小军每月借书少于20册时,采用零星方式租书合算;当每月租书20册时,两种方式费用一样;当每月租书多于20册时,采用会员的方式更合算...........10分23.证明:延长BF,交DA的延长线于点M,连接BD……………2分∵四边形ABCD是矩形∴MD∥BC∴∠AMF=∠EBF ∠E=∠MAF又FA=FE∴△AFM≌△EFB……………5分AM=BE FB=FM矩形ABCD中,AC=BD,AD=BC∴BC+BE=AD+AM即CE=MD∵CE=AC∴DB=DM∵FB=FM∴BF⊥DF……………12分24.(1)第一组的频率为=…………………………………………2分第二组的频率为…………………………………………3分错误!=150(人),这次共抽调了150人……………………………………6分(2)第一组人数为150×=6(人),第三、四组人数分别为51人,45人………8分这次测试的优秀率为5150×100%=24%………………………………10分(3)成绩为120次的学生至少有7人…………………………………………12分七、25.解:(2)证明:过点A作AF ⊥AB ,使AF=AB,连接DF∵△ABC是等腰直角三角形∴AC=AB ∠CAB=∠B=45°,∴∠FAC=45°∴△CAF≌△CBE…………………………………………3分∴CF=CE ∠ACF=∠BCE∵∠ACB=90°,∠DCE=45°∴∠ACD+∠BCE=45°∴∠ACD+∠ACF=45°即∠DCF=45°∴∠DCF=∠DCE又CD=CD∴△CDF≌△CDE∴DF=DE∵AD2+AF2=DF2∴AD2+BE2=DE2…………………………………………7分(3)结论仍然成立如图证法同(2)…………………………………………12分八、(本题14分)26.(1)∵抛物线y=x2-ax+a2-4a-4经过点(0,8)∴a2-4a-4=8解得:a1=6,a2=-2(不合题意,舍去)∴a的值为6…………………………………………4分(2)由(1)可得抛物线的解析式为y=x2-6x+8当y=0时,x2-6x+8=0解得:x1=2,x2=4∴A点坐标为(2,0),B点坐标为(4,0)当y=8时,x=0或x=6∴D点的坐标为(0,8),C点坐标为(6,8)DP=6-2t,OQ=2+t当四边形OQPD为矩形时,DP=OQ2+t =6-2t ,t =34,OQ =2+34=310 S =8×310=380 即矩形OQPD 的面积为380…………………………………………8分 (3)四边形PQBC 的面积为8)(21⨯+PC BQ ,当此四边形的面积为14时, 21(2-t +2t )×8=14 解得t =23(秒) 当t =23时,四边形PQBC 的面积为14…………………………………………12分(4)t =56时,PBQ 是等腰三角形.…………………………………………14分。
