摩擦力做功地特点
摩擦力做功与产生热能的关系
摩擦力做功与产生热能的关系众所周知，恒力做功的公式为W=F.Scos B ,但当做功的力涉及到摩擦力时，往往会使问题变的复杂化•我们知道摩擦力属于“耗散力”，做功与路径有关，如果考虑摩擦力做功的过程中与产生热能关系时，很多学生就会对之束手无策，从近几年的高考命题中，这类问题是重点也是难点问题，以下就针对摩擦力做功与产生热能的关系作一总结的分析1. 摩擦力做功的特点与产生热能的机理•根据，＜费曼物理学讲义＞中的描述：“摩擦力的起因：从原子情况来看，相互接触的两个表面是不平整的，它们有许多接触点，原子好象粘接在一起，于是，当我们拉开一个正在滑动的物体时，原子啪的一下分开，随及发生振动，过去，把这种摩擦的机理想象的很简单，表面起因只不过布满凹凸不同的形状，摩擦起因于抬高滑动体越过突起部分，但是事实不可能是这样的，因为在这种情况中不会有能量损失，而实际是要消耗动力的。
动力消耗的机理是当滑动体撞击突起部分时，突起部分发生形变，接着在两个物体中产生波和原子运动，过了一会儿，产生了热。
”从以上对摩擦力做功与产生热能的机理的描述，我们从微观的角度了解到摩擦生热的机理，"所以，我们对“做功”和“生热”实质的解释是：做功是指其中的某一个摩擦力对某一个物体做的功，而且一般都是以地面为参考系的，而“生热”的实质是机械能向内能转化的过程。
这与一对相互作用的摩擦力所做功的代数和有关。
为了说明这个问题，我们首先应该明确摩擦力做功的特点.2 .摩擦力做功的特点.我们学习的摩擦力包括动摩擦力和静摩擦力，它们的做功情况是否相同呢？下面我们就分别从各自做功的特点逐一分析。
2.1 静摩擦力的功静摩擦力虽然是在两个物体没有相对位移条件下出现的力，但这不等于静摩擦力做功一定为零。
因为受到静摩擦力作用的物体依然可以相对地面或其它参考系发生位移，这个位移如果不与静摩擦力垂直，则静摩擦力必定做功，如果叠在一起的两个木块A、E，在拉力F的作用下沿着光滑水平面发生一段位移s，图一所示，则A物体受到向前的静摩擦力f。
物理摩擦力知识考点总结
物理摩擦力知识考点总结（实用版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的实用范文，如学习资料、英语资料、学生作文、教学资源、求职资料、创业资料、工作范文、条据文书、合同协议、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of practical sample essays, such as learning materials, English materials, student essays, teaching resources, job search materials, entrepreneurial materials, work examples, documents, contracts, agreements, other essays, etc. Please pay attention to the different formats and writing methods of the model essay!物理摩擦力知识考点总结对物理概念的理解，不能单纯地去背诵。
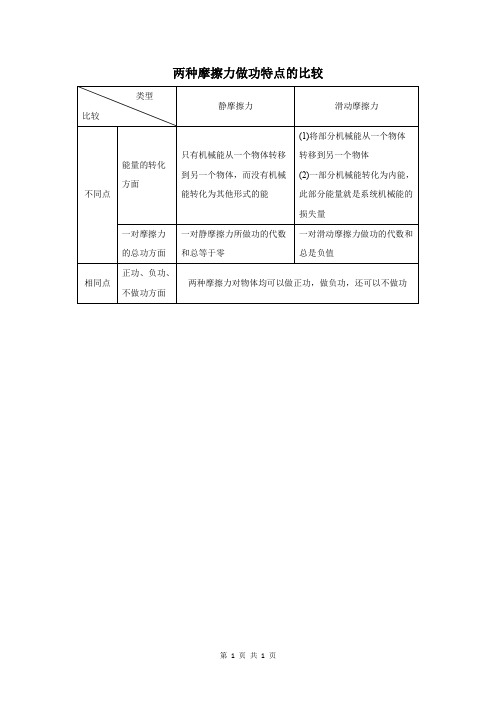
两种摩擦力做功特点的比较
类型
比较
静摩擦力
滑动摩擦力
不同点
能量的转化方面
只有机械能从一个物体转移到另一个物体，而没有机械能转化为其他形式的能
(1)将部分机械能从一个物体转移到另一个物体
(2)一部分机械能转化为内能，此部分能量就是系统机械能的损失量
一对摩擦力的总功方面
一对静摩擦力所做功的代数和总等于零
一对滑动摩擦力做功的代数和总是负值
相同点
正功、负功、不做功方面
两种摩擦力对物体均可以做正功，做负功，还可以不做功
摩擦力做功的特点
摩擦力做功的特点 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】摩擦力做功的特点南阳市五中李彩芹摩擦力做功问题，一直是高中物理教学的重点，更是教学难点。
在具体问题中涉及到摩擦力是否做功、做功的正负，以及作为作用力反作用力的一对摩擦力（以下简称“一对摩擦力”）所做功的代数和的正负等问题，学生往往纠缠不清，理不清思路，甚至发生谬误。
摩擦力大小和方向的不确定性，使得摩擦力做功有其自身的特殊性，本文简单归纳摩擦力做功的一些特点,仅供大家参考。
一、滑动摩擦力对物体可以做正功，可以做负功，也可以不做功。
1、滑动摩擦力可以对物体做负功这种情况最为常见，当滑动摩擦力阻碍物体运动或物体克服滑动摩擦力运动时，其对物体做负功．例1.如图1所示，一物块放在静止的粗糙水平桌面上，外力F把它拉着向右运动，在产生位移ｓ的过程中，摩擦力对物块做功情况如何？已知物块的质量为ｍ，与桌面之间的摩擦因数为μ分析与解物块在水平桌面上运动时，受到的滑动摩擦力大小为ｆ＝μｍｇ，其方向向左，而位移ｓ的方向向右，代入公式Ｗ＝ｆｓｃｏｓα，得Ｗ＝μｍｇｓｃｏｓπ＝－μｍｇｓ．即摩擦力对物体做了负功．2、滑动摩擦力可以对物体不做功在例1中水平桌面虽然受到物体对它的滑动摩擦力作用，但桌面并没有运动，即在滑动摩擦力作用下，桌面相对于地面的位移ｓ＝０，则Ｗ＝０，因而滑动摩擦力对桌面不做功．3、滑动摩擦力可以对物体做正功当滑动摩擦力的作用效果是加快物体运动时，其对物体做正功．例2.如图2所示，水平地面上有辆平板车，其粗糙的表面上放有一质量为ｍ的木块，当平板车向右加速运动的位移为ｓ时，发现木块在它上面发生向左方向的相对运动位移ｓ′，则滑动摩擦力对木块的做功情况如何？分析与解小车向右加速运动时，木块相对于小车向左滑动，所以木块受到的滑动摩擦力方向向右，在小车运动过程中，车上的木块相对于地面的位移为ｓ－ｓ′，方向向右（如图2所示）．所以，此过程中滑动摩擦力对木块做正功，其大小为Ｗ＝Ｆsｃｏｓα＝μｍｇ（ｓ－ｓ′）．同时滑动摩擦力对小车做负功Ｗ′＝μｍｇｓｃｏｓπ＝－μｍｇｓ，则一对滑动摩擦力分别对两物体所做功之和为Ｗ合＝Ｗ＋Ｗ′＝－μｍｇｓ′．即两物体之间的一对滑动摩擦力总做负功。
静摩擦力做功的特点
静摩擦力做功的特点
静摩擦力是指在物体表面接触处，当两个物体相对运动或尝试相对运动时，由于表面间的不规则性而产生的阻力。
当物体相对运动时，静摩擦力阻碍了物体的运动，并且在某些情况下可以做功。
以下是静摩擦力做功的特点：
1.只有在物体没有相对滑动时，静摩擦力才能做功。
当物体开
始移动时，摩擦力转变为滑动摩擦力，其方向与运动方向相反，并且不再做功。
2.静摩擦力做功的大小取决于物体之间的相对运动尝试程度。
如果施加在物体上的外力大于静摩擦力，则物体会继续保持静止。
在这种情况下，静摩擦力与外力大小相等，做正功，即朝着施加外力的方向做功。
如果施加的外力小于或等于静摩擦力，则物体仍然保持静止，静摩擦力不做功。
3.静摩擦力的功与位移成正比。
如果物体通过外力施加的力量
克服了静摩擦力，并且发生位移，那么静摩擦力所做的功就等于摩擦力乘以物体的位移。
4.静摩擦力的功可以使能量转化。
当物体受到静摩擦力做功时，
它的机械能会发生变化。
如果外力施加的功大于静摩擦力所做的功，物体的机械能增加；如果外力施加的功小于静摩擦力所做的功，物体的机械能减小。
静摩擦力的功也可能转化为其他形式的能量，例如热能。
总之，静摩擦力做功的特点包括：只在物体没有相对滑动时产
生，大小与物体间的相对运动尝试程度有关，与位移成正比，可以使能量转化。
了解这些特点有助于我们理解静摩擦力对物体运动的作用和能量转化的过程。
静摩擦力做功的特点
静摩擦力做功的特点
静摩擦力是指当两个物体相对运动时互相抵抗的力，不可避免地会使得运动变得困难。
静摩擦力做功的特点如下：
1. 静摩擦力对物体不会做功：在物体静止不动的情况下，静摩擦力不会做功。
因为静摩擦力的方向与物体相对运动的方向相反，两者之间没有相对运动，故静摩擦力不对物体做功。
2. 静摩擦力最大值与所需的力相等：当我们试图把一个静止的物体推动或拉动时，物体受到的静摩擦力将达到最大值。
此时，静摩擦力与所需的力相等，正好抵消物体运动的势能或动能的增加。
只有当所作用的力大于静摩擦力的最大值时，物体才能开始运动。
3. 静摩擦力与物体间的接触面质量有关：静摩擦力的大小与物体间的接触面之间的粗糙度及压力有关。
接触面越大、粗糙度越高或压力越大时，静摩擦力的最大值也会相应增加。
4. 静摩擦力与物体间的相对速度无关：静摩擦力与物体间的相对速度无关，只与物体间的接触状态和相互作用有关。
即使物体之间有一定的相对速度，只要它们没有相对滑动，静摩擦力仍然存在，且不会改变。
只有当相对速度大到一定程度时，静摩擦力会变为动摩擦力。
综上所述，静摩擦力做功的特点包括不对静止物体做功，最大值与所需的力相等，与接触面质量有关，与相对速度无关。
滑动摩擦力做功特点
滑动摩擦力做功特点
滑动摩擦力做功的特点包括以下几个方面：
1. 方向性：滑动摩擦力的方向与物体的运动方向相反。
当物体沿着滑动方向运动时，摩擦力的方向与物体的运动方向相反，因此滑动摩擦力做的功通常是负功。
2. 功率与速度的关系：滑动摩擦力做功的大小与物体的速度有关。
根据摩擦力的公式F = μN，其中F为摩擦力，μ为摩擦系数，N为物体受力面的压力，可以看出摩擦力与物体之间的垂直压力成正比。
随着物体速度的增加，垂直压力也会增加，从而导致滑动摩擦力的增大。
3. 能量转化：滑动摩擦力做功时，将物体的机械能转化为热能。
由于滑动摩擦力会使物体表面的分子发生热运动，这部分能量被转化为了热能而不是作为有用的机械能。
4. 能量损失：滑动摩擦力做功时，由于能量的转化与热量的损失，会导致能量的损耗。
这也是为什么滑动摩擦力做的功通常是负功的原因之一。
5. 与速度无关：滑动摩擦力做功与物体的速度并不完全成比例。
虽然滑动摩擦力随着速度的增加而增大，但其增长并不是严格线性的，而是存在阈值。
当速度超过一定阈值时，滑动摩擦力的增长趋势会变得平缓。
总之，滑动摩擦力做功通常是负功，能量会转化为热能并存在能量损耗，且其大小与物体的速度有关。
一对相互作用的摩擦力做功的特点
一对相互作用的摩擦力做功的特点湖北枣阳二中 张锋在高中阶段，许多学生对于相互作用力的做功情况尤其是一对相互作用的摩擦力做功的情况感觉很模糊，甚至是束手无策。
现在我就一对相互作用的摩擦力做功的特点发表一下我的看法。
一．一对静摩擦力做功特点（1） 单个静摩擦力可以做正功，也可以做负功，还可以不做功。
例如在斜面上静止不动的物体，静摩擦力不做功；与倾斜的传送带一起匀速上升的物体，静摩擦力做正功；与倾斜的传送带一起匀速下降的物体，静摩擦力做负功。
（2） 相互摩擦的系统内，一对静摩擦力所做功的代数和总为零，即021=+W W 。
由于受静摩擦力的物体相对静止，所以他们的位移相等，而一对静摩擦力等大反向，故有0)(21=⋅-+⋅==s f s f W W 。
（3） 在静摩擦力做功的过程中，只有机械能的相互转移（静摩擦力起着传递机械能的作用），而没有机械能转化为其他形式的能。
二．一对滑动摩擦力做功特点（1） 滑动摩擦力总是阻碍物体的相对运动，但不一定阻碍物体的运动，故单个滑动摩擦力可以对物体做正功，也可以对物体做负功，当然也可以不做功。
例如沿粗糙的斜面下滑的物体，滑动摩擦力对物体做负功而对斜面不做功。
（2） 相互摩擦的系统内，一对滑动摩擦力所做功的代数和总为负值，其绝对值恰等于于相对位移的乘积，即恰等于系统因摩擦而损失的机械能。
(Q W W -=+21，其中Q 就是在摩擦过程中产生的内能）。
（3） 一对滑动摩擦力做功的过程中，能量的转化有两种情况：一是相互摩擦的物体之间机械能的转移；二是机械能转化为内能。
转化为内能的数值等于滑动摩擦力于相对位移的乘积，即相对s F Q f ⋅=。
例如：质量为1m 的木板A 静止在光滑的水平面上，A 的上表面动摩擦因数为u,质量2m为物体B 左端以0v 水平冲上A 的上表面，当B 恰好到达A 的右端时二者相对静止。
求:(1)该过程中摩擦力分别对A,B 和系统做的功;(2)系统产生的内能。
摩擦力做功和产生热能的关系
摩擦力做功与产生热能的关系众所周知,恒力做功的公式为W=F.Scosθ, 但当做功的力涉及到摩擦力时,往往会使问题变的复杂化. 我们知道摩擦力属于“耗散力”，做功与路径有关，如果考虑摩擦力做功的过程中与产生热能关系时，很多学生就会对之束手无策,从近几年的高考命题中,这类问题是重点也是难点问题,以下就针对摩擦力做功与产生热能的关系作一总结的分析.1．摩擦力做功的特点与产生热能的机理.根据，<费曼物理学讲义>中的描述：“摩擦力的起因:从原子情况来看,相互接触的两个表面是不平整的,它们有许多接触点,原子好象粘接在一起,于是,当我们拉开一个正在滑动的物体时,原子啪的一下分开，随及发生振动，过去，把这种摩擦的机理想象的很简单，表面起因只不过布满凹凸不同的形状，摩擦起因于抬高滑动体越过突起部分，但是事实不可能是这样的，因为在这种情况中不会有能量损失，而实际是要消耗动力的。
动力消耗的机理是当滑动体撞击突起部分时，突起部分发生形变，接着在两个物体中产生波和原子运动，过了一会儿，产生了热。
”从以上对摩擦力做功与产生热能的机理的描述，我们从微观的角度了解到摩擦生热的机理，”所以，我们对“做功”和“生热”实质的解释是：做功是指其中的某一个摩擦力对某一个物体做的功，而且一般都是以地面为参考系的，而“生热”的实质是机械能向内能转化的过程。
这与一对相互作用的摩擦力所做功的代数和有关。
为了说明这个问题，我们首先应该明确摩擦力做功的特点．２．摩擦力做功的特点．我们学习的摩擦力包括动摩擦力和静摩擦力，它们的做功情况是否相同呢？下面我们就分别从各自做功的特点逐一分析。
２．１静摩擦力的功静摩擦力虽然是在两个物体没有相对位移条件下出现的力，但这不等于静摩擦力做功一定为零。
因为受到静摩擦力作用的物体依然可以相对地面或其它参考系发生位移，这个位移如果不与静摩擦力垂直，则静摩擦力必定做功，如果叠在一起的两个木块Ａ、Ｂ，在拉力Ｆ的作用下沿着光滑水平面发生一段位移s，图一所示，则Ａ物体受到向前的静摩擦力f０对Ａ作正功W= f０s图一图二在圆柱体沿水平面向前无滑滚动时，（图二所示），虽然圆柱体相对地面存在位移，但地面对车轮的静摩擦力f ０并不做功，这时，不能认为滚动的圆柱体是一个质点，从地面参考系来看，在一段微小时间间隔内，f ０作用于地面接触的圆柱体边缘一点Ａ，对于静摩擦力f ０而言Ａ的瞬时速度v Ａ＝０，故Ａ的微小位移dr ＝v Ａdt ＝０，元功为零，下一个微小时间间隔内，静摩擦力f ０则作用在另一个质点Ｂ，同样元功为零．所以滚动过程中静摩擦力f ０对圆柱体做功为零．在此过程中，滚动摩擦要阻止圆柱体滚动，柱体需要克服这种阻碍消耗能量做功，但这主要是克服滚动过程中地面形变后产生的支持力所导致的阻力矩的功．高中阶段，一般我们只分析第一种情况的静摩擦力的做功情况．由以上分析，我们可以归纳出静摩擦力做功有以下特点：1、静摩擦力可以做正功，也可以做负功，还可以不做功．2、在静摩擦力做功的过程中，只有机械能的相互转移，而没有机械能相互为其它形式的能．3、相互作用的系统内，一对静摩擦力所做的功的和必为零。
一对相互作用的摩擦力做功的特点
一对相互作用的摩擦力做功的特点相互作用的摩擦力是一种常见的力，它是由两个物体相对运动或者因运动而试图相对运动时产生的阻碍力。
当两个物体之间存在相互作用的摩擦力时，这些力会对物体产生功。
下面将详细探讨相互作用的摩擦力做功的特点。
摩擦力是相互作用力之一，是由物体之间的表面接触带来的。
相互作用的摩擦力有两种常见的类型：静摩擦力和动摩擦力。
静摩擦力是指两个物体相对静止且试图相对运动时产生的阻碍力，动摩擦力则是指两个物体相对运动时产生的阻碍力。
首先，相互作用的摩擦力做功是有限制的。
当两个物体相对运动或者试图相对运动时，摩擦力会阻碍物体的运动，并产生与运动方向相反的力。
假设一个物体在沿着水平方向运动，受到了摩擦力的阻碍。
由于摩擦力与运动方向相反，所以物体的速度会减小。
随着速度的减小，摩擦力的大小也会减小，直到两者达到平衡。
其次，摩擦力做功时，功的大小与物体的位移有关。
功是力和位移的乘积，当物体受到的摩擦力不变时，物体移动的距离越大，摩擦力所做的功就越大。
这是因为力和位移都是矢量量，相互的乘积和求积会产生一个矢量量。
另外，摩擦力做功时的功率是有限制的。
功率是功对时间的比值，描述了单位时间内所做的功。
摩擦力所做的功越大，其所需的时间也就越长。
这是因为相互作用的摩擦力通常带有较大的阻碍性质，需要更长的时间才能将物体从一个位置移动到另一个位置。
此外，摩擦力做功时会产生热能。
摩擦力会导致物体表面的摩擦区域产生热量，这是由于运动的摩擦表面之间摩擦力的互相作用所形成的。
这部分热能以热量的形式被释放出来，同时也导致摩擦表面的温度升高。
最后，摩擦力做功时会损耗机械能。
由于摩擦力的存在，物体在移动过程中会损耗一定的机械能。
这是由于摩擦力将一部分作用于物体的机械能转化为热能而引起的。
这种机械能的损耗使得物体在移动过程中逐渐减速，最终停止。
总之，相互作用的摩擦力做功具有以下特点：有限制、与位移相关、功率有限制、产生热能、损耗机械能。
摩擦力做功与能量转化问题
专题专题专题 摩擦力做功与能量转化问题摩擦力做功与能量转化问题【学习目标】【学习目标】1.1.理解静摩擦力和滑动摩擦力做功的特点；理解静摩擦力和滑动摩擦力做功的特点；理解静摩擦力和滑动摩擦力做功的特点；2.2.2.理解摩擦生热及其计算。
理解摩擦生热及其计算。
理解摩擦生热及其计算。
【知识解读】【知识解读】1.1.静摩擦力做功的特点静摩擦力做功的特点静摩擦力做功的特点如图5－1515－－1，放在水平桌面上的物体A 在水平拉力F 的作用下未动，则桌面对A 向左的静摩擦力不做功，因为桌面在静摩擦力的方向上没有位移。
如图5－1515－－2，A 和B 叠放在一起置于光滑水平桌面上，在拉力F 的作用下，的作用下，A A 和B 一起向右加速运动，则B 对A 的静摩擦力做正功，的静摩擦力做正功，A A 对B 的静摩擦力做负功。
可见静摩擦力做功的特点是：的静摩擦力做负功。
可见静摩擦力做功的特点是： （1）静摩擦力可以做正功，也可以做负功，还可以不做功。
功，还可以不做功。
（2）相互作用的一对静摩擦力做功的代数和总等于零。
数和总等于零。
（3）在静摩擦力做功的过程中，只有机械能的相互转移（静摩擦力起着传递机械能的作用），而没有机械能转化为其它形式的能。
，而没有机械能转化为其它形式的能。
2.2.滑动摩擦力做功的特点滑动摩擦力做功的特点滑动摩擦力做功的特点如图5－1515－－3，物块A 在水平桌面上，在外力F 的作用下向右运动，桌面对A 向左的滑动摩擦力做负功，A 对桌面的滑动摩擦力不做功。
力不做功。
如图5－1515－－4，上表面不光滑的长木板，放在光滑的水平地面上，一小铁块以速度，上表面不光滑的长木板，放在光滑的水平地面上，一小铁块以速度v 从木板的左端滑上木板，当铁块和木板相对静止时木板相对地面滑动的距离为s，小铁块相对木板滑动的距离为d ，滑动摩擦力对铁块所做的功为：W 铁＝－f(s+d)―――①―――①根据动能定理，铁块动能的变化量为：k w =f s+d ED 铁铁＝－（）―――②―――②②式表明，铁块从开始滑动到相对木板静止的过程中，其动能减少。
摩擦力做功的特点
摩擦力做功的特点
以下是 7 条关于摩擦力做功特点的内容：
1. 嘿，你知道吗？摩擦力做功有时可真是让人又爱又恨啊！就好比你在冰面上走路，滑溜溜的很难前进，这就是摩擦力小导致它做功少呀！摩擦力做功的一个特点就是，它的大小和方向都挺复杂呢！
2. 哇塞，想想看啊，当你推一个很重的箱子，使出浑身力气它才慢慢动起来，这就是摩擦力在“作祟”呀！摩擦力做功还跟接触面的粗糙程度有很大关系哦，这就好像在爬山时，陡峭的路走起来就费劲，就像摩擦力做功大一样！
3. 哎呀呀，你有没有发现啊，摩擦力做功有时候能帮大忙呢！像刹车的时候，没有摩擦力做功车子怎么停下来？它就像是个默默守护的“小卫士”！但有时候它又很“调皮”，消耗好多能量呢！比如一部机器的零件摩擦久了会发热，这不就是摩擦力做功在“捣蛋”嘛？
4. 嘿，你想啊，骑自行车的时候，轮子和地面的摩擦力做功让车子前进，多神奇呀！摩擦力做功会让物体的能量发生变化，这不是像一个神奇的“魔法”在起作用吗？
5. 哦哟，有些时候呢，摩擦力做功能成就一些美好的事情哦，比如你能稳稳地站在地上，就是摩擦力在好好工作，让它做功呀！但要是没有控制好，它也可能带来麻烦，就好像在一些光滑的表面容易滑倒，就是它在“捣乱”啦！
6. 哈哈，你说摩擦力做功是不是很有个性呀！有时你需要它，有时又想摆脱它。
就好比走路和滑冰，一个靠它前进，一个想减少它，多有趣的“两面派”啊！
7. 瞧瞧，摩擦力做功就是这样特别呢！时而让人高兴，时而让人烦恼。
说它简单吧，又挺复杂；说它复杂吧，又在生活中无处不在。
它就是这么神奇呀！总之，摩擦力做功既有好处又有坏处，关键看我们怎么利用和应对它啦！。
斜面上摩擦力做功的特点及应用
斜面上摩擦力做功的特点及应用斜面上的摩擦力是指当物体在斜面上运动或试图运动时，斜面对物体施加的抵抗运动的力。
摩擦力是由物体之间的接触面之间的粗糙程度决定的，它可以阻碍物体在斜面上滑动或滚动。
在斜面上，摩擦力可以对物体做功，从而改变物体的动能。
摩擦力做功的特点主要有以下几个方面：1. 功与位移方向相反：斜面上的摩擦力始终与物体的运动方向相反，所以摩擦力所做的功始终与物体的位移方向相反。
这是因为摩擦力的方向总是阻碍物体的运动，使物体减速或停止。
2. 功与摩擦力大小成正比：摩擦力所做的功与摩擦力的大小成正比。
当斜面上的摩擦力较大时，它对物体所做的功也较大；反之，当摩擦力较小时，所做的功也较小。
3. 功与物体在斜面上的高度变化有关：当物体沿斜面下滑时，它的高度会不断减小，而斜面上的摩擦力所做的功正是将物体的动能转化为势能。
因此，物体在下滑过程中的高度变化越大，摩擦力所做的功也就越大。
斜面上摩擦力做功的应用十分广泛，以下是一些常见的应用场景：1. 刹车系统：汽车、自行车等交通工具的刹车系统利用斜面上的摩擦力做功来减速或停止运动。
当刹车踏板被踩下时，刹车片与刹车盘之间的摩擦力会将车辆的动能转化为热能，从而实现刹车效果。
2. 斜面运动：滑雪、滑板等运动中，运动员利用斜面上的摩擦力做功来调整速度和方向。
通过控制身体的重心和斜面的倾斜度，运动员可以在斜面上获得所需的摩擦力，从而实现加速、减速或转向。
3. 倾斜平台：某些工业场景中，需要将物体从低处抬升到高处，但由于物体较重且体积较大，无法通过直接抬起。
此时可以使用倾斜平台，通过斜面上的摩擦力做功，将物体从低处推到高处。
4. 滚动阻力：斜坡上滚动的物体会受到斜面上的摩擦力的阻碍，这种摩擦力会将物体的动能转化为热能，使物体减速。
这一原理被广泛应用于滚动轴承、滚筒输送机等设备中，用于控制物体的速度和运动。
斜面上的摩擦力做功的特点是与位移方向相反，与摩擦力大小成正比，与物体在斜面上的高度变化有关。
斜面上摩擦力做功的特点和推广应用
斜面上摩擦力做功的特点和推广应用
一、斜面上摩擦力做功的特点
1. 斜面上的物体受到重力和斜面法向力的作用，同时也受到摩擦力的阻碍。
2. 当物体在斜面上运动时，摩擦力始终与物体运动方向相反，并且大小随着物体运动的速度和斜面角度的变化而变化。
3. 斜面上摩擦力做功的特点是摩擦力始终阻碍物体运动，并减少了物体的动能，同时使物体的机械能逐渐转化为热能，最终以热能的形式散失到周围环境中。
4. 斜面上的摩擦力做功量由于摩擦力的大小和物体在斜面上移动的距离而不同。
二、斜面上摩擦力做功的推广应用
1. 斜面上摩擦力做功可以应用于机械能的转换，在机械工程领域中有广泛的应用。
例如，利用坡道或斜面将物体提升到高处，或将物体从高处移动到低处，可将势能转化为动能或反之，从而实现机械能的转换。
2. 斜面上摩擦力做功还可以应用于制动系统中。
例如，汽车的制动系统利用摩擦力产生制动力，将车辆的动能转化为热能，从而实现车辆的停止。
3. 在科学实验中，斜面上摩擦力做功可以用于测量物体的动能和摩擦力的大小。
例如，利用斜面实验测量汽车刹车摩擦系数，通过实验得
到摩擦系数的大小，可为制动系统的设计和升级提供理论基础。
4. 斜面上摩擦力做功还可以用于能量转化中。
例如，利用坡道或斜面来蓄能，可以将机械能转化为电能，用于驱动电动汽车、制造储能装置等。
综上所述，斜面上摩擦力做功是机械能转换、制动系统、科学实验和能量转化等领域中广泛应用的原理和方法，对推动科技进步和提高生活质量具有重要作用。
斜面上摩擦力做功的特点及应用
斜面上摩擦力做功的特点及应用
斜面上的摩擦力是物体在斜面上运动时所受到的一种阻力，在物理学中具有重要的地位。
当物体沿着斜面运动时，摩擦力始终与物体运动的方向相反，由此可以计算出斜面上摩擦力所做的功。
下面我们来探讨一下斜面上摩擦力做功的特点与应用。
首先，斜面上摩擦力做功的特点是随着斜面角度的变化而变化。
当斜面的角度较小时，摩擦力所做的功非常小，甚至可以忽略不计。
而当斜面的角度增大时，摩擦力所做的功也相应增大，能够对物体的运动产生明显的影响。
其次，斜面上摩擦力做功的应用十分广泛。
例如在斜面上升降机、滑雪运动、汽车爬坡等方面都有重要的应用。
在这些应用中，我们需要计算出斜面上摩擦力所做的功以及对物体运动的影响，以便能够更好地进行设计和控制。
最后，斜面上摩擦力做功也可以被应用到机械能守恒定律的研究中。
根据机械能守恒定律，物体在斜面上运动时，斜面上摩擦力所做的功与物体的重力势能的变化量相等，因此可以通过计算斜面上摩擦力所做的功来研究物体的机械能守恒问题。
总之，斜面上摩擦力做功是物理学中的一个重要概念，具有广泛的应用价值。
我们需要充分认识其特点和应用，以便更好地进行研究和应用。
- 1 -。
摩擦力做功的特点解析
摩擦力做功的特点解析摩擦力是物体之间相对运动时产生的阻碍运动的力，它对物体的运动有着重要的影响。
当物体受到摩擦力作用时，摩擦力会对物体进行功的转化。
摩擦力做功的特点可以从以下几个方面进行解析。
首先，摩擦力做功的特点之一是能量转化。
在物体相对运动时，摩擦力将部分物体的机械能转化为热能。
当两个物体相互摩擦时，由于摩擦力的作用，物体的动能会逐渐减小，同时热能会逐渐增加。
这是因为摩擦力背后的机理是由两个物体之间的相互作用引起的微观力。
其次，摩擦力做功的特点之二是方向相反。
摩擦力的方向与物体相对运动的方向相反，这意味着摩擦力对物体的运动起到了阻碍的作用。
摩擦力的大小与物体之间的接触面积、表面粗糙程度、受力物体的质量以及动摩擦系数等因素有关。
当物体与支持面之间没有相对滑动时，称为静摩擦。
当物体具有相对滑动时，称为动摩擦。
此外，摩擦力做功的特点之三是与速度相关。
摩擦力的大小与物体相对速度有关。
当物体的速度增大时，摩擦力也随之增大。
相反，当物体的速度减小时，摩擦力也会减小。
这与物体表面的粗糙程度有关，当物体的相对速度增加时，物体表面的接触点也随之增多，从而增大了摩擦力的大小。
此外，摩擦力做功的特点之四是滑动摩擦与滚动摩擦的不同。
滑动摩擦是指物体相对滑动时产生的摩擦力，例如两个物体在相对滑动时，摩擦力将物体的机械能转化为热能。
而滚动摩擦是指物体进行滚动时产生的摩擦力，例如一个轮子在地面上滚动时，摩擦力既可减小物体的速度，也可增加物体的速度。
总结起来，摩擦力做功的特点主要包括能量转化、方向相反、与速度相关以及滑动摩擦与滚动摩擦的不同。
这些特点在物体的运动过程中起着重要的作用，使物体的运动受到了限制或改变。
在实际生活中，我们需要充分理解和利用摩擦力的作用，以便更好地控制和调节物体的运动。
高中物理摩擦力做功的特点
一、静摩擦力做功的特点1．静摩擦力可以做正功，也可以做负功，还可以不做功。
2．在静摩擦力做功的过程中，只有机械能的相互转移（静摩擦力起着传递机械能的作用），而没有机械能转化为其他形式的能。
3．相互作用的系统内，一对静摩擦力所做功的代数和总为零。
二、滑动摩擦力做功的特点1．滑动摩擦力可以不做功若相对运动的两物体之一对地面静止，则滑动摩擦力对该物体不做功。
2．滑动摩擦力可以做正功如：货车车厢内放一木箱，货车突然加速，木箱相对货车向后滑动，但相对地面向前运动，则货车对木箱的滑动摩擦力做正功。
3．滑动摩擦力可以做负功如：货车车厢内放一木箱，货车突然加速，木箱相对货车向后滑动，但相对地面向前运动，则木箱对货车的滑动摩擦力对货车做负功。
4.相互作用的系统内，一对滑动摩擦力所做的功总不为零，其绝对值恰等于滑动摩擦力与相对位移的乘积，即等于系统损失的机械能。
5．一对滑动摩擦力做功的过程中，能量的转化有两种情况：一是相互摩擦的物体之间机械能的转移；二是机械能转化为内能，转化为内能的量值等于滑动摩擦力与相对位移的乘积。
三、斜面上摩擦力做功的特点模型：单个物体在斜面上滑动，不受其它外力作用时，滑动摩擦力做功Wf=-μGx(x为物体运动的水平位移)。
特点：①一个物体在斜面上滑动；②FN=mgcosα；③摩擦力为阻力；④摩擦阻力做功为Wf=-μGx(x为物体运动的水平位移)；⑤μ=h/X例1、如图1所示，木块A放在木板B上表面左端，现用水平恒力F将A 拉至B的右端，已知A、B间的摩擦力大小为f。
第一次将木板固定在地面上，f对A做功数值为W1，此次过程中产生热量为Q1；第二次木板B 可以在光滑水平地面上自由滑动，这一次f对A做功数值为W2，此过程中产生热量为Q2，则（）A、W1<W2，Q1=Q2B、W1≠W2，Q1=Q2C、W1<W2，Q1<Q2D、Wl=W2，Q1<Q2解析：设木板长为L，木块边长为a，当木板固定时，摩擦力f对A做负功，大小为W1=f（L－a）该过程产生的热量Q1=W1=f（L－a）当木板B可以在光滑水平面上运动时，在A被拉至木板右端的过程中，木板将向右移动，设移动距离为l，此过程中A相对于B的位移仍为（L－a），如图1所示摩擦力f对A做负功，大小为W2=f（L+l－a）木板受到的摩擦力f对木板做正功WB，WB=fl使木板的动能增大。
分析摩擦力做功
--精品 分 析 摩 擦 力 做 功 的 特 点浙江省苍南县求知中学（灵溪第三高级中学） 李求龙 （325800）在相当多的问题里,摩擦力都是阻碍物体的运动,对物体做负功,这就很容易给人一种感觉-----摩擦力一定做负功,实际上,因摩擦力的方向与物体的运动方向之间没有必然的联系所以摩擦力可以做负功,也可以做正功,也可以不做功,下面按静摩擦力的功和滑动摩擦力的功分述如下:一.关于静摩擦力做的功1.静摩擦力可以对物体不做功（1）当物体受静摩擦力作用时，若物体相对地面处于静止状态，静摩擦力对物体不做功，因为物体相对于地面的位移为零.相对于地面静止的物体受到静摩擦力是不做功的,那运动的物体受到静摩擦力是否也可能不做功呢?（2）如右图所示，有一水平圆形转盘绕竖直轴以角速度ω转动，在离轴心为r 处放一块质量为m 的木块，随圆盘一起做匀速圆周运动.在转动过程中，木块m 有沿半径向外运动的趋势，则它所受静摩擦力F f 方向沿半径指向圆心，所以该力始终与速度方向垂直，即在F f 方向没有位移,在任何时刻木块所受的静摩擦力F f 对它不做功.再如:人掉在向右运动车厢的细绳上,则它所受静摩擦力F f 方向竖直向上,该力始终与速度方向垂直，人所受的静摩擦力F f 对它不做功.由此可看出，物体在静摩擦力作用下相对于地面运动，此时静摩擦力也可以对物体不做功.2.静摩擦力可以对物体做负功，也可以对物体做正功如图所示，在一与水平方向夹角为θ的传送带上，有一装满玉米的麻袋相对于传送带静止.（1）当麻袋随传送带一起匀速向下运动时，麻袋相对于地面的位移方向沿斜面斜向下，传送带对它的静摩擦F f 力与它的重力的下滑分力相平衡，即沿斜面向上.在这里，静摩擦力对物体做负功.（2）当麻袋随传送带一起匀速向上运动时，麻袋所受静摩擦力F f 与物体位移方向一致，静摩擦力F f 对麻袋做正功.综上所述，物体之间的静摩擦力F f 可以对其中一个物体做正功，也可以做负功，甚至不做功，关键看物体受到的静摩擦力和它运动方向的关系.一对静摩擦力对两物体所做的总功为零，这是因为物体间的静摩擦力总是大小相等、静止 F f F 麻袋F f ω r v方向相反，而它们运动时相对于地面的位移是相同的，所以它们之间的静摩擦力若做功时，必定对一个物体做正功，对另一个物体做等量的负功，要么静摩擦力对两物体都不做功，这就是在静摩擦力作用下的两物体，即使发生运动也不会产生内能的原因.二.滑动摩擦力做的功在分析滑动摩擦力做功的时候要正确理解“运动”和“相对运动”的关系。
摩擦力做功的特点及应用
摩擦力做功的特点及应用1．静摩擦力做功时，只有机械能的相互转移，不会转化为内能．2．滑动摩擦力做功的特点相互间存在滑动摩擦力的系统内，一对滑动摩擦力做功将产生两种可能效果：(1)机械能全部转化为内能；(2)有一部分机械能在相互摩擦的物体间转移，另外一部分转化为内能．例1 如图1所示，质量为m ＝1 kg 的滑块，在水平力作用下静止在倾角为θ＝30°的光滑斜面上，斜面的末端B 与水平传送带相接(滑块经过此位置滑上传送带时无能量损失)，传送带的运行速度为v 0＝3 m/s ，长为l ＝1.4 m ；今将水平力撤去，当滑块滑到传送带右端C 时，恰好与传送带速度相同．滑块与传送带间的动摩擦因数为μ＝0.25，g 取10 m/s 2.求：图1(1)水平作用力F 的大小；(2)滑块下滑的高度；(3)若滑块滑上传送带时速度大于3 m/s ，滑块在传送带上滑行的整个过程中产生的热量．答案 (1)1033N (2)0.1 m 或0.8 m (3)0.5 J 解析 (1)滑块受到水平力F 、重力mg 和支持力F N 作用处于平衡状态，水平力F ＝mg tan θ，F ＝1033N. (2)设滑块从高为h 处下滑，到达斜面底端速度为v ，下滑过程机械能守恒mgh ＝12m v 2， 得v ＝2gh若滑块冲上传送带时的速度小于传送带速度，则滑块在传送带上由于受到向右的滑动摩擦力而做匀加速运动；根据动能定理有μmgl ＝12m v 02－12m v 2 则h ＝v 202g－μl ，代入数据解得h ＝0.1 m 若滑块冲上传送带时的速度大于传送带的速度，则滑块由于受到向左的滑动摩擦力而做匀减速运动；根据动能定理：－μmgl ＝12m v 02－12m v 2 则h ＝v 202g＋μl 代入数据解得h ＝0.8 m.(3)设滑块在传送带上运动的时间为t ，则t 时间内传送带的位移x ＝v 0t ，mgh ＝12m v 2，v 0＝v －at ，μmg ＝ma滑块相对传送带滑动的位移Δx ＝l －x相对滑动生成的热量Q ＝μmg ·Δx代入数据解得Q ＝0.5 J.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
摩擦力做功的特点1.静摩擦力做功的特点如图5－15－1，放在水平桌面上的物体A 在水平拉力F 的作用下未动，则桌面对A 向左的静摩擦力不做功，因为桌面在静摩擦力的方向上没有位移。
如图5－15－2，A 和B叠放在一起置于光滑水平桌面上，在拉力F 的作用下，A 和B 一起向右加速运动，则B 对A 的静摩擦力做正功，A 对B 的静摩擦力做负功。
可见静摩擦力做功的特点是： （1）静摩擦力可以做正功，也可以做负功，还可以不做功。
（2）相互作用的一对静摩擦力做功的代数和总等于零。
（3）在静摩擦力做功的过程中，只有机械能的相互转移（静摩擦力起着传递机械能的作用），而没有机械能转化为其它形式的能。
一对相互作用的静摩擦力做功的代数和必为零，即对相互有静摩擦力作用的两物体A 和B 来说，A 对B 的摩擦力和B 对A 的摩擦力是一对作用力和反作用力：大小相等，方向相反。
由于两物体相对静止，其对地位移必相同，所以这一对静摩擦力一个做正功，一个做负功，且大小相等，其代数和必为零， 即例1. 如图1所示，物体在水平拉力下静止在粗糙水平面上，物体与桌面间有静摩擦力，该摩擦力不做功。
图1如图2所示，光滑水平面上物体A 、B 在外力F 作用下能保持相对静止地匀加速运动，则在此过程中，A 对B 的静摩擦力对B 做正功。
FA5-15-1图FAB 5152图－－图2如图3所示，物体A、B以初速度滑上粗糙的水平面，能保持相对静止地减速运动，则在此过程中A对B的静摩擦力对B做负功。
图3例2. 在光滑的水平地面上有质量为M的长平板A（如图4），平板上放一质量的物体B，A、B之间动摩擦因数为。
今在物体B上加一水平恒力F，B和A发生相对滑动，经过时间，求：（1）摩擦力对A所做的功；（2）摩擦力对B所做的功；（3）若长木板A固定时B对A的摩擦力对A做的功。
解析（1）平板A在滑动摩擦力的作用下，向右做匀加速直线运动，经过时间，A的位移为因为摩擦力的方向和位移相同，即对A做正功，其大小为。
（2）物体B在水平恒力F和摩擦力的合力作用下向右做匀加速直线运动，B的位移为摩擦力方向和位移方向相反，所以对B做负功为。
（3）若长木板A固定，则A的位移，所以摩擦力对A做功为0，即对A不做功。
2.滑动摩擦力做功的特点滑动摩擦力做功与路程有关，其值等于滑动摩擦力的大小和物体沿接触面滑动的路程的乘积，即例3. 滑雪者从山坡上A点由静止出发自由下滑，设动摩擦因数为常数，他滑到B点时恰好停止，此时水平位移为（如图5所示）。
求 A、B两点间的高度差。
图5解析：设滑雪者质量为，取一足够小的水平位移，对应的滑行路线可视为小直线段，该处滑雪者所受的摩擦力为所以在段摩擦力所做的功为对滑行路线求和可得摩擦力的总功从A到B的过程中，重力做功，而动能的变化为，所以由动能定理得，即，可解得A、B两点间的高度差为。
一对滑动摩擦力做功的代数和必不为零，且等于滑动摩擦力的大小与两物体间相对位移的乘积，即例4. 如图6，一质量为M的木板，静止在光滑水平面上，一质量为的木块以水平速度滑上木板。
由于木块和木板间有摩擦力，使得木块在木板上滑动一段距离后就跟木板一起以相同速度运动。
试求此过程中摩擦力对两物体做功的代数和。
图6解析：设木块与木板的共同速度为，以木块和木板整体为研究对象，则由动量守恒定律可得①摩擦力对木板做正功，对木块做负功。
由动能定理得②③由①②③可知，摩擦力对两物体做功的代数和为④上式即表明：一对滑动摩擦力做功的代数和必不为零，且等于滑动摩擦力的大小与两物体间的相对位移的乘积。
对于与外界无能量交换的孤立系统而言，滑动摩擦产生的热等于滑动摩擦力的大小与两物体间相对路程的乘积，即例5. 如图7（a）所示，质量为的木板静止在光滑水平面上，板的右端放一质量为的小铁块，现给铁块一个水平向左速度，铁块在木板上滑行，与固定在木板左端的水平轻弹簧相碰后又返回，且恰好停在木板右端，求整个过程中，系统机械能转化为能的多少？图7解析：在铁块运动的整个过程中，系统的动量守恒，因此弹簧压缩到最短时和铁块最终停在木板右端对系统的共同速度（铁块与木板的速度相同），由动量守恒定律得代入数据得从开始滑动到弹簧压缩到最短的过程中（如图7b），摩擦力铁块做负功；摩擦力对木板做正功从弹簧压缩最短到铁块最终停在木板右端的过程中（如图7c），摩擦力对铁块做正功；摩擦力对木板做负功故整个过程中，摩擦力做功的代数和为（弹簧力做功代数和为零）（式中就是铁块在木板上滑过的路程）根据动能定理有。
由功能关系可知，对于与外界无能量交换的孤立系统而言，系统克服摩擦力做功将这的动能转化为了系统的能，即，这表明滑动摩擦产生的热等于滑动摩擦力的大小与两物体间相对路程的乘积。
系统机械能的损失等于滑动摩擦力的大小与两物体间的相对位移的乘积，即例6. 设木块与木板间的摩擦系数为，则木块在木板上滑动过程中，在摩擦力作用下，木板做匀加速运动，木块做匀减速运动直至达到共同速度为止。
图8以木块和木板整体为研究对象，由动量守恒定律可得这一过程中，木板的位移为木块的位移为摩擦力对木板做正功对木块做负功则摩擦力对两物体做功的代数和为①整个过程中木板动能的增量为木块动能的增量为系统动能的总增量为②上述①、②表明：系统机械能的减少刚好与一对摩擦力做功的代数和的绝对值对等。
静摩擦力可以做正功，也可以做负功，还可以不做功。
如图5－15－3，物块A 在水平桌面上，在外力F 的作用下向右运动，桌面对A 向左的滑动摩擦力做负功，A 对桌面的滑动摩擦力不做功。
如图5－15－4，上表面不光滑的长木板，放在光滑的水平地面上，一小铁块以速度v 从木板的左端滑上木板，当铁块和木板相对静止时木板相对地面滑动的距离为s ，小铁块相对木板滑动的距离为d ，滑动摩擦力对铁块所做的功为：W 铁＝－f(s+d)―――①根据动能定理，铁块动能的变化量为：k w =f s+d E ∆铁铁＝－（）―――②②式表明，铁块从开始滑动到相对木板静止的过程中，其动能减少。
那么，铁块减少的动能转化为什么能量了呢？以木板为研究对象，滑动摩擦力对木板所做的功为：w fs 板＝――――――③ 根据动能定理，木板动能的变化量为：k E w fs ∆板板＝＝――④④式表明木板的动能是增加的，由于木板所受摩擦力的施力物体是铁块，可见木块减小的动能有一部分（fs ）转化为木板的动能。
将②、④两式相加得：k k E E fd ∆∆物板＋＝－―――――――⑤⑤式表明铁块和木板组成的系统的机械能的减少量等于滑动摩擦力与铁块相对木板FA 5153图－－0sd5154图－－的位移的乘积，这部分能量转化为系统的能。
综上所述，滑动摩擦力做功有以下特点：①滑动摩擦力可以对物体做正功，也可以对物体做负功，还可以不做功。
②相互摩擦的系统，一对滑动摩擦力所做的功总为负值，其绝对值等于滑动摩擦力与相对位移的乘积，且等于系统损失的机械能。
③一对滑动摩擦力做功的过程中，能量的转化有两种情况：一是相互摩擦的物体间机械能的转移；二是机械能转化为能。
滑动摩擦力、空气阻力等，在曲线运动或者往返运动时所做的功等于力和路程（不是位移）的乘积。
3.摩擦生热摩擦生热是指滑动摩擦生热，静摩擦不会生热。
产生的热Q 等于系统机械能的减少，又等于滑动摩擦力乘以相对位移，即Q=fd=E ∆机 【案例剖析】例.如图5－15－5，质量为M 的足够长的木板，以速度0v 在光滑的水平面上向左运动，一质量为m （M m 〉）的小铁块以同样大小的速度从板的左端向右运动，最后二者以共同的速度013v v =做匀速运动。
若它们之间的动摩擦因数为μ。
求：（1）小铁块向右运动的最大距离为多少？ （2）小铁块在木板上滑行多远？【解析】小铁块滑上木板后，由于铁块相对木板向右滑动，铁块将受到向左的滑动摩擦力作用而减速，木板将受到向右的滑动摩擦力作用而减速。
由于M m 〉，所以当m 的速度减为零时，M 仍有向左的速度，m 相对于M 仍向右滑行，m 将在向左的滑动摩擦力作用下相对地面向左做初速为零的匀加速运动，木板M 继续向左减速，直到二者达到相同的速度，而后保持相对静止一起向左匀速运动。
正确理解“小铁块向右运动的最大距离”和“在木板上滑行距离”的区别是解决问题的关键。
（答案：（1）2012v s g μ=；（2）204()9v M m L mgμ+=）3.综合分析例 1、一传送带以速度v o 匀速运行，左端上方有一漏斗，单位时间漏下的砂子质量恒定，即（恒量），设传送带足够长，求传送带运行功率P=？v 0v Mm5155图－－解析：砂子在水平方向靠摩擦力作功，使砂子获得动能设△t时间落在带上砂子质量为△m。
依功能关系。
在△t砂子获得能量的功率在这段时间砂子的位移带的位移 s2=v o△t其相对位移△s=s2-s1=s1部分机械能转化的能△E=f△s=s1f=W1传送带消耗的功率为砂子获得功率与转化的热功率之和例 2、如图所示，一小木块以初速v0=10m/s，沿倾角为30°的固定斜面向上运动，木块与斜面间的滑动摩擦因数为，求木块上升的最大高度。
（方法一）：设木块上升的最大高度为 h，此时木块速度为零，由功能关系，系统的机械能改变量为。
其值应等于合外力做的功。
有（方法二）：用动能定理 W=E k2-E k1(方法一)错解的错因是：关于重力功应等于其重力势能变化，不能同时考虑，否则重复了。
方法一中：合外力功不应包括重力或弹力功，（它不会转移机械能。
）方法二中：合外力功为所有外力功。
例 3、如图所示，质量为m的物体（可视为质点）以水平速度v0滑上原来静止在光滑水平面上质量为M的小车上，物体与小车之间的动摩擦因数为μ，小车足够长。
求：（1）物体从滑上小车到相对小车静止所经历的时间；（2）物体相对小车滑行的距离；（3）到物体相对小车静止时，小车通过的距离。
解析：物体滑上小车后，物体受到向后的摩擦力为 f＝mg而做匀减速直线运动，小车受到向前的摩擦力为f＝mg而做匀加速直线运动，物体相对小车静止时，物体与小车以相同的速度v共做匀速直线运动。
（1）由于物体加速度为摩擦力产生，有mg＝ma1∴a1＝g.小车加速度为 a2＝mg/M. v共＝v0－gt＝∴ t＝∴v共＝（2）物体相对小车的位移L可由一对摩擦力做的总功（即摩擦力与相对位移的乘积）等于系统机械能的增量求得，即：W f＝-mgL,△E＝可解得： L＝。
也可对物体和小车分别用动能定理，列出二式进行联立求解。
（3）对小车用动能定理可求出小车对地位移s:得： s＝.例 4、一木块静止在光滑水平桌面上，被水平飞来的子弹击中，并未穿出，深入深度为d，此过程木块位移为s2，子弹位移为s1，（子弹阻力恒为f），则：A．子弹损失的动能为fs1. B．子弹损失的动能为fd.C．系统增加的能为fd. D．子弹对木块做的功为fs2.E．子弹损失的动能等于木块获得的动能解析：由动能定理，子弹对木块做的功等于木块动能的改变量 W1＝fs2＝M.阻力对子弹做的功 W2＝－fs1＝－.其系统机械能损失△E=Q=综合上述分析，正确选项为 A、C、D。