初一平面直角坐标系动点问题(经典难题)

合集下载

(完整版)初一平面直角坐标系动点问题(经典难题)

(1)求点C，D的坐标及四边形ABDC的面积
(2)在y轴上是否存在一点P，连接PA，PB，使＝，
若存在这样一点，求出点P的坐标，若不存在，试说明理由．
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）给出下列结论：的值不变，的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．
5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣ ）（﹣9，）…根据你发现的规律，第100个有序数对是．
6、观察下列有规律的点的坐标：
依此规律，A11的坐标为，A12的坐标为．
7、以0为原点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系，一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2，再向正西方向走9米到达A3，再向正南方向走12米到达A4，再向正东方向走15米到达A5，按此规律走下去，当机器人走到A6时，A6的坐标是．
平面直角坐标系动点问题
（一）找规律
1．如图1，一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）
图1
A．（4，0）B．（5，0）C．（0，5）D．（5，5）
（1）汽车行驶到什么位置时离A村最近？写出此点的坐标．
（2）汽车行驶到什么位置时离B村最近？写出此点的坐标．
（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？
4．如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．

七年级平面直角坐标系动点规律问题(经典难题)

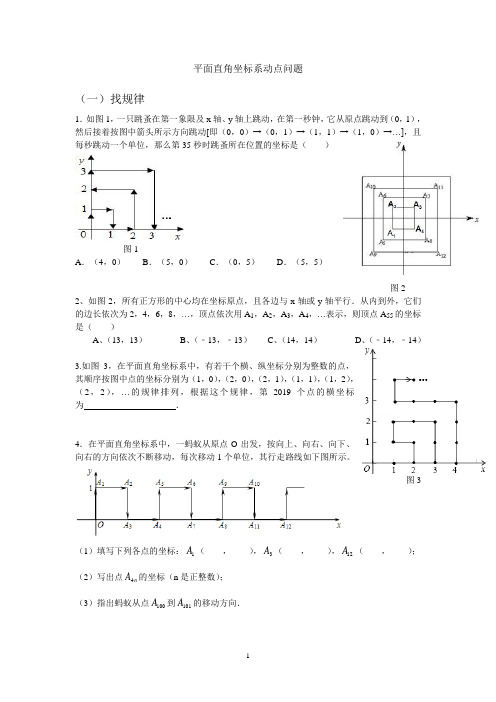
平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A ．（4，0）B ．（5，0）C ．（0，5）D ．（5，5）图22、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（） A 、（13，13） B 、（﹣13，﹣13） C 、（14，14） D 、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2019个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3（1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是．6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次，点P 依次落在点201921,,,P P P 的位置，则点2019P 的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2019次跳动至点P 2019的坐标是．图4 图5 10、如图5，已知A l （1，0），A 2（1，1），A 3（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2019的坐标为．1PAOyxP1. 如图，一个粒子在第一象限内及x 、y 轴上运动，在第一分钟内它从原点运动到()1,0，而后它接着按图所示在x 轴、y 轴平行的方向上来回运动，且每分钟移动1个长度单位，那么，在1989分钟后这个粒子所处的位置是（）．A ．()35,44B ．()36,45C ．()37,45D ．()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合，那么称点P 与点Q 关于点M 对称，定点M 叫做对称中心，此时，点M 是线段PQ 的中点，如图，在直角坐标系中，ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0，点1P ，2P ，3P ，…中相邻两点都关于ABO △的一个顶点对称，点1P 与点2P 关于点A 对称，点2P 与点3P 关于点B 对称，点3P 与点4P 关于点O 对称，点4P 与点5P 关于点A 对称，点5P 与点6P 关于点B 对称，点6P 与点7P 关于点O 对称，…对称中心分别是A ，B ，O ，A ，B ，O ，…且这些对称中心依次循环，已知1P 的坐标是()1,1．试写出点2P 、7P 、100P 的坐标．3. 如图，在平面直角坐标系中，四边形各顶点的坐标分别为：()0,0A ，()7,0B ，()9,5C ，()2,7D ．（1）求此四边形的面积．（2）在坐标轴上，你能否找到一点P ，使50PBC S =△?若能，求出P 点坐标；若不能，请说明理由．4. 如图①，已知OABC 是一个长方形，其中顶点A 、B 的坐标分别为()0,a 和()9,a ，点E在AB 上，且13AE AB =，点F 在OC 上，且13OF OC =．点G 在OA 上，且使GEC △的面积为20，GFB △的面积为16，试求a 的值．图②5. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如()1,0，()2,0，()2,1，()1,1，()1,2，()2,2……根据这个规律，第2019个点的横坐标为_______．6. 在平面直角坐标系xOy 中，我们把横、纵坐标都是整数的点叫做整点．已知点()0,4A ，点B 是x 轴正半轴上的整点，记AOB △内部（不包括边界）的整点个数为m ，当3m =时，点B 的横坐标的所有可能值是_______；当点B 的横坐标为4n （n 为正整数）时，m =________（用含n 的代数式表示）．7. 如图，把自然数按图的次序排在直角坐标系中，每个自然数都对应着一个坐标．如1的对应点是原点()0,0，3的对应点是()1,1，16的对应点是()1,2-，那么2019的对应点的坐标是_______．8．如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙由点()2,0A 同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以每秒1个单位长度的速度匀速运动，物体乙按顺时针方向以每秒2个单位长度的速度匀速运动，求两个物体开始运动后的第2019次相遇地点的坐标．9. 在平面直角坐标系中，如图①，将线段AB 平移至线段CD ，连接AC 、BD ．（1）直接写出图中相等的线段、平行的线段；（2）已知()3,0A -、()2,2B --，点C 在y 轴的正半轴上．点D 在第一象限内，且5ACD S =△，求点C 、D 的坐标；（3）如图②，在平面直角坐标系中，已知一定点，()1,0M ，两个动点(),21E a a +、(),23F b b -+，请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM ．若存在，求以点O 、M 、E 、F 为顶点的四边形的面积，若不存在，请说明理由．图②10 . 如图，AOCD 是放置在平面直角坐标系内的梯形，其中O 是坐标原点．点A 、C 、D 的坐标分别为()0,8，()5,0，()3,8，若点P 在梯形内，且PAD POC S S =△△，PAO PCD S S =△△，求P 点的坐标．11. 操作与研究（1）对数轴上的点P 进行如下操作：先把点P 表示的数乘以13，再把所得数对应的点向右平移1个单位，得到点P 的对应点'P B ．点A ，B 在数轴上，对线段AB 上的每个点进行上述操作后得到线段''A B ，其中点A ，B 的对应点分别为'A ，'B ．如图①，若点A 表示的数是3-，则点'A 表示的数是______；若点'B 表示的数是2，则点表示的数是______；已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合，则点E 表示的数是_________．（2）如图②，在平面直角坐标系xOy 中，对正方形ABCD 及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a ，将得到的点先向右平移m 个单位，再向上平移n 个单位()0,0m n >>，得到正方形''''A B C D 及其内部的点，其中点A ，B 的对应点分别为'A ，'B ．已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合，求点F 的坐标．图①A B'-1-2-3-412340图②（二）几何综合问题1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标2、如图，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．(3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）给出下列结论：①DCP BOP CPO ∠+∠∠的值不变，②DCP CPOBOP∠+∠∠的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°，AB ∥CD ,AB =CD =8cm ，AD =BC =6cm ，D 点与原点重合，坐标为(0,0). （1）写出点B 的坐标.（2）动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?（3）在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b 满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ONF的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

平面直角坐标系。动点问题。好

平面直角坐标系。

动点问题。

好平面直角坐标系动点问题已知平面直角坐标系中，点A(4,0)，点B(0,3)，点P从点A出发，以每秒1个单位的速度在x轴上向右平移，点Q从B 点出发，以每秒2个单位的速度沿直线y=3向右平移，又P、Q两点同时出发，设运动时间为t秒。

1) 求当t为多少时，四边形OBPQ的面积为8.首先，可以求出四边形OBPQ的坐标：O(0,0)，B(0,3)，P(4+t,0)，Q(2t,3)。

由于四边形OBPQ是平行四边形，所以它的面积可以用它的对角线之积来表示：S(OBPQ) = |OB| × |PQ|× sinθ。

其中，|OB| = 3，|PQ| = √[(4+t-2t)²+3²] = √(t²+16)，θ是OB与PQ之间的夹角。

由于OB与PQ平行，所以θ = 0，sinθ = 0，因此S(OBPQ) = 0.所以，四边形OBPQ的面积始终为0，无法等于8，因此无解。

2) 连接AQ，当△APQ是直角三角形时，求Q的坐标。

由于△APQ是直角三角形，所以根据勾股定理，有AP²+PQ² = AQ²。

又因为AP = 4+t，PQ = 3-2t，所以可以列出方程：(4+t)² + (3-2t)² = AQ²。

化简后得到：AQ² = 25-8t+5t²。

又因为Q在直线y=3上，所以可以列出另一个方程：yQ = 3.将Q的坐标表示为(xQ。

yQ)，则有xQ² + yQ² = AQ²，代入上面的方程，得到xQ² + 9 = 25-8t+5t²，化简后得到：xQ² = 16-8t+5t²。

因为Q在第二象限，所以xQ<0，因此xQ = -√(16-8t+5t²)，yQ = 3.所以Q的坐标为(-√(16-8t+5t²)。

七年级下册数学平面直角坐标系中的动点问题

1.如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．(3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）给出下列结论：①DCP BOP CPO ∠+∠∠的值不变，②DCP CPOBOP∠+∠∠的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．2.如图，在长方形OABC 中，O 为平面直角坐标系的原点，点A 的坐标为（4，0），点C 的坐标为（0,6），点B 在第一象限内，点P 从原点出发，以每秒2个单位长度的速度沿着 O —A —B —C —O 的路线移动（即沿着长方形的边移动一周）. （1）点B 的坐标为_______________.（2）当点P 移动了4秒时，描出此时点P 的位置，并求出点P 的坐标；（3）在移动过程中，当点P 到x 轴的距离为5个单位长度时，求点P 移动的时间.3.如图，在平面直角坐标系中，四边形OABC 为正方形，A 点在x 轴负半轴上，C 点在y 轴负半轴上，边长为4，有一动点P 自O 点出发，以每秒2个单位长度的速度沿O —A —B —C —O 运动，则何时S △PBC =4？并求出此时P 点的坐标.4 ．如图， △ A BO 的三个顶点的坐标分别为 O ( 0 ， 0 ) ， A ( 5 ， 0 ) ， B ( 2 ， 4 ) ．( 1 ) 求 △O AB 的面积； ( 2 ) 若 O ， B 两点的位置不变，点 M 在 x 轴上，则点 M 在什么位置时， △O BM 的面积是 △ O AB 的面积的 2 倍？ ( 3 ) 若 O ， A 两点的位置不变，点 N 由点 B 向上或向下平移得到，则点 N 在什么位置时， △O AN 的面积是 △ O AB 的面积的 2 倍？ O AB C yA B C O yP。

七年级下册数学动点问题及压轴题(带答案)

七年级下册动点问题及压轴题1．如图1，在平面直角坐标系中，A（a，0）是x轴正半轴上一点，C是第四象限一点，CB⊥y轴，交y轴负半轴于B（0，b），且（a﹣3）2+|b+4|=0，S四边形AOBC=16．（1）求C点坐标；（2）如图2，设D为线段OB上一动点，当AD⊥AC时，∠ODA的角平分线与∠CAE 的角平分线的反向延长线交于点P，求∠APD的度数．（3）如图3，当D点在线段OB上运动时，作DM⊥AD交BC于M点，∠BMD、∠DAO的平分线交于N点，则D点在运动过程中，∠N的大小是否变化？若不变，求出其值，若变化，说明理由．【解答】解：（1）∵（a﹣3）2+|b+4|=0，∴a﹣3=0，b+4=0，∴a=3，b=﹣4，∴A（3，0），B（0，﹣4），∴OA=3，OB=4，∵S四边形AOBC=16．∴（OA+BC）×OB=16，∴（3+BC）×4=16，∴BC=5，∵C是第四象限一点，CB⊥y轴，∴C（5，﹣4）（2）如图，延长CA，∵AF是∠CAE的角平分线，∴∠CAF=∠CAE，∵∠CAE=∠OAG，∴∠CAF=∠OAG，∵AD⊥AC，∴∠DAO+∠OAG=∠PAD+∠PAG=90°，∵∠AOD=90°，∴∠DAO+∠ADO=90°，∴∠ADO=∠OAG，∴∠CAF=∠ADO，∵DP是∠ODA的角平分线∴∠ADO=2∠ADP，∴∠CAF=∠ADP，∵∠CAF=∠PAG，∴∠PAG=∠ADP，∴∠APD=180°﹣（∠ADP+∠PAD）=180°﹣（∠PAG+∠PAD）=180°﹣90°=90°即：∠APD=90°（3）不变，∠ANM=45°理由：如图，∵∠AOD=90°，∴∠ADO+∠DAO=90°，∵DM⊥AD，∴∠ADO+∠BDM=90°，∴∠DAO=∠BDM，∵NA是∠OAD的平分线，∴∠DAN=∠DAO=∠BDM，∵CB⊥y轴，∴∠BDM+∠BMD=90°，∴∠DAN=（90°﹣∠BMD），∵MN是∠BMD的角平分线，∴∠DMN=∠BMD，∴∠DAN+∠DMN=（90°﹣∠BMD）+∠BMD=45°在△DAM中，∠ADM=90°，∴∠DAM+∠DMA=90°，在△AMN中，∠ANM=180°﹣（∠NAM+∠NMA）=180°﹣（∠DAN+∠DAM+∠DMN+∠DMA）=180°﹣[（∠DAN+DMN）+（∠DAM+∠DMA）]=180°﹣（45°+90°）=45°，∴D点在运动过程中，∠N的大小不变，求出其值为45°2．如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．【考点】JB：平行线的判定与性质．【分析】（1）利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补，所以易证AB∥CD；（2）利用（1）中平行线的性质推知°；然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°，即EG⊥PF，故结合已知条件GH⊥EG，易证PF∥GH；（3）利用三角形外角定理、三角形内角和定理求得∠4=90°﹣∠3=90°﹣2∠2；然后由邻补角的定义、角平分线的定义推知∠QPK=∠EPK=45°+∠2；最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变，是定值45°．【解答】解：（1）如图1，∵∠1与∠2互补，∴∠1+∠2=180°．又∵∠1=∠AEF，∠2=∠CFE，∴∠AEF+∠CFE=180°，∴AB∥CD；（2）如图2，由（1）知，AB∥CD，∴∠BEF+∠EFD=180°．又∵∠BEF与∠EFD的角平分线交于点P，∴∠FEP+∠EFP=（∠BEF+∠EFD）=90°，∴∠EPF=90°，即EG⊥PF．∵GH⊥EG，∴PF∥GH；（3）∠HPQ的大小不发生变化，理由如下：如图3，∵∠1=∠2，∴∠3=2∠2．又∵GH⊥EG，∴∠4=90°﹣∠3=90°﹣2∠2．∴∠EPK=180°﹣∠4=90°+2∠2．∵PQ平分∠EPK，∴∠QPK=∠EPK=45°+∠2．∴∠HPQ=∠QPK﹣∠2=45°，∴∠HPQ的大小不发生变化，一直是45°．3.如图①，在矩形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A→B→C→D 路线运动，到D停止，点P的速度为每秒1cm，a秒时点P改变速度，变为每秒bcm，图②是点P出发x秒后△APD的面积S（cm2）与x（秒）的关系图象，（1）参照图②，求a、b及图②中的c值；（2）设点P离开点A的路程为y（cm），请写出动点P改变速度后y与出发后的运动时间x（秒）的关系式，并求出点P到达DC中点时x的值．（3）当点P出发多少秒后，△APD的面积是矩形ABCD面积的．4．星光橱具店购进电饭煲和电压锅两种电器进行销售，其进价与售价如表：进价（元/台）售价（元/台）电饭煲200250电压锅160200（1）一季度，橱具店购进这两种电器共30台，用去了5600元，并且全部售完，问橱具店在该买卖中赚了多少钱？（2）为了满足市场需求，二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的，问橱具店有哪几种进货方案？并说明理由；（3）在（2）的条件下，请你通过计算判断，哪种进货方案橱具店赚钱最多？【考点】一元一次不等式组的应用；二元一次方程组的应用．【分析】（1）设橱具店购进电饭煲x台，电压锅y台，根据图表中的数据列出关于x、y的方程组并解答即可，等量关系是：这两种电器共30台；共用去了5600元；（2）设购买电饭煲a台，则购买电压锅（50﹣a）台，根据“用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的”列出不等式组；（3）结合（2）中的数据进行计算．【解答】解：（1）设橱具店购进电饭煲x台，电压锅y台，依题意得，解得，所以，20×+10×=1400（元）．答：橱具店在该买卖中赚了1400元；（2）设购买电饭煲a台，则购买电压锅（50﹣a）台，依题意得，解得22≤a≤25．又∵a为正整数，∴a可取23，24，25．故有三种方案：①防购买电饭煲23台，则购买电压锅27台；②购买电饭煲24台，则购买电压锅26台；③购买电饭煲25台，则购买电压锅25台．（3）设橱具店赚钱数额为W元，当a=23时，W=23×+27×=2230；当a=24时，W=24×+26×=2240；当a=25时，W=25×+25×=2250；综上所述，当a=25时，W最大，此时购进电饭煲、电压锅各25台．5．（本题12分）已知：在平面直角坐标系中，直线AB 分别与x 轴负半轴、y 轴正半轴交于点B (b ，0)、点A (0，a )，且a 、b 满足0|32|34=++++--b a b a ，点D (h ，m )是直线AB 上且不与A 、B 两点重合的动点(1) 求△AOB 的面积;(2) 如图1，点P 、点T 分别是线段OA 、x 轴正半轴上的动点，过T 作TE ∥AB ，连接TP ．若∠ABO ＝n °，请探究∠APT 与∠PTE 之间的数量关系？（注：可用含n 的式子表达并说明理由）(3) 若32S △BOD ≥S △AOD ，求出m 的取值范围.。

动点问题经典例题

动点问题经典例题在数轴上，点A从原点出发，以每秒2个单位长度的速度向右运动，同时点B也从原点出发，以每秒3个单位长度的速度向左运动。

经过5秒，A、B两点之间的距离是多少？A. 5个单位长度B. 10个单位长度C. 15个单位长度D. 25个单位长度在一条直线上，甲车以每小时40千米的速度从A地出发向B地行驶，同时乙车以每小时60千米的速度从B地出发向A地行驶。

若A、B两地相距200千米，则两车相遇时，它们各自行驶了多少千米？A. 甲车100千米，乙车100千米B. 甲车80千米，乙车120千米C. 甲车120千米，乙车80千米D. 甲车60千米，乙车140千米在平面直角坐标系中，点P从原点出发，沿x轴正方向以每秒1个单位长度的速度移动。

同时，点Q从点(0,4)出发，沿y轴负方向以每秒2个单位长度的速度移动。

当P、Q两点之间的距离达到5个单位长度时，它们各自移动了多少秒？A. 1秒B. 2秒C. 3秒D. 4秒在一条环形跑道上，甲、乙两人同时同地同向出发进行跑步比赛。

甲的速度是每分钟400米，乙的速度是每分钟500米。

经过多少分钟，两人会再次相遇？A. 1分钟B. 5分钟C. 10分钟D. 无法确定在数轴上，点A和点B分别表示-3和7。

点A以每秒2个单位长度的速度向右移动，同时点B以每秒1个单位长度的速度向左移动。

经过多少秒，A、B两点之间的距离为15个单位长度？A. 2秒B. 4秒C. 6秒D. 8秒在平面直角坐标系中，点A从(0,0)出发，沿x轴正方向以每秒1个单位长度的速度移动。

同时，点B从(4,0)出发，沿x轴负方向以每秒2个单位长度的速度移动。

当A、B两点之间的距离为2个单位长度时，它们各自移动了多少秒？A. 1秒B. 1.5秒C. 2秒D. 2.5秒在一条直线上，甲、乙两人相距100米，甲以每秒6米的速度向乙走去，乙以每秒4米的速度向甲走来。

经过多少秒，甲、乙两人会相遇？A. 5秒B. 10秒C. 15秒D. 20秒在平面直角坐标系中，点P从原点出发，沿x轴正方向以每秒2个单位长度的速度移动。

七年级下册数学压轴题训练——坐标系动态问题

压轴题训练——坐标系动态问题1．如图，在平面直角坐标系中，A（4，0），B（0，4），C是第一象限内一点，且BC∥x轴．（1）连接AC，当S∥ABC＝6时，求点C的坐标；（2）设D为y轴上一动点，连接AD，CD，作∥BCD、∥DAO的平分线相交于点P，在点D的运动过程中，试判断等式∥CPA＝2∥CDA是否始终成立，并说明理由．2．如图,在直角坐标系中,点A．C分别在x轴、y轴上,CB∥OA，OA=8,若点B的坐标为(4,4).(1)直接写出点A，C的坐标；(2)动点P从原点O出发沿x轴以每秒2个单位的速度向右运动，当直线PC把四边形OABC分成面积相等的两部分时停止运动，求P点运动时间；(3)在(2)的条件下，点P停止运动时，在y轴上是否存在一点Q，连接PQ，使三角形CPQ的面积与四边形OABC 的面积相等?若存在，求点Q的坐标；若不存在，请说明理由。

3．如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b﹣6|=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O 的线路移动．（1）a=，b=，点B的坐标为；（2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标；（3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．4．已知点A（1，a），将线段OA平移至线段BC，B（b，0），a是m+6n＝3，n，且m ＜n，正数b满足（b+1）2＝16．（1）直接写出A、B两点坐标为：A，B；（2）如图1，连接AB、OC，求四边形AOCB的面积；（3）如图2，若∥AOB＝a，点P为y轴正半轴上一动点，试探究∥CPO与∥BCP之间的数量关系．5．如图1,在平面直角坐标系中，点A(a，0)，B(0，b),且a、b2(2)0a b++=.(1)请直接写出A、B两点的坐标：点A为_______,点B为________.(2)若点P的坐标为(-2，n)，且三角形PAB的面积为7，求n的值.(3)如图2，过点B作BC//x轴，点Q为x轴上点A左侧的一动点，连结QB，BM平分∥QBA，BN平分∥CBA，当点Q运动时，∥MBN:∥AQB的值是否发生变化？如果变化，请说明理由；如果不变，请求出其值.6．如图1，在平面直角坐标系中，点A为x轴负半轴上一点，点B为x轴正半轴上一点，C(0，a)，D(b，a)，其中a，b满足关系式：|a+3|+(b-a+1)2=0.（1）a=___，b=___，∥BCD的面积为______；（2）如图2，若AC∥BC，点P线段OC上一点，连接BP，延长BP交AC于点Q，当∥CPQ=∥CQP时，求证:BP 平分∥ABC；（3）如图3，若AC∥BC，点E是点A与点B之间一动点，连接CE,CB始终平分∥ECF,当点E在点A与点B之间运动时，BECBCO∠∠的值是否变化？若不变，求出其值；若变化，请说明理由.7．如图，以直角∥AOC 的直角顶点O 为原点，以OC ，OA 所在直线为x 轴和y 轴建立平面直角坐标系，点A （0，a ），C （b ，080b +-=．（1）点A 的坐标为________；点C 的坐标为________．（2）已知坐标轴上有两动点P ，Q 同时出发，P 点从C 点出发沿x 轴负方向以每秒2个单位长度的速度匀速移动，Q 点从O 点出发沿y 轴正方向以每秒1个单位长度的速度匀速移动，点P 到达O 点整个运动随之结束．AC 的中点D 的坐标是（4，3），设运动时间为t 秒．问：是否存在这样的t ，使得∥ODP 与∥ODQ 的面积相等？若存在，请求出t 的值；若不存在，请说明理由．（3）在（2）的条件下，若∥DOC=∥DCO ，点G 是第二象限中一点，并且y 轴平分∥GOD ．点E 是线段OA 上一动点，连接接CE 交OD 于点H ，当点E 在线段OA 上运动的过程中，探究∥GOA ，∥OHC ，∥ACE 之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．8．如图，在平面直角坐标系中，点A 、B 分别是x 轴、y 轴上的点，且OA=a ，OB=b ，其中a 、b 满足|a ﹣20|+（﹣2b+a ﹣8）2=0，将点B 向左平移16个单位长度得到点C ．（1）求点A 、B 、C 的坐标；（2）如图，点M 为线段BC 上的一个动点，点F 在x 轴的正半轴上，点E 、D 在直线BC 上，∥FOE=23∥MOF ，∥MOD=13∥BOM ．请问当点M 运动时，∥DOE 的大小是否发生变化？如果变化请说明理由；如果不变，求出其大小；（3）如图2，当点M 从点B 以1个单位长度/秒的速度向左运动时，线段OA 上的动点N 同时从点A 以2个单位长度/秒的速度向右运动，设运动时间为t 秒（0＜t≤10）．是否存在某个时间，使得S 四边形NACM ＜12S 四边形BOAC ？若存在，求出t 的取值范围；若不存在，说明理由．9．如图1，在平面直角坐标系中，A（a，0）是x轴负半轴上一点，C是第三象限内一点，CB∥y轴交y轴负半轴于B（0，b），且|a+3|+(b+4)2=0，S四边形AOBC=16．（1）求点A、B、C的坐标；（2）如图2，设D为线段OB上一动点，当AD∥AC时，∥ODA的平分线与∥CAN的平分线的反向延长线交于点E，求∥AED的度数（点N在x轴的负半轴）；（3）如图3，当点D在线段OB上运动时，作DP∥AD交BC于P点，∥BPD、∥DAO的平分线交于Q点，则点D 在运动过程中，∥Q的大小是否会发生变化？若不变化，求出其值；若变化，请说明理由．．10．如图，已知点A（﹣m，n），B（0，m），且m、n（n﹣5）2=0，点C在y轴上，将∥ABC沿y 轴折叠，使点A落在点D处．（1）写出D点坐标并求A、D两点间的距离；（2）若EF平分∥AED，若∥ACF﹣∥AEF=20°，求∥EFB的度数；（3）过点C作QH平行于AB交x轴于点H，点Q在HC的延长线上，AB交x轴于点R，CP、RP分别平分∥BCQ 和∥ARX，当点C在y轴上运动时，∥CPR的度数是否发生变化？若不变，求其度数；若变化，求其变化范围．11．如图，在平面直角坐标系中，点A，B的坐标为（a，0），（0，b），且满足（a﹣4）2＝0，现将OA平移到BC的位置，连接AC，点P从点B出发，沿BC﹣CA运动，速度为每秒1个单位长度，设运动时间为t 秒．（1）求出a和b的值，并写出点C的坐标；（2）求点P在运动过程中的坐标（用含t的式子表示）．（3）点Q以每秒3.5个单位长度的速度从点A出发，在AO间往返运动，（两个点同时出发，当点P到达点A停止时点Q也停止），在运动过程中，直接写出当PQ∥OB时，点P的坐标．12．如图，在平面直角坐标系中，已知点A（0，4），B（3，0），线段AB平移后对应的线段为CD，点C在x轴的负半轴上，B、C两点之间的距离为8．（1）求点D的坐标；（2）如图（1），求∥ACD的面积；（3）如图（2），∥OAB与∥OCD的角平分线相交于点M，探求∥AMC的度数并证明你的结论．。

动点问题一

动点问题（一）【解题关键】抓住变化中的不变量、不变关系，化动为静．【经典例题】例1．如图，平面直角坐标系中，四边形OABC 为矩形，点A B ，的坐标分别为(40)43()，，，，动点M N ，分别从O B ，同时出发，以每秒1个单位的速度运动．其中，点M 沿OA 向终点A 运动，点N 沿BC 向终点C 运动，过点M 作MP OA ⊥，交AC 于P ，连结NP ，已知动点运动了x 秒．（1）P 点的坐标为（，）（用含x 的代数式表示）；（2）试求NPC △面积S 的表达式，并求出面积S 的最大值及相应的x 值；（3）当x 为何值时，NPC △是一个等腰三角形？简要说明理由．例2．如图，正方形ABCD 的边长为1，点E 是AD 边上的动点，从点A 沿AD 向D 运动．．，以BE 为边，在BE 的上方作正方形BEFG ，连接CG 。

请探究：（1）线段AE 与CG 是否相等？请说明理由：（2）若设x AE =，y DH =，当x 取何值时，y 最大？（3）连接BH ，当点E 运动到AD 的何位置时，△BEH ∽△BAE ？Ｎ BA M PCO y x （第3题图）G例3．如图，在平面直角坐标系中，点A 、B 分别在x 轴、y 轴上，线段OA 、OB 的长(0A<OB) 是方程x 2-18x+72=0的两个根，点C 是线段AB 的中点，点D 在线段OC 上，OD=2CD ． (1)求点C 的坐标；(2)求直线AD 的解析式；(3)P 是直线AD 上的点，在平面内是否存在点Q ，使以0、A 、P 、Q 为顶点的四边形是菱形?若存在，请直接写出点Q 的坐标；若不存在，请说明理由．例4．如图，△OAB 是边长为23+的等边三角形，其中O 是坐标原点，顶点B 在y 轴正方向上，将△OAB 折叠，使点A 落在边OB 上，记为A ′，折痕为EF. （1）当A ′E//x 轴时，求点A ′和E 的坐标；（2）当A ′E//x 轴，且抛物线216y x bx c =-++经过点A ′和E 时，求抛物线与x 轴的交点的坐标；（3）当点A ′在OB 上运动，但不与点O 、B 重合时，能否使△A ′EF 成为直角三角形？若能，请求出此时点A ′的坐标；若不能，请你说明理由.例5．等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/s 的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交与点D．设P点运动时间为t，△PCQ的面积为S．(1)求出S关于t的函数关系式；(2)当点P运动几秒时，S△PCQ=S△ABC？(3)作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．QCDEB【拓展练习】1．已知：如图矩形ABCD中，AB=4m，BC=6m，E为BC的中点，动点P以每秒2m的速度从A 出发，沿着△AED的边，按照从A→E→D→A的顺序环行一周，设P从A出发经x秒后，△ABP 的面积为ym2，求y与x的函数关系式．2.如图，在ΔABC 中，AC ＝15，BC ＝18，sinC=45，D 是AC 上一个动点（不运动至点A ，C),过D 作DE ∥BC ，交AB 于E ，过D 作DF ⊥BC ，垂足为F ，连结 BD ，设 CD ＝x ．（1）用含x 的代数式分别表示DF 和BF ；（2）如果梯形EBFD 的面积为S ，求S 关于x 的函数关系式；（3）如果△BDF 的面积为S 1，△BDE 的面积为S 2，那么x 为何值时，S 1＝2S 2．3.如图：已知A 为∠POQ 的边OQ 上一点，以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点，且∠MAN ＝∠POQ ＝α（α为锐角），当∠MAN 以点A 为旋转中心，AM 边从与AO 重合的位置开始，按逆时针方向旋转（∠MAN 保持不变）时，M 、N 两点在射线OP 上同时以不同的速度向右平行移动，设OM ＝x ，ON ＝y （y ＞x ≥0），△AOM 的面积为S ，若αcos 、OA 是方程02522=+-z z 的两个根．（1）当∠MAN 旋转300（即∠OAM ＝300）时，求点N 移动的距离；（2）求证：MN ON AN ⋅=2（3）求y 与x 之间的函数关系式及自变量x 的取值范围；（4）试写出S 随x 变化的函数关系式，并确定S 的取值范围．αα第28题图PNMOAQ4．用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD .把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A 重合，两边分别与AB ，AC 重合.将三角尺绕点A 按逆时针方向旋转．（1）当三角尺的两边分别与菱形的两边BC ，CD 相交于点E ，F 时，（如图13—1），通过观察或测量BE ，CF 的长度，你能得出什么结论？并证明你的结论；（2）当三角尺的两边分别与菱形的两边BC ，CD 的延长线相交于点E ，F 时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由．5．如图，A 、B 是直线L 上的两点，AB =4厘米，过L 外一点C 作CD ∥L ，射线BC 与Ｌ所成的锐角∠1=60°，线段BC =2厘米，动点P 、Q 分别从B 、C 同时出发，P 以每秒1厘米的速度沿由B 向C 的方向运动，Q 以每秒2厘米的速度沿由C 向D 的方向运动．设P ，Q 运动的时间为t （秒），当t ＞2时，P A 交CD 于E ．（1）用含t 的代数式分别表示CE 和QE 的长．（2）求△APQ 的面积S 与t 的函数关系式．（3）当QE 恰好平分△APQ 的面积时，QE5、如图，四边形AOBC是菱形，点B的坐标为（4，0）。

七年级平面直角坐标系动点规律问题

平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A ．（4，0）B ．（5，0）C ．（0，5）D ．（5，5）图22、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（）A 、（13，13）B 、（﹣13，﹣13）C 、（14，14）D 、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2019个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3（1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是．6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次，点P 依次落在点201921,,,P P P 的位置，则点2019P 的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2019次跳动至点P 2019的坐标是．图4 图510、如图5，已知A l （1，0），A 2（1，1），A 3（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2019的坐标为．1. 如图，一个粒子在第一象限内及x 、y 轴上运动，在第一分钟内它从原点运动到()1,0，而后它接着按图所示在x 轴、y 轴平行的方向上来回运动，且每分钟移动1个长度单位，那么，在1989分钟后这个粒子所处的位置是（）．A ．()35,44B ．()36,45C ．()37,45D ．()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合，那么称点P 与点Q 关于点M 对称，定点M 叫做对称中心，此时，点M 是线段PQ 的中点，如图，在直角坐标系中，ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0，点1P ，2P ，3P ，…中相邻两点都关于ABO △的一个顶点对称，点1P 与点2P 关于点A 对称，点2P 与点3P 关于点B 对称，点3P 与点4P 关于点O 对称，点4P 与点5P 关于点A 对称，点5P 与点6P 关于点B 对称，点6P 与点7P 关于点O 对称，…对称中心分别是A ，B ，O ，A ，B ，O ，…且这些对称中心依次循环，已知1P 的坐标是()1,1．试写出点2P 、7P 、100P 的坐标．3. 如图，在平面直角坐标系中，四边形各顶点的坐标分别为：()0,0A ，()7,0B ，()9,5C ，()2,7D ．（1）求此四边形的面积．（2）在坐标轴上，你能否找到一点P ，使50PBC S =△若能，求出P 点坐标；若不能，请说明理由．4. 如图①，已知OABC 是一个长方形，其中顶点A 、B 的坐标分别为()0,a 和()9,a ，点E 在AB 上，且13AE AB =，点F 在OC 上，且13OF OC =．点G 在OA 上，且使GEC △的面积为20，GFB △的面积为16，试求a 的值．5. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如()1,0，()2,0，()2,1，()1,1，()1,2，()2,2……根据这个规律，第2019个点的横坐标为_______．6. 在平面直角坐标系xOy 中，我们把横、纵坐标都是整数的点叫做整点．已知点()0,4A ，点B 是x 轴正半轴上的整点，记AOB △内部（不包括边界）的整点个数为m ，当3m =时，点B 的横坐标的所有可能值是_______；当点B 的横坐标为4n （n 为正整数）时，m =________（用含n 的代数式表示）．7. 如图，把自然数按图的次序排在直角坐标系中，每个自然数都对应着一个坐标．如1的对应点是原点()0,0，3的对应点是()1,1，16的对应点是()1,2-，那么2019的对应点的坐标是_______．8．如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙由点()2,0A 同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以每秒1个单位长度的速度匀速运动，物体乙按顺时针方向以每秒2个单位长度的速度匀速运动，求两个物体开始运动后的第2019次相遇地点的坐标．9. 在平面直角坐标系中，如图①，将线段AB 平移至线段CD ，连接AC 、BD ．（1）直接写出图中相等的线段、平行的线段；（2）已知()3,0A -、()2,2B --，点C 在y 轴的正半轴上．点D 在第一象限内，且5ACD S =△，求点C 、D 的坐标；（3）如图②，在平面直角坐标系中，已知一定点，()1,0M ，两个动点(),21E a a +、(),23F b b -+，请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM ．若存在，求以点O 、M 、E 、F 为顶点的四边形的面积，若不存在，请说明理由．10 . 如图，AOCD 是放置在平面直角坐标系内的梯形，其中O 是坐标原点．点A 、C 、D 的坐标分别为()0,8，()5,0，()3,8，若点P 在梯形内，且PAD POC S S =△△，PAO PCD S S =△△，求P 点的坐标．11. 操作与研究（1）对数轴上的点P 进行如下操作：先把点P 表示的数乘以13，再把所得数对应的点向右平移1个单位，得到点P 的对应点'P B ．点A ，B 在数轴上，对线段AB 上的每个点进行上述操作后得到线段''A B ，其中点A ，B 的对应点分别为'A ，'B ．如图①，若点A 表示的数是3-，则点'A 表示的数是______；若点'B 表示的数是2，则点表示的数是______；已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合，则点E 表示的数是_________．（2）如图②，在平面直角坐标系xOy 中，对正方形ABCD 及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a ，将得到的点先向右平移m 个单位，再向上平移n 个单位()0,0m n >>，得到正方形''''A B C D 及其内部的点，其中点A ，B 的对应点分别为'A ，'B ．已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合，求点F 的坐标．（二）几何综合问题1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB x ABDC S 四边形PAB S ∆ABDC S 四边形DCP BOP CPO ∠+∠∠DCP CPO BOP∠+∠∠知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°，AB ∥CD ,AB =CD =8cm ，AD =BC =6cm ，D 点与原点重合，坐标为(0,0).（1）写出点B 的坐标.（2）动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC（3）在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9 求出此时Q 点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b 满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ON F的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

完整版)初一平面直角坐标系动点问题(经典难题)

完整版)初一平面直角坐标系动点问题(经典难题)一）找规律1.如图1，一只跳蚤在第一象限及x轴、y轴上跳动。

在第一秒钟，它从原点跳动到（0，1），然后按照箭头所示方向跳动（即（0，0）→（0，1）→（1，1）→（1，0）→…），每秒跳动一个单位。

那么第35秒时跳蚤所在位置的坐标是（4，1），因此答案为A。

2.如图2，所有正方形的中心都在坐标原点，且各边与x轴或y轴平行。

从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示。

顶点A55的坐标是（54，54），因此答案为A。

3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列。

根据这个规律，第2015个点的横坐标为1，因此答案为A。

4.在平面直角坐标系中，一只蚂蚁从原点O出发，按照向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如图3所示。

1）填写下列各点的坐标：A1（0，1），A3（2，1），A12（6，﹣2）；2）点A4n的坐标为（2n，﹣2n+1）；3）蚂蚁从点A100到A101的移动方向为向上。

5.观察下列有序数对：（3，﹣1），（﹣5，0），（7，﹣1），（﹣9，0），…根据你发现的规律，第100个有序数对是（195，﹣1）。

6.观察下列有规律的点的坐标：A1（1，0），A2（2，1），A3（4，0），A4（8，1），…依照规律，A11的坐标为（1024，1），A12的坐标为（2048，0）。

7.以原点为起点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系。

一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2，再向正西方向走9米到达A3，再向XXX方向走12米到达A4，再向正东方向走15米到达A5，按此规律走下去，当机器人走到A6时，A6的坐标是（﹣3，﹣3）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平面直角坐标系动点问题
（一）找规律
1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）
图1
A ．（4，0）
B ．（5，0）
C ．（0，5）
D ．（5，5）
图2
2、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（） A 、（13，13） B 、（﹣13，﹣13） C 、（14，14） D 、（﹣14，﹣14）
3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2015个点的横坐标为．
4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。