平面弯曲习题解答1
平面弯曲习题解答1
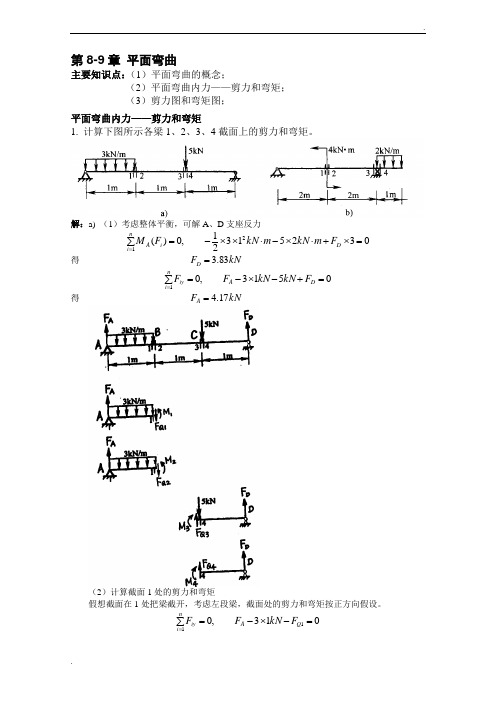
..第8-9章 平面弯曲主要知识点:(1)平面弯曲的概念;(2)平面弯曲内力——剪力和弯矩; (3)剪力图和弯矩图; 平面弯曲内力——剪力和弯矩1. 计算下图所示各梁1、2、3、4截面上的剪力和弯矩。
解:a) (1)考虑整体平衡,可解A 、D 支座反力03251321,0)(21=⨯+⋅⨯-⋅⨯⨯-=∑=D ni i A F m kN m kN F M 得 kN F D 83.3=0513,01=+-⨯-=∑=D A ni iy F kN kN F F得 kN F A 17.4=(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,011=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.11=011321,0)(1121=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.21(3) 计算截面2处的剪力和弯矩假想截面2在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,021=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.12=011321,0)(2221=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.22(4) 计算截面3处的剪力和弯矩假想截面在3处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
05,031=+-=∑=D Q ni iy F kN F F得 kN F Q 17.13=01,0)(31=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.33(5) 计算截面4处的剪力和弯矩假想截面在4处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
0,041=+=∑=D Q ni iy F F F得 kN F Q 83.34-=01,0)(41=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.34b) (1)考虑整体平衡,可解A 、C 支座反力05.41244,0)(1=⋅⨯⨯-⨯+⋅=∑=m kN F m kN F M C ni i A得 kN F C 25.1=012,01=⨯-+=∑=kN F F F C A ni iy得 kN F A 75.0=..(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
第1节 平面弯曲的概念和实例

第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
二、静定梁的基本形式 梁的支座形式:工程中常见的梁的支座有以下三 种形式。 1)固定铰支座:如图a所示,固定铰支座限制梁在 支承处任何方向的线位移,其支座反力可用两个正 交分量表示,即沿梁轴线方向的 FAx 和垂直于梁轴 线方向的FAy。
第七章 直梁弯曲时的内力和应力
第一节
平面弯曲的概念和实例
一、平面弯曲 弯曲变形:当杆件受到垂直于轴线的外力作用或 受到作用面平行于轴线的外力偶作用时,杆件的 轴线会由直线变为曲线,这种变形称弯曲变形。 梁:以弯曲变形为主的杆件称作梁。 直梁:工程中常见的轴线是直线的梁。 平面弯曲:若梁的外力及支 座反力都作用在纵向对称面 内,则梁弯曲时轴线将变成 此平面内的一条平面曲线, 该弯曲变形称为平面弯曲。
或
第七章 直梁弯曲时的内力和应力 2)活动铰支座:如图b所示,活动铰支座只能限制 梁在支承处垂直于支承面的线位移,支座反力可用 一个分量FRA表示。 3)固定端支座:如图c所示,固定端支座限制梁在 支承处的任何方向线位移和角位移,其支座反力有 两个正交力FAx、FAy和一个力偶分量MA。
或
MA
第七章 直梁弯曲时的内力和应力 静定梁的形式:根据梁的支座情况,工程中常见 的静定梁可以简化成以下三种形式。 1)简支梁:梁的支座一端是 固定铰支座,另一端是活 动铰支座。 2)外伸梁:梁的支座与简支 梁相同,只是梁的一端或 两端伸出在支座之外。 3)悬臂梁:梁的一端自由, 另一端是固定支座。
第七章 直梁弯曲时的Biblioteka 力和应力三、梁上载荷的简化
1)集中力:集中力作用在梁上的很小一段范围内, 可近似简化为作用于一点,如图所示的力F。单位 为牛顿(N)或千牛顿(kN)。 2)集中力偶:作用在微小梁段上的力偶,可近似 简化为作用于一点,如图所示的力偶M。单位为牛 顿· 米(N· m)或千牛顿· 米(KN· m)。 3)分布载荷:沿梁轴线方 向、在一定长度上连续分布 的力系,如图所示的均布载 荷q。其大小用载荷集度表 示,单位为牛顿/米(N/m) 或千牛/米(kN/m)。
工程力学习题及答案

工程力学习题及答案1.力在平面上的投影(矢量)与力在坐标轴上的投影(代数量)均为代数量。
正确2.力对物体的作用是不会在产生外效应的同时产生内效应。
错误3.在静力学中,将受力物体视为刚体(D)A. 没有特别必要的理由B. 是因为物体本身就是刚体C. 是因为自然界中的物体都是刚体D. 是为了简化以便研究分析。
4.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确5.轴力图、扭矩图是内力图,弯矩图是外力图。
错误6.胡克定律表明,在材料的弹性变形范围内,应力和应变(A)A .成正比B .相等C .互为倒数 D. 成反比7.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体8.通常工程中,不允许构件发生(A)变形A.塑性B.弹性C.任何D.小9.圆轴扭转时,同一圆周上的切应力大小(A)A.全相同B.全不同C.部分相同D.部分不同10.杆件两端受到等值、反向且共线的两个外力作用时,一定产生轴向拉伸或压缩变形。
正确1.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体2.构件的许用应力是保证构件安全工作的(B)A.最低工作应力B.最高工作应力C.平均工作应力D.极限工作应力3.低碳钢等塑性材料的极限应力是材料的(A)A.屈服极限B.许用应力C.强度极限D.比例极限4.一个力作平行移动后,新点的附加力偶矩一定(B)A.存在B.存在且与平移距离有关C.不存在D.存在且与平移距离无关5.力矩不为零的条件是(A)A.作用力和力臂均不为零B.作用力和力臂均为零C. 作用力不为零D.力臂不为零6.构件抵抗变形的能力称为(B)B.刚度C.稳定性D.弹性7.工程实际计算中,认为切应力在构件的剪切面上分布不均匀。
错误8.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确9.圆轴扭转时,横截面上的正应力与截面直径成正比。
错误10.扭转时的内力是弯矩。
错误1.各力作用线互相平行的力系,都是平面平行力系。
《材料力学》弯曲计算-习题

②无均布载荷段弯矩图均为直线。有均布载荷段,弯矩图为
抛物线,其开口与均布载荷方向相同。
(3)弯矩、剪力、载荷集度的关系
①
M '(x) F S (x) F S'(x) q(x)
② FS=0的点是M图的取极值的点,FS=0的段M图是平行
于轴线的直线。
注意: 内力图上要注明控制面值、特殊点纵坐标值。
利用微分关系绘内力图
y
B截面 30.3 +
z
C截面 15.1 z
-
+
69
34.5
(d) 单位:MPa
Engineering Mechanics
四、弯曲 弯曲强度计算
例3 之二
解:(1)求截面形心轴,即中性轴z轴。
yC
( yi Ai ) Ai
170 30 170 30 200 (170 30)
2
2
17030 30 200
解:(1)外力分析,判变形。
10kN
50kN
(a) A
CD
B
z
4m
2m
4m
求得支坐反力
FA 26kN ,FB 34kN
荷载与梁轴垂直,梁将发
26kN 26 16
34kN
生平面弯曲。中性轴z过形心
+ (b)
与载荷垂直,沿水平方向。
FQ(kN)
104 136
34
(2)内力分析,判危险面。剪力
+
(c)
⑤解题步骤:
1)外力分析,判变形、中性轴,求截面的几何性质、支反力。 2)内力分析,判危险面,画剪力图、弯矩图(可只画弯矩图)
3)应力分析,判危险点。 4)强度计算。
材料力学第四章平面弯曲

得
∫ A ydA =0
M
dA
z
y z ζdA
My
横截面对中性轴 zdA 的面积矩为零, A 中性轴过形心。 E yzdA 0
A
y
Iyz =0——梁发生平面弯曲的条件
E I E 2 ∫ AσdA· z ∫ A y dA = Mz= y = ρ ρ 1 Mz = EIz —— 梁的弯曲刚度 中性层曲率公式 EI ρ z
y
m MB=-40kN· m MD=22.5kN· B M y B截面 上部受拉、下部受压 tBmax B t max 21.4MPa Iz B yt max 100mm B M y I z 186.6 106 m 4 B B c max 38.6MPa B c max yc max 180mm Iz
max
FQ S
* z max
Izd
d FQ 4 FQ 12 4 d 3 A d 64
3
d/2
z
max
四、薄壁圆环截面梁 中性轴处:
r0
z
max 2
FQ A
max
例 如图所示一T形截面。某截面上的剪力FQ=50kN,与y 轴重合。试求腹板的最大切应力,并画出腹板上的切应力分布图。
1
* FQ S z 1
I zd
4.13MPa
例 一矩形截面外伸梁,如图所示。现自梁中1、2、 3、4点处分别取四个单元体,试画出单元体上的应力,并 写出应力的表达式。
q
1 2 h/4 4 3
z l/4 b
l/4
l
解: (1)求支座反力:
FRA
FRB
1 l/4
工程力学习题册第八章 - 答案

第八章 直梁弯曲一、填空题1.工程中 发生弯曲 或以 弯曲变形 为主的杆件称为梁。
2.常见梁的力学模型有 简支梁 、 外伸梁 和 悬臂梁 。
3.平面弯曲变形的受力特点是 外力垂直于杆件的轴线,且外力和力偶都作用在梁的纵向对称面内 ;平面弯曲变形的变形特点是 梁的轴线由直线变成了在外力作用面内的一条曲线 ;发生平面弯曲变形的构件特征是 具有一个以上对称面的等截面直梁 。
4.作用在梁上的载荷有 集中力 、 集中力偶 和 分布载荷 。
5.梁弯曲时,横截面上的内力一般包括 剪力 和 弯矩 两个分量,其中对梁的强度影响较大的是 弯矩 。
6.在计算梁的内力时,当梁的长度大于横截面尺寸 五 倍以上时,可将剪力略去不计。
7.梁弯曲时,某一截面上的弯矩,在数值上等于 该截面左侧或右侧梁上各外力对截面形心的力矩 的代数和。
其正负号规定为:当梁弯曲成 凹面向上 时,截面上弯矩为正;当梁弯曲成凸面向上 时,截面上弯矩为负。
8.在集中力偶作用处,弯矩发生突变,突变值等于 集中力偶矩 。
9.横截面上弯矩为 常数 而剪力为 零 的平面弯曲变形称为 纯弯曲变形 。
10.梁纯弯曲变形实验中,横向线仍为直线,且仍与 梁轴线 正交,但两线不再 平行 ,相对倾斜角度θ。
纵向线变为 弧线 ,轴线以上的纵向线缩短,称为 缩短 区,此区梁的宽度 增大 ;轴线以下的纵向线伸长,称为 伸长 区,此区梁的宽度 减小 。
情况与轴向拉伸、压缩时的变形相似。
11.中性层与横截面的交线称为 中性轴 ,变形时梁的 所有横截面 均绕此线相对旋转。
12.在中性层凸出一侧的梁内各点,其正应力均为 正 值,即为 拉 应力。
13.根据弯曲强度条件可以解决 强度校核 、 截面选取 和 确定许可载荷 等三类问题。
14.产生最大正应力的截面又称为 危险截面 ,最大正应力所在的点称为 危险点 。
15.在截面积A 相同的条件下, 抗弯截面系数 越大,则梁的承载能力就越高。
平面弯曲
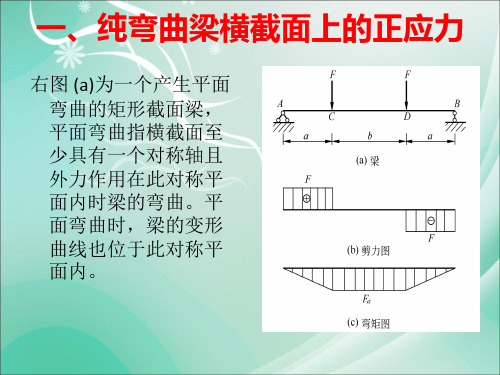
•
有
EIz
1 M = M及 = ρ ρ EIz
式中,1/ρ表示中性层的曲率。反映梁产生弯曲变 形的程度;EIz表示梁抵抗弯曲变形的能力,称为 抗弯刚度。由式(4-44)可知,在指定截面上M为一 定值时,梁的抗弯刚度越大,曲率越小,梁的弯 曲变形也越小。 将 σ = E ⋅ ε = E y 代入得
ρ
My σ = Iz
式(4-45)是计算梁在纯弯曲时横截面上任意一点的 正应力公式。 式中,M——横截面上的弯矩; y——所求点到中性轴的距离; Iz——整个截面对中性轴的惯性矩。 正应力σ的正负号可根据变形判断,以中性轴为界 ,变形后凸边的纤维受拉,应力为正(拉 应力) ,凹边的纤维受压,应力为负(压应力)。
(2) 求梁的最大正应力值,及最大正应力值发生的 位置。该梁为等截面梁,在全梁范围内惯性矩为 一常数,任意截面的上下边缘至截面中性轴的距 离均相等。所以最大正应力发生在最大弯矩截面 的上下边缘处。 则最大正应力为
M max
ql 2 2 × 52 = = kN ⋅ m = 6.25kN ⋅ m 8 8 M max ymax M max h 6.25 × 106 × 200 = = = = 6.25N/mm 2 = 6.25MPa 8 IZ 2I Z 2 × 10
距中性轴y处的纵向纤维 a1a2的原长为,变形后 的长度,所以纤维的 伸长量为,相应的纵 向线应变为: ydφ y ε= = ρ dφ ρ 上式表明:各纤维的纵 向线应变与它到中性 层的距离成正比
距中性层最远的上、下 边缘处的线应变最大 ,而中性层上线应变 为零。
2. 物理方面 假设梁在纯弯曲时纵向 纤维之间无挤压作用 ,梁内各点处于单向 受力状态,材料在线 弹性范围内。则
平面弯曲1(内力及内力图)
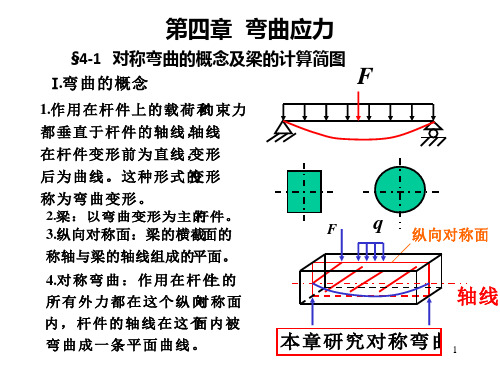
ΙΙ. ΙΙ. 梁的计算简图
一、载荷和约束力的类 型
1.集中力 2.集中力偶 3.分布力
F
m
q
二、梁的支座类型
1.固定铰支座
2.活动铰支座
3.固定端
三、梁的类型
1.简支梁
2.外伸梁 3.悬臂梁
约束力不超过三个, 以上三种梁统称为 : 静定梁(约束力不超过三个, 可由平衡方程求解。) 可由平衡方程求解。) 2
11
由外力写内力
力引起正剪力; 1.相对于横截面来说,左 段向上、右段向下的外 力引起正剪力; 相对于横截面来说, 段向上、 反之则反。 反之则反。
2.相对于横截面来说,左 、右段向上的外力引起 正弯矩; 相对于横截面来说, 正弯矩; 反之则反。 反之则反。
3.相对于横截面来说,外 力矩或外力偶,左段顺 时针转, 相对于横截面来说, 力矩或外力偶, 时针转, 反之则反。 右段逆时针转引起正弯 矩;反之则反。
3 .根据方程作图
Pa (a<x<l) l Pa (a ≤ x ≤ l ) M = FB ( l − x ) = (l − x ) l
Pa l
x
0
+
M
Pab l
8
例二、 作图示梁的剪力图和弯矩图,并标出控制点的数据。 例二、 作图示梁的剪力图和弯矩图,并标出控制点的数据。 解:
FA = FB = ql 2
18
例. 作图示梁的Fs、M图 作图示梁的F
y
解:
Fa Fa FA = (↓),FB = + F(↑) l l
x1
A
B
x2
C
FxBiblioteka axlAB段
Fa Fs = − l Fa M=− x l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8-9章 平面弯曲主要知识点:(1)平面弯曲的概念;(2)平面弯曲内力——剪力和弯矩; (3)剪力图和弯矩图; 平面弯曲内力——剪力和弯矩1. 计算下图所示各梁1、2、3、4截面上的剪力和弯矩。
解:a) (1)考虑整体平衡,可解A 、D 支座反力03251321,0)(21=⨯+⋅⨯-⋅⨯⨯-=∑=D ni i A F m kN m kN F M 得 kN F D 83.3=0513,01=+-⨯-=∑=D A ni iy F kN kN F F得 kN F A 17.4=(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,011=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.11=011321,0)(1121=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.21(3) 计算截面2处的剪力和弯矩假想截面2在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,021=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.12=011321,0)(2221=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.22(4) 计算截面3处的剪力和弯矩假想截面在3处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
05,031=+-=∑=D Q ni iy F kN F F得 kN F Q 17.13=01,0)(31=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.33(5) 计算截面4处的剪力和弯矩假想截面在4处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
0,041=+=∑=D Q ni iy F F F得 kN F Q 83.34-=01,0)(41=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.34b) (1)考虑整体平衡,可解A 、C 支座反力05.41244,0)(1=⋅⨯⨯-⨯+⋅=∑=m kN F m kN F M C ni i A得 kN F C 25.1=012,01=⨯-+=∑=kN F F F C A ni iy得 kN F A 75.0=(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
0,011=-=∑=Q A ni iy F F F得 kN F Q 75.01=02,0)(111=+⨯-=∑=M F F M Q ni i A得 m kN M ⋅=5.11 (3) 计算截面2处的剪力和弯矩假想截面2在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
0,021=-=∑=Q A ni iy F F F得 kN F Q 75.02=042,0)(221=+⋅+⨯-=∑=M m kN F F M Q ni i A得 m kN M ⋅-=5.22(4) 计算截面3处的剪力和弯矩假想截面在3处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
012,031=⨯-+=∑=kN F F F C Q ni iy得 kN F Q 75.03=01221,0)(231=⋅⨯⨯--=∑=m kN M F M ni i C得 m kN M ⋅-=13(5) 计算截面4处的剪力和弯矩假想截面在4处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
0)(1A =∑=i n i M F l M F M l F ==+⋅-B B 00)(1B =∑=i ni M F lM F M l F ==+⋅-A A 0)0()(A Q a x l M F x F ≤≤==)()(A Q l x a lMF x F ≤≤==)0( )(Q l x lMx F ≤≤=⎪⎩⎪⎨⎧≤≤--≤≤=)()()0()(l x a x l l Ma x x l Mx M012,041=⨯-=∑=kN F F Q ni iy得 kN F Q 24=01221,0)(241=⋅⨯⨯--=∑=m kN M F M ni i C得 m kN M ⋅-=14剪力图和弯矩图2. 建立图示梁的剪力方程和弯矩方程,并画剪力图和弯矩图。
(a ) (b )解:a)(1)求支座反力(2)求剪力方程和弯矩方程(分段建立方程)AC 段CB 段(3)作剪力图和弯矩图弯矩图是两斜直线,在C 截面处有突变,突变量为M 。
)0()(Aa x x l M x F x M ≤≤=⋅=)()()()(B l x a x l lMx l F x M ≤≤--=-⋅=b) (1)求支座反力由整体平衡方程(见图8-2b ):0)(1=∑=ni i A F M , 03102=⋅⨯+⨯-m kN F B , kN F B 15= 0)(1=∑=ni i B F M , 01102=⋅⨯+⨯-m kN F A , kN F A 5-=(2)求剪力方程和弯矩方程梁上任取一截面(见图8-2b),到支座A 的距离为x ,由截面法得该截面的剪力方程和弯矩方程AB 段:kN x F Q 5)(-=, x x M 5)(-=, (m x 20<≤)BC 段: kN x F Q 10)(=, )(x x M --=310)(,即3010)(-=x x M ,(m x m 32≤<)图8-2b(3)作剪力图和弯矩图:AB 、BC 段剪力都为常数,剪力图各为一水平直线。
AB 、BC 段弯矩方程是x 的一次函数,弯矩图各为一斜直线。
两点可以确定一条直线,当0=x 时,0)0(=M ;当m x 2=时,m kN M ⋅-=10)2(;当m x 3=时,0)3(=M ,连A 、B 两点可得AB 段弯矩图,连B 、C 两点可得BC 段弯矩图,如图8-2b 所示。
3. 剪力和弯矩的正负号如何确定?梁在集中力、集中力偶及均布载荷作用下的剪力图和弯矩图有何特点?答:在计算内力时,为了使考虑左段梁平衡与考虑右段梁平衡的结果一致,对剪力和弯矩的正负号作以下规定: 剪力:使截面绕其内侧任一点有顺时针转趋势的剪力为正,反之为负。
弯矩:使受弯杆件下侧纤维受拉为正,使受弯杆件上侧纤维受拉为负。
或者使受弯杆件向下凸时为正,反之为负。
(1) 当梁上有集中力作用时,剪力图在集中力作用处有突变,突变量是集中力的大小; 弯矩图在集中力作用处产生尖角。
(2) 当梁上有集中力偶作用时,剪力图在集中力偶作用处不变;弯矩图在集中力偶作用处有突变,突变量是集中力偶的大小。
(3)梁的某一段内有均布载荷作用,则剪力)(x F Q 是x 的一次函数,弯矩)(x M 是x 的二次函数。
剪力图为斜直线;若)(x q 为正值,斜线向上倾斜;若)(x q 负值,斜线向下倾斜。
弯矩图为二次抛物线,当)(x q 为正值,弯矩图为凹曲线;当)(x q 为负值,弯矩图为凸曲线。
4. 什么是剪力、弯矩和载荷集度的微分关系?如何利用微分关系作梁的剪力图和弯矩图?答:载荷集度)(x q 、剪力)(x F Q 和弯矩)(x M 之间的微分关系如下:)(d )(d x q x x F Q = )(d )(d x F x x M Q =)(d )(d 22x q x x M =利用微分关系作梁的剪力图和弯矩图:1. 无分布载荷作用的梁段(q =0)由于0)(=dx x dF Q ,因此)(x F Q =常数,即剪力图为水平直线。
而)()(x F dxx dM Q =为常数,)(x M 是x 的一次函数,即弯矩图为斜直线,其斜率由)(x F Q 值确定。
(1) 当梁上仅有集中力作用时,剪力图在集中力作用处有突变,突变量是集中力的大小;弯矩图在集中力作用处产生尖角。
(2) 当梁上仅有集中力偶作用时,剪力图在集中力偶作用处不变;弯矩图在集中力偶作用处有突变,突变量是集中力偶的大小。
2. 均布载荷作用的梁段()(x q 为常数)由于q x q =)(,因此q dxx dF Q =)(,即)(x F Q 是x 的一次函数,M(x)是x 的二次函数,所以剪力图为斜直线,其斜率由q 确定;弯矩图为二次抛物线。
当分布载荷向上(即q >0)时,q xd x M d =22)(>0,弯矩图为凹曲线;反之,当分布载荷向下(即q <0)时,q xd x M d =22)(<0,弯矩图为凸曲线。
5. 指出下图所示各弯矩图的错误,画出正确的弯矩图。
解:a )弯矩图的斜率、起点错误,图8-5a 为正确的弯矩图;b )弯矩图应该是斜直线,图8-5b 为正确的弯矩图;图8-5d)弯矩图在支撑处没有突变,图8-5d为正确的弯矩图(设l>2a)。
6. 利用剪力、弯矩与载荷集度的微分关系作图示各梁的剪力图和弯矩图。
由整体平衡方程(见图8-6a):01=∑=ni iy F , 0=--qa qa F A , qa F A 2=0)(1=∑=ni i A F M , 05.2=⨯-⨯--a qa a qa M A , 25.3qa M A -=图8-6a(2)作剪力图AC 段剪力图是水平线,大小为2qa ,CD 段剪力图也是水平线,大小为qa ,DB 是斜直线,确定两个控制点qa F QD =,0=QB F ,作剪力图如图8-6a 所示。
(3)作弯矩图AC 段与CD 段的弯矩图是斜直线,求出以下控制截面的弯矩25.3qa M A -=,25.1qa M C -=,25.0qa M D -=,可作这两段斜直线。
DB 段由于有均布载荷作用,弯矩图是一段抛物线,如图8-6a 所示。
b) (1)求支座反力由整体平衡方程(见图8-6b ):0)(1=∑=ni i A F M , 0322=⨯++⨯⨯-a F qa a a q B , 得3qaF B = 01=∑=ni iy F , 02=+⨯-B A F a q F , 得35qaF A =图8-6b(2)作剪力图CB 段剪力图是水平线,大小为3qa-。
AC 段剪力图是斜直线,确定两个控制点35qa F QA =,=QC F 3qa-。
作剪力图如图8-6b 所示。
(3)作弯矩图CB 段的弯矩图是斜直线,求出以下控制截面的弯矩:231qa M C =+,0=B M ,作出这段斜直线。
AC 段由于有均布载荷作用,弯矩图是一段抛物线。
当剪力为0时(见图7-21所示D 点),弯矩出现极值,即当a x 35=时,2m a x 389.1)35(qa a M =。
再求出以下控制截面的弯矩:0=A M ,234qa M C =-。
画弯矩图如图8-6b 所示。
