黔东南州2014年初中毕业生学业(升学)统一考试
黔东南州2014年初中毕业生学业(升学)统一考试

机密★启用前黔东南州2014年初中毕业生学业(升学)统一考试数学试题卷(全卷总分150分,考试时间120分钟)注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其它答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.5.考试结束后,将试题卷和答题卡一并交回.一、选择题(本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符号题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满.)1.=()A.3 B.﹣3 C.D.﹣2.下列运算正确的是()A.a2•a3=a6B.(a2)3=a6C.(a+b)2=a2+b2D.+=3.掷一枚质地均匀的硬币10次,下列说法正确的是()A.可能有5次正面朝上B.必有5次正面朝上C.掷2次必有1次正面朝上D.不可能10次正面朝上4.如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是()A.AB∥DC,AD=BC B.AB∥DC,AD∥BCC.AB=DC,AD=BC D.OA=OC,OB=OD(4题图) (5题图)5.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B.1.5 C.D.16.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2014的值为()A.2012 B.2013 C.2014 D.20157.如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为()A.4cm B.3cm C.2cm D.2cm(7题图) (8题图)8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为()A.1 B.2C.D.9.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有()A.①②③B.①②④C.①③④D.②③④(9题图) (10题图)10.如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A 重合,则折痕EF的长为()A.6 B.12 C.2D.4二、填空题(每个小题4分,共24分)。
2014年贵州省黔西南州中考试题(word版含答案)

贵州黔西南州2014初中毕业生学业与升学统一考试试卷数学(满分150分,考试时间120分钟)一、选择题(每小题4分,共40分)1.(2014黔西南州1,4分)12-的倒数A.12B.2-C.2D.12-2.(2014黔西南州2,4分)不等式240x->的解集为A.12x>B.2x>C.2x>-D.8x>3.(2014黔西南州3,4分)已知等腰三角形ABC中,腰AB=8,底BC=5,则这个三角形的周长A.21 B.20 C.19 D.184.(2014黔西南州4,4分)在一个不透明的盒子中装12个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是13,则黄球的个数A.18 B.20 C.24 D.285.(2014黔西南州5,4分)如图1,已知AB=AD,那么添加下列一个条件后,仍无法判定∆ABC ≌∆ADC的是A.CB=CD B.∠BAC=∠D AC C.∠BCA=∠D CA D.∠B=∠D=90°6.(2014黔西南州6,4分)已知两圆的半径分别为3、5,圆心距为8,则这两圆的位置关系为A.外离B.相含C.相交D.外切7.(2014黔西南州7,4分)如图所示,是由5个相同的小正方体组成的几何体,它的左视图是8.(2014黔西南州8,4分)下列图形中,既是中心对称,又是轴对称的是9.(2014黔西南州9,4分)已知如图2,一次函数y ax b =+和反比例函数ky x=的图象相交于A 、B 两点,不等式kax b x+>的解集为 A .3x <- B .30x -<<或1x > C .3x <-或1x > D .31x -<<10.(2014黔西南州10,4分)甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息。
已知甲先出发2秒,在跑步的过程中,甲乙两人之间的距离()y cm 与乙出发的时间t(s)之间的函数关系如图3所示,给出以下结论①8a =,②92b =,③123c =,其中正确的是A .①②③B .仅有①②C .仅有①③D .仅有②③二、填空题(每小题3分,共30分,共30分)11.(2014黔西南州11,3分)1x =时,代数式21____________x +=.12.(2014黔西南州12,3分)21040000用科学记数法表示(保留3个有效数字)为_____________ 13.(2014黔西南州13,3分)已知甲数据的平均数为x 甲,乙数据的平均数为x 乙,且x x =乙甲,而甲数据的方差为2 1.25S =甲;乙数据的方差为23S =乙,则_______较稳定 14.(2014黔西南州14,3分)点P (2,3)关于x 轴的对称点的坐标为________15.(2014黔西南州15,3分)函数y x 的取值范围_____________.16.(2014黔西南州16,3分)四边形的内角和________. 17.(2014黔西南州17,3分)如图4,已知a ∥b ,小时把三角板的直角顶点放在直线b 上,若∠1=35°则∠2的度数为____________18.(2014黔西南州18,3分)如图5,AB 是⊙O 的直径,AB=15,AC=9,则ta n ADC ∠=_________19、(2014黔西南州19,3分)如图6,将矩形纸片ABCD 折叠,使边AB 、CB 均落在对角线BD 上,使得折痕BE 、BF ,则∠EBF 的大小为___________20、(2014黔西南州20,3分)在平面直角坐标系中,对于平面内在一点(,)m n ,规定以下两种变化,①f(m,n)(,)m n =-;②f(2,1)(21)=-;②g(,)(m,n)m n =--; g(2,1)(2,1)=--按照以上变换有,按照以上变换有:f[g(3,4)](3,4)(3,4)f =--=-;那么g[f(3,2)]-=__________三、解答题(本题共12分) 21.(2014黔西南州21,12分) (1)计算:201()(2014)sin 6023π---+︒;(2)解方程:21424x x =--四.(本题共12分) 22.(2014黔西南州22,12分)如图7,点B 、C 、D 都在⊙O 上,过C 点作CA ∥BD 交OD 的延长线于点A ,连接BC ,∠B=∠A=30°,BD =(1)求证:AC 是⊙O 的切线;(2)求曲线段AC 、AD 与弧CD 所围成的阴影部分的面积(结果保留π)五.(本题共14分) 23.(2014黔西南州23,14分)我州实施新课程改革后,学生的自主学习、合作交流能力有很大提高,某学校为了了解学生自主学习、合作交流的具体情况,对部分学生进行了为期半个月的跟踪调查,并将调查结果分类,A :特别好;B :好;C :一般;D :较差.现将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题.(1)本次调查中一共调查了__________名同学,其中C 类女生有____________名. (2)将下面的条形统计图补充完整.(3)为了共同进步,学校想从被调查的A 类和D 类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰恰好是一位男生、一位女生的概率.六.(本题共14分) 24.(2014黔西南州24,14分)为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具某居民五月份用电190千瓦时,缴纳电费90元. (1) 求x 和超出部分电费单价;(2) 若该户居民六月份缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围. 七.(阅读材料题,本题12分) 25.(2014黔西南州25,12分)已知点00(,)P x y 和直线y kx b =+,则点P 到直线y kx b =+的距离d 可用公式d =计算.例如:求点(2,1)P -到直线1yx =+的距离.解:因为直线1y x =+可变形为10x y -+=,其中1,1k b == 所以点(2,1)P -到直线1y x =+的距离为:d ====根据以上材料,求:(1)点(1,1)P 到直线32y x =-的距离,并说明点P 与直线的位置关系; (2)点(2,1)P -到直线21y x =-的距离;(3)已知直线1y x =-+与3y x =-+平行,求这两条直线的距离.八 .(本题共16分)26.(2014黔西南州26,16分)如图9所示,在平面直角坐标系中,抛物线2y ax bx c =++经过(3,0)A -、B(1,0)、(0,3)C 三点,其顶点为D ,连接AD ,点P 是线段AD 上一个动点(不与A 、D 重合).经过点P 作y 轴的垂线,重足为E ,连接AE . (1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)如果P 点的坐标为(,)x y ,∆PAE 的面积为S ,求S 与x 之间的函数关系式,直接写出自变量x 的取值范围,并求S 的最大值;(3)在(2)的条件下,当S 取到最大值时,过点P 作x 轴的垂线,垂足为F ,连接EF ,把∆PEF 沿直线EF 折叠,点P 的对应点为点P ',求出P '的坐标,并判断P '是否在该抛物线上.图9贵州黔西南州2014初中毕业生学业与升学统一考试试卷数学参考答案(满分150分,考试时间120分钟)一、选择题(每小题4分,共40分) 1.【答案】B. 2.【答案】B. 3.【答案】A. 4.【答案】C. 5.【答案】C. 6.【答案】D. 7.【答案】D.8.【答案】A. 9.10.二、填空题(每小题3分,共30分,共30分) 11.【答案】2 12.【答案】72.0110⨯ 13.【答案】甲 14.【答案】(2,3)- 15.【答案】12x ≥16.【答案】360° 17.【答案】55°18. 【答案】3419、【答案】45° 20、【答案】(3,2)三、解答题(本题共12分) 21.(2014黔西南州21,12分) (1)计算:201()(2014)sin 6023π---+︒;【答案】(1)解:9122=-++10= (2)解方程:21424x x =-- 【答案】解:24x +=,2x =;把2x =代入24x -,240x -=所以方程无解四.(本题共12分) 22.(2014黔西南州22,12分)如图7,点B 、C 、D 都在⊙O 上,过C 点作CA ∥BD 交OD 的延长线于点A ,连接BC ,∠B=∠A=30°,BD =(1)求证:AC 是⊙O 的切线;(2)求曲线段AC 、AD 与弧CD 所围成的阴影部分的面积(结果保留π)(1) 证明:连接OC ,与BD 相交于点E∵CD CD = 且∠B=∠A=30°∴∠AOC=60°∴∠OCD=180°-∠A -∠AOC=90° 即:AC 是⊙O 的切线(2) 解:∵CA ∥BDA∴ ∠OED=∠OCD=90°,∠ODE=∠A=30°∵BD =∴12DE BD ==即:2cos DEOD ODE==∠ ∴OC=OD=2,cot 2AC OC A ==∴0216022223603S ππ=⨯⨯⨯⨯=︒阴 五.(本题共14分)23.(2014黔西南州23,14分)我州实施新课程改革后,学生的自主学习、合作交流能力有很大提高,某学校为了了解学生自主学习、合作交流的具体情况,对部分学生进行了为期半个月的跟踪调查,并将调查结果分类,A :特别好;B :好;C :一般;D :较差.现将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题.(1)本次调查中一共调查了__________名同学,其中C 类女生有____________名. (2)将下面的条形统计图补充完整.(3)为了共同进步,学校想从被调查的A 类和D 类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰恰好是一位男生、一位女生的概率.【答案】 解: 六.(本题共14分) 24.(2014黔西南州24,14分)为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准如下表:某居民五月份用电190千瓦时,缴纳电费90元.(3) 求x 和超出部分电费单价;(4) 若该户居民六月份缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围. 【答案】解:(1)依题意得:160(190160)(0.15)90x x +-+=;解得:0.45x = (2)∵1600.457275⨯=< ∴190x >依题意得:75720.6(160)84x ≤+-≤;解得:165180x ≤≤ 七.(阅读材料题,本题12分)25.(2014黔西南州25,12分)已知点00(,)P x y 和直线y kx b =+,则点P 到直线y kx b =+的距离d可用公式d =计算.例如:求点(2,1)P -到直线1y x =+的距离.解:因为直线1y x =+可变形为10x y -+=,其中1,1k b == 所以点(2,1)P -到直线1y x =+的距离为:d ====根据以上材料,求:(1)点(1,1)P 到直线32y x =-的距离,并说明点P 与直线的位置关系; (2)点(2,1)P -到直线21y x =-的距离;(3)已知直线1y x =-+与3y x =-+平行,求这两条直线的距离. 【答案】解:(1)∵点(1,1)P 在直线32y x =-的图象上∴0d =(2)因为直线21y x =-可变形为210x y --=,其中2,1k b ==- 所以点(2,1)P -到直线21y x =-的距离为:d ====(3)∵直线1y x =-+、3y x =-+平行∴任取直线1y x =-+上的一点到直线3y x =-+的距离即为两直线之间的距离∴取1y x =-+上的一点(0,1)P 到直线3y x =-+的距离d ====八 .(本题共16分)26.(2014黔西南州26,16分)如图9所示,在平面直角坐标系中,抛物线2y ax bx c =++经过(3,0)A -、B(1,0)、(0,3)C 三点,其顶点为D ,连接AD ,点P 是线段AD 上一个动点(不与A 、D 重合).经过点P 作y 轴的垂线,重足为E ,连接AE .(1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)如果P 点的坐标为(,)x y ,∆PAE 的面积为S ,求S 与x 之间的函数关系式,直接写出自变量x 的取值范围,并求S 的最大值;(3)在(2)的条件下,当S 取到最大值时,过点P 作x 轴的垂线,垂足为F ,连接EF ,把∆PEF 沿直线EF 折叠,点P 的对应点为点P ',求出P '的坐标,并判断P '是否在该抛物线上.【答案】解:(1)∵抛物线过点(3,0)A -、B(1,0)∴设其解析式为:(3)(1)y a x x =+-且过点(0,3)C∴1a =-即解析式为:223y x x =--+,顶点坐标为:(2)过点A 作AH ⊥CF 交CP 的延长线于点H∵(3,0)A -、(1,4)D -∴直线AD 的解析式为:26y x =+ 图9∴21139(3)()2224APE S AH EP xy x x x ∆==-=-+=-++ (31)x -≤≤-当32x =-时,S 取得最大值,最大值为:94;此时点P 的坐标为:3(,3)2-,且点E 与点C 重合(5) 如图,过点P '作y 轴的垂线交y 轴于点N ,交PE 的延长线于点M∵PE=1.5,PF=3且∆FPE ≌∆FP E '∴P F 3PF '==,P 1.5E PE '==设点P '的坐标为:P (,)x y ',可得:ME x =、3MP y '=-、P N y '=、 1.5FN x =+ 易证:∆MEP '∽∆NP F '∴ 1.53ME MP EP NP NF FP ''==='' 即:311.52x y y x -==+ 解得:P (0.9,1.8)'代入抛物线:223y x x =--+知该点不在抛物线上.。
1066贵州省黔东南州2014年中考历史试题(word版有答案)

黔东南州2014年初中毕业升学统一考试试题文科综合(历史卷)(本试卷为5-8页,共五个大题,23个小题,满分75分)一、选择题(本大题共15个小题,每小题2分,共30分)本题共有A、B、C、D四个备选答案,其中只有一个正确,请你将正确答案的序号填涂在相应的答题卡上。
) (2014·贵州黔东南)1.央视热播纪录片《舌尖上的中国》,从最平凡的一锅米饭,到一个馒头,到……不管吃下多少酒食菜肴,主食,永远都是中国人餐桌上最后的主角。
以下古人类最早有可能享受米饭的是()A.北京人 B.山顶洞人C.半坡居民 D.河姆渡居民【答案】D(2014·贵州黔东南)2.周杰伦创作的“中国风”歌曲:“兰亭临帖,行书如行云流水。
……忙不迭,千年碑易拓却难拓你的美……”。
你唱到他的这首歌时会想到以下哪位书法家()A.张旭B.王羲之C.柳公权D.颜真卿【答案】B(2014·贵州黔东南)3.2011年4月28日至10月22日的西安世园会的会徽取名为“长安花”,取意于“春风得意马蹄疾,一日看尽长安花”。
而这取意源自我国古代的()A.分封制B.郡县制C.科举制D.三省六部制【答案】C(2014·贵州黔东南)4.从电视剧《贞观长歌》中可以看出:统治者重视发展生产、减轻农民负担,从而开创了“贞观之治”的局面。
这位统治者是()A.秦始皇B.汉武帝C.唐太宗D.唐玄宗【答案】C(2014·贵州黔东南)5.当你去购买商品的时候,你一定会体会到人民币(纸币)给人们的生活带来了极大的便利。
世界上最早的纸币出现在中国古代的北宋时期。
请你指出它是()A.会子B.交子C.关子D.瓦子【答案】B(2014·贵州黔东南)6.“国父”孙中山在领导中国民主革命斗争中愈挫愈奋直到临终前还在遗嘱中告诫革命党人:“革命尚未成功,同志仍须努力。
”这里“革命尚未成功”主要指()A.没有建立起中华民国B.没有促进资本主义发展C.没有完成反帝反封建的革命任务D.辛亥革命的果实被袁世凯窃取了【答案】C(2014·贵州黔东南)7.五四运动中青年学生高喊:“外争国权,内惩国贼”、“誓死力争,还我青岛”、“废除二十一条”等口号,上述口号所体现出的五四精神主要是()A.爱国B.进步C.民主D.科学【答案】A(2014·贵州黔东南)8.“战士双脚走天下,四渡赤水出奇兵。
【精校】2014年贵州省黔东南州中考真题数学

2014年贵州省黔东南州中考真题数学一、选择题:每个小题4分,10个小题共40分1.(4分)=( )A. 3B. -3C.D. -解析:根据负数的绝对值是它的相反数,得:|-|=.答案:C.2.(4分)下列运算正确的是( )A. a2·a3=a6B. (a2)3=a6C. (a+b)2=a2+b2D. +=解析:A、原式=a5,错误;B、原式=a6,正确;C、原式=a2+b2+2ab,错误;D、原式不能合并,错误,答案:B3.(4分)如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD 是平行四边形的是( )A. AB∥DC,AD=BCB. AB∥DC,AD∥BCC. AB=DC,AD=BCD. OA=OC,OB=OD解析:A、“一组对边平行,另一组对边相等”是四边形也可能是等腰梯形,故本选项符合题意;B、根据“两组对边分别平行的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;C、根据“两组对边分别相等的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;D、根据“对角线互相平分的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;答案:A.4.(4分)掷一枚质地均匀的硬币10次,下列说法正确的是( )A. 可能有5次正面朝上B. 必有5次正面朝上C. 掷2次必有1次正面朝上D. 不可能10次正面朝上解析:A、是随机事件,故A正确;B、不是必然事件,故B错误;C、不是必然事件,故C错误;D、是随机事件,故D错误;答案:A.5.(4分)如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D 恰好落在BC边上.若AC=,∠B=60°,则CD的长为( )A. 0.5B. 1.5C.D. 1解析:∵∠B=60°,∴∠C=90°-60°=30°,∵AC=,∴AB=×=1,∴BC=2AB=2,由旋转的性质得,AB=AD,∴△ABD是等边三角形,∴BD=AB=1,∴CD=BC-BD=2-1=1. 答案:D.6.(4分)如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )A. 4cmB. 3cmC. 2cmD. 2cm解析:连结OA,如图,∵∠ACD=22.5°,∴∠AOD=2∠ACD=45°,∵⊙O的直径CD垂直于弦AB,∴AE=BE,△OAE为等腰直角三角形,∴AE=OA,∵CD=6,∴OA=3,∴AE=,∴AB=2AE=3(cm).答案:B.7.(4分)已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )A. 2012B. 2013C. 2014D. 2015解析:∵抛物线y=x2-x-1与x轴的一个交点为(m,0),∴m2-m-1=0,解得 m2-m=1.∴m2-m+2014=1+2014=2015.答案:D.点评:本题考查了抛物线与x轴的交点.解题时,注意“整体代入”数学思想的应用,减8.(4分)如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )A. 1B. 2C.D.解析:∵正比例函数y=x与反比例函数y=的图象相交于A、B两点,∴点A与点B关于原点对称,∴S△AOC=S△BOC,∵BC⊥x轴,∴△ABC的面积=2S△BOC=2××|1|=1.答案:A.9.(4分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2-4ac>0其中正确结论的有( )A. ①②③B. ①②④C. ①③④D. ②③④解析:由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于正半轴知:c>0,由对称轴直线x=2,可得出b与a异号,即b<0,则abc<0,故①正确;把x=-1代入y=ax2+bx+c得:y=a-b+c,由函数图象可以看出当x=-1时,二次函数的值为正,即a+b+c>0,则b<a+c,故②选项正确;把x=2代入y=ax2+bx+c得:y=4a+2b+c,由函数图象可以看出当x=2时,二次函数的值为负,即4a+2b+c<0,故③选项错误;由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2-4ac>0,故④D 选项正确;答案:B.10.(4分)如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A 重合,则折痕EF的长为( )A. 6B. 12C. 2D. 4解析:设BE=x,则CE=BC-BE=16-x,∵沿EF翻折后点C与点A重合,∴AE=CE=16-x,在Rt△ABE中,AB2+BE2=AE2,即82+x2=(16-x)2,解得x=6,∴AE=16-6=10,由翻折的性质得,∠AEF=∠CEF,∵矩形ABCD的对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AE=AF=10,过点E作EH⊥AD于H,则四边形ABEH是矩形,∴EH=AB=8,AH=BE=6,∴FH=AF-AH=10-6=4,在Rt△EFH中,EF===4.答案:D.二、填空题:每个小题4分,6个小题共24分11.(4分)cos60°=.解析:cos60°=.答案:12.(4分)函数y=自变量x的取值范围是.解析:有意义的条件是x-1≥0,解得x≥1;又分母不为0,x-1≠0,解得x≠1.∴x>1.答案:x>1.13.(4分)因式分解:x3-5x2+6x= .解析:x3-5x2+6x=x(x2-5x+6)=x(x-3)(x-2).答案:x(x-3)(x-2).14.(4分)若一元二次方程x2-x-1=0的两根分别为x1、x2,则+= .解析:∵一元二次方程x2-x-1=0的两根分别为x1、x2,∴x1+x2=1,x1x2=-1,∴+= ==-1.答案:-1.15.(4分)在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为.解析:底层正方体最少的个数应是3个,第二层正方体最少的个数应该是2个,因此这个几何体最少有5个小正方体组成,答案:5.16.(4分)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为.解析:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,此时PA+PB最小,由题意可得出:OA′=1,BO=2,PA′=PA,∴PA+PB=A′B==.答案:.三、解答题:8个小题,共86分17.(8分)计算:2tan30°-|1-|+(2014-)0+.解析:本题涉及零指数幂、绝对值、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.答案:原式=2×-(-1)+1+=-+1+1+=2.18.(8分)先化简,再求值:÷-,其中x=-4.解析:原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算得到最简结果,将x的值代入计算即可求出值.答案:原式=·-=-=,当x=-4时,原式==.19.(10分)解不等式组,并写出它的非负整数解.解析:分别求出各不等式的解集,再求出其公共解集,找出符合条件的x的非负整数解即可.答案:,由①得,x>-,由②得,x<,故此不等式组的解集为:-<x<,它的非负整数解为:0,1,2,3.20.(12分)黔东南州某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:根据图表解答下列问题:(1)在女生的频数分布表中,m= ,n= .(2)此次调查共抽取了多少名学生?(3)此次抽样中,学习时间的中位数在哪个时间段?(4)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽到男女生各一名的概率是多少?解析:(1)根据第一段中有4人,占20%,即可求得女生的总人数,然后根据频率的计算公式求得m、n的值;(2)把直方图中各组的人数相加就是男生的总人数,然后加上女生总人数即可;(3)求得每段中男女生的总数,然后根据中位数的定义即可判断;(4)利用列举法即可求解.答案:(1)女生的总数是:4÷20%=20(人),则m=20×15%=3(人),n==0.3;(2)男生的总人数是:6+5+12+4+3=30(人),则此次调查的总人数是:30+20=50(人);(3)在第一阶段的人数是:4+6=10(人),第二阶段的人数是:3+5=8(人),第三阶段的人数是:5+12=17(人),则中位数在的时间段是:60≤t<90;(4)如图所示:共有20种等可能的情况,则恰好抽到男女生各一名的概率是=.21.(12分)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.(1)求证:△ACB∽△CDB;(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.解析:(1)由CP是⊙O的切线,得出∠BCD=∠BAC,AB是直径,得出∠ACB=90°,所以∠ACB=∠CDB=90°,得出结论△ACB∽△CDB;(2)求出△OCB是正三角形,阴影部分的面积=S扇形OCB-S△OCB=π-.答案:(1)如图,连接OC,∵直线CP是⊙O的切线,∴∠BCD+∠OCB=90°,∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°∴∠BCD=∠ACO,又∵∠BAC=∠ACO,∴∠BCD=∠BAC,又∵BD⊥CP∴∠CDB=90°,∴∠ACB=∠CDB=90°∴△ACB∽△CDB;(2)如图,连接OC,∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,故阴影部分的面积=S扇形OCB-S△OCB=π-.22.(10分)黔东南州某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:≈1.41,≈1.73)解析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.25m.由小明站在B点测得旗杆顶端E点的仰角为45°,可得△AEM是等腰直角三角形,继而得出得出AM=ME,设AM=ME=xm,则CN=(x+6)m,EN=(x-0.25)m.在Rt△CEN中,由tan∠ECN==,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.答案:过点A作AM⊥EF于M,过点C作CN⊥EF于N,∴MN=0.25m,∵∠EAM=45°,∴AM=ME,设AM=ME=xm,则CN=(x+6)m,EN=(x-0.25)m,∵∠ECN=30°,∴tan∠ECN===,解得:x≈8.8,则EF=EM+MF≈8.8+1.5=10.3(m).答:旗杆的高EF为10.3m.23.(12分)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.(1)求每件甲种、乙种玩具的进价分别是多少元?(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.解析:(1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,根据“5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元”列出方程组解决问题;(2)分情况:不大于20件;大于20件;分别列出函数关系式即可;(3)设购进玩具x件(x>20),分别表示出甲种和乙种玩具消费,建立不等式解决问题. 答案:(1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,由题意得,解得,答:件甲种玩具的进价是30元,每件乙种玩具的进价是27元;(2)当0<x≤20时,y=30x;当x>20时,y=20×30+(x-20)×30×0.7=21x+180;(3)设购进玩具x件(x>20),则乙种玩具消费27x元;当27x=21x+180,则x=30所以当购进玩具正好30件,选择购其中一种即可;当27x>21x+180,则x>30所以当购进玩具超过30件,选择购甲种玩具省钱;当27x<21x+180,则x<30所以当购进玩具少于30件,选择购乙种玩具省钱.24.(14分)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.解析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)根据直线AB的解析式,可求得直线AC的解析式y=-x+b,已知了点A的坐标,即可求得直线AC的解析式,联立抛物线的解析式,可求得C点的坐标;答案:(1)∵B(4,m)在直线线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx-4上,∴,∵c=6,∴a=2,b=-8,∴y=2x2-8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2-8n+6),∴PC=(n+2)-(2n2-8n+6),=-2n2+9n-4,=-2(n-)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)当∠PAC=90°时,设直线AC的解析式为y=-x+b,把A(,)代入得:=-+b,解得:b=3,∴直线AC解析式:y=-x+3,点C在抛物线上,设C(m,2m2-8m+6),代入y=-x+3得:2m2-8m+6=-m+3,整理得:2m2-7m+3=0,解得;m=3或m=(舍去)∴P(3,5),当∠PCA=90°时,把y=代入y=2x2-8x+6,得x=,x=代入y=x+2得:y=,∴P(,),所以P的坐标为(3,5)或(,).考试高分秘诀是什么?试试这四个方法,特别是中考和高考生谁都想在考试中取得优异的成绩,但要想取得优异的成绩,除了要掌握好相关的知识定理和方法技巧之外,更要学会一些考试技巧。
2014 黔南州中考数学试卷
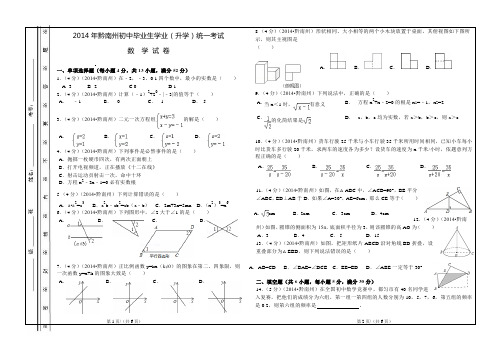
2014年黔南州初中毕业生学业(升学)统一考试数 学 试 卷一、单项选择题(每小题4分,共13小题,满分52分)1.(4分)(2014•黔南州)在﹣2,﹣3,0.1四个数中,最小的实数是( ) A.-3 B.-2 C.0 D.12.(4分)(2014•黔南州)计算(﹣1)2+20﹣|﹣3|的值等于( ) A . ﹣1B . 0C . 1D . 53.(4分)(2014•黔南州)二元一次方程组的解是( )A .B .C .D .4.(4分)(2014•黔南州)下列事件是必然事件的是( ) A . 抛掷一枚硬币四次,有两次正面朝上B . 打开电视频道,正在播放《十二在线》C . 射击运动员射击一次,命中十环D . 方程x 2﹣2x ﹣1=0必有实数根5.(4分)(2014•黔南州)下列计算错误的是( ) 6.(4分)(2014•黔南州)下列图形中,∠2大于∠1的是( )A .B .C .D .7.(4分)(2014•黔南州)正比例函数y=kx (k≠0)的图象在第二、四象限,则一次函数y=x+k 的图象大致是( ) A .B .C .D .8.(4分)(2014•黔南州)形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )9.(4分)(2014•黔南州)下列说法中,正确的是( )10.(4分)(2014•黔南州)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是( )11.(4分)(2014•黔南州)如图,在△ABC 中,∠ACB=90°,BE 平分∠ABC ,ED ⊥AB 于D .如果∠A=30°,AE=6cm ,那么CE 等于( )12.(4分)(2014•黔南州)如图,圆锥的侧面积为15π,底面积半径为3,则该圆锥的高AO 为( )A . 3B . 4C . 5D . 1513.(4分)(2014•黔南州)如图,把矩形纸片ABCD 沿对角线BD 折叠,设重叠部分为△EBD ,则下列说法错误的是( )二、填空题(共6小题,每小题5分,满分30分)14.(5分)(2014•黔南州)在全国初中数学竞赛中,都匀市有40名同学进入复赛,把他们的成绩分为六组,第一组一第四组的人数分别为10,5,7,6,第五组的频率是0.2,则第六组的频率是 。
贵州省黔东南州2014年中考语文试题(word版,无答案)

黔东南州2014年初中毕业升学统一考试试题语文本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间150分钟,第Ⅰ卷l至2页,第Ⅱ卷3至6页,考试结束后本卷与答题卡一并收回。
注意事项:1.第Ⅰ卷共10小题,每题3分,共30分。
2.答题前,考生必须使用0. 5毫米黑色签字笔先将姓名、准考证号填写在答题卡规定的位置上。
3.必须使用2B铅笔将答题卡上对应标号涂黑,如需改动,用橡胶擦擦干净后再重新选潦其它答案标号,所有题目必须在答题卡上作答,在试题卷上答题无效。
第Ⅰ卷一、(21分)(每小题3分)1.下列词语中加点字注音完全正确..的一项是()A.抽搐.(chù) 静谧.(mì) 心宽体胖.(pán)B.伧.俗(cāng) 骸.骨(hé) 浑身解.数(xiè)C.秫.秸(shǔ) 讪.笑(shān) 龙吟凤哕.(suì)D.荸.荠(pǔ)荇.藻(xìng) 猝.然长逝(cù)2.下列对加点字词的解释完全正确..的一项是()A.伫立..(长时间站着)警报迭.(突然)起B.羁.(约束)绊进退维.(是)谷C.臆.(主观的)测触日伤怀.(怀念)D.荣膺.(胸中)不言而喻.(说明)3下列句子中没有语病....的一项是()A.通过开展党的群众路线教育实践活动,当地的老百姓得到了实惠。
B.环境的好坏、服务质量的优劣,是我州旅游业健康发展的重要保证。
C.苗乡侗寨原生态的自然环境和浓郁的民族风情,成为众多游客心驰神往的旅游胜地。
D.伴随《舌尖上的中国》第二部的全国热播,不仅让大家了解各地美食,而且引发了人们对“文化认同”的思考。
4.下列句子中加点词语运用恰当..的一项是()A.其实,这两篇文章的主题思想大相径庭....,都是歌颂母爱,赞美亲情的。
B.相比“地沟油”而言,那些“毒大米”对人们身体健康的危害有过之无不及......。
贵州省黔东南州2014年中考数学试卷及答案(解析word版)
2014年贵州省黔东南州中考数学试卷一、选择题:每个小题4分,10个小题共40分1.(4分)(2014年贵州黔东南)=()A. 3 B.﹣3 C.D.﹣考点:绝对值.分析:按照绝对值的性质进行求解.解答:解:根据负数的绝对值是它的相反数,得:|﹣|=.故选C.点评:绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.(4分)(2014年贵州黔东南)下列运算正确的是()A.a2•a3=a6B.(a2)3=a6C.(a+b)2=a2+b2D.+=考点:完全平方公式;实数的运算;同底数幂的乘法;幂的乘方与积的乘方.专题:计算题.分析:A、原式利用同底数幂的乘法法则计算得到结果,即可做出判断;B、原式利用幂的乘方运算法则计算得到结果,即可做出判断;C、原式利用完全平方公式展开得到结果,即可做出判断;D、原式不能合并,错误.解答:解:A、原式=a5,错误;B、原式=a6,正确;C、原式=a2+b2+2ab,错误;D、原式不能合并,错误,故选B点评:此题考查了完全平方公式,实数的运算,同底数幂的乘法,以及幂的乘方与积的乘方,熟练掌握公式及法则是解本题的关键.3.(4分)(2014年贵州黔东南)如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是()A.AB∥DC,AD=BC B.A B∥DC,AD∥BC C.AB=DC,AD=BC D.OA=OC,OB=OD考点:平行四边形的判定.分析:根据平行四边形的判定定理分别进行分析即可.解答:解:A、“一组对边平行,另一组对边相等”是四边形也可能是等腰梯形,故本选项符合题意;B、根据“两组对边分别平行的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;C、根据“两组对边分别相等的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;D、根据“对角线互相平分的四边形是平行四边形”可判定四边形ABCD为平行四边形,故此选项不符合题意;故选:A.点评:此题主要考查了平行四边形的判定,关键是掌握判定定理:(1)两组对边分别平行的四边形是平行四边形.(2)两组对边分别相等的四边形是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.(4)两组对角分别相等的四边形是平行四边形.(5)对角线互相平分的四边形是平行四边形.4.(4分)(2014年贵州黔东南)掷一枚质地均匀的硬币10次,下列说法正确的是()A.可能有5次正面朝上B.必有5次正面朝上C.掷2次必有1次正面朝上D.不可能10次正面朝上考点:随机事件.分析:根据随机事件是指在一定条件下,可能发生也可能不发生的事件,可得答案.解答:解:A、是随机事件,故A正确;B、不是必然事件,故B错误;C、不是必然事件,故C错误;D、是随机事件,故D错误;故选:A.点评:解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.5.(4分)(2014年贵州黔东南)如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B. 1.5 C. D. 1考点:旋转的性质.分析:解直角三角形求出AB,再求出CD,然后根据旋转的性质可得AB=AD,然后判断出△ABD是等边三角形,根据等边三角形的三条边都相等可得BD=AB,然后根据CD=BC ﹣BD计算即可得解.解答:解:∵∠B=60°,∴∠C=90°﹣60°=30°,∵AC=,∴AB=×=1,∴BC=2AB=2,由旋转的性质得,AB=AD,∴△ABD是等边三角形,∴BD=AB=1,∴CD=BC﹣BD=2﹣1=1.故选D.点评:本题考查了旋转的性质,等边三角形的判定与性质,解直角三角形,熟记性质并判断出△ABD是等边三角形是解题的关键.6.(4分)(2014年贵州黔东南)如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为()A.4cm B.3cm C.2cm D.2cm考点:圆周角定理;等腰直角三角形;垂径定理.专题:计算题.分析:连结OA,根据圆周角定理得∠AOD=2∠ACD=45°,由于3⊙O的直径CD垂直于弦AB,根据垂径定理得AE=BE,且可判断△OAE为等腰直角三角形,所以AE=OA=,然后利用AB=2AE进行计算.解答:解:连结OA,如图,∵∠ACD=22.5°,∴∠AOD=2∠ACD=45°,∵⊙O的直径CD垂直于弦AB,∴AE=BE,△OAE为等腰直角三角形,∴AE=OA,∵CD=6,∴OA=3,∴A E=,∴AB=2AE=3(cm).故选B.点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰直角三角形的性质和垂径定理.7.(4分)(2014年贵州黔东南)已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2014的值为()A.2012 B.2013 C.2014 D. 2015考点:抛物线与x轴的交点.分析:把x=m代入方程x2﹣x﹣1=0求得m2﹣m=1,然后将其整体代入代数式m2﹣m+2014,并求值.解答:解:∵抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),∴m2﹣m﹣1=0,解得m2﹣m=1.∴m2﹣m+2014=1+2014=2015.故选:D.点评:本题考查了抛物线与x轴的交点.解题时,注意“整体代入”数学思想的应用,减少了计算量.8.(4分)(2014年贵州黔东南)如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为()A.1 B.2C.D.考点:反比例函数系数k的几何意义.专题:计算题.分析:由于正比例函数y=x与反比例函数y=的图象相交于A、B两点,则点A与点B 关于原点对称,所以S△AOC=S△BOC,根据反比例函数比例系数k的几何意义得到S△BOC=,所以△ABC的面积为1.解答:解:∵正比例函数y=x与反比例函数y=的图象相交于A、B两点,∴点A与点B关于原点对称,∴S△AOC=S△BOC,∵BC⊥x轴,∴△ABC的面积=2S△BOC=2××|1|=1.故选A.点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数y=的图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.9.(4分)(2014年贵州黔东南)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有()A.①②③B.①②④C.①③④D.②③④考点:二次函数图象与系数的关系.分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=﹣1时,x=2时二次函数的值的情况进行推理,进而对所得结论进行判断.解答:解:由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于正半轴知:c>0,由对称轴直线x=2,可得出b与a异号,即b<0,则abc<0,故①正确;把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c,由函数图象可以看出当x=﹣1时,二次函数的值为正,即a+b+c>0,则b<a+c,故②选项正确;把x=2代入y=ax2+bx+c得:y=4a+2b+c,由函数图象可以看出当x=2时,二次函数的值为负,即4a+2b+c<0,故③选项错误;由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2﹣4ac>0,故④D选项正确;故选B.点评:本题考查二次函数图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=4a+2b+c,然后根据图象判断其值.10.(4分)(2014年贵州黔东南)如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为()A. 6 B.12 C.2D. 4考点:翻折变换(折叠问题).分析:设BE=x,表示出CE=16﹣x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.解答:解:设BE=x,则CE=BC﹣BE=16﹣x,∵沿EF翻折后点C与点A重合,∴AE=CE=16﹣x,在Rt△ABE中,AB2+BE2=AE2,即82+x2=(16﹣x)2,解得x=6,∴AE=16﹣6=10,由翻折的性质得,∠AEF=∠CEF,∵矩形ABCD的对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AE=AF=10,过点E作EH⊥AD于H,则四边形ABEH是矩形,∴EH=AB=8,AH=BE=6,∴FH=AF﹣AH=10﹣6=4,在Rt△EFH中,EF===4.故选D.点评:本题考查了翻折变换的性质,矩形的判定与性质,勾股定理,熟记各性质并作利用勾股定理列方程求出BE的长度是解题的关键,也是本题的突破口.二、填空题:每个小题4分,6个小题共24分11.(4分)(2014年贵州黔东南)cos60°=.考点:特殊角的三角函数值.分析:根据特殊角的三角函数值计算.解答:解:cos60°=.点评:本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要掌握特殊角度的三角函数值.12.(4分)(2014年贵州黔东南)函数y=自变量x的取值范围是x>1.考点:函数自变量的取值范围.分析:根据二次根式被开方数非负、分母不等于0列式计算即可得解.解答:解:有意义的条件是x﹣1≥0,解得x≥1;又分母不为0,x﹣1≠0,解得x≠1.∴x>1.故答案为:x>1.点评:本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.13.(4分)(2014年贵州黔东南)因式分解:x3﹣5x2+6x=x(x﹣3)(x﹣2).考点:因式分解-十字相乘法等;因式分解-提公因式法.分析:先提取公因式x,再利用十字相乘法分解因式.解答:解:x3﹣5x2+6x=x(x2﹣5x+6)=x(x﹣3)(x﹣2).故答案是:x(x﹣3)(x﹣2).点评:本题考查了用提公因式法和十字相乘法分解因式,一个多项式有公因式首先提取公因式,然后用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.14.(4分)(2014年贵州黔东南)若一元二次方程x2﹣x﹣1=0的两根分别为x1、x2,则+=﹣1.考点:根与系数的关系.分析:欲求+的值,先把此代数式变形为两根之积或两根之和的形式,再代入数值计算即可.解答:解:∵一元二次方程x2﹣x﹣1=0的两根分别为x1、x2,∴x1+x2=1,x1x2=﹣1,∴+===﹣1.故答案为﹣1.点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.15.(4分)(2014年贵州黔东南)在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为5.考点:由三视图判断几何体.分析:易得此几何体有三行,三列,判断出各行各列最少有几个正方体组成即可.解答:解:底层正方体最少的个数应是3个,第二层正方体最少的个数应该是2个,因此这个几何体最少有5个小正方体组成,故答案为5.点评:本题考查了由三视图判断几何体的知识,解决本题的关键是利用“主视图疯狂盖,左视图拆违章”找到所需最少正方体的个数.16.(4分)(2014年贵州黔东南)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为.考点:轴对称-最短路线问题;一次函数图象上点的坐标特征.分析:利用一次函数图象上点的坐标性质得出OA′=1,进而利用勾股定理得出即可.解答:解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,此时PA+PB最小,由题意可得出:OA′=1,BO=2,PA′=PA,∴PA+PB=A′B==.故答案为:.点评:此题主要考查了利用轴对称求最短路线以及一次函数图象上点的特征等知识,得出P点位置是解题关键.三、解答题:8个小题,共86分17.(8分)(2014年贵州黔东南)计算:2tan30°﹣|1﹣|+(2014﹣)0+.考点:实数的运算;零指数幂;特殊角的三角函数值.分析:本题涉及零指数幂、绝对值、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=2×﹣(﹣1)+1+=﹣+1+1+=2.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是掌握零指数幂、绝对值、特殊角的三角函数值、二次根式化简等考点的运算.18.(8分)(2014年贵州黔东南)先化简,再求值:÷﹣,其中x=﹣4.考点:分式的化简求值.专题:计算题.分析:原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算得到最简结果,将x的值代入计算即可求出值.解答:解:原式=•﹣=﹣=,当x=﹣4时,原式==.点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.19.(10分)(2014年贵州黔东南)解不等式组,并写出它的非负整数解.考点:解一元一次不等式组;一元一次不等式组的整数解.分析:分别求出各不等式的解集,再求出其公共解集,找出符合条件的x的非负整数解即可.解答:解:,由①得,x>﹣,由②得,x<,故此不等式组的解集为:﹣<x<,它的非负整数解为:0,1,2,3.点评:本题解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.20.(12分)(2014年贵州黔东南)黔东南州某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:学习时间t(分钟)人数占女生人数百分比0≤t<30 4 20%30≤t<60 m 15%60≤t<90 5 25%90≤t<120 6 n120≤t<150 2 10%根据图表解答下列问题:(1)在女生的频数分布表中,m=3,n=0.3.(2)此次调查共抽取了多少名学生?(3)此次抽样中,学习时间的中位数在哪个时间段?(4)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽到男女生各一名的概率是多少?考点:频数(率)分布直方图;频数(率)分布表;中位数;列表法与树状图法.分析:(1)根据第一段中有4人,占20%,即可求得女生的总人数,然后根据频率的计算公式求得m、n的值;(2)把直方图中各组的人数相加就是男生的总人数,然后加上女生总人数即可;(3)求得每段中男女生的总数,然后根据中位数的定义即可判断;(4)利用列举法即可求解.解答:解:(1)女生的总数是:4÷20%=20(人),则m=20×15%=3(人),n==0.3;(2)男生的总人数是:6+5+12+4+3=30(人),则此次调查的总人数是:30+20=50(人);(3)在第一阶段的人数是:4+6=10(人),第二阶段的人数是:3+5=8(人),第三阶段的人数是:5+12=17(人),则中位数在的时间段是:60≤t<90;(4)如图所示:共有20种等可能的情况,则恰好抽到男女生各一名的概率是=.点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.21.(12分)(2014年贵州黔东南)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B 作BD⊥CP于D.(1)求证:△ACB∽△CDB;(2)若⊙O的半径为1,∠B CP=30°,求图中阴影部分的面积.考点:切线的性质;扇形面积的计算;相似三角形的判定与性质.分析:(1)由CP是⊙O的切线,得出∠BCD=∠BAC,AB是直径,得出∠ACB=90°,所以∠ACB=∠CDB=90°,得出结论△ACB∽△CDB;(2)求出△OCB是正三角形,阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.解答:(1)证明:∵直线CP是⊙O的切线,∴∠BCD=∠BAC,∵AB是直径,∴∠ACB=90°,又∵BD⊥CP∴∠CDB=90°,∴∠ACB=∠CDB=90°∴△ACB∽△CDB;(2)解:如图,连接OC,∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,∴阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.点评:本题主要考查了切线的性质及扇形面积,三角形的面积,解题的关键是利用弦切角找角的关系.22.(10分)(2014年贵州黔东南)黔东南州某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:≈1.41,≈1.73)考点:解直角三角形的应用-仰角俯角问题.分析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.25m.由小明站在B 点测得旗杆顶端E点的仰角为45°,可得△AEM是等腰直角三角形,继而得出得出AM=ME,设AM=ME=xm,则CN=(x+6)m,EN=(x﹣0.25)m.在Rt△CEN中,由tan∠ECN==,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.解答:解:过点A作AM⊥EF于M,过点C作CN⊥EF于N,∴MN=0.25m,∵∠EAM=45°,∴AM=ME,设AM=ME=xm,则CN=(x+6)m,EN=(x﹣0.25)m,∵∠ECN=30°,∴tan∠ECN===,解得:x≈8.8,则EF=EM+MF≈8.8+1.5=10.3(m).答:旗杆的高EF为10.3m.点评:本题考查了解直角三角形的问题.该题是一个比较常规的解直角三角形问题,建立模型比较简单,但求解过程中涉及到根式和小数,算起来麻烦一些.23.(12分)(2014年贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.(1)求每件甲种、乙种玩具的进价分别是多少元?(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.考点:一次函数的应用;二元一次方程组的应用;一元一次不等式的应用.分析:(1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,根据“5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元”列出方程组解决问题;(2)分情况:不大于20件;大于20件;分别列出函数关系式即可;(3)设购进玩具x件(x>20),分别表示出甲种和乙种玩具消费,建立不等式解决问题.解答:解:(1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,由题意得,解得,答:件甲种玩具的进价是30元,每件乙种玩具的进价是27元;(2)当0<x≤20时,y=30x;当x>20时,y=20×30+(x﹣20)×30×0.7=21x+180;(3)设购进玩具x件(x>20),则乙种玩具消费27x元;当27x=21x+180,则x=30所以当购进玩具正好30件,选择购其中一种即可;当27x>21x+180,则x>30所以当购进玩具超过30件,选择购甲种玩具省钱;当27x<21x+180,则x<30所以当购进玩具少于30件,选择购乙种玩具省钱.点评:此题考查二元一次方程组,一次函数,一元一次不等式的运用,理解题意,正确劣势解决问题.24.(14分)(2014年贵州黔东南)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A (,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.考点:二次函数综合题.分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)根据直线AB的解析式,可求得直线AC的解析式y=﹣x+b,已知了点A的坐标,即可求得直线AC的解析式,联立抛物线的解析式,可求得C点的坐标;解答:解:(1)∵B(4,m)在直线线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx﹣4上,∴,∵c=6,∴a=2,b=﹣8,∴y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)设直线AC的解析式为y=﹣x+b,把A(,)代入得:=﹣+b,解得:b=3,∴直线AC解析式:y=﹣x+3,点C在抛物线上,设C(m,2m2﹣8m+6),代入y=﹣x+3得:2m2﹣8m+6=﹣m+3,整理得:2m2﹣7m+3=0,解得;m=3或m=,∴P(3,0)或P(,).点评:此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识;。
2014年贵州省黔南州中考英语(word版,有解析)
2014年黔南州初中毕业生学业(升学)统一考试英语试卷注意事项:1、答题前,考生务必用直径0.5毫米黑色签字笔将自己的姓名、准考证号清楚地填写在答题卡规定的位置上。
2、答题时,卷I必须用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号;卷II必须用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上,在试卷上作答无效。
3、本试卷共8页,满分150分,考试时间120分钟。
4、考试结束后,试卷和答题卡一并交回。
第I卷(选择题共1 05分)A)从下面各题所给的A、B、C、D四个选项巾,选出可以填入空白处的最佳选项。
(2014年黔南州)1. -We have ________ 8-day holiday.-Why not go to West Lake?A. an; theB. a; aC. a; theD. an; a1. A【解析】考查冠词的用法。
句意为:——我们有八天的假期。
——为什么不去西湖呢?不定冠词a/an表泛指;在辅音音素前用a;在元音音素前用an;the表特指,也用在由普通名词变来的专有名词前。
8-day以元音音素开头,表示一个,用an;West Lake是由普通名词变来的专有名词。
故选A。
(2014年黔南州)2. -Which class won the basketball match?did.A. Class ThirdB. Class ThreeC. Third ClassD. Three Class2. B【解析】考查数词的用法。
句意为:——哪个队赢了篮球赛?——________赢了。
在英语中表示几年级班级时,一般用基数词,放在年级或班级之后,并且首字母都要大写,故选B。
(2014年黔南州)3.The Spring Festival in January or February.A. celebratesB. was celebratedC. celebratedD. is celebrated3. D【解析】考查被动语态。
2014年贵州省黔南州中考英语试题(含答案)
2014年黔南州初中毕业生学业(升学)统一考试英语试卷注意事项:在答题卡规定的位置上。
2、答题时,卷I必须用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦的位置上,在试卷上作答无效。
3、本试卷共8页,满分150分,考试时间120分钟。
4、考试结束后,试卷和答题卡一并交回。
第I卷(选择题共1 05分)A)从下面各题所给的A、B、C、D四个选项巾,选出可以填入空白处的最佳选项。
1. -W e have ________ 8-day holiday.-Why not go to West Lake?A. an; theB. a; aC. a; theD. an; a2. -Which class won the basketball match?did.A. Class ThirdB. Class ThreeC. Third ClassD. Three Classin January or February.A. celebratesB. was celebratedC. celebratedD. is celebrated4. -Exercising more is good for us.-So, I'd rather _ an hour's walk to school than consider _ a bus.A. take; takeB. taking; takingC. take; takingD. taking; take5. We should remember to spend some time _ your loved ones, because they're not going to be around forever.A. fromB. withC. inD. on6. Jimmy has sixteen broken bikes to and gives away to kids who don't have bikes.A. look upB. set upC. put upD. fix up7. Hi, guy! You _ _ not park your car here. It's for our customers only.A. needB. canC. willD. may8. -His friend wants to go swimming _ it's very hot.-it’s OK. But allow him to do that alone!A. so; notB. so; don'tC. because; notD. because; don't9. After a long walk in the sun, they wanted to drinkA. cold somethingB. something coldC. nothing coldD. cold anything10. -David has been away for more than 25days.-I miss him very much. You know, 25days _ short.A. isB. isn'tC. areD. aren't11. the mountain is, the air is.A. The higher;the thinnerB. Higher; thinnerC. The higher; the thinnerD. More higher; more thinner12. -Do you know ?-Oh, it means a healthy, encouraging and hopeful power.A. what does 'positive energy' meanB. what 'positive energy' meansC. if it means 'positive energy'D. that it means 'positive energy'13. -We couldn't find you anywhere around 8:00 yesterday evening.-I am sorry for it. My mother and I in the square.A. dancedB. will danceC. were dancingD. are dancing14. The boy called his teacher for help because he couldn't solve the problem by _A. herselfB. himselfC. yourselfD. themselves15. -Ann, could you help me?-Wait a minute. IA. am locking the doorB. have locked the doorC. lock the doorD. was locking the door16. Do you know the man is talking to our English teacher?A. whomB. whoC. whichD. what17. -Mr. Miller, I am afraid that I can't finish this work in a week.-My boy, be brave and tell yourselfA. don't give upB. not give upC. not to give upD. to give up18. -Do you think yesterday's math problem was difficult?-Yes, I could _ work it out.A. easilyB. hardlyC. finallyD. nearly19. - is it from the village to your school?-About 5 kilometers.A. How oftenB. How soonC. How longD. How far20. -We're doing really well this term. We believe we will win!--_______________.A. Nice idea!B. You are in with a chance to win.C. I bet you do!D. Thank you.B)从下面各题所给的A. B. C. D四个选项中,选出与划线部分意思相同或相近的最佳选项。
黔东南州2014年初中毕业升学统一考试试卷——物理卷及答案解析
黔东南州2014年初中毕业升学统一考试试卷理科综合(本试题包含物理卷和化学卷,满分150分。
考试时间150分钟)注意事项:1、答题时务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2、答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3、答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4、所有题目必须在答题卡上作答,在试卷上答题无效。
5、考试结束后,将试卷和答题卡一并收回。
物理卷(本试卷为1~6页,共六个大题,25个小题。
满分90分)一、选择题(每小题3分,共24分,每小题只有一个答案是正确的,请用2B铅笔将答题卡上对应字母标号涂黑)1.如图所示是描述地球上不同位置的人释放手中石块的四个示意图,图中的虚线表示石块下落的路径,则对石块下落路径的描述最接近实际的示意图是()A B C D2.如图所示的四种物态变化的实例中,属于凝华的是()A.山间形成浓雾B.冰雪消融C.草叶上形成“白霜”D.草叶上形成“露珠”3.如图所示的四种现象中,属于光的折射现象的是()A. 通过汽车后视镜看到该车后面的其他车辆B. 钢勺子好像在水面处折断了C. 车子在水中形成“倒影”D. 点燃的蜡烛通过小孔成像4.有一种“光控开关”能在天黑时自动闭合,天亮时自动断开;而另一种“声控开关”能在有声音时自动闭合,无声音时自动断开利用“光控开关”和“声控开关”来控制居民楼里楼道灯可以节约电,要求灯白天不会亮,天黑后楼道有人走动发出声音时灯会自动亮,下列如图4所示的电路图中合理的是()A B C D5.关于电流表和电压表的使用,下列说法错误的是()A.使用前都应检查指针是否指零B.若有两个量程,一般都先用大量程“试触”C.两表都不能将两接线柱直接接到电源的两极上D.接入电路时,都应使电流从正接线柱流入,从负接线柱流出6.如图所示,人沿水平方向拉牛,但没有拉动.其中说法正确的是()A.绳拉牛的力小于牛拉绳的力B.绳拉牛的力小于地面对牛的摩擦力C.绳拉牛的力与牛拉绳的力是一对平衡力D.绳拉牛的力与地面对牛的摩擦力是一对平衡力7.如图所示,已知人造地球卫星绕地球运行的轨道是椭圆形的,有一近地点和远地点,下面关于卫星的说法正确的是()A.当卫星从远地点向近地点运动时,速度变大B.当卫星从近地点向远地点运动时,速度变大C.当卫星在远地点时,动能最大,重力势能最小D.当卫星在近地点时,动能最小,重力势能最大8.如图的电路中,电源电压保持不变.闭合开关S,当滑动变阻器的滑片P向右移动时,不变的是()A.电流表A示数与电流表A1示数的差值B.电压表V示数与与电流表A示数的比值C.电压表V示数与与电流表A示数的乘积D.电压表V示数与与电流表A1示数的乘积二、填空题(每空1分,共15分)9.如图所示,近年在黔东南州“一事一议”财政奖补政策的支持下,农村道路两旁安装有太阳能路灯,这样改善了农村的村容村貌,灯杆顶端是太阳能电池板,它能将能转化为能,并向放在灯杆中的蓄电池充电,充电时把能转化为能蓄存起来,夜晚蓄电池给路灯供电。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机密★启用前
黔东南州2014年初中毕业生学业(升学)统一考试
数学试题卷
(全卷总分150分,考试时间120分钟)
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其它答案标号.
3.答非选择题时,必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上.
4.所有题目必须在答题卡上作答,在试题卷上答题无效.
5.考试结束后,将试题卷和答题卡一并交回.
一、选择题(本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项
是符号题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满.)
1.=()
A.3 B.﹣3 C.D.﹣
2.下列运算正确的是()
A.a2•a3=a6B.(a2)3=a6C.(a+b)2=a2+b2D.+=
3.掷一枚质地均匀的硬币10次,下列说法正确的是()
A.可能有5次正面朝上B.必有5次正面朝上
C.掷2次必有1次正面朝上D.不可能10次正面朝上
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是()
A.AB∥DC,AD=BC B.AB∥DC,AD∥BC
C.AB=DC,AD=BC D.OA=OC,OB=OD
(4题图) (5题图)
5.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()
A.0.5 B.1.5 C.D.1
6.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2014的值为()A.2012 B.2013 C.2014 D.2015
7.如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为()
A.4cm B.3cm C.2cm D.2cm
(7题图) (8题图)
8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为()
A.1 B.2C.D.
9.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0
其中正确结论的有()
A.①②③B.①②④C.①③④D.②③④
(9题图) (10题图)
10.如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A 重合,则折痕EF的长为()
A.6 B.12 C.2D.4
二、填空题(每个小题4分,共24分)。
11.cos60°=.
12.函数y=自变量x的取值范围是.
13.因式分解:x3﹣5x2+6x=.
14.若一元二次方程x2﹣x﹣1=0的两根分别为x1、x2,则+=.
15.在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为.
(15题图) (16题图)
16.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为.
三、解答题(8个小题,共86分)。
17.(8分)计算:2tan30°﹣|1﹣|+(2014﹣)0+.
18.(8分)先化简,再求值:÷﹣,其中x=﹣4.
19.(10分)解不等式组,并写出它的非负整数解.
20.(12)黔东南州某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
根据图表解答下列问题:
(1)在女生的频数分布表中,m=,n=.
(2)此次调查共抽取了多少名学生?
(3)此次抽样中,学习时间的中位数在哪个时间段?
(4)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽
到男女生各一名的概率是多少?
21.(12)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠B CP=30°,求图中阴影部分的面积.
22.(10)黔东南州某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:≈1.41,≈1.73)
23.(12)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
24.(14)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),
点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.。
