基本不等式―最值―对勾函数-耐克函数(学案 附答案)
基本不等式—最值—对勾函数耐克函数(学案 附答案)

基本不等式——形式一:a b +≥(a>0,b>0)____a b +( )——形式二:2a b+≥ (a__0,b__0)__(a >0,b >0)2a b + ——形式三:22a b ab +⎛⎫≤ ⎪⎝⎭( )(a>0,b>0)2a b+≤2a b+? 用分析法证明:要证2a b+ (1) 只要证 a b +≥ (2)要证(2),只要证____0a b +-≥ (3) 要证(3),只 要证2(__________)0-≥ (4)显然(4)是成立的. 当且仅当a=b 时,(4)中的等号成立.探究3:使用基本不等式的三个条件:一正二定三相等思考:(1)已知y=x+x1 ( x>0 ) ,求y 的范围.(2)已知y=x+x1( x≠0 ) ,求y 的范围.例题拓展【例1 】已知0x >,则xx 432++的最小值是________。
【 例2 】下列不等式一定成立的是 ( )A .xy y x 2≥+B .21≥+xx C .xy y x 222≥+ D .xyxy y x 12≥+【 例3 】下列结论中,错用基本不等式做依据的是( )基础回顾1、对于____ _ ,a b ,有22____2a b ab +,当且仅当____ _ 时,等号成立.2、基本不等式:对于____ _,a b ,则2a b+___ _时,不等式取等号.注意:使用基本不等式时,应具备三个条件:____ _ ____ _【例1 】(1)已知x >0,且y = x +81x,x =_________时,y 取最小值 (2)已知0x >,则xx 432++的最小值是________。
(3)y x x=++23122的最小值是(4)a+b=2,则3a +3b 的最小值是______________(5)a+2b=4,则3a +9b 的最小值是______________【 例2】设x ,y 为正数, 求14()()x y x y++的最小值【例4 】若0,0,x y >>且211x y+=,则2x y +的最小值为________练兵场:1、函数y =31-x + x (x>3) 的最小值是_________。
高考数学复习专题系列学案:基本不等式对勾函数

基本不等式与对勾函数b、对勾函数y = ax • b (a . 0,b .0)的图像与性质x性质: 1.定义 '*_f(x) =aj+ —>C.A A 0) 当孟a 0*. == 3 + —2石瓦f 当 且仅当站=—)」AX当孟= —(iix + —}台 2-Jab,X所臥得到血点坐标A (£.2加)』,_2石咬一41 I I 1*iI I i i| I I5-—_—M —— —三 <_ — ■. ■■ ■■ ■ ■“ ■ ■■ tM' — —' "W— ■* ~ — 1(-=,0) (0,二)2. 值域:(-::,-2 . ab) (2、ab,::)3. 奇偶性:奇函数,函数图像整体呈两个“对勾”的形状,且函数图像关于原点呈中心对称,即 f(x) f(-x) =0 4. 图像在一、三象限当x =0时,由基本不等式知 yuax + PzzJab (当且仅当x = J 匕取等号),xV a由奇函数性质知: 当x<0时,f (x)在x= — 时,取最大值 -^ab\ a一、对勾函数的变形形式 类型一:函数y =ax • b (a ::: 0, b ::: 0)的图像与性质 x此函数与对勾函数 y =(-a)x • J?关于原点对称,故函数图像为x即f (x)在x=—时,取最小值a2 . ab5.单调性:增区间为( 减区间是(0,性质: 类型二:斜勾函数y = ax • b (ab ::: 0)xf(x)二2ax bx c(ac 0)此类函数可变形为cc f(x)二ax b ,贝y f(x)可由对勾函数 y 二ax上下平移得到xx性质: ②a 0,b . 0作图 如下: 类型三:函数例1作函数f (x) x2 x 1的草图解:f(x)二匚x1f(x)=x 1作图如下:x类型四:函数f(x)=x・a(a 0,k") x k此类函数可变形为a t af(x)=(x,k )-k ,则f (x)可由对勾函数y = x 左右平移,x上下平移得到例2作函数f (x)的草图x -2解:f (x) 例3作函数f(x)=x-2 12作图如下:x — 2=xx -2x 3x 2x 3x「f(x)二x的作图:x 2 1 1 1 f (x) x=1 x=x 2 1 x+2 x+2 x+21 练习:1.求函数f(x) =x 在(2/ ::)上的最低点坐标2x —4 解:f (x)X2.求函数f(X )= X的单调区间及对称中心X —1a.若a • 0 ,则f (x)的单调性和对勾函数 y = x •巴的单调性相反,图像如下: x1 .定义域:(一匚片•::)由奇函数性质知: 当x<0时,f (x)在x= - b 时,取最小值-—a _2Jb5.单调性:减区间为( Jb, +30 ), (一00,-Jb )增区间是[- b, b]类型五: ax函数 f (X )二 2(a = 0,b . 0)f (x)二x 2 b3.奇偶性:奇函数,函数图像整体呈两个倒着的“对勾”的形状,且函数图像关于原点呈 中心对称,即f(x) f (-x) =04.图像在一、三象限 当x 0时,由基本不等式知f (x) V ——a 二a (当且仅当X 二• b 取等号2": 2"即f (x)在x - b 时,取最大值a2“b此类函数定义域为R ,且可变形为性质:3当 x=1 时,f(x)二X-12(x —1)23(xT) 4 (X-1)3(xT) 4 x 〔4x — 1问:若区间改为[4,则f (x)的最大值为2x 7x 10类型七:函数f(x)2x max +bx+cx 1x例4作函数f(x)二—X x 解:f(x)二: x +1 11 x - xb.若acO ,作出函数图像: 2x r 的草图 x 2 4 例5作函数f (x)二类型六:函数 f (x)二 ax bx c(a = 0) x 十m 2 此类函数可变形为f(xH a(X m) S(X m)=a(x m) —t — s(at 0)x+ m则f (x)可由对勾函数 y 二ax •丄左右平移,上下平移得到 xx 2+x +1 1 例6说明函数f(x) 由对勾函数y=x 如何变换而来 ■ x 解:f(x)= (x 1)2 -(x 1) ^x . 1 1 X 十1 故 此函数f (x)可由对勾函数 (填“上”、“下”)平移*1宀 y = x 向 __________ x单位.草图如下:(填 “左”、“右”)平移 单位,2.已知x 1 ,求函数f (X )口x 2 9x -10x-1的最大值练习:1.已知x ^ -1,求函数f(x)=的最小值例7求函数f ( X )工 在区间(1, •二)上的最大值解:当x =1时,f (1)=0x + b 类型八:函数f (x)=Jx + a此类函数可变形为标准形式:f(x^x a ^^./xb-a (b_a.O) v x + ax + 3例8求函数f(x)的最小值 <x 解:f(x) =x "4Jx —1x + 5 •求函数f(x)的值域J x +1函数 f(x)=—— v'x 十此类函数可变形为标准形式:解: y =x…x 2 aa2xf (x )= ( X 2 * * a)2 b-ax 2 a二 x 2 a 「Tag °〉工的最小值4x 2 5 =解:f(x) = x 2 4x 2 4 1 f (x)' = lx 2 +4 十 1 Jx 2 +4 lx 2+4练习:1.求函数f (X )例10已知a 0,求函数y= X 2 1、—2 的值域X 2 17x 2a 1 .X 2—a 的最小值。
高中数学专题7-1 基本不等式和对钩函数(解析版)

4
4
无法直接使用基本不等式,需要凑配位和定:
f (x) 4x(3 2x) 22x(3 2x) 2( 2x 3 2x)2 9 ;
2
2
再如:f (x) 4x 2 1 直接使用基本不等式,则 f (x) 4x 2 1 2 (4x 2) 1 ,
4x 5
4x 5
4x 5
发现积不定,则需要凑配为积定:
【答案】1
【详解】因为 a 1,所以 a 2 a 1 2 1 2 a 1 2 1 2 2 1,
a 1
a 1
a 1
当且仅当 a 1 2 时取等号.故 m 2 2 1, n 2 1,所以, 2n m 1. 故答案为:1. 2.(2022·云南·屏边苗族自治县第一中学高一阶段练习)( 若 x 2 ,求: x 2 的最小值.
【答案】(1) 9
【详解】(1)由题得 y 4x 1 1 4(x 1) 1 5,
x 1
x 1
因为 x 1,所以 x 1 0 ,
所以 4(x 1) 1 5 2 4(x 1) 1 5 9 ,
x 1
x 1
当且仅当 4(x 1) 1 ,即 x 3 时取得等号,
x 1
2
所以 y 4x 1 1 的最小值为 9 . x 1
y
4x2
9 x2
2
4x2
9 x2
12 ,
当且仅当 4x2
9 x2
,即 x
6 时取等号,
2
所以 ymin 12 , 故选:C.
2.(2022·黑龙江·哈尔滨工业大学附属中学校高二学业考试)若 x 0 ,则 x 1 1的最小 x
值是( )
A.0 【答案】B
B.1
C. 3 2
基本不等式(学案)-高中数学人教A版(2019)必修—(Word含解析)

第二章 一元二次函数、方程和不等式2.2 基本不等式学案一、学习目标1. 通过对基本不等式的学习,能够对其进行证明,并会用几种语言来进行解释.2. 能够运用基本不等式来求代数式的最值.3. 能够使用基本不等式解决实际生活中的最值问题,提高用数学手段解答现实生活中的问题的能力.二、基础梳理1. 若00a b >>,≤2a b +,当且仅当a b =时,等号成立. 其中,2a b +叫做正数a ,ba ,b 的几何平均数.2. 基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.三、巩固练习1.已知正数a ,b 满足4a b +=,则1113a b +++的最小值为( ) A.1 B.2 C.4 D.122.如果实数,x y 满足4x y +=,则222x y ++的最小值是( )A .4B .6C .8D .10 3.已知实数0,0a b >>,若21a b +=,则12a b +的最小值是( ) A .83 B .113 C . 4 D .84.已知0x >,0y >,228x y xy ++=,则2x y +的最小值是( )A.3B.4C.92D.1125.若111111M a b c ⎛⎫⎛⎫⎛⎫=--- ⎪⎪⎪⎝⎭⎝⎭⎝⎭,且1a b c ++=(其中a ,b ,c 均为正实数),则M 的取值范围是( ) A.10,8⎡⎫⎪⎢⎣⎭ B.1,18⎡⎫⎪⎢⎣⎭C.[1,8)D.[8,)+∞6.已知0a >,0b >,则11a b ++的最小值是( )A.2B.C.4D.57.若x,y均为正实数,且111223x y+=++,则xy的最小值为( )A.2B.12C.14D.168.已知01x<<,则1221x x+-的最小值为( )A.9B.92C.5D.52参考答案巩固练习1.答案:D解析:因为4a b +=,所以(1)(3)8a b +++=, 所以11111[(1)(3)]13813a b a b a b ⎛⎫+=++++ ⎪++++⎝⎭ 1312813b a a b ++⎛⎫=++ ⎪++⎝⎭128⎛≥+ ⎝ 11(22)82=⨯+=, 当且仅当13a b +=+且4a b +=,即3a =,1b =时,等号成立,所以1113a b +++的最小值为12. 2.答案:D 解析:因222()422x y x y ++=,故22x y +,所以应选D 3.答案:D解析:∵实数0,0a b >>,21a b +=,则()121242448b a a b a b a b a b ⎛⎫==++=++≥+ ⎪⎝⎭,,当且仅当122b a ==时取等号。
耐克函数
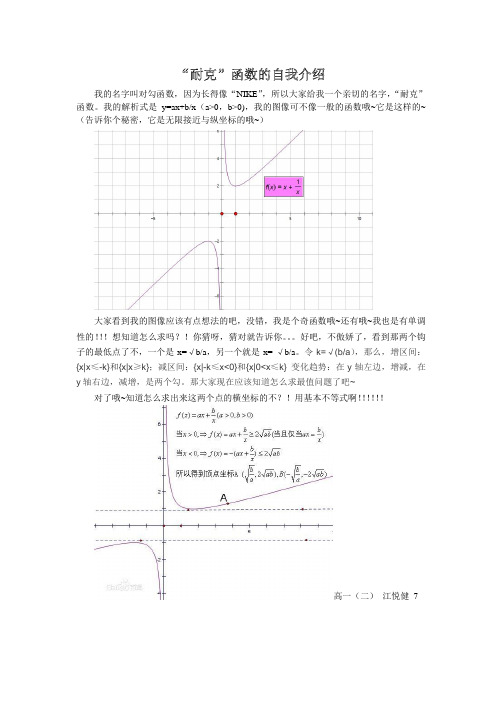
我的名字叫对勾函数,因为长得像“NIKE”,所以大家给我一个亲切的名字,“耐克”函数。
我的解析式是y=ax+b/x(a>0,b>0),我的图像可不像一般的函数哦~它是这样的~(告诉你个秘密,它是无限接近与纵坐标的哦~)
大家看到我的图像应该有点想法的吧,没错,我是个奇函数哦~还有哦~我也是有单调性的!!!想知道怎么求吗?!你猜呀,猜对就告诉你。
好吧,不傲娇了,看到那两个钩子的最低点了不,一个是x=√b/a,另一个就是x=-√b/a。
令k=√(b/a),那么,增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y轴左边,增减,在y轴右边,减增,是两个勾。
那大家现在应该知道怎么求最值问题了吧~ 对了哦~知道怎么求出来这两个点的横坐标的不?!用基本不等式啊!!!!!!
高一(二)江悦健7。
一类“对勾函数”型函数最值求法

教学信息新教师教学近年来高考对函数求最值问题一直都是热点,特别有一类“对勾函数”型的函数的最值越来越明显,对勾函数是一种类似于反比例函数的一般函数。
所谓的对勾函数,函数,是一种教材上没有但考试老喜欢考的函数意和学习。
而函数的最值求法必须注意其定义域,同时其最值求解及研究也离不开均值不等式,所以本文先简单介绍一下对勾函数图像与性质,再通过举例来说明对勾函数最值求解的方法。
对勾函数,的函数,此函数的图像与其参数a ,b ab >0时图像,其图像如下:在本文的例题当中只对参数a >0,b >0时进行研究,当a >0,为单调递增,在特别地当a =b =1时,:即x=1时取等号);当即x上为单调递增,在递减。
一、例题讲解例1(1)数最大值;(2)的最值解(1)令,由对勾函数的性质可知:即t =1,也即x =0时取等号),于是有(2)(x >0,x ≠1)可令,当时,当时所以当时,即f (x )取极大值-1;当时,即f (x )取极小值7。
从上例可知求解函数最值时要注意函数定义域,函数的最值也即函数值域,因此注意函数定义域是必须的。
练习1 已知x >1求下列函数最值:(1(2;(3答案:(18,无最大值;(2)f (x )=3x+无最大值;(3)f (x )最小值为3,无练习2。
(答案:f (x )最小值为。
二、小结本文主要介绍了一下对勾函数型函数最值求解方法,对于对勾函数型函数是指可以通过转化化成对勾函数,所以在求解时首先是先把函数转化成对函数,再利用对勾函数的图像用及性质求解,当然在求解过程中,有些问题可以利用均值不等式来解,但利用均值不等式求解时要注意取等号时是否能成立,若不能成立,文中采用了函数的单调性来求解,如文中的例题3就说明了这一些问题的处理方法。
一类“对勾函数”型函数最值求法左锦辉(丰城市丰城二中 江西 丰城 331100)【中图分类号】G634.6【文献标识码】B【文章编号】2095-3089(2015)24-0258-01Copyright©博看网 . All Rights Reserved.。
对勾函数的性质及应用(史上上最完整版)

对勾函数的性质及应用一、概念:【题型1】函数()(0,0)af x x a k =+>≠【例1】函数1()f x x =+的值域为【例2】函数3()x f x x +=+的值域为【题型2】函数()(0)ax bx cf x ac ++=>。
【例3】函数1()x x f x ++=的值域为【题型3】函数2()(0,0)axf x a b =≠>。
【例4】函数2()1xf x x =+的在区间[)2,+∞上的值域为 【解析】2x ≥,∴,函数15222≥+=【例5】如2214xa x +=-+,(1,2)x ∈,则实数a 的取值范围是(1,2)x ∈4y x x =+1144x x <+,7352a <-<【题型4】函数2()(0)ax bx cf x a ++=≠.【例6】已知1x >-,求函数710()1x x f x x ++=+的最小值。
,1x >-,7101x ++的最小值【例7】已知1x <,求函数299()x x f x +-=的最大值。
,1x <,2991x x +--的最大【题型5】函数2()(0)x mf x a +=≠ 【例8】求函数21()2x f x x x -=++在区间(1,)+∞上的最大值。
【例9】求函数2223()x x f x ++=在区间[0,)+∞上的最大值。
【例10】求函数()f x =的最小值。
类型九:函数2()0)f x a>。
【例12】求函数2()f x=的最小值。
【解析】由题可知,函数22()f x===2t=,则1()()f xg t tt==+,显然在[)2,+∞上单调递增,故min15()(2)222g t g==+=,此时0x=,故函数2()f x=的最小值为52。
【例13】求函数()f x=的值域.。
耐克函数

定义对勾函数是一种类似于反比例函数的一般函数,又被称为“双勾函数”、"勾函数"等。
也被形象称为“耐克函数”所谓的对勾函数(双曲线函数),是形如f(x)=ax+b/x 的函数。
由图像得名。
图像对勾函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。
奇偶性与单调性当x>0时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=sqrt(b/a)的时候(sqrt表示求二次方根)奇函数。
令k=sqrt(b/a),那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y 轴左边,增减,在y轴右边,减增,是两个勾。
渐近线耐克函数的图像是分别以y轴和y=ax为渐近线的两支双曲线。
编辑本段均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,就得到了平均值定理的公式:a+b≥2sqrt(ab)。
现在把ax+b/x套用这个公式,得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
编辑本段导数求解其实用导数也可以研究对勾函数的性质。
不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本不等式―最值―对勾函数-耐克函数(学案附答案)
同步:基本不等式 22 探究1:你能给出a?b?2ab的证明吗?
基本不等式――形式一:a?b?2ab(a>0,b>0)
2ab____a?(b )
――形式二:
a?bab___2(a>0, b>0)2a?b?ab2 (a__0,b__0)
a?b? ――形式三:ab????() 2??
通常我们把上式写作:ab?a?b(a>0,b>0) 2问:由不等式的性质证明基本不等ab?用
分析法证明:要证
a?b? 2a?b?ab (1) 2只要证 a?b? (2)
要证(2),只要证a?b?____?0 (3)要证(3),只要证(_____?_____)2?0 (4)
显然(4)是成立的. 当且仅当a=b时,(4)中的等号成立.
探究3:使用基本不等式的三个条件:一正二定三相等
1思考:(1)已知y=x+ ( x>0 ) ,求y的范围.
x1(2)已知y=x+ ( x≠0 ) ,求y的范围.
x
例题拓展
【例1 】已知x>0,则2?3x?4的最小值是________。
x
【例2 】下列不等式一定成立的是()
A.x?y?2xy B.x? C.x2?y2?2xy D.
1?2 xx?y1 ?2xyxy
【例3 】下列结论中,错用基本不等式做依据的是()
2abx2?2??2 B. A. a,b均为负数,则?2 2b2ax?1C.
D.a?R,(3?a)(1?)?0
?x?3a2?22,x?R x C专题:利用基本不等式的求最值基础回顾
1、对于____ _ a,b,有a2?b2____2ab,当且仅当____ _ 时,等号成立.
2、基本不等式:对于____ _ a,b,则时,不等式取等号.
a?b_____ab,当且仅当___ _2注意:使用基本不等式时,应具备三个条件:____ _ ____ _
题型1 当积ab为定值时,求和a?b最小值【例1 】(1)已知x?0,且y = x+
81,x=_________时,y取最小值 x(2)已知x>0,则2?3x?4的最小值是________。
x3x2?(3)y?2的最小值是 21?x
(4)a+b=2,则3a+3b的最小值是______________
(5)a+2b=4,则3a+9b的最小值是______________
【例2】设x,y为正数,求(x?y)(?
1x4)的最小值 y
【例4 】若x?0,y?0,且
21??1,则x?2y的最小值为________ xy
练兵场:
感谢您的阅读,祝您生活愉快。
