挡土墙土压力计算
(完整word)砌体挡土墙计算实例
(完整word)砌体挡土墙计算实例砌体地下室外墙（挡土墙)验算：已知地下室370mm厚挡土墙，高2.5m墙背直立、光滑、填土面水平.填土的物理力学指标如下:r=18kN/m³。
计算过程:土压力为：q=Ko r HKo=0.5，r=18kN/m³，现在标高-1。
090处加圈梁，所以H取两圈梁之间的高度1。
5m，故q=0。
5x18x1.5=13.5（kN/m）上下有圈梁约束,墙体按固端考虑，则在三角形侧向土压力作用下：弯矩Ma=rG1/20L²=1.2x1/20x13。
5x1。
5²=1.82（kN/m）剪力Va= rG7/20L=1。
2x7/20x13.5x1。
5=8。
5（kN）受弯、受剪承载力计算:墙体MU10烧结页岩实心砖,M10水泥砂浆,370mm墙厚M≤ftmW，V≤fvbz 砌体沿齿缝弯曲抗拉强度设计值ftm=0.8x0.33=0。
264（Mpa）抗剪强度设计值fv=0。
8x0。
17=0.136（Mpa）取1m宽墙体计算单元且按矩形截面计算：截面抵抗距W=bh²/6=1000x370²/6=22.82x1000000 （mm³）截面内力臂z=2h/3=2x370/3=246（mm)砌体受弯承载力ftmW=0。
264x22。
82x1000000=6.0（kN/m）> Ma=1。
82（kN/m）砌体受剪承载力fvbz=0。
136x1000x246=33。
45(kN）> Va=8.5(kN) 综上所诉:370mm厚地下室外墙（挡土墙）受弯、受剪承载力均满足要求.。
挡土墙土压力计算书
式中：S 为破裂棱体 ABC 的面积。通过几何关系分析得破裂棱体面积为：
S sin(90 ) 1 1 1 cos( ) AB BC sin( ) AB AB sin( ) H 2 sec 2 sin( ) 2 2 2 cos( ) sin(90 )
Ex Ea cos( ) E y Ea sin( )
路 基 路 面 工 程 -----李强
长 沙 理 工 大 学 备 课 纸
H Z x 土压力作用点： 3 Z y B Z x tan
2. 破裂角交于路基面 ⑴ 破裂面交于荷载中部（P127） 关键是确定破裂棱体的面积。将破裂棱体分解为三部分：大三角形－虚三角形＋荷载土柱，即：
★ 路基挡土墙一般都可能有向外的位移或倾覆，因此在设计中按墙背土体达到主动极限平衡状态，并取 一定的安全系数， 以保证墙背土体的稳定。 对于墙趾前土体的被动土压力 Ep， 在挡土墙基础一般埋深的情况下， 考虑到各种自然力和人畜活动的作用，一般均不计，以偏于安全。 ㈢ 库伦理论基本假定（教材无） ⑴ 墙后填料为均质散粒体（无粘聚力 c=0） ； ⑵ 挡土墙和滑动土楔视为无压缩或拉伸变形的刚体； ⑶ 滑动土楔沿着墙背和一个通过墙踵的平面滑动； ⑷ 土楔向下滑动时处于主动土压力状态，向上滑动时处于被动土压力状态； ⑸ 滑动土楔刚体形成时，土的自重与墙背反力及破裂反力保持静力平衡状态。 路 基 路 面 工 程 -----李强
第 1 页
㈠ 影响土压力的因素：① 墙体的位移方式；② 计算方法；③ 挡墙的几何尺寸；④ 墙后填土的边界条 件；⑤ 墙后填土的性质与状态；⑥ 荷载的分布与大小；⑦ 自然因素的作用；⑧ 各种因素的组合。<教材无> ㈡ 土压力分类：挡土墙的位移情况不同，可以形成不同性质的土压力。 （P125） 当挡土墙向外移动时（位移或倾覆） ，土压力随之减少，直到墙后土体沿破裂面下滑而处于极限平衡状态， 作用于墙背的土压力称主动土压力 Ea； 当墙向土体挤压移动，土压力随之增大，土体被推移向上滑动处于极限平衡状态，此时土体对墙的抗力称 为被动土压力 Ep； 墙处于原来位置不动，土压力大小介于两者之间，称为静止土压力。
挡土墙土压力计算
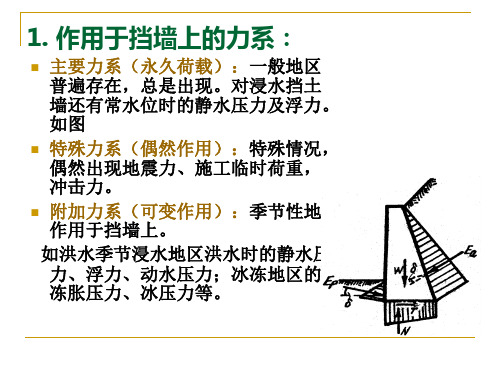
（3）Ea
r ( A0tg
cos(25031' 350 ) B0 ) sin(25031' 690 )
17 (22.8 tg25031'
5.6847)
cos(25031'350 ) sin(25031' 690 )
139.05KN
/
m
Ex Ea cos( ) 139 .05 cos(20 0 14 0 ) 115 .28KN / n Eg Ea sin( ) 77.76KN / m
a)ctg1
Htg ]2
* cos sin 1 cos( 1)
其中： AB (b L) (H a)ctg1 Htg
在ABC
中，由正弦定理：CD
BC
sin
1
AB
cos sin 1 cos( 1)
BC
sin(90
)
AB
sin(90
1)
BC
AB
sin(900 ) sin(900 1)
b
d ]H 0
1 2
(a
H
2h0
)(a
H )tg
1 2
ab
(b
d )h0
1 2
H
(H
2a
2h0
)tg
令： A0
1（a 2
H
2h0
)(a
H
)
B0
1 2
ab
(b
d )h0
1 2
H(H
2a
2h0 )tg
则： S A0tg B0
破裂棱体的重：G rs r( A0tg B0 )
Ea
r ( A0tg
S Somnp SpnB SQmp SOQA SABC Sklij
各个挡土墙详细计算和计算图形
目录1.重力式挡土墙 (2)1.1土压力计算 (2)1.2挡土墙检算 (4)2.2设计计算 (6)3.扶壁式挡土墙 (9)3.1土压力计算 (9)5.2锚杆设计计算 (16)5.3锚杆长度计算 (17)6.锚定板挡土墙 (17)6.1土压力计算 (17)6.3抗拔力计算 (18)7.土钉墙 (18)7.1土压力计算 (18)7.2土钉长度计算和强度检算 (18)7.3土钉墙内部整体稳定性检算 (19)7.4土钉墙外部整体稳定性检算 (19)1.重力式挡土墙 1.1土压力计算⑴第一破裂面ψϕδα=++tan tan θψ=-±土压力系数：()()()cos tan tan sin θϕλθαθψ+=-+土压力：()()()00cos tan sin a E A B θϕγθθψ+=-+()cos ax a E E δα=- ()sin ay a E E δα=-① 破裂面在荷载分布内侧()2012A A a H =+ ()012tan 22H B ab H a α=-+ a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 21h H h =-()()32211223332x H a H h H h Z H a H h +-+=⎡⎤+-⎣⎦tan y x Z B Z α=-②破裂面在荷载分布范围中()()00122A a H h a H =+++ ()()000122tan 22HB ab b d h H a h α=++-++00h σγλ= a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 2tan tan dh θα=+ 312h H h h =--()()322211032103333322x H a H h H h h h Z H aH ah h h +-++=+-+ tan y x Z B Z α=-③破裂面在荷载分布外侧()2012A a H =+ ()00012tan 22HB ab l h H a α=--+00h σγλ= a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 2tan tan dh θα=+ 03tan tan l h θα=+ 4123h H h h h =---()()()322211033421033332322x H a H h H h h h h h Z H aH ah h h +-+++=+-+tan y x Z B Z α=-⑵第二破裂面 查有关的计算手册。
砌体挡土墙计算实例
砌体挡土墙计算实例在土木工程中，砌体挡土墙是一种常见的结构，用于支撑土体，防止其坍塌或滑移。
为了确保挡土墙的稳定性和安全性，需要进行精确的计算。
下面，我们将通过一个具体的实例来详细介绍砌体挡土墙的计算过程。
假设我们要设计一个高度为 5 米的砌体挡土墙，墙背填土为砂土，填土表面水平，墙后地下水位在墙底以下 1 米处。
挡土墙采用 MU30 毛石、M75 水泥砂浆砌筑，墙身重度为 22kN/m³。
一、土压力计算首先，我们需要计算作用在挡土墙上的土压力。
根据库仑土压力理论，主动土压力系数可以通过以下公式计算：Ka ＝tan²(45° φ/2)其中，φ 为填土的内摩擦角。
假设填土的内摩擦角为 30°，则主动土压力系数 Ka 为：Ka ＝ tan²(45° 30°／2) ＝ 033土压力的分布呈三角形，顶部为零，底部最大。
土压力强度可以通过以下公式计算：σa ＝γhKa其中，γ 为填土的重度，h 为计算点距离填土表面的高度。
假设填土重度为 18kN/m³，则墙顶处土压力强度为零，墙底处土压力强度为：σa ＝ 18×5×033 ＝ 297kN/m²土压力的合力可以通过三角形面积计算：Ea ＝ 05×297×5 ＝ 7425kN/m合力作用点距离墙底的高度为：h ＝ 5/3 ＝ 167m二、抗滑移稳定性验算为了保证挡土墙不会沿基底滑移，需要进行抗滑移稳定性验算。
抗滑移稳定系数 Ks 可以通过以下公式计算：Ks ＝（μ∑Gn ＋ Ep) ／ Ea其中，μ 为基底摩擦系数，∑Gn 为垂直于基底的重力之和，Ep 为墙前被动土压力。
由于本例中不考虑墙前被动土压力，Ep 为零。
假设基底摩擦系数为 04，重力之和为：∑Gn ＝ G ＋ Ey其中，G 为挡土墙自重，Ey 为墙后土压力的水平分力。
挡土墙自重 G 可以通过墙身体积乘以重度计算：G ＝ 05×5×22 ＝ 55kN/m墙后土压力的水平分力 Ey 为：Ey ＝Ea×cos(δ)其中，δ 为墙背与填土之间的摩擦角，假设为 15°。
挡土墙土压力计算
Ea
sin(
)
（2）破裂面交于路基 以图b为例，破裂棱体的断面面积S为
S
1 2
(a
H
)2 (tan
tan )
1 2
(b
a
tan )a
a
H
tan
H
tan
b
a h0
G (A0 tan B0)
Ea
A0
t an
B0
cos( sin(
) )
dEa / d 0
tan tan cot tan ( B0 tan )
Ea 1 H 2 sec2 cos( )sin( ) cos( )
2
cos( )
sin( )
Ea
1
2
H 2Ka
1
2
H2
cos2
cos(
cos2 ( ) )[1 sin( )sin(
)
]2
cos( ) cos( )
令dEa/dθ=0
Ex Ea cos( )
Ey
1.4车辆荷载换算及计算参数
1.车辆荷载换算
原则：近似地按均布荷载来考虑，并将 其换算为容重与墙后填土相同的均布土 层。
1）按墙高确定的附加荷载强度进行换算
2）根据破裂棱体范围内布置的车辆荷裁 换算
墙后破裂棱体上的车辆荷载换算为重度 与墙后填土相同的均布土层，其厚h0为
h0
Q
B0L
2.计算参数
（1）填料的计算内摩擦角和重度 当缺乏可靠试验数据时，填料内摩擦角φ可选用经验数据
（2）墙背摩擦角δ 主要有墙背的粗糙度(墙背愈粗糙，δ值愈大)、填料的性质(φ值愈大，δ值愈大)
和墙后排水条件(排水条件愈好，δ值愈大)等。
挡土墙工程土压力计算、边坡整体稳定性计算方法
附录A 土压力计算A.0.1侧向岩土压力可采用库伦土压力或郎肯土压力公式计算，侧向岩土压力分布应根据支护类型确定。
A.0.2当墙后土体倾斜时，墙后主动土压力合力用公式（A.0.2-1）计算，侧向土压力分布形式为三角形，合力作用点位置距墙底1/3H 处，计算简图见图A.0.2。
2ak a12E H K γ=（A.0.2-1）{[22sin()sin()sin()sin sin ()a q K K αβαβαδααβϕδ+=+-+--]sin()sin()2sin cos cos()ϕδϕβηαϕαβϕδ++-++---（A.0.2-2）2sin cos 1sin()q q K H αβγαβ=++（A.0.2-3）2c Hηγ=（A.0.2-4）式中：ak E —主动土压力合力标准值（kN/m ）；a K —主动土压力系数；H —挡土墙高度（m ）；γ—土体重度（kN/m 3）。
；c —土的黏聚力（kPa ）；ϕ—土的内摩擦角（°）；q —地表均布荷载标准值（kN/m 2）；δ—土对挡土墙墙背的摩擦角（°），可按表A.0.2取值；β—填土表面与水平面的夹角（°）；α—挡土墙墙背的倾角（°）；θ—滑裂面与水平面的夹角（°）。
图A.0.2库伦土压力计算表A.0.2土对挡土墙墙背的摩擦角δ挡土墙情况摩擦角δ墙背平滑，排水不良（0~0.33）ϕ墙背粗糙，排水良好（0.33~0.50）ϕ墙背很粗糙，排水良好（0.50~0.67）ϕ墙背与填土间不可能滑动（0.67~1.00）ϕA.0.3当墙后土体水平，墙后主动土压力标准值可按公式（A.0.3）计算。
aikj j ai 12i j e h q K c γ=⎛⎫=+- ⎪⎝⎭∑（A.0.3）式中：aik e —计算点处的主动土压力标准值（kN/m 2），当aik e <0时取aik e ＝0；ai K —计算点处的主动土压力系数，取2o aii tan (452)K ϕ=-；i c —计算点处土的黏聚力（kN/m 2）；i ϕ—计算点处土的内摩擦角（°）。
挡土墙计算
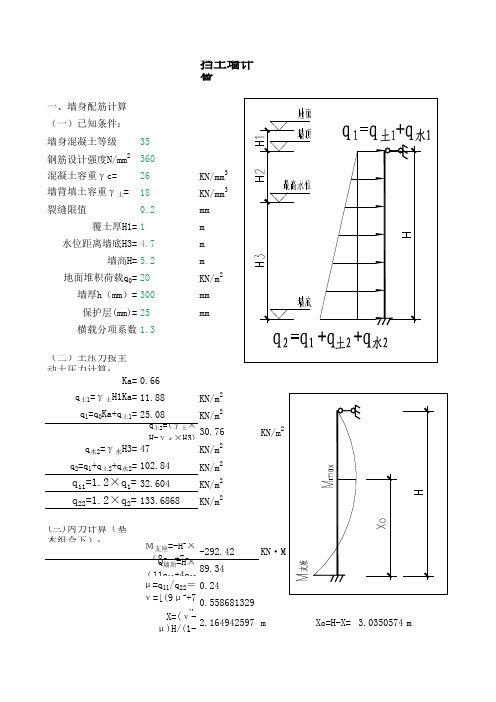
挡土墙计算一、墙身配筋计算（一）已知条件：墙身混凝土等级35钢筋设计强度N/mm 2360混凝土容重γc=26KN/mm 3墙背填土容重γ土=18KN/mm 3裂缝限值0.2mm 覆土厚H1=1m 水位距离墙底H3=4.7m 墙高H=5.2m 地面堆积荷载q 0=20KN/m 2墙厚h（mm）=300mm 保护层(mm)=25mm 横载分项系数1.3（二）土压力按主动土压力计算：Ka=0.66q土1=γ土H1Ka=11.88KN/m 2q 1=q 0Ka+q 土1=25.08KN/m 2q 土2=(γ土×H-γ水×H3)30.76KN/m 2q 水2=γ水H3=47KN/m 2q 2=q 1+q 土2+q 水2=102.84KN/m 2q 11=1.2×q 1=32.604KN/m 2q 22=1.2×q 2=133.6868KN/m 2(三)内力计算（基本组合下）：Ｍ支座=-H 2×（8q 22+7q 11-292.42KN·M Q 墙顶=H×（11q 11+4q 2289.34μ=q 11/q 22＝0.24ν=[(9μ2+7μ0.558681329X=(ν-μ)H/(1-2.164942597m Xo=H-X= 3.0350574mＭmax =Q 墙顶X-q 11X 2/2+84.13227KN·M （四）配筋计算混凝土抗压强度fcd=16.7N/mm 2ho=265mm 钢筋设计强度fy=360N/mm 2计算宽度b=1000mm Ｍ支座 =f cd bx(h 0-x/2)292420114.00 =16700x(265-x/2)x =77.371 m ≤ξb h 0 =0.53×265.00 =140.5mm 解得A s = Ｍ支座/(ho-3691mm 2Ｍmax =f cd bx(h 0-x/2)84000000.00 =16700x(265-x/2)x =19.714 mm ≤ξb h 0 =0.53×265.00 =140.5mm 解得跨中A s = Ｍmax/(ho-940mm 2（五）裂缝计算钢筋直径d=22mm 钢筋间距75mm 每延米实配钢筋A s =5068.44mm 2标准组合下Ｍk 支座=-H 2×-224.94KN·M σsk=Ｍk支座192.4974N/mm2αcr=2.1ρte=0.033789574ftk=2.2ψ=0.880148956< 1 且>0.2所以ψ取0.880148956Es=200000c=25deq=22裂缝宽度W fk =0.177163082mm 裂缝满足要求。
挡土墙及土压力计算
RD 一定位于 R 的下方，即 RD 与 N 之间的夹角φD 一定大于 R 与 N 之间的夹角φ ，鉴于
挡土墙：为G防止12土体 坍H 塌2 而sin修(9建0第o的s六i挡n章(土：结挡)构土)s。inc墙土(o9及s压02 o土力压：墙力后计 )土算体对墙背的作用力称为土压力。
一、三种土压力——根据墙、土间可能的位移方向的不同，土压力可以分为三种类型：
1.主动土压力 Ea——在土压力作用下，挡土墙发生离开土体方向的位移，墙后填土达到极
2.被动土压力 压力系数，应用时，查表。
其中
库仑被动土
Ep 沿深度呈三角形分布，其作用点距墙底 H/3，位于墙背法线下方，与墙背法线成δ角。 库仑理论应用中的几个问题 1. 关于δ的取值: δ值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于 0～φ之间，实用中常取δ =1/2～1/3φ。 2. 当墙后填土为粘性土时——为了得到确切的解析解，库仑理论假设墙后填土为无粘性土，
二、三种土压力在数量上的关系
墙、土间无位移，墙后填土处于弹性平衡状态，与天然状态相同，此时的土压力为静止土压
力；在此基础上，墙发生离开土体方向的位移，墙、土间的接触作用减弱，墙、土间的接触
压力减小，因此主动土压力在数值上将比静止土压力小；而被动土压力是在静止土压力的基
础上墙挤向土体，随着墙、土间挤压位移量的增加，这种挤压作用越来越强，挤压应力越来
此，实用中，可考虑将粘性土的φ值适当增大，用增大后的Δφ来近似考虑 c 值对土压力的
挡土墙计算公式
挡土墙计算公式挡土墙是一种用于支撑填土或山坡土体，防止其变形失稳的结构物。
在工程设计中，准确计算挡土墙的各项参数至关重要，这需要依靠一系列的计算公式。
下面我们就来详细介绍一下常见的挡土墙计算公式。
一、土压力计算土压力是作用在挡土墙上的主要荷载之一，常见的土压力计算方法有朗肯土压力理论和库仑土压力理论。
1、朗肯土压力理论朗肯主动土压力强度计算公式为：＄e_a ＝＼gamma z tan^2(45°＼frac{＼varphi}｛2}） 2c tan(45°＼frac{＼varphi}｛2}）＄朗肯被动土压力强度计算公式为：＄e_p ＝＼gamma z tan^2(45°＋＼frac{＼varphi}｛2}）＋ 2ctan(45°＋＼frac{＼varphi}｛2}）＄其中，＄＼gamma$为填土的重度，＄z$为计算点深度，＄＼varphi$为填土的内摩擦角，＄c$为填土的粘聚力。
2、库仑土压力理论库仑主动土压力系数：＄K_a ＝＼frac{cos^2(＼varphi ＼alpha)｝｛cos^2\alpha cos(＼alpha ＋＼delta)1 ＋＼sqrt{＼frac{sin(＼varphi ＋＼delta) sin(＼varphi ＼beta)｝｛cos(＼alpha ＋＼delta) cos(＼alpha ＼beta)｝｝＾2}＄库仑被动土压力系数：＄K_p ＝＼frac{cos^2(＼varphi ＋＼alpha)｝｛cos^2\alpha cos(＼alpha ＼delta)1 ＼sqrt{＼frac{sin(＼varphi ＋＼delta) sin(＼varphi ＋＼beta)｝｛cos(＼alpha ＼delta) cos(＼alpha ＋＼beta)｝｝＾2}＄主动土压力：＄E_a ＝＼frac{1}｛2}＼gamma H^2 K_a$被动土压力：＄E_p ＝＼frac{1}｛2}＼gamma H^2 K_p$其中，＄＼alpha$为墙背与水平面的夹角，＄＼beta$为填土面与水平面的夹角，＄＼delta$为墙背与填土之间的摩擦角，＄H$为挡土墙的高度。
挡土墙上土压力的计算
郎 肯 土 压
γz(σ3)
移，竖向应力保持不变， 水平应力逐渐增大，位移
增大到△p，墙后土体处
h
z
力
σp(σ1)于朗肯被动状态时，墙后
的
土体出现一组滑裂面，它
计 算
45o－ϕ/2
与小主应力面夹角45o－
ϕ/2，水平应力增大到最
大值
极限平衡条件
朗肯被动土压力强度
σ1
=
σ
3
tan2
⎜⎛ ⎝
45o＋ϕ
2
⎟⎞＋2c ⎠
哪种情况下墙后土体更密实，挡土墙上的土压力更大？
挡土结构与基坑工程
挡土墙上土压力的计算
1.主动土压力（Ea）
土 当墙在土压力作用下
压 力 的
向前移动或转动时， 达到一定位移量时，
类 墙后土体达到极限平
型 衡状态，此时的土压
力叫主动土压力
2.被动土压力（Ep） 3.静止土压力（Eo）
挡土墙在外力作用 下向后移动，压缩 填土达到极限平衡 状态，此时作用于
Kp
挡土结构与基坑工程
挡土墙上土压力的计算
滑动面
450 + ϕ / 2
σ3
σ1 = γ z
γz K0γ z
主动土压力
静止土压力
滑动面
450 −ϕ / 2
σ3
=
σ γ
1
z
被动土压力
挡土结构与基坑工程
挡土墙上土压力的计算
库
理论假设
仑
土 压
1. 墙背倾斜，具有倾角α；
力
2. 墙后填土为砂土，表面倾角为角β；
H
2
Ea
H 3
γ HKa
1.无粘性土主动土压力强度与z成正比，沿墙高呈三角形分布
第五章 挡土墙土压力计算
求E2最大值，令dE2/dθ=0，得：
由于力多边形法分析折线形挡土墙下墙土压力计算
是满足思了考楔体：静比力较平衡两中种的土力矢压量力闭计合条算件方，法用此。法推
导出的下墙土压力计算公式来计算下墙土压力较为合理。
第五节 粘性土土压力计算
当墙后填土为粘性土时，由于粘结力的存在， 致使土压力减少。采用库仑理论分析时，主要有等 效内摩擦角法和力多边形法。
裂缝深度
hc
=
2c
γ
tan(45°
+
ϕ
) 2
hc'
=
hc
−
h0
=
2c
γ
tan(45°
+
ϕ)−
2
h0
墙后填料受局部荷载 作用时，不考虑其对 裂缝深度的影响。
土压力计算
Ec = Ea − Ec'
=
G
cos(θ sin(θ
+ϕ +ψ
) )
−
cLcosϕ sin(θ +ϕ
)
令： dEc = 0
dθ
tan
α
适用范围
（1）库仑理论较适用于砂性土，计算所得主动土压力与实 际情况比较接近。应用于粘性土时，计算误差并不太大，常 常采用 “换算内摩阻角法” 计算。
（2）库仑理论仅适用于刚性墙。柱板式、锚杆式和加筋土 等柔性挡墙，可作某些近似假设后按库仑理论计算。
（3）库仑理论用于仰斜墙背时，墙背坡度以不缓于 1:0.3或 1:0.35为宜，以免出现较大误差，并偏于安全。
1、等效内摩擦角法 将粘性土的内聚力折算成内摩擦角，折算后的
内摩擦角称为等效内摩擦角或等值内摩擦角。 主要方法有：
各种挡土墙计算公式
各种挡土墙计算公式在土木工程中，挡土墙是一种常见的结构，用于支撑填土或山坡土体，防止其坍塌或滑坡。
为了确保挡土墙的稳定性和安全性，需要进行精确的设计和计算。
下面我们将介绍一些常见的挡土墙计算公式。
一、重力式挡土墙重力式挡土墙主要依靠自身的重量来抵抗土压力，其稳定性取决于墙体的自重、墙底摩擦力和墙背与填土之间的摩擦力。
1、土压力计算静止土压力：＄P_0 ＝ K_0 ＼gamma z$，其中$K_0$为静止土压力系数，＄＼gamma$为填土的重度，＄z$为计算点距离墙顶的深度。
主动土压力：＄P_a ＝＼frac{1}｛2} ＼gamma z^2 K_a$，＄K_a$为主动土压力系数，可通过库仑土压力理论或朗肯土压力理论计算得出。
2、稳定性验算抗滑移稳定性：＄K_s ＝＼frac{（W ＋ E_{px}）＼mu}｛E_{py}｝＄，＄W$为挡土墙自重，＄E_{px}＄和$E_{py}＄分别为主动土压力的水平和垂直分量，＄＼mu$为墙底与地基之间的摩擦系数。
要求$K_s ＼geq 13$。
抗倾覆稳定性：＄K_t ＝＼frac{M_R}｛M_O}＄，＄M_R$为抗倾覆力矩，＄M_O$为倾覆力矩。
要求$K_t ＼geq 15$。
3、基底应力验算偏心距：＄e ＝＼frac{B}｛2} ＼frac{M_R}｛W}＄，＄B$为基底宽度。
基底最大应力：＄＼sigma_{max} ＝＼frac{W}｛B}（1 ＋＼frac{6e}｛B}）＄基底最小应力：＄＼sigma_{min} ＝＼frac{W}｛B}（1 ＼frac{6e}｛B}）＄二、悬臂式挡土墙悬臂式挡土墙由立壁、趾板和踵板组成，其稳定性主要依靠墙身的抗弯能力和踵板上的土重。
1、土压力计算同重力式挡土墙。
2、内力计算立壁弯矩：根据墙后土压力分布，计算立壁在不同高度处的弯矩。
踵板弯矩：考虑踵板上的土重和作用在踵板上的土压力，计算踵板的弯矩。
3、截面设计根据内力计算结果，确定立壁和踵板的截面尺寸和配筋。
第六章：挡土墙及土压力计算
RD 一定位于 R 的下方，即 RD 与 N 之间的夹角φD 一定大于 R 与 N 之间的夹角φ ，鉴于
库仑主动土压力系数，应用时，查表。
Ea 沿深度呈三角形分布，其作用点距墙底 H/3，位于墙背法线上方，与墙背法线成δ角。
E
1 2
H
2
s具in(90o sin(
) sin(90o体 ) cos2
)
sin(如 ) sin(90o
)
图
：
Ea
Em a x
1 2
H
2
Ka
Ka f (,, , )
越大，因此被动土压力最大。即：Ea<Eo<Ep 三、静止土压力 Eo 的计算
E
sin( ) sin(90o
)
G
Eo =Ko *γ*H2/2，(kN/m)
式中： γ为填土的容重(kN/m3) ，Ko 为静止土压力系数，可近似取 Ko =1-sinφ'，φ'为土
的有效内摩擦角。
H 为挡土墙高度，m。
2.被动土压力 压力系数，应用时，查表。
其中
库仑被动土
Ep 沿深度呈三角形分布，其作用点距墙底 H/3，位于墙背法线下方，与墙背法线成δ角。 库仑理论应用中的几个问题 1. 关于δ的取值: δ值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于 0～φ之间，实用中常取δ =1/2～1/3φ。 2. 当墙后填土为粘性土时——为了得到确切的解析解，库仑理论假设墙后填土为无粘性土，
挡土墙的土压力计算(朗肯_库仑)
处。
第六章
第18页/共43页
三、被动土压力的计算
同计算主动土压力一样用1、3作摩尔应力圆，如下图。 使挡土墙向右方移动，则右半部分土体有压缩的趋势，墙 面的法向应力h增大 。h、 v为大小主应力。当挡土墙的位 移使得h增大到使土体达到极限平衡状态时，则h达到最高限 值pp ，即为所求的朗肯被动土压力强度。
当墙背倾角α>45°-/2时，滑动土楔不再沿墙背滑动， 墙后土体中出现两个滑动面的挡土墙称为坦墙。
第六章
第23页/共43页
αcr=45°-/2
第六章 第24页/共43页
第六章
第25页/共43页
（四）填土成层和有地下水时的土压力计算
(a)
1 1
h1
(b)
(c)
1 h1 K a 1
第六章
第16页/共43页
对于无粘性土 主动土压力强度为： p a 3 ztg（45
2 O
2 1 2
） zK a
总的土压力为： Pa 作用点位置在墙高 1 3
第六章
1 2
2 H 2 tg（45 O
2
）
H 2 K a
H处。
第17页/共43页
对于粘性土：
主动土压力强度为： p a 3 ztg（45
第六章
挡土墙在土压力作用下，不向任何方向发生位移和转动 时，墙后土体处于弹性平衡状态，作用在墙背上的土压力 称为静止土压力。 当挡土墙沿墙趾向离开填土方向转动或平行移动，且位 移达到一定量时，墙后土体达到主动极限平衡状态，填土 中开始出现滑动面 ，这时在挡土墙上的土压力称为主动土 压力。 当挡土墙在外力作用下向墙背填土方向转动或平行移动 时，土压力逐渐增大，当位移达到一定量时，潜在滑动面 上的剪应力等于土的抗剪强度，墙后土体达到被动极限平 衡状态，填土内开始出现滑动面 ，这时作用在挡土墙上的 土压力增加至最大，称为被动土压力。
挡土墙设计主动土压力计算
土压力的水平 和垂直为：
E x E a cos( ) E y E a sin( )
1 2 cos( ) sin( ) 2 G H sec 2 cos( )
1.破裂面交于内边坡
sin(90 ) cos( ) Ea G G sin( ) sin( )
1 2 cos( ) sin( ) 2 G H sec 2 cos( )
8、一般条件下库伦主动土压力计算
挡土墙库仑土压力理论
挡土墙土压力计算时应用了库仑（Coulomb）土压 力理论，通过对墙背后破坏棱体的受力分析，得到土 压力的反力E是破裂角的函数，即 E f ()，再求E的极 值可以得到主动土压力和被动土压力。 库仑法的假定为：破裂面为平面且通过墙踵、填 料为砂性土(c=0)、墙背存在摩擦、挡墙和破坏土体为 刚体。
南京工业大学交通学院
挡土墙土压力考虑
1、主动土压力与被动土压力的区分：
假定挡土墙处于极限移动状态，土体有沿墙及假 想破裂面移动的趋势，则土推墙即为主动土压力， 墙推土即为被动土压力。
2、路基挡土墙的土压力考虑：
路基挡土墙一般都有可能有向外的位移或倾覆， 因此，在设计中按墙背土体达到主动极限平衡状态 考虑，且取一定的安全系数以保证墙背土体的稳定。 墙趾前土体的被动土压力一般不计。
南京工业大学交通学院
用土压应力分布图计算主动土压力
挡土墙主动土压力计算公式
挡土墙主动土压力计算公式
1.土壤的重力是均匀分布的；
2.土壤的内摩擦角和墙与土壤的摩擦角没有明显差异；
3.挡土墙和土壤之间的界面摩擦是充分发展的。
根据这些假设，挡土墙主动土压力可以通过卡诺定理进行计算。
卡诺定理的基本原理是，土壤对挡土墙产生的压力可以分解为水平分量和垂直分量，其中水平分量对应于土壤壁面的水平压力，垂直分量对应于土壤壁面的垂直压力。
Pa=1/2*γ*H^2*Ka,
其中
Pa为挡土墙的主动土压力（单位为kN/m）；
γ为土壤的干容重（单位为kN/m^3）；
H为挡土墙的高度（单位为m）；
Ka为活动土压力系数，其大小取决于土壤的内摩擦角和挡土墙的后坡角度。
活动土压力系数Ka的取值通常根据实际情况进行确定，可以通过查表或进行现场试验得到。
常见的Ka值范围在0.15到0.45之间，取决于土壤的类型和挡土墙的几何形状。
需要注意的是，挡土墙的主动土压力只是整个挡土墙稳定性计算中的一个因素，还需要考虑其他因素，如墙体的抗滑稳定性、抗倾覆稳定性和
抗底部推力等。
因此，在实际工程中，对挡土墙的设计和计算需要综合考虑各种因素的影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
动，且位移达到一定量
时，墙后土体达到主动 极限平衡状态，填土中
墙位移与土压力
开始出现滑动面 ，这时
在挡土墙上的土压力称 为主动土压力。
Ea
滑裂面
根据墙的位移情况和墙后 土体所处的应力状态， 土压力可分为三种： 3）被动土压力（Ep）对应于图中 C点墙向填土的方向位移
当挡土墙在外力作用下向墙背填 土方向转动或平行移动时，土压 力逐渐增大，当位移达到一定量 时，潜在滑动面上的剪应力等于 土的抗剪强度，墙后土体达到被 动极限平衡状态，填土内开始出 现滑动面 ，这时作用在挡土墙上 的土压力增加至最大，称为被动 土压力。
H
z0
Ea ( H z0 )(HKa 2c K a ) / 2
HKa-2c√Ka
负侧压力深度为临界深度z0
a z0 K a 2c K a 0
z0 2c /( Ka )
当c＞0, 粘性土
2c√ Ka (H-z0)/3
a zK a 2c K a
Ea ( H z0 )(HKa 2c K a ) / 2
v
z
h
h
v
土体内每一竖直面都是对称面，地 面下深度z处的M点在自重作用下，垂直 截面和水平截面上的剪应力均为零，该 点处于弹性平衡状态（静止土压力状 态），其大小为：
(a)
1 v z 3 h P K 0z
z
大主应力 小主应力
K 0 z
p
(d)
按常用的结构形式分： 重力式、悬壁式、扶臂式、锚式挡土墙
按刚度及位移方式分：
刚性挡土墙、柔性挡土墙、 临时支撑
墙体位移与土压力类型
试验表明： (1)挡土墙所受到的土压力类型，首先取决于墙 体是否发生位移以及位移方向； (2) 挡土墙所受土压力的大小随位移量而变化， 并不是一个常数； (3) 主动和被动土压力是特定条件下的土压力， 仅当墙有足够大位移或转动时才能产生。
岩石地基上的挡土墙（牢固联结）
拱座（不允许产生位移）
第三节 朗肯土压力理论
1857年英国学者朗肯（Rankine）的土压力理论按 半无限弹性体的应力状态研究土体极限平衡状态的条件， 并提出相应计算挡土墙土压力的方法。又称极限应力法。 一、基本原理 朗肯理论的基本假设： 1.墙本身是刚性的，不考虑墙身的变形； 2.墙后填土延伸到无限远处，填土表面水平 （=0）； 3.墙背垂直光滑（墙与垂向夹角 =0，墙与土的 摩擦角=0）。
C 土 压 力 Pp E
p
A P0 E 0 B Pa Ea 墙向前移 位移
墙向后移
墙位移与土压力
Ep 滑裂面
三种土压力之间的关系 -△ +△
E
Ep Ea -△
o
△a
Eo
△p
+△
对同一挡土墙，在填土 的物理力学性质相同的 条件下有以下规律：
1. 2.
Ea<E0<Ep
△p ＞＞△a
第三节 静止土压力计算
h
z
朗肯被动土压力强度
朗肯被动土压 力系数Kp
p zK p 2c K p
即三角形面积
3.合力Ea作用点在三角形形心，
即作用在离墙底H/3处
当c＞0, 粘性土
2c√ Ka (H-z0)/3
a zK a 2c K a
粘性土主动土压力强度包括两部分 1. 土的自重引起的土压力zKa 2. 粘聚力c引起的负侧压力2c√Ka 说明：负侧压力是一种拉力，由于土与 结构之间抗拉强度很低，受拉极易开裂， Ea 在计算中不考虑
C 土 压 力 A P0 E 0 墙向后移 B
Ea Pa 墙向前移
位移
墙位移与土压力
根据墙的位移情况和墙后 土体所处的应力状态， 土压力可分为三种： 2）主动土压力（Ea）对应 Pp Ep 于图中B点墙前位移。
当挡土墙沿墙趾向离开 填土方向转动或平行移
P0 E 0 墙向后移
C
土 压 力 A B Pa Ea 墙向前移 位移
2
z
讨论： 朗肯主动土压力强度
a zK a 2c K a
当c=0,无粘性土
a zK a
1.无粘性土主动土压力强度作用
方向垂直于墙背
2.无粘性土主动土压力强度与z成
H
Ea (1 / 2)H 2 Ka 正比，沿墙高呈三角形分布 H/3
合力Ea大小为分布图形的面积，
HKa
例题分析 【例】有一挡土墙，高5米，墙背直立、光滑，墙后填土
面水平。填土为粘性土，其重度、内摩擦角、粘聚力如下 图所示 ，求主动土压力及其作用点，并绘出主动土压力 分布图
h=5m
=18kN/m3
c=10kPa
=20o
2 c√ Ka
【解答】 主动土压力系数
z0
K a t an2 45o ＝0.49 2
小 主 应 力 方 向
v z
小主应力
3
h K 0 z 大主应力 1 p
剪切破坏面与水 平面夹角为 45 0
2
应力圆III 主动土压力
3
1
f
伸展
45o-/2
45o＋/2
压缩
pa K0z
z
pp
被动极限 平衡状态 被动朗 肯状态
主动极限 水平方向均匀伸展 土体处于水平方向均匀压缩 弹性平衡 平衡状态 状态 主动朗 处于主动朗肯状态，σ1方向竖直，剪切 肯状态 破坏面与竖直面夹角为45o-/2 处于被动朗肯状态，σ3方向竖直，剪切 破坏面与竖直面夹角为45o＋/2
E
E
隧道侧墙
（a）边坡挡土墙
第一节 概述
（c）基坑围护结构
（d）桥台
填土面
E E
码头
桥台
第二节 土压力的基本概念
挡土墙的常见类型：
P
P
土压力通常是指挡土墙 后的填土因自重或外荷 载作用对墙背产生的侧
P 地下室 P
压力
挡土墙的几种类型
（a）支撑土坡的挡土墙（b）堤岸挡土墙 （c）地下室侧墙（d）拱桥桥台
c=8kPa
=20o
2 c√ Ka
【解答】
z0
主动土压力系数
(H-z0)/3
K a t an2 45o ＝0.49 2
6m
墙底处土压力强度
Ea
pa hKa 2c K a＝ 38.8kPa
临界深度
HKa-2c√Ka
z0 2c /(
K a )＝ 1.34m
挡土墙土压力计算
第一节 第二节 第三节 第四节 第五节 第六节 概述 土压力的基本概念 静止土压力计算 朗肯土压力理论 库伦土压力理论 若干问题的讨论
第一节 概述
挡土墙：用来侧向支持土体的结构物，统称为挡土墙。
挡土墙应用很广：地下室的外墙，重力式码头的岸壁，桥 梁接岸的桥台，以及矿石或碎石堆的围墙等都支持着这些侧向 土体。它们都是一种防止土体下滑或截断土坡延伸的构筑物。
z(σ1) h
pa(σ3)
45o＋/2
极限平衡条件
3 1 tan2 45o 2c tan 45o
2 2
朗肯主动土压力系数
o o a z tan 45 2c tan 45 2 2
主动土压力分布图 主动土压力作用点 距墙底的距离
Ea (h z0 )(hKa 2c K a ) / 2 ＝ 90.4kN / m
(1 / 3)(h z0 ) 1.55m
三、被动土压力的计算
同计算主动土压力一样用1、3作摩尔应力圆，如下图。 使挡土墙向右方移动，则右半部分土体有压缩的趋势， 墙面的法向应力h增大 。h、 v为大小主应力。当挡土墙的 位移使得h增大到使土体达到极限平衡状态时，则h达到最高 限值pp ，即为所求的朗肯被动土压力强度。
剪切面方向
土体静止不动时，深度z处单元体应力
v z h K 0 z
大主应力
1
小主应力
3
应力圆I 静止土压力
3
1
剪切面方向
当土体向左侧平移时， h 将逐渐减小，而 v 不变， 应力圆直径逐渐增大。直至达 到应力圆与土体抗剪强度包络 线相切，如图中II
大 主 应 力 方 向
HKa-2c√Ka
主动土压力分布图
主动土压力作用点 距墙底的距离
(1/ 3)(H z0 ) 1.14m
例题分析 【例】有一挡土墙，高6米，墙背直立、光滑，墙后填土
面水平。填土为粘性土，其重度、内摩擦角、粘聚力如下 图所示 ，求主动土压力及其作用点，并绘出主动土压力 分布图
h=6m
=17kN/m3
z
h=p0
z
H
H
E0 p
K0H (c) (d)
3
z
(b)
静止土压力沿墙高呈三角形分布，作用于墙背面单位 长度上的总静止土压力（E0）：
H
P0
0
1 p0 dz K 0H 2 2
E0的作用点位于墙底面往上1/3H处，单位[kN/m]。 （d）图是处在静止土压力状态下的土单元的应力摩 尔圆，可以看出，这种应力状态离破坏包线很远，属于弹 性平衡应力状态。
将 z0 2c /( K a ) 代入上式，得
Ea
H
z0
1 2 2c 2 Ea H K a 2cH Ka 2
HKa-2c√Ka
1.粘性土主动土压力强度存在负侧压力区（计算中不考虑） 2.合力大小为分布图形的面积（不计负侧压力部分） 3.合力作用点在三角形形心，即作用在离墙底(H-z0)/3处