运用完全平方公式进行因式分解ppt课件
第2课时 用完全平方公式进行因式分解

解:原式=a(x2+2ax+a2) =a(x+a)2
解:原式=-3(x2-2xy+y2) =-3(x-y)2
能提公因式的,要先提公因式再用完全平方公式进行因式分解
【例4】 利用完全平方公式分解因式:(1)1002-2×100×99+99²;(2)342+34×32+162.
解:(1)原式=(100-99)²
(2)原式=(34+16)2
=1.
=2500.
【例5】 已知x2-4x+y2-10y+29=0,求x2y2+2xy+1的值.
第十四章 整式的乘法与因式分解14.3 因式分解14.3.2 公式法第2课时 运用完全平方公式因式分解
1.能够运用完全平方公式进行因式分解(重点)2.能综合运用各种方法进行因式分解(难点)
学习目标
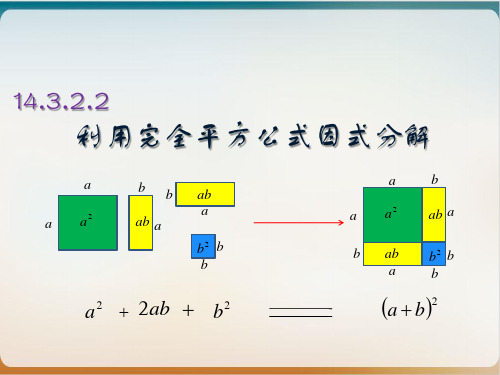
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
1.完全平方式
问题四 这两个多项式有什么共同的特点?
(4m)2
16m2 +8mn+n2;
=(4m+n)2 .
+2•(4m)
+n2
a2 - 2 ab + b2
y2
解:原式=
【例2】分解因式:(1)16x2+24x+9;(2)-x2+4xy-4y2.
解:原式=(4x)2+2∙4x∙3+32 =(4x+3)2
解:原式=-(x2-4xy+4y2) =-[x2-2∙x∙2y+(2y)2] =-(x-2y)2.
因式分解(完全平方公式)精选教学PPT课件

现在我们把这个公式反过来
a2 2abb2 ab2
a2 2abb2 ab2
很显然,我们可以运用以上这个公式 来分解因式了,我们把它称为“完全 平方公式”
a2 2abb2 a2 2abb2
我们把以上两个式子叫做完全平方式
我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
最后,我打他一巴掌。干脆痛快,出手的瞬间,像那位绝望的母亲,远远掷出她的高跟鞋。掷中没有?并不重要。 有多爱,就有多不舍;有多温柔,就有多暴烈,爱得唇边有血,眼中有泪,胸口有纠缠的爱与恨,爱到如连体婴般骨肉相连。割爱,就一定不可能如拈去一片花叶般轻松微笑。 明知留不住,收不下,却不能自控我颠倒狂乱的脚步。那一遭,我是夜深街上,追逐汽车的女子。而我无声的哭泣,他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼,不慕荣利。假如你喜欢武侠小说,你没有必要愧对红楼梦; 假如你喜欢的人突然销声匿迹,你没有必要寻死觅活地断言他一定洒脱地离去;假如你的朋友不幸,你没有必要怨天尤人;假如你认为张曼玉艳美绝俗,你没有必要眼馋肚饱虐待老婆;假如你已经身心交病,那就去教堂忏悔,没有必要仇视别人的平庸;坦然面对心融神会,快乐就在你心里。我怜悯一个有点荣誉的人,就旁若无人而因此失 去快乐的人。能把名利得失置之度外,而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会,如:赤城待人的那种快乐。低待遇下一如既往工作的快乐,助人为乐一介不取的快乐,一片至诚去感化恶人的快乐,热心被人误解依然如故的快乐,信实可靠的服务态度为目的的快乐,尽责任吃苦耐劳的快乐,因为这些 “快乐”能保持住人内心的快乐,使人的容貌永远那么牵挂,一句亲切的问候。甚至一个关切的眼神,快乐无处不有,唯有胸襟开阔的人,才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作,摄影、观鸟,我们仍然兴复不浅,乐不可支。人生苦短,岁月如流,乐天知命,为什么不乐乐陶陶的。为什么要疾首蹙额,为眼前一时的顿挫心胆俱碎?为什么要对那些你看不惯的人和事心烦率乱?岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地,无妄之灾,荣 华富贵,香娇玉嫩……都将随身亡命殒。而人生长着百年,短则数十寒暑,又有何值得耀武扬威的,不过是烟云过眼矣?人生如月,月满则亏,凡事岂能尽人意,但求于心无愧。无愧我心,则恩同再造,那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉,快乐起来吧!芸芸众生,绿水青山,名胜古迹,
初中数学《完全平方公式》优秀课件北师大版2
a2 2• a •bb2
(1)、解:16x2 24x 9
方法:当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时,可直 接分解因式。结果为这两平
4x 32
方项底数和或差的平方,是
和是差看中间项的符号
分析:- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点:
运用完全平方公式分解因式.
学习难点:综合运用提公因式和公式法分解
因式
复习引入
问题一:大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的 积的形式
即: 和
积
问题二:我们已经学习了分解因式的哪
些方法?
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即:两个数的平方差等于 这两个数的和与差的积
方法:若式子有整体满足完全平方 式可直接进行因式分解,需注意中 间项的符号
练习2 将下列多项式分解因式:
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案:
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现?请尝试概括 你的发现.
把整式的乘法公式——完全平方公式 倒过来 就得到因式分解的完全平 方公式:
a2 2ab+b2 =(a b)2
首2 2 首 尾 尾2 首 尾2
即两个数的平方和加上(或减去)这两个 数的积的2倍,等于这两个数的和(或差) 的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解
利用完全平方公式进行因式分解ppt课件

④ 4x2 – 8xy + 4y2 = 4 (x2–2xy+y2) = 4 (x–y)2
例3 把下列完全平方式因式分解。
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
例4 把下列各式因式分解。
(1)3ax2+6axy+3ay2; (2)-x2-4y2+4xy。
补例 把9x2 3x 1 因式分解
试计算:9992 + 2×1999998×1 + 1 = (999+1)2 = 106
就像平方差公式一样,完全平方公式也可 以逆用,从而进行一些简便计算与因式分解。 即:
a 2 2 a b b 2 a b 2
a 2 2 a b b 2 a b 2
这个公式可以用文字表述为:
两个数的平方和加上(或减去)这两个数的 积的两倍,等于这两个数的和(或差)的平方。
a 2 2 a b b 2 a b 2
牛刀小试(对下列各式因式分解):
① a2+6a+9 = _______(a_+__3)_2______ ② n2–10n+25 = ____(n_–_5_)_2_______ ③ 4t2–8t+4 = _____4_(t_–_1_)_2 _______ ④ 4x2–12xy+9y2 = _(_2_x_–_3_y_)2______
形如a2±2ab+b2的式子称为完全平方式。
① 16x2 + 24x + 9
② – 4x2 + 4xy – y2 ③ x2 + 2x – 1
完全平方式
④ 4x2 – 8xy + 4y2 ⑤ 1 – 2a2 + a4 ⑥ (p+q)2 – 12(p+q) + 36
因式分解法ppt课件

(1)提公因式法:am+bm+cm= m(a+b+c)
;
( 2)公式法:a²-b²= (a+b)(a-b) ,a²±2ab+b²= (a± b)²
(3)十字相乘法 X
)(x
根据物理学规律,如果把一个物体从地面以10 m/s的速度竖直上抛, 那么物体经过xs 离地面的高度(单位:m) 为10-4.9x².
解 :(1) x(x-4)=2-8x
方程整理,得x²+4x=2,
配方,得x²+4x+4=6, 即(x+2)²=6 开平方,得x+2=± √6,
解得x
=-2+√6,x₂=-2-√6.
解 :(2) x²-4x=0
分解因式,得x(x-4)=0, 所以x=0 或x-4=0, 解得x=0,x₂=4.
解:(3)2 x(x+4)=1
解得
,X
₂
解 :2(x-3)²=x²-9,
2(x-3)²=(x-3)(x+3) (x-3)[2(x-3)-(x+3)]=0 (x-3)[x-9]=0 x₁=3,x₂=9.
练习6 按要求解一元二次方程.
(1)x(x-4)=2-8x
(配方法) .
(2)x²-4x=0
(因式分解法).
(3)2x(x+4)=1 (公式法) .
元
先配方,再用直接开平方法降
二 配方法 次 方
次
适用于全部
一
程 公式法
直接利用求根公式
元二次方程
的 方
先使方程一边化为两个一次因
法
因式分解法
式乘积的形式,另一边为0,适用于部分一
《公式法》因式分解PPT课件(第2课时)

B. + −
C. − +
D. − + +
D
)
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是(
A . 11
B. 9
C. -11
)
B
D. -9
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
∴++=(+) =112=121.
连接中考
(2020•眉山)已知 + = − − ,则 −
. 4
的值为
解析:由 +
得
+
= − − ,
− + + = ,
即 − + + + + = ,
∵ − = , = ,
∴原式=2.
巩固练习
变式训练
已知-+-+=,求++的值.
解:∵x2-4x+y2-10y+29=0,
∴(-)+(-)=.
∵(-) ≥ ,(-) ≥ ,
∴-=,-=,∴=,=,
是.
巩固练习
变式训练
将前面例题的(2)(3)(4)变为完全平方式?
(2) + ²;
+ ² + ;
(3) + − ;
+ + ;
(4) + + .
+ + .
探究新知
知识点 2
用完全平方公式因式分解
111111完全平方公式进行因式分解一ppt课件

2 2
2
(2) 49b a 14ab (3) a 10a 25
2 3 2 2 3
(4) 4 x y 4 x y xy
例2:因式分解
(1) x 18 x 81
4 2
(2)
(2 x y ) 6(2 x y ) 9
2
(3)
1 2 2 x 3xy 9 y 4
2 2
(x 7)
2
(2)
(m n) 6(m n) 9
2
原式 (m n) 2 2 (m n) 3 32 解:
(m n 3) 2
请运用完全平方公式把下 列各式分解因式: 2 2 1 x 4 x 4 原式 x 2 2 2 2 a 6a 9 原式 x 3 2 2 3 4a 4a 1 原式 2a 1 2 2 2 4 9m 6mn n 原式 3m n
2
a表示:2x+y b表示:3
(2 x y) 2 2 (2 x y) 3 32
( 2 x y 3) 2
填一填
多项式
x2 6x 9
是否是完全 平方式
是
是
4 y 4 y 1
2
a、b各表 表示(a+b)2 示什么 或(a-b)2 a表示x, ( x 3) 2 b表示3 a表示2y, ( 2 y 1) 2 b表示1
9a b 3ab 1
2 2
是否是完全 平方式
a、b各表 示什么
表示(a+b)2 或(a-b)2
是 否
a表示x, b表示1/2
1 2 (x ) 2
利用完全平方公式因式分解

利用完全平方公式因式分解当我们遇到一个多项式无法因式分解的时候,可以考虑使用完全平方公式来进行因式分解。
完全平方公式是一种通过加减法将一个二次多项式转化为一个平方的方法。
完全平方公式如下:(a+a)^2=a^2+2aa+a^2(a−a)^2=a^2−2aa+a^2我们以一个具体例子来说明这个方法。
假设我们要因式分解a^2+6a+9这个二次多项式。
我们可以将这个多项式写成一个完全平方的形式。
根据完全平方公式,(a+a)^2=a^2+2aa+a^2,我们可以将a^2+6a+9写成(a+3)^2的形式。
因此,a^2+6a+9=(a+3)^2接下来我们来看一个更复杂的例子。
假设我们要因式分解a^2+8a+12这个二次多项式。
我们可以尝试将这个多项式写成两个完全平方的和的形式。
首先,我们需要找到两个数,它们的乘积等于12,而它们的和等于8、通过试错的方法,我们可以得出这两个数是2和6然后,我们可以使用这两个数将a^2+8a+12进行因式分解。
a^2+8a+12=(a+2)(a+6)通过这种方法,我们成功将a^2+8a+12因式分解为两个一次多项式的乘积。
(a+2)(a+6)即为该多项式的因式分解形式。
除了上述的二次多项式,我们还可以使用完全平方公式来因式分解更复杂的多项式。
例如,a^4+10a^2+25这个四次多项式。
我们可以将a^4+10a^2+25写成一个完全平方的形式。
根据完全平方公式,(a+a)^2=a^2+2aa+a^2,我们可以尝试将a^4+10a^2+25写成(a^2+5)^2的形式。
通过这种方法,我们成功将a^4+10a^2+25因式分解为一个完全平方的平方。
(a^2+5)^2即为该多项式的因式分解形式。
总结一下,完全平方公式是一种因式分解多项式的方法。
通过将一个二次多项式转化为一个平方的形式,我们可以更容易地因式分解一个多项式。
通过试错的方法或其他的求解技巧,我们可以找到适合使用完全平方公式的例子来进行因式分解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习
已经学过的因式分解的哪些方法?
1、提取公因式法 ma+mb+mc=m(a+b+c) 2、运用公式法
(1)平方差公式
a2 b2 (a b)(a b)
2
练习
把下列各式分解因式
① a3-a
② x4-16
解:原式=a(a2-1)
解: 原式=(x2+4)(x2-4)
=a(a+1)(a-1)
=(x2 +4)(x+2)(x-2)
3
引入 口算:
1. (x 2)2 x2 4x 4 2. (1 3a)2 1 6a 9a2 3.(3x 5y)2 9x2 30xy 25 y2 4.( y 3z)2 y2 6yz 9z2
4
回顾与思考:
上面计算过程中运用了哪个乘法公式? 完全平方公式:
(a b)2 a2 2ab b2 (a b)2 a2 2ab b2
x2-2·x·3+32
x2-2·x·0.5+0.52
12+2·1·0.5m+(0.5m)2 (2y)2-2·2y·3x+(3x)2
7
课内练习
2、填空 :
(1)a2+ 2ab +b2=(a+b)2 (2)a2-2ab+ b2 =(a-b) 2 (3)m2+2m+ 1 =( m+1) 2 (4)n2-2n+ 1 =( n-1 ) 2 (5)x2-x+0.25=( x-0.5 ) 2 (6)4x2+4xy+( y ) 2=( 2x+y) 2
公式:a2+2ab+b2=(a+b)2
{ a2-2ab+b2=(a-b)2
①三项式
完全平方式,特征: ②两平方项的符号同正
③首尾2倍中间项
例1 把下列各式分解因式:
(1)4a2+12ab+9b2
(2)-x2+4xy-4y2
解:原式=(2a)2 + 2·2a·3b+ (3b)2 解:原式=-(x2-4xy+4y2)
9
课本P162 T1、T2 想一想
10
7.5运用完全平方公式分解因式
公式:a2-2ab+b2=(a-b)2
完全平方式,特征:
①三项式
整式乘法
(a+b)2
a2+2ab+b2
②两平方项的符号同正
因式分解
③首尾2倍中间项
整式乘法(a-b)2a2-2ab+b2
因式分解
11
7.5运用完全平方公式分解因式
5
a2 2abb2 a2 2abb2
我们把以上两个式子叫做完全平方式
完全平方式又怎样的特征呢?
①三项式; ②其中两项是两个整式的和; ③另一项是这两个整式积的2倍。
6
课内练习
1、下列多项式哪些是完全平方式?哪些不是?
√(1)x2-6x+9 ×(2)1+4a2 ×(3)x2-0.5x+0.25 ×(4)4x2+4x-1 √(5)1+m+0.25m2 √(6)4y2-12xy+9x2
(5)xn+2xn+1+xn+2
(n为正整数)
13
1.已知 4x2+kxy+9y2 是一个完全平方
式,则k=
2.已知
a(a+1)-(a2-b)=-2,
求
a2+b2 2
+ab
的值。
3.已知x2+4x+y2-2y+5=0,求 x-y 的值。
14
15
=(2a+3b)2
=-[x 2 -2·x·2y+(2y) 2 ]
(3)0.25x2+xy+y2
=-(x-2y) 2
解:原式=(0.5x)2+2·0.5x·y+y2
=(0.5x+y) 2
12
练习 把下列各式分解因式:
(1)9-6y3+6y6 (2)m2-2m(p+q)+(p+q)2 (3)27a2+18ab+3b2 (4)x3-4x2y+4xy2
8
练习
例1 把下列各式分解因式:
(1) x2 2 xy 1 y2 (2) 2ax2 12axy 18ay2
39
(3)(x y)2 8(x y) 16
分析:(1)首先要提取负号,使其变成为完全平方式。 (2 ) 因式分解时,如果多项式有公因式一般 先提取公因式,再用其他方法分解因式。
(3)把 ( x y) 看作一个整体。
