19次课 夫琅禾费单缝衍射
夫琅和费单缝衍射实验报告

夫琅和费单缝衍射实验报告夫琅和费单缝衍射实验报告夫琅和费单缝衍射实验是光学领域中的一项重要实验,它揭示了光的波动性质。
本文将介绍夫琅和费单缝衍射实验的原理、实验装置和实验结果,并探讨其对光学理论的贡献。
一、实验原理夫琅和费单缝衍射实验是基于光的波动性质而进行的。
当光通过一个狭缝时,光波会发生衍射现象,即光波会弯曲并扩散到周围空间。
夫琅和费单缝衍射实验利用单缝的特性来观察光的衍射现象,从而揭示光的波动性。
二、实验装置夫琅和费单缝衍射实验的装置相对简单,主要包括光源、单缝、屏幕和测量仪器。
光源可以使用激光器或者单色光源,确保光的单色性。
单缝通常是一个细长的狭缝,可以是金属制成。
屏幕用于接收光的衍射图样,可以是白色的墙壁或者特制的屏幕。
测量仪器可以是尺子或者显微镜,用于测量衍射图样的尺寸。
三、实验过程实验开始时,将光源对准单缝,并调整光源的位置和角度,使得光线垂直射向单缝。
然后,在屏幕上观察到的光的衍射图样。
根据实验需要,可以调整单缝的宽度和光源的强度,观察不同条件下的衍射现象。
四、实验结果夫琅和费单缝衍射实验的结果是一系列明暗相间的条纹,称为衍射图样。
衍射图样的中央区域亮度最高,称为中央极大。
中央极大两侧是一系列暗条纹,称为暗纹。
暗纹两侧又是一系列亮条纹,称为亮纹。
亮纹和暗纹的宽度和间距与单缝的宽度和入射光的波长有关。
五、实验分析夫琅和费单缝衍射实验的结果可以用光的波动理论解释。
当光通过单缝时,光波会向前传播,并在缝后形成球面波。
这些球面波相互干涉,形成衍射图样。
中央极大对应光波的相干增强,而亮纹和暗纹对应光波的相干减弱。
夫琅和费单缝衍射实验的结果还验证了赫兹斯普龙光波理论。
根据赫兹斯普龙光波理论,光波可以看作是一系列波长和振幅不同的波组成的。
夫琅和费单缝衍射实验的结果与赫兹斯普龙光波理论预测的衍射图样相吻合,进一步证明了光的波动性。
六、实验应用夫琅和费单缝衍射实验的结果在实际应用中有着广泛的应用。
光的衍射夫琅禾费单缝衍射

k
0
1
-1
-2
-3
2
3
f
sin
0.047
0.017
1
I / I0
0
相对光强曲线
0.047
0.017
四. 光强:
中央明纹最亮,其它明纹光强迅速下降。
条纹间距
五、讨论
波长对衍射条纹的影响
缝宽对衍射条纹的影响
单缝位置对衍射条纹的影响
光源位置对衍射条纹的影响
ห้องสมุดไป่ตู้
Single slit Double slit Three slit Seven slit More slit Double hole Square aperture
惠更斯- 菲涅耳原理:波前S上每一个面元dS都可以看成是发射球面子波的新波源,波场中P点的强度由各个子波在该点的相干叠加决定。
菲涅耳在惠更斯子波假说的基础上补充了子波相干叠加的概念。
波在前进过程中引起前方某点的总振动,为面 S 上各面元 dS 所产生子波在 P 点引起分振动的总和,即这些子波在 P 点的相干叠加。
夫琅禾费单缝衍射
单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。
01
夫琅禾费 (Joseph von Fraunhofer 1787—1826)
夫琅禾费是德国物理学家。1787年3月6日生于斯特劳宾,父亲是玻璃工匠,夫琅禾费幼年当学徒,后来自学了数学和光学。1806年开始在光学作坊当光学机工,1818年任经理,1823年担任慕尼黑科学院物理陈列馆馆长和慕尼黑大学教授,慕尼黑科学院院士。夫琅禾费自学成才,一生勤奋刻苦,终身未婚,1826年6月7日因肺结核在慕尼黑逝世。
(3)当 时会出现明显的衍射现象。 a <λ时条纹太暗。
单缝和圆孔的夫琅禾费衍射介绍

明纹在屏上的位置
x f sin f (2k 1)
2a
k ax 1 3.5 0.5 3
f 2
第3级明 纹
(2)对应于 p点缝可分成多少个半波带?
asin (2k 1)
2
(23 1) 7
22
7个半波带
(3)将缝宽增加1倍,p 点将变为什么条纹?
y2 = u
-2 - o
··
··
2 u
-2.46π -1.43π
+1.43π +2.46π
u 1.43, 2.46, 3.47,…
相应 asin 1.43, 2.46, 3.47,…
三、入射光非垂直入射时光程差的计算
DB BC
b(sin sin)
“半波带”发的光在 P处干涉相消形成暗纹。
当asin=3/2时,可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第 3个“半波带”发的光在 P形成明纹。
一般情况下,可将缝分为k个半波带,当k为偶数 时,p点为暗纹,当k为奇数时,p点为明纹。
例3 在单缝衍射中,若使单缝和透镜分别 稍向上移,则衍射条纹将如何变化? 解:
o
⑴单缝上移衍射光束向上平移经透镜聚焦后, 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后,位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中,缝宽a=10,缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度,线 宽度以及中央明纹的线宽度。
第19章 光的衍射

第19章 光的衍射思考题19-1 在日常生活中,为什么声波的衍射比光波的衍射显著?答:因为耳朵能听到的声波波长在0.017-17米之间,这与通常的障碍物的尺寸基本相同,故声波的衍射很显著.而可见光的波长在400-700nm 之间,远小于通常的障碍物的尺寸,故光的衍射在通常情况下不太容易观察到.19-2 夫琅禾费衍射实验中,透镜的作用是什么? 图19-16 答:夫琅禾费衍射实验中,透镜的作用是把有限远的光源成像到无穷远,或把无穷远处的衍射图样成像到有限远处.19-3 夫琅禾费单缝衍射实验中,若入射的平行光束与狭缝平面不垂直(如图19-16),干涉条纹的分布将发生什么变化?答:夫琅禾费衍射实验中,若入射的平行光束与狭缝平面不垂直,干涉条纹在观察屏幕上的位置将发生偏移,即中央明纹将偏离观察屏的中心点O ,但干涉花样的形状保持不变.19-4若放大镜的放大倍数足够高,是否能看清任何细小的物体?答:放大镜的放大倍数足够高,也不一定能看清任何细小的物体.因为,要看清细小物体不仅需要有一定的放大能力,还要有足够的分辨本领,才能把微小物体放大到清晰可见的程度.19-5 为什么天文望远镜的物镜直径都很大? 答:由光学仪器的分辨率λθ22.11D R R ==,可知天文望远镜的分辨率与物镜直径D 成正比.物镜的直径越大,分辨率越高.为分辨无限远处的天体,天文望远镜的物镜直径都做得尽可能的大.19-6 如何理解光栅的衍射条纹是单缝衍射和多缝干涉的总效益?答:光栅是由许多等宽的狭缝等距离地排列起来构成的,光栅衍射实际上是每个狭缝的单缝衍射光再相互干涉的结果,所以多缝干涉的效果必然受到单缝衍射效果的影响,也即光栅的衍射条纹是单缝衍射和多缝干涉的总效益.19-7 光栅的光谱和棱镜的光谱有什么区别?答:光栅的光谱是由于光在光栅上的衍射引起的,而棱镜的光谱是光在棱镜两个表面的折射引起的.19-8 为什么用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长? 答:因为杨氏双缝干涉的条纹间距太小,亮度很暗,不易观测,而光栅衍射的条纹间距较大、极细、亮度很高. 因此用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长.19-9 为什么不能用一般光栅观察X 射线的衍射现象?答:X 射线的波长很短(介于20~0.06nm ),而普通光栅的缝宽在μm 量级.由于X 射线的波长远小于光栅的缝宽,因此无法观察到衍射现象.习题19-1 用波长为500nm 的单色平行光,垂直入射到缝宽为1mm 的单缝上,在缝后放一焦距f =50cm 的凸透镜,并使光聚焦在观察屏上,求衍射图样的中央到一级暗纹中心、二级明纹中心的距离各是多少?解:(1)已知λ=500nm ,a =1mm ,f =50cm.根据夫琅禾费单缝衍射公式, 可知一级暗纹位置sin f x f aλθ==±可得衍射图样的中央到一级暗纹中心的距离为 7115050010cm 0.025cm 0.25mm 110f x a λ--⨯⨯≈===⨯ (2)二级明纹位置为5sin 2f x f aλθ==±可得衍射图样的中央到二级明纹中心的距离为 7221555050010sin cm 0.063cm 0.63mm 22110f x f a λθ--⨯⨯≈==⨯==⨯ 即衍射图样的中央到一级暗纹中心、二级明纹中心的距离分别为0.25mm 和0.63mm.19-2 在夫琅禾费单缝衍射实验中,以波长λ为589 nm 的平行光垂直入射到单缝上.若缝宽为0.10 mm ,试问一级暗纹中心出现在多大的角度上?若要使一级暗纹中心出现在0.50︒的方向上,则缝宽应多大?解:(1) 已知λ=589nm ,a =0.10mm.根据夫琅禾费单缝衍射公式,可得一级暗纹中心的角位置为661158910sin rad 5.8910rad 0.34a 0.1λθθ--⨯≈=±=±=±⨯=± 故衍射图样的一级暗纹中心出现在0.34︒的方向上.(2) 若一级暗纹中心出现在0.50︒的方向上,即10.5θ=,则62158910a mm 6.7510mm 0.5/180 3.14λθ--⨯≈==⨯⨯ 即要使一级暗纹中心出现在0.50︒的方向上,则缝宽应为26.7510mm -⨯.19-3 波长λ=500nm 的平行单色光,垂直入射到缝宽为0.25mm 的单缝上,紧靠缝后放一凸透镜,在凸透镜的焦平面上测得第二条暗纹间距离为2x 2=2mm ,求凸透镜的焦距f 为多少?解:已知λ=500nm ,a =0.25mm ,x 2=1mm.根据夫琅禾费单缝衍射公式 af f x λθ2sin 2±== 可得 260.251mm 250mm 25cm 2250010x a f λ-⨯====⨯⨯ 凸透镜的焦距f 为25cm. 19-4 用水银灯发出的波长为546 nm 的绿色平行光垂直入射到一单缝上,紧靠缝后放一的焦距为40 cm 凸透镜,在位于凸透镜的焦平面处的观察屏上测得二级暗纹中心至衍射图样中心的线距离为0.30 cm. 若用一波长未知的光作实验时,测得三级暗纹中心到衍射图样中心的线距离为0.42 cm ,试求未知波长.解:已知1λ=546nm , f =40cm ,x 2=0.30cm ,x 3=0.42cm.根据夫琅禾费单缝衍射公式a f kf x λθ±==sin 可得 1122sin 2f x f a λθ==,2233sin 3f x f aλθ== 解上述方程可得 232112220.42546nm 510nm 330.30x x λλ==⨯= 即未知波的波长为510nm.19-5 在单缝夫琅禾费衍射装置中,用细丝代替单缝,就构成了衍射细丝测径仪.已知光波波长为632.8 nm, 透镜焦距为50 cm, 今测得零级衍射斑的宽度为1.0 cm, 试求该细丝的直径.解:已知λ=632.8 nm ,a =1 mm ,f =50 cm ,0x ∆=1.0 cm .根据夫琅禾费单缝衍射公式,得零级衍射斑的宽度021.0cm f x aλ∆== 可得细丝的直径为 295205010632.81022m 6.3310m 63.3μm 110f a x λ----⨯⨯⨯==⨯≈⨯≈∆⨯ 19-6 在迎面驶来的汽车上,两盏前灯相距1.0 m ,试问在汽车离人多远的地方,眼睛恰好能分辨这两盏灯?设夜间人眼瞳孔的直径为5.0 mm ,入射光波长为550 nm ,而且仅考虑人眼瞳孔的衍射效应.解:已知λ=550nm ,d =1.0m ,D =5.0mm.由最小的分辨角公式可得人眼的最小分辨角为943550101.22 1.22rad 1.3410rad 510λθ---⨯==⨯=⨯⨯R D 设人和汽车的距离为x 时,眼睛恰好能分辨这两盏灯,则有θ≈R d x 即 341m 7.4610m=7.46km 1.3410θ-≈=≈⨯⨯R dx 人和汽车的距离为7.46km 时,眼睛恰好能分辨这两盏灯.19-7 一架生物显微镜,物镜的标号为20×0.25, 即物镜的放大率为20倍,数值孔径sin n u 为0.25;若光波的波长以550 nm 计算,试问可分辨的最小距离是多大?目镜物方焦平面上恰可分辨的两物点的艾里斑中心间距是多大?解:已知λ=550nm ,sin n u =0.25,可得m μ3.1m 103.1m 25.01055061.0sin 61.069=⨯=⨯⨯==∆--u n y λ 目镜物方焦平面上恰可分辨两物点的艾里斑中心间距等于物镜的放大率乘以y ∆, 即26μm .19-8 对于可见光,平均波长为λ = 550 nm ,试比较物镜直径为5.0 cm 的普通望远镜和直径为6.0 m 的反射式天文望远镜的分辨本领.解: 由光学仪器的分辨率公式,可知物镜直径为D 1 = 5.0 cm 和D 2 = 6.0 m 的望远镜的最小分辨角为:rad 103.1rad 100.51055022.122.152911---⨯=⨯⨯⨯==D λθ rad 101.1rad 0.61055022.122.17922--⨯=⨯⨯==D λθ 它们的比值为12016100.522112=⨯==-D D θθ 即这台天文望远镜的分辨本领是普通望远镜的120倍19-9用λ=589.3nm 的钠黄光垂直入射到一个平面透射光栅上,测得第三级谱线的衍射角为10.18︒, 而用未知波长的单色光垂直入射时,测得第二级谱线的衍射角为6.20︒, 试求此未知波长.解:已知1λ=589.3nm ,13θ=10.18︒,22θ=6.20︒.由光栅方程λθk d ±=sin 可得 sin10.183589.3nm =⨯d ,2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯= 19-10 用每毫米内有400条刻痕的平面透射光栅观察波长为589nm 的纳光谱.试问:光垂直入射时,最多能观察到几级光谱?解:已知1λ=589.3nm ,依题意可得光栅常数d =1mm/400=0.0025mm.由光栅方程λθk d ±=sin ,可知90θ=对应光栅光谱的最高衍射级次,即max 6sin 900.00251 4.2589.310λ-⨯==≈⨯d k 即最多能观察到4级光谱 2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯= 19-11 以波长范围为400~700 nm 的白光,垂直入射到一块每厘米有6000条刻线的光栅上.试分别计算第一级和第二级光谱的角宽度,两者是否重叠?解:已知1λ=400nm ,2λ=700nm ,依题意可得光栅常数d =1/6000cm.由光栅方程λθk d ±=sin ,可得第一级和第二级光谱的角宽度11θ、21θ和12θ、22θ分别为711140010asin asin 0.24rad 1/6000λθ-⨯==≈d 722170010asin asin 0.43rad 1/6000λθ-⨯==≈d 71122240010asin asin 0.50rad 1/6000λθ-⨯⨯==≈d 72222270010asin asin 1.00rad 1/6000λθ-⨯⨯==≈d 即白光的一级衍射光谱的角范围为0.24~0.43rad ,二级衍射光谱的角范围为0.50~1.00rad. 一级衍射光谱的角宽度为0.19rad ,二级衍射光谱的角宽度为0.50rad. 显然,白光的第一级和第二级光谱的不会重叠.19-12 用氦氖激光器发出的λ=632.8nm 的红光,垂直入射到一平面透射光栅上,测得第一级极大出现在38︒的方向上,试求这一平面透射光栅的光栅常量d ,这意味着该光栅在1 cm 内有多少条狭缝?第二级谱线的衍射角是多大?解:(1) 已知λ=632.8nm ,1θ=38︒,k =1.由光栅方程λθk d ±=sin ,可得7411632.810cm 1.0010cm sin sin 38λθ--⨯⨯==≈⨯k d 即光栅在1 cm 内有10000条狭缝.(2) 当k =2时,由光栅方程得22sin dλθ=,即 72422632.810sin 1.211.0010d λθ--⨯⨯==≈>⨯ 表明该光栅的第二级谱线实际上是不存在的.19-13 已知氯化钠的晶体结构是简单的立方点阵,且相邻两离子之间的平均距离(即晶格常量)d =0.2819nm .若用波长λ = 0.154 nm 的X 射线照射在氯化钠晶体表面上,且只考虑与表面平行的晶面系,试问当X 射线与表面分别成多大掠射角时,可观察到第一级和第二级主极大谱线.解:(1) 已知λ=0.154nm ,a =0.2819nm ,k =1和k =2时,由布拉格方程得10.154arcsin arcsin 15.85220.2819d λθ==≈⨯ 220.154arcsin arcsin 33.1120.2819d λθ==≈ X 射线与表面分别成15.85︒和33.11︒大掠射角时,可观察到第一级和第二级主极大谱线.。
19.2单缝衍射

b (sin sin )
由暗纹条件
b (sin sin ) k
( k 1, 2 , 3 , )
b
C
A
D
B
arcsin(
k b
sin )
19.2 单缝夫琅禾费衍射
19.2 单缝夫琅禾费衍射
夫 琅 禾 费 单 缝 衍 射
R
衍射角
第十九章 光的衍射
L
f
P
Q
A
b
C
o
B
b sin
2
(衍射角 :向上为正,向下为负 .)
菲涅尔波带法
BC b sin
k
19.2 单缝夫琅禾费衍射
一 半波带法
R
第十九章 光的衍射
A
b
B
缝长 b sin 2 k
第十九章 光的衍射
例2 如图,一雷达位于路边 15m 处,它的射束与 公路成15 角. 假如发射天线的输出口宽度 b 0 . 10 m , 发射的微波波长是18mm ,则在它监视范围内的公路长 度大约是多少? 解 将雷达天线输出口看成是发出衍射波的单缝, 衍射波能量主要集中在中央明纹范围内.
第十九章 光的衍射
单缝宽度变化,中央明纹宽度如何变化?
19.2 单缝夫琅禾费衍射
第十九章 光的衍射
入射波长变化,衍射效应如何变化 ?
越大, 1越大,衍射效应越明显.
19.2 单缝夫琅禾费衍射
(3)条纹宽度(相邻条纹间距)
b sin 2 k
第十九章 光的衍射
夫琅禾费单缝衍射

当 = 2 时,可将缝分成四个“半波带”,
它们发的光在 P 处两两相消,又形成暗纹……
菲涅耳半波带的数目决定于 bsin
P•
•
•
2
f
对应沿方向衍射
的平行光狭缝,波 阵面可分半波带数
k
b sin
2
1、k 由 b、、 确定。
2、k 不一定是整数。
三、单缝衍射明暗条纹条件
由半波带法可得明暗纹条件为:
a sin1
0 21
1 sin1
中央明纹
1
a
k 1
k2
0
2
a
上式为中央明纹角宽度
中央明纹线宽度
x
x0
2 x1
2
ftg 0
2
f 0
2 f
a
xk
k2
x0
2 f
a
(a, )
其他明纹宽度
0 2 1
f
k 1 O中明央纹
a sin k k
tg k
xk f
tg k sin k
xk
k
f
a
f xk a
0.017 0.047
0.047 0.017
-2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。
明纹暗纹的图示
sin Δ x / f
中央亮纹的半角宽
1
x
f
(1)明纹宽度
中央明纹:两个一级暗纹间的距离,
为1
1
级暗纹对应的衍射角
xkk
条纹散开了 b
光通量减少,
清晰度变差。
分析与讨论:
夫琅禾费单缝衍射
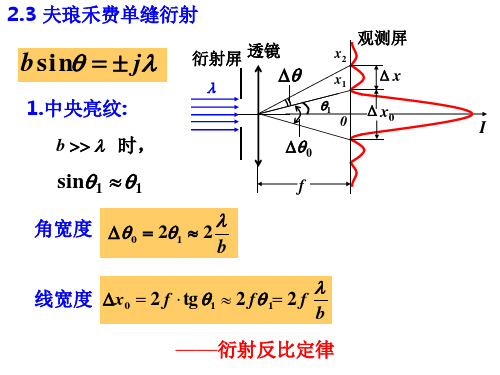
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝(设宽度分别为a、b) 衍射光在x, y方向的衍射角分别为
x, y
衍射光场:两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角:
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛(正常人眼) a=D/2=1mm,n=1,n'=1.336,
0=550nm,f '=2.2cm
角分辨极限: m=0.610/n'a ≈2.511×10-4 rad
线分辨极限:
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
2.3 夫琅禾费单缝衍射
bsin j
夫琅禾费单缝衍射实验报告

夫琅禾费单缝衍射实验报告
夫琅禾费单缝衍射实验是一项经典的物理实验,通过这个实验可以直观地观察到单缝衍射现象,验证光的波动性质。
在本次实验中,我们使用了一束激光作为光源,通过单缝进行衍射,观察到了清晰的衍射条纹,得到了有意义的实验结果。
以下将对实验过程和结果进行详细的报告。
首先,我们准备了一台激光器作为光源,保证光线的单色性和平行性。
然后,我们利用微米级的细缝装置,制备了单缝装置。
在实验过程中,我们需要保证光线垂直射向缝隙,并且尽量减小其他杂散光的干扰。
在实验过程中,我们发现了一些问题,比如光源的稳定性、缝隙的制备等,但通过反复调整和实验,最终得到了可靠的实验结果。
在观察实验结果时,我们发现了清晰的衍射条纹,这些条纹的间距与光的波长有关,这验证了光的波动性质。
通过测量条纹间距和光源波长的比值,我们可以得到比较准确的光的波长数据。
此外,我们还观察到了衍射条纹的明暗变化规律,这也与单缝衍射理论相符合。
通过本次实验,我们深刻地理解了夫琅禾费单缝衍射现象,加深了对光的波动性质的认识。
同时,我们也意识到了实验中一些细节对结果的影响,比如光源的稳定性、缝隙的制备等,这些都需要我们在今后的实验中加以注意和改进。
总的来说,夫琅禾费单缝衍射实验是一项非常有意义的物理实验,通过这个实验,我们可以直观地观察到光的波动性质,验证了光的波动理论。
同时,实验过程中也锻炼了我们的实验操作能力和问题解决能力。
希望通过今后的学习和实验,我们可以更深入地理解光的波动性质,并将这些知识运用到实际生活和工作中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迈克尔逊(1852-1931)美 国实验物理学家,毕业于安那坦 利斯海军学院,在该院任物理教 官,退役后在芝加哥大学任教。 将毕生精力献给了研制干涉仪和 精确测定光速的事业,为之奋斗 了半个世纪,在最后一次光速测 量中中风去世,因为在研制迈克 尔逊干涉仪方面的成就,1907年 获得诺贝尔物理学奖,成为获得 该奖的第一个美国人。
k:衍射级次, 2k和2k 1 是单缝面上可以分 成的半波带的数目。
a sin : 最大光程差
四、单缝衍射条纹的特点
1. 光强分布规律 中央明纹最亮,各级明纹的光 强随级数增加而迅速减弱。
பைடு நூலகம்
a P
y
光 强
明纹 a sin 2k 1
2
k级明纹,狭缝分成(2k+1)个半波带,
a
x f
a
1.一定时, 改变缝宽a ,单缝衍射条纹如何变化?
缝宽a越小,条纹间隔拉大,衍射作用越明显;
当a= ,整个屏幕被中央明纹所占据;
当缝宽a较宽,a>> ,光的传播遵从直线传播规律. 通常实验室选择缝宽 a 10 ~ 100 。
讨论2
x0 2 f
a
x f
衍射:连续的无限多个子波的相干叠加;
强调:偏离直线传播而进入阴影区域;
杨氏双缝干涉:是缝间干涉和每个缝自 身发出光的衍射的综合效果。
例1:缝宽a=0.5mm,焦距f=100cm, P处(x=1.5mm)为明纹 求:(1)单色可见光的 ; a (2)P处k, 对应的衍射角 ,此时单缝面可分 的半波带数; (3)中央明纹的宽度。 解:(1) P点满足: a sin
解:(1)a sin1 1
x f tan
a sin 2 22
1 2 1 22
a (2) sin k11 k22
1 22 k 2k 2 1
即 k2 2k1 , 衍射极小都重合。
2
G2
L
2 1 E
M2
2
1. 在迈克耳孙干涉仪的一条光路中,放入一 折射率为 n ,厚度为 d的透明薄片,放入后, 这条光路的光程改变了( A ) (A) 2(n 1)d (B) 2nd (D) nd (C) (n 1)d
2. 迈克耳逊干涉仪可用来测单色光的波长,当干涉仪 的动镜 M2 移动d 距离时,测得某单色光的干涉条 纹移过N条,则该光的波长为( A ) (A)2d/N (B)d/N (C) 4d/N (D) 2N/d
一、构造及光路图
L:透镜
M1、M2:反射镜
M1 M2
S L
1
G1 2
G2
G1--分光板(有镀银膜) G2--补偿板(无镀银膜)
2 1 E
M2
二、干涉条纹的形状
若M1 与M2: 严格垂直: 等倾干涉 不严格垂直: 等厚干涉 M2平移的距离与条纹 移动数N的关系为:
d N
M1 M2
1
S
G1
§18.1 光的衍射现象
一、光的衍射现象
光遇到障碍物时偏离直线传播,使光的强 度重新分布的现象。
圆孔衍射
钉子衍射
当缝宽较大时
K
S b
当缝宽减小时
K
S b
a
Sc a
光的直线传播
光的衍射现象
障碍物几何尺寸D,光波长 • D •D 直线传播 光的衍射
二、惠更斯—菲涅尔原理
1.惠更斯原理——子波原理 媒质中传播到的各点都可 看作发射子波的子波源。 2.菲涅耳原理——相干叠加 同一波阵面上各点发出的子 波相遇时会产生干涉现象。
B A
2
P
C
P点出现暗纹
BC a sin
3
P
2
a
B
P点出现明纹
C
P点形成明纹还是暗纹,取决于BC等于半波长的奇 数倍还是偶数倍。
三、衍射条件
0
( 2k 1)
中央明纹
2
k 1,2,3... 明纹
a sin
2k
2
k
k 1,2,3... 暗纹
非以上值
明纹与暗纹之间
a sin k k
x
P0
f
k 1 k sin k 1 sin k
1 a
( k 1)
1 a
k
a
(各级明纹角宽度约为为中央明纹的一半) 线宽度:x
f ( tg k 1 tg k )
a
f f
讨论1
x0 2 f
r
P
dE C
S
S
三、衍射的分类
1.菲涅耳衍射 2.夫琅和费衍射
光源、屏与缝相距有限远。 光源、屏与缝相距无限远。
K
S
Sc
K
夫琅和费衍射的实现
L1
K
L2
Sc
S
§18.2 单缝的夫琅禾费衍射
单缝:宽度远小于长度的矩形孔
一、装置和现象 透镜 L1
L2
S
f
单缝
屏幕
二、菲涅耳半波带法分析 A a B
称为衍射角
P
P0
1. = 0
P0干涉相长 形成中央明纹
2. 0
菲涅尔半波带法
A
a B
A P
菲 涅 尔 半 波 带 A1 A2 A3 A4
C
2
C
B
2
2
2
最大光程差: BC a sin
2
任何两个相邻的半波带发出的衍射光在P点完全抵消。
BC a sin
2
A
a
S
n r
u
P
惠更斯-菲涅耳原理: 波阵面上任一点均可视为发射子波的子波源,波 阵面前方某点处的光振动取决于到达该点的所有子波 相干叠加。 dS发出的子波在P点引起的光振动:
dE C dS K ( ) r cos ( t r u )
n
dS
K ( )
E
倾斜因子
dS K ( ) r cos ( t r u )
a
2.缝宽a一定,条纹随波长的变化如何变化?
a 一定, ,
同一级 , 中央明纹越宽;
若用白光照射单缝,则中央为白光,两侧各 级条纹都为彩色条纹,内--- 外 ;紫--- 红 。
讨论3
3.上下移动单缝位置,衍射图像是否改变?
讨论4
4.干涉和衍射的关系?
本质:相干叠加 干涉:有限个分立光束的相干叠加; 强调:不同光束相互影响而相长相消;
2a sin 2k 1
x
P
x o
( 2k 1)
2
x f
f
2a tan 2k 1
tan
1.5 10
3
k 1 : 500 nm
k 2 : 300 nm
舍去!
(2) P点对应的衍射角
tan 1.5 10
3
rad
P点的明纹级次:k=1,为第一级明纹 单缝分出的半波带数:2k+1=3 (3)中央明纹的宽度:
x 2 f
a
2 mm
例2.在某个单缝衍射实验中,光源发出的光有两 种波长1和2,若1的第一级衍射极小与2的第二 级衍射极小相重合,求: (1)这两种波长之间有何关系? (2)在这两种波长的光所形成的衍射图样中,是否 还有其他极小相重合?
2. 条纹位置及宽度
中央明纹线宽度
a sin 1
1 sin 1
a
--- 两个第一级暗纹间距
1
1
x
P0
中央明纹角宽度 0 21 2 中央明纹线宽度
x0 2 f tg 1
2 f a
f
a
其他各级明纹的角宽度 第k+1级暗纹和第k级暗纹之间
